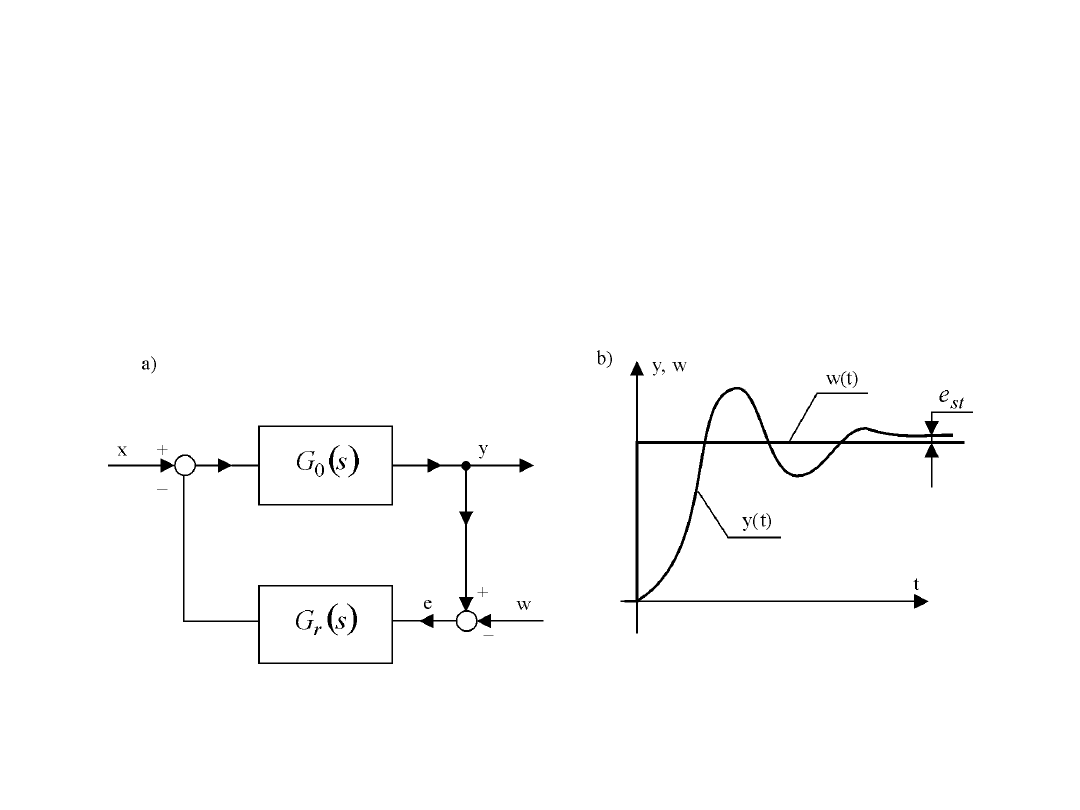
Dokładność statyczna
Wymaganie dokładności w stanie ustalonym, której miarą jest uchyb
ustalony:
jest jednym z podstawowych wymagań stawianych układowi regulacji.
Uchyb zależy od wielkości wymuszającej i wartości zadanej wielkości
regulowanej.
Układ automatyki: a) schemat blokowy, b) przebieg w(t) i y(t)
,
t
w
t
y
e
t
ust
lim
Dokładność statyczna
• Ponieważ rozpatrywany jest układem liniowym, a sygnały x(t) i
w(t) są wzajemnie niezależne, to ich wpływ na uchyb statyczny
można rozpatrywać oddzielnie, czyli:
• gdzie:
• Exust – odchylenie wywołane wymuszeniem x (uchyb nadążania)
• Ewust – odchylenie wywołane zmianą wartości wielkości zadanej
w (uchyb zakłóceniowy).
• Warunki na uchyby ustalone formułuje się oddzielnie dla i
.
• gdzie:
• e1, e2 - dopuszczalne wartości odchyleń statycznych wywołane
odpowiednio zmianami x i w.
• O wartości uchybu statycznego decyduje dynamika
rozpatrywanego układu. Zastanówmy się, jak kształtuje się uchyb
ustalony w zależności od właściwości transmitancji operatorowej
układu.
wust
xust
ust
e
e
e
ust
x
e
ust
w
e
1
max
100
e
w
e
o
o
ust
w
2
max
100
e
y
e
o
o
ust
x
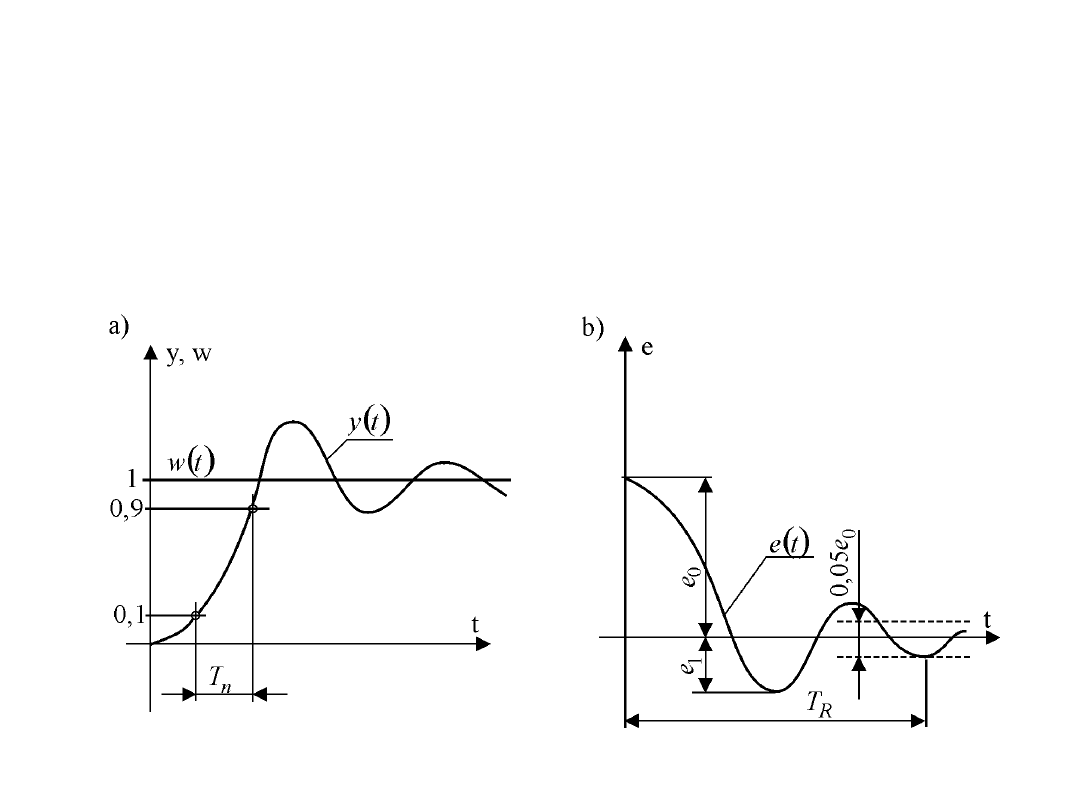
Jakość dynamiczna
• Oceny własności dynamicznych układów regulacji dokonuje się na
podstawie:
• 1) odpowiedzi układu na wymuszanie skokowe (przebiegu
przejściowego),
• 2) charakterystyk częstotliwościowych.
• Przebieg wielkości regulowanej i uchybu regulacji , po wymuszeniu
skokowym sygnałem x(t) pokazano na rysunku.
Wskaźniki jakości
• Przebieg odpowiedzi skokowej charakteryzują następujące wskaźniki:
•
– czas regulacji - jest to czas od chwili wprowadzenia
wymuszenia do chwili, gdy uchyb zmaleje poniżej dopuszczalnej
wartości , którą zwykle przyjmuje się równą 5% wartości początkowej
. Czas regulacji jest określony czasem trwania stanu przejściowego.
•
– czas narastania - jest to czas potrzebny, aby charakterystyka
skokowa osiągnęła od 10% do 90% wartości ustalonej.
• – przeregulowanie,
•
• gdzie:
• e0 – początkowa maksymalna wartość uchybu przejściowego,
• e1 – największa wartość uchybu o znaku przeciwnym niż e0.
• Przeregulowanie χ można uważać za miarę zapasu stabilności
układu. Dla układów znajdujących się na granicy stabilności
. W przemysłowych układach automatyki
przeregulowanie zawiera się w granicach od 0 do 40%.
• Całkowe wskaźniki jakości
o
o
e
e
100
0
1
r
T
n
T
%
100
1
0
e
e
Skalowanie obiektu
• Punktem wyjścia przy projektowaniu układów regulacji jest
modelowanie i analiza dynamiki obiektu. Jak już wiemy ten sam
obiekt możemy modelować na wiele sposobów. Jeśli układ jest liniowy
lub zlinearyzowany w pewnym punkcie pracy, to może to być model
operatorowy lub w przestrzeni stanu.
• Pierwszym etapem analizy obiektu sterowania jest skalowanie. Jest
ono bardzo ważne w praktycznych aplikacjach, tak samo jak analiza
modelu i projektowanie regulatora. W przypadku skalowanego
obiektu łatwiej podawać zmianę jakości układu przy zastosowaniu
różnych regulatorów. Również niektóre metody sterowania wymagają
skalowania obiektu. Ponadto współczesne sterowniki
mikroprocesorowe (cyfrowe) muszą mieć skalowane sygnały
wejściowe. Aby skalować układ należy znać wielkość zaburzenia lub
zmianę sygnału odniesienia, wymaganą wielkość sygnału
wejściowego oraz wymagane odchylenie od sygnału wyjściowego. Na
potrzeby skalowania model liniowy obiektu powinien być opisany
równaniem:
• gdzie znak „۸” jest użyty w celu pokazania, że zmienna jest
wielkością nie skalowaną.
z
d
G
u
G
y
w
y
e
Skalowanie-cd
• Praktycznym podejściem do skalowania jest stworzenie zmiennej o
wartości mniejszej od 1. Można to uzyskiwać dzieląc zmienną przez
maksymalną wartość oczekiwaną lub maksymalną dozwoloną zmianę.
Dla zakłócenia i sygnału wejściowego, użyjemy zmienną skalowaną:
• ,
• gdzie:
• - największa oczekiwana zmiana zakłócenia;
• - największa dopuszczalna zmiana sygnału wejściowego.
• Maksymalna odchyłka od wartości nominalnej zostałaby dobrana po
przeanalizowaniu maksymalnej akceptowanej wartości lub
dopuszczalnej zmiany funkcji w czasie.
•
Zmienne , , są jednakowymi sygnałami fizycznymi z
takimi samymi współczynnikami skalowania. Dwie możliwości są
dopuszczalne:
• - największy dopuszczalny uchyb;
• - największa akceptowalna zmiana wartości odniesienia.
• Jednocześnie głównym punktem widzenia w układach sterowania jest
minimalizacja wartości uchybu . Dopuszczalne jest skalowanie z
uwzględnieniem maksymalnego uchybu:
• W celu sformalizowania procedury skalowania dla układu MIMO
zostanie wprowadzony wektor skalowania:
,
/
max
d
d
d
max
/u
u
u
max
d
max
u
y
e
r
max
e
max
r
e
,
/
,
/
,
/
max
max
max
e
e
e
e
r
r
e
y
y
max
max
max
max
,
,
,
r
D
d
D
u
D
e
D
r
d
u
e
Skalowanie-cd
• Dla układów MIMO zmienne , , i mogą mieć różne
wartości maksymalne, w tym przypadku Dd , Dr, Du , De , są
diagonalnymi macierzami skalowania. Zapewnione jest na
przykład, że wszystkie uchyby (wyjścia) są wartościami o
porównywalnej wielkości.
•
Zmienne skalowane używane w układach sterowania, to:
• Podstawiając równanie (11.20) do równania (11.16)
otrzymamy:
• oraz wprowadzając transformatę funkcji skalowanej:
• ,
•
• otrzymujemy model o następujących wartościach skalowania:
•
dˆ
rˆ
uˆ
eˆ
,
1
d
D
d
d
,
1
u
D
u
u
,
1
y
D
y
e
,
1
e
D
e
e
w
D
w
e
1
,
d
D
G
u
D
G
y
D
u
d
u
e
w
D
y
D
e
D
e
e
e
d
d
e
d
u
e
D
G
D
G
D
G
D
G
1
1
,
;
d
G
Gu
y
d
w
y
e
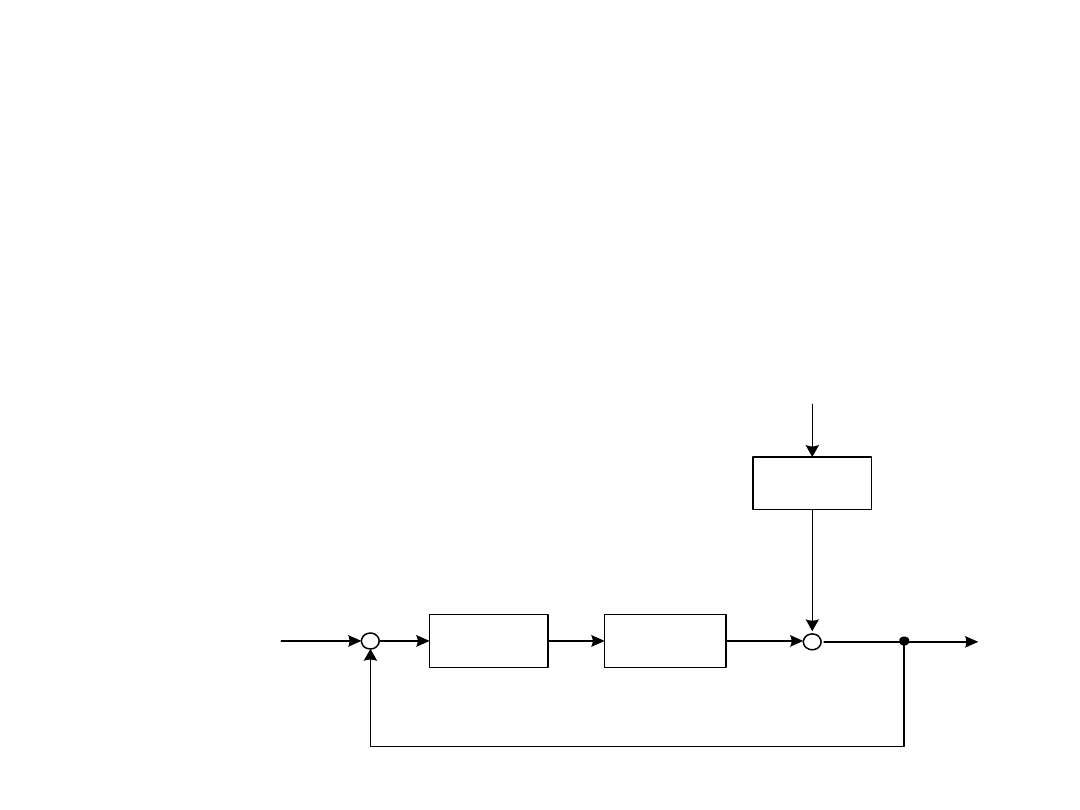
Układ zamknięty
• Obiekt sterowania generuje odpowiedź y(s) w określony sposób w zależności od
reakcji obiektu na sygnał wejściowy u(s) (rys.11.5). Zadaniem regulatora K(s)
jest dokonanie zmiany parametru u(s) w zależności od sygnału uchybu e(s).
Problemem układów sterowania jest zmiana parametru u(s), w taki sposób aby
wyjście układu Y(s) nadążało za sygnałem wejściowym w(s). a maksymalnie
ignorowało zakłócenia d(s). W ten sposób dążymy do uzyskania niewielkiego
sygnału uchybu e(s)=y(s)-w(s). Algorytm regulacji sygnału u(s) bazuje na
dostępnej informacji z regulatora K(s). Aby zaprojektować właściwie regulator
K(s) należy posiadać informację na temat oczekiwanych zakłóceń, sygnału
odniesienia oraz informację o obiekcie sterowania G(s) i modelu zakłóceń Gd(s).
• Do analizy przyjmiemy model liniowy o następującym równaniu:
G
d
(s)
K(s)
G(s)
y(s)
u(s)
d(s)
+
+
+
-
w(s)
y(s)
s
d
s
G
s
u
s
G
s
y
d
Odporna stabilność i jakość
• Istotnym źródłem trudności jest to, że modele obiektu sterowania G(s) i
zakłócenia Gd(s) mogą być nieścisłe lub mogą zmieniać się w czasie. W
szczególności, niedokładność w opisie transmitancji układu G(s) może
powodować problemy, ponieważ obiekt sterowania może mieć wpływ na
pętlę sprzężenia zwrotnego. W celu rozwiązania tego problemu zostanie
sprecyzowany model niepewności. Na przykład, zamiast pojedynczego
modelu G(s) można analizować zachowanie modelu Gp(s)=G(s)+E(s), z
uwzględnieniem zmian "niepewności" lub "zakłóceń" E(s), które mogą
być nieznane. W wielu przypadkach używane są specjalne funkcje w(s)
do wyrażenia E(s)=w(s)
, gdzie rozmiary
są mniejsze lub równe 1.
Podczas analizy układów wykorzystujemy następujące pojęcia:
• - stabilność nominalna układu (ang. nominal stability) – układ nominalny
jest stabilny bez modelu niepewności.
• - jakość nominalna układu (ang. nominal performance) – osiągi układu
nominalnego są zadowalające bez modelu niepewności.
• - stabilność odporna układu (ang. robust stability) – układ jest stabilny
dla wszystkich zakłóceń obiektu o nominalnych parametrach modelu z
uwzględnieniem modelu niepewności.
• - jakość odporna układu (ang. robust performance) – układ osiąga
satysfakcjonujące wyniki dla wszystkich zakłóceń obiektu o
nominalnych parametrach modelu z uwzględnieniem modelu
niepewności.
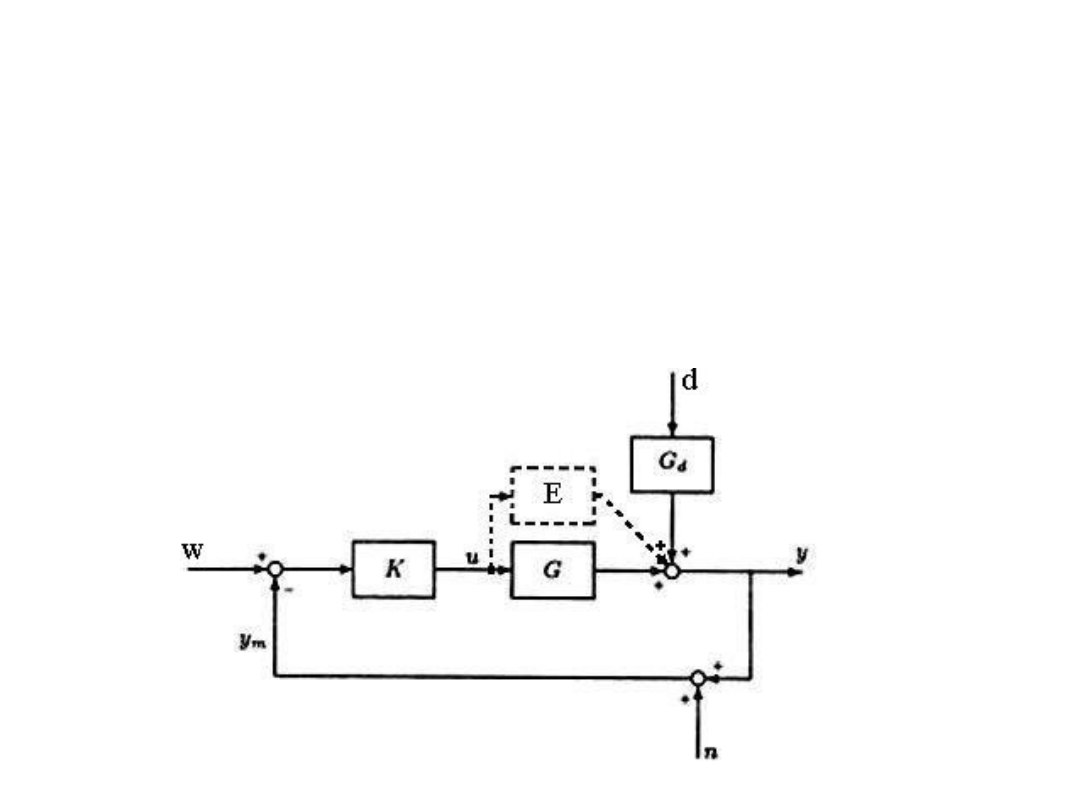
Definicje układów:
• Układ G(s) jest ściśle właściwy (ang. strictly proper), jeżeli: G(s) 0 przy
s
;
• Układ jest średnio właściwy (ang. semi-proper) lub właściwy (ang. bi-
proper), jeżeli: G(s)
D0 przy s ;
• Układ G(s), który jest ściśle lub średnio właściwy jest właściwy;
• Układ G(s) jest niewłaściwy (ang. improper), jeżeli G(s) przy s .
Funkcje wraźliwości
• Wprowadzając zakłócenie pomiarowe n, sygnał wyjściowy opisuje zależność ym=y+n,
gdzie ym jest mierzonym sygnałem wyjściowym. Uwzględniając te zależności układ
sterowania opisują następujące zależności:
•
• oraz:
• .
• Łącząc powyższe równania otrzymujemy:
•
• W związku z tym układ ze sprzężeniem opisują równania:
• Z kolei sygnał sterujący obiektem regulacji opisuje zależność:
•
• W równaniach zostały użyte następujące transmitancje, charakteryzujące właściwości
dynamiczne układu zamkniętego:
• L=GK- transmitancja układu otwartego;
• S=(I+GK)-1=(I+L)-1- funkcja wrażliwości;
• T=(I+GK)-1GK=(I+L)-1L- komplementarna funkcja wrażliwości.
• Należy zauważyć, że S jest funkcją przejścia układu zamkniętego pomiędzy
zakłóceniem a wyjściem, natomiast T jest funkcją przejścia pomiędzy sygnałem
zadanym a wyjściem. Termin wrażliwość komplementarna wynika z faktu, że funkcje te
spełniają związek:
• S+T=I,
• czyli dopełniają się do jedności (macierzy jednostkowej), co łatwo wykazać przez
podstawienie wyrażeń na te funkcje.
d
s
G
u
s
G
y
d
m
y
n
y
w
s
K
u
d
G
n
y
w
GK
y
d
GKn
d
G
GKw
y
GK
I
d
n
GK
GK
I
d
G
GK
I
w
GK
GK
I
y
T
d
S
T
1
1
1
Tn
d
SG
Sw
w
y
e
d
KSn
d
KSG
KSw
u
d
Funkcje wrażliwości układu
zamkniętego
• Funkcje wrażliwości pozwalają, na przykład, ocenić wrażliwość transmitancji układu
zamkniętego na zmianę parametrów układu otwartego. Aby to pokazać założymy, że
mamy układ (SISO), a ponadto pominiemy szum pomiarowy i wymuszenia.
• Mamy następującą funkcję przejścia pomiędzy wielkością zadaną a wielkością
mierzoną:
• .
•
• Z kolei funkcja przejścia pomiędzy sygnałem uchybu i sygnałem mierzonym
ma postać:
•
• Wrażliwość funkcji przejścia układu zamkniętego będziemy badać różniczkując
cząstkowo funkcję przejścia układu zamkniętego względem dowolnego parametru p:
• Przechodząc do wariacji, mamy:
• Jeśli przyrównamy wariację funkcji przejścia do samej funkcji, to znajdziemy związek
pomiędzy zmianą funkcji układu zamkniętego a zmianą funkcji układu otwartego:
• W powyższym wzorze widać w sposób oczywisty, że funkcję S(s) można nazwać
funkcją wrażliwości, gdyż określa wrażliwość funkcji przejścia układu zamkniętego
na zmiany parametrów układu otwartego.
)
(
)
(
)
(
)
(
)
(
)
(
s
s
s
s
s
s
L
I
L
w
y
T
G
z
.
)
(
1
1
)
(
1
)
(
)
(
)
(
)
(
)
(
)
(
s
s
s
s
s
s
s
s
L
T
w
y
w
w
e
S
.
)
1
(
1
2
p
p
L
L
G
z
.
)
1
(
1
2
L
L
G
z
.
)
1
(
1
L
L
S
L
L
L
G
G
z
z
Porównanie kryteriów jakości
• Celem projektowania układu sterowania jest, obok
zapewnienia stabilności, uzyskanie układu
zamkniętego o odpowiedniej jakości działania. Tę jakość
działania ocenia się poprzez odpowiednie kryteria
nałożone na charakterystyki czasowe lub
częstotliwościowe układu otwartego lub układu
zamkniętego. Zazwyczaj kryteria stabilności i jakości
układu prowadzą projektanta w dwóch przeciwnych
kierunkach. Dlatego jest istotnym podczas
projektowaniu układu znalezienia kompromisu
pomiędzy wszystkimi wymaganiami.
• Kryteria jakości opieramy na:
• - Parametrach odpowiedzi układu na skok jednostkowy;
• - Parametrach charakterystyk częstotliwościowych
układu otwartego;
• - Parametrach charakterystyk częstotliwościowych
układu zamkniętego.
Czasowe kryteria jakości
• Wśród kryteriów związanych z odpowiedzią układu na skok
jednostkowy możemy wyróżnić:
• - Czas podniesienia (Tn) – jest to czas po którym odpowiedź
układu osiągnie po raz pierwszy 90% jej końcowej wartości.
• - Czas regulacji (Tr) – jest to czas po którym odpowiedź
pozostaje w przedziale 5% jej ostatecznej (ustalonej)
wartości.
• - Przeregulowanie – jest to stosunek maksymalnej wartości
odpowiedzi do jej wartości ustalonej. W typowych układach
powinien wynosić 1.2 (20%) lub mniej.
• - Stopień tłumienia – jest to stosunek drugiego względem
pierwszego maksymalnego wychylenia. W typowych układach
powinien wynosić 0.3 lub mniej.
• - Błąd ustalony – jest to różnica pomiędzy wartością zadaną a
wartością wyjściową układu dla ich ustalonych wartości.
• Czas podniesienia i czas regulacji są miernikami prędkości
odpowiedzi układu, natomiast przeregulowanie, stopień
tłumienia i błąd ustalony są miernikami jakości odpowiedzi.
Kryteria oparte na normach
• Ponadto często oceniamy jakość układu zamkniętego przez
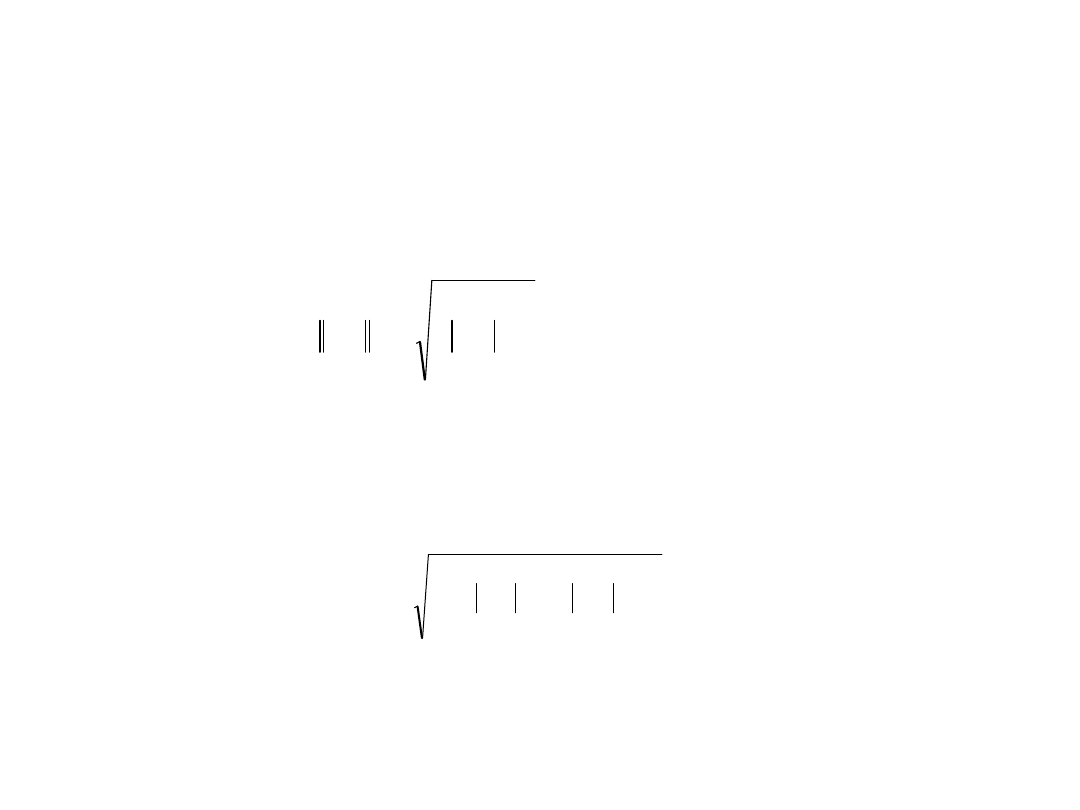
normy nałożone na uchyb regulacji: e(t)=y(t)-w(t). Może to być
na przykład całka z kwadratu uchybu lub pierwiastek z tej całki,
który jest 2-normą (euklidesową):
• .
Zauważmy że w przypadku tego kryterium uwzględniamy
zarówno prędkość jak i jakość odpowiedzi układu zamkniętego.
Inną zaletą 2-normy jest łatwa optymalizacja układu przez
numeryczne obliczanie minimum tego kryterium w funkcji
parametrów regulatora. Można również brać pod uwagę w
rozważaniach wielkość sygnałów wejściowych przez
wprowadzenie kryterium w postaci:
• gdzie Q, R są stałymi dodatnimi. To podejście jest podobne do
LQR – liniowego kwadratowego sterowania optymalnego, lecz w
LQR na wejściu (wielkość zadana – w(t)) rozpatruje się zazwyczaj
impuls a nie skok.
dt
t
e
t
e
2
0
2
)
(
)
(
dt
t
u
R
t
e
Q
J
0
2
2
)
(
)
(
Zapas modułu
• W oparciu o charakterystyki układu otwartego budujemy kryteria zapasu
wzmocnienia i zapasu fazy. W tym celu wykreślamy charakterystyki
częstotliwościowe Bodego dla L(j
).
• Zapas modułu M jest definiowany jako:
•
gdzie fazowa częstotliwość przecięcia odpowiada częstotliwości, dla której
wykres Nyquista funkcji L(j) przecina ujemną gałąź osi rzeczywistej pomiędzy
punktami 0 i –1, gdzie mamy:
L(j180)=-180o.
• Gdy mamy więcej niż jednokrotne przecięcie tego poziomu przez charakterystykę
fazową, to największa z wartości |L(j180)| brana jest pod uwagę. Na wykresie
Bodego z logarytmiczną skalą modułu |L| przyjmujemy zapas modułu jako
odwrotność pionowej odległości od poziomu 0 [dB],. ∆M jest współczynnikiem, o
który można podnieść wzmocnienie układu otwartego |L(j)| aby znaleźć się na
granicy stabilności układu zamkniętego. Tym samym GM jest zabezpieczeniem
przed niepewnością wzmocnienia układu. Zazwyczaj wymagamy, aby GM>2. Jeśli
wykres Nyquista przekroczy ujemną gałąź osi rzeczywistej pomiędzy –1 i , to
wzmocnienie, które redukuje zapas modułu można podobnie zdefiniować na
podstawie najmniejszej wartości |L(j180)| .
180
1
(
)
M
L jw
D =
180
Zapas fazy
• Zapas fazy może być definiowany jako:
• PM=L(jc) +180o
• gdzie częstotliwość przecięcia c ma miejsce wówczas, gdy |
L(j)| przecina po raz pierwszy poziom 0 [dB], to znaczy, gdy:
• |L(jc)| = 1.
• Zapas fazy określa, ile należy dodać opóźnienia fazowego do
charakterystyki L(s), aby dla częstotliwości –180o układ
zamknięty znalazł się na granicy stabilności. Zazwyczaj
wymagamy, aby PM był większy niż 30o. Zapas fazy
zabezpiecza przed niepewnością opóźnień czasowych. Jeśli
dodamy opóźnienie czasowe:
• to układ staje się niestabilny. Należy zwrócić uwagę na spójność
układu jednostek. Jeśli c jest w rad/s to i PM musi być w
radianach. Należy zauważyć, że jeśli będziemy obniżać wartość
c ( a tym samym skracać pasmo przenoszenia układu
zamkniętego), to układ będzie w stanie tolerować większe
opóźnienie czasowe.
c
PM
/
max
Kryteria układu zamkniętego
• Dla charakterystyk układu zamkniętego wprowadzimy
kryteria maksymalnych wartości funkcji wrażliwości i funkcji
komplementarnej wrażliwości. Zdefiniujemy je następująco:
• Można zauważyć, że: są tak
zwaną normą H,. W typowych układach wymaga się aby MS
było mniejsze niż 2 (6 [dB]) a MT było mniejsze niż 1.25 (2
[dB]). Większe wartości tych wskaźników świadczą, że układ
charakteryzuje się niską jakością oraz gorszą odpornością na
zmiany parametrów. Ponieważ zachodzi S+T=1, to dla
dowolnej częstotliwości mamy:
• ||S|-|T|||S+T|=1
• a tym samym MS i MT mogą wzajemnie różnić się co najwyżej
o wartość 1. Tym samym duże wartości MS pojawiają się
wtedy i tylko wtedy, gdy MT jest duże. Dla układów stabilnych
zazwyczaj mamy MS > MT lecz nie jest to regułą.
T
M
S
M
T
S
max
,
max
,
)
(
max
,
)
(
max
j
T
M
j
S
M
T
s
Związki pomiędzy kryteriami
• Pomiędzy kryteriami MS, MT oraz zapasem modułu i fazy
istnieją ścisłe relacje:. Na przykład dla danego MS zachodzi:
• Z powyższych zależności wynika, że dla Ms=2 mamy
zagwarantowane, że GM≥2, a PM≥29o.Podobnie dla danego
MT otrzymamy:
• Ponownie, dla MT=2 mamy zapewnione, że GM≥1.5, a
PM≥29o.
• Podsumowując, jeśli przyjmiemy i utrzymamy ograniczenia na
wartości maksymalne funkcji wrażliwości |S(jω)| lub funkcji
komplementarnej wrażliwości |T(jω)|, to badanie zapasu
modułu i fazy okazuje się niepotrzebne. Na przykład przy
zapewnieniu, że: Ms<2 mamy natychmiast GM>2 i PM>30o.
rad
M
M
PM
M
M
GM
s
s
s
s
1
2
1
arcsin
2
~
,
1
rad
M
M
PM
M
GM
T
T
T
1
2
1
arcsin
2
~
,
1
1