Materiały pochodzą z Platformy 

Edukacyjnej Portalu 

www.szkolnictwo.pl

Wszelkie  treści  i  zasoby  edukacyjne  publikowane  na  łamach  Portalu  www.szkolnictwo.pl    mogą  być  wykorzystywane  przez  jego 
Użytkowników 

wyłącznie 

w  zakresie  własnego  użytku  osobistego  oraz  do  użytku  w  szkołach  podczas  zajęć  dydaktycznych.  Kopiowanie,  wprowadzanie  zmian, 
przesyłanie, 

publiczne 

odtwarzanie 

i  wszelkie  wykorzystywanie  tych  treści  do  celów  komercyjnych  jest  niedozwolone.  Plik  można  dowolnie  modernizować  na  potrzeby 
własne 

oraz 

do 

wykorzystania 

w szkołach podczas zajęć dydaktycznych.

„Kto lekceważy osiągnięcia 

matematyki przynosi szkodę 

całej nauce,

ponieważ ten, kto nie zna 

matematyki,

nie może poznać innych nauk 

ścisłych i nie może poznać 

świata.”

Roger Bacon

Koło. Okrąg. Liczba π.

Koło i okrąg to figury dobrze Ci znane ze 
szkoły podstawowej.  W tej lekcji 
przypomnimy parę ważnych pojęć z nimi 
związanych. Powiemy też, co to takiego jest 
liczba π.

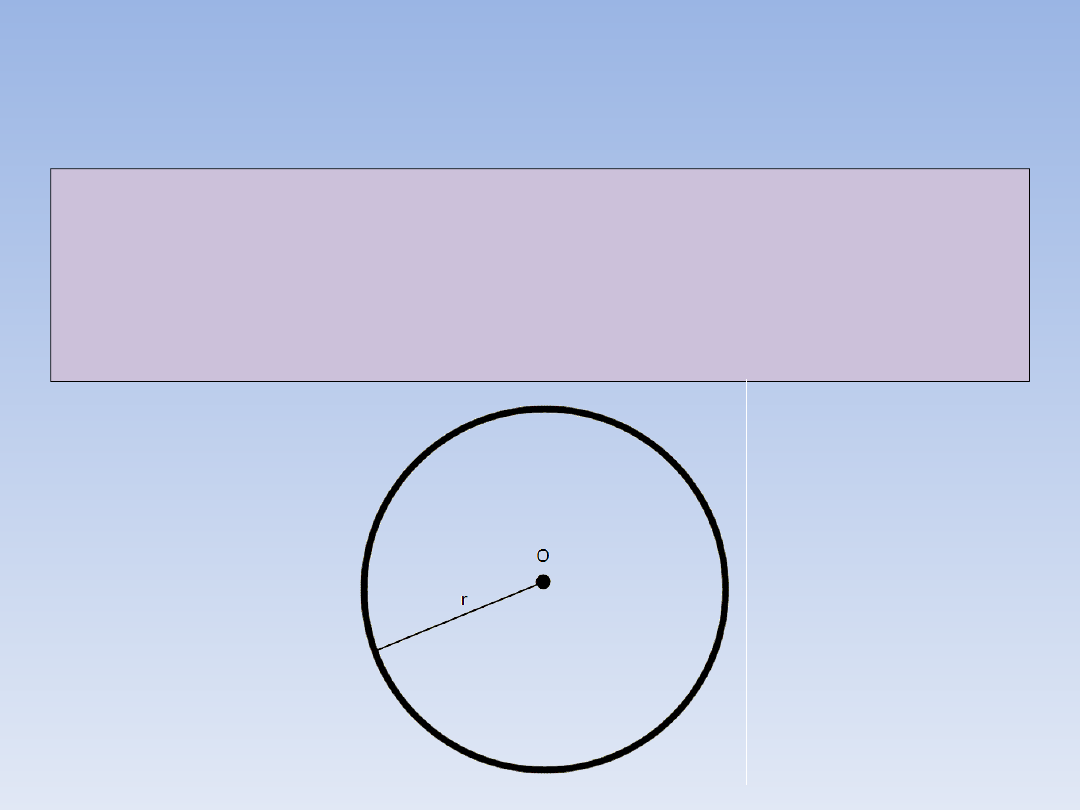
DEFINICJA OKRĘGU.

Okręgiem o środku O i promieniu r 

nazywamy figurę geometryczną utworzoną 

ze wszystkich punktów płaszczyzny, które 

leżą w tej samej odległości r od środka O.

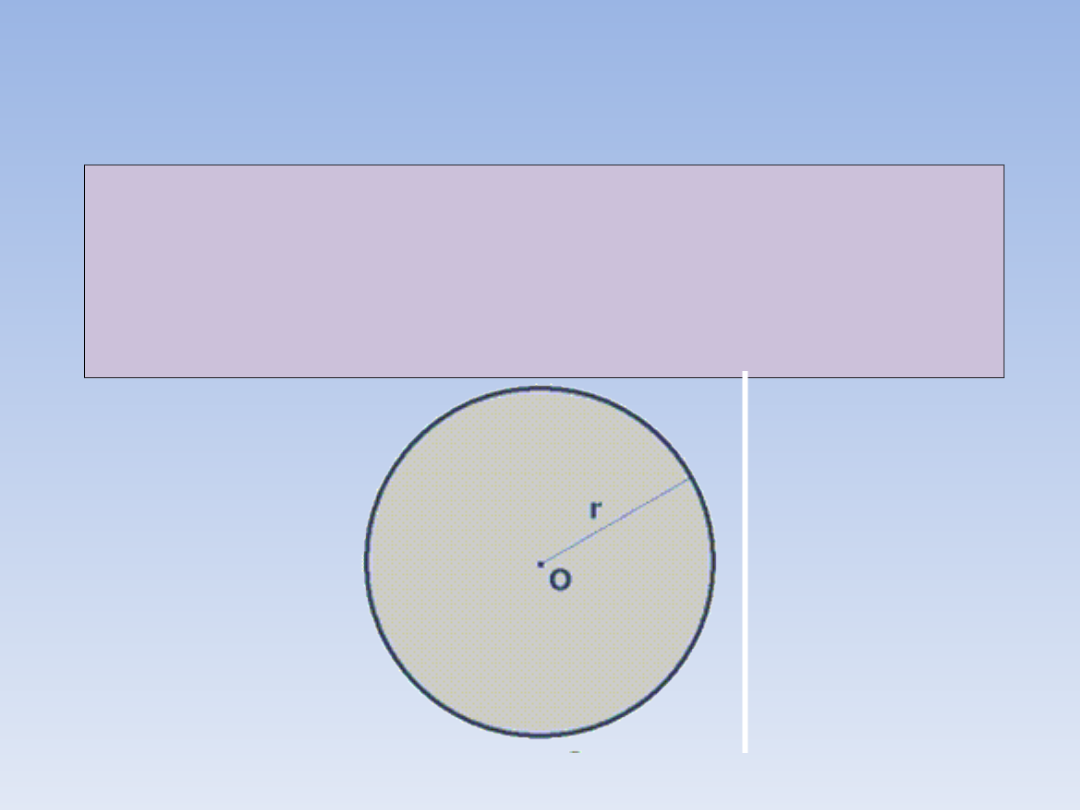
DEFINICJA KOŁA.

Kołem o środku O i promieniu r 

nazywamy figurę utworzoną ze wszystkich 

punktów płaszczyzny, ograniczonych 

okręgiem o środku O i promieniu r.

CZYM SIĘ RÓŻNIĄ?

Czym okrąg różni się od koła? Po prostu 
okrąg „jest pusty w środku” a koło „jest 
wypełnione”.

okrąg

koło

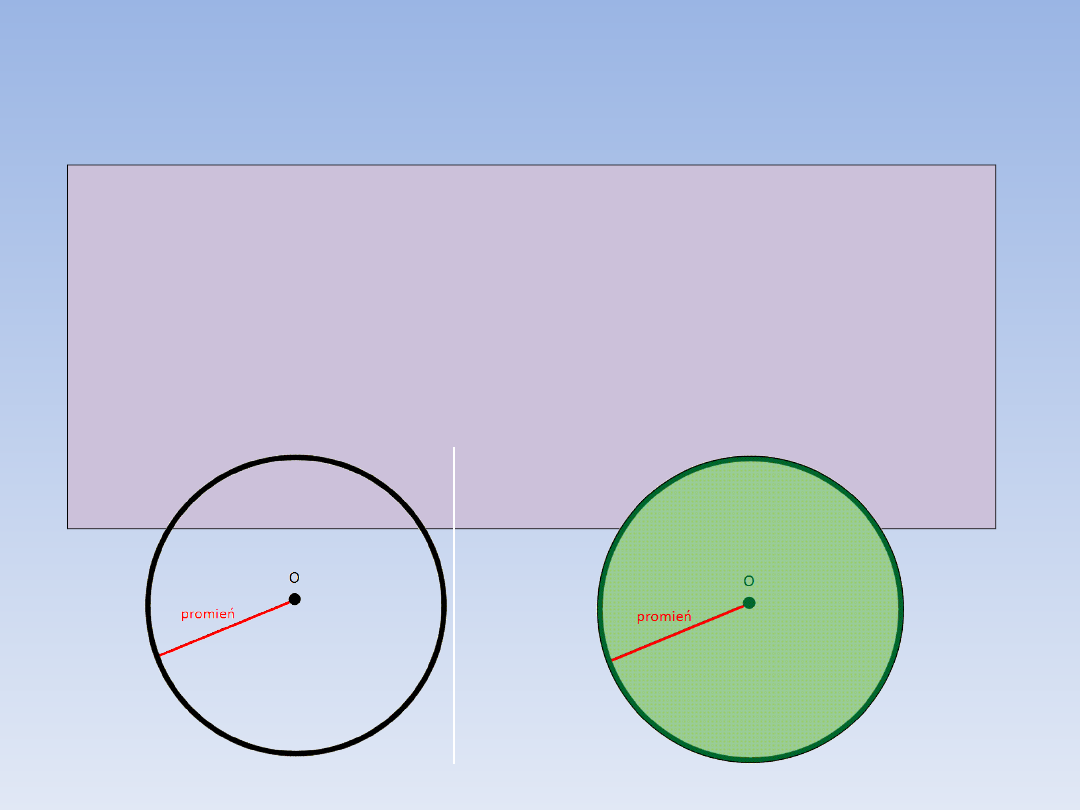
PROMIEŃ.

Promieniem okręgu [koła] nazywamy 

każdy odcinek, którego jednym końcem 

jest środek okręgu [koła] a drugim punkt 

leżący na tym okręgu [okręgu 
ograniczającym to koło].

Długość promienia oznaczamy małą literą 

r.

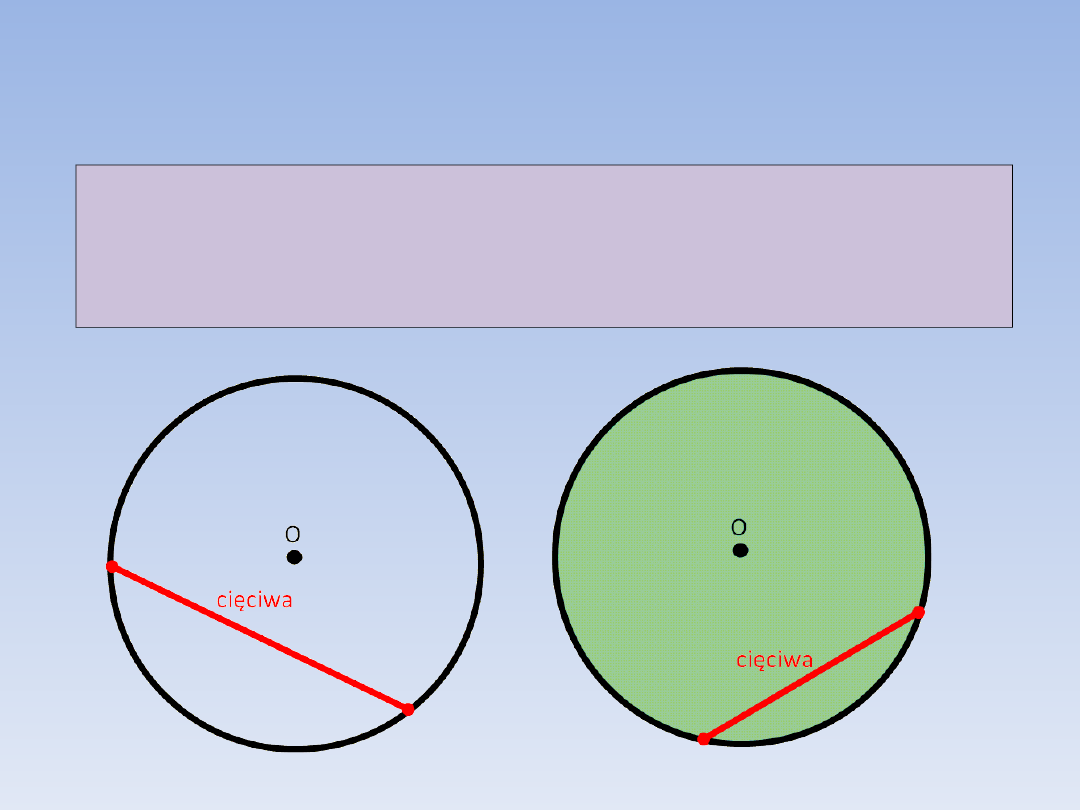
Cięciwa.

Cięciwą okręgu [koła] nazywamy każdy 

odcinek łączący dwa dowolne punkty tego 

okręgu [okręgu ograniczającym to koło].

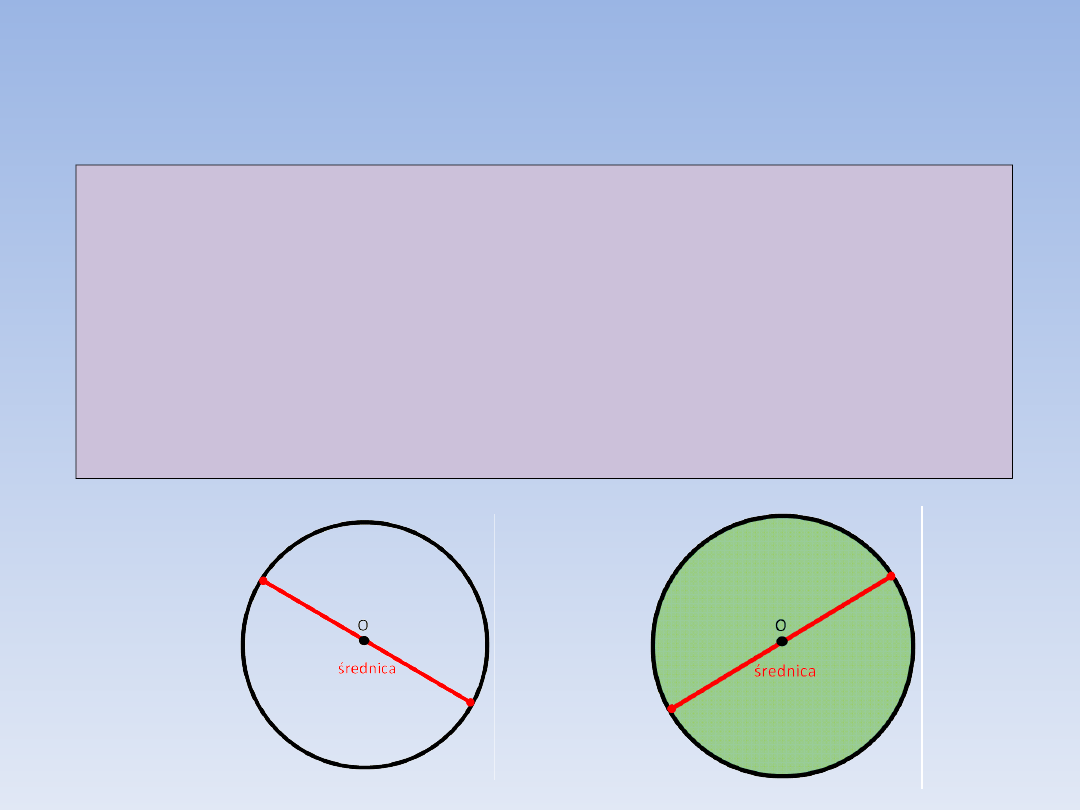
ŚREDNICA.

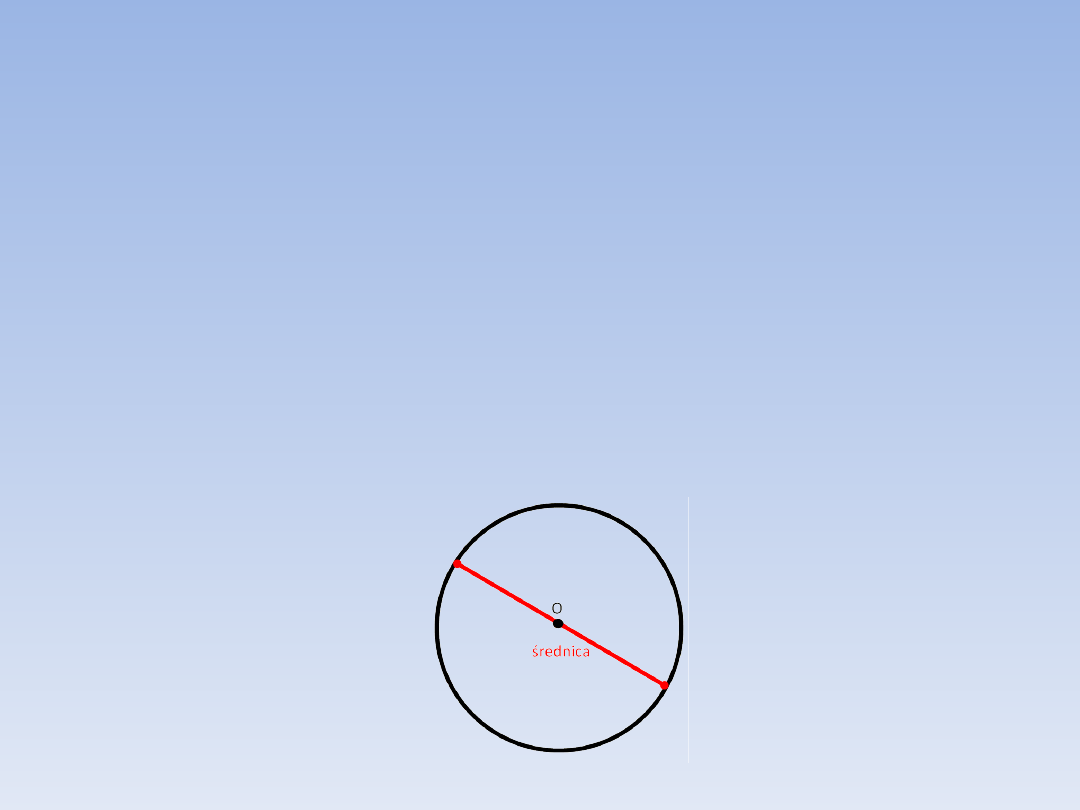
Średnicą okręgu [koła] nazywamy cięciwę 

przechodzącą przez jego środek.

Długość średnicy oznaczamy mała literą d.

d = 2r

Długość średnicy jest dwa razy większa od 

długości promienia.

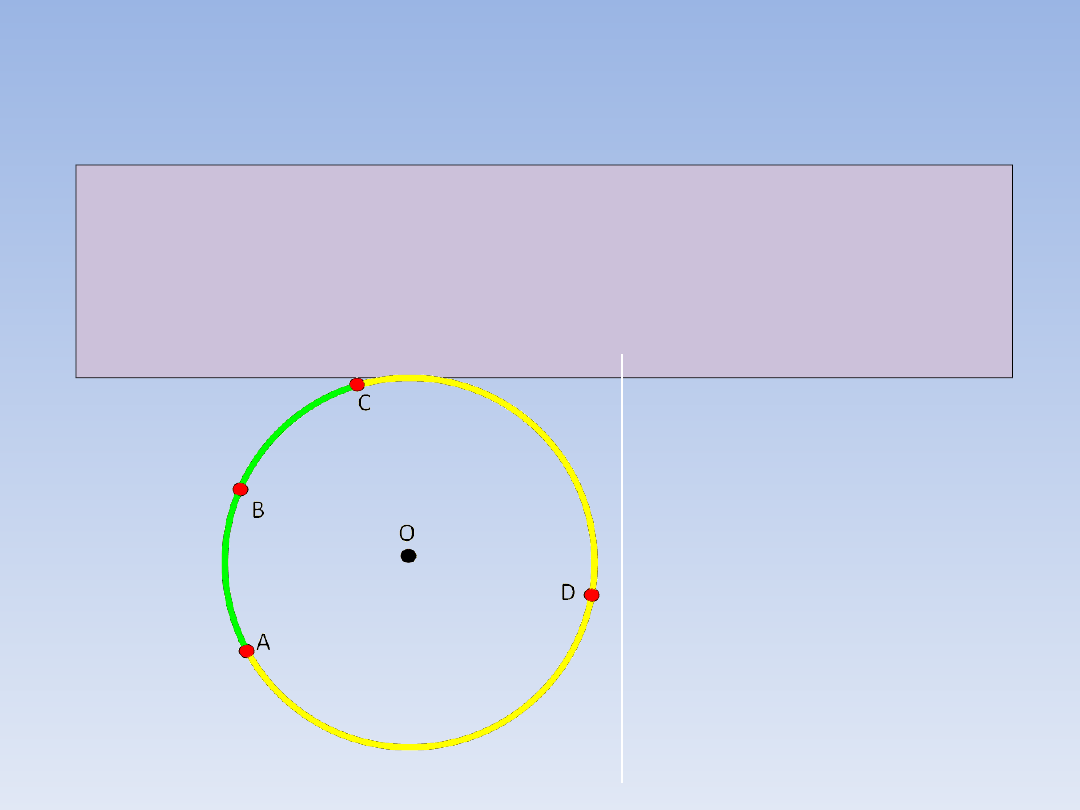
ŁUK.

Łukiem nazywamy część okręgu 

ograniczoną dwoma punkami. 

Dwa punkty okręgu wyznaczają dwa różne 

łuki.

ABC 

- łuk

CDA 

- łuk

LICZBA π.

Liczba π (czyt. „pi”) to liczba niewymierna ściśle 

związana z okręgami i kołami.
Jeśli podzielimy długość obwodu koła (długość 

okręgu) i podzielimy go przez jego średnicę 

otrzymamy liczbę π.

Sprawdź: używając sznurka i linijki zmierz obwody 

różnych okrągłych przedmiotów oraz ich średnice (rura od 

odkurzacza, słoik, szklanka itp.), podziel zgodnie z 

powyższą definicją a przekonasz się że dla każdego 

okrągłego przedmiotu wynik jest bardzo zbliżony (aby 

wyszedł ten sam wynik należy dokonywać bardzo 

dokładnych pomiarów).

PRZYBLIŻENIE LICZBY π.

Liczba π jest niewymierna, ma więc 
rozwinięcie dziesiętne nieskończone, 
nieokresowe. Oto liczba π z dokładnością do 
50 miejsc po przecinku:
π = 3,14159 26535 89793 23846 26433 832
79 50288 41971 69399 37510...
Do konkretnych obliczeń używamy 
najczęściej takich przybliżeń:

   π ≈ 3,14

PAMIĘTAJ!

•π (czyt. „pi”) to symbol za którym kryje 

się liczba niewymierna.

•Używając symbolu π w obliczeniach, 

podajemy dokładną wartość – liczbę 
niewymierną.

•Jeśli chcemy podać wartość przybliżoną 

zamiast symbolu π musimy wstawić 
przybliżenie liczby π, np. 3,14.

PRZYKŁADOWE ZADANIA.

ZADANIE 1.
Jaką długość ma promień okręgu, którego 
najdłuższa cięciwa ma długość 9 cm?
Najdłuższą cięciwą w okręgu jest jego 
średnica. A więc promień tego okręgu ma 
długość r = 4,5 cm (ponieważ długość 
średnicy d = 2r)

PRZYKŁADOWE ZADANIA.

ZADANIE 2. 
Czy na dnie garnka o średnicy 24 cm można 
ustawić 4 słoiki o promieniu dna 6 cm?
Oczywiście nie. Skoro promień dna ma 
długość 6 cm jego średnica ma 12 cm. 
2 ∙ 12 = 24 a więc już ustawienie dwóch 
słoików obok siebie sprawiłoby trudność a co 
dopiero czterech.

PRZYKŁADOWE ZADANIA.

ZADANIE 3.
Zapisz w jak najprostszej postaci:

a) 3π ∙ 4π
b) 5π + 2π

c) 4π : 2π
Obliczenia wykonujemy zgodnie z zasadami 

działań na wyrażeniach algebraicznych

a) 3π ∙ 4π = 12π

2

 

b) 5π + 2π = 7π

c) 4π : 2π = 2

π

Obwód koła o średnicy 1 wynosi π.

Symbol π wprowadził w 1706 roku William 
Jones a rozpowszechnił go później 
Leonhard Euler. Symbol pochodzi od 
greckiego słowa περίμετρον - perimetron, 
czyli obwód.

π

Liczba π występuje w tak wielu zagadnieniach 
w matematyce i fizyce oraz pełni tak 
szczególną rolę, że uczeni poszukujący 
kontaktu z cywilizacjami pozaziemskimi 
wysłali w kosmos drogą radiową informację o 
wartości liczby π, wierząc, że inteligentne 
istoty spoza Ziemi znają tę liczbę i rozpoznają 
komunikat.