„Dlaczego liczby są piękne?

To jak pytać, dlaczego

dziewiąta symfonia

Beethovena jest piękna.

Jeżeli nie rozumiesz dlaczego,

nikt ci ni może powiedzieć. Ja

wiem, że liczby są piękne.

Jeśli one nie są, nic nie jest.”

Pal Erdos

WIELKOŚCI ODWROTNIE

PROPORCJONALNE.

Nie

wszystkie

wielkości

spotykane

w

codziennym życiu są wprost proporcjonalne,
istnieje także proporcjonalność odwrotna. Jeśli
nauczysz

się

odróżniać

oba

rodzaje

proporcjonalności rozwiązywanie większości
problemów z nimi związanych będzie bardzo
proste.

WIELKOŚCI ODWROTNIE

PROPORCJONALNE.

O dwóch wielkościach mówimy, że są

odwrotnie proporcjonalne, jeśli wraz ze

wzrostem jednej, druga maleje tyle samo

razy.

PRZYKŁADY.
Cena benzyny i ilość benzyny, którą można
kupić za
30 zł – im wyższa cena, tym proporcjonalnie
mniej benzyny.
Ilość kolegów i liczba chipsów przypadająca
na osobę – im więcej osób tym każda z nich
otrzyma proporcjonalnie mniej chipsów.

PRZYKŁADY WIELKOŚCI

ODWROTNIE

PROPORCJONALNYCH.

Średnia prędkość skutera i czas potrzebny na
przejechanie danego odcinka drogi – im
większa prędkość tym mniej czasu potrzeba
na przejechanie określonej trasy.

Liczba osób na przyjęciu i wielkość kawałka
tortu przypadającego na osobę – im więcej
osób, tym proporcjonalnie mniejszy kawałek
tortu otrzyma każda z nich.

Grubość książki i ilość jednakowych książek
na półce – im grubsza książka, tym mniej
takich zmieści się na półce.

PROPORCJONALNOŚĆ

ODWROTNA.

Zależność między dwiema wielkościami,

których iloczyn jest stały nazywamy

proporcjonalnością odwrotną.

xy = a

gdzie a ≠ 0. O wielkościach x i y mówimy,

że są odwrotnie proporcjonalne.

UWAGA.

Z powyższej definicji wynika, że zależność
między wielkościami wprost proporcjonalnymi
możemy zapisać
przy pomocy wzoru

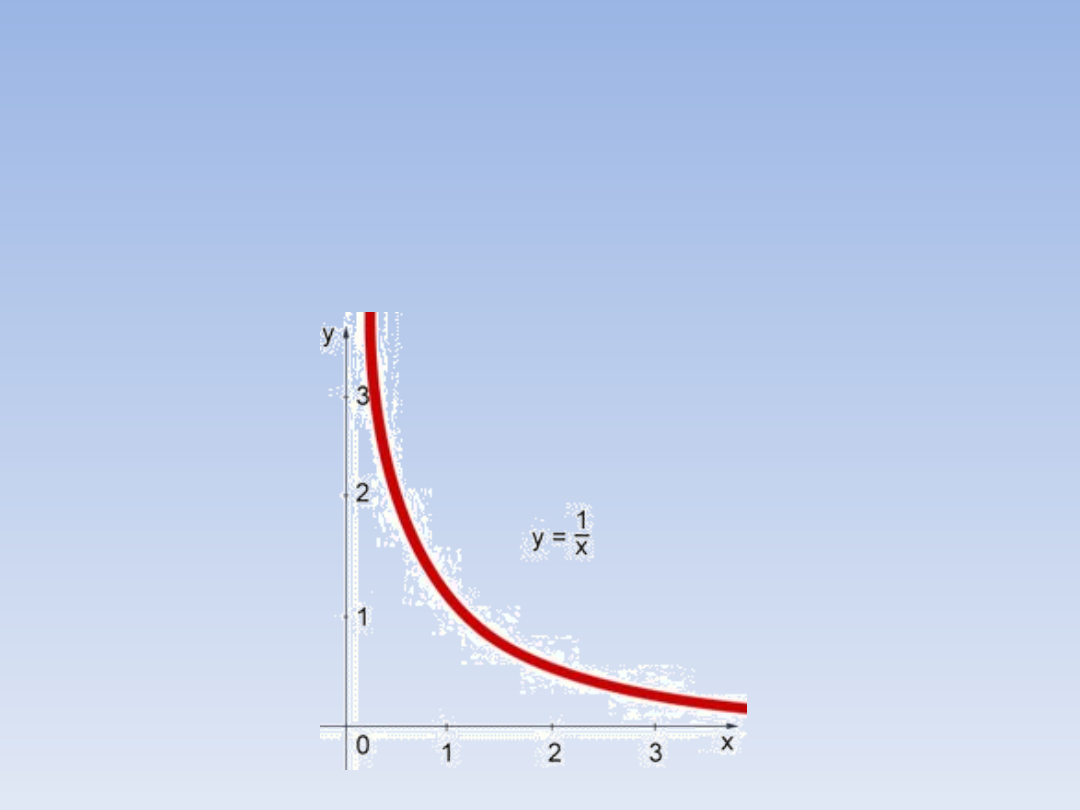
WYKRES

PROPORCJONALNOŚCI

ODWROTNEJ.

Wykres proporcjonalności odwrotnej to jedno
z ramion hiperboli, dla a = 1 wygląda on
następująco:

PRZYKŁADOWE ZADANIA.

ZADANIE 1.
Sprawdź, czy wielkości podane w tabelce są
odwrotnie proporcjonalne.

Aby

podane

wielkości

były

odwrotnie

proporcjonalne, ich iloczyn musi być stały,
liczymy więc x · y
0,3 · 4 = 1,2
1 · 1,2 = 1,2
3 · 0,4 = 1,2
2 · 0,6 = 1,2

x

0,3

1

3

2

0,2

y

4

1,2

0,4

0,6

6

PRZYKŁADOWE ZADANIA.

ZADANIE 1 – ciąg dalszy.
0,2 · 6 = 1,2
Iloczyn jest stały więc podane wielkości są

odwrotnie proporcjonalne.
Współczynnik proporcjonalności dla podanych

wielkości to a = 1,2 a wzór wygląda

następująco:

UWAGA.

Gdybyśmy w chociaż jednym mnożeniu

otrzymali inną liczbę, podane wielkości nie

byłyby odwrotnie proporcjonalne.

PRZYKŁADOWE ZADANIA.

ZADANIE 2.
Uzupełnij tabelkę tak, aby podane wielkości
były odwrotnie proporcjonalne.

Należy wstawić takie liczby, aby iloczyn był
stały. Obliczamy x · y z kolumny, w której
mamy podane obie wartości

0,1 · 36 = 3,6

Pozostałe komórki musimy uzupełnić tak,
aby x · y = 3,6

x

3,6

0,1

144

y

0,6

36

PRZYKŁADOWE ZADANIA.

ZADANIE 2 – ciąg dalszy.

3,6 · y = 3,6
y = 1

x · 0,6 = 3,6 / : 0,6
x = 6

144 · y = 3,6 /: 144
y = 0,025

x

3,6

0,1

144

y

0,6

36

x

3,6

6

0,1

144

y

1

0,6

36

0,025

Uzupełniona
tabela:

PRZYKŁADOWE ZADANIA.

ZADANIE 3.
Robotnicy stawiali mur. Po wykonaniu pracy
każdy z nich otrzymał 12 dukatów zapłaty.
Gdyby robotników było o 4 mniej, to każdy z
nich otrzymałby 3 razy większą zapłatę. Ilu
robotników stawiało mur?

Wielkości występujące w tym zadaniu są
odwrotnie proporcjonalne, nie możemy więc
skorzystać z proporcji do jego rozwiązania.
Korzystamy z własności wielkości odwrotnie
proporcjonalnych (ich iloczyn jest stały).

Oznaczmy:
x – ilość robotników

PRZYKŁADOWE ZADANIA.

ZADANIE 3 – ciąg dalszy.
x – 4 – ilość robotników zmniejszona o 4
3 · 12 = 36 – zapłata, którą otrzymaliby
robotnicy, gdyby było ich o 4 mniej
12x = 36(x – 4) – równanie wynikające z
własności

wielkości

odwrotnie

proporcjonalnych
12x = 36x – 144
144 = 36x – 12x
144 = 24x / ; 24
6 = x
Mur stawiało sześciu robotników.

PRZYKŁADOWE ZADANIA.

ZADANIE 4.
Koło zębate o 120 zębach napędza koło zębate
o 48 zębach. Ile razy obróciło się małe koło,
gdy duże w tym czasie obróciło się 40 razy?

Im mniejsze koło tym proporcjonalnie więcej
obrotów mamy więc do czynienia z
wielkościami odwrotnie proporcjonalnymi.

Oznaczmy:
x – ilość obrotów małego kola

Musimy rozwiązać równanie wynikające z
własności wielkości odwrotnie
proporcjonalnych.

PRZYKŁADOWE ZADANIA.

ZADANIE 4 – ciąg dalszy.
120 · 40 = 48 · x – iloczyn ilości zębów i
obrotów jest stały
4800 = 48x / : 48
100 = x

Małe koło obróciło się 100 razy.

PRZYKŁADOWE ZADANIA.

ZADANIE 5.
Kierowca pokonał pewną trasę jadąc ze średnią
szybkością 90 km/h. O ile kilometrów na godzinę
powinien zwiększyć szybkość, aby pokonać tę
samą trasę w czasie o 25% krótszym?

Oznaczmy:
t – czas potrzebny na pokonanie trasy
0,75t – czas o 25% krótszy (100% - 25% = 75%)
x – nowa szybkość

Układamy i rozwiązujemy równanie zgodne z
własnościami

wielkości

odwrotnie

proporcjonalnych.

PRZYKŁADOWE ZADANIA.

ZADANIE 5.
90t = 0,75t · x
Zauważmy, że niewiadomej t możemy łatwo
się pozbyć dzieląc przez nią obie strony
równania (warunek t ≠ 0 wynika z zadania),
jest to tzw. niewiadoma pomocnicza.
90 = 0,75x / : 0,75
120 = x
120 – 90 = 30

Kierowca powinien zwiększyć szybkość o 30
km/h

UWAGA.

Zawszę zwracaj uwagę z jakimi wielkościami

masz do czynienia – wprost, czy odwrotnie

proporcjonalnymi.

Proporcji możemy używać tylko do zadań, w

których występują wielkości wprost

proporcjonalne.