Referat. Architektura Systemów Komputerowych

Opracował: Dariusz Zagórski

Warszawa, Uczelnia Vistula 2012

W systemach pamięci mogą występować dwa rodzaje błędów: błędy stałe i
przypadkowe.



Błąd stały (czyli uszkodzenie sprzętowe) jest trwałym defektem fizycznym

nośnika powodującym, że uszkodzona komórka pamięci nie jest w stanie
przechowywać danych – pozostają one trwale w stanie 0 lub 1, ewentualnie
zmieniają swój stan przeskakując chaotycznie pomiędzy 0 i 1.



Błąd przypadkowy jest zjawiskiem losowym i nieniszczącym, które zmienia

zawartość komórek pamięciowych bez ich fizycznego uszkodzenia. Błąd taki
może być spowodowany przez problemy z zasilaniem lub naturalnie i
powszechnie występujące zjawiska emisji cząsteczki alfa w procesie
promieniotwórczości

.



Bitem parzystości nazywamy bit kontrolny, który przyjmuje wartość 1, gdy
liczba jedynek w przesyłanej wiadomości jest nieparzysta lub 0, gdy
odwrotnie. Innymi słowy – bit parzystości sprawia, że wiadomość ma
zawsze parzystą liczbę jedynek. W tym wariancie bit parzystości możemy
obliczyć wykonując

sumę modulo dwa

na wszystkich bitach wiadomości:

gdzie n to liczba bitów wiadomości.

Przykłady



Wiadomość 10111101

2

ma parzystą liczbę jedynek, więc bit parzystości

wynosi 0. Wiadomość z dołączonym bitem parzystości to 101111010

2

.



Wiadomość 01110011

2

ma nieparzystą liczbę jedynek, więc bit parzystości

wynosi 1. Wiadomość z dołączonym bitem parzystości to 011100111

2

.



W wielu systemach kodowania (kody kreskowe, numery ISBN, numery
rachunków bankowych, numery NIP) stosuje się sumy kontrolne. Są to
specjalne kody, które pozwalają szybko ustalić, czy któryś z
poprzedzających je znaków nie został przypadkiem błędnie odczytana.



CRC (cykliczna kontrola nadmiarowa) to technika opierająca się na sumach
kontrolnych, którą stosuje się głównie przy przesyłaniu danych w celu
sprawdzenia , czy w jakimś bloku lub strumieniu bajtów nie wkradł się błąd.
Istnieje tutaj prosta zależność, że im większy blok danych jest do
sprawdzenia, tym większa musi być suma kontrolna. Sumy kontrolne i
techniki CRC zaliczamy do grupy regularnych systemów detekcji błędów.
Bity kontrolne są doklejane do bajtów danych nie powodując ich zmiany.
Grupę takich bitów nazywamy syndromem. Techniki CRC są oparte na
arytmetyce modulo 2.

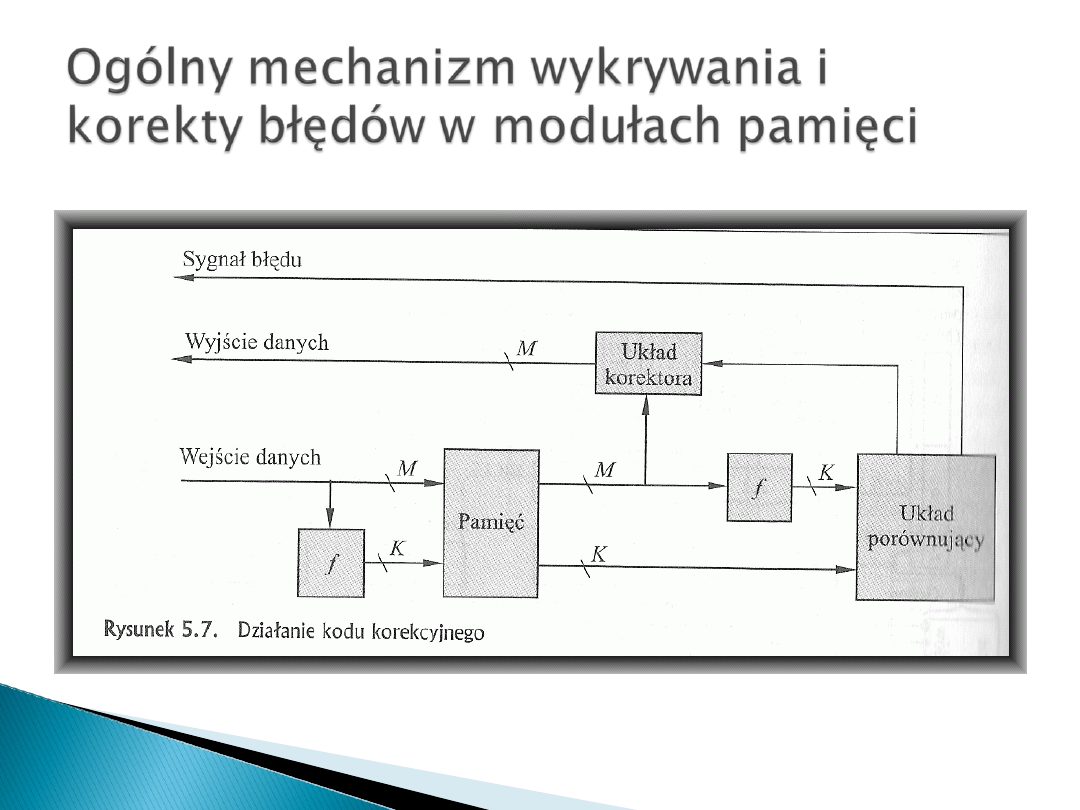
W momencie, gdy dane mają być wczytane do pamięci przeprowadza się na

tych danych obliczenia, określane jako funkcja f, w celu utworzenia kodu, przy

czym dane i kod zostają przechowywane i w efekcie powstaje M+K bitowe

słowo (M-bitów danych i K-bitów kodu).

W trakcie odczytu uprzednio zmagazynowanego słowa kod korekcyjny jest

wykorzystywany do wykrycia i ewentualnej korekty błędów. Najpierw

generowany jest nowy zestaw K-bitów kodowych z M-bitów danych, po czym

następuje porównanie go z pobranymi bitami kodowymi. W wyniku porównania

następuje jeden z 3 stanów:



- nie wykryto żadnych błędów więc przesyłamy pobrane bity



- wykryto błąd i jest możliwa jego korekta – bity danych i bity korekty błędu sa

przesyłane do układu korektora, gdzie jest tworzony poprawiony zestaw M-

bitów przeznaczonych do wysłania



- wykryto błąd niemożliwy do poprawienia – zgłaszamy alarm

Wszystkie kody działające na tej zasadzie nazywamy kodami korekcyjnymi.

Kod korekcyjny jest opisywany przez liczbę błędnych bitów w danym słowie.



Jednym z najstarszych, a zarazem jednym z najwydajniejszych kodów

zapewniających możliwość korygowania błędów jest kod Hamminga. Został on

opracowany przez Richarda Hamminga z Bell Laboratories. Kody Hamminga

stosuje się wszędzie tam, gdzie zachodzi duże prawdopodobieństwo pojawienia

się losowych błędów, tj. takich, dla których prawdopodobieństwo wystąpienia

błędu na pozycji danego bitu jest takie samo, jak na wszystkich pozostałych

pozycjach, niezależnie od liczby błędów, które już wystąpiły w danym bajcie.

Tego typu błędy pojawiają się w pamięciach komputerów.



Kod Hamminga wykorzystuje kontrolę parzystości, w której zdolność do

wykrywania i korygowania błędów rośnie proporcjonalnie do bitów parzystości

dodawanych do każdego słowa właściwej informacji. Samo słowo maszynowe

składa się z m bitów, ale dodaje się do niego r bitów kontrolnych(bitów

parzystości), które pozwalają na stosowanie mechanizmów kontroli i korekcji

błędów. Otrzymujemy w ten sposób tzw. słowo kodowe.



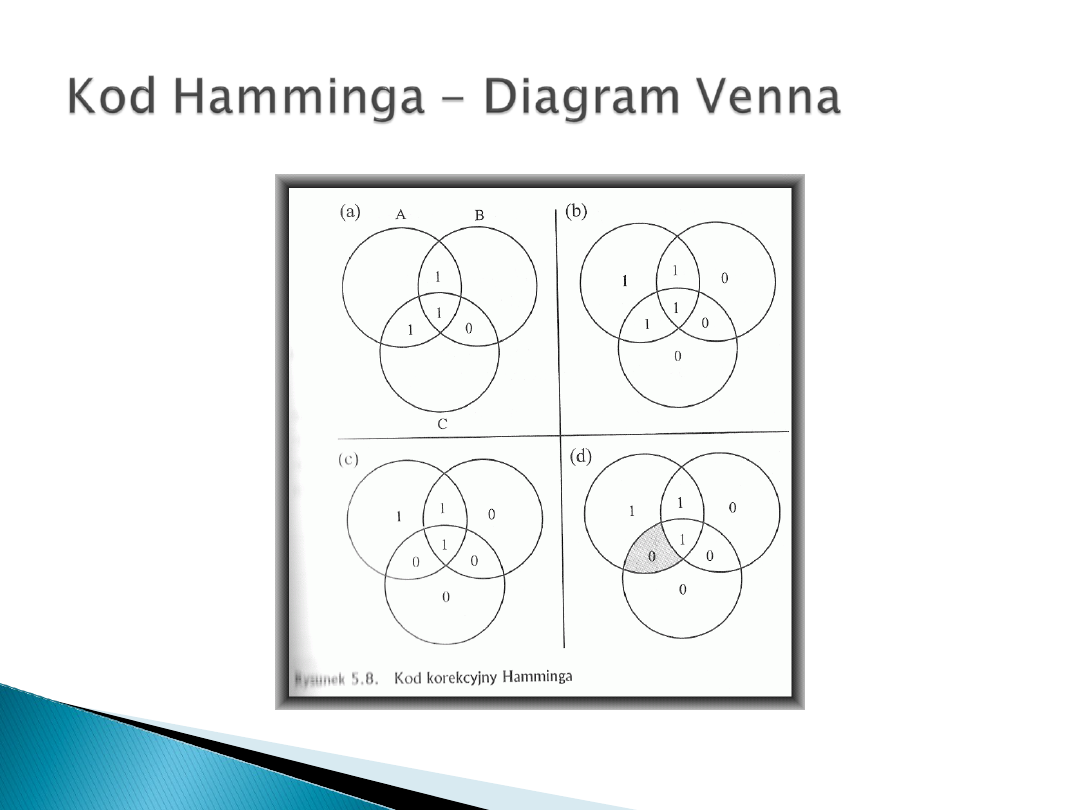
Działanie Kodu Hamminga najlepiej zrozumieć na podstawie Diagramu Venna.,

czyli schematu ilustrującego zależność pomiędzy zbiorami, co znacznie ułatwia

dostrzeżenie relacji pomiędzy zbiorami.

Odległością Hamminga będziemy nazywać liczbę bitów, którymi różnią się
dwa słowa. Np.

10001001
10110001
- - ***- - -

różnią się trzema bitami, więc ich odległość Hamminga jest równa 3.

Odległość Hamminga między dwoma słowami kodowymi ma istotne znaczenie
dla wykrywania błędów. Jeżeli dla dwóch różnych słów kodowych wynosi ona d,
to wystarczy d jednobitowych błędów, aby z jednego z nich zrobiło się drugie i
aby błąd pozostał niezauważony. W związku z tym, jeżeli chcemy tworzyć kod,
który zagwarantuje nam wykrycie wszystkich jednobitowych błędów, dla
wszystkich par słów kodowych odległość musi wynosić przynajmniej 2. Jeżeli
dane n-bitowe słowo nie zostanie rozpoznane jako dozwolone słowo kodowe,
będzie ono uznane za błędne.

W celu wyjaśnienia wykorzystanej koncepcji opracujemy kod, który może

posłużyć do wykrycia i skorygowania 1-bitowego błędu w słowach 8-

bitowych. Zaczniemy od określenia wymaganej długości kodu. Zgodnie z

ogólnym schematem działania kodów korekcyjnych (rys. 5.7) układy

porównujące otrzymują na wejściu dwie wartości k-bitowe. Porównanie jest

dokonywane przez bramki XOR. Otrzymany wynik nosi nazwę syndromu, a

każdy jego bit przyjmuje wartość 0 lub 1 w zależności od wyniku

porównania zgodności bitów na 2 wejściach.

Słowo syndrom ma więc k bitów i zakres wartości pomiędzy 0 a 2

k

-1.

Wartość 0 wskazuje, że nie został wykryty żaden błąd, natomiast wartości

2

k

-1 wskazują na zaistnienie błędu i jego lokalizację bitową. Ponieważ błąd

może wystąpić w dowolnym z m bitów danych lub k bitów kontrolnych musi

być spełniona nierówność 2

k

-1 >=m+k, określająca ilośc bitów

wymaganych do skorygowania błędu 1-bitowego w słowie zawierającym m

bitów danych.

W naszym przypadku k=4: bo

2

4

>8+4

- 8 bitów danych wymaga 4 bitów kontrolnych.

Chcemy aby utworzony prze nas 4-bitowy syndrom miał następujące
właściwości:



Jeżeli syndrom zawiera same 0 to znaczy że nie został wykryty żaden

błąd



Jeżeli syndrom zawiera jedną i tylko jedną 1, błąd wystąpił w jednym z

bitów kontrolnych – korekta nie jest potrzebna



Jeżeli syndrom zawiera więcej niż jedną 1, to wartość numeryczna

syndromu wskazuje pozycję błędnego bitu danych. Korekta polega na
zamianie wskazanego bitu

Aby uzyskać zamierzony efekt bity danych i bity kontrolne są aranżowane
jako słowa 12-bitowe. Pozycje bitowe są ponumerowane od 1 do 12. Bity
na pozycjach będących potęgą 2 są bitami kontrolnymi.

Pozycja

bitowa

12

11

10

9

8

7

6

5

4

3

2

1

Numer

pozycji

1100

1011

1010

1001

1000

0111

0110

0101

0100

0011

0010

0001

Bit

danych

D8

D7

D6

D5

 

D4

D3

D2

 

D1

 

 

Bit

kontrolny

 

 

 

 

C8

 

 

 

C4

 

C2

C1

Pozycj

a

bitowa

12

11

10

9

8

7

6

5

4

3

2

1

Numer

pozycji

1100 1011 1010 1001 1000 0111 0110 0101 0100 0011 0010 0001

Bit

danych

D8

D7

D6

D5

 

D4

D3

D2

 

D1

 

 

Bit

kontrol

ny

 

 

 

 

C8

 

 

 

 

C4

 

 

C2

C1

Słowo

zapisa

ne

0

0

1

1

0

1

0

0

1

1

1

1

Słowo

pobran

e

0

0

1

1

0

1

1

0

1

1

1

1

Bit

kontrol

ny

 

 

 

 

0

 

 

 

0

 

0

1

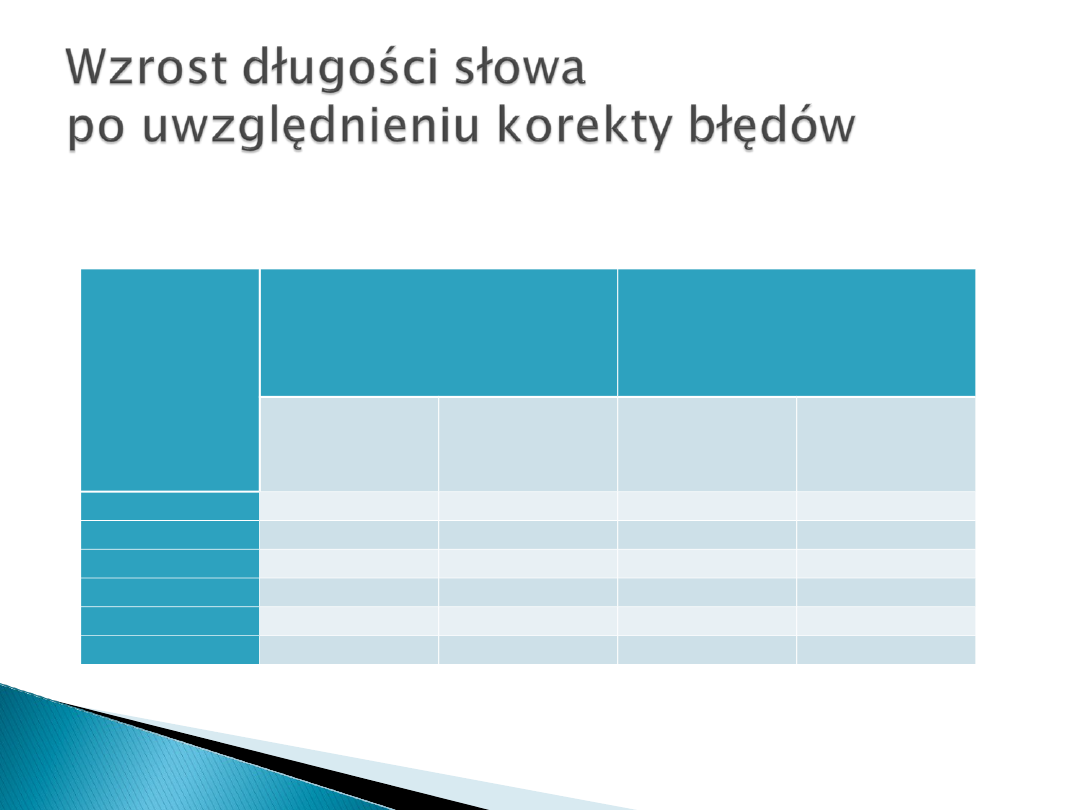
Tabela. Wzrost długości słowa po uwzględnieniu korekty błędów.

Liczba

bitów

danych

Poprawianie

pojedynczego błędu

Poprawianie

pojedynczego błędu

Wykrywanie błedu

podwójnego

Bity

kontrolne

% wzrostu

Bity

kontrolne

% wzrostu

8

4

50

5

62,5

16

5

31,25

6

37,5

32

6

18,75

7

21,875

64

7

10,94

8

12,5

128

8

6,25

9

7,03

256

9

3,52

10

3,91

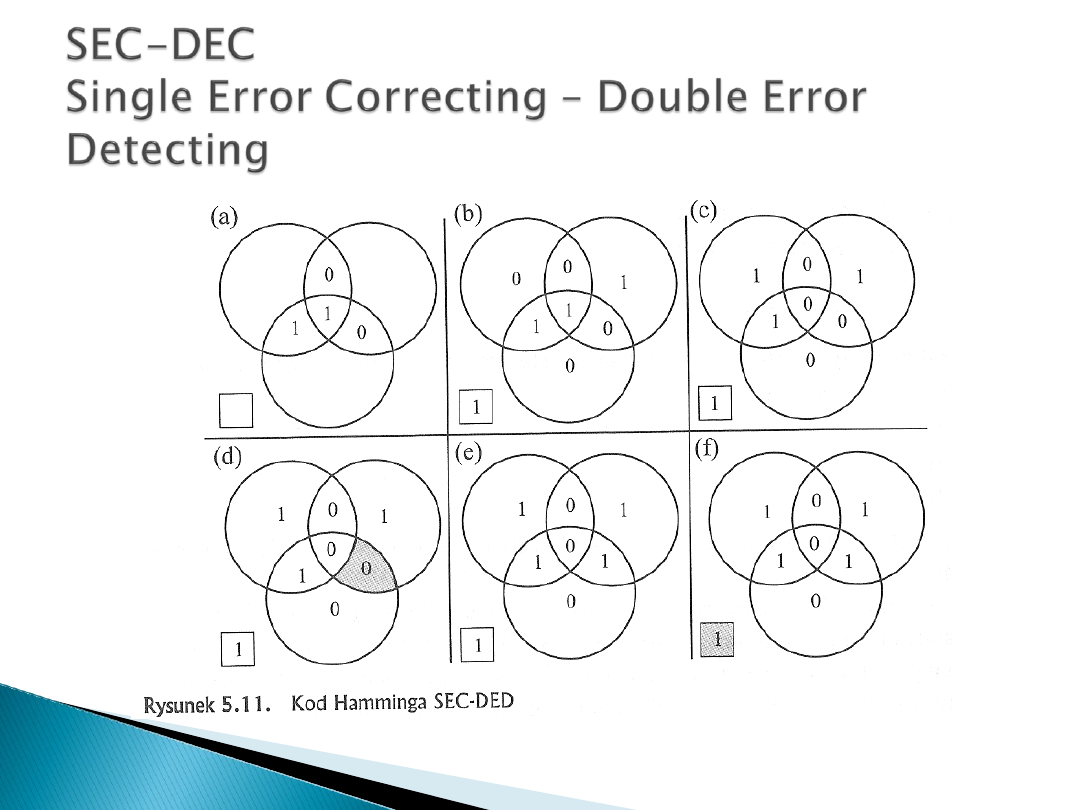
Kody Hamminga sprawdzają się w sytuacjach w których błędy występują stosunkowo

rzadko. We współczesnych dyskach twardych błąd pojawia się średnio raz na 100

milionów bitów a 3-bitowy kod Hemminga pozwoliłby na jego bezproblemowe usunięcie.

Jednakże kody te są bezużyteczne w sytuacji gdy istnieje prawdopodobieństwo, że

uszkodzonych będzie kilka kolejnych bitów (powstanie tzw. błąd sekwencyjny. Błędy te są

charakterystyczne dla przenośnych nośników pamięci, o których użytkonik nie dba tak

jak powinien. Gdy przewidujemy, że błędy będą występowały całymi blokami, należałoby

zastosować kod korekcji błędów, który operuje na poziomie bloków, nie zaś pojedynczych

bitów. Przykładem takiego kodu jest kod Reeda-Solomana (RS), który można traktować

tak, jak gdyby był on właśnie kodem CEC odnoszącym się do większej grupy znaków.

Kody RS, podobnie jak CRC, są symetryczne. Bity parzystości są doklejane do bloków

zawierających bity danych.

Kody RS (n,k) definiowane są za pomocą następujących parametrów:



S = liczba bitów w znaku (zwanym też symbolem)



K = liczba k-bitowych znaków składających się na blok danych



n = liczba bitów w słowie kodowym



RS (n,k) jest w stanie skorygować (n-k)/2 błędów w k bajtach informacji.

Najbardziej popularny kod RS (255,223) wykorzystuje więc 223 8-bitowe bajty informacji i

32 bajty kontrolne, które składają się na 255-bajtowe słowa kodowe. Jest on w stanie

skorygować do 16 błędnych bajtów występujących w danym bloku informacji.

BIBLIOGRAFIA



William Stallings, Orgaizacja i Architektura Systemu Komputerowego



Wikipedia



Inne źródła