Statystyka II-4
1
Testowanie hipotez statystycznych
(1)
• Drugim (obok teorii estymacji) ważnym działem
wnioskowania statystycznego jest testowanie
hipotez statystycznych, obejmu-jące zasady i
metody sprawdzania określonych przypuszczeń
(założeń), dotyczących parametrów lub postaci
rozkładu cech statystycznych populacji
generalnej na podstawie wyników z próby.
Hipotezą statystyczną nazywamy każdy sąd o
zbiorowości generalnej, wydany bez
przeprowadzenia badania całkowitego.
Prawdziwość hipotezy statystycznej orzeka się na
podstawie próby losowej.
• Hipotezy mogą być parametryczne, gdy dotyczą
wartości odpowiednich parametrów
statystycznych populacji generalnej, takich jak
wartość przeciętna, wariancja czy wskaźnik
struktury, lub nieparametryczne, gdy dotyczą np.
postaci rozkładu cechy statystycznej,
współzależności cech lub losowości próby.
Statystyka II-4
2
Testowanie hipotez statystycznych
(2)
• Hipotezą zerową H
0
nazywamy hipotezę sprawdzaną
(testowaną, weryfikowaną).
• Hipotezą alternatywną H
1
nazywamy hipotezę, którą
jesteśmy skłonni przyjąć, gdy odrzucamy hipotezę H
0
.
• Test statystyczny jest to reguła postępowania, która
przyporządkowuje wynikom próby losowej decyzję
przyjęcia lub odrzucenia hipotezy H
0
.
• Bląd I rodzaju polega na odrzuceniu hipotezy H
0
, mimo
że jest ona prawdziwa.
• Poziomem istotności nazywamy prawdopodobieństwo
popełnienia błędu I rodzaju. Wartości są bliskie zera i
na ogół są równe 0,01; 0,02; 0,05; 0,1.
• Bląd II rodzaju polega na przyjęciu hipotezy H
0
, gdy
jest ona fałszywa. Prawdopodobieństwo popełnienia
tego błędu oznacza się przez . Dobry test statystyczny
powinien mieć tę własność, że również powinno być
bliskie zera.
Statystyka II-4
3
Testowanie hipotez statystycznych
(3)
• W statystycznej kontroli jakości (SKJ) określane jest
często jako ryzyko producenta, zaś jako ryzyko
odbiorcy. Wartości i są wzajemnie powiązane i
zmniejszanie jednej z nich powoduje zwiększenie
drugiej.
• Pewnym kompromisem są tzw. testy istotności, które
dla zadanego z góry poziomu istotności a zapewniają
możliwie najmniejszą wartość prawdopodobieństwa .
• Sprawdzianem hipotezy nazywamy taką statystykę T
(o znanym rozkładzie), której wartość t
e
, policzona na
podstawie próby losowej, pozwala na podjecie decyzji,
czy odrzucić hipotezę H
0
. Dla hipotez parametrycznych
sprawdzianami są estymatory odpowiednich
parametrów, natomiast dla hipotez nieparametrycznych
rolę sprawdzianów pełnią mierniki rozbieżności między
rozkładem empirycznym a teoretycznym,
sformułowanym w hipotezie H
0
.
Statystyka II-4
4
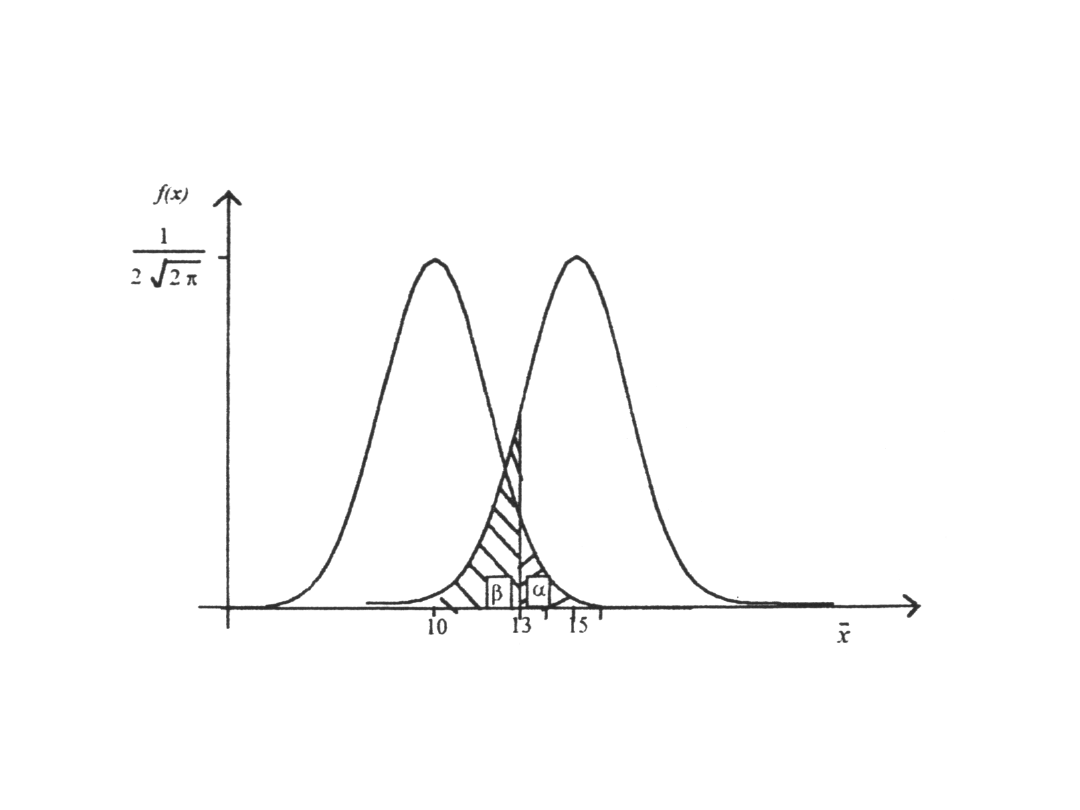
Testowanie hipotez statystycznych
(4)
Ilustracja graficzna wielkości i
Statystyka II-4
5
Testowanie hipotez statystycznych
(5)
• Zbiorem krytycznym Z nazywamy zbiór tych
wartości sprawdzianu hipotezy, które
przemawiają za odrzuceniem hipotezy H
0
.
• Zbiór Z może być w zależności od postaci
hipotezy alternatywnej zbiorem
jednostronnym (prawostronnym lub
lewostronnym) albo zbiorem dwustronnym.
Mówimy wtedy również, że test statystyczny
jest jednostronny (prawostronny, lewostronny)
lub dwustronny. Rozkład sprawdzianu
hipotezy określa, z jakich tablic należy
odczytać wartość krytyczną t
wyznaczającą
zbiór Z, a zatem zbiór Z zależy również od
liczebności próby n, od tego, czy znamy
parametry (m lub ) w zbiorowości generalnej
oraz od poziomu istotności .
Statystyka II-4
6
Testowanie hipotezy o wartości
przeciętnej (1)
• Konstrukcję testu statystycznego omówimy na
przykła-dzie. Zakłada się, że długość życia
opon ma rozkład
N(m,). Producent twierdzi, że wartość
przeciętna tej charakterystyki jest równa 50
tys. km. Na podstawie 100 losowo wybranych
opon otrzymano = 45 tys. km i
s = 8 tys. km. Czy na poziomie istotności
=0,05 można uważać, że producent ma
rację?
• 1
o
Sformułowanie hipotezy H
0
i H
1
W testach istotności hipoteza H
0
jest hipotezą
„o równoś-ci”. Hipoteza alternatywna H
1
może
być prostym zaprzeczeniem H
0
albo hipotezą
„o większości” lub „o mniejszości”. W tym
przypadku:
• H
0
: m = 50
H
1
: m 50
• W testach istotności wartość jest z góry
zadana
x
Statystyka II-4
7
Testowanie hipotezy o wartości
przeciętnej (2)
• 2
o
Zakładając, że długość życia opon ma
rozkład N(m,) wybór sprawdzianu hipotezy
zależy od liczebności próby n oraz od tego, czy
parametr w zbiorowości generalnej jest
znany: jeśli
• jest znane i n30 lub
• jest znane i n>30 lub
• jest nieznane i n>30, ale wówczas S
to sprawdzianem hipotezy H
0
jest statystyka:
o rozkładzie N(0,1).
• Gdy jest nieznane i n 30, to sprawdzianem
hipotezy jest
o rozkładzie Studenta z (n-1)
st.swobody
n
m
X
T
1
1
n
S
m
X
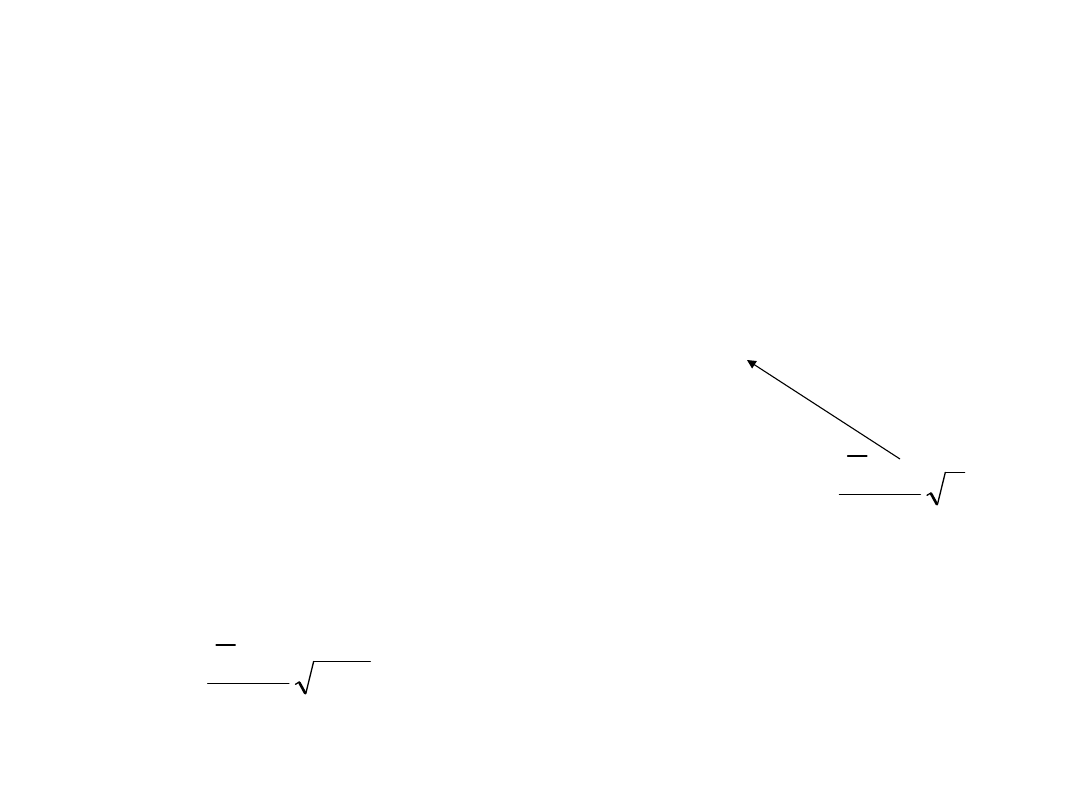
T
n
T
e
=(45-
50)/8·100=-6,25
Statystyka II-4
8
Testowanie hipotezy o wartości
przeciętnej (3)
• 3
o
Wyznaczanie zbioru krytycznego
Wartość krytyczną t
odczytujemy w danym
przykładzie z tablic funkcji (t) w ten sposób,
że przy zbiorze dwustron-nym (t
)=(1- )/2, a
przy jednostronnym (t
)=1/2- . Jeżeli relacja
wyznaczająca zbiór krytyczny jest spełniona,
czyli wartość t
wpada w zbiór krytyczny, to
hipotezę H
0
należy odrzucić. W przeciwnym
przypadku nie ma podstaw do odrzucenia H
0
.
W przypadku przyjęcia sprawdzianu hipotezy
T
n-1
wartość krytyczną t
odczytujemy z tablic
rozkładu Studenta dla n-1 stopni swobody i:
a)P(t
)= przy zbiorze jednostronnym;
b) P(t
)= 2 przy zbiorach dwustronnych. W
przykładzie H
1
: m 50, więc zbiór krytyczny
jest dwustronny.
Statystyka II-4
9
Testowanie hipotezy o wartości
przeciętnej (4)
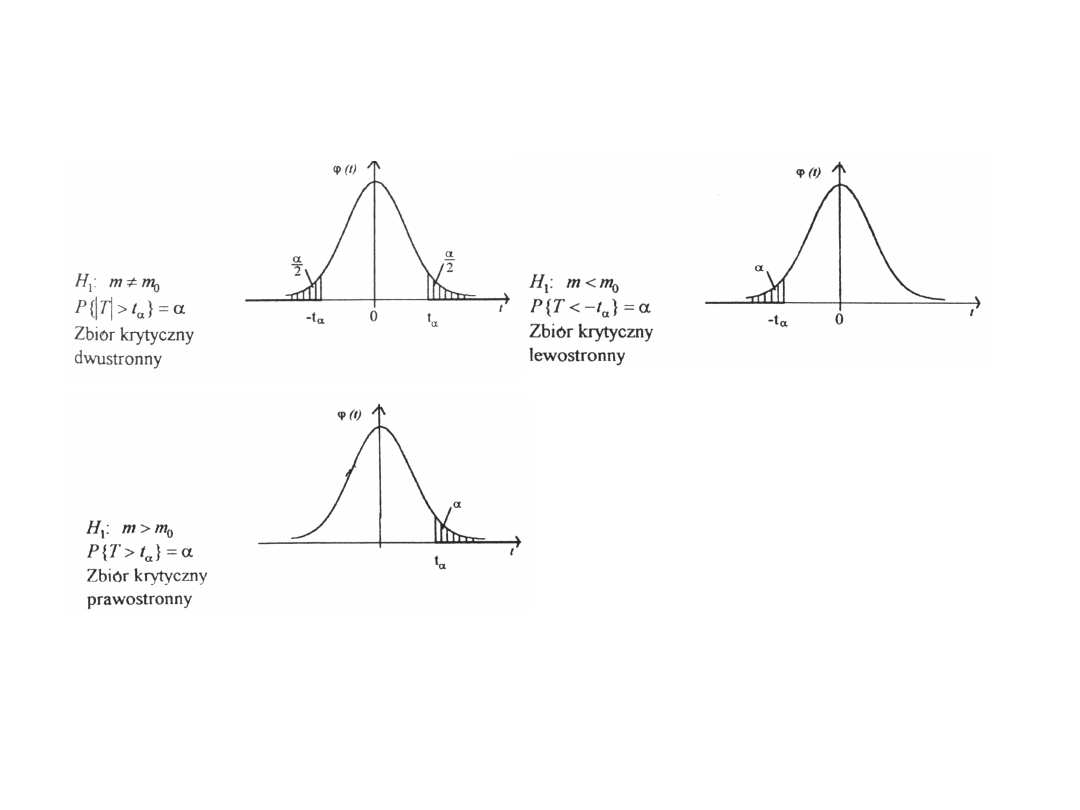
Zbiory krytyczne
w zależności od
postaci hipotezy
alternatywnej
Statystyka II-4
10
Testowanie hipotez
parametrycznych
• W przypadku testowania hipotezy H
0
: m = m
0
wobec
hipotezy alternatyw-nej postaci H
1
: m m
0
można
podejmować decyzję o odrzuceniu (lub nie) H
0
na
podstawie przedziału ufności wyznaczonego dla
parametru m na poziomie ufności l-.
Jeśli wartość m
0
wpada do przedziału ufności, to nie ma
podstaw do odrzucenia H
0
; jeśli nie, to H
0
należy odrzucić,
ponieważ zbiór leżący poza przedziałem ufności jest
zbiorem krytycznym.
• Korzystając z gotowych pakietów statystycznych, takich
jak np. „Statgra-phics", otrzymujemy wśród wyników, na
wydrukach, wartość określaną jako „P-value". Wartość ta
jest równa prawdopodobieństwu zajścia odpowiednich
zdarzeń: a) P
V
= P(T>t
e
) przy testach dwustronnych,
b) P
V
= P(T>t
e
) przy testach prawostronnych, c) P
v
=P(T<
-t
e
) przy testach lewostronnych, gdzie T — oznacza
sprawdzian hipotezy, t
e
— wartość sprawdzianu T
policzoną na podstawie wyników z próby. Jeśli wartość
obliczonego prawdopodobieństwa P jest nie większa od
zadanego poziomu istotności (P
v
), to hipotezę H
0
należy odrzucić na korzyść odpowiedniej hipotezy
alternatywnej. W przeciwnym wypadku, gdy
P
v
> , nie ma podstaw do odrzucenia H
0
.
Podsumowanie przykładu
• W rozpatrywanym przykładzie H
1
: m ≠ 50,
więc zbiór krytyczny jest dwustronny.
Sprawdzianem hipotezy jest
(t
) = (1 – 0,05)/2 = 0,95/2 = 0,475
stąd t
= 1,95
• W przykładzie wyznaczyliśmy wartość t
e
=
-6,25. Wynika stąd, że t
e
wpada w zbiór
krytyczny, należy zatem odrzucić hipotezę H
0
i
w konsekwencji przyjąć hipotezę alternatywną
H
1
. Zatem producent opon nie ma racji
twierdząc, że przeciętna długość życia opon
wynosi 50 tys. km.
Statystyka II-4
11
Podsumowanie
• W przypadku testowania hipotezy H
0
: m
≠ m
0
można podejmować decyzję o
odrzuceniu (lub nie) H
0
na podstawie
przedziału ufności wyznaczonego dla
parametru m na poziomie ufności 1 - .
Jeśli wartość m
0
wpada do przedziału
ufności, to nie ma podstaw do
odrzucenia H
0
; jeśli nie, to H
0
należy
odrzucić, ponieważ zbiór leżący poza
przedziałem ufności jest zbiorem
krytycznym.
Statystyka II-4
12
P-value
• Korzystając z gotowych pakietów statystycznych, np.
pakietu „Statistica”, na wydrukach wyników
otrzymujemy wartość określaną jako „P-value”. Wartość
ta jest równa prawdopodobieństwu zajścia odpowiednich
zdarzeń:
a) P
v
= P(|T| > t
e
) przy testach dwustronnych,
b) P
v
= P(T > t
e
) przy testach prawostronnych,
c) P
v
= P(T < -t
e
) przy testach lewostronnych,
gdzie T – oznacza sprawdzian hipotezy, t
e
–wartość
sprawdzianu T policzoną na podstawie wyników z próby.
Jeśli wartość obliczonego prawdopodobieństwa P jest
nie większa od zadanego poziomu istotności (P
v
≤ ),
to hipotezę H
0
należy odrzucić na korzyść odpowiedniej
hipotezy alternatywnej. W przeciwnym przypadku, gdy
P
v
> , nie ma podstaw do odrzucenia H
0
.
Statystyka II-4
13
Testowanie hipotezy o
równości dwóch wartości
przeciętnych
• Dane są dwie zbiorowości generalne o
rozkładach normalnych N(m
1
,
1
) i N(m
2
,
2
). Chcemy zweryfikować hipotezę H
0
:
m
1
= m
2
wobec hipotezy H
1
: m
1
≠ m
2
(lub
H
1
: m
1
< m
2
albo H
1
: m
1
> m
2
). Niech n
1
,
n
2
oznaczają wielkości prób prostych,
wylosowanych z każdej zbiorowości , a
oraz oznaczają
odpowiednio średnie arytmetyczne i
wariancje z prób.
Statystyka II-4
14
2
1
, X
X
2
)
2
(
2
)
1
(
S
i
S
Testowanie hipotezy o
równości dwóch wartości
przeciętnych (2)
• W zależności od założeń
dotyczących zbiorowości
generalnych oraz od liczebności
prób, sprawdzian hipotezy H
0
ma
różną postać i jest związany z
rozkładem normalnym lub
rozkładem Studenta.
Statystyka II-4
15
Testowanie hipotezy o
równości dwóch wartości
przeciętnych (3)
• Jeżeli
1
,
2
znane i n
1
≤ 30, n
2
≤ 30 lub
•
1
,
2
znane i n
1
> 30, n
2
> 30 lub
•
1
,
2
nieznane i n
1
> 30, n
2
> 30 i
przyjmujemy, że
, to
sprawdzian hipotezy ma postać:
Statystyka II-4
16
2
)
2
(
2
2
\
2
)
1
(
2
1
,
S
S
2
2
2
1
2
1
2
1
n
n
X
X
T
Rozkład statystyki przy
założeniu prawdziwości
H
0
, jest N(0, 1).
Testowanie hipotezy o równości
dwóch wartości przeciętnych (4)
• W przypadku, gdy s
1
, s
2
— nieznane, lecz s
1
=
s
2
i n
1
≤ 30, n
2
≤ 30, to korzystamy ze
sprawdzianu:
który, przy założeniu prawdziwości H
0
, ma
rozkład Studenta o (n
1
+ n
2
– 2) stopniach
swobody.
• Dalszy tok postępowania związanego z
testowaniem H
0
: m
1
= m
2
przebiega tak samo
jak przy testowaniu hipotezy o jednej średniej.
Statystyka II-4
17
Testowanie hipotezy o równości
dwóch wartości przeciętnych (5)
• Przykład. Stalowe obręcze produkowane są
na dwóch maszynach A i B. Kontroler jakości
uważa, że obręcze produkowane przez
maszynę A mają średnicę istotnie większą od
średnicy obręczy produkowanych przez
maszynę B. Zakładamy, że rozkłady średnic
obręczy dla maszyn A i B są: N(m
1
, s
1
) i N(m
1
,
s
2
) oraz że s
1
= s
2
. Sprawdzić, czy kontroler
jakości ma rację, jeśli dla 10 losowo
wybranych obręczy z maszyny A otrzymano
x
1
= 1,051 i s
1
2
= 0,000397 a dla 15 obręczy z
maszyny B mamy x
2
= 1,036 i s
2
2
= 0,00021.
Poziom istotności a = 0,01.
Statystyka II-4
18
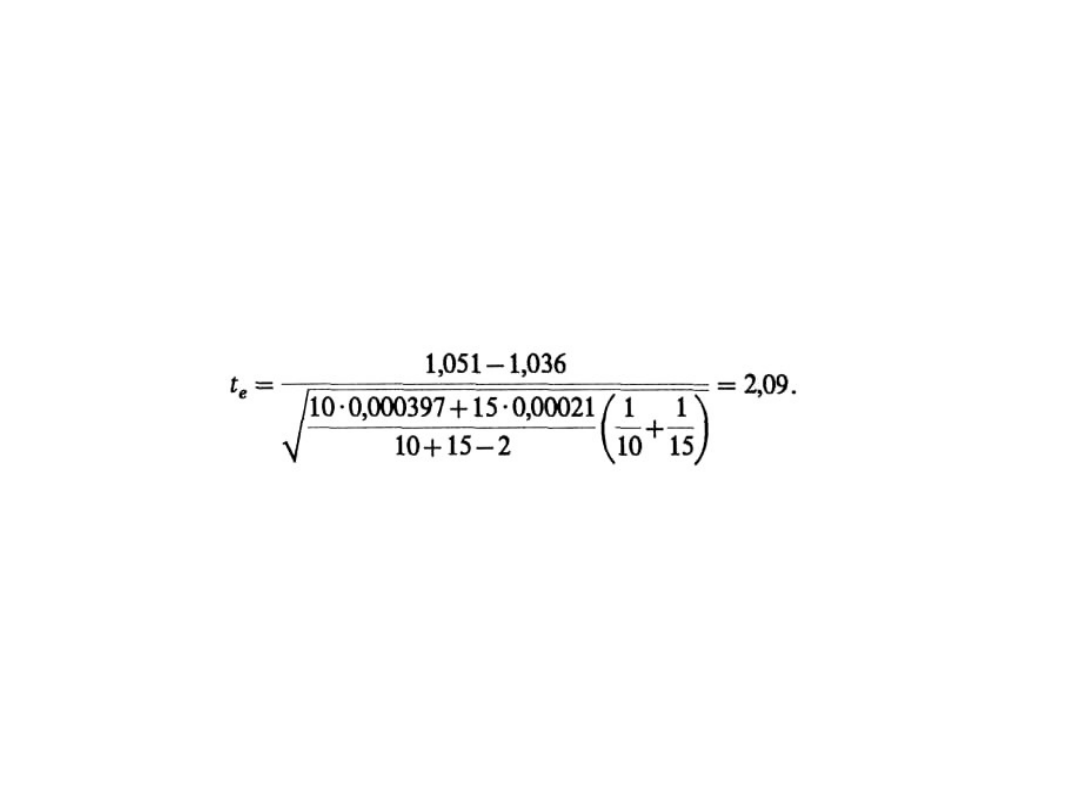
Etapy konstrukcji testu
statystycznego
• H
0
: m
l
= m
2
, H
1
: m
1
>m
2
, a = 0,01.
• Ponieważ s
1
, s
2
— nieznane, a n
1
= 10 < 30 i n
2
= 15 < 30, to sprawdzian hipotezy ma postać:
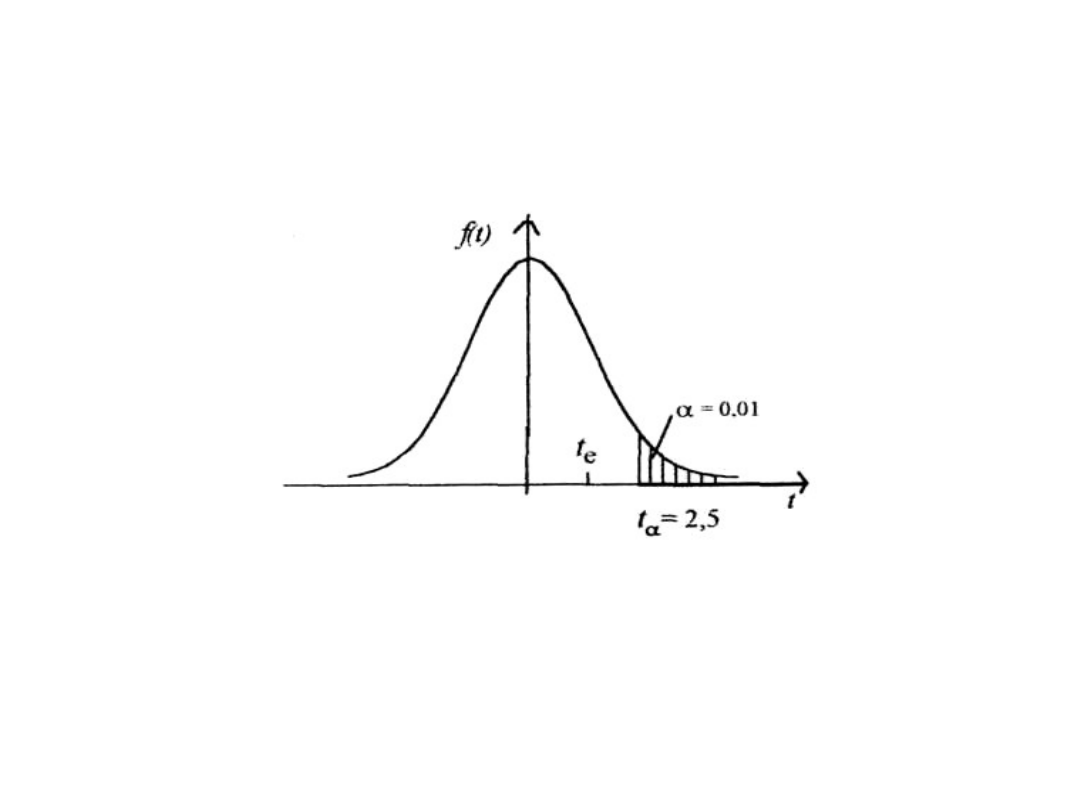
• T ma rozkład Studenta o 23 stopniach
swobody i H
1
: m
1
> m
2
zbiór krytyczny jest
prawostronny i t
a
odczytujemy dla P (t
a
) = 2∙a
= 2∙0,01 = 0,02 i 23 stopni swobody z tablic
rozkładu Studenta, zatem t
a
= 2,5. Rysunek na
następnym slajdzie przedstawia zbiór
krytyczny i wartość t
e
.
Statystyka II-4
19
Etapy konstrukcji testu
statystycznego
Statystyka II-4
20
Otrzymaliśmy t
e
< t
a
, czyli nie ma podstaw do
odrzucenia H
0
, więc kontroler jakości nie ma
racji twierdząc, że obręcze produkowane przez
maszynę A mają średnicę istotnie większą niż
obręcze produkowane przez maszynę B.
Testowanie hipotezy o wskaźniku
struktury
• Niech populacja generalna ma rozkład dwupunktowy z
parametrem p oznaczającym prawdopodobieństwo, że badana
cecha przyjmie wyróżnioną wartość. Chcemy zweryfikować na
podstawie n-elementowej próby (n ≥ 100) hipotezę zerową
H
0
: p = p
0
.
• Hipoteza alternatywna może przyjmować jedną z
następujących postaci:
H
1
: p ≠ p
0
, H
1
: p < p
0
, lub H
1
: p > p
0
,
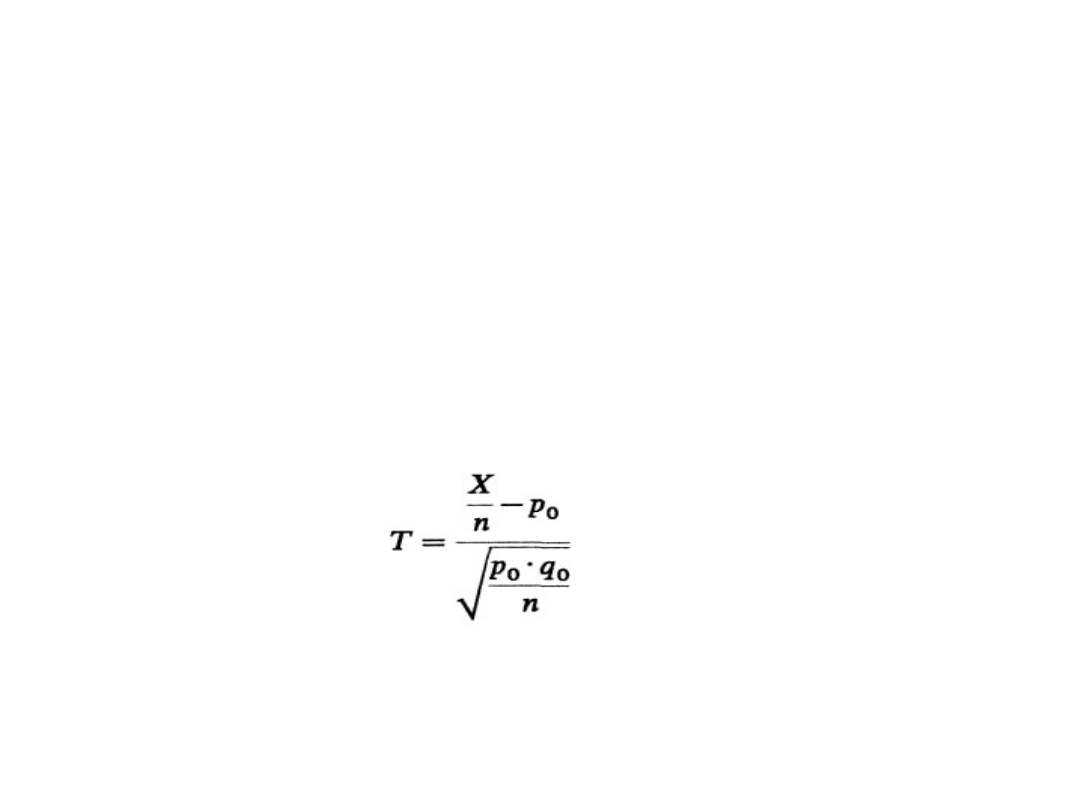
• Sprawdzianem hipotezy H
0
: p = p
0
jest statystyka:
Statystyka II-4
21
która przy prawdziwości H
0
ma w przybliżeniu rozkład N(0, 1),
przy czym X oznacza ilość jednostek o wyróżnionej wartości
cechy w n-elementowej próbie.
Testowanie hipotezy o wskaźniku
struktury (2)
• Przykład: Firma zatrudniająca około
2000 pracowników ma zamiar budować
parking, ponieważ przypuszcza się, że
ponad 60% pracowników przyjeżdża do
pracy samochodem. Sprawdzić, czy
przypuszczenie jest prawdziwe, jeśli
spośród 250 losowo wybranych osób
206 przyjeżdża do pracy swoim
samochodem. Poziom istotności a =
0,02.
Statystyka II-4
22
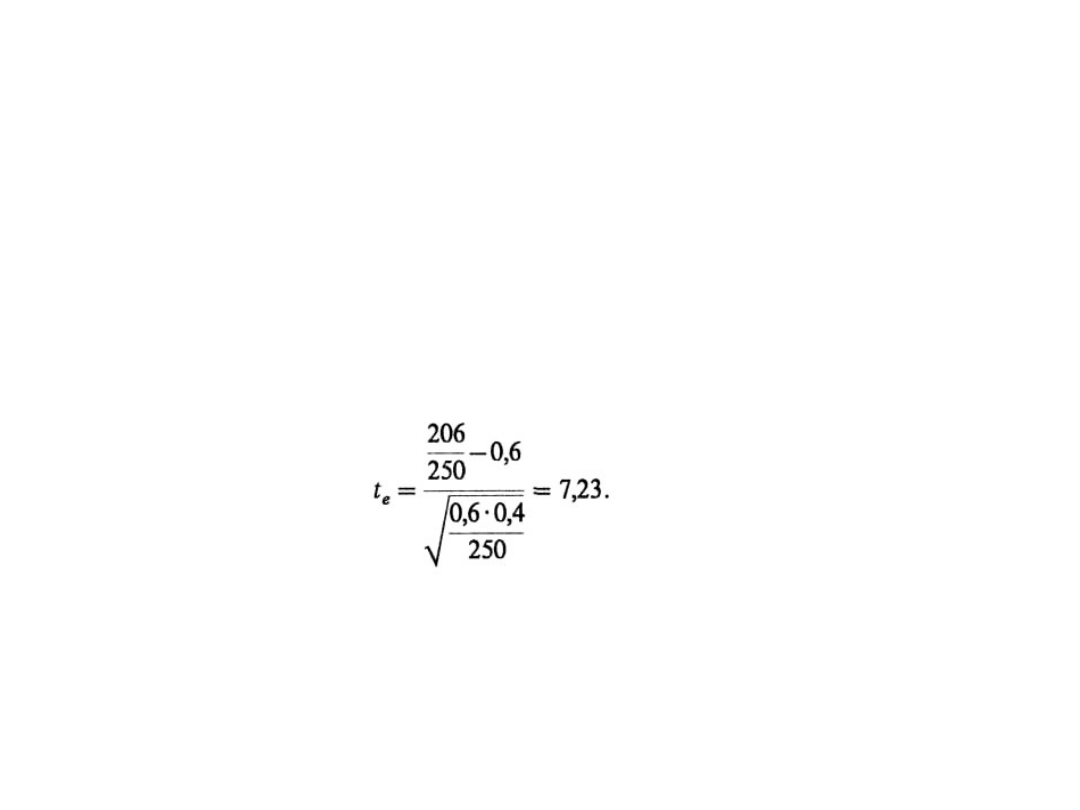
Testowanie hipotezy o wskaźniku
struktury (3)
• Test statystyczny jest następujący:
• H
0
: p = 0,6, H
1
: p> 0,6, a = 0,02,
• X określa ilość osób przyjeżdżających do pracy swoim
samochodem wśród 250 wylosowanych osób, czyli x =
206.
• Sprawdzianem hipotezy H
0
: p = p
0
dla wskaźnika
struktury jest statystyka:
Statystyka II-4
23
T – N(0, 1). Z uwagi na to, że H
1
: p > 0,6, zbiór krytyczny jest
prawostronny i t
a
znajdujemy z warunku F(t
a
) = 1/2 – 0,02 = 0,48,
więc t
a
= 2,05. Ponieważ t
e
> t
a
, zatem należy odrzucić H
0
na
korzyść H
1
, czyli przypuszczenie, że ponad 60% pracowników
przyjeżdża swoim samochodem, można uznać za prawdziwe.
Testowanie hipotezy o dwóch
wskaźnikach struktury
• Zakładamy, że badana cecha ma w dwóch populacjach
rozkład dwupunktowy z parametrami p
1
i p
2
. Należy
zweryfikować hipotezę H
0
: p
1
= p
2
. Hipoteza
alternatywna może mieć postać H
1
: p
1
≠ p
2
lub H
1
: p
1
>
p
2
lub H
1
: p
1
< p
2
.
• Z obu populacji losujemy próby proste o liczebności n
1
i
n
2
, przy czym obydwie próby muszą być duże, tzn. n
1
≥
100 i n
2
≥ 100. Niech X
1
/n
1
i X
2
/n
2
oznaczają wskaźniki
struktury z pierwszej i drugiej próby. Sprawdzianem
hipotezy H
0
: p
1
= p
2
jest statystyka:
Statystyka II-4
24
Testowanie hipotezy o dwóch
wskaźnikach struktury (2)
• Statystyka ta, przy założeniu prawdziwości
hipotezy H
0
, ma rozkład zbliżony do N(0, 1).
Sposób weryfikacji hipotezy będzie więc
identyczny jak w przypadku hipotezy o jednej
średniej.
• Przykład: Panuje przekonanie, że studenci
stacjonarni pewnej uczelni zdają lepiej egzamin ze
statystyki niż studenci zaoczni. Wylosowano w tym
celu grupę 100 osób na studiach stacjonarnych i
okazało się, że wśród nich 35 uzyskało ocenę
przynajmniej dobrą. Wśród 100 osób
wylosowanych z grupy studentów zaocznych
podobną ocenę uzyskało 16 osób. Czy rzeczywiście
studenci stacjonarni zdają lepiej egzamin ze
statystyki niż studenci zaoczni? Poziom istotności
a = 0,05.
Statystyka II-4
25
Etapy budowy testu
statystycznego
• W zadaniu interesuje nas procent studentów,
którzy na egzaminie uzyskali ocenę
przynajmniej dobrą. Chcemy zweryfikować
hipotezę:
H
0
: p
1
= p
2
przeciwko H
l
: p
1
> p
2
,
przy czym indeks 1 odpowiada zbiorowości
studentów stacjonarnych, 2 zaś zbiorowości
studentów zaocznych.
• Z danych w zadaniu otrzymujemy:
Statystyka II-4
26
Etapy budowy testu
statystycznego (2)
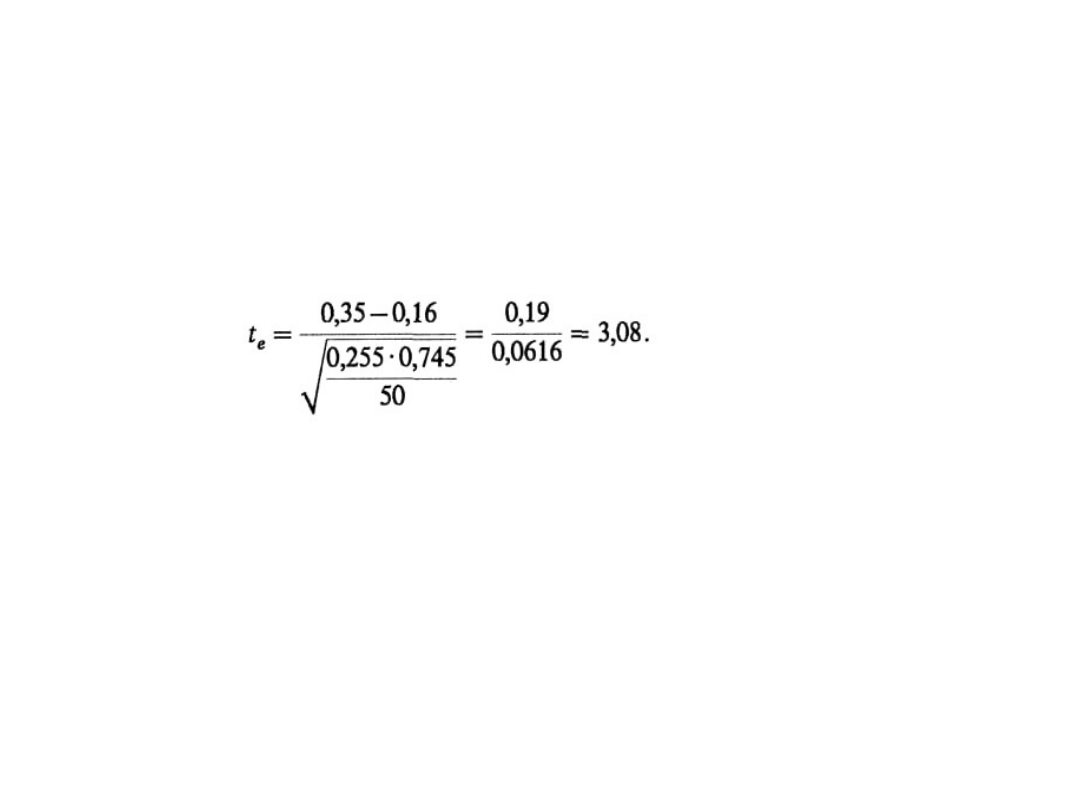
• Znajdujemy wartość t
e
sprawdzianu hipotezy:
Statystyka II-4
27
Ponieważ H
1
: p
1
> p
2
, więc zbiór krytyczny jest
prawostronny i t
a
spełnia równość F(t
a
) = 1/2 –
a = 0,45. Stąd t
a
= 1,65.
Otrzymaliśmy t
e
> t
a
, odrzucamy więc H
0
: p
1
=
p
2
na korzyść H
1
. Mamy zatem prawo sądzić,
że studenci stacjonarni zdają egzamin ze
statystyki lepiej niż studenci zaoczni.
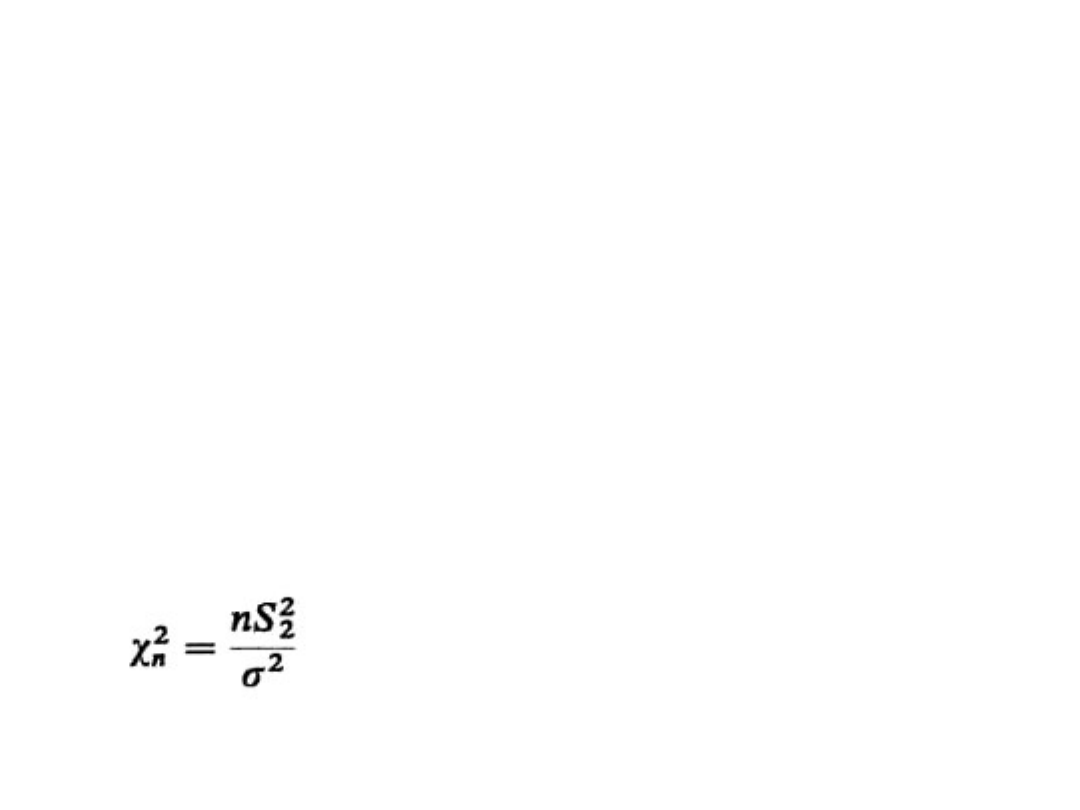
Testowanie hipotezy o
wariancji
• Niech cecha X ma w zbiorowości generalnej
rozkład N(m, s). Należy zweryfikować hipotezę
H
0
: s
2
= s
0
2
przeciwko
H
1
: s
2
> s
0
2
.
• Taką hipotezę alternatywną przyjmuje się
najczęściej, gdyż zwykle sytuacja, gdy wariancja
cechy w zbiorowości jest duża, jest niekorzystna.
• Jeśli m jest znane, to sprawdzian hipotezy H
0
ma
postać:
Statystyka II-4
28
Przy założeniu prawdziwości H
0
statystyka ta ma rozkład
2
o n
stopniach swobody.
Testowanie hipotezy o
wariancji (2)
• Jeśli m jest nieznane, sprawdzianem hipotezy
H
0
jest:
Statystyka II-4
29
lub
Obydwie te statystyki mają rozkład
2
o (n - 1)
stopniach swobody. Z uwagi na postać H
1
relacja P
= P(
2
>
a
2
) = a wyznacza prawostronny zbiór
krytyczny, gdzie jest wartością krytyczną
odczytaną z tablic rozkładu
2
dla odpowiedniej
liczby stopni swobody i P = a.
Jeśli dla danej próby losowej relacja wyznaczająca
zbiór krytyczny jest spełniona, to H
0
należy
odrzucić na korzyść H
1
.
Testowanie hipotezy o
wariancji (3)
• Przykład: W zakładzie A otrzymano
następujące informacje o 16 pracownikach:
Statystyka II-4
30
Wiek pracowników
20-24
24-28
28-32
32-36
Liczba pracowników
4
6
4
2
Zakładając, że wiek ma rozkład N(m, s) –
czy można uważać, że wariancja wieku
jest większa niż 10, na poziomie istotności
a = 0,05?
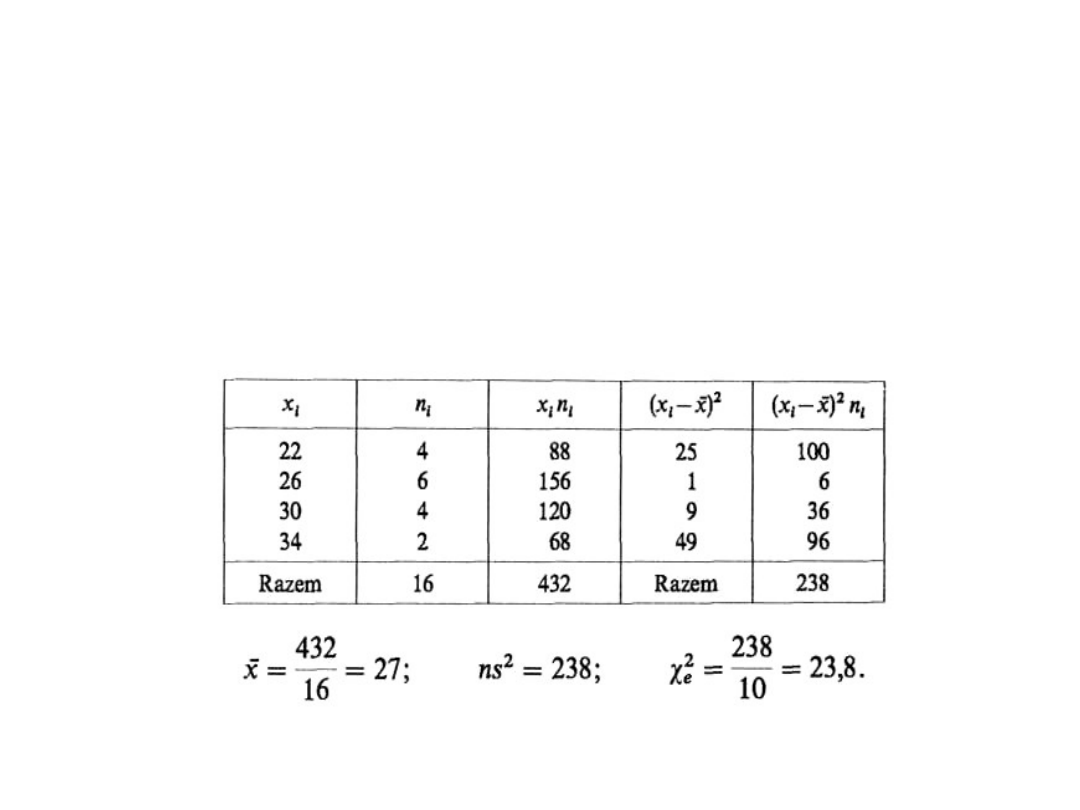
Testowanie hipotezy o
wariancji (4)
• H
0
: s
2
= 10, H
1
: s
2
> 10, a = 0,05.
• m jest nieznane, więc obliczamy s
2
Statystyka II-4
31
Testowanie hipotezy o
wariancji (5)
• Z tablic rozkładu
2
dla 15 stopni
swobody i P = =a = 0,05 otrzymujemy
a
2
= 24,996.
• Ponieważ
e
2
= 23,8 < 24,996 =
a
2
,
więc relacja wyznaczająca zbiór
krytyczny nie jest spełniona, tzn. nie ma
podstaw do odrzucenia hipotezy H
0
. Nie
można zatem twierdzić, że wariancja
wieku jest większa niż 10.
• Opisany powyżej test stosuje się, gdy
liczebność próby jest n ≤ 30.
Statystyka II-4
32
Testowanie hipotezy o
wariancji (6)
• Jeśli n > 30, sprawdzian hipotezy przyjmuje
jedną z poniższych postaci:
– jeśli m jest znane w zbiorowości generalnej, to:
Statystyka II-4
33
- jeśli m jest nieznane, wówczas:
Statystyka T ma rozkład zbliżony do N(0, 1), zatem
dalsze postępowanie jest identyczne jak w opisanych
wyżej testach istotności wykorzystujących statystyki o
rozkładzie N(0, 1).
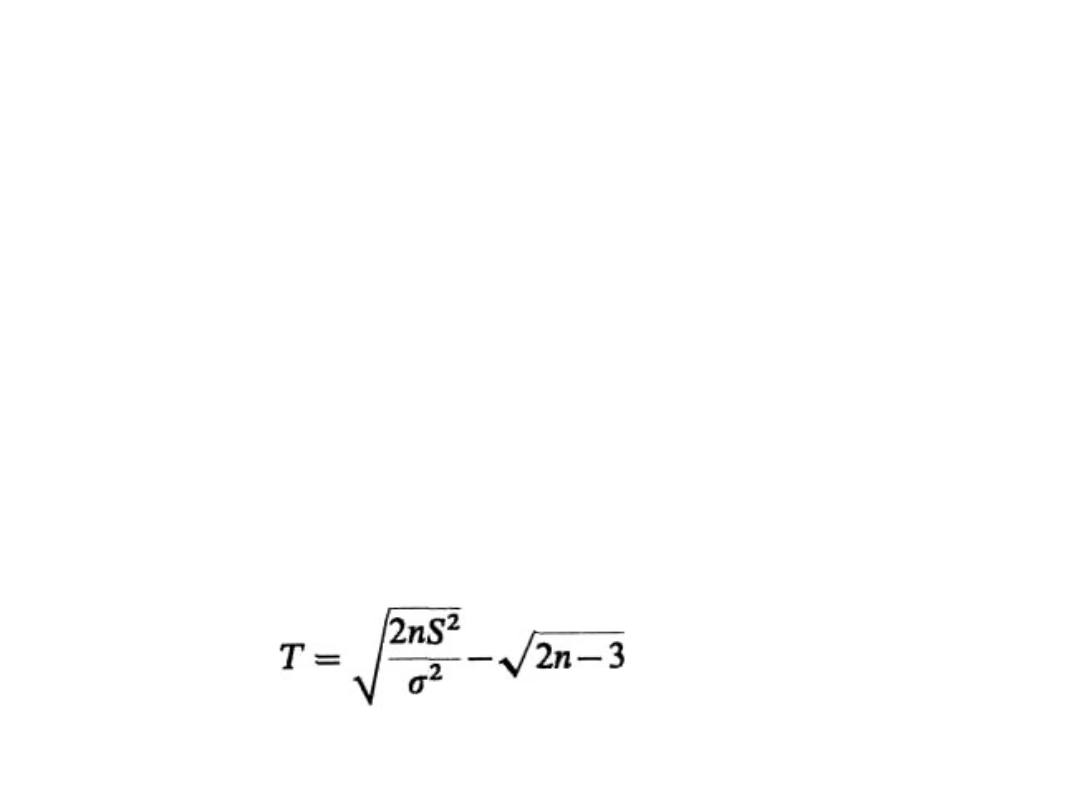
Testowanie hipotezy o
wariancji (7)
• Przykład: Zweryfikować hipotezę, że wariancja
wieku pracowników pewnego zakładu jest
większa niż 16, jeśli na podstawie 100-
elementowej próby pracowników otrzymano
odchylenie standardowe wieku równe 5 lat (a =
0,05).
• Etapy budowy testu są następujące:
1. H
0
:s
2
= 16, H
1
: s
2
> 16, a = 0,05.
2. Ponieważ n > 30 i m jest nieznane,
korzystamy ze sprawdzianu hipotezy postaci
Statystyka II-4
34
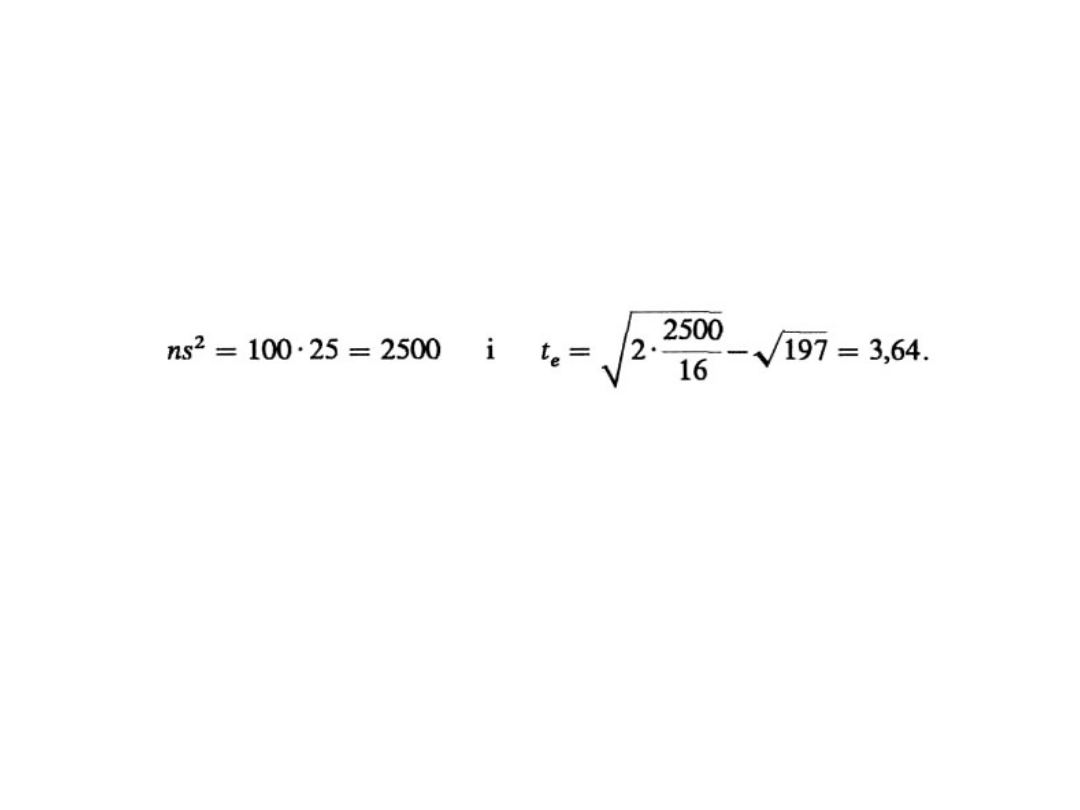
Testowanie hipotezy o
wariancji (8)
• Obliczamy:
Statystyka II-4
35
3. Zbiór krytyczny jest prawostronny, zatem
t
a
odczytujemy dla F(t
a
= 1/2 – a = 0,45, t
a
=
1,65. Relacja t
e
= 3,64 > t
a
= 1,65 jest
spełniona, więc należy odrzucić H
0
, na
poziomie istotności 0,05 można zatem
uważać, że wariancja wieku jest większa niż
16.
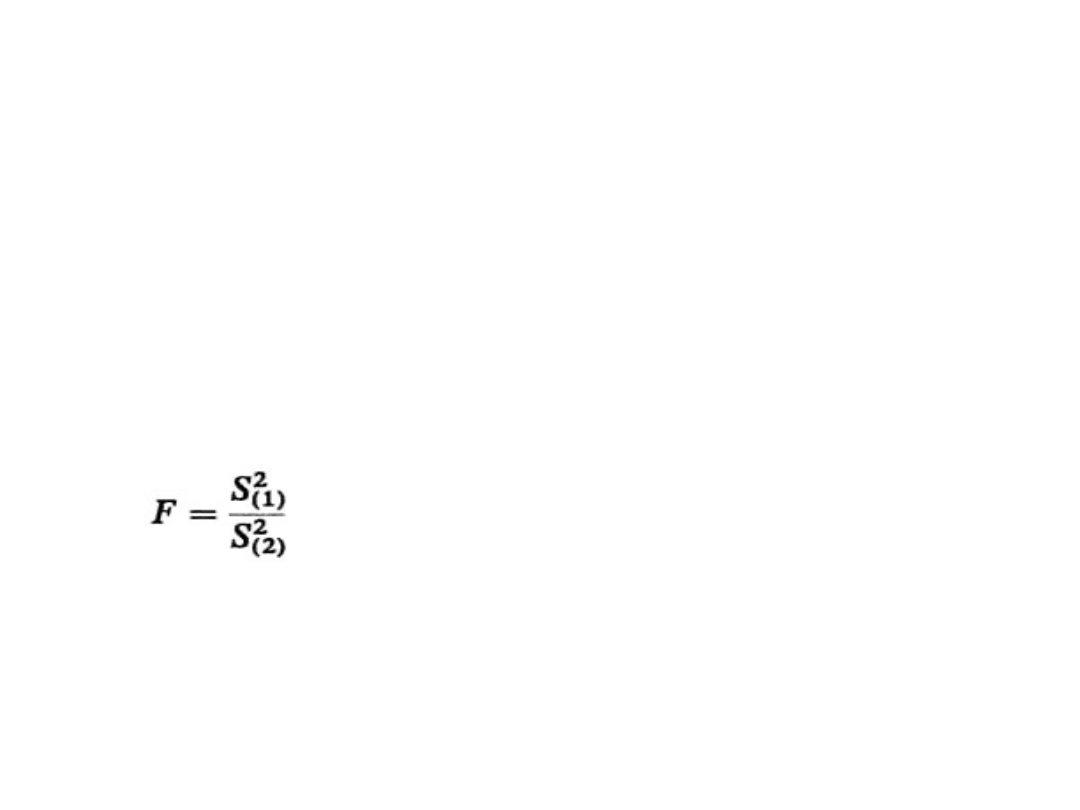
Testowanie hipotezy o dwóch
wariancjach
Statystyka II-4
36
Badamy dwie zbiorowości o rozkładzie normalnym N(m
1
,
s
1
) i N(m
2
, s
2
). Należy zweryfikować hipotezę:
H
0
: s
1
2
= s
2
2
przy H
1
: s
1
2
> s
2
2
.
Z obydwu populacji losuje się próby proste o liczebności n
1
i n
2
. Niech S
(1)
2
i S
(2)
2
oznaczają wariancję S
1
2
obliczoną dla
każdej z prób. Ze względu na postać hipotezy H
1
tak
numerujemy zbiorowości, aby S
(1)
2
> S
(2)
2
.
Sprawdzianem hipotezy jest statystyka:
o wartości empirycznej F
e
.
Statystyka ta ma rozkład F-Snedecora o r
1
= (n
1
– 1)
i r
2
= (n
2
– 1) stopniach swobody.
Testowanie hipotezy o dwóch
wariancjach (2)
Statystyka II-4
37
Relacja wyznaczająca prawostronny zbiór
krytyczny jest postaci:
P(F > F
a
) = a,
gdzie F
a
— odczytujemy z tablic rozkładu F-
Snedecora dla r
1
i r
2
stopni swobody.
Jeśli relacja ta jest spełniona, należy H
0
odrzucić, w przeciwnym wypadku nie ma
podstaw do odrzucenia H
0
.
Przedstawiony powyżej test wykorzystuje się
najczęściej do sprawdzenia prawdziwości
założenia, że s
1
= s
2
, które jest konieczne, aby
można było testować hipotezę o równości
wartości przeciętnych w dwóch populacjach,
gdy n
1
≤ 30,
n
2
≤ 30, s
1
i s
2
zaś — nieznane.
Testowanie hipotezy o dwóch
wariancjach (3)
Statystyka II-4
38
Uwagi:
• Jeśli w zadaniach dane są wartości wariancji
S
2
, to wartości S
1
2
, z których korzystamy w
omawianym teście, wyznacza się z równości
• Jeśli w tablicy zawierającej wartości rokładu
F-Snedecora brakuje wartości dla pewnej
liczby stopni swobody r
1
lub r
2
, to odczytujemy
je dla najbliższej liczby stopni swobody, np. gdy
r
1
= 19, to odczytujemy dla r
1
= 20 (lub 18).
Testowanie hipotezy o dwóch
wariancjach (4)
Statystyka II-4
39
Przykład: W dwóch firmach przewozowych
badano odległości przejazdów i otrzymano:
dla firmy A: wielkość próby — 15 przewozów i
odchylenie standardowe z próby — 158 km,
dla firmy B: wielkość próby — 10 przewozów i
odchylenie standardowe w tej próbie 283 km.
Czy można na poziomie istotności a = 0,05
uważać, że wariancje odległości przewozów w
obu firmach są takie same?
Testowanie hipotezy o dwóch
wariancjach (5)
Statystyka II-4
40
Test statystyczny jest następujący:
1. H
0
: s
1
= s
2
, H
1
: s
1
> s
2
, a = 0,05.
2. Oznaczamy:
n
1
= 10 i s
(1)
2
= (283)
2
= 80089
n
2
= 15 i s
(2)
2
= (158)
2
= 24964
i otrzymujemy:
Z tablic rozkładu Snedecora dla P = 0,05 oraz
r
1
= 9 i
r
2
= 14 otrzymujemy F
a
= 2,65. Ponieważ F
e
>
F
a
, odrzucamy hipotezę H
0
, że wariancja
odległości przewozów w obu firmach jest
jednakowa.
Statystyka II-4
41
Hipotezy nieparametryczne (1)
• Nieparametryczne testy istotności dzielimy na trzy
zasadnicze grupy: testy zgodności, testy
niezależności oraz testy losowości próby. Testy
nieparametryczne, w przeciwieństwie do testów
parametrycznych, mają tę zaletę, że nie wymagają
założeń w odniesieniu do postaci rozkładu cechy w
zbiorowości generalnej.
• Do najczęściej stosowanych testów nieparametrycznych
należy test zgodności chi-kwadrat (
2
). Test zgodności
2
służy do weryfikowania hipotezy, że obserwowana
cecha X w zbiorowości generalnej ma określony typ
rozkładu, np. dwumianowy, Poissona, normalny itd.
Poniżej podajemy kilka sposobów formułowania takiej
hipotezy:
a. H
0
: cecha X ma rozkład określony dystrybuantą F(x)
= F
0
(x).
b. H
0
: cecha X ma rozkład N(m,).
c. H
0
: cecha X ma rozkład N (100, 5).
d. H
0
: cecha X ma rozkład Poissona.
e. H
0
: cecha X ma rozkład Poissona z parametrem m =
2.
Statystyka II-4
42
Hipotezy nieparametryczne (2)
• W celu jednoznacznego określenia rozkładu
teoretycznego (hipote-tycznego) w danej ich klasie
niejednokrotnie należy najpierw na pod-stawie próby
oszacować odpowiednie parametry. Dla zweryfikowania
hipotezy przedstawionej w b) należy oszacować m i w
d) parametr m; w c) i e) parametry są podane. W
omawianych przykładach hipoteza alternatywna jest
prostym zaprzeczeniem hipotezy zerowej. Test
zgodności
2
można stosować, jeśli:
1° dane pochodzą z dużej n-elementowej próby
wylosowanej w sposób niezależny,
2° dane są przedstawione w postaci szeregu
rozdzielczego o r przedziałach klasowych, o
liczebnościach przedziałów n
1
, n
2
,..., n
r
spełniających
warunek n
1
+ n
2
+...+ n
r
= n. Na ogół przyjmuje się, że
n
j
5, j = l, 2,..., r,
3° rozkład hipotetyczny (sprecyzowany w H
0
) może być
zarówno rozkładem typu ciągłego, jak i skokowego.
Statystyka II-4
43
Hipotezy nieparametryczne (3)
• Sprawdzianem hipotezy H
0
jest statystyka
• Statystyka ta ma, przy założeniu prawdziwości hipotezy H
0
,
rozkład
2
o k = (r-s-1) stopniach swobody, przy czym s
oznacza liczbę parametrów, które należy wstępnie
wyznaczyć na podstawie próby; r — liczbę przedziałów
klasowych.
• We wzorze (*) p
i
oznacza prawdopodobieństwo, że cecha X
przyjmuje wartość należącą do i-tego przedziału klasowego
(gdy rozkład cechy jest zgodny z H
0
), np
i
, zaś oznacza liczbę
jednostek, które powinny znaleźć się w i-tym przedziale,
przy założeniu, że cecha ma rozkład zgodny z
hipotetycznym. Określa się je jako liczebności teoretyczne.
Wartość empiryczną statystyki (*) oznaczamy przez
e
2
.
Statystyka
2
jest miarą rozbieżności między rozkładem
empirycznym a teoretycznym, a zatem zbyt duże wartości
2
powodują odrzucenie H
0
. Z tego względu relacja
wyznaczająca zbiór krytyczny ma postać
gdzie
2
oznacza wartość krytyczną odczytaną z tablic
dla k = r – s – 1 stopni swobody i P = a.
(*)
1
2
2
r
i
i
i
i
np
np
n
2
2
P
Statystyka II-4
44
Test zgodności -Kołmogorowa (1)
• Test służy do weryfikowania hipotezy, że cecha
X ma w zbiorowości generalnej określony
rozkład typu ciągłego; najczęsciej jest to
rozkład normalny. Warunki dotyczące danych
z próby są takie same, jak w teście
2
.
Hipotezy H
0
i H
1
formułuje się następująco:
H
0
: F(x) = F
0
(x)
H
1
: F(x) F
0
(x)
Sprawdzian hipotezy ma postać:
F(x) oznacza dystrybuantę hipotetyczną
(teoretyczną), a F*(x) – dystrybuantę
empiryczną.
)
(
*
)
(
sup
x
F
x
F
D
D
n
x
n
n
Statystyka II-4
45
Test zgodności -Kołmogorowa (2)
• Wartość dystrybuanty empirycznej dla danego
x oblicza się z zależności: F*(x)=n
isk
/n, w
której n
isk
jest skumulowaną liczebnością,
odpowiadającą wartościom cechy nie
większym od x.
• Statystyka przy założeniu prawdziwości H
0
ma asymptotyczny rozkład - Kołmogorowa. Z
uwagi na fakt, iż D
n
mierzy rozbieżność
między dystrybuantą teoretyczną i
empiryczną, zbiór krytyczny będą tworzyły
tylko zbyt duże wartości , tak więc będzie to
zbiór prawostronny określony równością:
odczytuje się z tablic, przy czym Q(
) =
P
Test zgodności -Kołmogorowa
(3)
• Przykład: Producent proszku do prania uważa,
że rozkład wagi pudełka proszku jest N(m, s).
Na podstawie 150 wylosowanych niezależnie
do próby pudełek otrzymano:
• Na poziomie istotności a = 0,05 należy
zweryfikować hipotezę o prawdziwości
przekonania producenta.
• H
0
: X — waga proszku w pudełku ma rozkład
N(m, s) wobec hipotezy:
• H
1
: X — ma rozkład różny od rozkładu N(m, s).
Statystyka II-4
46
Waga
pudełka [g]
575-585
585-
595
595-
605
605-
615
615-
625
Liczba pudełek
16
34
50
38
12
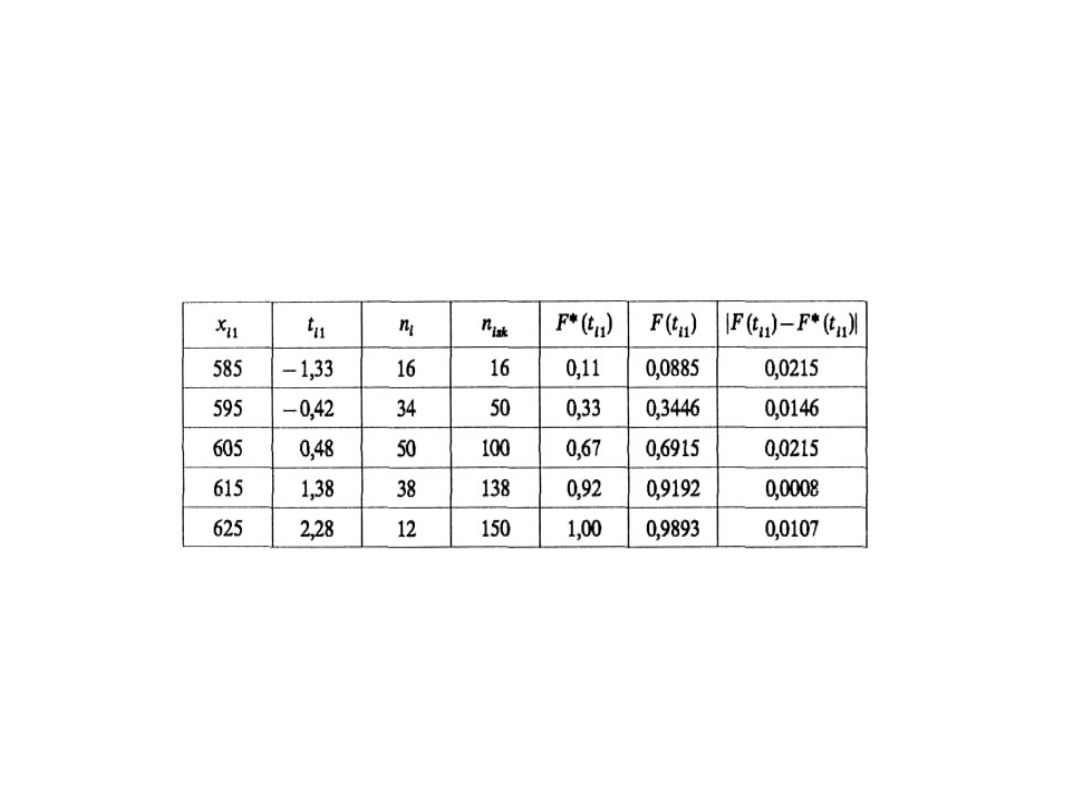
Test zgodności -Kołmogorowa
(4)
• Obliczenia pomocnicze związane z
wyznaczeniem statystyki l przedstawiono w
tabeli.
Statystyka II-4
47
Otrzymaliśmy więc D
n
= 0,0215 i l
e
= 150∙
0,0215 = 0,263.
Z tablicy rozkładu l dla Q(l
a
) = 1 – 0,05 = 0,95
odczytujemy
l
a
= 1,36. l
e
< l
a
, nie ma zatem podstaw do
odrzucenia hipotezy H
0
, że rozkład wagi pudełka
proszku jest N(m, s).
Test zgodności Kołmogorowa-
Smirnowa
• Test służy do weryfikacji hipotezy, że
dwie populacje mają jednakowy
rozkład, co jest równoważne ze
stwierdzeniem, że dwie próby pochodzą
z tej samej populacji. Badamy dwie
populacje, w których cecha ma rozkład
ciągły opisany odpowiednio
dystrybuantami F
l
(x) i F
2
(x). Hipotezy
H
0
i H
1
mają postać
• H
0
: F
1
(x) = F
2
(x),
• H
1
: F
1
(x) ≠ F
2
(x).
Statystyka II-4
48
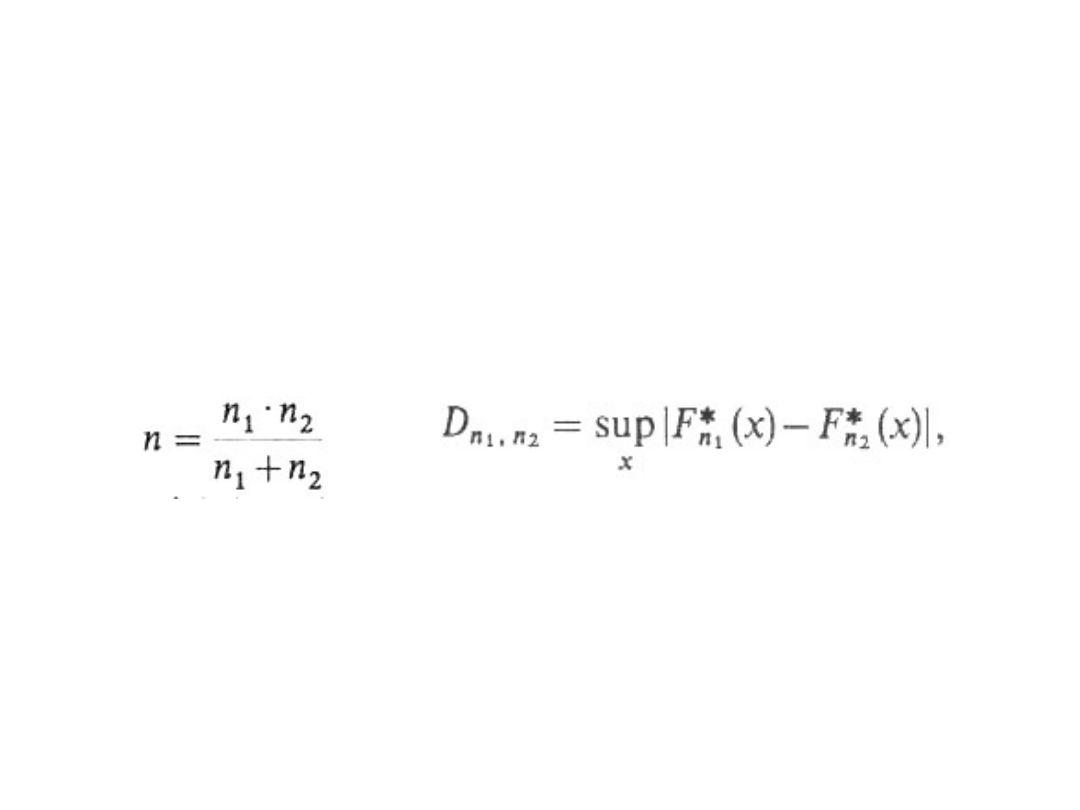
Test zgodności Kołmogorowa-
Smirnowa (2)
• Sprawdzianem hipotezy jest statystyka:
l
n
= n D
n1,n2
, gdzie
przy czym n
1
, n
2
oznaczają liczebności
dużych prób z obu populacji, a F*
n1
(x),
F*
n2
(x) - dystrybuanty empiryczne,
wyznaczone na podstawie prób.
Statystyka II-4
49
Test zgodności Kołmogorowa-
Smirnowa (3)
• Statystyka l
n
ma przy założeniu
prawdziwości H
0
asymptotyczny rozkład l-
Kołmogorowa. Zbyt duże wartości
sprawdzianu wskazują, że hipoteza H
0
może być nieprawdziwa, a więc relacja
wyznaczająca zbiór krytyczny oraz sposób
wyznaczania wartości krytycznej są takie
same jak w teście l –Kołmogo-rowa, tzn.
P(l
n
≥ l
a
) = a, przy czym l
a
odczytuje się z
tablicy rozkładu, tak że Q(l
a
) = 1 – a.
Statystyka II-4
50
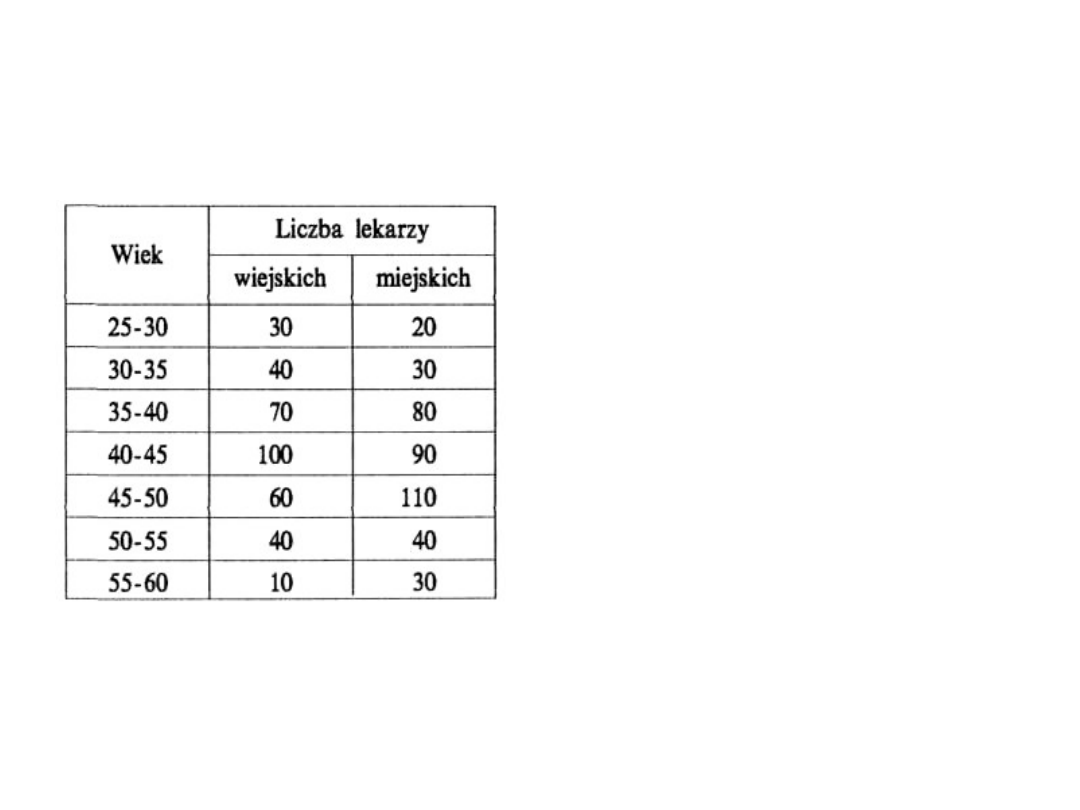
Test zgodności Kołmogorowa-
Smirnowa (4)
Statystyka II-4
51
Przykład : Na podstawie
danych otrzymanych w
dwóch wylosowanych
niezależnie próbach na
poziomie istotności a =
0,05 zweryfikować
hipotezę, że rozkład
wieku lekarzy na wsi i w
mieście jest taki sam.
H
0
: F
1
(x) = F
2
(x),
H
1
: F
1
(x) ≠ F
2
(x).
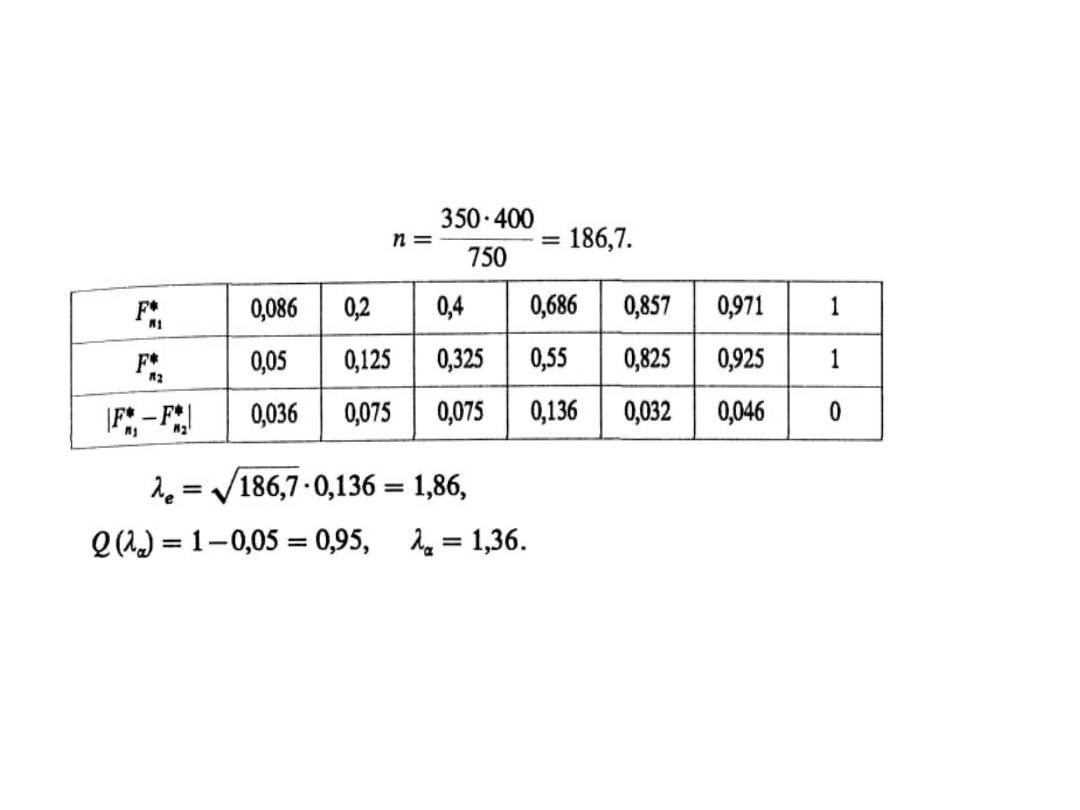
Test zgodności Kołmogorowa-
Smirnowa (5)
Statystyka II-4
52
n
1
= 350, n
2
= 400,
Ponieważ l
e
> l
a
, odrzucamy hipotezę, że rozkład
wieku lekarzy w mieście na wsi jest taki sam, co
jest równoznaczne ze stwierdzeniem, że struktury
wieku lekarzy w mieście i na wsi są różne.
Testowanie niezależności testem
chi-kwadrat
Statystyka II-4
53
W praktyce badań statystycznych występuje
często konieczność oceny niezależności
stochastycznej:
— dwóch cech jakościowych,
— dwóch cech ilościowych lub
— cech: ilościowej i jakościowej, opisujących
zbiorowość generalną.
W tym celu weryfikuje się odpowiednio
sformułowaną hipotezę nieparametryczną za
pomocą testu niezależności
2
.
W przypadku odrzucenia hipotezy zerowej,
mówiącej o tym, że dwie cechy opisujące daną
zbiorowość statystyczną są niezależne,
korzystając z wybranej miary, ocenia się siłę
zależności stochastycznej tych cech.
Testowanie niezależności testem chi-
kwadrat (2)
Statystyka II-4
54
Hipotezę zerową orzekającą, że cechy X i Y są
niezależne, można formalnie zapisać (por. rozdział
5):
H
0
: p
ij
= p
i∙
p
∙j
, H
1
: p
ij
≠ p
i∙
p
∙j
gdzie p
ij
oznacza łączny rozkład zmiennej (X, Y), a
p
i
. oraz p.
j
- rozkłady brzegowe cechy X i cechy Y.
Dla zweryfikowania tej hipotezy należy
dysponować dużą próbą, tzn. n > 30. Wyniki tej
próby przedstawiamy w postaci tzw. tablicy
dwudzielnej o r-wierszach i s-kolumnach, przy
czym r oznacza liczbę wariantów cechy X, a s –
liczbę wariantów
cechy Y.
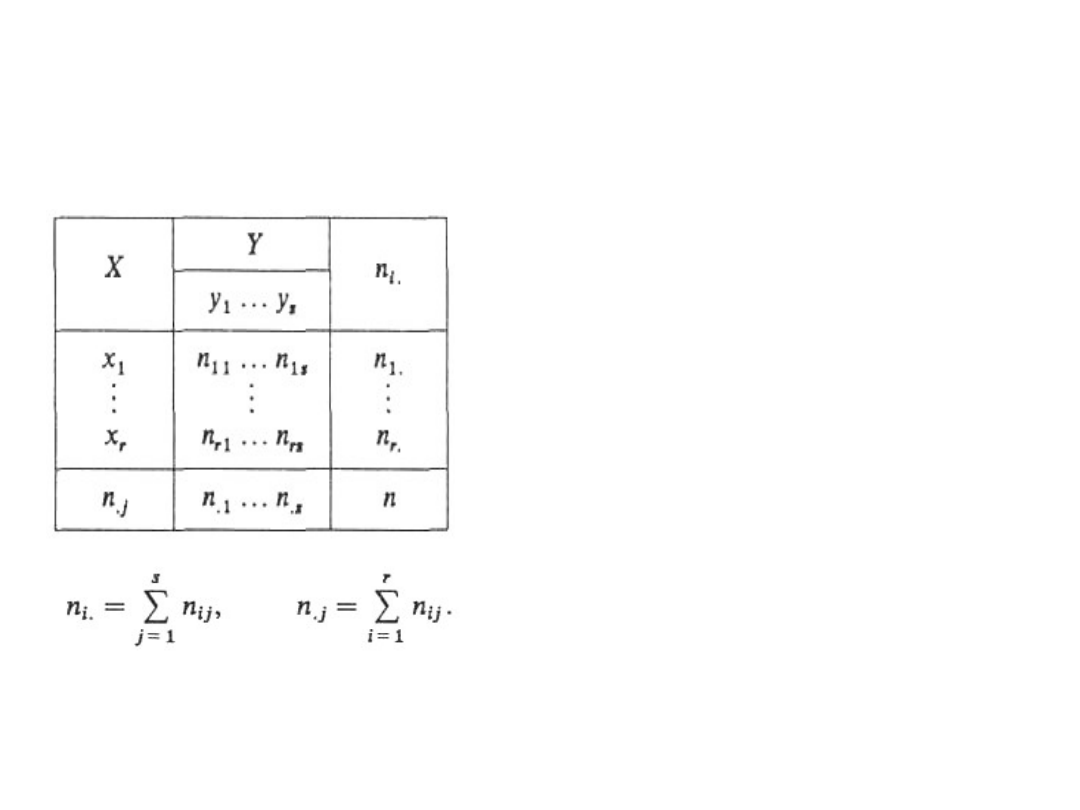
Testowanie niezależności testem chi-
kwadrat (3)
Statystyka II-4
55
Wnętrze tablicy dwudzielnej
stanowią liczebności
empiryczne n
ij
tych
elementów w próbie, dla
których cecha X przyjęła
wariant x
i
, a cecha Y —
wariant y
j
.
Jak widać, n
ij
są to liczby
leżące na przecięciu i-tego
wiersza oraz j-tej kolumny,
przy czym wymaga się na
ogół, aby n
ij
≥ 8 dla każdej
kombinacji i i j.
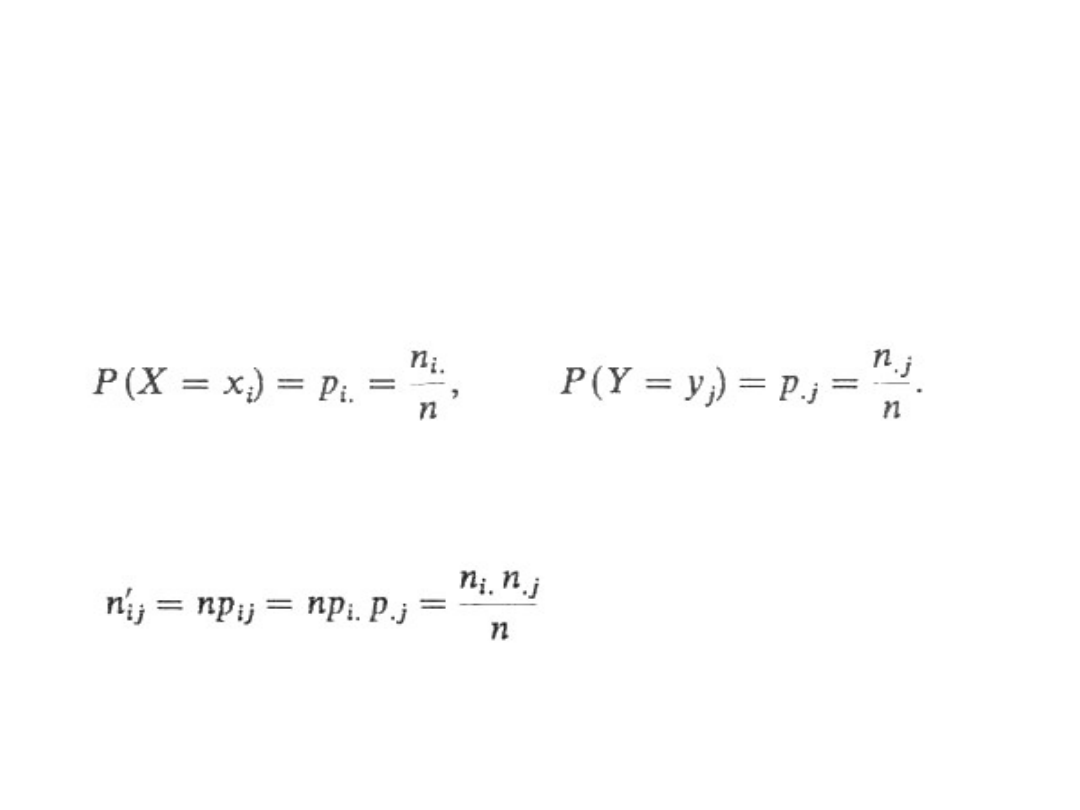
Testowanie niezależności testem chi-
kwadrat (4)
Statystyka II-4
56
Obliczając n
i∙
/n, n
∙j
/n znajdujemy empiryczne
rozkłady brzegowe i przyjmujemy je jako
oszacowania rozkładów brzegowych cechy X i
cechy Y:
Liczebności teoretyczne n'
ij
znajdujemy,
zakładając prawdziwość hipotezy H
0
, w ten
sposób, że
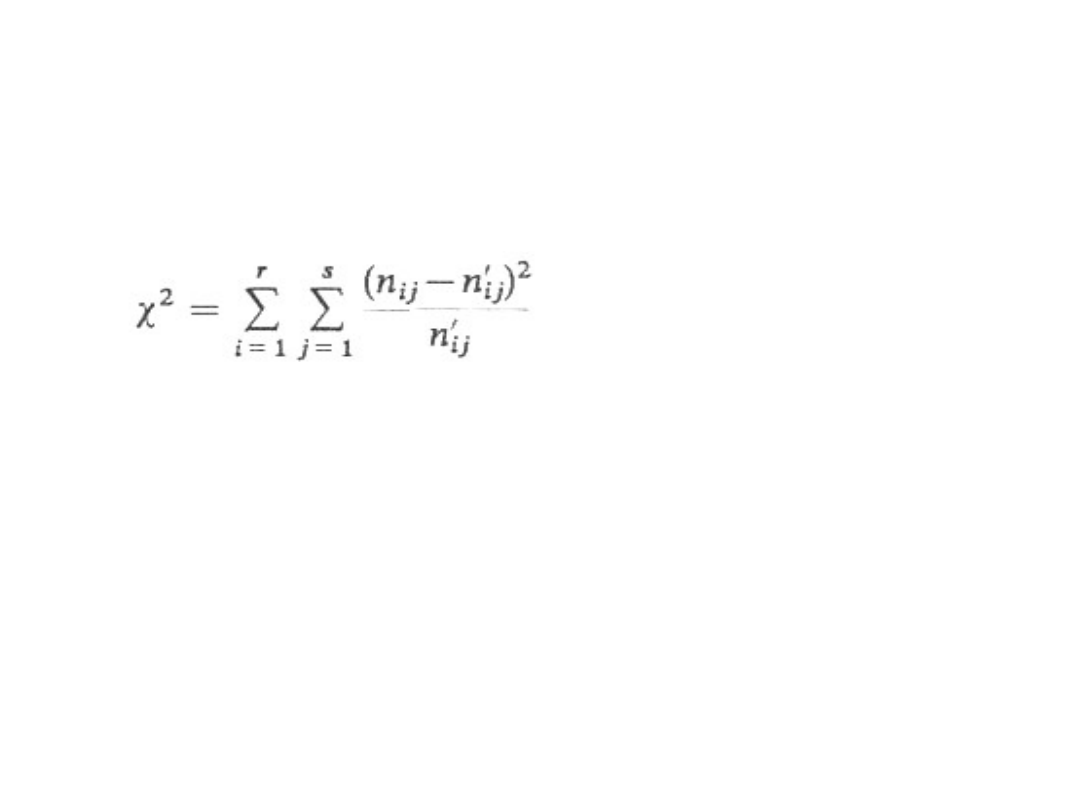
Testowanie niezależności testem chi-
kwadrat (5)
Statystyka II-4
57
Sprawdzianem hipotezy H
0
jest statystyka
Statystyka ta przy założeniu prawdziwości H
0
ma
asymptotyczny rozkład
2
o k = (r – l)(s – 1)
stopniach swobody. Duże wartości empiryczne
sprawdzianu hipotezy oznaczają, że liczebności
empiryczne i teoretyczne istotnie różnią się
między sobą, powodują więc odrzucenie hipotezy
zerowej.
Testowanie niezależności testem chi-
kwadrat (6)
Statystyka II-4
58
Obszar krytyczny jest prawostronny, określony
relacją
P(
2
>
e
2
) = a
Jeśli wartość empiryczna sprawdzianu hipotezy
spełnia relację
2
>
e
2
na
przyjętym poziomie
istotności należy hipotezę o niezależności X i Y
odrzucić. Oznacza to, że cechy X i Y są zależne.
A więc można ocenić siłę tej zależności
korzystając z jednej z zaprezentowanych poniżej
miar.
Większość spośród istniejących miar zależności
cech, zwłaszcza jakościowych, bazuje na
wartości statystyki
2
, obliczonej dla tablicy
dwudzielnej o wymiarach (rs)
Najczęściej stosowane miary
zależności
Statystyka II-4
59
Współczynnik -Yule'a postaci:
przy czym gdy:
r = 2, s — dowolne, to 0 ≤ ≤ 1,
r > 2, s — dowolne, to może być większe od 1.
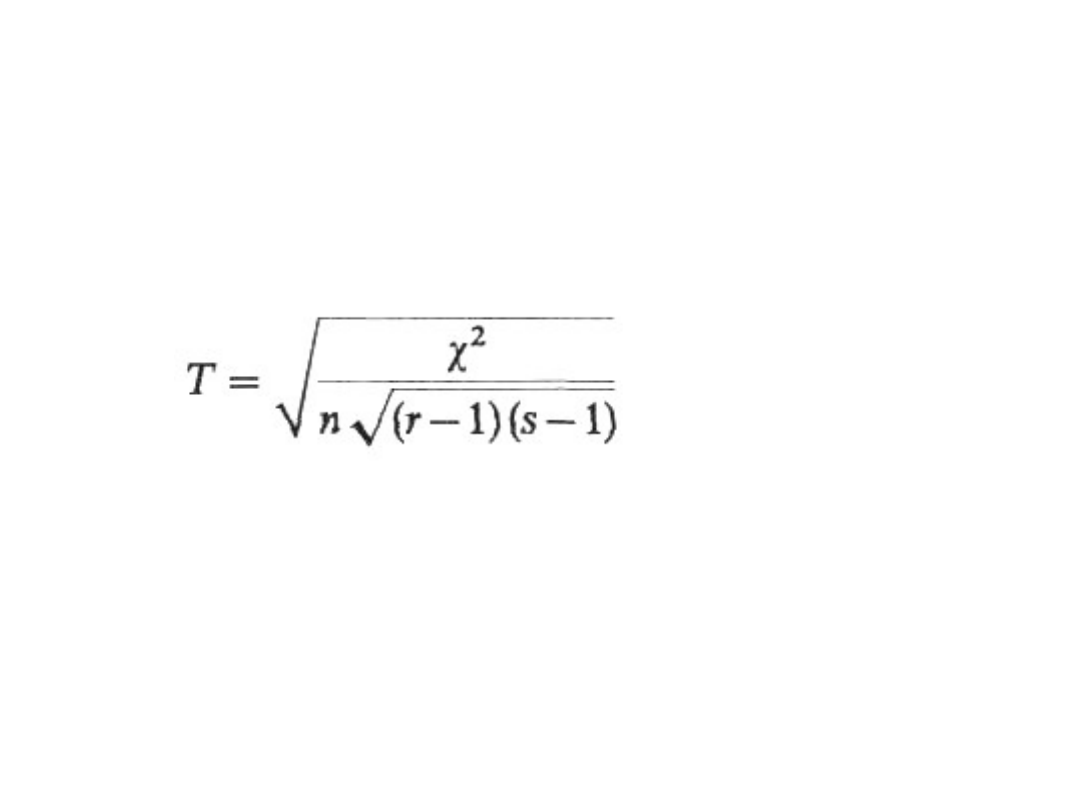
Najczęściej stosowane miary
zależności (2)
Statystyka II-4
60
Współczynnik zbieżności T-Czuprowa postaci:
gdy r = s, to 0 ≤ T ≤ 1,
r ≠ s, T może być znacznie mniejsze od 1.
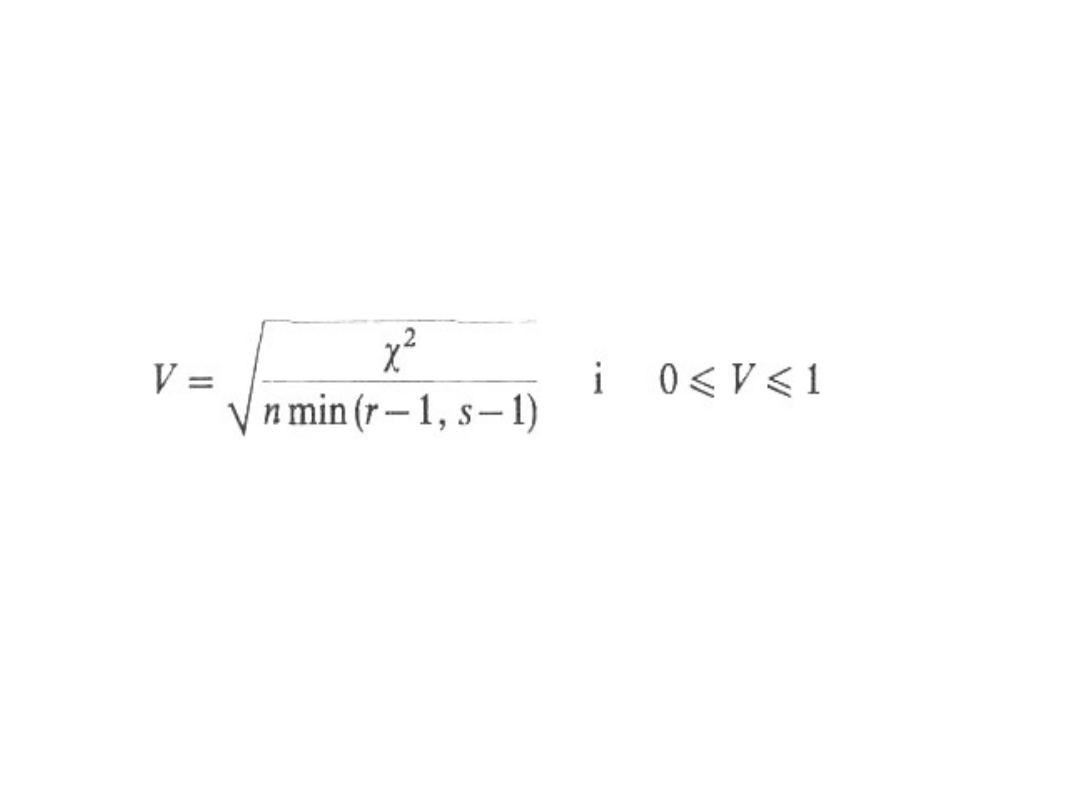
Najczęściej stosowane miary
zależności (3)
Statystyka II-4
61
Współczynnik V-Cramera postaci:
gdy: r = s, to V = T,
r ≠ s, to V > T.
Interpretacja każdego z podanych
współczynników
Statystyka II-4
62
- jeśli przyjmuje on wartość zero, oznacza to,
że cechy X i Y są stochastycznie niezależne,
- im bliższa jedności jest wartość danego
współczynnika, tym silniejsza zależność
między badanymi cechami X i Y.
Oczywiście, w przypadku tablic o wymiarach
(2x2),
= V = T.
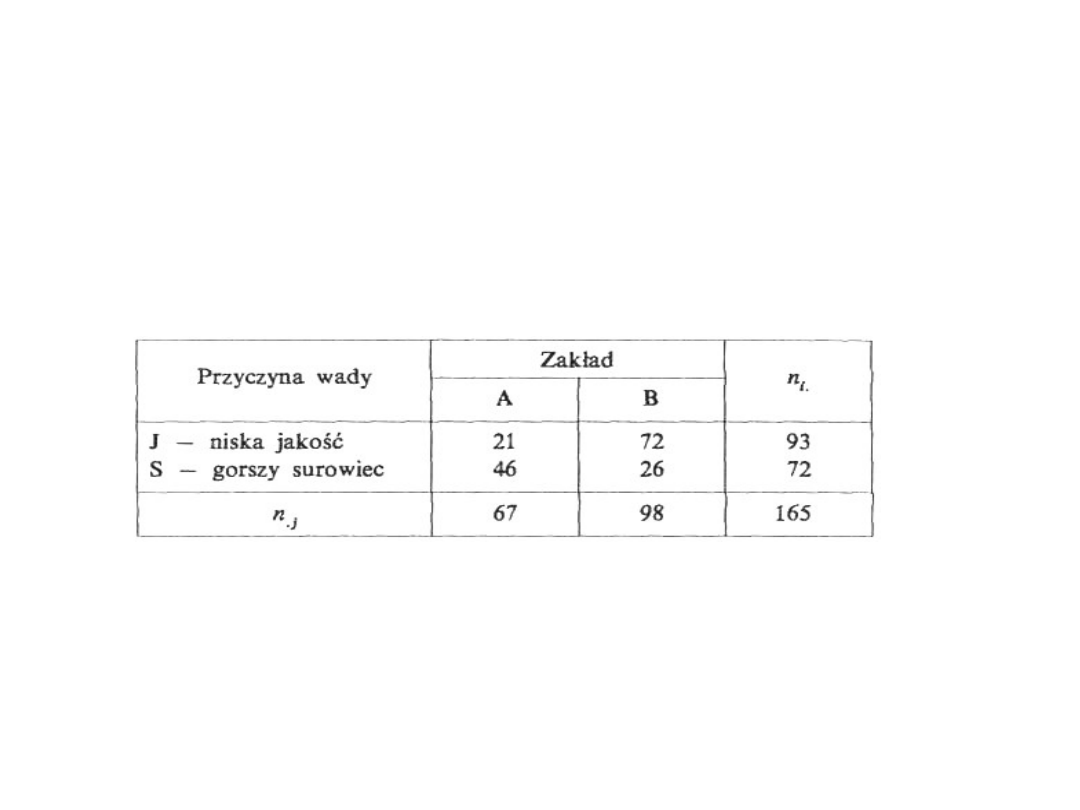
Miary zależności - przykład
Statystyka II-4
63
Przykład: Wyrób produkowany w dwóch zakładach A i B
może być uznany jako wadliwy z dwóch powodów: J —
niskiej jakości wykonania lub S - użycia gorszego surowca.
Analizując 165 wyrobów wadliwych otrzymano wyniki:
Na
poziomie istotności a = 0,01 zweryfikujemy hipotezę
o niezależności między miejscem powstania wyrobu a
przyczyną uznania wyrobu za wadliwy.
H
0
: p
ij
= p
i∙
p
∙j
, H
1
: p
ij
≠ p
i∙
p
∙j
Miary zależności –
przykład (2)
Statystyka II-4
64
Jak widać, dane tworzą tablicę dwudzielną o
wymiarach (2x2). Np. liczba 21 oznacza, że wśród
165 badanych wyrobów 21 wyprodukowano w
zakładzie A i zakwalifikowano je jako wadliwe z
powodu niskiej jakości wykonania. Można podać
analogiczną interpretację pozostałych elementów
tej tablicy.
Korzystając z wzoru
wyznaczamy tablicę liczebności teoretycznych n’
ij
.
Dla przykładu liczebność teoretyczna
Miary zależności –
przykład (3)
Statystyka II-4
65
Analogicznie obliczamy pozostałe elementy
tabeli.
Zgodnie z zależnością:
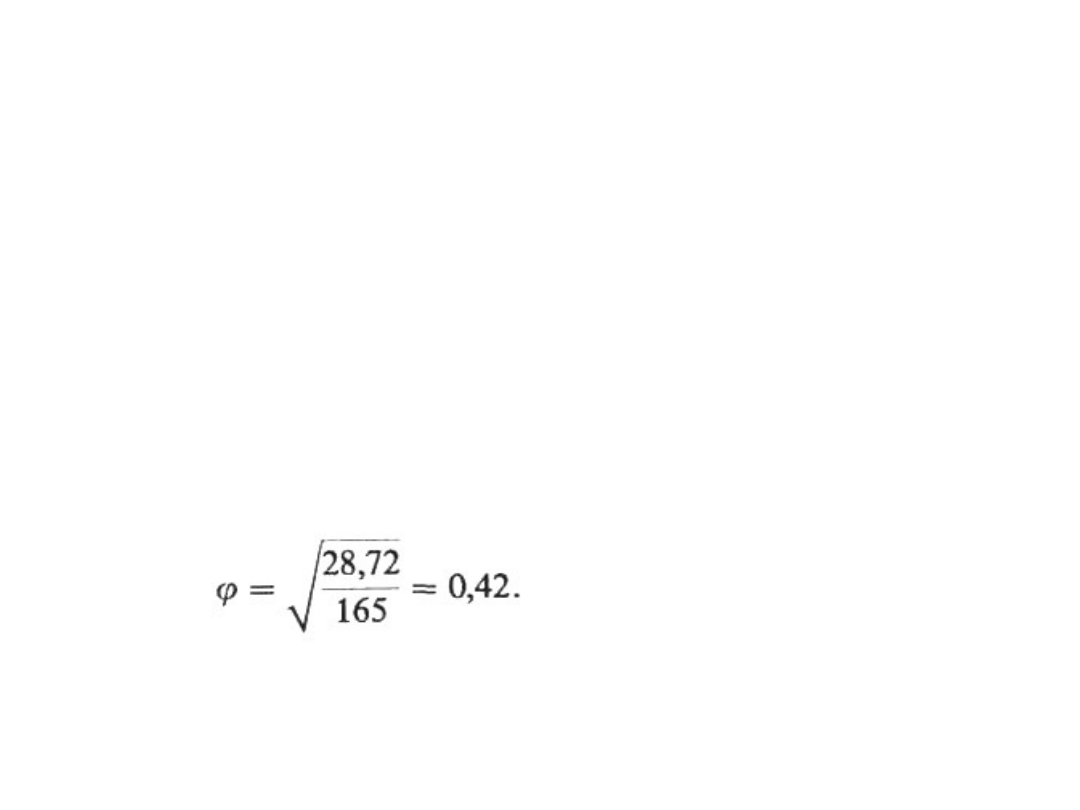
Miary zależności –
przykład (4)
Statystyka II-4
66
Z tablic rozkładu
2
dla P = 0,01 i dla k = (r - l)(s -
1) =
= (2 - 1)(2 - 1) = 1 stopni swobody mamy = 6,63.
Ponieważ
e
2
>
a
2
, należy odrzucić H
0
, a zatem można
powiedzieć, że istnieje zależność między przyczyną
uznania wyrobu za wadliwy a miejscem, gdzie
został wyprodukowany.
Miarą tej zależności jest jeden z przedstawionych
wyżej współczynników. Dla analizowanego
przykładu = T = V i wynosi
Jak widać, jakość wyrobu zależy od miejsca jego
powstania.
Miary zależności – uwagi
• Prezentowane powyżej miary
stosowane są przede wszystkim do
oceny zależności stochastycznej
cech niemierzalnych.
• W przypadku cech mierzalnych,
zwłaszcza o dużej liczbie
wariantów, stosuje się różne
mierniki zależności korelacyjnej.
Statystyka II-4
67
Document Outline