CHEMIA 1



Termochemia

◦

Równanie stanu gazu doskonałego i rzeczywistego

◦

Podstawy termodynamiki

◦

Prawo Hessa

Wykład 11

Równanie stanu gazu

doskonałego

i rzeczywistego

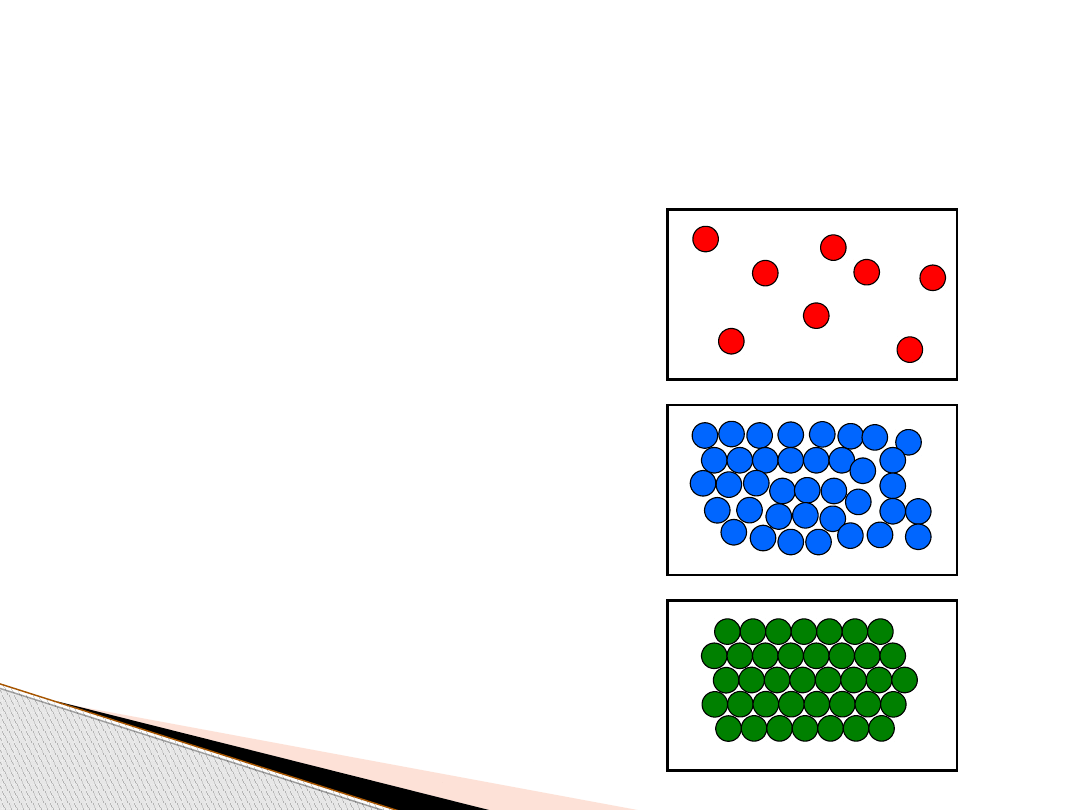
Stany skupienia materii –
przypomnienie

1. Gaz (wypełnia całkowicie

objętość naczynia w którym
się znajduje)

2. Ciecz (przybiera kształt

naczynia w którym się
znajduje)

3. Ciało stałe (zachowuje swój

własny kształt)

2-wymiarowy model

uporządkowania w skali atomowej

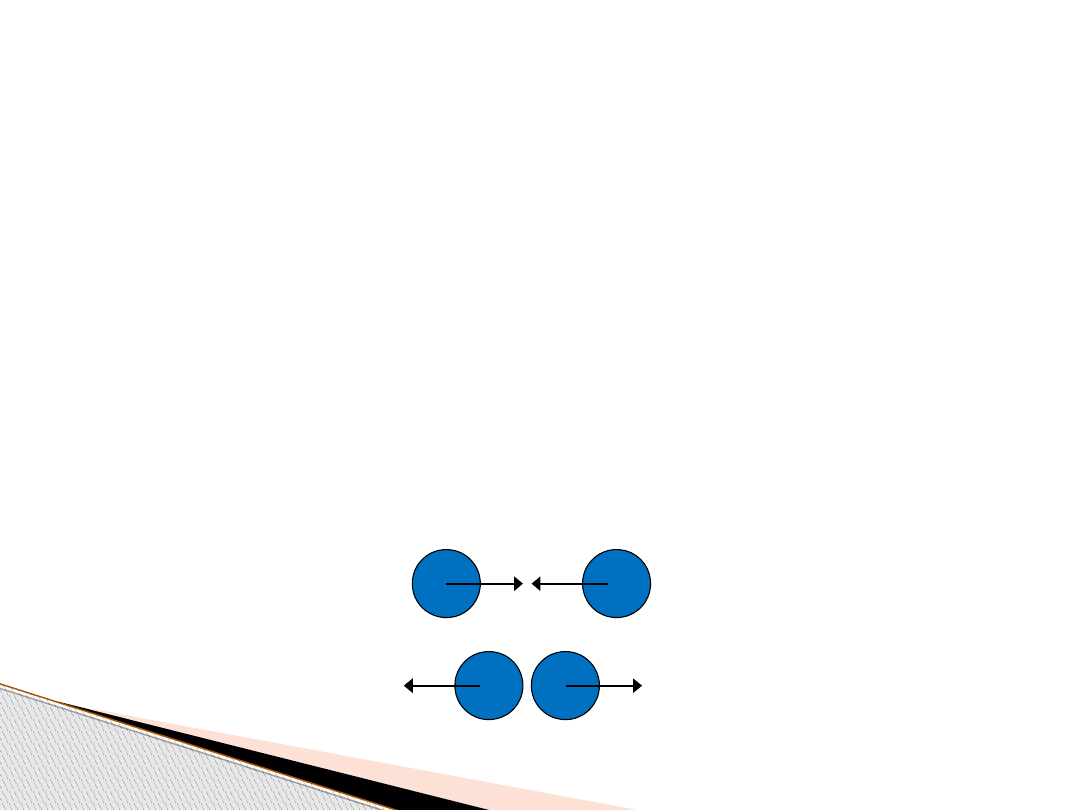
Gazy doskonałe – założenia teorii

1. Cząsteczki gazu zachowują się jak jednorodne kule, doskonale

sprężyste

2. Objętość własna, którą zajmują może być zaniedbana

3. Cząsteczki znajdują się w ciągłym ruchu postępowym,

zderzając się miedzy sobą doskonale sprężyście

4. Pomiędzy zderzeniami cząstki poruszają się ruchem

prostoliniowym

5. Generalnie, ruch cząsteczek nie ma uprzywilejowanego

kierunku

zderzenie doskonale sprężyste

Gazy doskonałe – parametry

Stan gazowy można określić parametrami:

p

– ciśnienie

jednostki: Pa (paskal), atm (atmosfera fizyczna), 1 Pa = 1 N/1

m

2

,

1 atm = 101325 Pa = 1013 hPa ~ 0,1 MPa

T

– temperatura

jednostki: K (kelwin),

o

C (stopień Celsjusza),

0

o

C = 273,15 K

V

– objętość

jednostki: m

3

, cm

3

, litr,

1 m

3

= 1000 litrów, 1 litr = 1000 cm

3

= 1 dm

3

n

– liczba moli

1mol zawiera N

A

cząsteczek

N

A

– liczba Avogadra = 6,022·10

23

mol

-1

Gazy doskonałe – historia

1662r – prawo Boyle’a:

p·V = const

w danej temperaturze

1802r – prawo Gay-Lussaca:

V = V

0

(1 + a·T)

dla danego ciśnienia (T w stopniach Celsjusza a

V

0

to objętość w temp. 0

o

C, a oznacza współczynnik

rozszerzalności cieplnej)

jeśli oznaczymy a = 1/T

0

to V = V

0

(1+T/T

0

), T

0

+ T daje

temperaturę w Kelwinach, więc V = V

0

T/T

0

, w efekcie

otrzymujemy:

V/T = const

1811r – prawo Avogadra:

Przy tym samym ciśnieniu i w tej samej temperaturze jednakowe
objętości różnych gazów zawierają taką samą liczbę cząsteczek.

Równanie stanu gazu doskonałego
(Clapeyron, 1834)

T

R

n

V

p









ciśnienie
[Pa]

objętość
[m

3

]

ilość moli
[mol]

stała gazowa
8,314 [J·mol

-1

·K

-1

]

temperatura
[K]

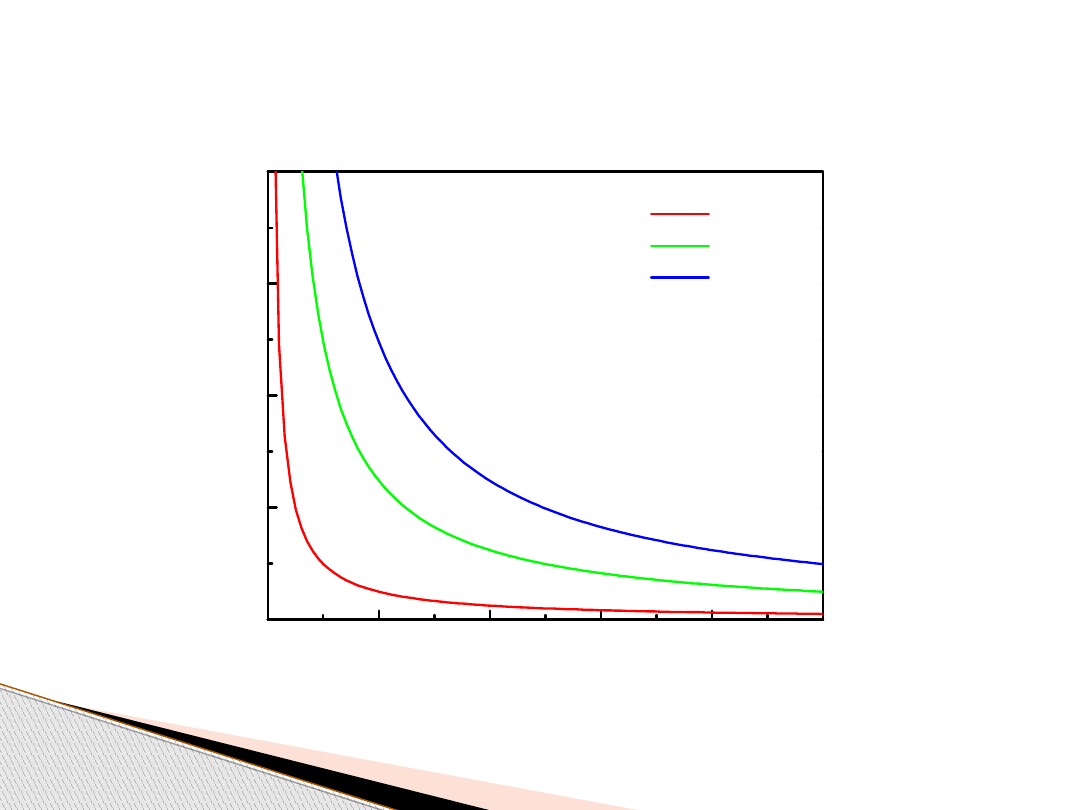
Gaz doskonały (izotermy, T = const)

0,0

0,2

0,4

0,6

0,8

1,0

0,0

5,0x10

4

1,0x10

5

1,5x10

5

2,0x10

5

Przykładowe izotermy gazu doskonałego (298K)

ci

śn

ie

ni

e

[P

a]

objętość [m

3

]

1 mol
5 moli
10 moli

p

1

V

1

= p

2

V

2

= const

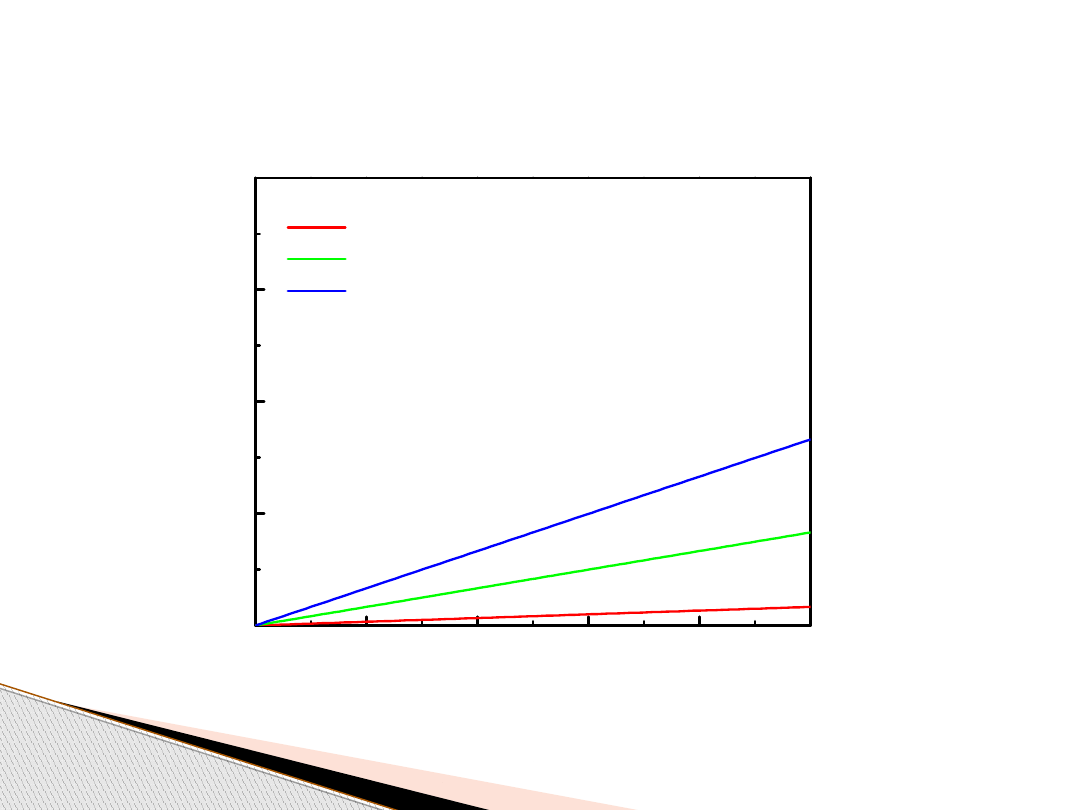
Gaz doskonały (izobary, p = const)

0

200

400

600

800

1000

0,0

0,2

0,4

0,6

0,8

1,0

Przykładowe izobary gazu doskonałego (p = 1013hPa = 1atm)

ob

ję

to

ść

[m

3

]

temperatura [K]

1 mol
5 moli
10 moli

V

1

/T

1

= V

2

/T

2

= const

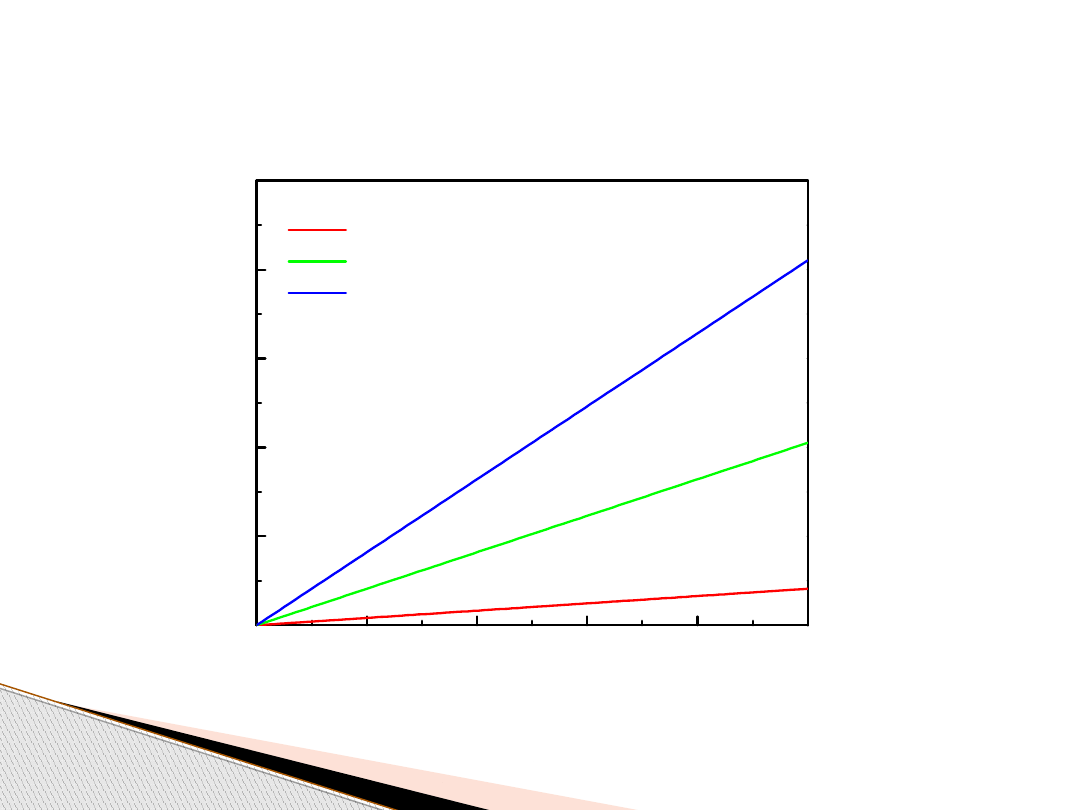
Gaz doskonały (izochory, V = const)

0

200

400

600

800

1000

0,0

5,0x10

4

1,0x10

5

1,5x10

5

2,0x10

5

Przykładowe izochory gazu doskonałego (V = 1m

3

)

ci

śn

ie

ni

e

[P

a]

temperatura [K]

1 mol
5 moli
10 moli

p

1

/T

1

= p

2

/T

2

= const

Gazy doskonałe – przykładowe
zadanie

Obliczyć objętość 1 mola gazu doskonałego w temperaturze 0

o

C

znajdującego się pod ciśnieniem 1 atm:

p·V = n·R·T

V = n·R·T/p

V = 1 mol · 8,314 J·mol

-1

·K

-1

· 273,15 K / 101300 Pa

V = 22,4 dm

3

= 0,0224 m

3

Co oznacza, że w warunkach normalnych (1 atm, 0

o

C) 1 mol gazu

doskonałego zajmuje objętość 22,4 dm

3

.

Gazy doskonałe – elementy
kinetycznej teorii gazów

Załóżmy, że gaz doskonały znajduje się w sześciennym
pojemniku o boku

a

.

Ciśnienie

p

wywierane na ściankę to całkowita zmiana pędu

cząsteczek zderzających się z daną ścianką liczona dla czasu 1
sekundy oraz przypadająca na jednostkową powierzchnię.

Pęd cząstki w kierunku osi

x

wynosi

m·u

x

gdzie

m

to masa

cząstki a

u

x

to składowa x-owa prędkości cząstki.

Zmiana pędu po zderzeniu doskonale sprężystym =

2m·u

x

.

Ilość zderzeń w ciągu sekundy z daną ścianką wynosi

u

x

/2a

.

Zmiana pędu podczas jednej sekundy dla 1 cząstki =

2m·u

x

·u

x

/2a

=

m·ū

x

2

/a

gdzie

ū

x

2

to średni kwadrat prędkości składowej x-owej.

Gazy doskonałe – elementy
kinetycznej teorii gazów

Wobec tego dla

N

cząstek wywierane ciśnienie na ściankę

wynosi:

bo składowe dla różnych kierunków są sobie równe, a
prawdopodobieństwo ruchu wzdłuż jednej osi wynosi 1/3, pole
ścianki wynosi

a

2

.

Dla jednego mola cząsteczek ciśnienie wynosi:

Wiedząc, że

p·V = n·R·T

i

n = 1

:

2

2

a

a

u

m

N

3

1

p









V

u

m

N

3

1

p

2

A







2

A

u

m

N

3

1

T

R









Gazy doskonałe – elementy
kinetycznej teorii gazów

Energia kinetyczna dana jest wzorem

E = 0,5m·ū

x

2

, a więc:

k

B

= 1,381·10

-23

J·K

-1

to jedna z głównych stałych fizycznych

(stała Boltzmanna).

Podstawowy wniosek:

temperatura jest miarą energii

kinetycznej cząsteczek

.

Na każdy z kierunków w przestrzeni (stopień swobody) dla
jednej cząsteczki (jednoatomowego) gazu doskonałego

E =

0,5k

B

·T

, a dla jednego mola:

E = 0,5R·T

T

k

2

3

2N

T

3R

E

E

N

3

2

T

R

B

A

A















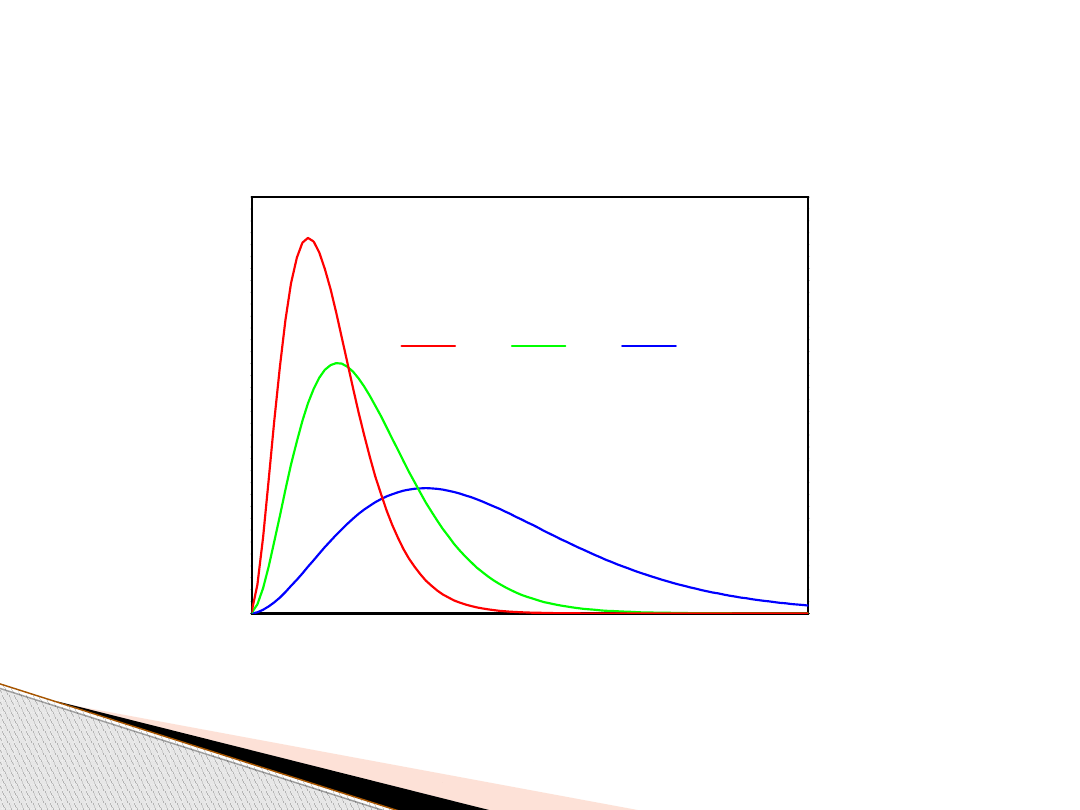
Gazy doskonałe – elementy
kinetycznej teorii gazów

Rozkłady prędkości cząsteczek gazu

dla różnych temperatur (na postawie rozkładu Boltzmanna)

ilo

ść

c

zą

st

ec

ze

k

o

da

ne

j p

rę

dk

oś

ci

prędkość cząsteczek gazu

T

1

<

T

2

<

T

3

Gazy rzeczywiste

Obserwowane parametry mikroskopowe:

1. Średnia prędkość cząsteczek

100-1000 m·s

-1

2. Średnia droga pomiędzy zderzeniami

100-1000 Å

(1 Å = 10

-10

m)

3. Częstość zderzeń

10

10

s

-1

Różnice pomiędzy gazami rzeczywistymi, a opisem prostej teorii
gazów doskonałych wynikają głównie z:

• wpływu oddziaływań międzycząsteczkowych w gazie,

• niezaniedbywalnej objętości własnej cząsteczek gazu.

Gazy rzeczywiste

Odstępstwa będą tym większe im niższa temperatura (małe
k

B

·T) oraz im wyższe ciśnienie (mniejsze odległości między

cząsteczkami).

Poprawione przez van der Waalsa równanie stanu dla gazów ma
postać:

gdzie:

a

– stała uwzględniająca oddziaływanie pomiędzy cząsteczkami

(m

3

·Pa·mol

-2

),

b

– stała uwzględniająca rozmiar cząsteczek (m

3

·mol

-1

).





T

R

n

b

n

V

V

a

n

p

2

2





















 

Podstawy termodynamiki i

prawo Hessa

Termodynamika – wstęp i definicje

Układ

– to wydzielona (umownie) przestrzeń wraz ze

znajdującymi się tam substancjami, w której będzie zachodził
interesujący nas proces.

Parametry stanu

– to zmienne określające stan

(termodynamiczny) układu.

•

Parametry ekstensywne

– to parametry, które zależą od

wielkości układu np. objętość układu

V

, masa układu

m

,

energia

E

.

•

Parametry intensywne

– ich wielkość nie zależy od wielkości

układu np. temperatura

T

, ciśnienie

p

.

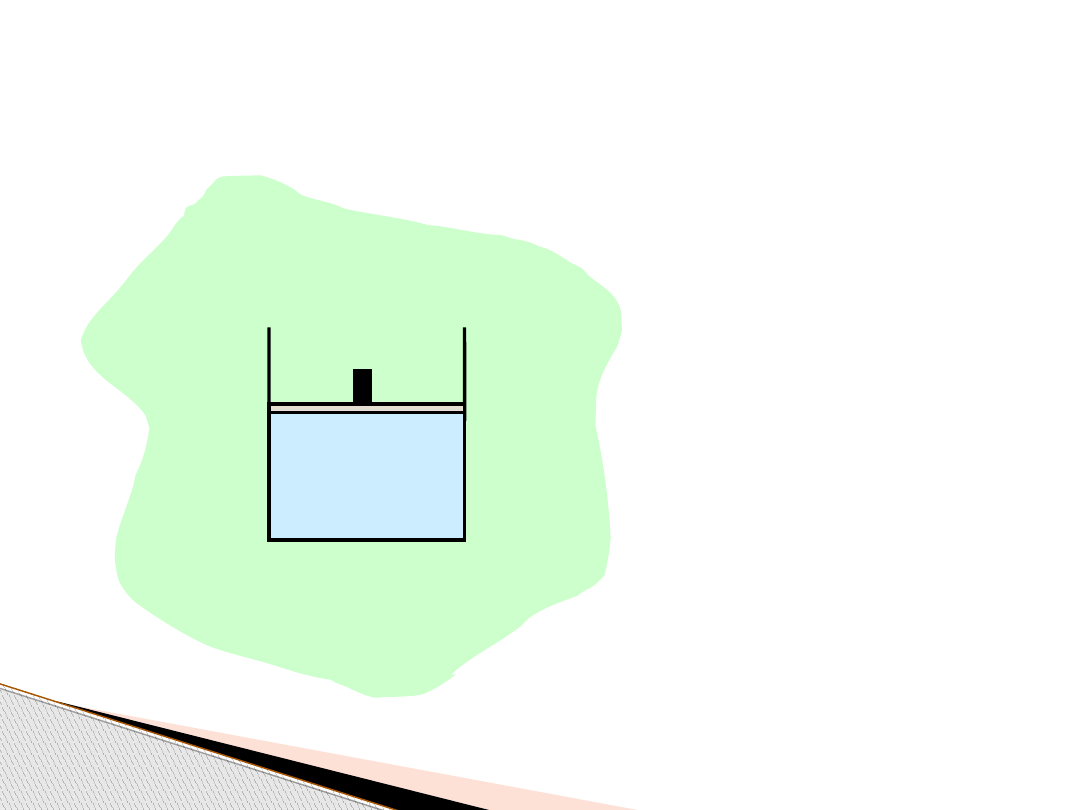
Termodynamika – wstęp i definicje

układ

V, p, T, n

otoczenie układu

Układ izolowany

– nie ma wymiany

masy ani energii (ciepła) z otoczeniem

Układ zamknięty

– nie ma wymiany

masy z otoczeniem

Układ otwarty

– jest wymiana

masy z otoczeniem

Termodynamika – I zasada

W układzie izolowanym energia wewnętrzna jest zachowana. U
= const. ΔU = 0.

Energia wewnętrzna jest sumą wszystkich rodzajów energii
układu: np. energii kinetycznej, oscylacji i rotacji cząstek
układu, energii elektronów, wiązań chemicznych, oddziaływań
międzycząsteczkowych, itd...

Zmiana energii wewnętrznej układu zamkniętego może nastąpić
na sposób ciepła albo na sposób pracy. DU = Q + W.

Q

– ciepło,

W

– praca. Q > 0 – do układu przepływa energia na

sposób ciepła, Q < 0 – układ traci energię na sposób ciepła. W >
0 – do układu przepływa energia na sposób pracy, W < 0 – układ
traci energię na sposób pracy.

Energia wewnętrzna jest funkcją stanu.

Jej zmiany zależą

jedynie od stanu początkowego i końcowego (przed i po dla
dowolnego procesu w układzie), nie zależą natomiast od drogi
tego procesu.

DU = U

2

– U

1

(w ogólnym przypadku Q i W

funkcjami stanu nie są!).

Dla tzw. procesu elementarnego (dowolnego, nieskończenie
małego):

dU = Q

el

+ W

el

(U posiada różniczkę zupełną, Q i W nie).

P

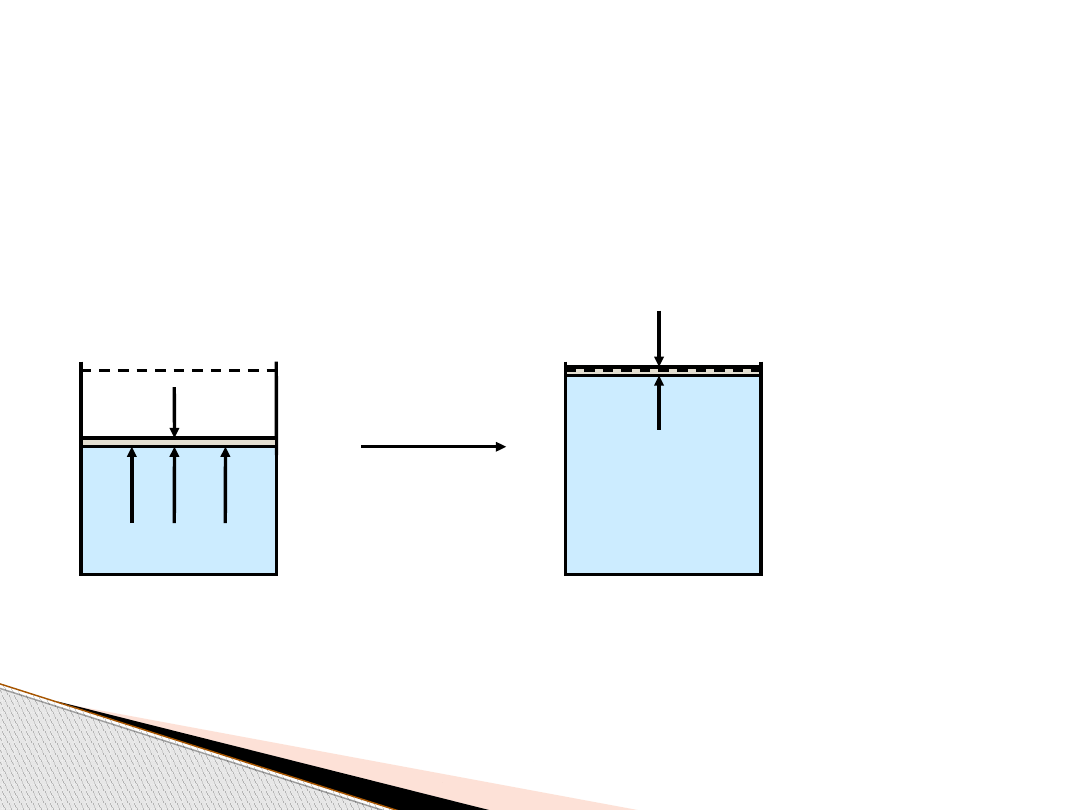
rocesy odwracalne i nieodwracalne

Nieodwracalne rozprężanie gazu

: ciśnienie zewnętrzne

jest stałe,
ciśnienie wewnętrzne maleje z początkowej wartości do
wartości ciśnienia
zewnętrznego

p

z

= const

p

w

p

z

V

1

V

2

p

w

p

z

V

2

P

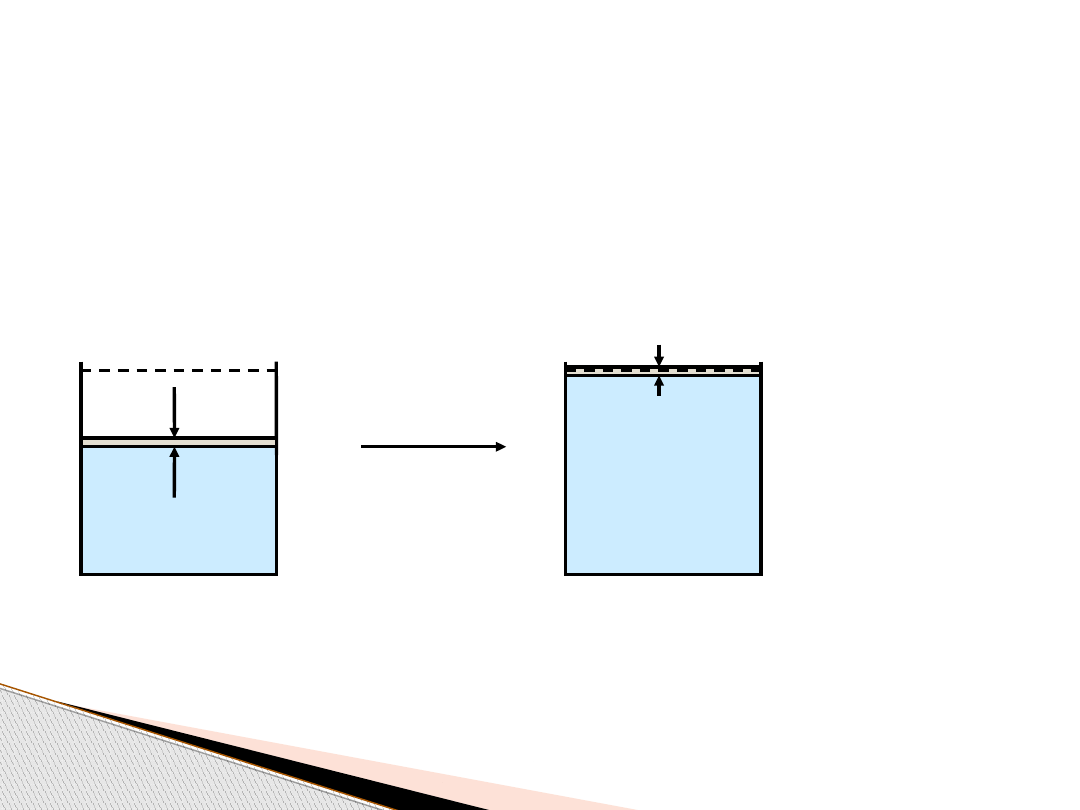
rocesy odwracalne i nieodwracalne

Odwracalne rozprężanie gazu

: ciśnienie zewnętrzne w

każdym momencie
równoważy ciśnienie wewnętrzne, oba ciśnienia
równocześnie maleją.

p

z

= p

w

p

w

p

z

V

1

V

2

p

w

p

z

V

2

W procesach odwracalnych przemiana następuje poprzez kolejne stany
równowagi.

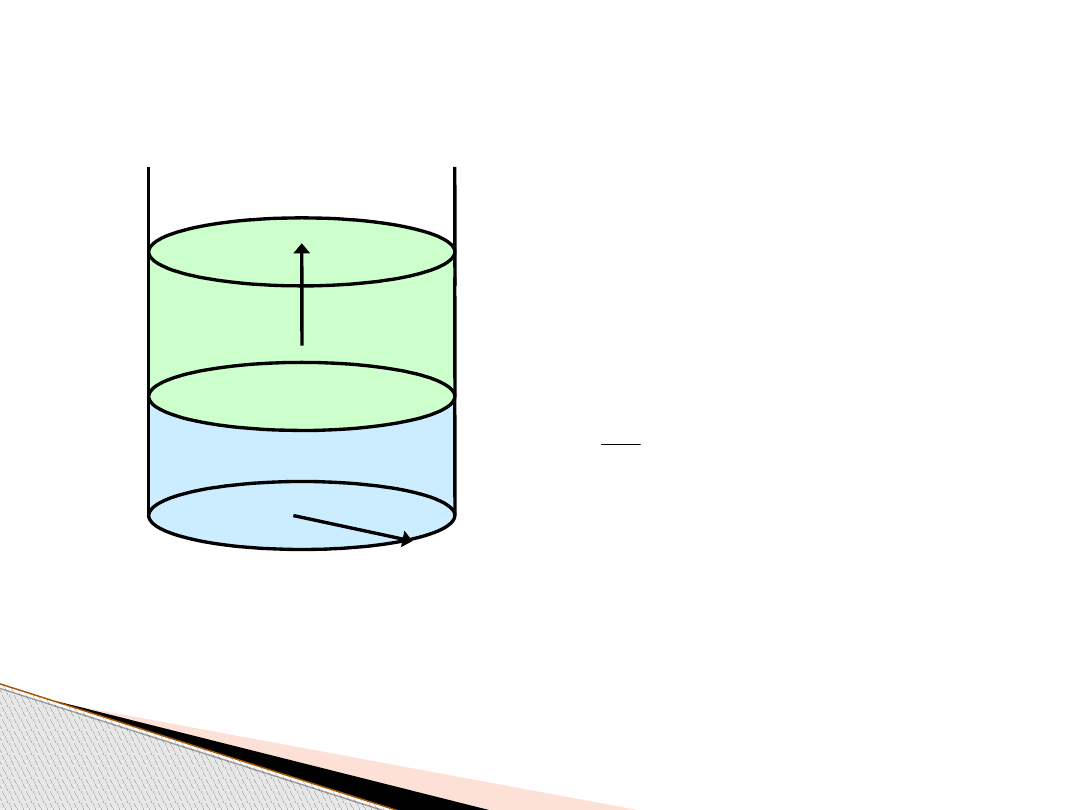
Praca objętościowa gazu – W

r

V

1

V

2

f

p

z

< p

w

, p

z

= const

f – siła działająca na tłok

pr

2

– pole powierzchni tłoka

V

p

Δl

πr

p

W

Δl

πr

V

V

ΔV

πr

f

p

Δl

f

W

2

2

1

2

2



























Jeśli układ traci energię (wykonuje pracę lub oddaje
ciepło) to znak pracy
i ciepła jest ujemny:

W

el

= –p·dV

. A więc:

dU = Q

el

–

p·dV

P

rocesy odwracalne i nieodwracalne

Nieodwracalne rozprężanie gazu doskonałego (p

z

< p

w

, p

z

=

const, T = const):

Odwracalne rozprężanie gazu doskonałego (p

z

= p

w

i maleją w

trakcie procesu,
T = const):























2

1

2

1

V

V

1

2

z

z

V

V

el

V

p

)

V

(V

p

dV

p

W

W















































2

1

2

1

V

V

V

V

1

2

el

el

V

V

ln

T

R

n

V

dV

T

R

n

W

W

dV

V

T

R

n

dV

p

W

T

R

n

V

p

I zasada termodynamiki dla procesów
izochorycznych

ΔU = Q + W

dU = Q

el

– p·dV

w procesach izochorycznych V = const, z czego wynika że dV =
0, a więc:

dU = Q

el

ΔU = U

2

– U

1

= Q

V

Ciepło reakcji (chemicznej) przebiegającej w stałej objętości jest
równe różnicy energii wewnętrznej w stanie końcowym i
początkowym – czyli Q

V

jest funkcją stanu.

I zasada termodynamiki dla procesów
izobarycznych

Wprowadźmy tzw. entalpię

H

jako:

H = U + p·V

dH = dU + p·dV +V·dp
dU = Q

el

– p·dV

dH = Q

el

+ V·dp

co jest równoważne z I zasadą termodynamiki dla procesu
izobarycznego.

Entalpia jest funkcją stanu.

Oznacza to, że jej zmiany zależą

jedynie od stanu początkowego i końcowego.

Dla procesu izobarycznego p = const co daje, że dp = 0 czyli:

dH = Q

el

Prawo Hessa

DH = H

2

– H

1

= Q

p

Ciepło reakcji (chemicznej) przebiegającej przy stałym ciśnieniu
jest równe różnicy entalpii w stanie końcowym i początkowym –
czyli Q

p

jest funkcją stanu.

Prawo Hessa:

Ciepło reakcji chemicznej (w warunkach izobarycznych lub
izochorycznych) nie zależy od drogi (reakcji), a jedynie od stanu
początkowego i końcowego reakcji. Czyli ciepło w takich
warunkach jest funkcją stanu.

Dla dowolnej reakcji chemicznej:

substraty ↔ produkty

w stanie

początkowym mamy substraty, a w końcowym produkty.

W

warunkach

izochorycznych

(

lub izobarycznych

) jeśli od sumy

energii wewnętrznych

(

entalpi

i) produktów odjąć sumę

energii

wewnętrznych

(

entalpii

) substratów otrzymamy wyrażenie na

ciepło reakcji

:











i

i

)

(substraty

i

i

(produkty)

i

i

V

ΔU

n

ΔU

n

Q

ΔU











i

i

)

(substraty

i

i

(produkty)

i

i

p

ΔH

n

ΔH

n

Q

ΔH