Równoważność wzorców
i wyrażeń regularnych

Kamila Borucka
Paweł Barud

Wydział Inżynierii Mechanicznej i Robotyki
Katedra Automatyzacji Procesów

09.06.2015 r.

Wzorce

• Wzorzec to zbiór obiektów o pewnej rozpoznawalnej

właściwości.

• Może to być:

– zbiór ciągów znaków, taki jak zbiór poprawnych

identyfikatorów języka C, z których każdy stanowi ciąg
znakowy, składający się z liter, cyfr i znaków
podkreślenia oraz rozpoczyna się od litery lub znaku
podkreślenia.

– zbiór tablic zer i jedynek o danym rozmiarze, które

czytnik znaków może interpretować jako reprezentację
tego samego symbolu. Zbiór wszystkich takich tablic
stanowiłby wzorzec o nazwie „A”.

Przykładowe wzorce

• [0-9]+ opisuje (niepuste) ciągi cyfr, czyli zapisy

dziesiętne liczb naturalnych.

• Do wzorca (a*bba*) ∩ (ab | ba)* pasuje tylko słowo abba.

Do a*bba* pasują słowa zawierające dokładnie dwie litery
b i to położone obok siebie, a do (ab | ba) pasują słowa
zbudowane z ,,cegiełek'' ab i ba. Jedynym słowem, które
pasuje do obydwu tych wzorców jest właśnie abba.

• Wzorzec [A-Z][A-Z] [0-9][0-9][0-9][0-9][0-9] opisuje jedną

z form numerów rejestracyjnych, złożonych z dwóch liter i
pięciu cyfr.

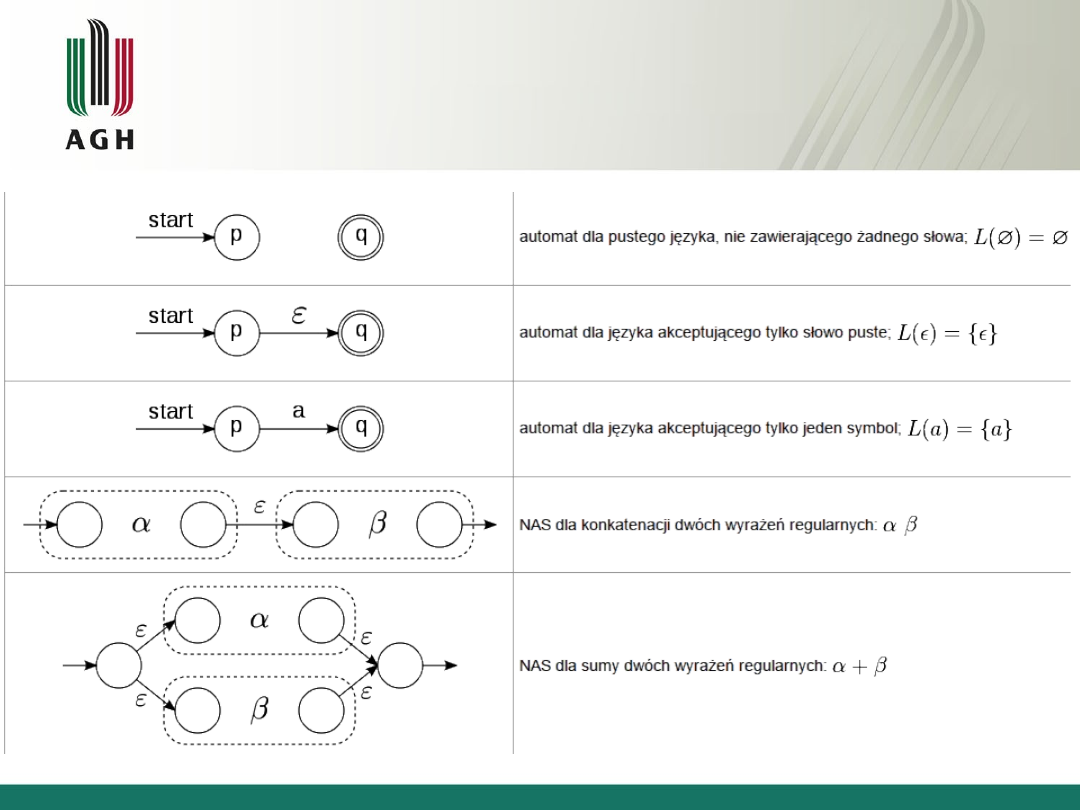
3 równoważne opisy wzorców

• oparty na teorii grafów, polegać będzie na wykorzystaniu

ścieżek w grafie szczególnego rodzaju, który nazwiemy
automatem,

• o charakterze algebraicznym, wykorzystujący notacje

wyrażeń regularnych,

• oparty o wykorzystanie definicji rekurencyjnych, nazwany

gramatyką bezkontekstową.

Wyrażenia regularne

• Wyrażenia regularne (ang. regular expressions, w skrócie

regex lub regexp) – stanowią algebraiczny sposób
definiowania wzorców. Teoria wyrażeń regularnych jest
związana z teorią języków regularnych.

• Wyrażenia regularne stanowią analogię do algebry

wyrażeń arytmetycznych oraz do algebry relacyjnej.

• Zbiór wzorców, które można wyrazić w ramach algebry

wyrażeń regularnych odpowiada dokładnie zbiorowi
wzorców, które można opisać za pomocą automatów.

Wyrażenia regularne

• Wyrażenia regularne posiadają pewne rodzaje operandów

niepodzielnych (ang. atomic operands): Znak, Symbol ɛ,
Symbol Φ oraz Zmienna - może być ona dowolnym
wzorcem zdefiniowanym za pomocą wyrażenia
regularnego.

• Wartość wyrażenia regularnego jest wzorcem

składającym się ze zbioru ciągów znaków, który często
określa się mianem języka (ang. language).

• Językiem regularnym nazywamy każdy język formalny L

nad danym alfabetem, dla którego istnieje wyrażenie
regularne A takie, że: L=L(A) . Klasę języków regularnych
oznaczamy przez JR.

Wyrażenia regularne

•

(A+B)+C≡A+(B+C)

•

A+Φ≡A

•

A+B≡B+A

•

A+A≡A

•

(A∙B)∙C≡A∙(B∙C)

•

A∙λ≡λ∙A≡A

•

A∙Φ≡Φ∙A≡Φ

•

(A+B)∙C≡A∙C+B∙C

•

A∙(B+C)≡A∙B+A∙C

Każdy język regularny może być generowany przez wiele wyrażeń
regularnych. Mówimy, że wyrażenia regularne A i B są równoważne,
gdy generują ten sam język, tzn.

A≡B↔L(A)=L(B)

Tw. Dla dowolnych wyrażeń regularnych A, B, C nad alfabetem Σ
zachodzą następujące równoważności:

Przykład

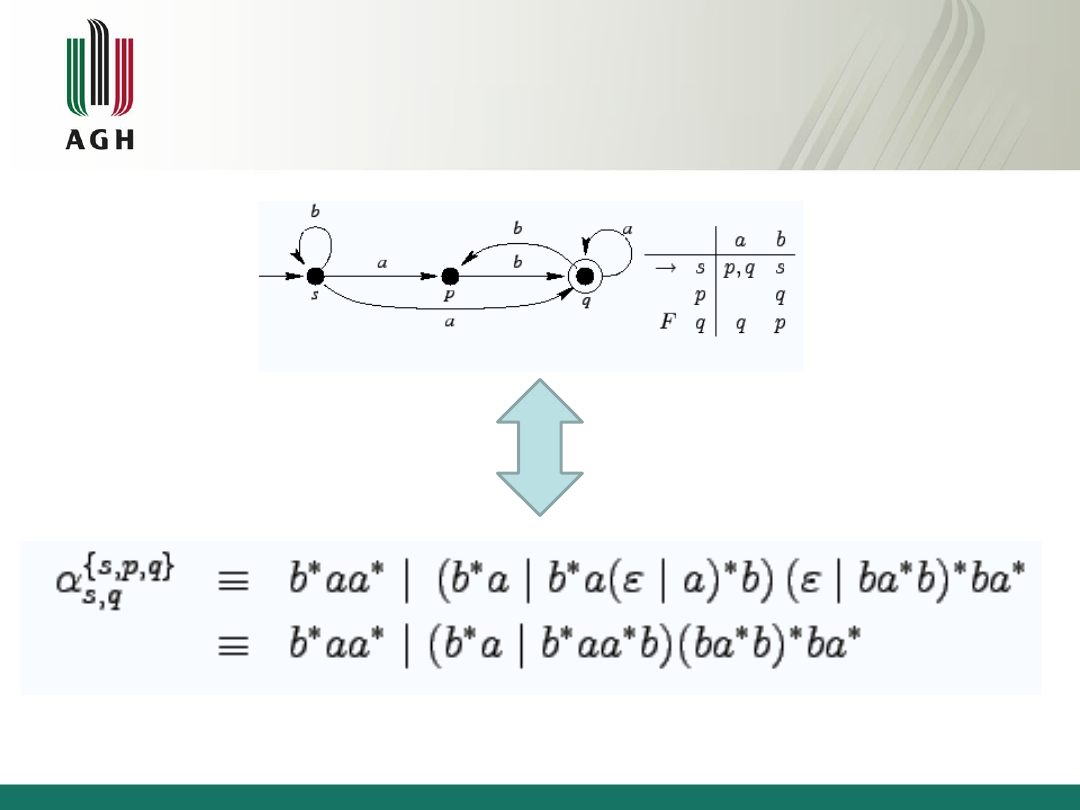
Przykład

Przykład