Stan gazowy

Gazy i środki lotne

Opis stanów materii

• Termin „stan” ma w chemii

fizycznej kilka różnych znaczeń

• Pierwsze znaczenie odnosi się do

form w jakich może występować
materia:

• Stan gazowy, ciekły i stały

STAN

• Stan będzie wyrażać opis pewnej

wybranej części materii
określający charakteryzujące
wartości objętości, ciśnienia,
temperatury, i ilości substancji.

• Dwie próbki tej samej substancji

są w tym samym stanie jedynie
wówczas, gdy mają taką samą
masę, objętość, ciśnienie i
temperaturę.

Objętość, temperatura

• Objętość

próbki V jest miarą

przestrzeni, jaka próbka zajmuje.

• Temperatura

ciała jest wielkością, która

określa kierunek przepływu energii,

gdy ciało znajduje się w kontakcie z

innym: energia przepływa od ciała o

temperaturze wyższej do ciała o

temperaturze niższej.

• Gdy dwa ciała maja tę samą

temperaturę, nie zachodzi miedzy nimi

przepływ ciepła i mówimy wówczas, że

znajdują się w

równowadze termicznej.

Jednostki ciśnienia

• W praktyce wielorakość.
• W układzie SI:
• 1 Pa = 1 N/m

2

• W równaniach należy stosować

jednostki Pa

• Inne jednostki:
• 1 bar = 10

5

Pa

• 1 mm Hg = 1 torr = 133.32 Pa

Jednostki ciśnienia

• 1 atm = 1,013 x 10

5

Pa

• 1 psi = 6894,76 Pa
• Ciśnienie w manometrach

pokazuje ciśnienie mierzone

względem ciśnienia

atmosferycznego:

• Psia = psig+14,7 (psi)
• Atmosfera standardowa = 760 mm

Hg = 760 torr = 1,013 bar =

1,013 x 10

5

Pa

Równanie stanu

• Stan dowolnej próbki danej

substancji możemy określić

podając wartości:

• V – objętość, jaką zajmuje próbka,
• P – ciśnienie, pod jakim się

znajduje,

• T – jej temperaturę
• N – ilość substancji, jaką zawiera
• Z doświadczenia wiemy, że te

cztery wielkości nie są od siebie

niezależne

Równanie stanu

• Co to oznacza?
• Np.. W 5,55 moli wody o objętości

100 cm

3

w temp. 500 K panujące

ciśnienie wynosiło by 100 kPa.

Doświadczalnie stwierdza się, że

taki stan nie istnieje.

• Jeżeli dobierzemy: n, V, T, to w

układzie ustali się ciśnienie p

niezależne od naszej woli.

Równanie stanu

• Prawidłowość ta odnosi się do

wszystkich substancji.

• Inaczej mówiąc stwierdza się, że

substancja spełnia określone

równanie stanu.

• Dla większości nie jest znane. W

szczególności znane jest równanie

stanu dla gazów pod niewielkim

ciśnieniem.

Równanie stanu gazu

doskonałego

• Równanie stanu gazów było

jednym z pierwszych praw chemii
fizycznej.

• Równanie Boyle’a Mariott’a
• Stanowi idealizację równań stanu

spełnianych w rzeczywistości
przez gazy.

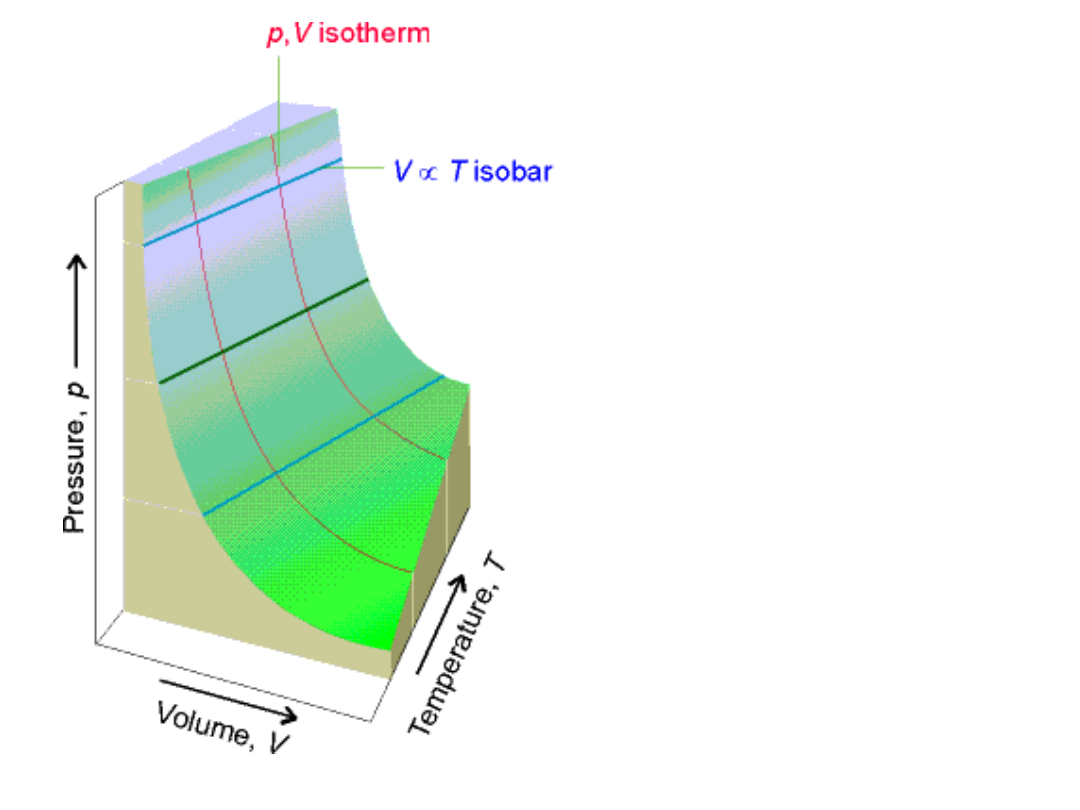
Gazy idealne i gazy

rzeczywiste

• Równanie
• P·V = n · R · T
• P – Pa
• V – m

3

• n – liczba moli gazu
• T – temperatura w K
• R – stała gazowa [ 8,314 J mol

-1

K

-1

]

Wartości stałej gazowej w

różnych jednostkach

• R = 8,31451• J • K

-1

• mol

-1

– 8,31451 • kPa • l • K

-1

• mol-1

– 8,20578 • 10

-2

• l • atm • K

-1

• mol-1

– 62,364 • l • Tr • K

-1

• mol

-1

– 1, 98722 • cal • K

-1

• mol

-1

Równania gazu

doskonałego

• Podstawą kinetyczna teoria gazu

– Doskonałe elastyczne kule
– Objętość kuli do pominięcia
– Brak występowania oddziaływań:

• przyciągających
• odpychających

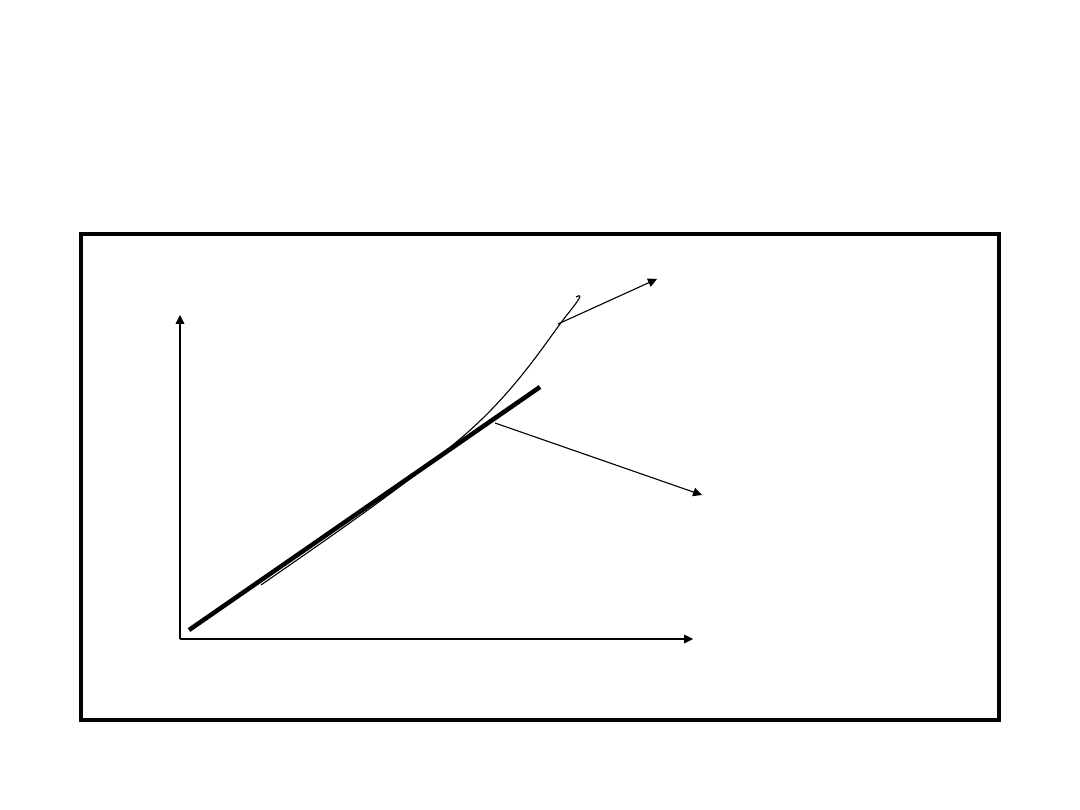
Prawo Boyle’a p versus

1/V

• P vs 1/V

p

1/objętość, 1/V

Ciśnienie
gazu
doskonałego

Ciśnienie
obserwowana

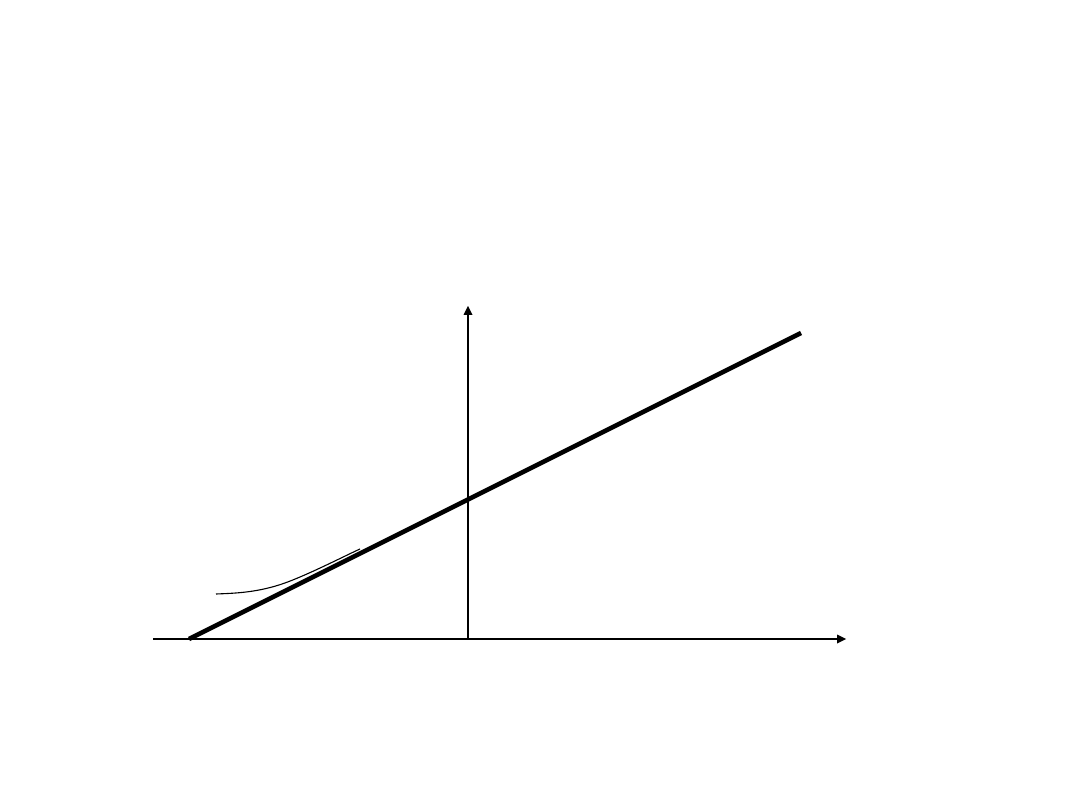
Prawo Charlesa V versus

t/°C

• V vs t/C

-273

0

Temperatura /°C

Objętość molowa

• Objętość molowa,

V

m

, dowolnej

substancji przedstawia objętość
zajmowaną przez mol cząsteczek
tworzących substancję:

• V

m

= V/n

• Z zasady Avogadra wynika, że

objętości molowe wszystkich
gazów w tych samych warunkach
p i T są jednakowe

Warunki standardowe

• Temperatura 25°C dokładnie (298,

15 K)

• Ciśnienie 100 kPa (tj. 1 bar)
• Ciśnienie standardowe p = p



= 1

bar

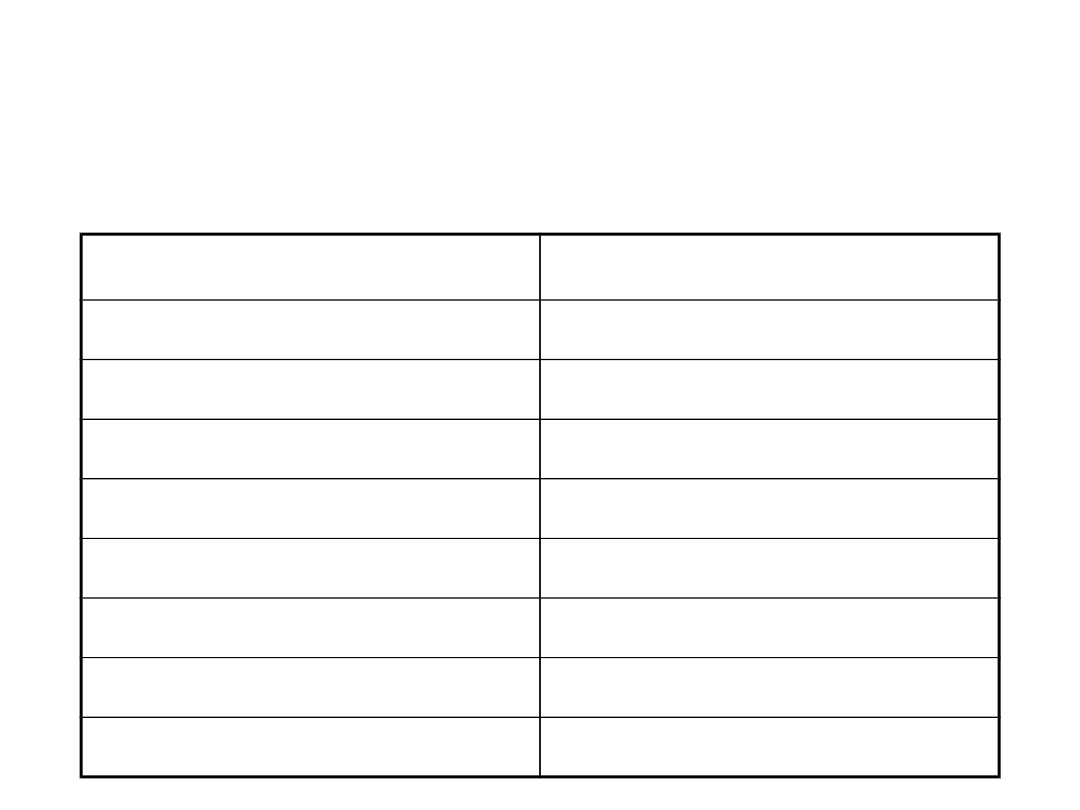
Objętości molowe gazów w

temperaturze 25 °C i pod

ciśnieniem 1 bar

Gaz

V

m

/l· mol

-1

Gaz doskonały

24,79

Amoniak

24,4

Argon

24,8

Dwutlenek węgla

24,6

Azot

24,8

Tlen

24,8

Wodór

24,8

Hel

24,8

Areozole

• W niektórych typach areozoli
• Gaz pod ciśnieniem

wykorzystywany jest do wydalenia
produktu jako strumienia ciała
stałego, mgły, lub piany.

• Ciśnienie gazu w areozolach

można obliczyć wykorzystując
prawo B

Obliczenie ciśnienia z

wykorzystaniem prawa B

• Oblicz ciśnienie gazu w pojemniku

zawierającym areozol, jeżeli
temperatura wynosi 25 °C,
objętość pojemnika V = 250 cm

3

,

objętość cieczy V

C

= 160 cm

3

. Do

pojemnika wprowadzono 0,04
mola azotu.

Rozwiązanie

• PV = n R T P = n R T / V
• P = ?
• V

g

=V – V

c

= 250 cm

3

-160 cm

3

= 90 cm

3

• 90 cm

3

x [1 m

3

/10

6

cm

3

]

• n = 0,04
• T = t °C + 273,15 K = 25 + 273,15 =

298,15

• P = (0,04 mol x 8,314 J/[mol K] x

298,15 K)/(90 cm

3

1 m

3

x 10

-6

cm

-3

) =

1,01 x 10

6

N m

-2

(lub Pa)

Równanie stanu gazów

rzeczywistych

• Napiszmy równanie stanu dla 1

mola gazu podzielmy stronami
przez n RT:

1

RT

1

pV

nRT

pV

m

m







Współczynnik ściśliwości

• Poprzednie równanie sugeruje wartość

jeden dla wszystkich gazów.

• Prawa strona wyrażenia oznaczana jest

jako z

• Zmiana ciśnienia nie powinna wpływać

na wartość tego wyrażenia.

• W rzeczywistości wartość ta różni się

od jedności i zależy od ciśnienia.

• Odchylenia są wywołane

oddziaływaniami

międzycząsteczkowymi.

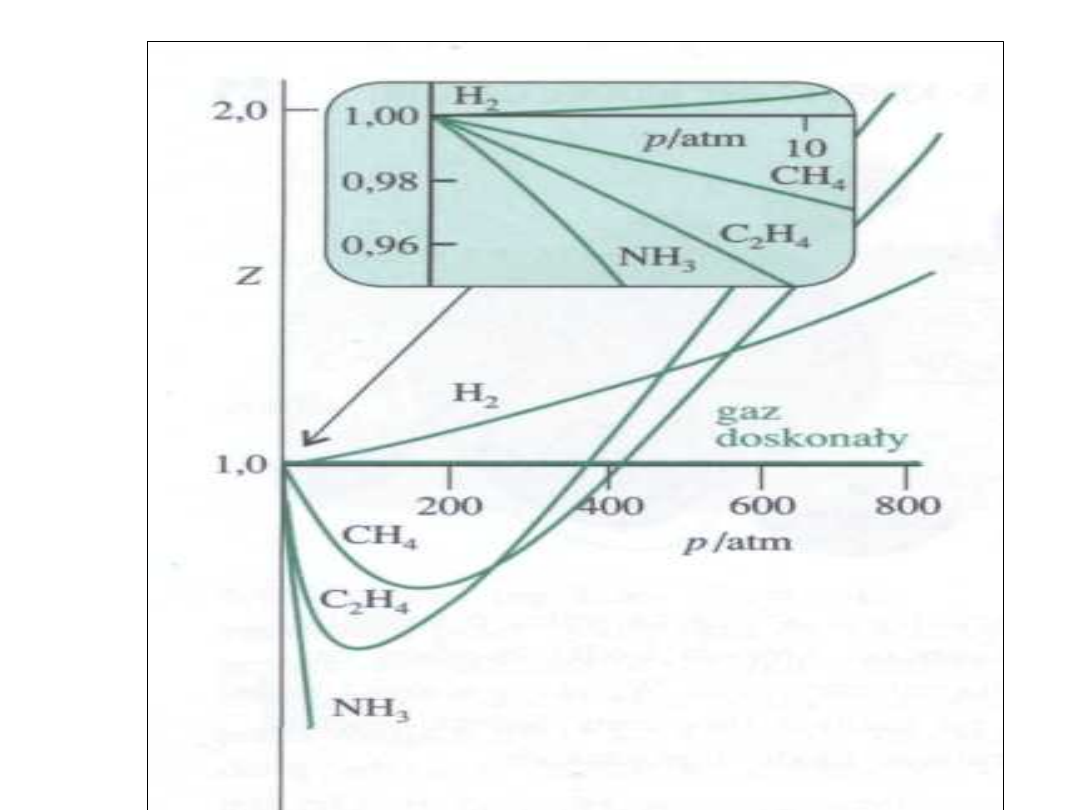
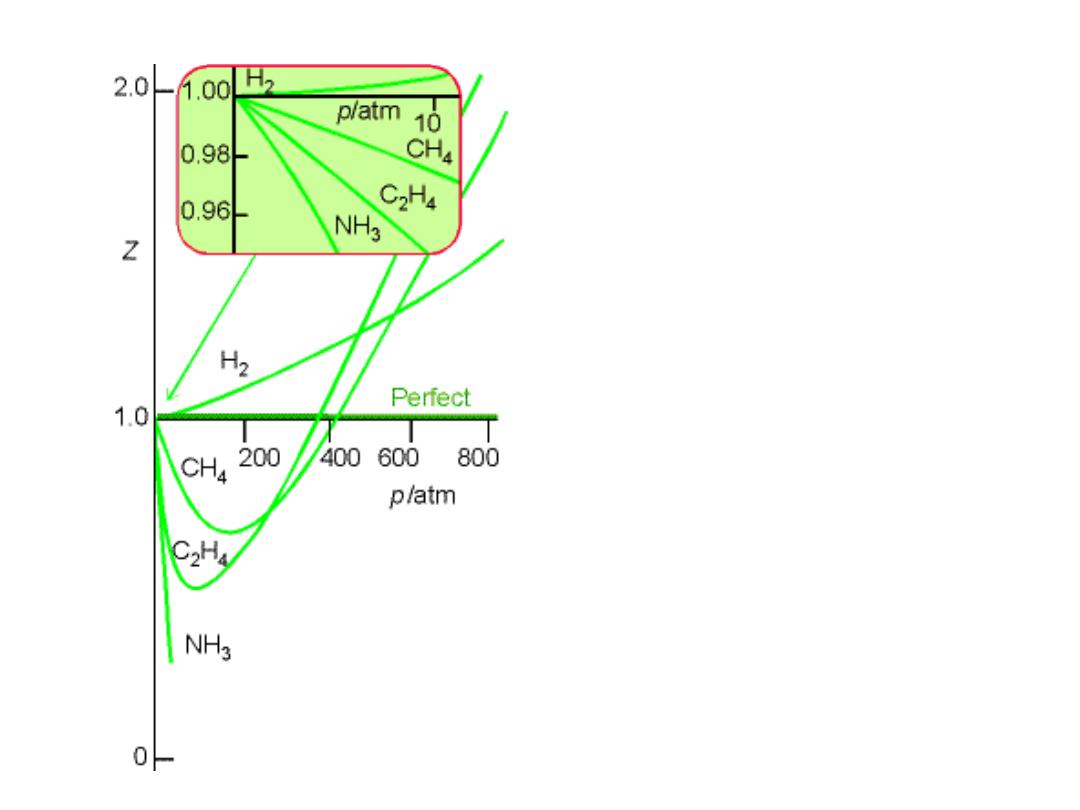
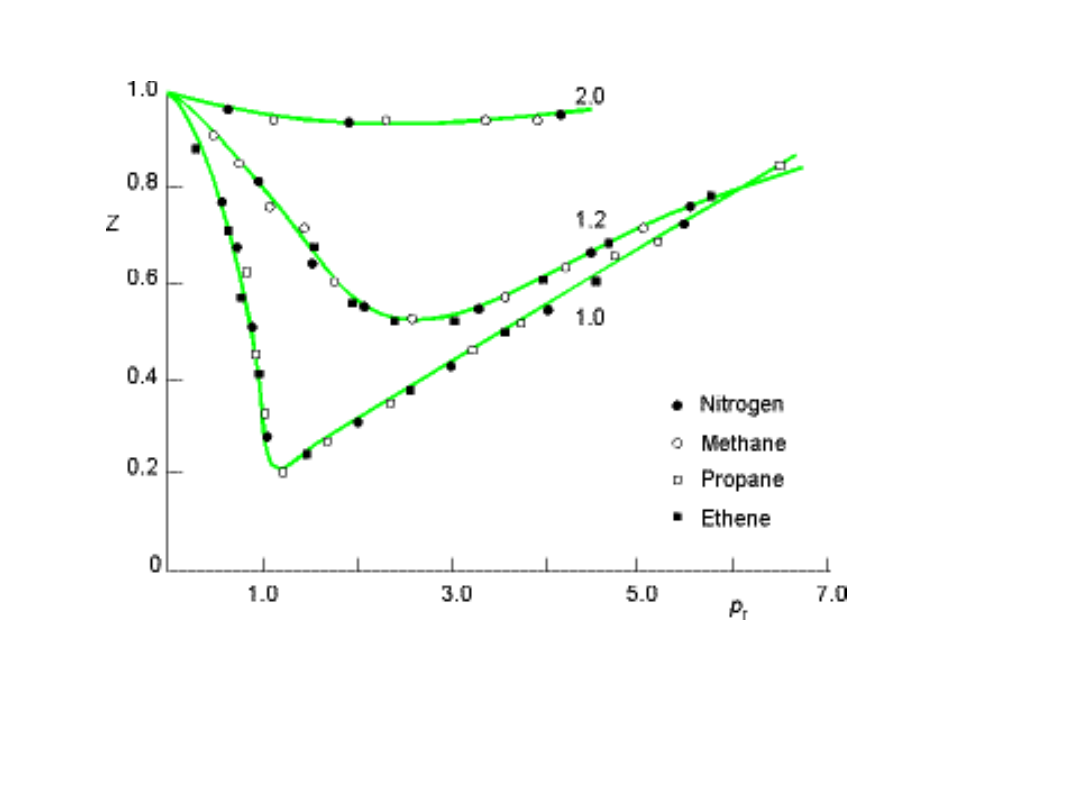
Z- odstępstwa od 1

• Wykres przedstawia z = f(p) dla

temperatury 0 °C.

• Wodór wykazuje z >1 zawsze
• Pozostałe gazy
• z < 1 w początkowej fazie
• z > 1 przy wysokich ciśnieniach
• z > 1 oznacza V

m

> od wartości

oczekiwanej (siły odpychania)

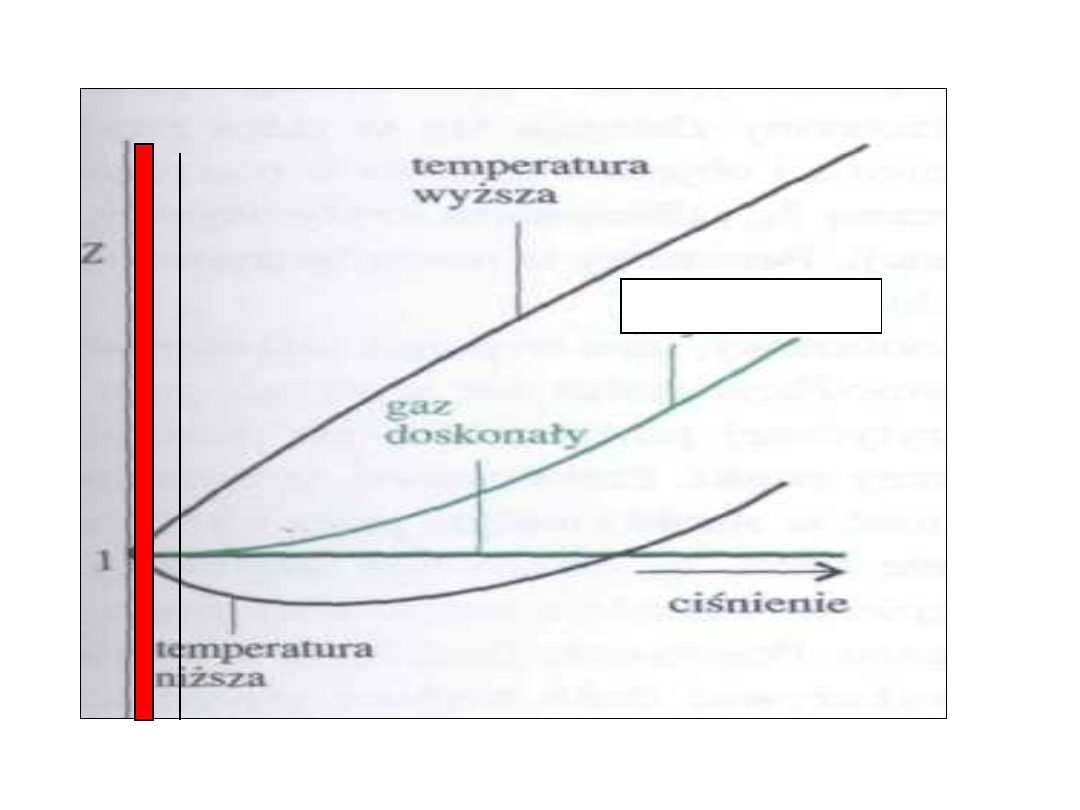
Systemy spotykane w

medycynie

• Obszar zaznaczony na czerwono

obejmuje zakres ciśnień z jakim
spotykamy się w medycynie, zatem
zastosowanie praw odnoszący się
do gazów idealnych jest słuszne

Gazy rzeczywiste

• Van der Waals wprowadził

poprawki do gazowego równania

stanu gazowego uwzględniające

wzajemne oddziaływanie

cząsteczek i objętość własną

cząsteczek.

• Dla 1 mola gazu rzeczywistego

równanie van der Waalsa ma

postać

• (p + a/V

2

)(V-b) = RT     

Gazy rzeczywiste

• gdzie: V - oznacza objętość gazu

rzeczywistego,

• p - ciśnienie,
• R - stała gazowa,
• T - temperatura w Kelvinach,
• a i b - stałe charakterystyczne dla

danego gazu rzeczywistego

Gazy rzeczywiste

• Wartość a jest stałą wynikająca z

istnienia sił przyciągania
międzycząsteczkowego, natomiast
b jest poprawką związaną z
objętością własną cząsteczek gazu.

Gazy rzeczywiste

• Poprawka a/V

2

nosi nazwę

ciśnienia wewnętrznego gazu.
Dodaje się ją do ciśnienia
zewnętrznego p dlatego, że
ciśnienia te mają zgodny kierunek
działania.

Gazy rzeczywiste

• Poprawka b zależy od wielkości i

kształtu cząsteczki gazu rzeczywistego,
oznacza tzw sferę działania
cząsteczek.

• b jest równe w przybliżeniu poczwórnej

objętości własnej cząsteczek.

• Poprawkę b wynikającą z istnienia

objętości własnej cząsteczek odejmuje
się od całkowitej objętości v zajmowanej
przez gaz.

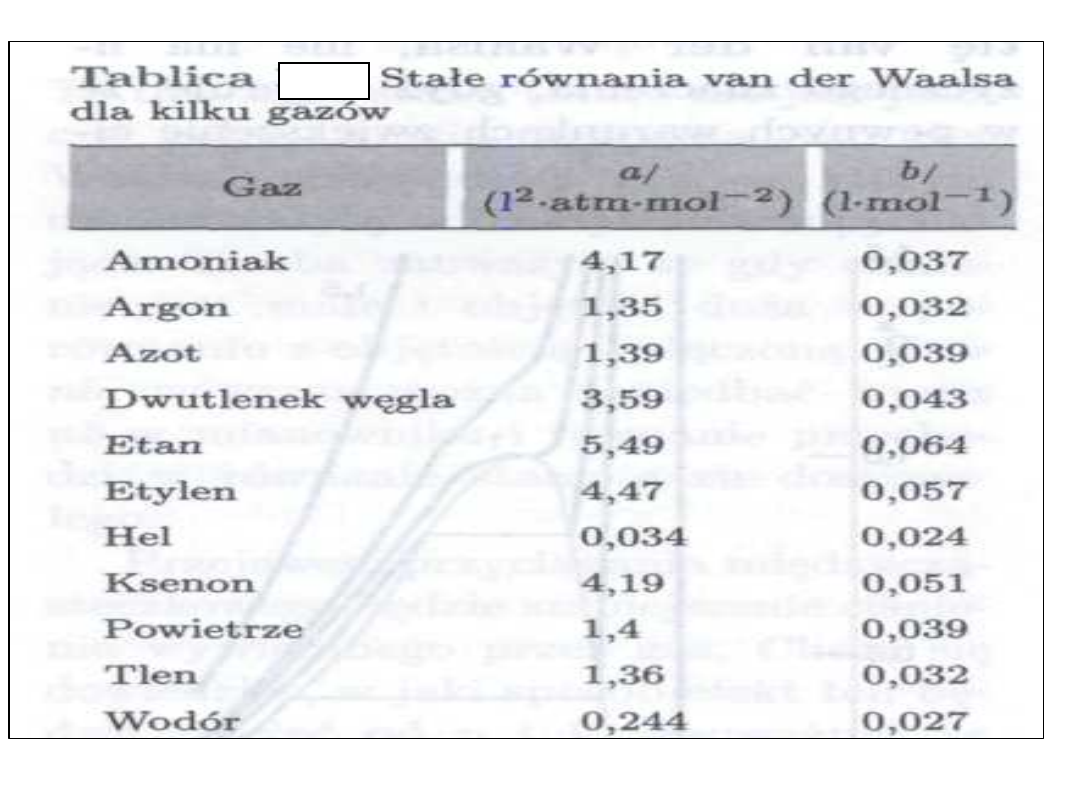
Porównanie zachowania

się gazów

• 0,193 mola eteru wypełnia

zbiornik o pojemności 7,35 litra w
temp. 295 K.

• Oblicz ciśnienie p stosując

równanie gazu idealnego i
rzeczywistego.

• Poprawka dla eteru a = 17,38 L

2

atm mol

-2

• Poprawka b = 0,1344 L mol

-1

.

Rozwiązanie

• P • V = n • R • T
• (P+a • n

2

/V

2

) •(V-b) = R • T

• P = R • T/(V-b)-a • n

2

/V

2

• P = (0,193 • mol • 0,0821 • l •

atm • deg • mol • 295 deg)/7,35 l
=

0,636 atm

• P= (0,193 • 0,0821 • 295)/[7,35-

(0,193 • 0,1344)]-17,38 • 0,193

2

=

0,626 atm

Gaz idealne i rzeczywiste

• Obliczyć ciśnienie 0,5 mola dwutlenku

węgla w gaśnicy o pojemności 1 litra w
temperaturze 27°C. Poprawki równania
van der Waalsa wyliczyć na podstawie
temperatury i ciśnienia krytycznego:

• Poprawka a = 27 R

2

T

2

c

/64 P

c

• Poprawka b = RT

c

/8P

c

• Temperatura krytyczna T

c

= 31,0 C

• Ciśnienie krytyczne P

C

= 72,9 atm

Rozwiązanie

• P = n • R • T/V=0,5 • 0,0821 •

300,15/1 = 12, 32 atm

• A = 27 • (0,0821)

2

(304.15)

2

/(64

72.9) = 3,608

• B = (0,0821 • 304,15)/(8 • 72,9) =

0,0428

• P = n • R • T/(V-n • b)-a •

n

2

/V

2

=(0,5 • 0,0821) • 300,15/(1-

(0,5 • 0,0428)-(3,608 • (0,5)

2

)/1

2

=

11, 69 atm

Mieszaniny gazów i

ciśnienia cząstkowe

• Mieszaniny gazów
• Skład atmosfery – meteorologia
• Wydychane powietrze – medycyna
• Synteza amoniaku – przemysł

chemiczny

• Jaki jest wkład każdego ze

składników mieszaniny do
całkowitego ciśnienia?

Prawo Daltona

• Ciśnienie wywierane przez

mieszaninę gazów doskonałych
jest sumą ciśnień, jakie
wywierałby każdy z gazów z
osobna.

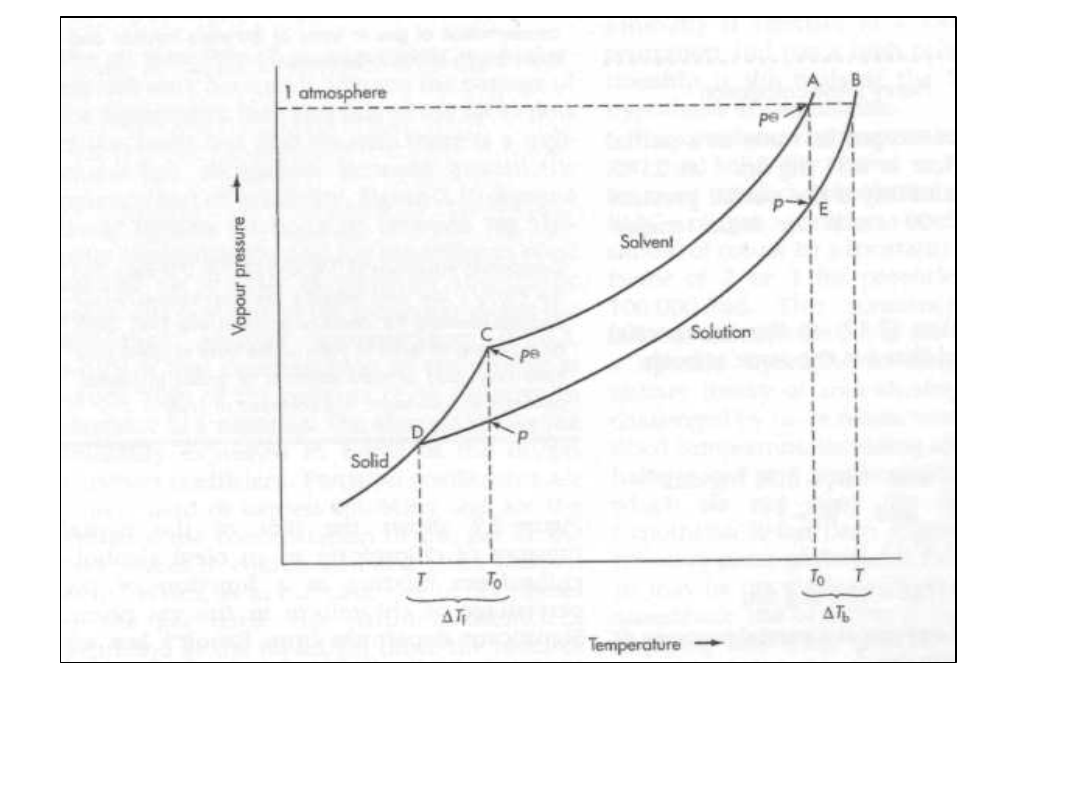
Ciśnienie par nad

roztworem

• Dla roztworu idealnego ciśnienie

par opisuje równanie Raoult’a”

i

0

i

i

x

p

p





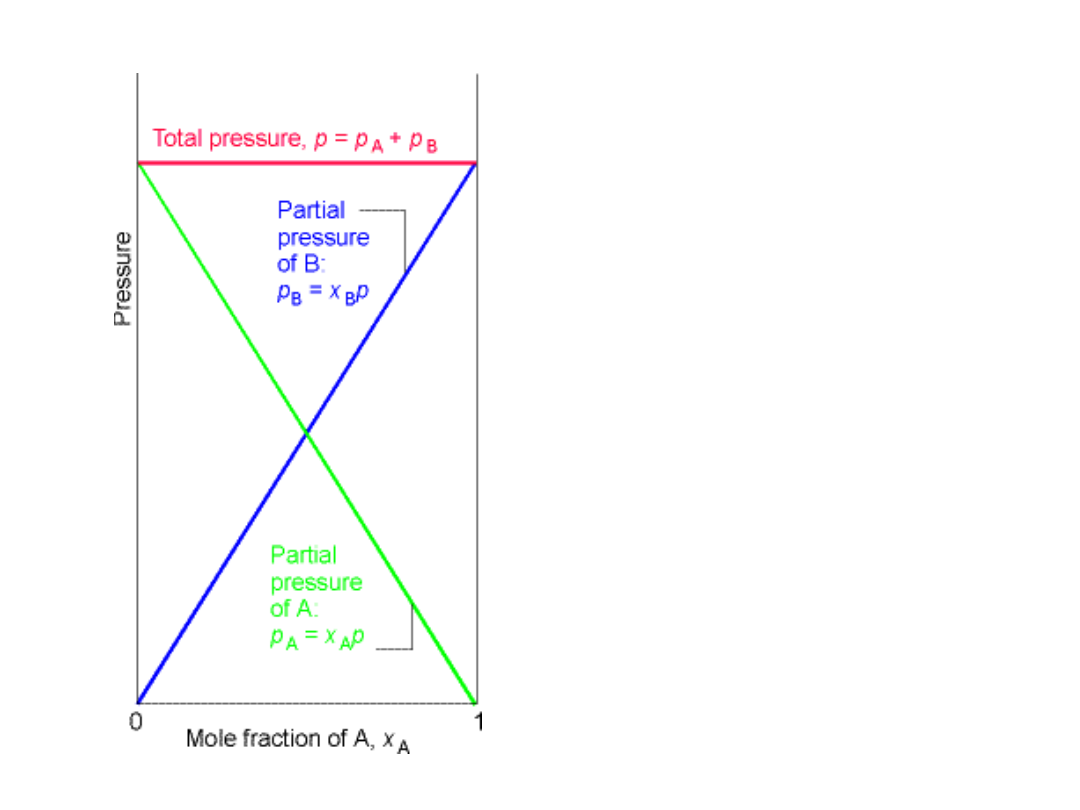
Prawo Rault’a

• Znaczenie polega na możliwości

obliczenia

• prężności par ze znajomości

składu roztworu.

• Ze względu na ochronę

środowiska w 1989 wprowadzono
zmiany w cieczach używanych do
wypełniania urządzeń,
chłodniczych, inhalatorów itp..

Dziura ozonowa

• Pochodne chlorofluoroalkanowe

(CFC) na pochodne
hydrofluoroalkanowe  znacząca
różnica we właściwościach
fizycznych i chemicznych.

• Właściwości najczęściej

stosowanych wypełniaczy
przedstawia następne przezrocze:

Właściwości pochodnych

fluorowcowych alkanów

Wypełniac

z

Wzór

M

T

wrz

(°C )

przy p = 1 atm

P (psig),

w 20 °C

HFA 134a C

2

H

2

F

4

102,0

-26,5

68,4

HFA

C

3

HF

7

170,0

-17,3

56,0

Dozowniki - inhalatory

• Ciśnienie w inhalatorach określa

wielkość kropli i wpływa na
skuteczność ich osadzania się w
płucach.

• Rozpatrzmy następujący przykład

w którym w zależności od rodzaju
wypełniacza istnieje równowaga
pomiędzy cieczą a parami.

Obliczenie ciśnienia par w

mieszaninie fluorowęglowodorów

• Mieszanina zawiera 30% w/w HFA

(składnik 1) 134a i 70% w/w HFA
227(składnik 2). Zakładamy
idealne zachowanie się
mieszaniny. Korzystamy z danych
w tabeli:

1

0

1

1

x

p

p





cd. zadania

• Dla drugiego składnika:

• Obliczmy ułamki molowe składników

mieszaniny:

• n

1

= 30/102 = 0,2941 mola

• n

2

= 70/170 = 0,4118 mola

• Suma = 0,2941 + 0,4118 = 0,7059 moli

2

0

2

2

x

p

p





Prawo Daltona

• X

1

= 0,2941/0,7059 = 0,4166

• X

2

= 0,4118/0,7059 = 0,5834

• Prawo Daltona – ciśnienie całkowite
• P =  ciśnień cząstkowych (zakładając

idealne zachowanie się gazów)

• P = (68,4 x 0,4166) + (56,0 x 0,5834) =

61,17 psig

• Przeliczając jednostki otrzymamy:
• Psia=psig+14,7 i 1psia = 6894,76 Pa P

= 5,23 x 10

5

Pa

Pompa infuzyjna

• Wykorzystanie stałego ciśnienia

nad roztworem
fluoroweglowodorów.

• Pompy infuzyjne:
• Wprowadzenie pod skórę brzucha
• Dostarczają płyn z stałą

szybkością:

• Np.., 1 cm

3

/dzień do żyły lub

tętnicy

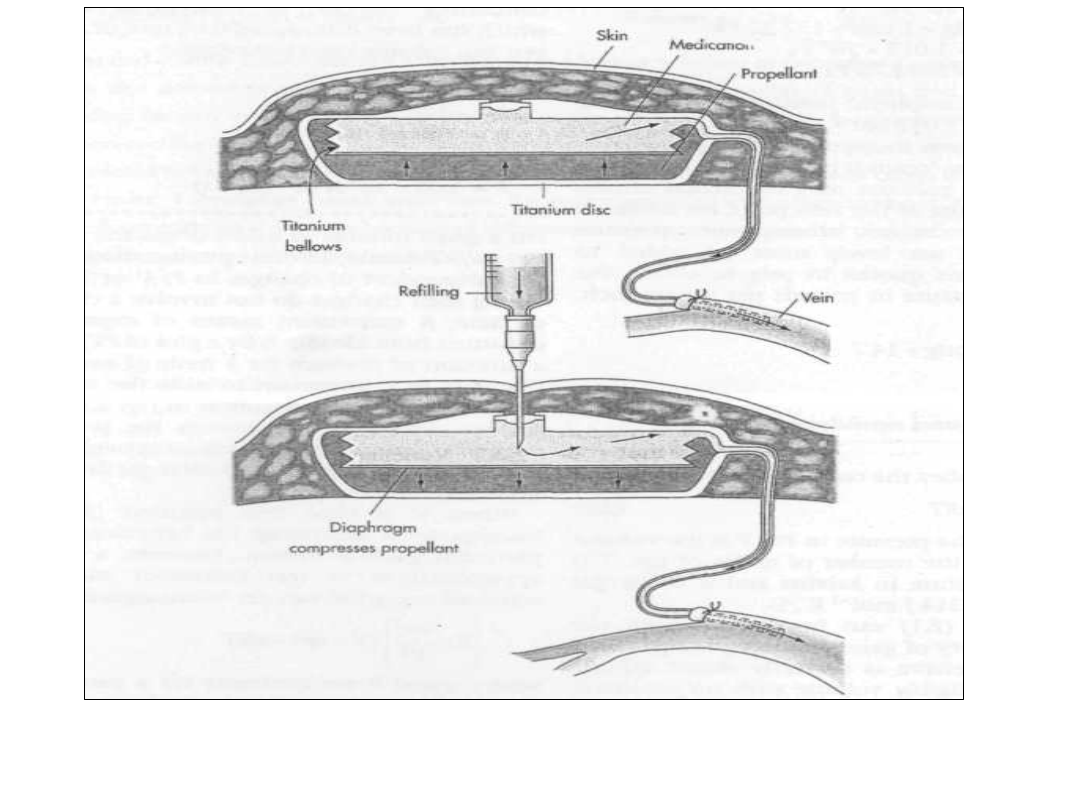
Zasada działania pompy

infuzyjnej

• Pierwsza podawana była heparyna
• Obecnie wiele leków
• Wymiar dysku 9 x 2,5 cm (tytan)
• Dwa zbiorniki przedzielone

nieprzepuszczalną membraną w
kształcie miechu.

• Zewnętrzny zawiera wypełniacz -

Freon

Zasada działania pompy

dyfuzyjnej

• Wewnętrzny zbiornik zawiera płyn

infuzyjny, który za pomocą cewnika
dostarczany jest do żyły(tętnicy),
poprzez filtry i oporniki regulujące
przepływ.

• Ponieważ ciśnienie par wypełniacza

pozostaje stałe (mała wrażliwość)-
temperatura ciała zmienia się w
niewielkim stopniu – stąd stałe
ciśnienie wywierane na brzuch, a w
konsekwencji stała szybkość
dostarczania płynu do krwi.

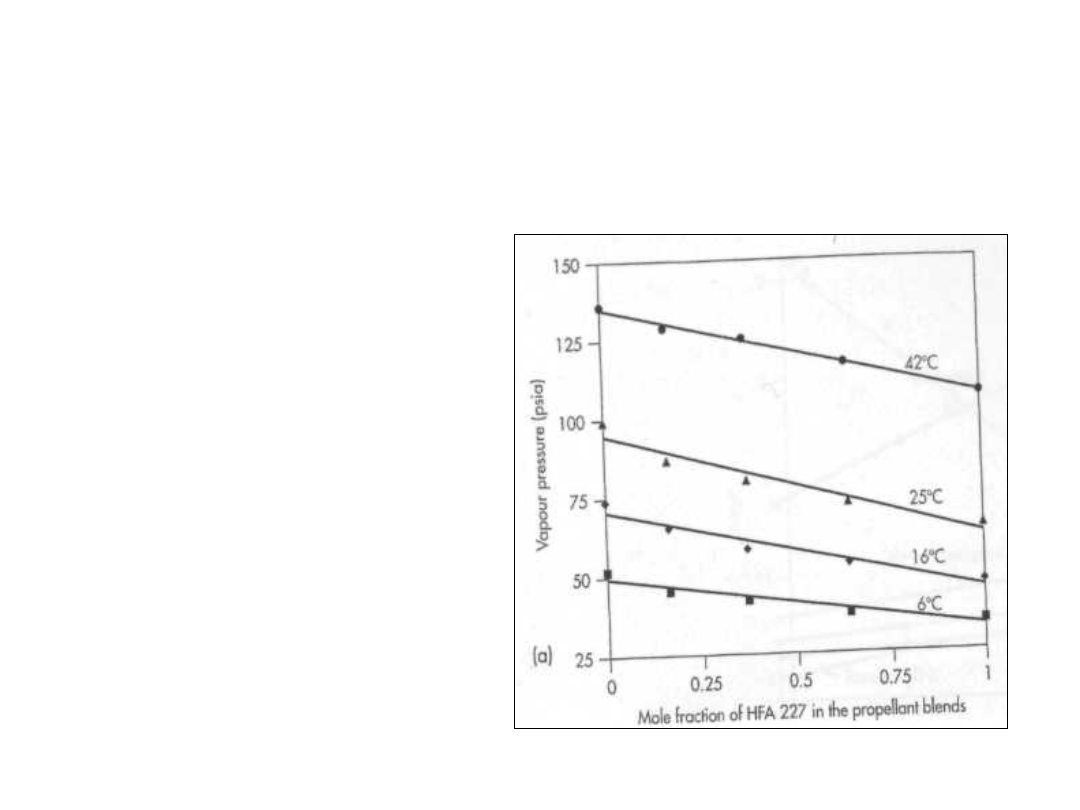
Wpływ temperatury

• Wykres obok

przedstawia

wpływ

temperatury na

zachowanie się

mieszaniny:

• Liniowość w

całym zakresie –

gaz idealny

• Tylko 2 psia w

zakresie 1 stopnia

czyli około 0,2

atm

Dodatek trzeciego

składnika

• Czasami należy poprawić właściwości

wypełniaczy przez dodatek
rozpuszczalnika.

• Poniższy diagram ilustruje zachowanie

się mieszaniny w sytuacji dodawania
etanolu.

• Należy rozpatrzyć oddziaływania –

pomiędzy samymi cząsteczkami CFC a
pomiędzy cząsteczką CFC a cząsteczka
alkoholu.

• CFC jest silnie niepolarną

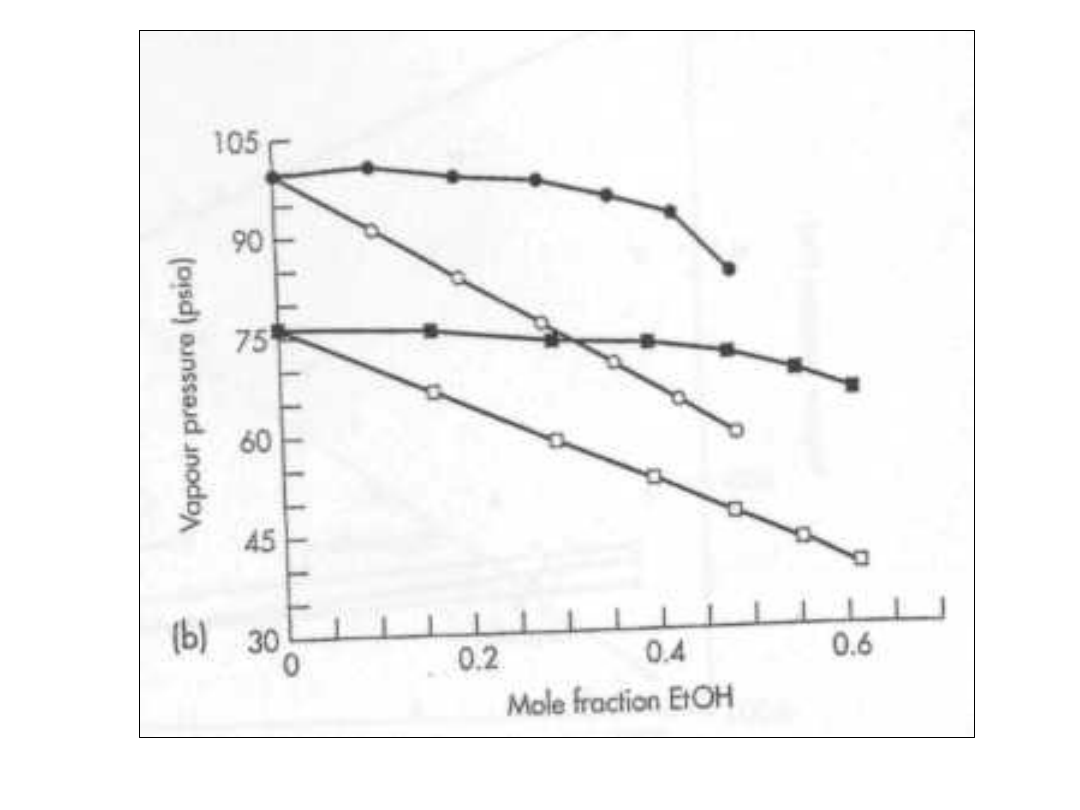
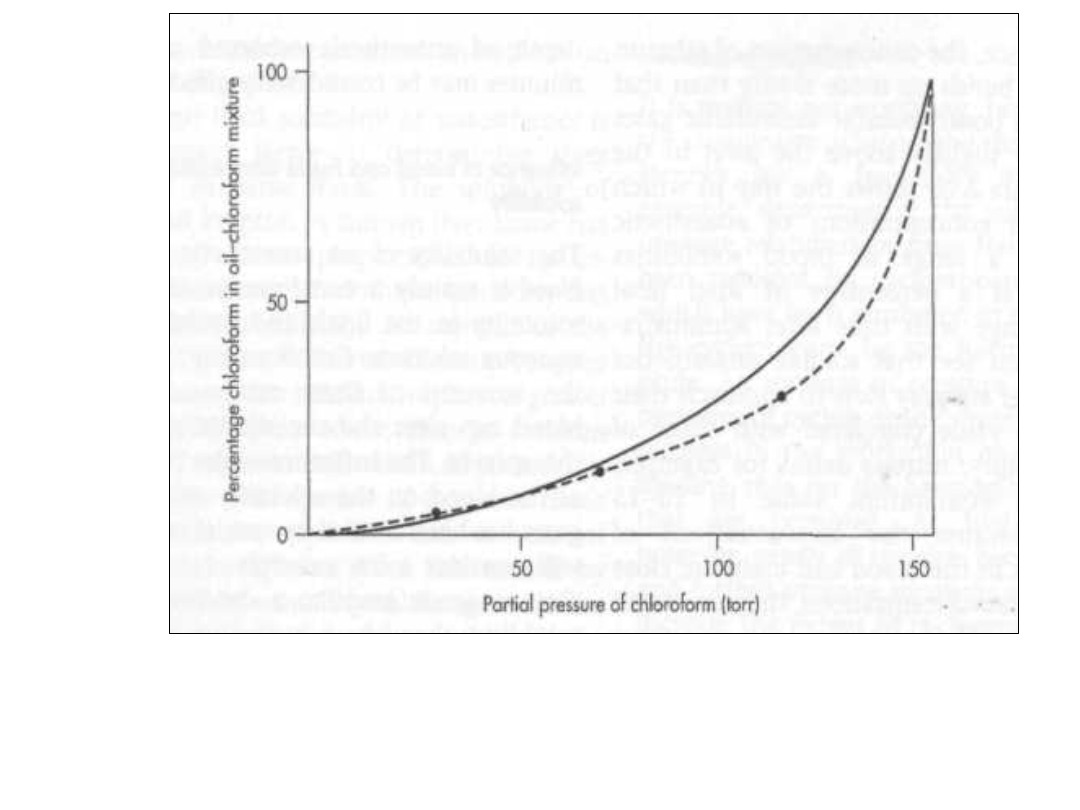
Dodatnie odchylenia od

prawa Rauolt’a

• Korzyści z dodatniego odchylenia

polegają na wzroście całkowitej

prężności a tym samym

właściwości nie ulęgają

pogorszeniu

• Wykres fazowy dla pary środków

znieczulających przedstawiony jest

poniżej:

• Enflurane – halothane
• Enflurane – znaczne odchylenie
• Laothane – niewielkie odchylenie

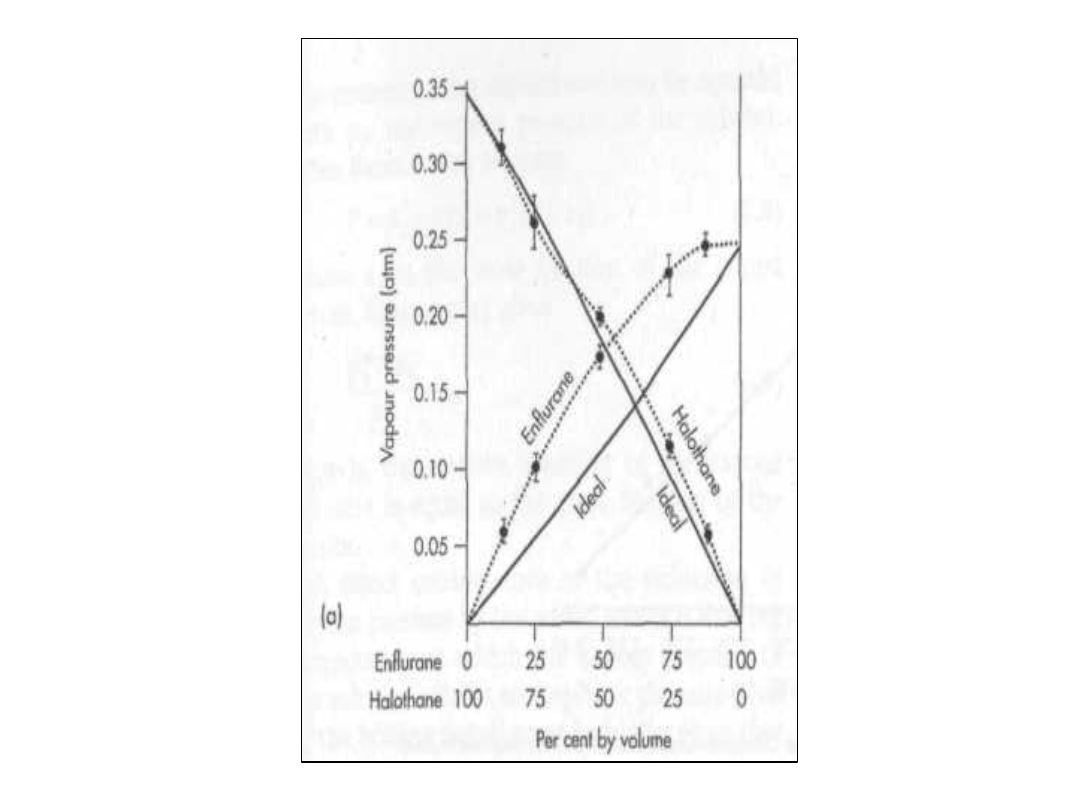
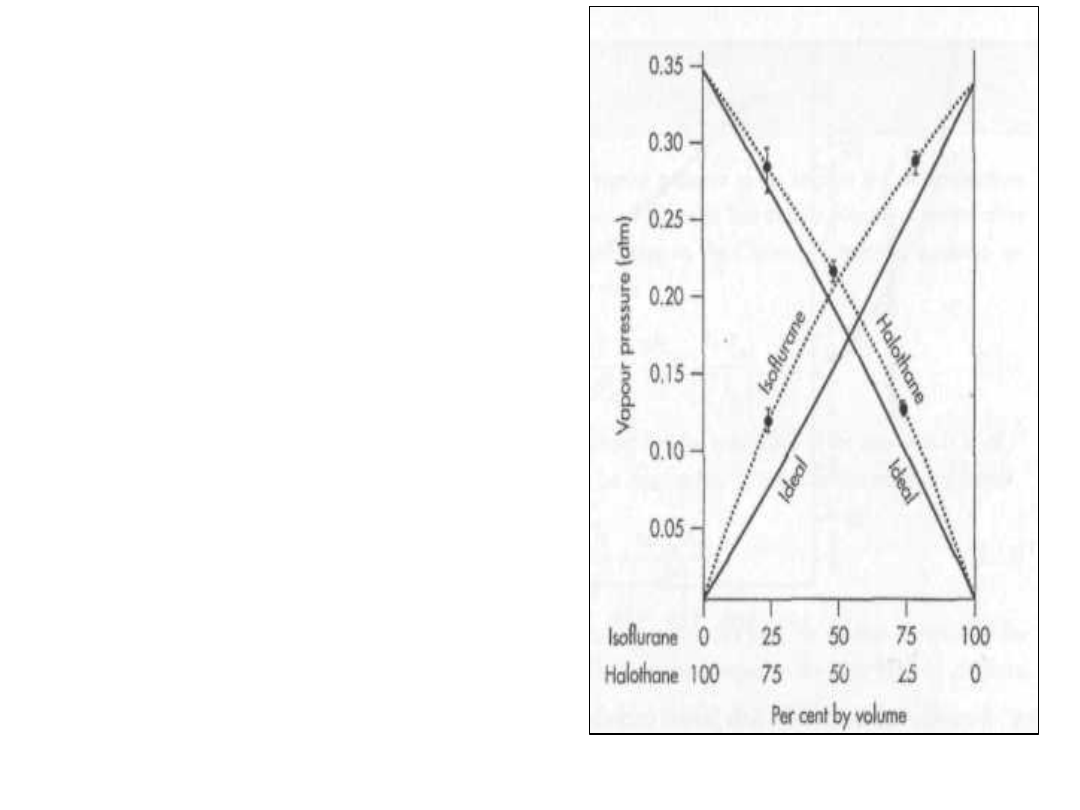
Asocjacja składnika

• Duże odchylenia są spowodowane

asocjacją jednego ze składników

• Gdzie wykorzystuje się praktycznie

takie diagramy fazowe:

• Środki znieczulające są podawane

poprzez wykorzystanie mieszanin ich z

gazem obojętnym.

• Jeżeli składniki są pomylone to wtedy

do organizmu są wprowadzone większe

ilości co może spowodować przykre

konsekwencje. Skład ten sam lecz

prężności par inne i inny skład w

mieszaninie.

Wpływ temperatury na ciśnienie p

• Temperatura powoduje wzrost

energii kinetycznej cząsteczek co
zwiększa tendencje do
opuszczenia powierzchni cieczy i
przechodzenia do fazy gazowej.

• Zmianę ciśnienia z temperaturą

określa równanie Claperon’a

Równanie Clausius -

Clapeyron

• Równanie różniczkowe:

V

T

H

dT

dP

par









Opis równania

• V – różnica objętości molowej w

stanie pary i stanie cieczy

• Ponieważ V

par

>>V

c

• Można różnice zastąpić przez V

par

• Zakładając idealne zachowanie się

pary można obliczyć V = n R T/p

Rózniczkowa postać

równania

• Równanie można całkować

2

par

2

par

T

dT

R

H

P

dP

lub

T

R

H

P

dT

dP















Całkowanie

• Log p vs 1/T

• Wykres linii prostej – nachylenie

s

RT

303

,

2

H

P

log

par









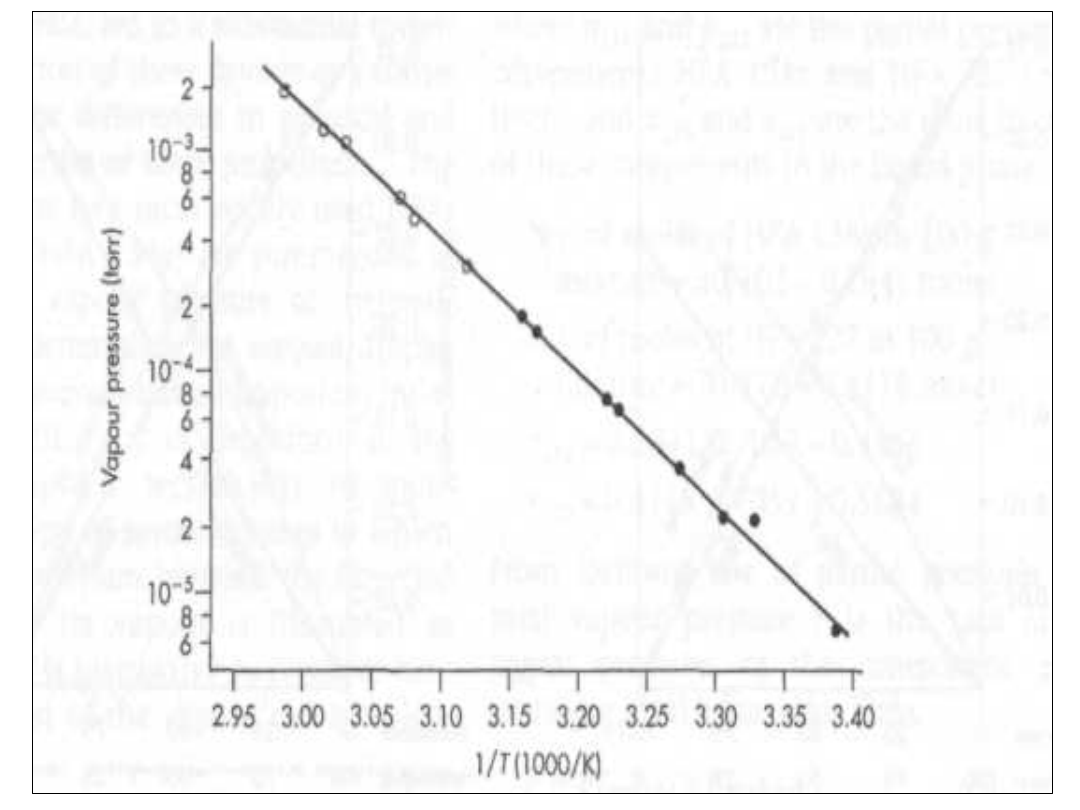
Wykorzystanie równanie

CC

• Równanie to można

wykorzystywać

• Do obliczenia entalpii parowania
• W przejściach fazowych

Sublimacja ibuprofenu

• Można porównać

prężność w
zakresie 23-64 C
przy entalpii
parowania 121 kJ
mol

-1

• W temp 23 jest

bardzo niska
rzędu 9 x 10

-6

ale

szybko rośnie o
kilka rzędów

Sublimacja

• Zmiana prężności powoduje, że w

temp. 55 C ubywa 4,15 mg w
ciągu dnia.

Ocena ryzyka

zawodowego

• Leki o działaniu cytostatycznym w

chemoterapii

• Zanieczyszczenia są wykrywane

bowiem ma miejsce rozlewanie,

• Wdychanie cieczy w postaci

areosolu (wyciąganie igieł)

• Bezpośredni kontakt z lekami -

rękawiczki

Parowanie

• Środki cytotoksyczne parują, i

tworzą pary

• Stwarzają ryzyko wdychania ich

przez personel

• Czynniki wpływające na szybkość

parowania

Szybkość parowania leku

• Ciśnienie par
• Wielkość cząsteczek (lek

sproszkowany)

• Camustine w temp. 40 C prężność

0,530 Pa oraz szybkość
wyparowania:

• d = 1 m 12 s
• d = 100 m 1,2 x 10

5

s [dodac

wykres]

Inne środki

antyneoplastyczne?

• Wykres p vs 1/T
• Im bardziej stromy wykres tym

większa entalpia a zatem
trudności w parowaniu tym
bezpieczniejszy środek dla
personelu go stosującego

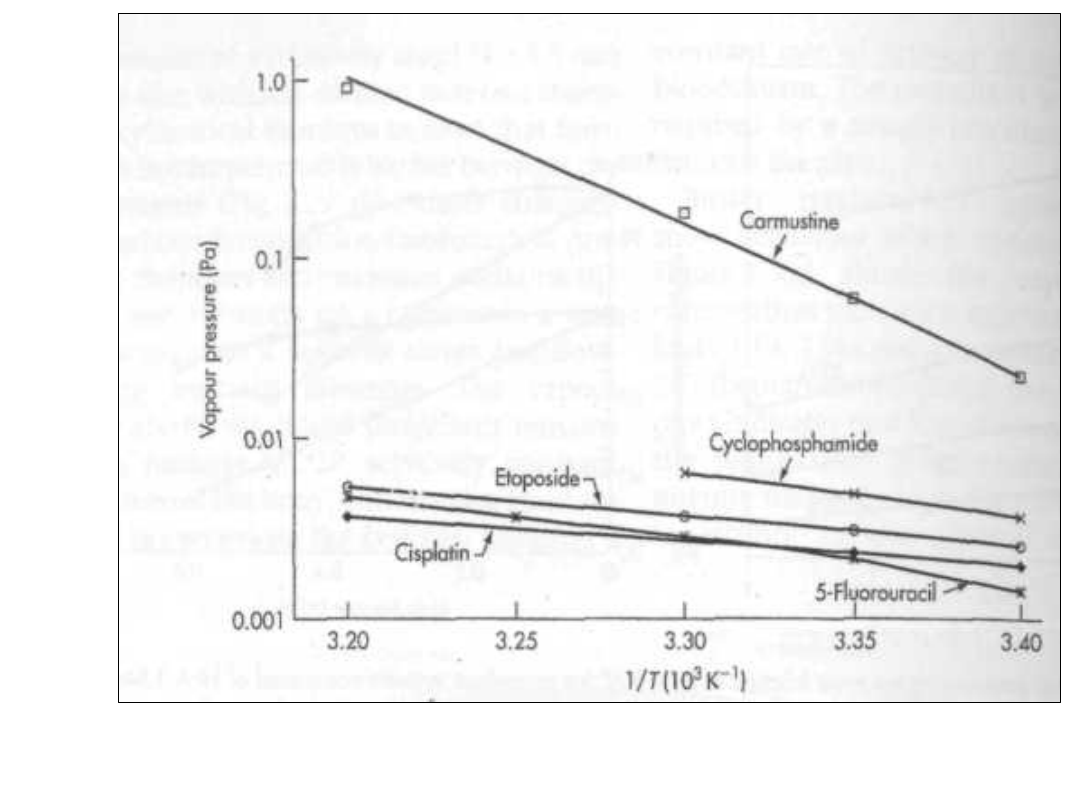
Obliczenie molowej entalpii

parowania

• Nachylenie wykresu p vs 1/T

wynosi:

• -2,727 x 10

3

K

• Obliczyć entalpię parowania:
• Nachylenie = -H

par

/(2,303 RT)=-

2.727 x 10

3

K

• H

pa

= -2,727 x 10

3

x 2,303x8,314=-

52,2 x 10

3

J mol

-1

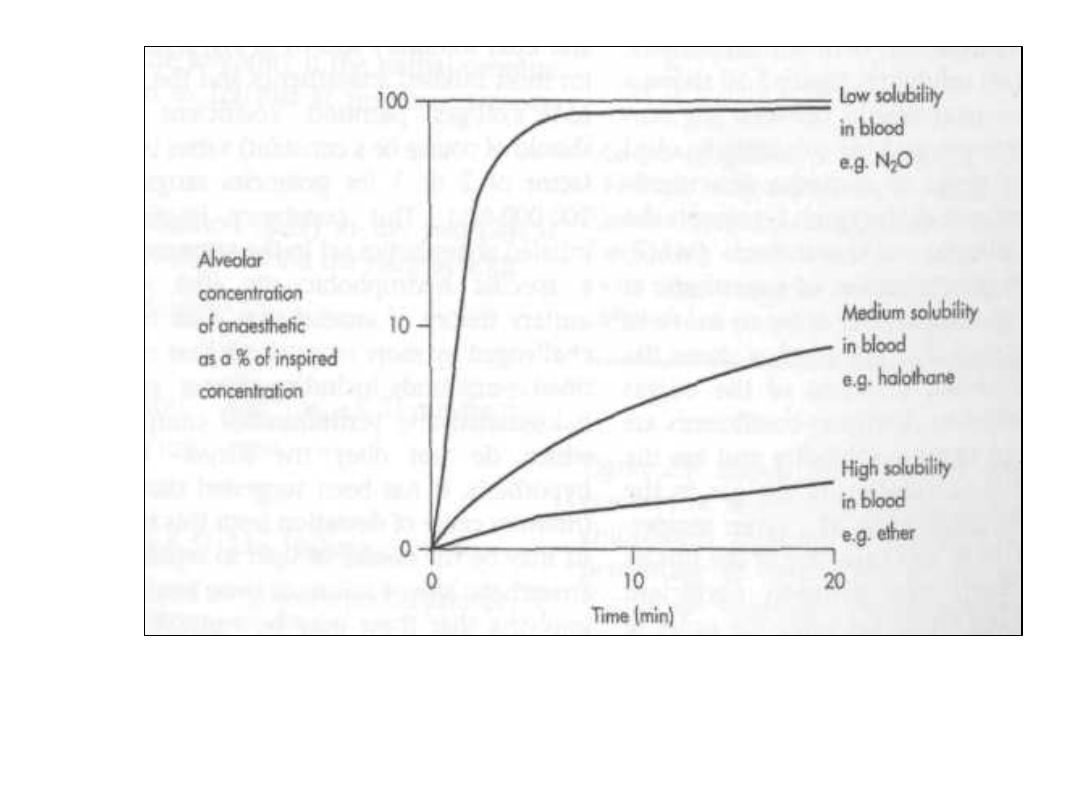
Gazowe znieczulanie

• Istnieje równowaga pomiędzy

gazem znieczulającym a gazem w
przestrzeni gdzie on działa:
biofazą. Prężność pary powinna
być opisywana równaniem C C.

• Dla celów porównawczych należy

równanie zmodyfikować tak aby
można było je zastosować do
każdego gazu

Wielkości zredukowane

• Należy wprowadzić wielkości

termodynamiczne-zredukowane

• Zredukowaną temperaturę

fizjologiczną T

f

• Można otrzymać dzieląc

temperaturę fizjologiczną (temp.,
ciała) prze temp. Wrzenia gazu

Wielkości zredukowane

• Powinno się otrzymać jedna linię

s

RT

303

,

2

H

P

log

r

par









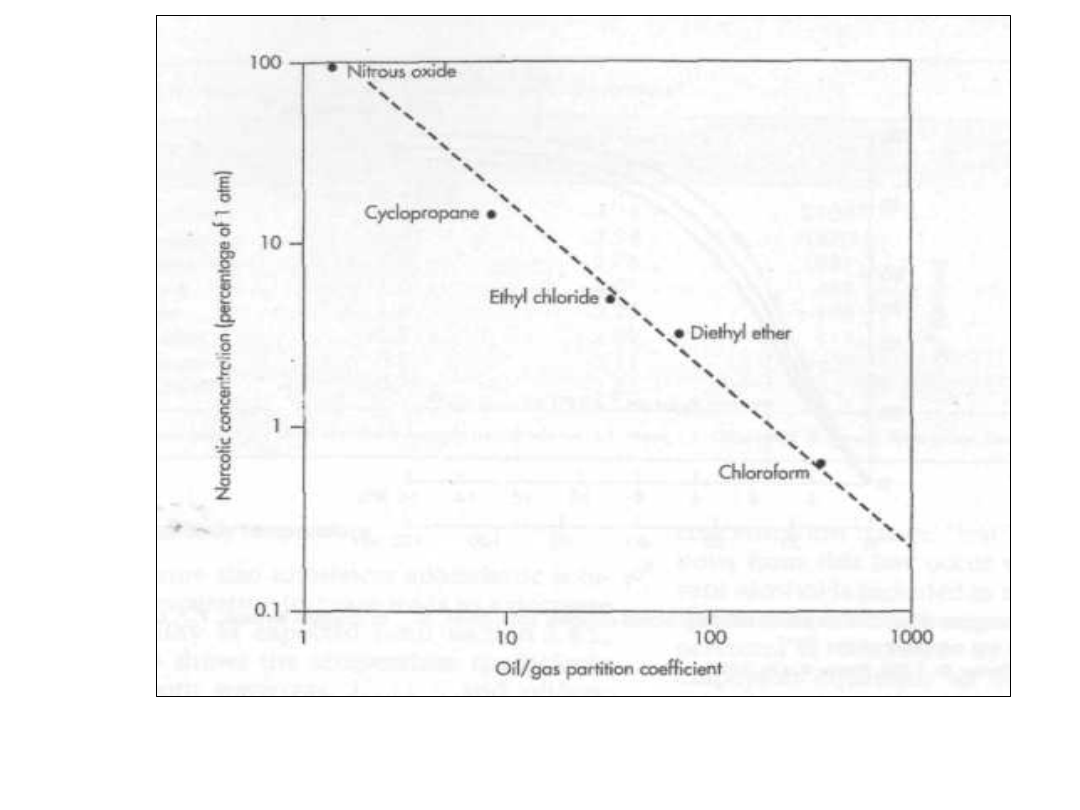
Ciśnienie znieczulające

• Log vs 1/T

r

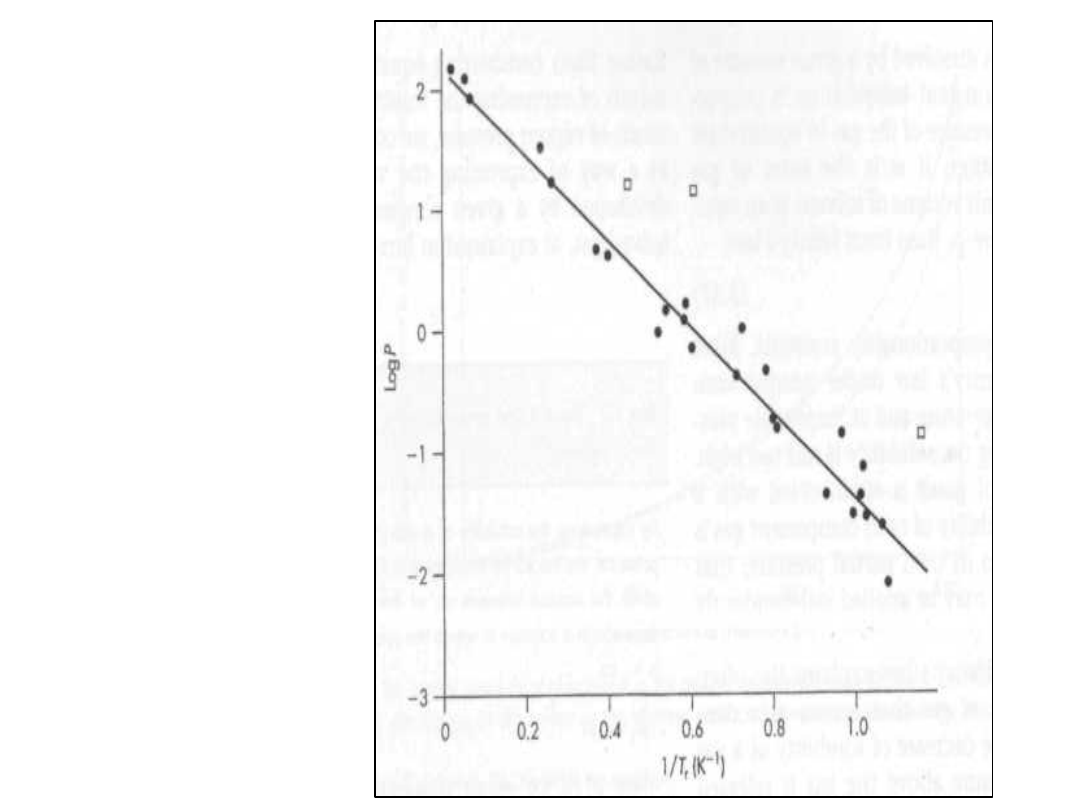
PODSUMOWANIE

• Barometr, manometr, jednostki

ciśnienia

• Prawa gazowe –równanie Clasiusa –

Clapeyrona

• Warunki standardowe STP
• Stała gazowa i stała Boltzmana
• Ułamek molowy
• Prawo Daltona i ciśnienia cząstkowe
• Prawo Grahama efuzji

Przykładowe zadania

• Zad 1.
• Przelicz 1,26 atm na Torr.
• Zad.2 Zakładając, że

skonstruowano barometr stosując
ciecz o gęstości 1,22 g/mL, Jaki
będzie poziom cieczy w
barometrze, jeżeli ciśnienie
atmosferyczne wynosiło 755 Torr.
Gęstość rtęci 13,6 g/mL

Zadania

• Wzór h

B

=h

A

x d

A

/d

B

• Zad.3
• Oblicz wartość stałej gazowej w

następujących jednostkach mL x Torr x
mol

-1

x K

-1

• Zad. 4
• Jaki jest skład procentowy powietrza

wewnątrz płuc jeżeli ciśnienie
cząstkowe wynoszą:

• N

2

= 570 Torr, O

2

= 103 Torr, CO

2

=

Torr

Zadania

• Zad. 5
• Gęstość CO

2

wynosi 1,96 gL

-1

i

gęstość N

2

1,25 gL

-1

. Który z

gazów wypływa szybciej? Jaki
będzie stosunek szybkości efuzji
azotu do ditlenku węgla.

•

A

B

A

B

B

A

M

M

d

d

v

v



