PROBLEM NIEPEWNOŚCI W
DZIAŁALNOŚCI
INŻYNIERSKIEJ I JEJ MODELOWANIE

Niedoskonałość
człowieka
Ograniczona wiedza

Niepewność wyników rozumowania,
obliczeń inżynierskich, trafności decyzji

Np. naprężeń σ i naprężeń
krytycznych σ

kr

2

Zmniejszanie niepewności
w procesie projektowania

• stosowanie w obliczeniach współczynników

bezpieczeństwa

• wykorzystywanie do obliczeń modeli

probabilistycznych

naprężeń i naprężeń krytycznych

• przeprowadzanie badań prototypu i serii

informacyjnej

3

Obliczenia probabilistyczne

Probabilistyczna forma warunków
ograniczających

σ

sup

≤ R

e

σ

max

≤ Z

X(t) ≤ X

kr

y ≤ y

kr

. .

.

P{ …} ≡ R(t) - funkcja
niezawodności

Np. R = P{σ

sup

≤ R

e

}

σ

sup

, σ

max

, R

e

,
Z, …

zmienne
losowe

4

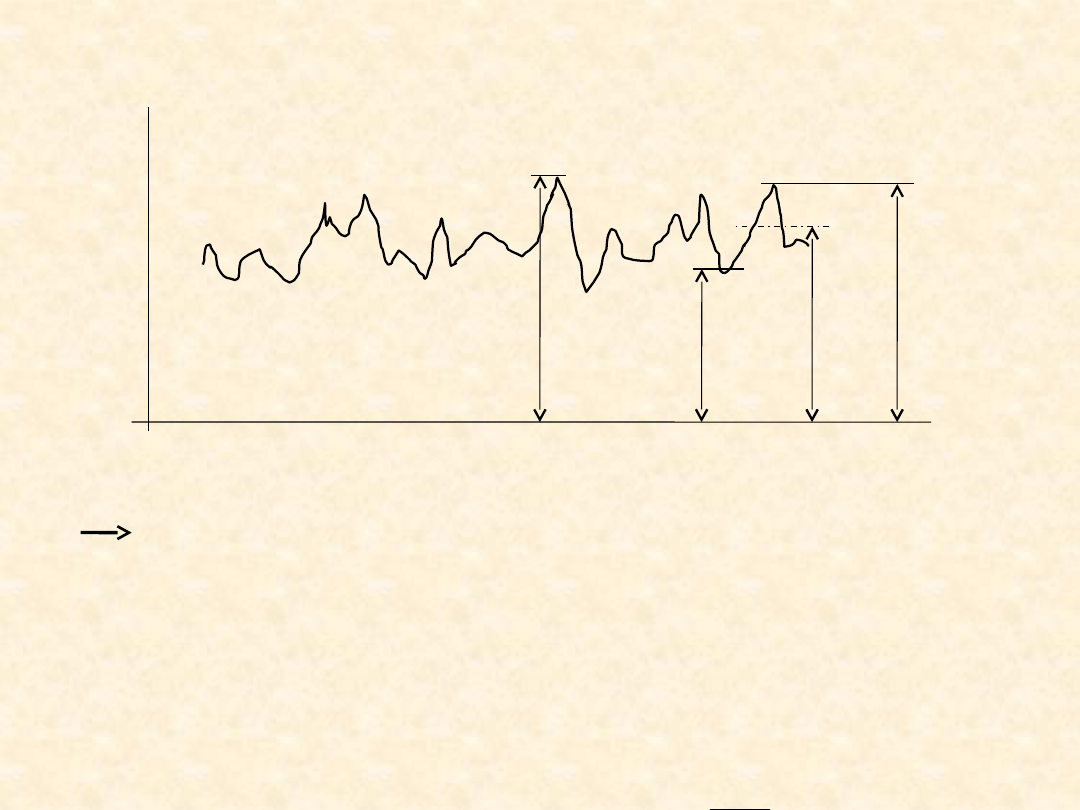
Probabilistyczny opis naprężeń

σ

sup

σ

max,i

σ

m,i

σ

min,

i

t

σ

Do probabilistycznych obliczeń na
wytrzymałość doraźną
rozkład prawdopodobieństwa σ

sup

w

postaci gęstości
prawdopodobieństwa f(σ

sup

)

5

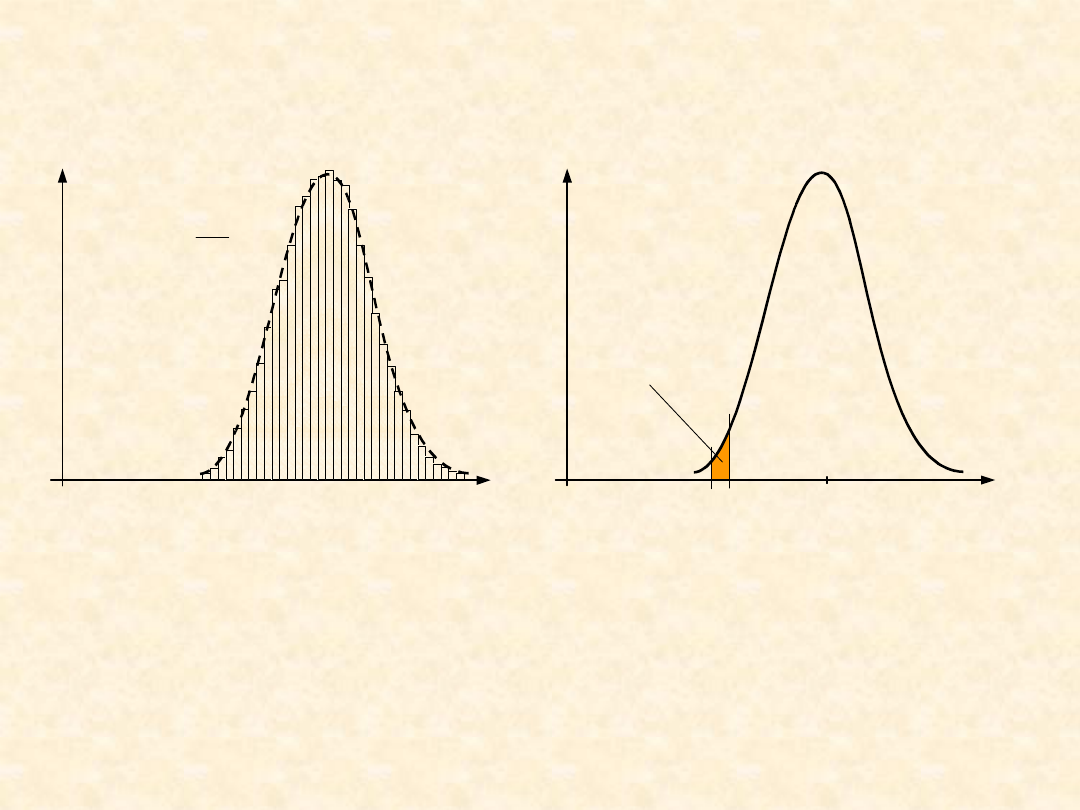
Przykłady typowych rozkładów

w

i

x

f

x

x

1

x

2

Ex

P{x

1

 x  x

2

}

N

n

w

i

i



w – częstość; f – gęstość
prawdopodobieństwa

x → σ

sup

, σ

max

, R

e

,

Z ,…

6

f

x

x

0

F(x

0

)

F(x

0

)

f

x

x

0

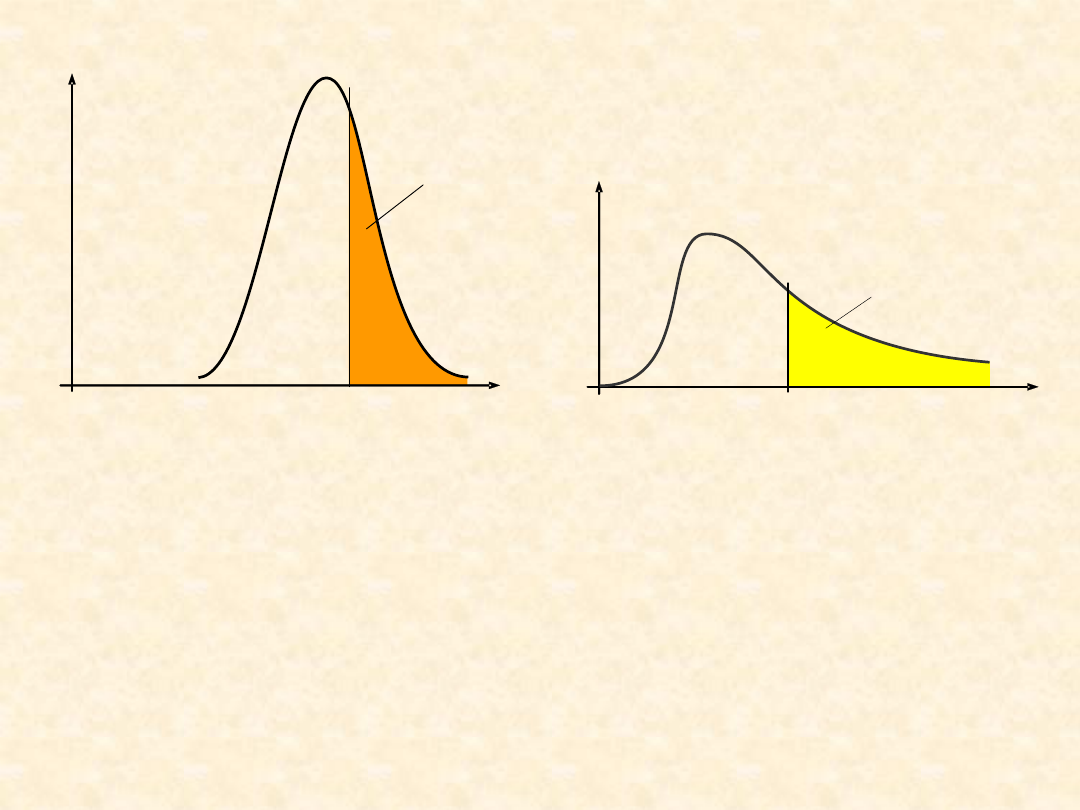
Gęstość rozkładu normalnego

Gęstość rozkładu
Weibulla

F(x

0

) = P{x ≥ x

0

}







xo

o

x

x

f

d

)

(

Duże rozrzuty cech, właściwości także
właściwości
obiektów technicznych
mechanicznych

R

e

, R

m

, Z , H , h , t

rw

,

…,wymiary

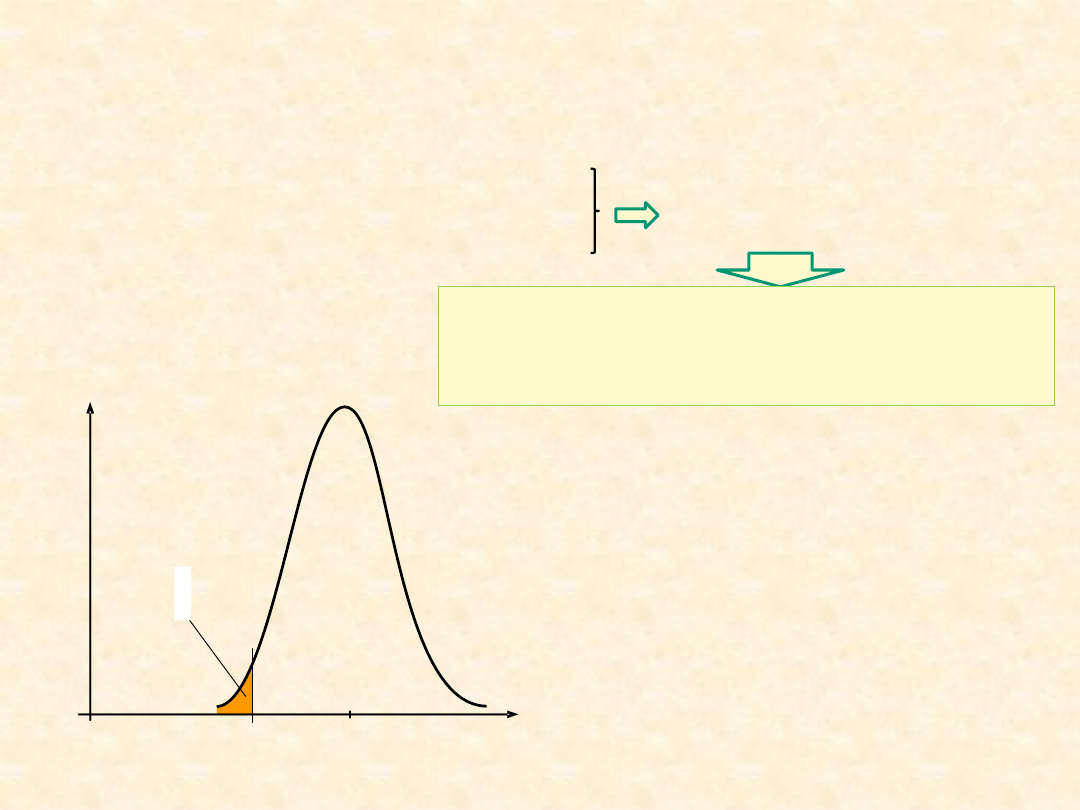
f

R

e

ER

e

R

e

P{R

e

≤ R

emin

}

R

emin

Probabilistyczny opis właściwości
mechanicznych

<

P{R

e

≥ R

emin

} ≈

0,98- 0,99

7

8

Uwzględnianie losowości w obliczeniach
inżynierskich

•

operowanie opisami probabilistycznymi naprężeń

(lub obciążeń)

oraz cech i właściwości (np.mechanicznych)

• stosowanie w obliczeniach deterministycznych

współczynników

uwzględniających wymagany poziom niezawodności,
np.
- a

Rwym

w obliczeniach łożysk tocznych

- c

r

w obliczeniach zmęczeniowych

P{war. ograniczający} ≡ R(t)

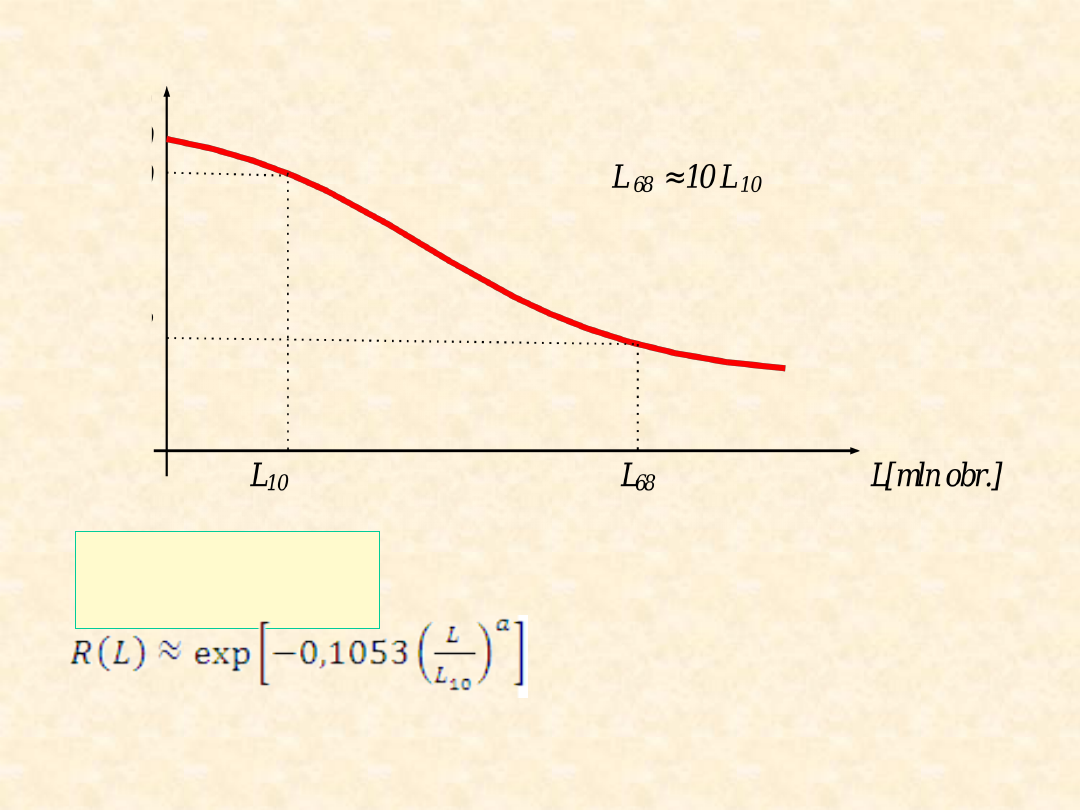
Trwałość łożyska
tocznego

R(L)

1,0
0

0,9
0

0,3
2

R(L) = P{ L ≥
L}

- rozkład Weibulla
zm. L

a = 10/9 dla łoż. kulk.; a = 9/8 dla łoż.
wałeczkowych

10

Trwałość umowna ( katalogowa)

α = 3 dla łoż. kulk.; α = 10/3 dla łoż.
wałeczkowych

L

10

R(L)

0,90

L

1,00

0,60

L

wym

R(L

wym

)

Np.
L

wym

= 10 mln

obr.

11

L

10

L

10

R(L)

0,90

L

1,00

0,60

L

wym

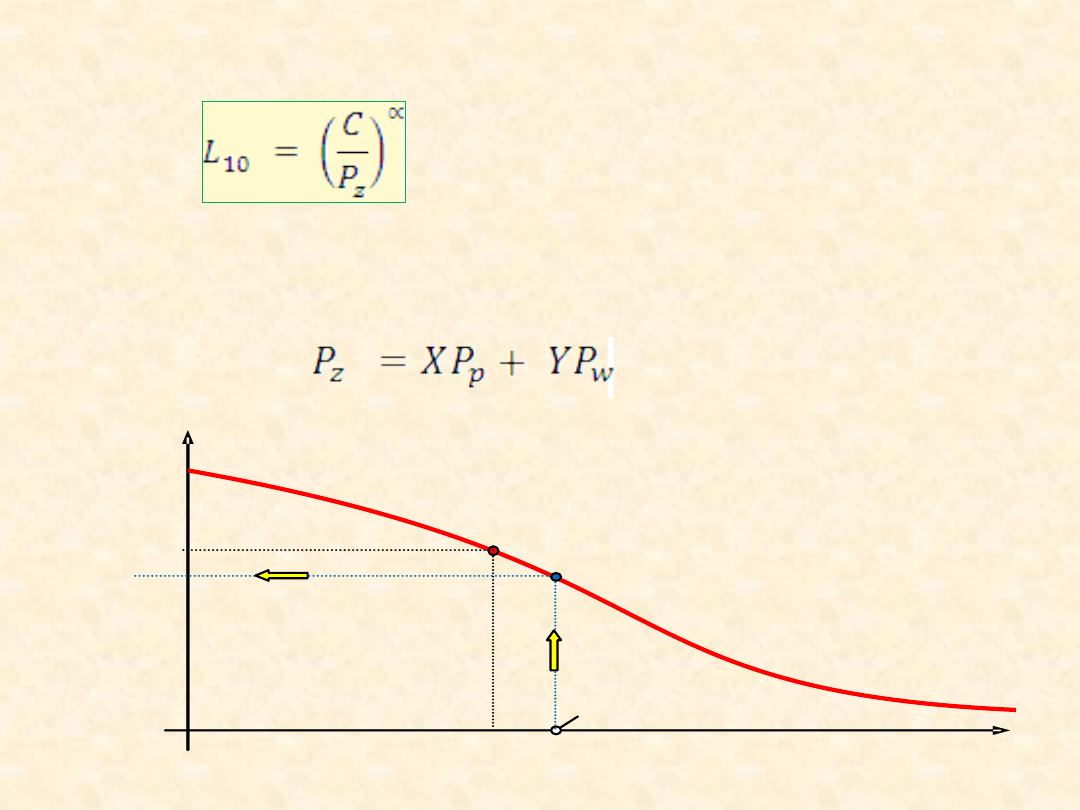
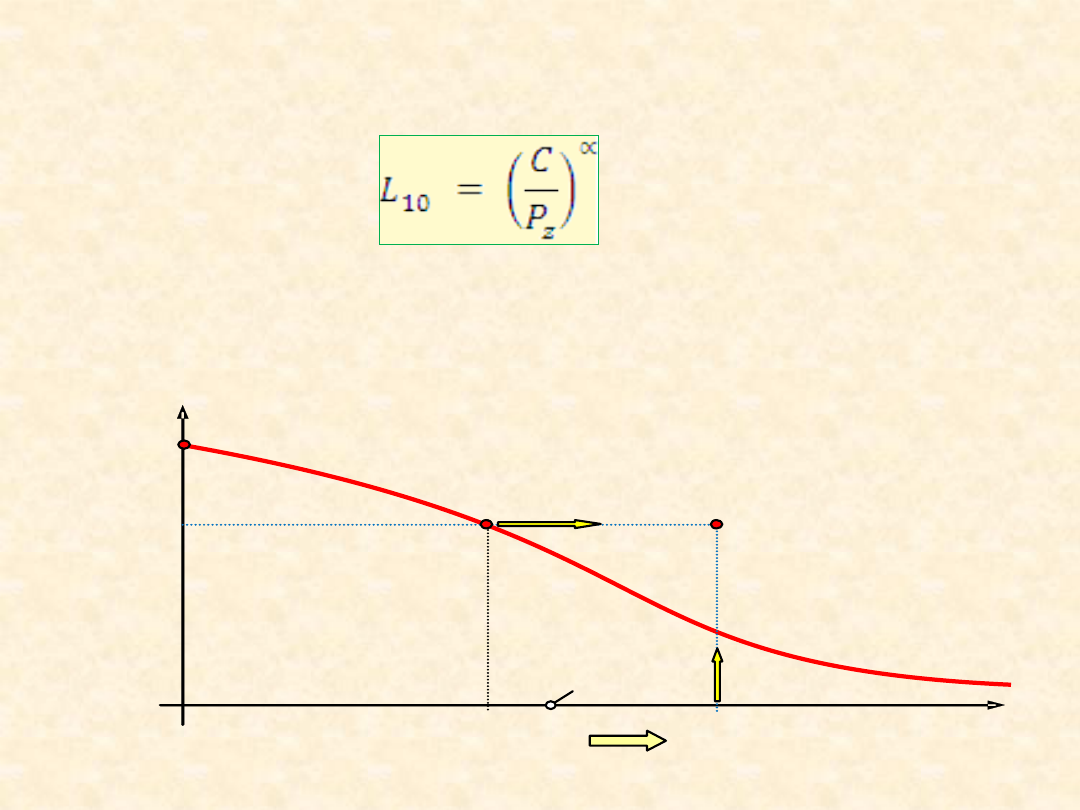
12

C/P

z

L

10

L

10

R(L)

0,90

L

1,00

0,60

L

wym

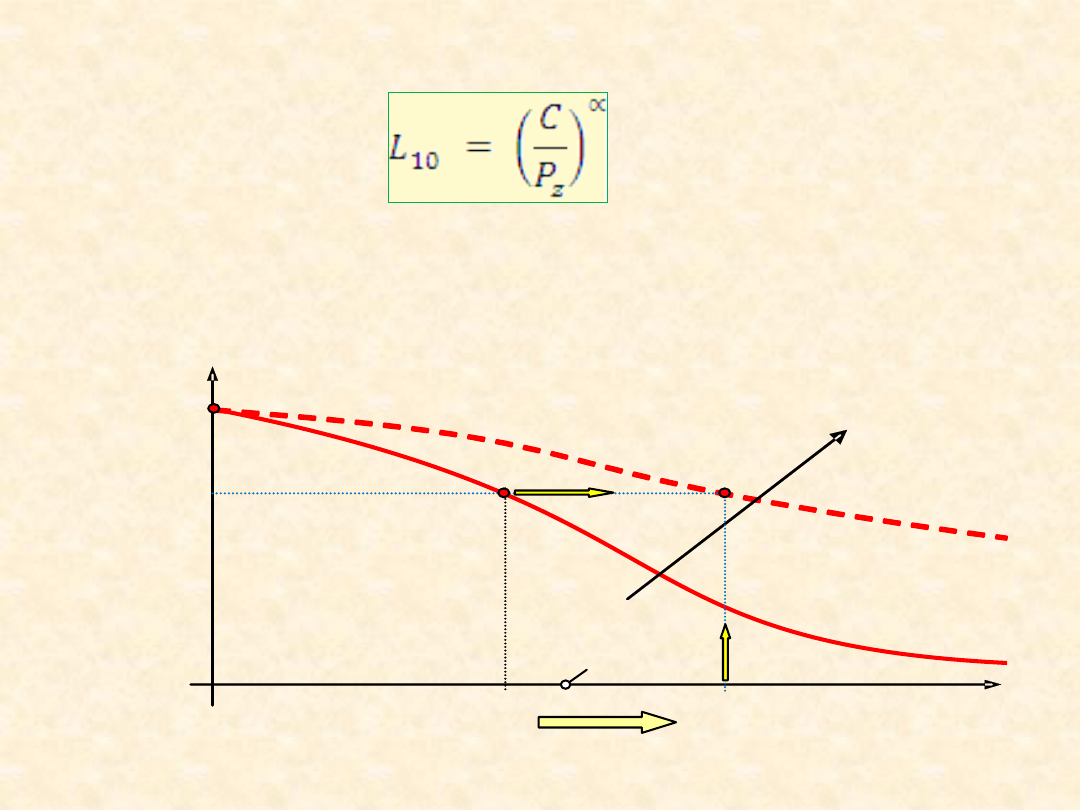
13

C/P

z

L

10

L

10

R(L)

0,90

L

1,00

0,60

L

wym

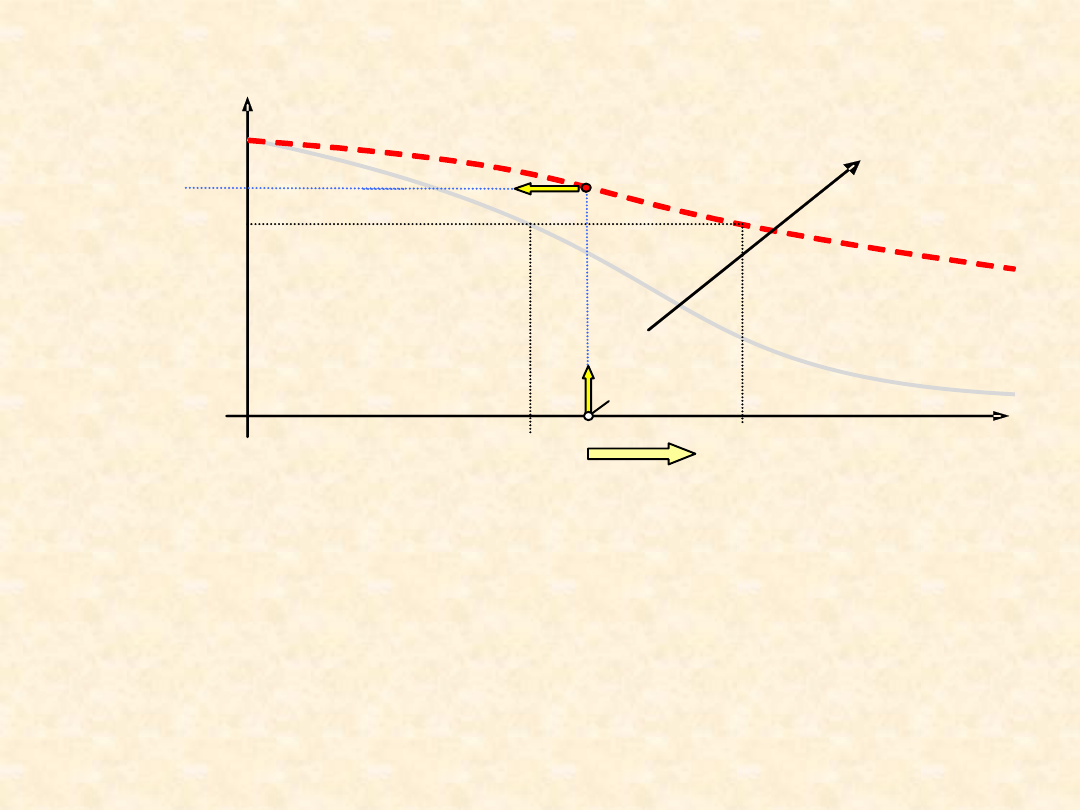
R(L

wym

)

R(L

wym

) ≥ R

wym

,

gdzie R

wym

= …. (np. R

wym

=

0,93 )

14

Dobór łożyska

Warunki ograniczające, gdy R

wym

≤

0,90

• warunki geometryczne d ≥

d

o

, …

• warunek trwałości

L

10

≥

L

wym

Gdy L

10

≈ L

wym

R(L

wym

) ≈ 0,90 b.

mało , gdyż

R(L) ≈ ∏ R

i

(L) , gdzie i = 1,2,…,n

Np. dla n =4 i R

i

(L) = 0,90 R(L)

≈ 0,64 !!

1

15

2

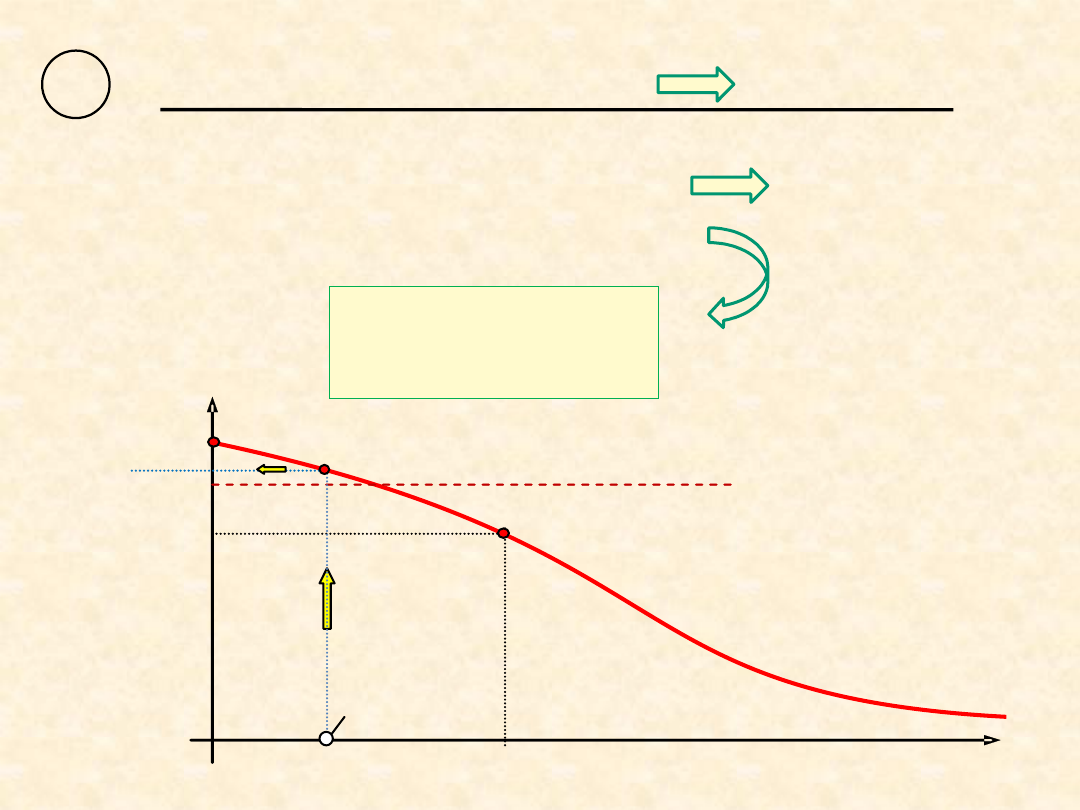
Warunki ograniczające, gdy R

wym

> 0,90

•

warunki geometryczne

d ≥ d

o

,…

• warunek niezawodności

R(L

wym

) ≥

R

wym

Np. R

wym

=

0,99

L

10

R(L)

0,90

L

1,00

0,60

L

wym

R

wym

R(L

wym

)

16

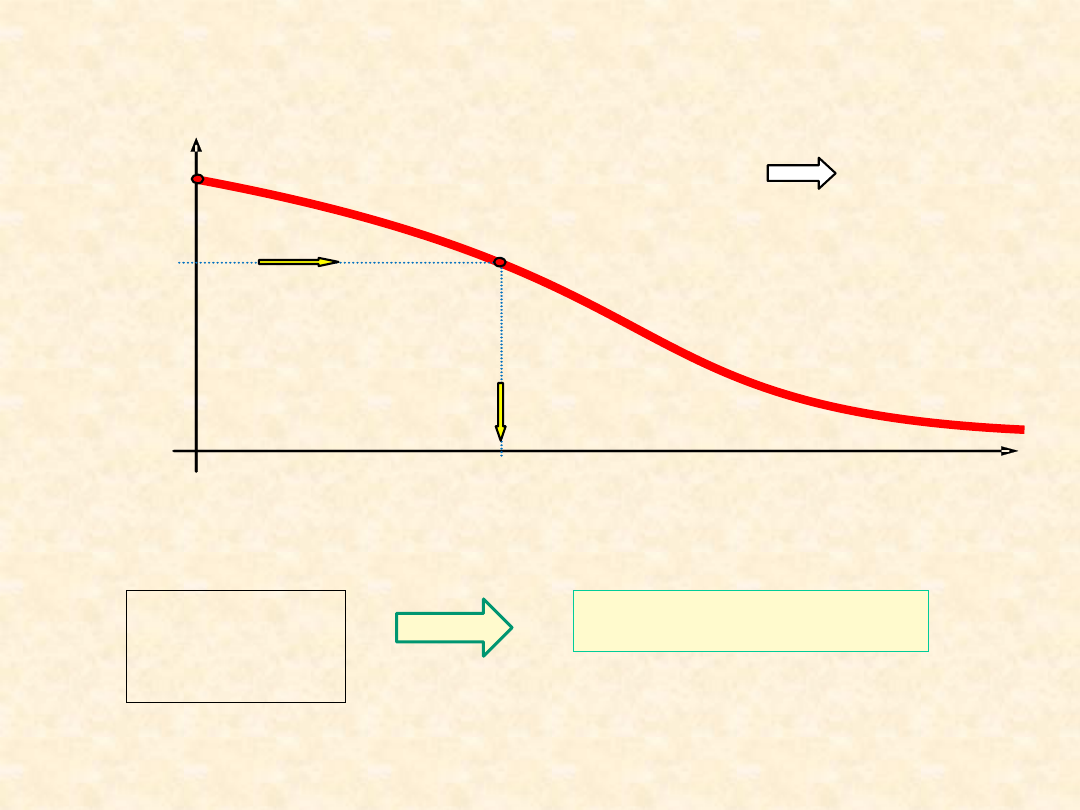
Inna postać metody (wg FAG,
SKF )

R(L)

L

R

wym

L(R

wym

)

Jeśli R(L),to L(R)

Warunek trwałości (+ niezawodności)

L(R

wym

) ≥ L

wym

L

10

≥

L

wym

gdzie L(R

wym

) =

a

Rwym

∙

a

23

∙ L

10

17

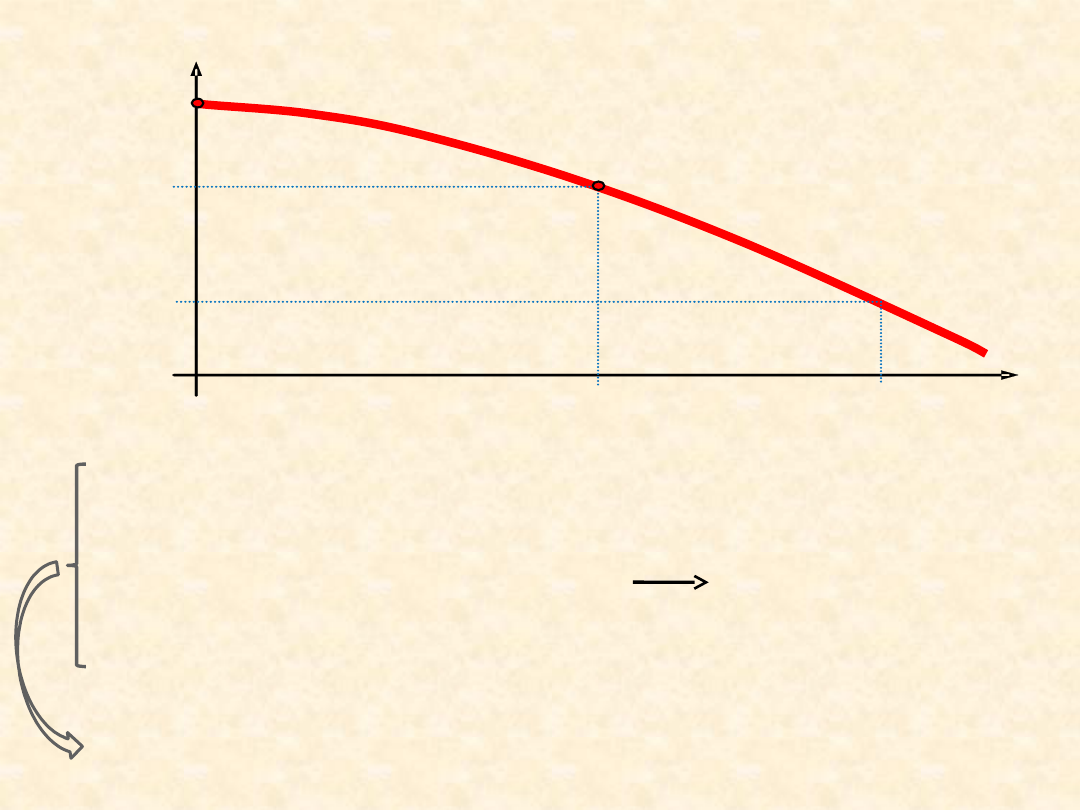
R(L)

L

R

wym

L(R

wym

)

0,90

L

10

1,00

a

Rwym

= L(R

wym

) ∕ L

10

Np. dla R

wym

= 0,99

a

Rwym

=

0,21

a

23

- wsp. materiałowy stali i oleju oraz war.

eksploat.
(w tym rodzaj i lepkość oleju)
wykresy w katalogu

18

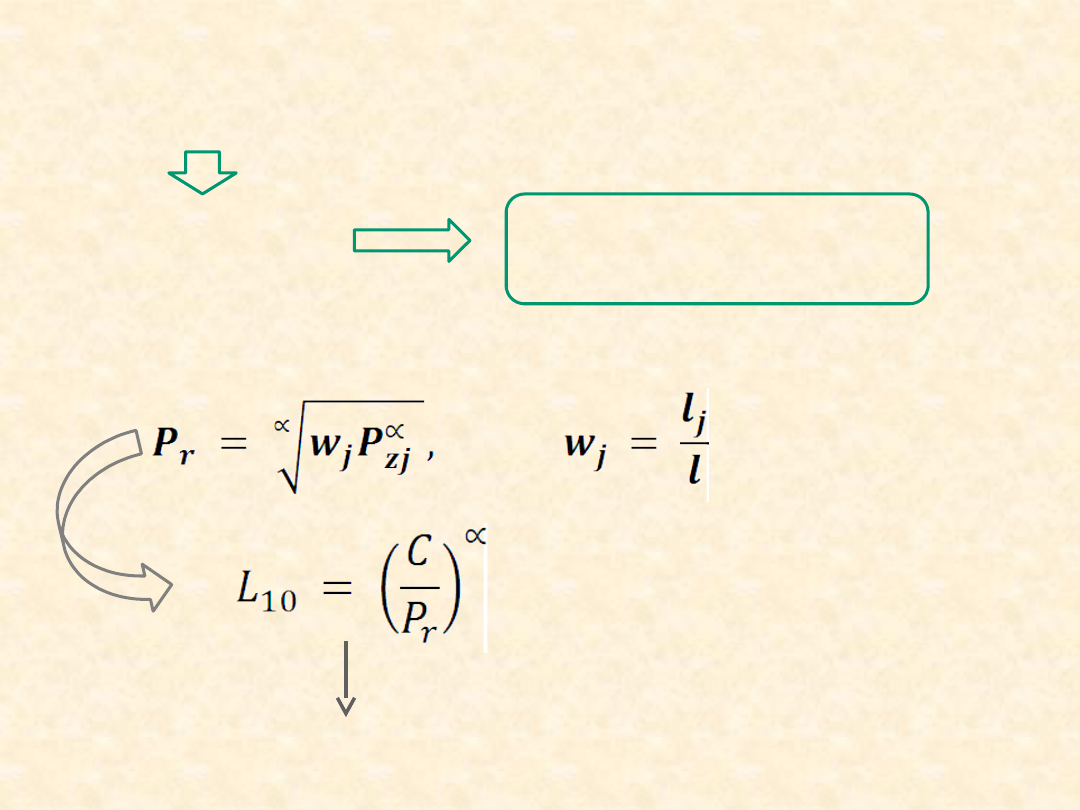
Dobór

łożyska, gdy obciążenie

niestałe
w czasie funkcjonowania
urządzenia

P

z

≠

const

obciążenie
zastępcze
równoważne P

r

●

●

●

19

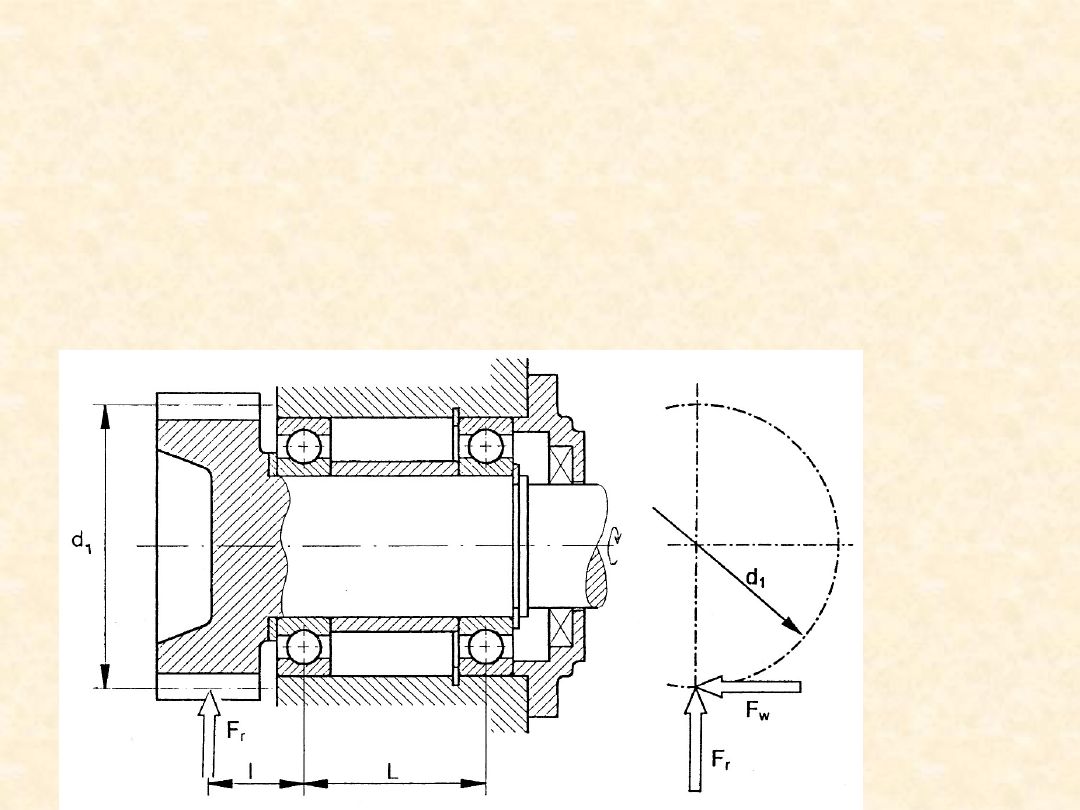
Zadanie

Do podparcia wałka przekładni zębatej (p. rysunek) użyto dwóch
jednakowych łożysk poprzecznych kulkowych o nośnościach ruchowych
każdego z nich C = 5,85 kN. W strefie zazębienia występuje obciążenie
poprzeczne o dwóch składowych, związanych relacją F

r

 = 0,364 F

w

. Przez

90% czasu funkcjonowania przekładni (liczonego w mln obrotów wałka)
siła obwodowa F

w

 = 2 kN, a w pozostałym czasie F

w

 = 4 kN.

Przewidywana trwałość pojedynczego łożyska L

wym

 = 10 mln obr., a

wymagana wartość funkcji jego niezawodności w tym okresie powinna być
nie mniejsza niż R

wym

 = 0,95. Sprawdzić prawidłowość doboru łożysk do

tych warunków.
Pozostałe dane: d

1

= 48 mm, l = 16 mm, L = 30 mm.

 
 

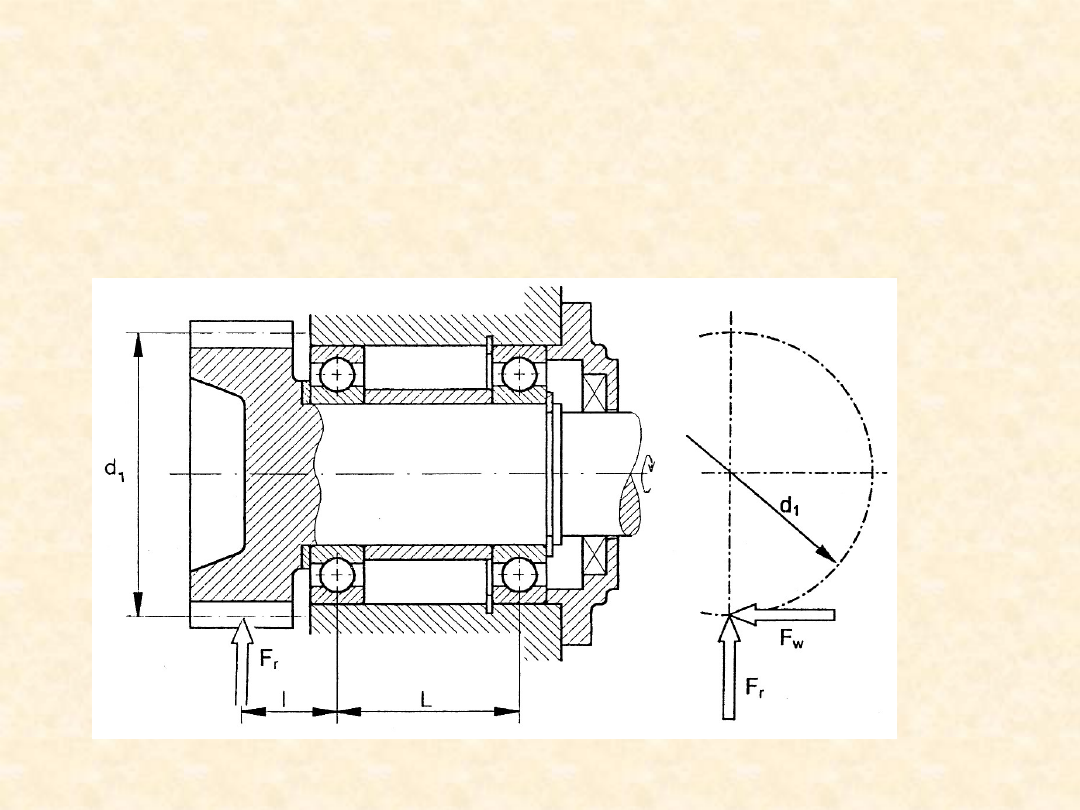
20

Zadanie

Narysować wykres funkcji niezawodności łożyska bardziej
obciążonego z dwóch łożysk, o których mowa w poprzednim
zadaniu i funkcjonujących w opisanych warunkach. Jakie są
dwa dominujące zjawiska fizyczne prowadzące do
uszkodzeń łożysk tocznych?

21

Zadanie

Łożysko poprzeczne kulkowe o nośności ruchowej
C = 3 kN jest obciążone siłą zastępczą P

z

= 1 kN.

Wymagana trwałość tego łożyska wynosi L

wym

= 27

mln obr. Przedstaw na wykresie funkcji
niezawodności tego łożyska, co stałoby się z jej
wartością, gdyby obciążenie zastępcze zmniejszyło
się do wartości P

z

´ = 0,5 kN.

 

Zadanie

Znana jest wartość trwałości umownej określonego
łożyska, wynikająca z jego obciążenia. Wynosi ona
5 mln obr. Z jakiego warunku można wyznaczyć
trwałość łożyska, oznaczoną symbolem L

5

?

Zaznacz ją na wykresie funkcji niezawodności
łożyska.

22

Zadanie

Łożysko wałeczkowe walcowe, podpierające czop
końcowy wałka ma nośność ruchową równą C. Siła
zastępcza P, obciążająca to łożysko, jest równa jego
nośności ruchowej. Należy wyznaczyć
prawdopodobieństwo nieuszkodzenia tego łożyska
w okresie L

wym

= 10

6

obrotów dla dwóch

następujących przypadków:

•  przedstawionego powyżej,

• gdy siła zastępcza jest równa 80% nośności

ruchowej.

Wyniki zilustrować na wykresach funkcji
niezawodności łożyska.
 

23