OBLICZENIA STATYCZNE

MASZTÓW

METODA DOKŁADNA

Wykonali:

Mariusz Chlebowicz

Łukasz Werpachowski

Za metodę dokładną uważa się obecnie

metodę elementów skończonych (MES) w jej
wersji przemieszczeniowej. Jej szczególną zaletą
jest nie tylko możliwość uwzględnienia dowolnej
konfiguracji konstrukcji i obciążenia (w tym
obliczania ustrojów belkowo-cięgnowych, jakimi są
maszty), ale również i to, że można ją stosować do
analizy statycznej i dynamicznej konstrukcji oraz
do analizy stateczności globalnej. Dokładność
metody rośnie w miarę zagęszczania podziału
konstrukcji na elementy skończone. Trzon masztu
należy podzielić tak, aby każde przęsło zawierało
co najmniej dwa elementy skończone.

Jeżeli weźmiemy pod uwagę dowolny j-ty element

skończony masztu, o początku l i końcu p, to pod
wpływem przemieszczeń jego końców oraz
obciążeń nań działających możemy napisać
zależność pomiędzy siłami [F

] a

przemieszczeniami węzłowymi [r

] w następującej

postaci macierzowej

] = [K

][r

gdzie:



]=[F

]



u, v, w - przemieszczenia odpowiednio wzdłuż osi
x, y, z lokalnego układu współrzędnych,



f, c , y kąty obrotu przekroju odpowiednio wzdłuż
osi x, y, z lokalnego układu współrzędnych,



] - macierz sztywności elementu belkowego, o

rozmiarach 12x12, którą można zapisać w postaci
sumy macierzy sprężystej pręta zginanego K

macierzy geometrycznej K

, uwzględniającej

wpływ siły podłużnej na sztywność pręta
zginanego, czyli:

] = [K

] + [K

]

[

]

ll j

�

=�

�

przy czym

[ ]

pp j

�

=�

�

[

]

[

]

lp j

pl j

�

=�

�

[

]

pp j

�

=�

�

W przypadku elementów skończonych odciągów,

w których występują siły rozciągające, należy w
licznikach poniższych wzorów zastąpić funkcje
trygonometryczne odpowiednimi im funkcjami
hiperbolicznymi, a równanie

należy zaś wzorem:

(

)

2 1 cos

sin

(

)

ch u

sh u

W metodzie elementów skończonych stosuje

się prawoskrętny układ współrzędnych, zarówno
lokalny (x, y, z), odnoszący się do poszczególnego
elementu skończonego, jak i globalny (X, Y, Z),
odnoszący się do całej konstrukcji. W układzie
lokalnym oś x jest zawsze osią podłużną
elementu, zaczynającą się w punkcie l i
skierowaną do punktu p, zaś osie y i z są
głównymi osiami centralnymi przekroju
poprzecznego danego elementu w punkcie l.
Składowe wektora przemieszczenia [r

]uważa się

za dodatnie, gdy mają zwroty zgodne z dodatnimi
zwrotami przyjętego lokalnego układu
współrzędnych. Podobnie znakuje się składowe
wektora sił węzłowych[F

Przemieszczenia translacyjne węzła u, v, w są

równoległe odpowiednio do osi x, y, z. Podobnie w
takiej samej kolejności oznaczono
przemieszczenia rotacyjne f, c , y .

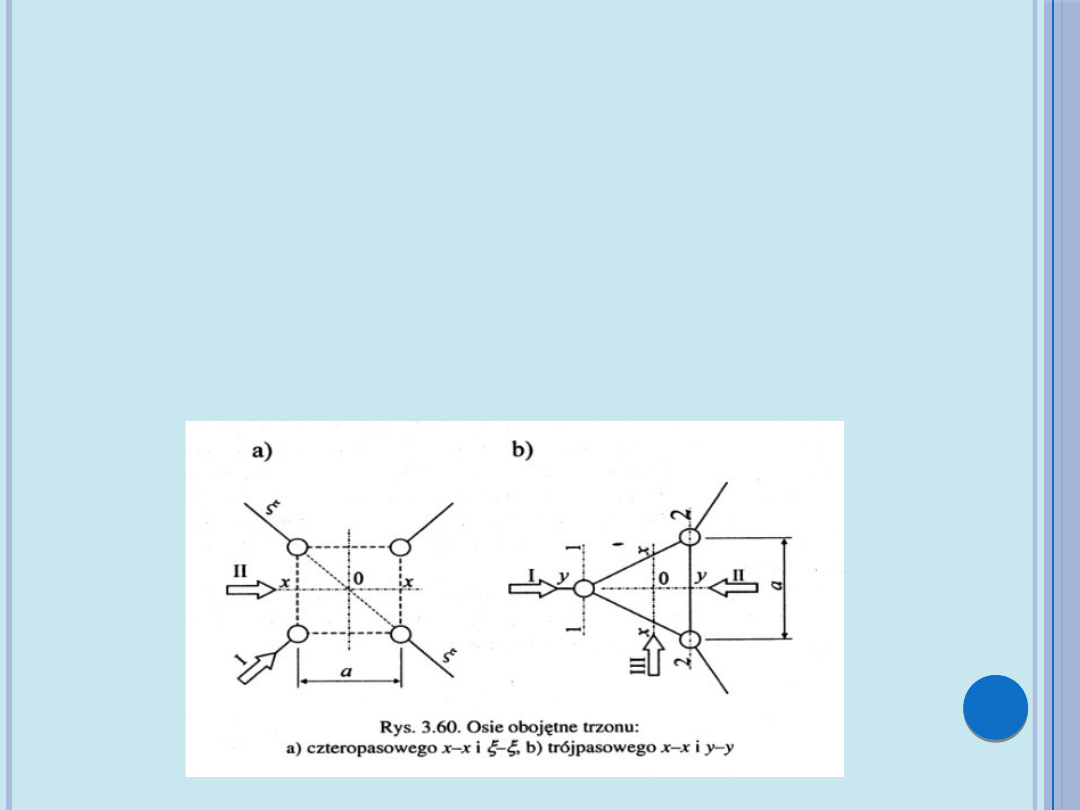
W podmacierzach występuje sztywność przekroju

na skręcanie GJ

, która dotyczy tylko elementów

skończonych trzonu. W przypadku trzonu
skratowanego mamy do czynienia z przekrojem
skrzynkowym quasi-zamkniętym.

Moment bezwładności na skręcanie możemy

obliczyć z drugiego wzoru Bredta :

gdzie:

-Ω - oznacza podwójne pole ograniczone liniami
środkowymi przekroju o boku a
-s - jest współrzędną skierowaną wzdłuż obwodu
przekroju trzonu
-t(s) - oznacza za stępczą grubość ścianki
przekroju trzonu, zależną od współrzędnej s

( )

t s

�

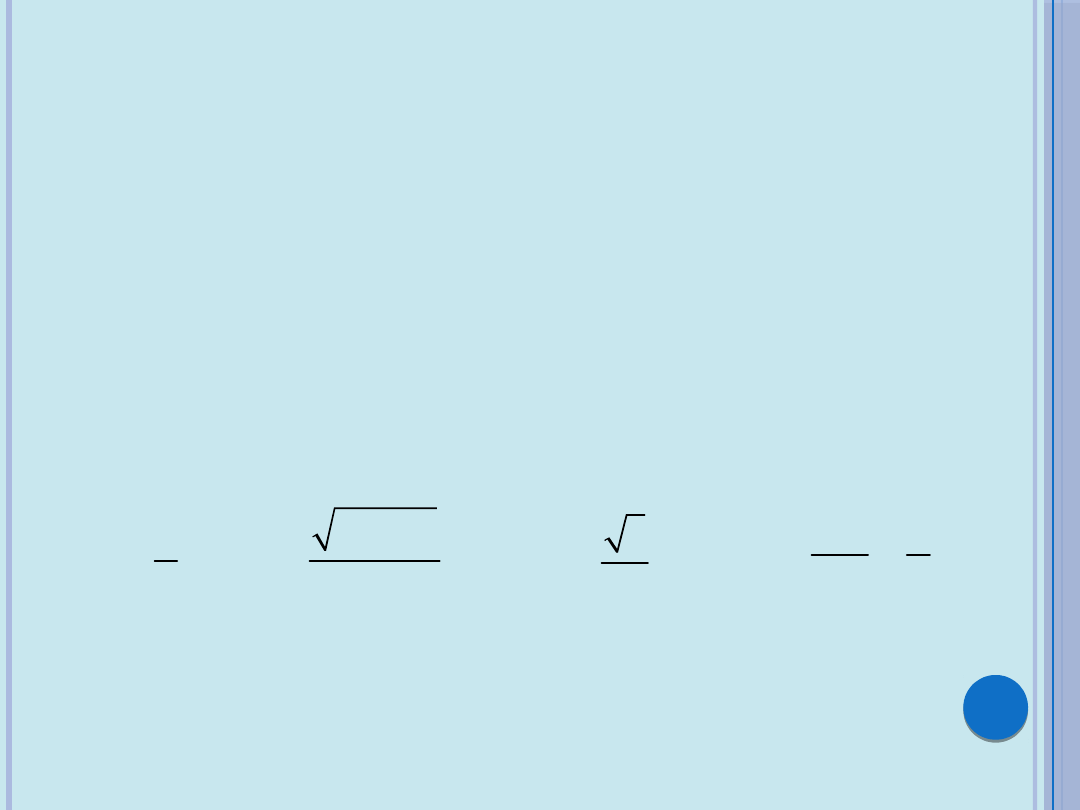
Zastępczą grubość ścianki wyznacza się na

podstawie porównania jej objętości z objętością
prętów kraty, ale bez rozpórek, które nie biorą
udziału w przenoszeniu momentu skręcającego. W
przypadku trzonu trójkątnego o długości boku
trójkąta a i długości przedziału kraty b, gdy pole
przekroju pojedynczego pasa wynosi A

zaś pole

przekroju krzyżulca wynosi A

, otrzymujemy:

A A

�

( )

t s

�

Składowe macierze, sprężystości [K

] i

geometryczną [K

], we wzorze uzyskuje się z

podmacierzy, po rozwinięciu jej wyrazów w szeregi
Taylora w otoczeniu N = 0, tzn. w otoczeniu u = 0.

Macierz sprężystości zależy tylko od geometrii
elementu skończonego, macierz geometryczna
zależy natomiast, oprócz geometrii, od siły
podłużnej N.

Taka postać zapisu ogólnej macierzy sztywności
[K

] jest bardzo przydatna do analizy stateczności

konstrukcji.

Macierz sztywności skończonego elementu cięgna

otrzymuje się przez wstawienie do macierzy
sztywności elementu belkowego EJ

= EJ

= 0.

Sprężysta macierz sztywności zależy tylko od EA/l,
a geometryczna od N/l.

Jeżeli znane są macierze sztywności wszystkich

elementów skończonych, wyrażone w lokalnych
układach współrzędnych poszczególnych
elementów, to następnym etapem obliczeń,
zwanym etapem agregacji lokalnych macierzy
sztywności, jest zbudowanie macierzy sztywności
[K] całego ustroju w globalnym układzie
współrzędnych. Odbywa się to za pomocą macierzy
transformacji, zależnej tylko od kątów zawartych
między osiami układu lokalnego i układu
globalnego.

Ostatecznie otrzymuje się następującą zależność

macierzową pomiędzy siłami węzłowymi a
przemieszczeniami węzłowymi:

w której:
[r] - wektor przemieszczeń węzłowych całego

ustroju,

[F] - wektor węzłowych obciążeń zewnętrznych.

[ ][ ] [ ]

K r

Wprowadzanie sił naciągu wstępnego odciągów

można uzyskać jednym z kilku możliwych
sposobów. Może to być np. założenie spadku
temperatury cięgien o takie DT, aby uzyskać
założoną siłę wstępną S

= (EA)

T,l

DT (wskaźnik l

oznacza tutaj linę).

Rozwiązanie wcześniejszego układu równań
jednym ze sposobów iteracyjnych, czyli
znalezienie składowych wektora przemieszczeń
[r], umożliwia wyznaczenie sił węzłowych we
wszystkich elementach skończonych ustroju.

STATECZNOŚĆ TRZONU

METODA PARAMETRÓW POCZĄTKOWYCH

Metoda ta jest też nazywana metodą macierzy

przeniesienia. Rozwiązanie zadania rozpoczyna się
od obliczenia stycznych współczynników
sprężystości podpór w kierunku poprzecznym C

t,y

przy działaniu wiatru „na odciąg" z kierunku I.

Oś odkształconą każdego przęsła trzonu w chwili

wyboczenia opisuje różniczkowe równanie
równowagi , którego rozwiązaniem jest funkcja .

y=C

sin(kz)+ C

cos(kz)+C

(kz)+C

Cztery stałe całkowania C

(j = 1, 2, 3, 4) w

każdym przęśle należy wyznaczyć z warunków
brzegowych. Jeżeli maszt ma n przęseł, a tym
samym n podpór sprężystych, to ogólna liczba
stałych całkowania wynosi 4n. Liczba stałych
całkowania ulega zmniejszeniu o 2(n-l), jeżeli
wykorzystamy warunki ciągłości konstrukcji,
zapisane dla ostatniego równania. Liczba stałych
całkowania ulega znacznej redukcji (do 2), jeżeli
zastosujemy metodę parametrów początkowych.

Warunki brzegowe na lewym końcu pierwszego

przęsła (przemieszczenie y

kąt obrotu przekroju



1,l

moment zginający M

1,l

siłę poprzeczną Q

1,l

)

można wyrazić za pomocą tylko dwóch
parametrów początkowych przy podparciu
przegubowym 

i Q

- następująco:

[ ]

� �

� �= � �

� �

gdzie macierz H ma postać:

Warunki brzegowe na prawym końcu pierwszego
przęsła można wyrazić za pomocą warunków
brzegowych na lewym końcu, korzystając z
macierzy przeniesienia A

0 0
1 0

[ ]

0 0
0 1

�

[ ][ ]

�

� �

�

�=

� �

�

� �

�

A H

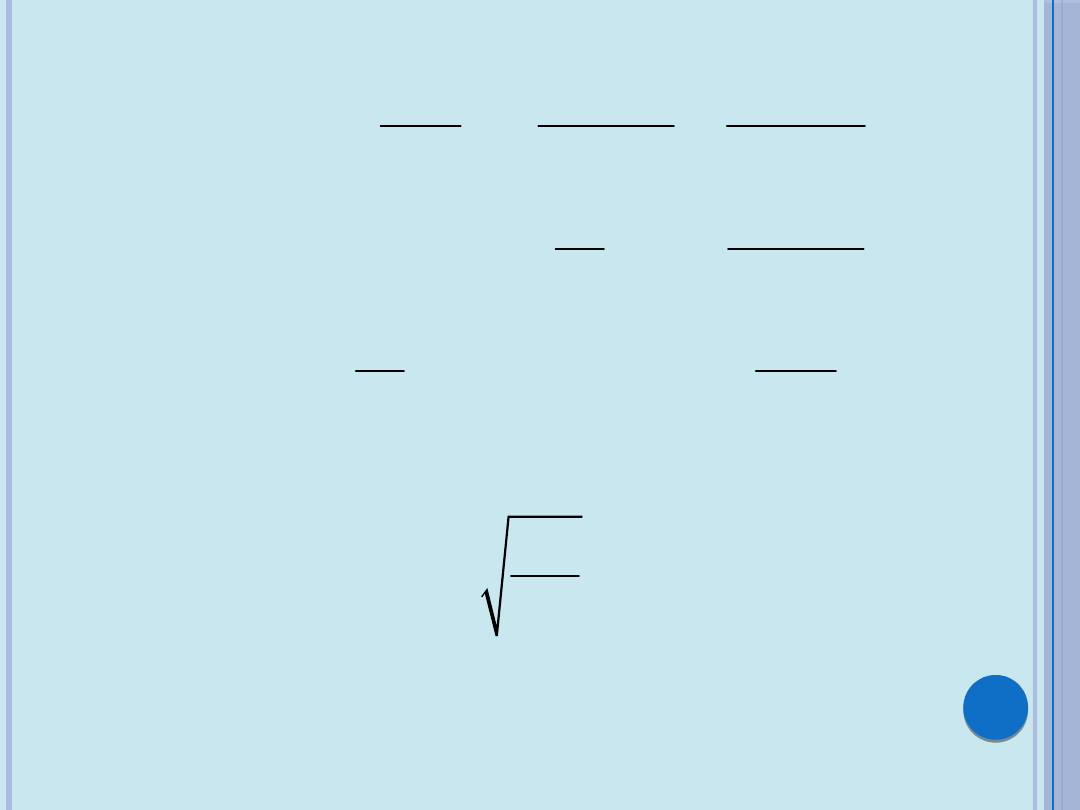
1 1

sin

cos

1 sin

cos

sin

[ ]

sin

cos

x x

k N

�

=�

�

1 1

x kl

Warunki brzegowe na lewej podporze przęsła

drugiego można zapisać za pomocą warunków
brzegowych na prawym końcu przęsła pierwszego,
korzystając z warunków ciągłości:

gdzie B

jest macierzą przejścia przez podporę

sprężystą o postaci:

[ ]

�

� �

�

� �

�

� �=

�

� �

�

� �

�

� �

�

0 0 0

1 0 0

[ ]

0 1 0
0 0 1

�

Warunki brzegowe na lewej podporze przęsła

drugiego można wyrazić za pomocą dwóch
parametrów początkowych, gdy zastosuje się
związki (warunki brzegowe na prawym końcu
pierwszego przęsła). Należy teraz powtarzać
algorytm przechodzenia z lewego końca do prawego
w każdym przęśle oraz przejścia n podpory
sprężyste.

Na prawym końcu n-tego (ostatniego) przęsła

warunki brzegowe są następujące:

Warunki można zapisać za pomocą warunków
brzegowych na lewym końcu n-tego przęsła i
macierzy końcowej K przy czym

0 ;

n p

n y n p

C y

0 1 0

[ ]

0 0 1

n y

�

=�

�

Po zapisaniu wszystkich warunków brzegowych za

pomocą parametrów początkowych y

i 

otrzymamy układ dwóch równań jednorodnych ze
względu na te dwie niewiadome. Niezerowe
rozwiązanie układu równań, odpowiadające
stanowi wyboczonemu konstrukcji, istnieje wtedy,
gdy wyznacznik główny macierzy współczynników
przy niewiadomych jest równy zeru. Równanie
wyznacznikowe ma postać:

det [ ][ ][ ][ ][ ]...[

][

][ ][ ][ ] 0

H A B A B

A B K

Z rozwinięcia wyznacznika otrzymuje się

równanie wiekowe, które w tym przypadku jest
równaniem przestępnym, gdyż niewiadoma x
występuje jako argument funkcji
trygonometrycznych. Z technicznego punktu
widzenia interesuje nas najmniejszy pierwiastek
dodatni niewiadomej X, na podstawie którego
obliczamy współczynniki długości
wyboczeniowych poszczególnych przęseł trzonu,
korzystając ze wzorów:

m =

l j

r x

m =

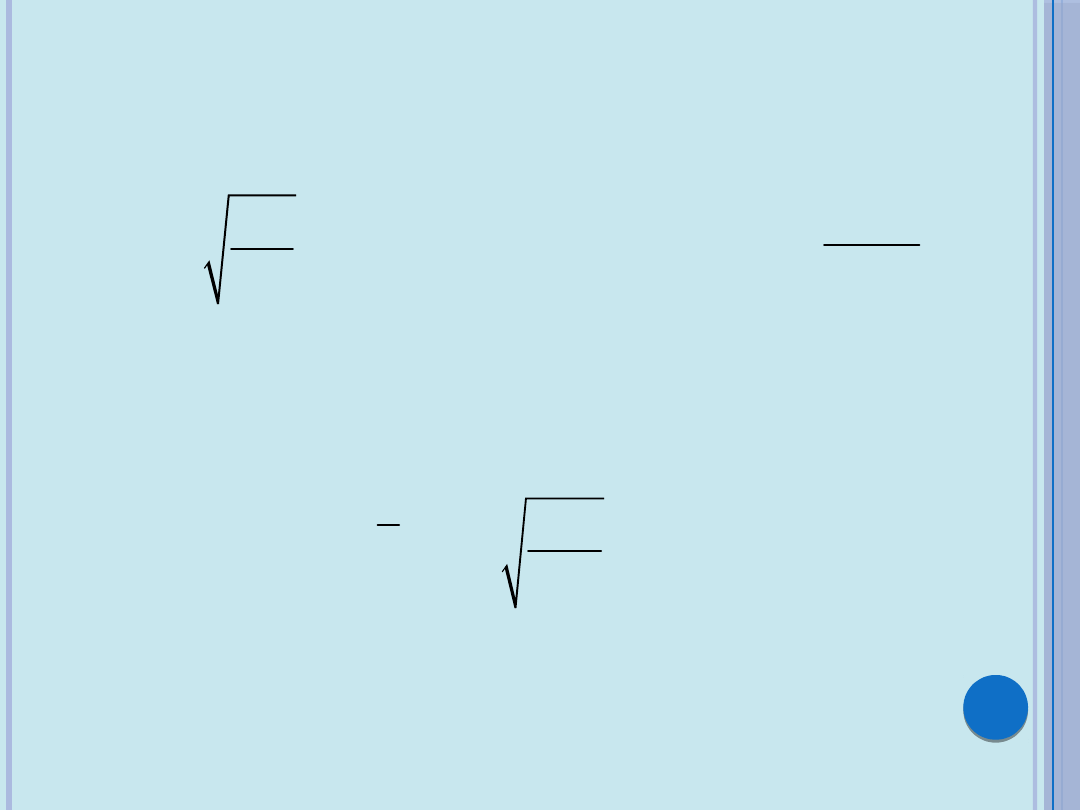
Siłę krytyczną N

1,kr

dla przęsła pierwszego według

wzorów:

Na tej podstawie oblicza się smukłość
sprowadzoną pierwszego przęsła trzonu

1 1

x kl

x EJ

1,15

l =

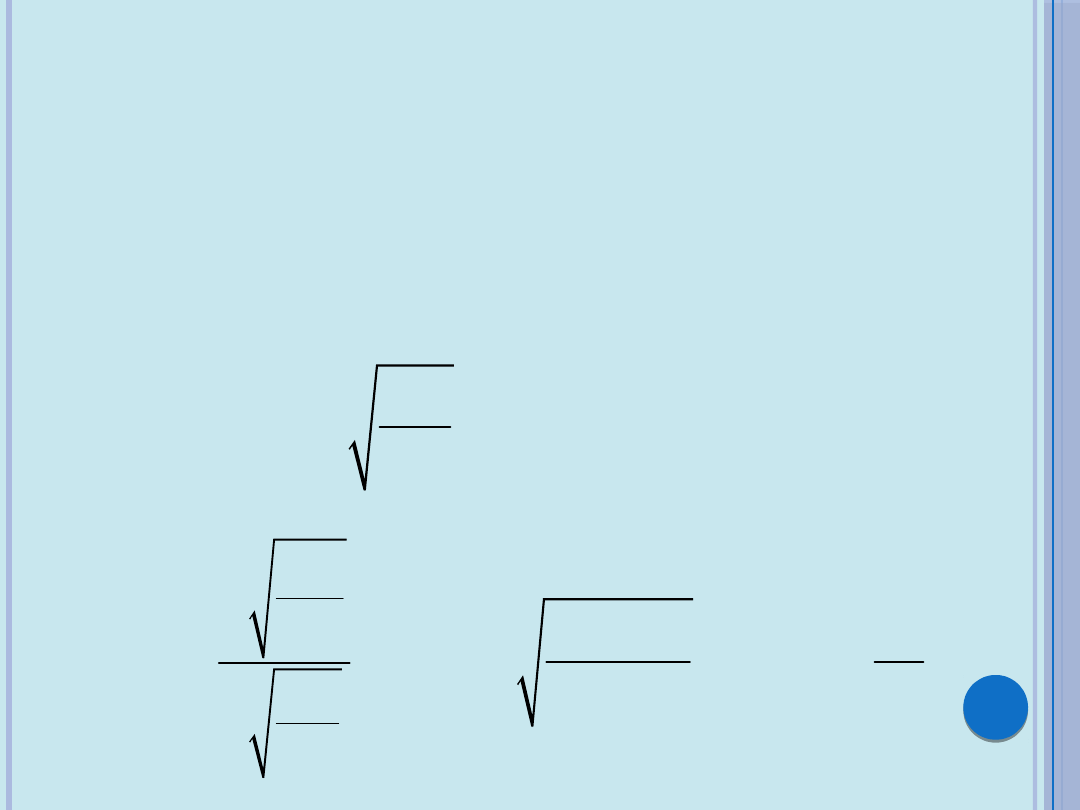
Podczas rozwiązywania równania

wyznacznikowego należy poczynić jeszcze dwie
uwagi, a mianowicie:

1. W macierzach [A

] (j = 2, 3, ..., n) niewiadome

iloczyny k

należy wyrazić poprzez niewiadomą x

= k

korzystając ze wzorów:

1 1

x kl

j j

k l

r x

N J

2. Podczas mnożenia dwóch kolejnych macierzy

należy zastosować inny sposób niż to jest przyjęte
w algebrze liniowej. Jeżeli wynikiem mnożenia
macierzy [A] przez macierz [B] jest macierz [C], to
w celu otrzymania elementu c w i-tej kolumnie i j-
tym wierszu należy pomnożyć pierwszy element i-
tej kolumny macierzy [A] przez pierwszy element
j-tego wiersza macierzy [B], następnie należy
dodać iloczyn drugiego elementu i-tej kolumny
macierzy [A] przez drugi element j-tego wiersza
macierzy [B] itd., aż do wyczerpania wszystkich
elementów i-tej kolumny macierzy [A] i wszystkich
elementów j-tego wiersza macierzy [B].

Praktyczne skorzystanie z opisanej metody przy

większej liczbie przęseł niż dwa wymaga
opracowania odpowiedniego programu
komputerowego. Autorski program o nazwie
MASZTY wykorzystuje niektóre segmenty pakietu
„Mathematica".

METODA ELEMENTÓW
SKOŃCZONYCH

Wykorzystajmy metodę elementów

skończonych do badania stateczności masztu.
Jak już wspomniano wcześniej, na utratę
stateczności trzonu są narażone przede
wszystkim maszty trójkątne podczas działania
wiatru z kierunku I („na odciąg"). Następuje
wtedy mocny spadek sztywności podpór w
kierunku prostopadłym do płaszczyzny
działania wiatru wskutek luzowania się dwóch
odciągów zawietrznych. Faktycznie więc bada
się stateczność ustroju płaskiego, po
uprzednim wyznaczeniu początkowych
sztywności podpór sprężystych C

t,y

Algorytm wyznaczania sztywności. Poszukując

w stanie obciążenia wiatrem masztu poziomych
przemieszczeń trzonu v

y,j

w kierunku osi y, od

przyłożonych sił poziomych W

o takich

wartościach, aby przemieszczenie wynosiło około
0,001 h

, gdzie h

jest odległością j-tej podpory od

przegubu centralnego. Zagadnienie wyznaczania
współczynnika sprężystości podpory jest tutaj
bardziej złożone niż w ustrojach prętowych, na
podstawie bowiem obliczonego przemieszczenia
v

i obliczonych zmian sił w linach DS

oblicza się

wydłużenie (skrócenie) ich cięciw oraz sztywności
odciągów na kierunkach ich cięciw

a następnie poszukiwaną sztywność:

gdzie drugi wskaźnik oznacza numer odciągu
drugiego (zawietrznego).

Dla płaskiego prętowego elementu skończonego

ścisła macierz sztywności przyjmie postać

2,1

2,2

0,75(

)

t y

[

]

a b a b

�

� ��

�

� ��

�

� ��

�

gdzie wprowadzono następujące oznaczenia,

wykorzystujące oznaczenie na u

sin

cos

sin

n =

Macierz uproszczoną zapisuje się teraz w postaci:
przy czym:

[

]

[

]

[

]

e j

g j

)

[

]

)

e j

�

� ��

�

� ��

�

+ � �

�

[

]

g j

a l

b l

c l

b l d l

a l

b l

b l d l

b l c l

�

� ��

�

=� ��

�

� �

�

=�

�

72 120(1

)

...,

60(1

)

g j

k k

6 30

...,

60(1

)

g j

- współczynnik podatności na ścinanie przekroju

pręta złożonego

x - mnożnik sił podłużnych w przęsłach trzonu,

dający obciążenie krytyczne, przy którym nastąpi
wyboczenie

8 (10 20 )

...,

60(1

)

g j

k k

2 10 (1

)

...,

60(1

)

g j

Dzięki zapisowi macierzy uproszczonej możemy

analizować konstrukcję tak samo obciążoną
poziomo w kierunku osi x, ale przy różnych
wartościach sił podłużnych w trzonie. Zauważmy,
że w kierunku osi y nie jest przyłożone żadne
obciążenie poziome. W tej sytuacji:

Rozwiązanie równania jest możliwe tylko dla
określonych wartości parametru  które
nazywamy wartościami własnymi, dla których
wyznacznik macierzy sztywności jest równy zeru,
czyli

[

][ ] 0

K r

det[

] 0

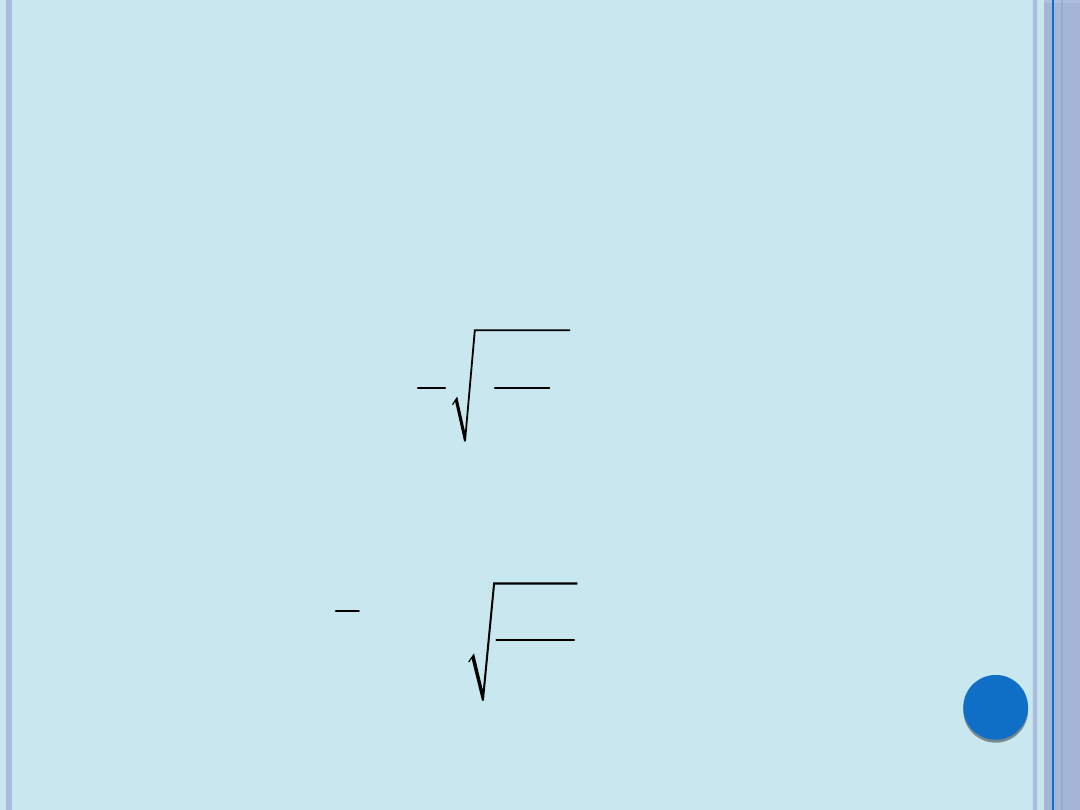
Z rozwinięcia wyznacznika otrzymujemy

równanie algebraiczne ze względu na parametr
 . Najmniejsza dodatnia wartość tego parametru
umożliwia obliczenie obciążenia krytycznego N

j,kr

a następnie współczynnika długości
wyboczeniowej każdego przęsła m

oraz smukłości względnej trzonu

� �

1,15

l =

DZIĘKUJEMY

UWAGĘ

Document Outline

Slide 1
Slide 2
Slide 3
Slide 4
Slide 5
Slide 6
Slide 7
Slide 8
Slide 9
Slide 10
Slide 11
Slide 12
Slide 13
Slide 14
Slide 15
STATECZNOŚĆ TRZONU Metoda parametrów początkowych
Slide 17
Slide 18
Slide 19
Slide 20
Slide 21
Slide 22
Slide 23
Slide 24
Slide 25
Slide 26
Slide 27
Slide 28
Slide 29
Metoda elementów skończonych
Slide 31
Slide 32
Slide 33
Slide 34
Slide 35
Slide 36
Slide 37
Slide 38
DZIĘKUJEMY ZA UWAGĘ