POJĘCIA PODSTAWOWE

(WYKŁAD ROZSZERZONY)

INSTYTUT SYSTEMÓW INFORMATYCZNYCH

WYDZIAŁ CYBERNETYKI WAT

WARSZAWA - 2012

WOJSKOWA AKADEMIA
TECHNICZNA

im. Jarosława Dąbrowskiego

TYTUŁ

- SYMBOL INKLUZJI (ZAWIERANIA SIĘ ZBIORÓW)
- JEST ELEMENTEM (ZBIORU) (NALEŻY DO ZBIORU)
- NIE JEST ELEMENTEM (ZBIORU) (NIE NALEŻY DO ZBIORU)
- JEŚLI … TO …
- WTEDY I TYLKO WTEDY

 

2

Wojskowa Akademia Techniczna

20.11.2021



 )

(

B

A

(DLA KAŻDEGO x, )

B

x

A

x







- NIE
- A NIE JEST PODZBIOREM B

 

B

A





























B

x

A

x

B

x

A

x

B

A

B

A

i

ISTNIEJE

~

i

ŻE

TAKIE,

x

ISTNIEJE

~

WOJSKOWA AKADEMIA
TECHNICZNA

im. Jarosława Dąbrowskiego

TYTUŁ

• Zbiory A i B są równe wtedy i tylko wtedy, gdy mają te same

elementy

• DLA DOWOLNYCH ZBIORÓW A, B, C ZACHODZI:

•
•
•
•
•

3

Wojskowa Akademia Techniczna

20.11.2021



 



B

x

x

x

B

A













:

każdego

dla

A





A

A

C

A

C

B

B

A







to

,

i

jeśli

B

A

A

B

B

A







to

,

i

jeśli

A

B

B

A

B

A







lub

to

,

jeśli

WOJSKOWA AKADEMIA
TECHNICZNA

im. Jarosława Dąbrowskiego

SUMA ZBIORÓW

• SUMA ZBIORÓW A, B

• DLA DOWOLNYCH ZBIORÓW A, B, C ZACHODZI:

•
•
•
•

4

Wojskowa Akademia Techniczna

20.11.2021



 



B

x

A

x

B

A

x











lub

A

A

(i)

oraz

"

"









"

"

lub

SYMBOLE

A

B

B

A









 



C

B

A

C

B

A











A

A





A

A

A





WOJSKOWA AKADEMIA
TECHNICZNA

im. Jarosława Dąbrowskiego

ILOCZYN ZBIORÓW

• ILOCZYN ZBIORÓW

• DLA DOWOLNYCH ZBIORÓW A, B, C ZACHODZI:

•
•
•
•

5

Wojskowa Akademia Techniczna

20.11.2021



 



B

x

A

x

B

A

x













"

"

B

A

A

B

B

A









 



C

B

A

C

B

A

















 A

A

A

A





WOJSKOWA AKADEMIA
TECHNICZNA

im. Jarosława Dąbrowskiego

RÓŻNICA ZBIORÓW

• RÓŻNICA ZBIORÓW

RÓŻNICĄ ZBIORÓW A i B nazywamy zbiór złożony z tych i tylko tych
elementów, które należą do A i nie należą do B.

• PRZESTRZEŃ. DOPEŁNIENIE ZBIORU

PRZESTRZEŃ X – ZBIÓR PEWNYCH ELEMENTÓW

• Podzbiór A przestrzeni X to zbiór elementów z X, które mają

pewną właściwość (A)

• PODZBIORY USTALONEJ PRZESTRZENI X NAZYWAMY RELACJAMI

JEDNOZNACZNYMI W X

6

Wojskowa Akademia Techniczna

20.11.2021



 



B

x

A

x

B

A

x













"

"

B

A

WOJSKOWA AKADEMIA
TECHNICZNA

im. Jarosława Dąbrowskiego

DOPEŁNIENIE ZBIORU

• DOPEŁNIENIE ZBIORU

DOPEŁNIENIEM ZBIORU A W PRZESTRZENI X NAZYWAMY ZBIÓR
DOPEŁNIENIE ZBIORU A OZNACZAMY

• DLA DOWOLNYCH PODZBIORÓW A, B PRZESTRZENI X

•
•
•
•
•
•
•
•

7

Wojskowa Akademia Techniczna

20.11.2021

"

"

A

X 

"

" A





 



A

x

A

x









A

A

X









 X

X

A

X





X







A

A





A

B

B

A

















 A

A

X

A

A















B

A

B

A

B

A

B

A

























MORGANA

DE

PRAWA

WOJSKOWA AKADEMIA
TECHNICZNA

im. Jarosława Dąbrowskiego

OBRAZY I PRZECIWOBRAZY WYZNACZANE PRZEZ FUNKCJE

• NIECH DANA BĘDZIE FUNKCJA

NIECH A BĘDZIE PODZBIOREM X

• NIECH , f(x) NAZYWAMY WARTOŚCIĄ (OBRAZEM) ELEMENTU

PRZY ODWZOROWANIU f

• OBRAZEM ZBIORU A WYZNACZONYM PRZEZ FUNKCJĘ f NAZYWAMY

ZBIÓR WARTOŚCI f(a) (ZBIÓR OBRAZÓW) WSZYSTKICH
ELEMENTÓW ZBIORU A

• OBRAZ ZBIORU OZNACZAĆ BĘDZIEMY SYMBOLEM f(A)

UWAGA!!!
(A nie jest elementem X)!

8

Wojskowa Akademia Techniczna

20.11.2021

X

x

Y

X

f



:

X

A

X

x

 





X

A

A

x

Y

y

x

f

A

f











,

)

(

X

A

WOJSKOWA AKADEMIA
TECHNICZNA

im. Jarosława Dąbrowskiego

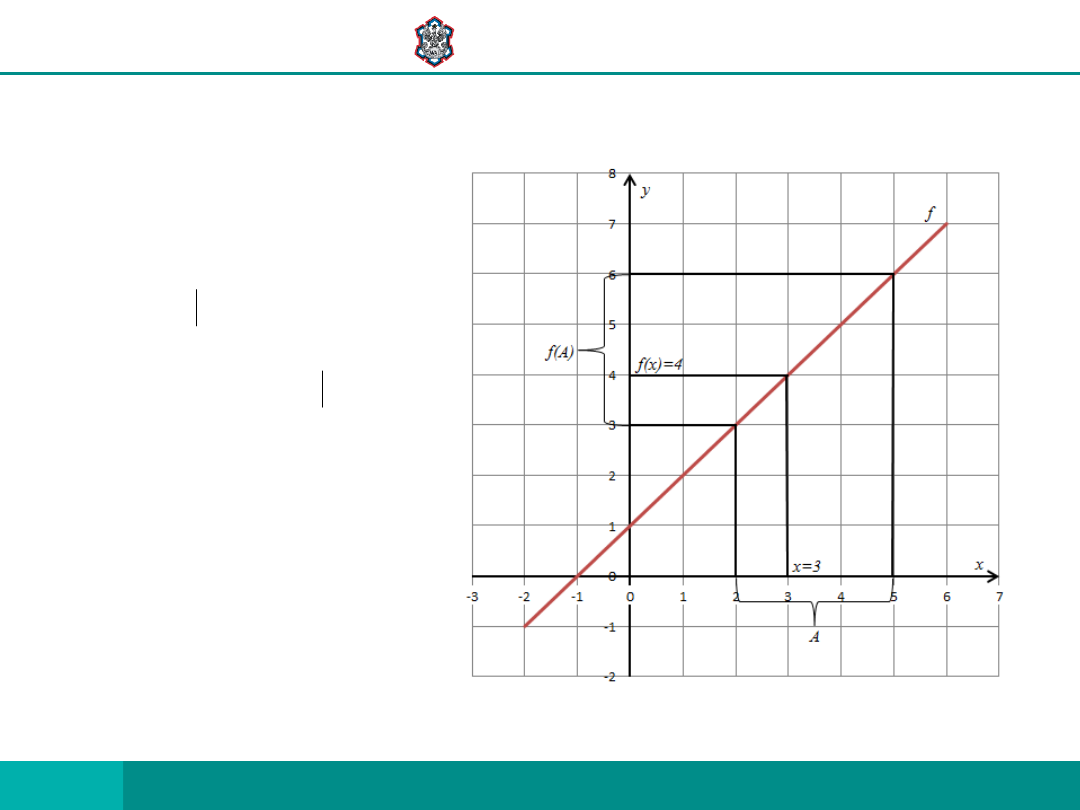
PRZYKŁAD 1

NIECH

9

Wojskowa Akademia Techniczna

20.11.2021

R

Y

R

X



 ,

1

)

(



x

x

f





5

2









x

R

x

A

 

 





6

3











y

R

y

x

f

A

f

WOJSKOWA AKADEMIA
TECHNICZNA

im. Jarosława Dąbrowskiego

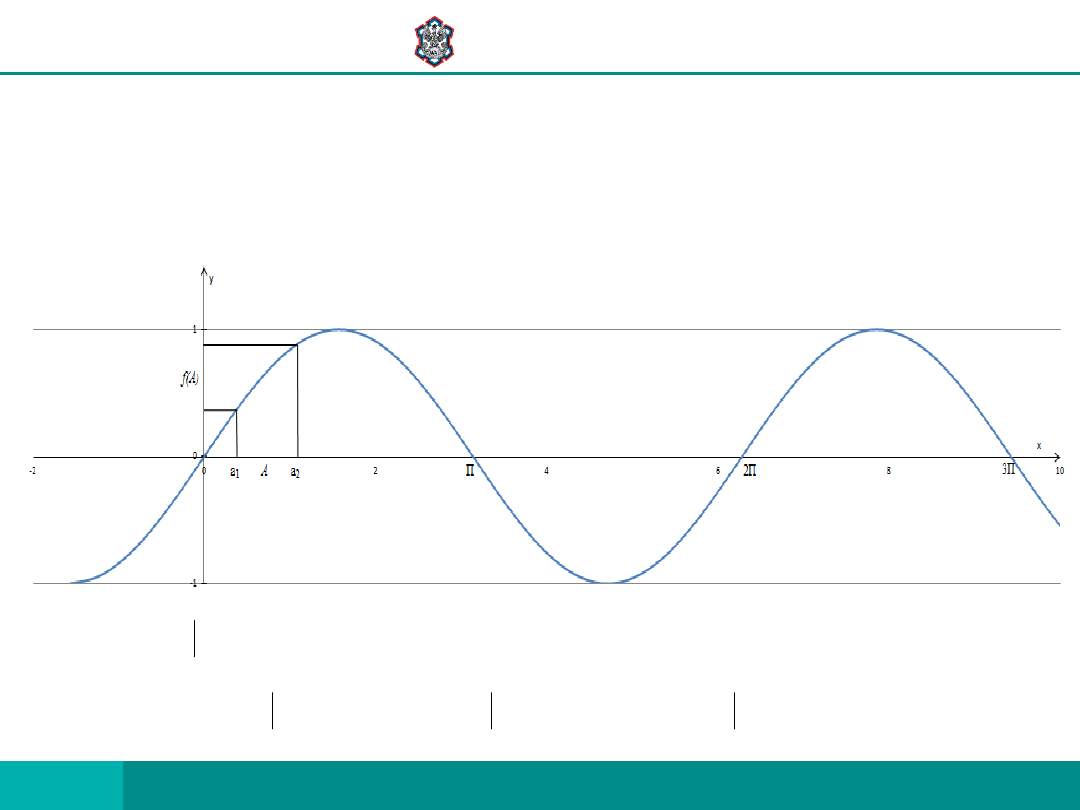
PRZYKŁAD 2

NIECH

10

Wojskowa Akademia Techniczna

20.11.2021

R

Y

R

X



 ,

x

x

f

sin

)

( 





2

1

a

x

a

R

x

A









 



 

 



2

1

2

1

sin

sin

sin

sin

a

y

a

R

y

a

x

a

R

x

A

x

R

x

A

f























WOJSKOWA AKADEMIA
TECHNICZNA

im. Jarosława Dąbrowskiego

PRZECIWOBRAZ

• NIECH (funkcja przekształcające zbiór X w zbiór Y)
• NIECH
• PRZECIWOBRAZEM ZBIORU C, WYZNACZANYM PRZEZ FUNKCJĘ f

NAZYWAMY ZBIÓR, KTÓREGO ELEMENTAMI SĄ TE ELEMENTY
ZBIORU X, KTÓRYCH OBRAZY NALEŻĄ DO C

• PRZECIWOBRAZ ZBIORU C, WYZNACZONY PRZEZ FUNKCJĘ f

OZNACZAMY SYMBOLEM

UWAGA!!!
(C nie jest elementem Y)!

11

Wojskowa Akademia Techniczna

20.11.2021

Y

X

f



:

 

 





Y

C

C

x

f

X

x

C

f











,

1

Y

C 

 

C

f

1



Y

C

WOJSKOWA AKADEMIA
TECHNICZNA

im. Jarosława Dąbrowskiego

PRZYKŁAD 1

NIECH

12

Wojskowa Akademia Techniczna

20.11.2021

)

,

(

:

R

Y

R

X

R

R

f







 

 

Q

f

h

wymiernyc

liczb

zbiór





1

1

 









Q

-Q

x

f

ych

x wymiern

dla

ych

niewymiern

x

dla

1

0

 

 

-Q

f

ych

niewymiern

liczb

zbiór





0

1

 

 

Q

f





1

1

 

 

Q

R

Q

f











0

1

WOJSKOWA AKADEMIA
TECHNICZNA

im. Jarosława Dąbrowskiego

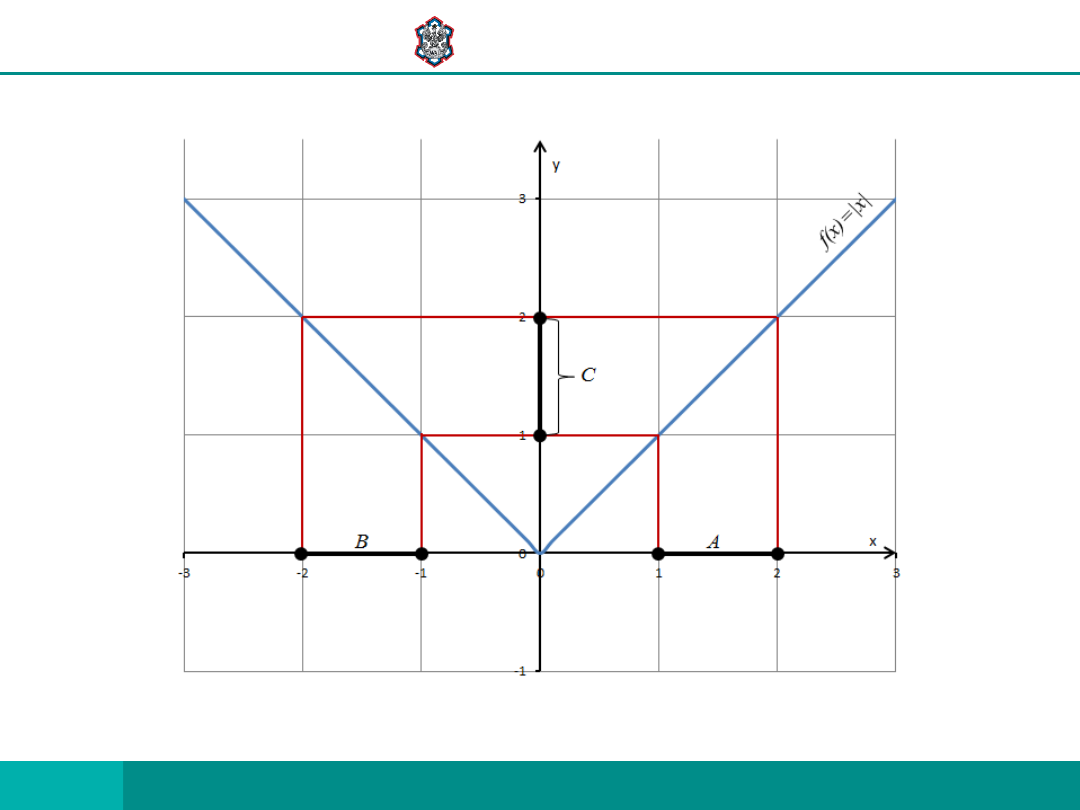
PRZYKŁAD 2

NIECH

13

Wojskowa Akademia Techniczna

20.11.2021

R

R

f



:

 

















0

0

x

x

x

x

x

x

f

dla

dla

  

 



B

A

x

R

x

x

R

x

C

f



























1

2

:

2

1

:

1

NIECH





2

1

:









y

R

y

C

WOJSKOWA AKADEMIA
TECHNICZNA

im. Jarosława Dąbrowskiego

c.d. PRZYKŁAD 2

14

Wojskowa Akademia Techniczna

20.11.2021

 

B

A

C

f





 1

WOJSKOWA AKADEMIA
TECHNICZNA

im. Jarosława Dąbrowskiego

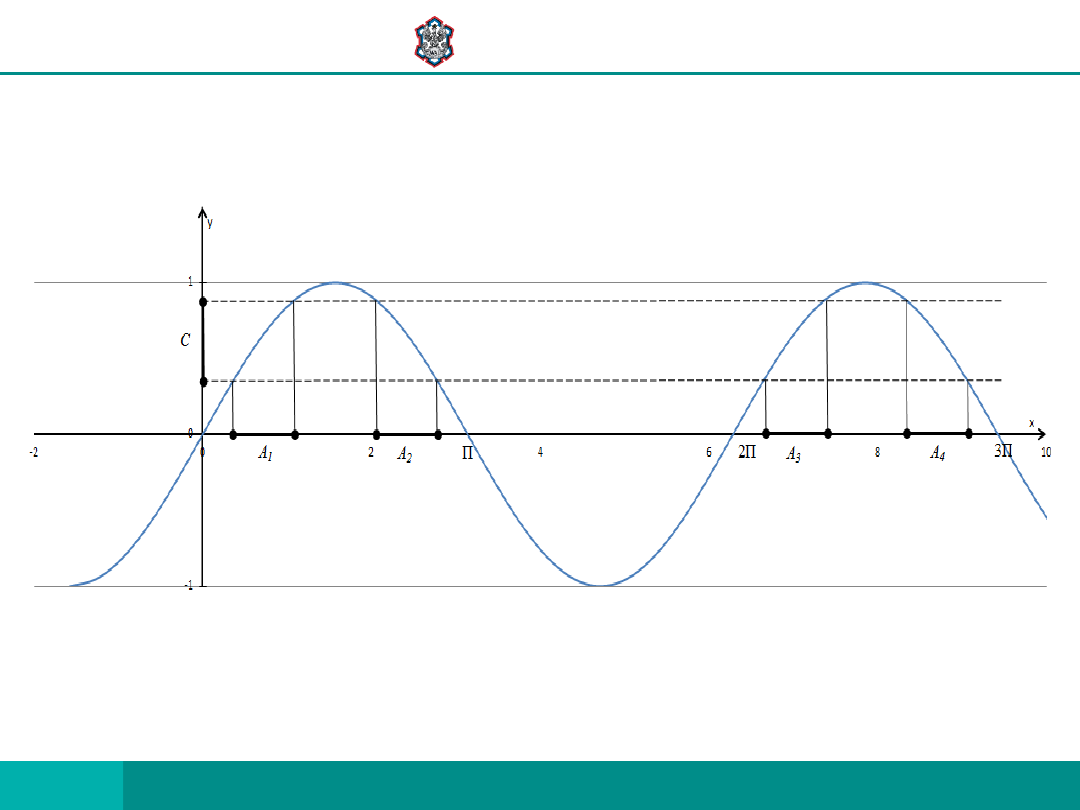
c.d. PRZYKŁADU (sinx)

15

Wojskowa Akademia Techniczna

20.11.2021

 

...

3

2

1

1

A

A

A

C

f









WOJSKOWA AKADEMIA
TECHNICZNA

im. Jarosława Dąbrowskiego

WYBRANE WŁASNOŚCI OBRAZÓW I PRZECIWOBRAZÓW

WYZNACZANYCH PRZEZ FUNKCJE (H.R., Rozdział V §5

NIECH
1)
2)
3)
4) JEŚLI JEST RÓŻNOWARTOŚCIOWA TO

5)
6)
7)
8) JEŚLI TO
9)
10) NIECH TO
JEŚLI „f RÓŻNOWARTOŚCIOWA” TO

16

Wojskowa Akademia Techniczna

20.11.2021

Y

D

C

X

B

A

Y

X

f







,

,

,

,

:





 

 

B

f

A

f

B

A

f











 

 

B

f

A

f

B

A

f







   





B

A

f

B

f

A

f







Y

X

f



:

   





B

A

f

B

f

A

f











 

 

B

f

A

f

B

A

f











 

 

D

f

C

f

D

C

f

1

1

1

















 

 

D

f

C

f

D

C

f

1

1

1

















 

 

D

f

C

f

D

C

f

1

1

1













D

C 

 

 

D

f

C

f

1

1







 





C

C

f

f



 1

X

A

 





A

f

f

A

1





 





A

f

f

A

1





WOJSKOWA AKADEMIA
TECHNICZNA

im. Jarosława Dąbrowskiego

FUNKCJE ZDANIOWE JEDNEJ

ZMIENNEJ

17

Wojskowa Akademia Techniczna

20.11.2021

Niech dana będzie przestrzeń
Wyrażenie , w którym występuje zmienna x
i które staje się zdaniem prawdziwym lub fałszywym, gdy zamiast
zmiennej x podstawimy nazwę dowolnego elementu przestrzeni X
nazywamy
FUNKCJĄ ZDANIOWĄ JEDNEJ ZMIENNEJ ,
której zakresem zmienności jest przestrzeń X





X

)

(x



FUNKCJĄ ZDANIOWĄ JEDNEJ ZMIENNEJ

WOJSKOWA AKADEMIA
TECHNICZNA

im. Jarosława Dąbrowskiego

RODZINA ZBIORU 2

x

18

Wojskowa Akademia Techniczna

20.11.2021

- zbiór wszystkich funkcji
Zbiór tych wszystkich wartości zmiennej , przy których funkcja
zdaniowa
staje się zdaniem prawdziwym oznaczamy
- jest to pewien podzbiór zbioru X, elementów,
które mają własność φ
Funkcja φ wyznacza pewien podzbiór zbioru X.

W skrócie

X

x

x



),

(



Zbió
r

 





1

,

0

: 





X



 

1

,

0

: 

X



X

x

X

x

x



),

(







)

(x

X

x

A











A





X

x

X

x

A









1

)

(









X

x

X

x

A







)

(









1

)

(

2

















x

X

x

A

A

X





WOJSKOWA AKADEMIA
TECHNICZNA

im. Jarosława Dąbrowskiego

PRZYKŁAD 1

19

Wojskowa Akademia Techniczna

20.11.2021

NIECH Z BĘDZIE ZBIOREM WSZYSTKICH LICZB CAŁKOWITYCH.
WYRAŻENIE:

JEST PRZYKŁADEM FUNKCJI ZDANIOWEJ ZMIENNEJ „z” O ZAKRESIE
ZMIENNOŚCI

np.:
DLA JEST ZDANIEM FAŁSZYWYM
DLA JEST ZDANIEM PRAWDZIWYM

Z

z

z

z







,

0

2

2

1

2

1

)

(

,

1











z

z







,...

3

,

2

,

1

,

0

,...,

z

Z





3

6

9

)

(

,

3









z

z



WOJSKOWA AKADEMIA
TECHNICZNA

im. Jarosława Dąbrowskiego

c.d. PRZYKŁAD 1

20

Wojskowa Akademia Techniczna

20.11.2021

WYZNACZMY ZBIÓR , CZYLI PODZBIÓR TYCH ELEMENTÓW ZE
ZBIORU Z, KTÓRE „MAJĄ WŁASNOŚĆ φ”

POWIEMY: „FUNKCJA φ WYZNACZA ZBIÓR (PODZBIÓR) ELEMENTÓW O
WŁASNOŚCI φ”
LUB INACZEJ: „FUNKCJA φ WYZNACZA PEWNĄ WŁASNOŚĆ ELEMENTÓW
ZBIORU X”

! PODZBIORY NAZYWAMY TEŻ RELACJAMI

JEDNOCZŁONOWYMI W X

Z

A 



 













2

,

1

,

0

0

2

1

2



















Z

z

z

Z

z

z

Z

z

A





X

A 



WOJSKOWA AKADEMIA
TECHNICZNA

im. Jarosława Dąbrowskiego

PRODUKTY KARTEZJAŃSKIE ZBIORÓW

RELACJE

FUNKCJE JAKO RELACJE

H. RASIOWA, ROZDZIAŁ V (W CAŁOŚCI)

str. 60

21

Wojskowa Akademia Techniczna

20.11.2021

WOJSKOWA AKADEMIA
TECHNICZNA

im. Jarosława Dąbrowskiego

POJĘCIE PARY UPORZĄDKOWANEJ I N-tki

UPORZĄDKOWANEJ

22

Wojskowa Akademia Techniczna

20.11.2021

MAJĄC DWA DOWOLNE PRZEDMIOTY (ELEMENTY) a, b MOŻEMY
UTWORZYĆ Z NICH ”PARĘ UPORZĄDKOWANĄ” O POPRZEDNIKU ”a” I
NASTĘPNIKU ”b”, KTÓRĄ OZNACZAĆ BĘDZIEMY (a, b).

PARĘ UPORZĄDKOWANĄ (a, b) UWAŻAMY ZA RÓŻNĄ OD PARY
UPORZĄDKOWANEJ (b, a) JEŚLI TYLKO a ≠ b .

PARY UPORZĄDKOWANE (a, b) I (c, d) UWAŻAMY ZA RÓWNE ((a, b) =
(c, d)) WTEDY I TYLKO WTEDY GDY MAJĄ RÓWNE POPRZEDNIKI I
NASTĘPNIKU, CZYLI GDY

a = c i b = d

CZYLI

   



 



d

b

c

a

d

c

b

a









 ,

,

WOJSKOWA AKADEMIA
TECHNICZNA

im. Jarosława Dąbrowskiego

POJĘCIE PARY UPORZĄDKOWANEJ I N-tki

UPORZĄDKOWANEJ

23

Wojskowa Akademia Techniczna

20.11.2021

RÓŻNE DEFINCJE PARY UPORZĄDKOWANEJ

     



 









c

b

a

b

a

a

b

a

,

,

,

,

,



 







N

N

N

a

a

a

a

a

,

,...,

,...,

1

1

1





KURATOWSKI (ROK 1921):

N-tka UPORZĄDKOWANA

WOJSKOWA AKADEMIA
TECHNICZNA

im. Jarosława Dąbrowskiego

PRODUKT (ILOCZYN) KARTEZJAŃSKI ZBIORÓW

24

Wojskowa Akademia Techniczna

20.11.2021

ILOCZYNEM KARTEZJAŃSKIM DWÓCH ZBIORÓW X i Y NAZYWAMY
ZBIÓR WSZYSTKICH PAR UPORZĄDKOWANYCH (x, y), TAKICH ŻE

• ILOCZYN KARTEZJAŃSKI DWÓCH ZBIORÓW X i Y, OZNACZAĆ

BĘDZIEMY

PRZYKŁADY:
1)
2)

•

 

Y

y

X

x





i

• ILOCZYNEM KARTEZJAŃSKIM

Y

X 

2

, X

X

X

Y

X







WOJSKOWA AKADEMIA
TECHNICZNA

im. Jarosława Dąbrowskiego

PRODUKT (ILOCZYN) KARTEZJAŃSKI ZBIORÓW

25

Wojskowa Akademia Techniczna

20.11.2021

3) OGÓLNIE:
NIECH

•
•
•

itd.

•

• PRODUKTEM (ILOCZYNEM) KARTEZJAŃSKIM ZBIORÓW

NAZYWAMY ZBIÓR ”N-tek” UPORZĄDKOWANYCH
GDZIE

X

A

1

A

A









W

w

C

c

B

b

A

a

w

c

b

a

z

Z

W

C

B

A





















,

,

,

:

,

,

,

2

A

A

A





3

A

A

A

A







N

n

A

A

A

A

,...,

,...,

,

2

1





N

n

a

a

a

,...,

,...,

1





N

n

A

a

n

n

,...,

1

,







N

WOJSKOWA AKADEMIA
TECHNICZNA

im. Jarosława Dąbrowskiego

RELACJE

26

Wojskowa Akademia Techniczna

20.11.2021

PODZBIORY USTALONEJ PRZESTRZENI X NAZYWAMY RELACJAMI
JEDNOCZŁONOWYMI W X
- FUNKCJA ZDANIOWA JEDNEJ ZMIENNEJ
PODZBIORY TE MOŻEMY UTOŻSAMIAĆ Z POJĘCIEM PEWNEJ
WŁASNOŚCI φ ”WYBRANYCH ELEMENTÓW” TEJ PRZESTRZENI, A
MIANOWICIE PODZBIÓR UTOŻSAMIANY Z WŁASNOŚCIĄ ” φ”
TAKĄ, ŻE DLA KAŻDEGO ” ”

 

1

,

0

: 

X



X

x

PODZBIORY

RELACJAMI

MIANOWICIE

X

A 



 





A

x

x







gdy

1

WŁASNOŚCI OZNACZAMY ZATEM JAKO ZBIORY
ZDANIA: ”x JEST ELEMENTEM A”

”x MA WŁASNOŚĆ A”

- SĄ RÓWNOWAŻNE

 





 





x

X

x

x

X

x

A







:

1











PODZBIORY NAZYWAMY

X

A 



RELACJAMI JEDNOCZŁONOWYMI W X

RELACJA ≡ PODZBIÓR ≡ WŁASNOŚĆ

WOJSKOWA AKADEMIA
TECHNICZNA

im. Jarosława Dąbrowskiego

RELACJE DWUCZŁONOWE

27

Wojskowa Akademia Techniczna

20.11.2021

NIECH DANE BĘDĄ DWA ZBIORY X, Y
ILOCZYN KARTEZJAŃSKI JEST TO ZBIÓR WSZYSTKICH PAR
UPORZĄDKOWANYCH (x, y) TAKICH ŻE

JEŚLI OZNACZYMY (NAZWIEMY) (x, y) = z TO

Z

Y

X





Y

y

X

x



 ,

RELACJĄ DWUCZŁONOWĄ NAZYWAMY DOWOLNY PODZBIÓR ILOCZYN
KARTEZJAŃSKIEGO

R JEST TO PODZBIÓR PAR UPORZĄDKOWANYCH POSIADAJĄCYCH
PEWNĄ WŁASNOŚĆ

 





Y

y

X

x

y

x

Y

X









,

,





Y

X

z

z

z

Z

Y

X









,...,

,

2

1

Y

X 

Y

X

R





WOJSKOWA AKADEMIA
TECHNICZNA

im. Jarosława Dąbrowskiego

RELACJE DWUCZŁONOWE

28

Wojskowa Akademia Techniczna

20.11.2021

NIECH FUNKCJA ZDANIOWA φ DWÓCH ZMIENNYCH x i y OZNACZA
PEWNĄ WŁASNOŚĆ φ PARY UPORZĄDKOWANEJ (x, y)

POWIEMY, ŻE FUNKCJA φ WYZNACZA PEWNĄ RELACJĘ

ZBIÓR TYCH PAR (x, y), KTÓRE MAJĄ WŁASNOŚĆ φ JEŚLI R JEST
RELACJĄ DWUCZŁONOWĄ W TO ZAMIAST
MOŻEMY PISAĆ, ŻE xRy I CZYTAĆ:
1) „para uporządkowana (x, y) należy do relacji R” lub
2) „x pozostaje w relacji R z elementem y”
DZIEDZINĄ RELACJI R NAZYWAMY ZBIÓR POPRZEDNIKÓW PAR
UPORZĄDKOWANYCH NALEŻĄCYCH DO RELACJI R,

PRZECIWDZIEDZINĄ RELACJI NAZYWAMY ZBIÓR
NASTĘPNIKÓW PAR UPORZĄDKOWANYCH NALEŻĄCYCH DO R

Y

X 



R

 

1

,

0

:



Y

X



 





1

)

,

(

,









y

x

Y

X

y

x

R





 

R

y

x



,

  



R

y

x

Y

y

X

x

R









)

,

(

:

że

,

istnieje

D

Y

X

R





  



R

y

x

X

x

Y

y

R









)

,

(

:

że

,

istnieje

*

D

WOJSKOWA AKADEMIA
TECHNICZNA

im. Jarosława Dąbrowskiego

RELACJE DWUCZŁONOWE

29

Wojskowa Akademia Techniczna

20.11.2021

• CZĘSTO BĘDZIEMY ZAKŁADAĆ, ŻE X=Y WTEDY
• ZBIÓR WSZYSTKICH RELACJI DWUCZŁONOWYCH W ILOCZNIE

OZNACZAĆ BĘDZIEMY

2

Y

Y

Y

Y

X













Y

Y

R

R

Y

Y









2

 

1

, 



y

x

y

xR





 

 





Y

X

y

x

Y

X

y

x

R













2

1

,

,





Y

X

R







• ZAPISZEMY WTEDY

FORMALNIE MOŻE BYĆ

• KAŻDA FUNKCJA ZDANIOWA WYZNACZA

PEWNĄ RELACJĘ

ILOCZYNIE

Y

Y

Y

Y

R



2





R

Y

Y

R





 

Y

y

X

x

y

x



 ,

,

,





R

WOJSKOWA AKADEMIA
TECHNICZNA

im. Jarosława Dąbrowskiego

RELACJE M-CZŁONOWE

30

Wojskowa Akademia Techniczna

20.11.2021

NIECH
NIECH
- ILOCZYN KARTEZJAŃSKI

• RELACJĄ ”M-CZŁONOWĄ” W PRODUKCIE JEST DOWOLNY

PODZBIÓR REGO PRODUKTU

JEŚLI JEST RELACJĄ M-CZŁONOWĄ TO ZAMIAST
MOŻEMY PISAĆ I CZYTAĆ ”RELACJA
ZACHODZI POMIĘDZY ” LUB ”M-tka
MA WŁASNOŚĆ ”





N

M





M

m,...,

,...,

2

,

1



M

m

m

X

X

X

X

X

X

M

m



,...,

,...,

,

2

1

M

m

X

X

X

X











...

...

2

1



M

m

m

X







M

m

m

M

X

R

M

R





M

m

m

R

x

x

x



,...,

,...,

1





M

m

M

x

x

x

R

,...,

,...,

1

M

R

M

m

x

x

x

,...,

,...,

1





M

m

x

x

x

,...,

,...,

1

M

R

WOJSKOWA AKADEMIA
TECHNICZNA

im. Jarosława Dąbrowskiego

RELACJE M-CZŁONOWE

31

Wojskowa Akademia Techniczna

20.11.2021

• NIECH BĘDZIE DANY PRODUKT ZBIORÓW

O LICZNOŚCIACH
W PRODUKCIE TYM ISTNIEJE DOKŁADNIE RELACJI
M-CZŁONOWYCH

PRZYKŁAD:
„WZÓR” x < y < z dla WYRAŻA PEWNĄ RELACJĘ
TRÓJCZŁONOWĄ W

WŁASNOŚĆ CIĄGÓW TRÓJELEMENTOWYCH
WŁASNOŚĆ „TRÓJEK UPORZĄDKOWANYCH”

M

m

X

X

X









...

...

1

m

X

M



m

k

m

,

M

m

k

k

k









...

...

1

2

M

m

X

X

X

M

R











...

...

1

2





z

y

x ,

,











3

3

















R





3

3

,

2

,

1

R







3

3

,

0

,

1







WOJSKOWA AKADEMIA
TECHNICZNA

im. Jarosława Dąbrowskiego

FUNKCJE ZDANIOWE M-ZMIENNYCH

32

Wojskowa Akademia Techniczna

20.11.2021

 

1

,

0

...

...

:

1











M

m

M

X

X

X



M

m

X

X

X

M

R











...

...

1

2













1

0

,...,

,...,

1

M

m

M

x

x

x



M

m

M

M

X

X

X

R













...

...

1



1

R

R

M

W

ZAMIANA"

"









Z

m

X

x

x

x

x

X

X

X

m

m

M

m

M

m

















M

,

,...,

,...,

...

...

1

1





Z

x

x

x

z

M

m





,...,

,...,

1

 

1

,

0

: 

Z



 





1

,











z

Z

z

A

Z

A









NIECH X i Y DOWOLNE ZBIORY

• SPEŁNIA

NASTĘPUJĄCY WARUNEK:
„DLA KAŻDEGO ISTNIEJE DOKŁADNIE JEDEN ELEMENT
TAKI ŻE TO RELACJĘ TĘ NAZYWAMY FUNKCJĄ”

•

• DLA KAŻDEGO ISTNIEJE , ŻE

• DLA KAŻDEGO I DLA KAŻDEGO

JEŻELI I TO

WOJSKOWA AKADEMIA
TECHNICZNA

im. Jarosława Dąbrowskiego

FUNKCJE JAKO

RELACJE

33

Wojskowa Akademia Techniczna

20.11.2021

Y

X

R





X

x

JEŻELI RELACJA DWUCZŁONOWA

Y

y

 

R

y

x



,

ZATEM FUNKCJA JEST SZCZEGÓLNEGO RODZAJU RELACJĄ

POWYŻSZY WARUNEK MOŻNA ZASTĄPIĆ DWOMA WARUNKAMI

X

x

Y

y

 

R

y

x



,

X

x

Y

y

y



2

1

,





R

y

x



1

,





R

y

x



2

,

2

1

y

y 

1) ZBIÓR X - POJĘCIE PIERWOTNE

2) PARA UPORZĄDKOWANA – ZBIÓR

3) RELACJA – ZBIÓR (PODZBIÓR ILOCZYNU KARTEZJAŃSKIEGO)

4) FUNKCJA – RELACJA „SZCZEGÓLNEGO RODZAJU”

SZCZEGÓLNEGO RODZAJU ZBIÓR

5) FUNKCJA ZDANIOWA WŁASNOŚĆ RELACJA

ZBIÓR

WOJSKOWA AKADEMIA
TECHNICZNA

im. Jarosława Dąbrowskiego

FUNDAMENTALNE ZNACZENIE POJĘCIA

„ZBIÓR”

34

Wojskowa Akademia Techniczna

20.11.2021

Y

X

R





     





b

a

a

b

a

,

,

, 

wyznacza

NIECH , X – PRZESTRZEŃ

• Z

RELACJĘ NAZYWAMY ZWROTNĄ, JEŚLI DLA KAŻDEGO

• P

RELACJĘ NAZYWAMY PRZECIWZWROTNĄ, JEŚLI DLA
KAŻDEGO

• S

RELACJĘ NAZYWAMY SYMETRYCZNĄ, JEŚLI DLA
KAŻDYCH , Z TEGO ŻE WYNIKA, ŻE

• P

RELACJĘ NAZYWAMY PRZECIWSYMETRYCZNĄ, JEŚLI
DLA KAŻDYCH , Z TEGO ŻE WYNIKA, ŻE

WOJSKOWA AKADEMIA
TECHNICZNA

im. Jarosława Dąbrowskiego

WŁASNOŚCI RELACJI

DWUCZŁONOWYCH

35

Wojskowa Akademia Techniczna

20.11.2021

X

X

R





ZWROTNOŚĆ:

X

X

R





 

R

x

x 

,

X

x

PRZECIWZWROTNOŚĆ:

X

X

R





X

x

 

R

x

x 

,

SYMETRYCZNOŚĆ:

X

X

R





X

y

x 

,

 

R

y

x



,

 

R

x

y 

,

PRZECIWSYMETRYCZNOŚĆ (ASYMETRYCZNOŚĆ):

X

X

R





X

y

x 

,

 

R

y

x



,

 

R

x

y 

,

• A

RELACJĘ NAZYWAMY ANTYSYMETRYCZNĄ, JEŚLI DLA
KAŻDYCH , Z TEGO ŻE I WYNIKA,
ŻE x=y

• P

RELACJĘ NAZYWAMY PRZECHODNIĄ, JEŚLI DLA
KAŻDYCH TRZECH ELEMENTÓW Z TEGO ŻE
I WYNIKA ŻE

• S

RELACJĘ NAZYWAMY SPÓJNĄ, JEŚLI DLA KAŻDYCH
ZACHODZI LUB

WOJSKOWA AKADEMIA
TECHNICZNA

im. Jarosława Dąbrowskiego

c.d. WŁASNOŚCI RELACJI

DWUCZŁONOWYCH

36

Wojskowa Akademia Techniczna

20.11.2021

ANTYSYMETRYCZNOŚĆ:

X

X

R





PRZECHODNIOŚĆ:

X

X

R





SPÓJNOŚĆ:

X

X

R





X

y

x 

,

 

R

y

x



,

 

R

x

y 

,

X

y

x 

,

 

R

y

x



,

 

R

y

x



,

X

z

y

x



,

,

 

R

z

y 

,

 

R

z

x 

,

 

R

x

y 

,

RODZINA ZBIORÓW R ≡ ZBIÓR ZBIORÓW
CIAŁO ZBIORÓW TO TAKA RODZINA R, ŻE

1) „RELACJA MNIEJSZOŚCI” W ZBIORZE R

a) JEST PRZECIWZWROTNA
b) JEST PRZECHODNIA

BO WARUNEK x<x NIE JEST SPEŁNIONY DLA ŻADNEJ
LICZBY RZECZYWISTEJ

2) „RELACJA RÓWNOLEGŁOŚCI PROSTYCH” W ZBIORZE WSZYSTKICH

PROSTYCH NA PŁASZCZYŹNIE
JEŚLI PROSTA L JEST RÓWNOLEGŁA DO PROSTEJ Q TO PROSTA Q
JEST RÓWNOLEGŁA DO PROSTEJ L

a) NIE JEST SPÓJNA
b) JEST SYMETRYCZNA
c) JEST ZWROTNA?

1)
2) JEŚLI TO
3) JEŚLI TO

WOJSKOWA AKADEMIA
TECHNICZNA

im. Jarosława Dąbrowskiego

PRZYKŁADY

37

Wojskowa Akademia Techniczna

20.11.2021

 

R

x

x 

,





...

, 





i

X

A

i

i

R





R

R



A

R



 A

R



B

A,

R



 B

A

3) RELACJA „≤” W ZBIORZE LICZB RZECZYWISTYCH JEST

ANTYSYMETRYCZNA, BOWIEM WARUNKI x≤y I y≤x POCIĄGAJĄ
WARUNEK x=y

4) RELACJA INKLUZJI „ ” W DOWOLNEJ DZIEDZINIE ZBIORÓW JEST

ANTYSYMETRYCZNA

5) „RELACJA PODZIELNOŚCI” W ZBIORZE LICZBA NATURALNYCH JEST

PRZECHODNIA, JEŚLI BOWIEM x JEST DZIELNIKIEM y, A y JEST
DZIELNIKIEM z, TO x JEST DZIELNIKIEM z

6) RELACJA INKLUZJI ZBIORÓW W DOWOLNEJ RODZINIE ZBIORÓW

JEST PRZECHODNIA
„JEŚLI I TO ” DLA DOWOLNYCH TRZECH
ZBIORÓW A, B, C

WOJSKOWA AKADEMIA
TECHNICZNA

im. Jarosława Dąbrowskiego

PRZYKŁADY

38

Wojskowa Akademia Techniczna

20.11.2021



B

A

C

A

C

B

• RELACJĘ NAZYWAMY RELACJĄ RÓWNOWAŻNOŚCI W

ZBIORZE X JEŻELI R JEST:

- ZWROTNA DLA KAŻDEGO

- SYMETRYCZNA DLA KAŻDYCH

- PRZECHODNIA

• NIECH R – RELACJA RÓWNOWAŻNOŚCI

NIECH DLA KAŻDEGO ZBIÓR OZNACZA ZBIÓR TYCH
WSZYSTKICH ELEMENTÓW , ŻE (KTÓRE
POZOSTAJĄ W RELACJI RÓWNOWAŻNOŚCI)

WOJSKOWA AKADEMIA
TECHNICZNA

im. Jarosława Dąbrowskiego

RELACJA

RÓWNOWAŻNOŚCI

39

Wojskowa Akademia Techniczna

20.11.2021

 

R

x

x 

,

X

X

R





X

x

 

 

R

x

y

R

y

x







,

,

X

y

x 

,

 

 

 

R

z

x

R

z

y

R

y

x









,

,

,

i

X

x

X

y

 

R

y

x



,

 









X

y

x

X

y

x

R

R

y

x

X

y

x

R

R



















"

"

,

ZWROTNA

x

SYMETRYCZNA

PRZECHODNIA

! ZBIORY DLA NAZYWAMY KLASY RÓWNOWAŻNOŚCI

RELACJI R W X (ALBO KLASĄ ABSTRAKCJI) O REPREZENTANCIE x
(LUB WYZNACZONĄ PRZEZ x)

• DOWOLNA RELACJA RÓWNOWAŻNOŚCI R W ZBIORZE

USTALA PODZIAŁ TEGO ZBIORU NA ROZŁĄCZNE I NIEPUSTE
PODZBIORY. MIANOWICIE NA KLASY RÓWNOWAŻNOŚCI TEJ RELACJI
W TAKI SPOSÓB, ŻE DWA ELEMENTY x, y ZBIORU X NALEŻĄ DO TEJ
SAMEJ KLASY RÓWNOWAŻNOŚCI GDY

WOJSKOWA AKADEMIA
TECHNICZNA

im. Jarosława Dąbrowskiego

c.d. RELACJA

RÓWNOWAŻNOŚCI

40

Wojskowa Akademia Techniczna

20.11.2021

x

X

x





X



 

R

y

x



,

ZBIÓR A NAZYWAMY WYPUKŁYM, JEŚLI Z TEGO, ŻE
WYNIKA, ŻE ELEMENT , PRZY CZYM .

PRZYKŁADY:
STOŻEK
ZBIÓR NAZYWAMY STOŻKIEM, JEŻELI Z TEGO, ŻE
WYNIKA, ŻE DLA KAŻDEGO .

PRZYKŁADY: KAŻDY STOŻEK ZAWIERA

WOJSKOWA AKADEMIA
TECHNICZNA

im. Jarosława Dąbrowskiego

RELACJE PORZĄDKU I ICH

WŁASNOŚCI

41

Wojskowa Akademia Techniczna

20.11.2021

A

x

x



2

1

,

POJĘCIA DODATKOWE

ZBIÓR WYPUKŁY









A

x

x







2

1

1





1

0







STOŻEK

N

R









x





x



0





 







1

2

R





2

 





x

y

y

x











R

R

,

3

 





0

,

0

,

4













y

x

y

x

R

R

 





1

,

5













x

y

y

x

R

R

 





0

,

1

,

6















x

x

y

y

x

R

R





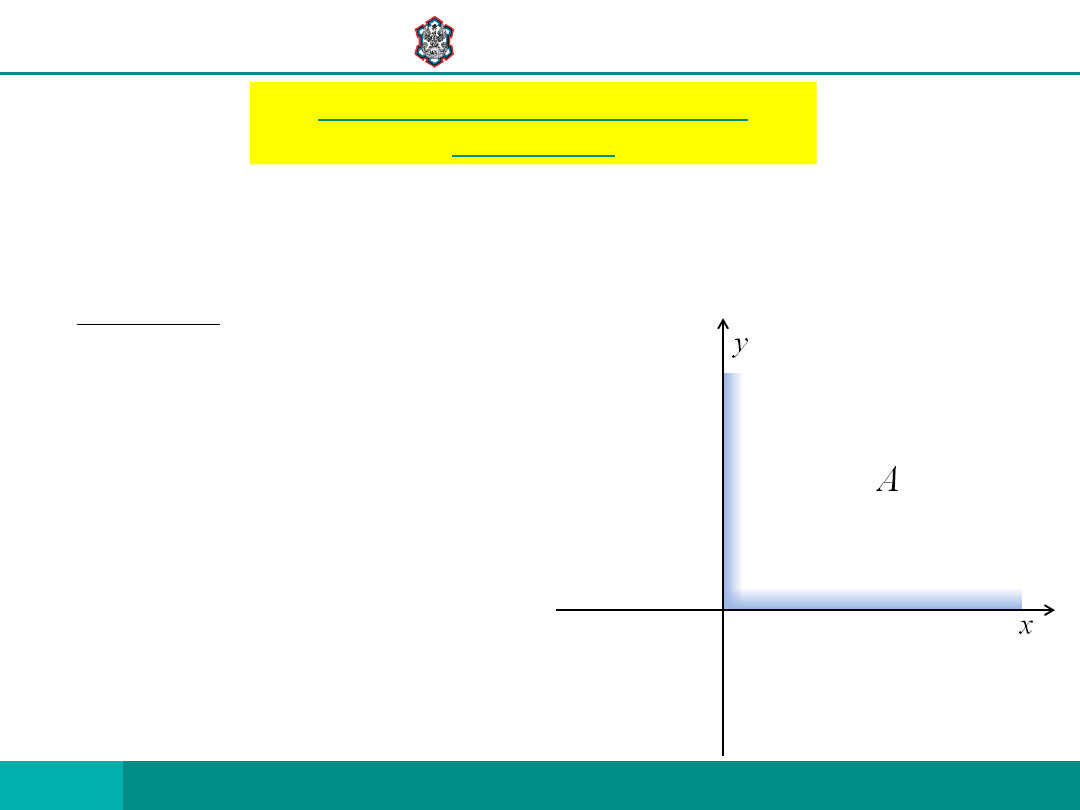
ELEMENT NAZWIEMY PUNKTEM WIERZCHOŁKOWYM ZBIORU
A, JEŚLI NIE ISTNIEJĄ RÓŻNE OD w, ŻE
DLA PEWNEGO . .

PRZYKŁAD

1) CZY A JEST ZBIOREM WYPUKŁYM?
2) CZY A JEST STOŻKIEM?
3) CZY A POSIADA PUNKT WIERZCHOŁKOWY?

WOJSKOWA AKADEMIA
TECHNICZNA

im. Jarosława Dąbrowskiego

PUNKT WIERZCHOŁKOWY

ZBIORU A

42

Wojskowa Akademia Techniczna

20.11.2021





2

1

1

x

x

w











1

0







 





0

,

0

:

,











y

x

y

x

A

R

R

A

w

A

x

x



2

1

,

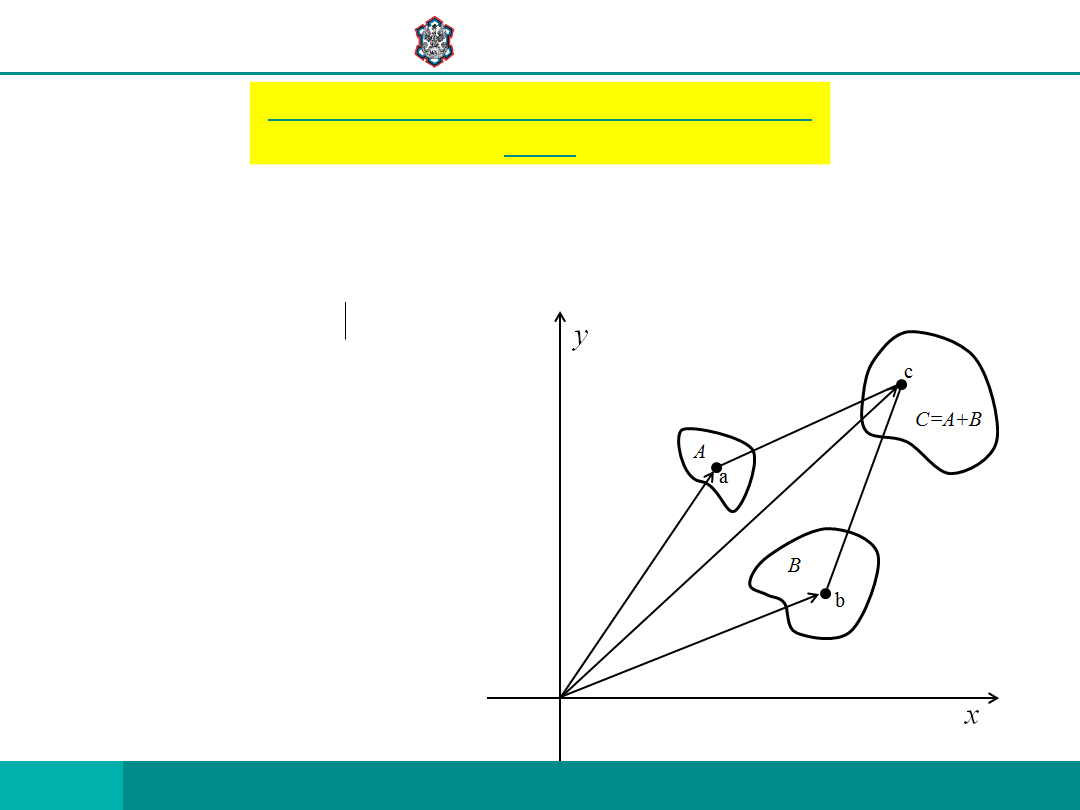
NIECH
SYMBOLEM A+B OZNACZAMY ZBIÓR WSZYSTKICH ELEMENTÓW
POSTACI

WOJSKOWA AKADEMIA
TECHNICZNA

im. Jarosława Dąbrowskiego

SUMA ALGEBRAICZNA ZBIORÓW

A+B

43

Wojskowa Akademia Techniczna

20.11.2021

N

B

A

R



,

R

R









b

a

b

a

c

,

,





R

R















b

a

b

a

c

C

B

A

,

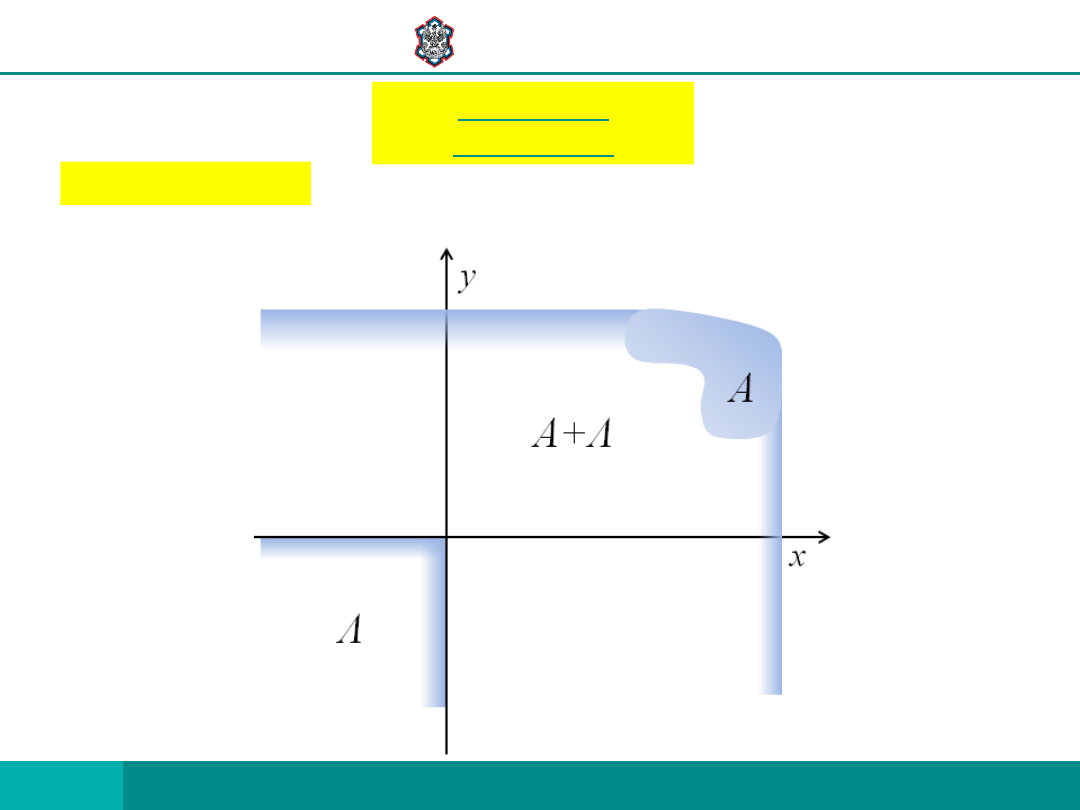
NIECH Λ STOŻEK W
ZBIÓR A NAZYWAMY Λ –WYPUKŁYM, JEŚLI ZBIÓR Λ+A JEST WYPUKŁY

WOJSKOWA AKADEMIA
TECHNICZNA

im. Jarosława Dąbrowskiego

ZBIÓR Λ-

WYPUKŁY

44

Wojskowa Akademia Techniczna

20.11.2021

N

N

A R

R



,

NIECH Λ STOŻEK

• NIECH Λ STOŻ (NIE MUSI)

• ZWIĄZKI STOŻKÓW Z RELACJAMI

NIECH - STOŻEK WYPUKŁY W
RELACJĄ - GENEROWANĄ PRZEZ STOŻEK Λ NAZYWAĆ
BĘDZIEMY TAKI ZBIÓR (y, z), ŻE

•

•

WOJSKOWA AKADEMIA
TECHNICZNA

im. Jarosława Dąbrowskiego

RELACJE PORZĄDKUJĄCE I STOŻKI (OW str.

16 →)

45

Wojskowa Akademia Techniczna

20.11.2021

CZY STOŻEK JEST ZBIOREM WYPUKŁYM?

ZWIĄZKI

N

N

z

y

R

R



,

,

N

R







R

 





 y

z

 

 























y

z

z

y

R

N

N

R

R

,

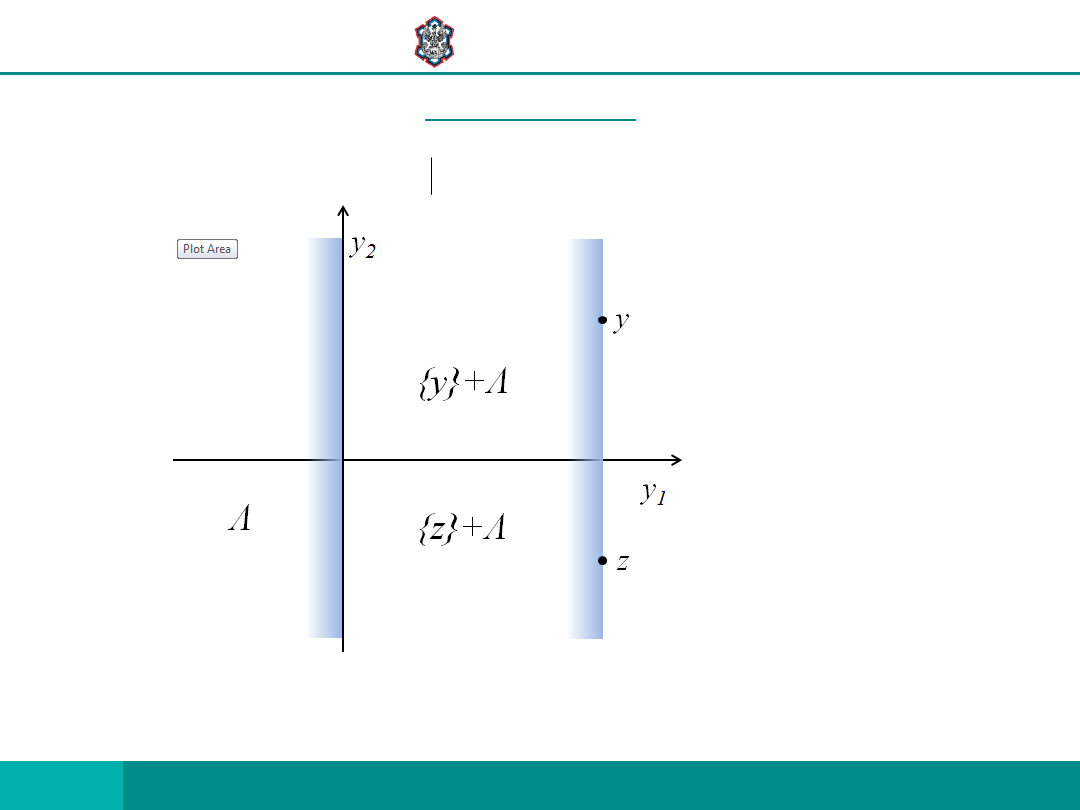
WOJSKOWA AKADEMIA
TECHNICZNA

im. Jarosława Dąbrowskiego

PRZYKŁAD 1

46

Wojskowa Akademia Techniczna

20.11.2021

RYCZNA

ANTYSYMET

JEST

NIE

-



R

 

 











z

y









0

,

,

1

2

2

1

2



















R

R

 

 











y

z

R

z

y

bo

,

 

 











z

y

R

y

z

bo

,

ZBIÓR UPORZĄDKOWANY TO PARA UPORZĄDKOWANA

GDZIE Y PEWIEN ZBIÓR
RELACJA PORZĄDKU

• ZBIORY QUASIUPORZĄDKOWANE

• ZBIORY UPORZĄDKOWANE

• ZBIORY LINIOWO UPORZĄDKOWANE

WOJSKOWA AKADEMIA
TECHNICZNA

im. Jarosława Dąbrowskiego

RELACJE

PORZĄDKU

47

Wojskowa Akademia Techniczna

20.11.2021

ZBIÓR UPORZĄDKOWANY

ZWROTNA
PRZECHODNIA
ANTYSYMETRYCZNA
SPÓJNA



 



R

B

R

Y

,

,



Y

Y

R





QUASIPORZĄDEK (PORZĄDEK CZĘŚCIOWY)
PORZĄDEK
PORZĄDEK LINIOWY

PRZESTRZEŃ

UPORZĄDKOWANA





Y

Y

R





WOJSKOWA AKADEMIA
TECHNICZNA

im. Jarosława Dąbrowskiego

c.d. RELACJE

PORZĄDKU

48

Wojskowa Akademia Techniczna

20.11.2021

KAŻDY STOŻEK WYPUKŁY Λ GENERUJE RELACJĘ
QUASIPORZĄDKU,



R









A

PRZECHODNI

ZWROTNA

R

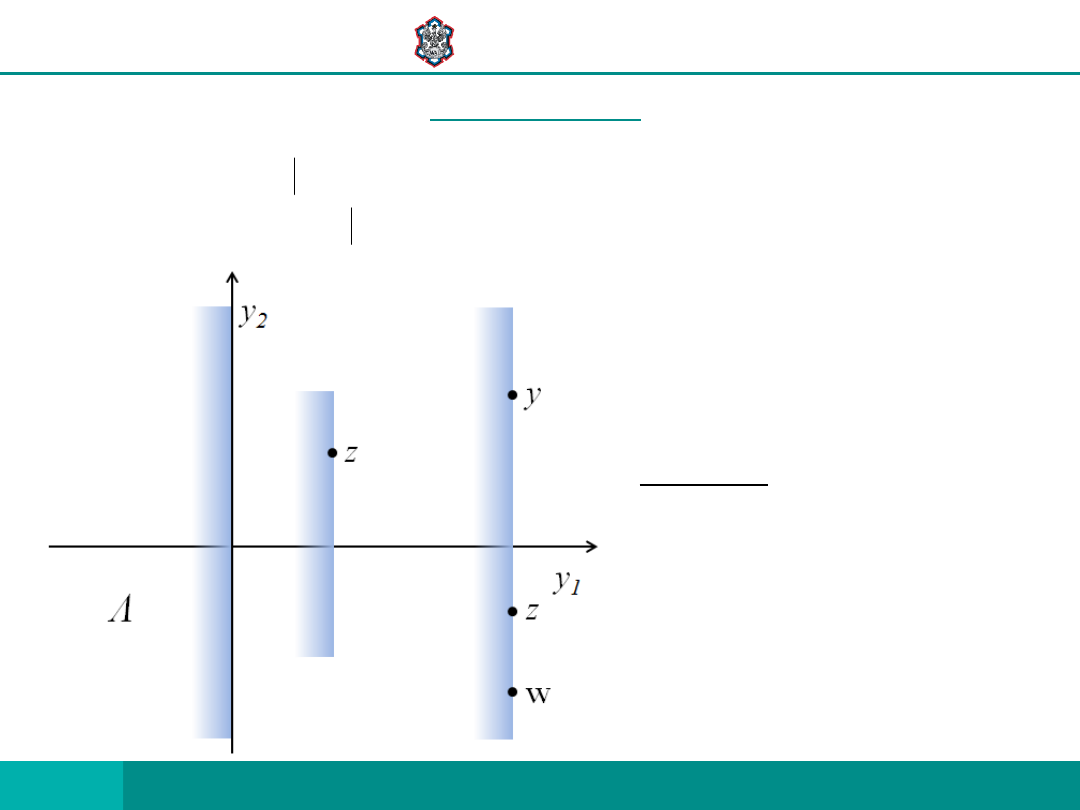
CZY JEST:

a) ZWROTNA?
b) PRZECHODNIA?

WOJSKOWA AKADEMIA
TECHNICZNA

im. Jarosława Dąbrowskiego

PRZYKŁAD 2

49

Wojskowa Akademia Techniczna

20.11.2021



R









0

,

1

2

2

1















R

 

 



















y

z

y

x

R

2

2

,

R

R

 











y

z

R

z

y

,

 











z

w

R

w

z

,







 R

w

y,

?

POKAZAĆ, ŻE
1) JEŚLI TO
2) JEŚLI TO
3) CZYLI
4) TO
5) TO





 y

w





 y

z

1

1

z

y 





 z

w

1

1

w

z 

1

1

1

w

z

y









 y

w

1

1

w

y 

WOJSKOWA AKADEMIA
TECHNICZNA

im. Jarosława Dąbrowskiego

c.d. RELACJE

PORZĄDKU

50

Wojskowa Akademia Techniczna

20.11.2021

STOŻEK WYPUKŁY POSIADAJĄCY PUNKT WIERZCHOŁKOWY GENERUJE
RELACJĘ: ZWROTNĄ
PRZECHODNIĄ PORZĄDKU
ANTYSYMETRYCZNĄ

ŁATWO POKAZAĆ, ŻE:

a) Λ - STOŻEK
b) Λ - ZBIÓR WYPUKŁY
c) Λ - POSIADA PUNKT WIERZCHOŁKOWY

WOJSKOWA AKADEMIA
TECHNICZNA

im. Jarosława Dąbrowskiego

PRZYKŁAD 3

51

Wojskowa Akademia Techniczna

20.11.2021









N

R











n

n

N

N

n

,

0

,...,

,...,

1









 

 



















y

z

z

y

R

N

N

R

R

,

NIECH ORAZ NIECH . OZNACZA TO ŻE
A WIĘC DLA PEWNEGO MAMY CZYLI
PONIEWAŻ
WIĘC

N

z

y

R



,

 





 y

z

















y

z











y

z

N







n

y

z

n

n

n

,



N



 n

n

,

0



N



 n

z

y

n

n

,

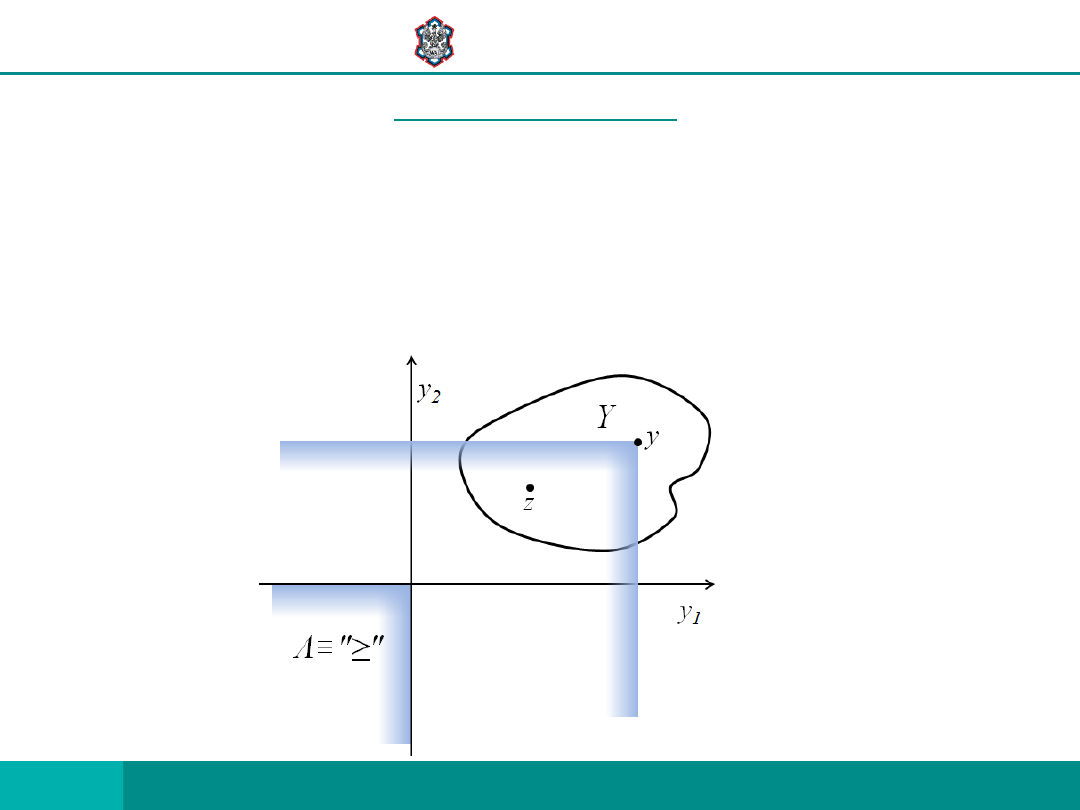
STOŻEK Λ GENERUJE
JEST RELACJĄ:

a) ZWROTNĄ
b) PRZECHODNIĄ
c) ANTYSYMETRYCZNĄ

A WIĘC RELACJĄ PORZĄDKU

WOJSKOWA AKADEMIA
TECHNICZNA

im. Jarosława Dąbrowskiego

c.d. PRZYKŁAD 3

52

Wojskowa Akademia Techniczna

20.11.2021







R





R

 





 y

z





y

z

WOJSKOWA AKADEMIA
TECHNICZNA

im. Jarosława Dąbrowskiego

PRZYKŁAD 3

53

Wojskowa Akademia Techniczna

20.11.2021













0

0

0

,

2

1

1

2

2

1



























i

lub

R

L

 

 



















y

z

z

y

R

N

N

R

R

,

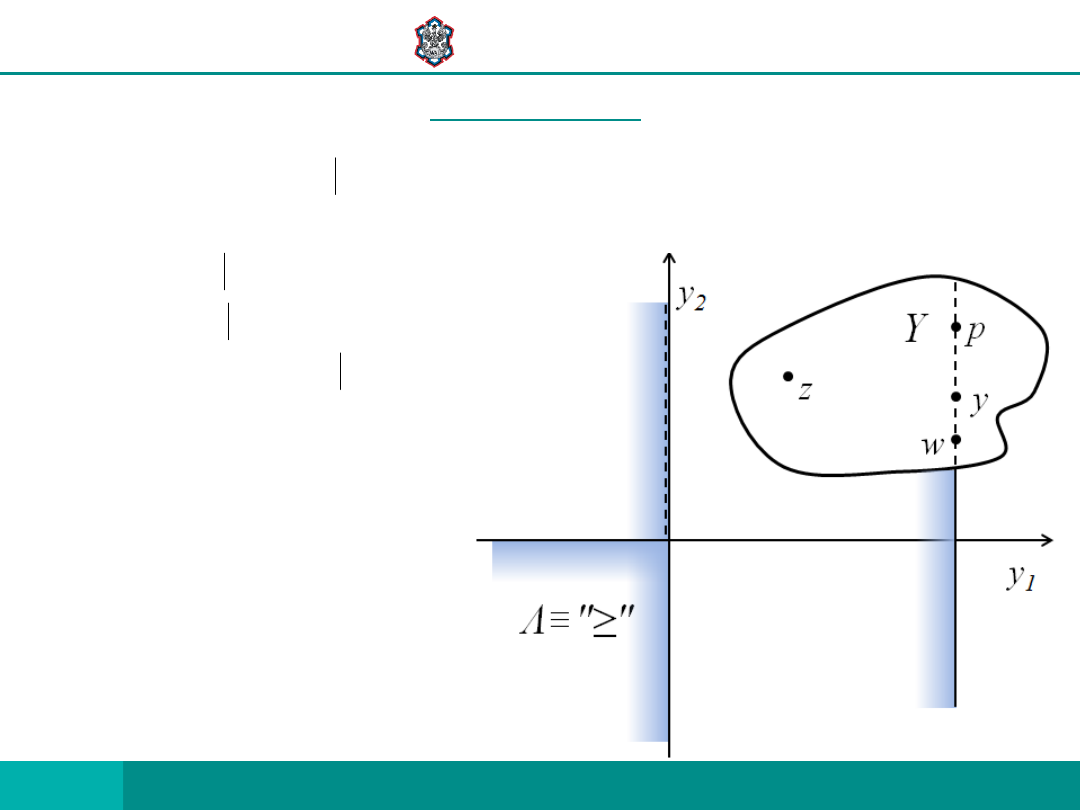
CZY JEST
a) STOŻKIEM?
b) ZBIOREM WYPUKŁYM?
c) CZY W Λ JEST WIERZCHOŁEK?

2

1











L





0

1

1













N

R





0

0

2

1

2

















i

N

R

L



1

1

y

w 

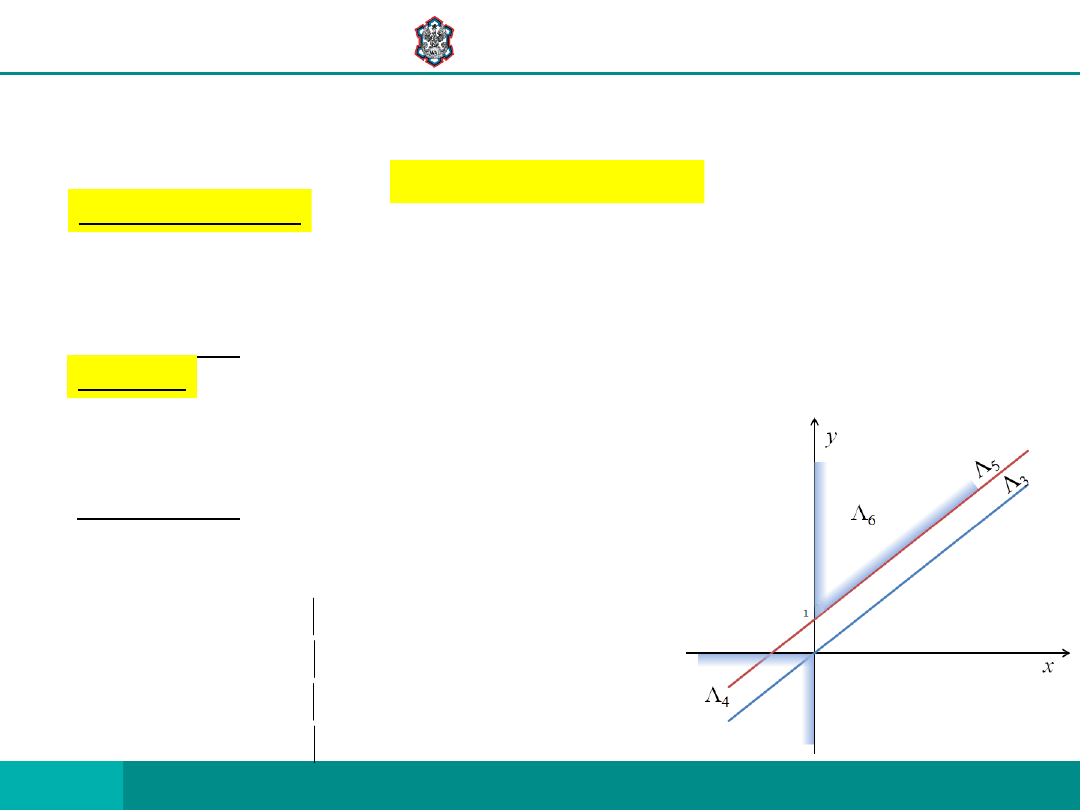
JAKI TO PORZĄDEK?

ZAUWAŻMY, ŻE
NATOMIAST
PONADTO
OZNACZA TO, ŻE DLA DOWOLNEJ PARY (y, z)

WOJSKOWA AKADEMIA
TECHNICZNA

im. Jarosława Dąbrowskiego

c.d. PRZYKŁAD 3

54

Wojskowa Akademia Techniczna

20.11.2021

 

L

R

z

y





,

RELACJĘ GENEROWANĄ STOŻKIEM MOŻEMY
ZAPISAĆ:

L

L

y

w

y

z













,

L

y

p







L

w

y







JEŚLI
LUB O ILE
GDY

1

1

z

y 

1

1

z

y 

2

2

z

y 

L

R



L



 



































z

y

l

k

z

y

z

y

l

z

y

R

k

k

l

l

N

N

L

LUB

DLA

ORAZ

ŻE

,

ISTNIEJE

N

R

R

,

 

"

lub

dla

oraz

że

,

istnieje

"

z

y

l

k

z

y

z

y

l

z

y

k

k

l

l













N

,

