Ćwiczenie 5

Analiza .AC - charakterystyka częstotliwościowa

1. Filtry RC. Proszę połączyć układ jak na rys. 1, realizujący najprostszą realizację filtru dolnoprzepustowego i górnoprzepustowego filtru 1-go rzędu.

Rysunek 1 Dolnoprzepustowy i górnoprzepustowy filtr RC

Badanie charakterystyki częstotliwościowej przeprowadza się przy użyciu analizy .AC. Okienko konfiguracji (EditSpice analysis) pokazane jest na rys. 2. Pole Type of sweep ustala sposób zmiany częstotliwości (Decade oznacza skalę logarytmiczną na której jedna działka oznacza 10-krotny wzrost wartości). Pole Number of points per decade ustala ile wartości częstotliwości zostanie rozmieszczonych w obrębie jednej dekady. Pola Start frequency oraz Stop frequency określają zakres częstotliwości zobrazowanych charakterystyką. Całkowita ilość punktów charakterystyki to iloczyn wartośc Number of points per decade i ilości dekad wynikających z podanego zakresu częstotliwości (np. zakres 1 do 1MEG to 6 dekad, przy 100 punktach na dekadę charakterystyka będzie się składała z 600 punktów).

Rysunek 2 Konfiguracja analizy .AC

Do przeprowadzenia charakterystyki konieczne jest zastosowanie źródła Voltage w trybie AC (rys. 3). Jeśli zostanie zastosowana wartość amplitudy 1V, to pokazywana na wykresie wartość amplitudy (20log(Uwy)) będzie odpowiadała wartości wzmocnienia w dB (20log(Uwy/Uwe), Uwe=1).

Rysunek 3 Konfiguracja źródła do wyznaczania charakterystyki częstotliwościowej

2. Charakterystyki uzyskane dla powyższego układu pokazane są na rys. 4

Rysunek 4 Charakterystyki częstotliwościowe układu z p. 1

1. Są to tzw. wykresy Body'ego. Ciągłą linią są wykreślone charakterystyki amplitudowe, linią przerywaną - charakterystyki fazowe. Płaski obszar na obu charakterystykach amplitudowych to obszar przepuszczania, obszar nachylony, to obszar zaporowy. W okolicach częstotliwości granicznej następuje załamanie charakterystyk, dla filtru dolnoprzepustowego charakterystyka przechodzi z zakresu przepuszczania do zaporowgo (zaczyna opadać), dla filtru górnoprzepustowego - odwrotnie. Jednocześnie charakterystyki fazowe wykazują zmianę fazy o 90 stopni. Takie przejście nazywane jest biegunem.

2. Proszę za pomocą kursorów pomiarowych wyznaczyć jaka jest amplituda w dB w zakresie przepuszczania, jakie jest nachylenie w dB na dekadę charakterystyk amplitudowych w zakresie zaporowym, jaka jest rozpiętość fazy wykazywana przez charakterystyki fazowe. Kursory pomiarowe wypisują jednocześnie fazę i amplitudę.

3. Charakterystyki amplitudowe i fazowe można rozdzielić na dwa okna. Prawy przycisk myszy na wykresie, opcja Add plot pane doda nowe okno wykresu. Prawy przycisk myszy, Add trace umożliwy wstawienie do nowego okno przebiegów (V(hipass), V(lopass)), lewy przycisk myszy na osi fazy w jednym oknie umożliwi zaznaczenie opcji Don't plot phase (rys. 5a), lewy przycisk myszy na osi fazy w drugim oknie umożliwi zaznaczenie opcji Don't plot magnitude (rys. 5b).

a)
b)

Rysunek 5 Wyłączanie kreślenia charakterystyki fazowej (a) oraz charakterystyki amplitudowej (b)

4. Możliwe jest też alternatywne zobrazowanie charakterystyki częstotliwościowej w układzie współrzędnych Re-Im. Należy kliknąć oś amplitudy i w okienku, w grupie Representation wybrać opcję Re-Im. Tego typu zobrazowanie szczególnie nadaje się do badania stabilności układu zgodnie z kryterium Nyquista (obejmowanie lub nie przez charakterystykę punktu (-1,j0)). Proszę użyć kursora pomiarowego, żeby przekonać się, że każdy punkt charakterystyki odpowiada innej częstotliwości.

3. Częstotliwość graniczna układów wynika z ich transmitancji. Dla filtru dolnoprzepustowego i górnoprzepustowego 1 rzędu o wzmocnieniu w paśmie przepustowym równym 1 (czyli dla takich układów jak w p. 1) są to odpowiednio:

Są to transmitancje zespolone. Ich moduły (odpowiadające charakterystykom amplitudowym wynoszą odpowiednio:

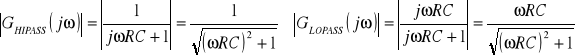
Często te wzory zapisuje się jako:

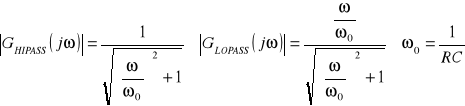
Jako częstotliwość graniczną przyjmuje się częstotliwość, dla której
, czyli:

Proszę wyznaczyć ze wzorów jaka powinna być częstotliwość graniczna dla układów z p. 1 oraz jakie powinno być wzmocnienie w dB dla tej częstotliwości granicznej, a następnie zweryfikować te wyniki za pomocą kursorów pomiarowych na charakterystyce amplitudowej.

4. Transmitancje wyrażone funkcją zespoloną można modelować w SPICE. We wszystkich źródłach sterowanych (E,F,G,H) atrybut Value odpowiadający transmitancji można podać w postaci: Laplace = ... , określając transmitancję za pomocą transformaty Laplace'a. Na rys. 6 przedstawiony jest układ realizujący filtr dolno- i górnoprzepustowy takie jak w p. 1 ale za pomocą źródeł typu E z transmitancjami wg wzorów z p. 3. Proszę zrealizować układ i sprawdzić zgodność charakterystyk.

Rysunek 6 Teoretyczna realizacja filtru dolno- i górnoprzepustowego

1. Związek między układem całkującym i filtrem dolnoprzepustowym. Proszę zmienić transmitancję źródła E2 z rys. 6 na Laplace=1/s, czyli na transmitancję idealnego członu całkującego. Jakie jest podobieństwo charakterystyk częstotliwościowych tych dwóch członów? Czy uzasadnione jest stwierdzenie, że idealny człon całkujący to graniczny przypadek filtru dolnoprzepustowego z częstotliwością graniczną równą 0 oraz z nieskończonym wzmocnieniem w paśmie przepustowym?

2. Związek między układem różniczkującym i filtrem górnoprzepustowym. Proszę przywrócić transmitancję źródła E2 z rys. 6 na Laplace=s*1u*1k/(s*1u*1k+1) i zmienić transmitancję E1 na Laplace=s, czyli na transmitancję idealnego członu różniczkującego. Jakie jest podobieństwo charakterystyk częstotliwościowych tych dwóch członów? Czy uzasadnione jest stwierdzenie, że idealny człon całkujący to graniczny przypadek filtru dolnoprzepustowego z częstotliwością graniczną równą ∞ oraz z nieskończonym wzmocnieniem w paśmie przepustowym?

5. Aktywne realizacje filtrów pierwszego rzędu. Idąc tropem ustaleń z p. 4 i wychodząc od aktywnych realizacji członu całkującego i różniczkującego można prosto zrealizować aktywne filtry pierwszego rzędu. Układ jest podany na rys. 7.

Rysunek 7 Aktywny filtr dolno- i górnoprzepustowy

6. Automatyczny pomiar częstotliwości granicznej. Układ z rys. 7 należy wzbogacić o dwie dyrektywy SPICE:

.measure tmp MAX mag(v(lopass))

.measure AC fg WHEN mag(v(lopass))=tmp/sqrt(2)

Dyrektywy należy wstawić do schematu za pomocą EditSpice directive. Polecenie .measure ma bardzo złożoną składnię - szerzej będzie omówione na wykładzie. Zastosowany wariant w pierwszej linii szuka maksimum mag(v(lopass)), czyli modułu przebiegu v(lopass) (maksimum charakterystyki amplitudowej) i zapisuje wynik w zmiennej tmp, w drugiej linii szuka na charakterystyce AC punktu (częstotliwości), dla której mag(v(lopass)) jest równe tmp/sqrt(2), czyli wykazuje spadek o 3dB. Wynik zostanie zapisany w zmiennej fg. Po przeprowadzeniu analizy wynik pomiaru można odczytać za pomocą ViewSpice Error Log (tak jak na rys. 8).

Rysunek 8 Wynik pomiaru częstotliwości granicznej

7. Ćwiczenie. Proszę wyznaczyć wgrać schemat C:/Program Files/LTC/SwCadIII/examples/Educational/MeasureBW.ASC i przeanalizować analogiczną do poprzedniej procedurę wyznaczania pasma przenoszenia wzmacniacza tranzystorowego.

8. Proszę zbadać charakterystykę częstotliwościową wzmacniacza operacyjnego pracującego w układzie wtórnika napięciowego jak na rys. 9. Wyznaczyć częstotliwość graniczną. Teraz proszę zmienić amplitudę źródła AC na 1000V. Jakie napięcie jest na wyjściu wzmacniacza wg charakterystyki częstotliwościowej? Dlaczego tak jest. Proszę teraz wrócić do amplitudy źródła AC równej 1V i rozewrzeć pętlę sprzężenia zwrotnego (podłączając wejście `-` wzmacniacza do masy). Przeprowadzić analizę i zmierzyć częstotliwość graniczną. Jak wyjaśnić różnicę tej częstotliwości w stosunku do wtórnika napięciowego?

Rysunek 9 Badanie częstotliwości granicznej wzmacniacza operacyjnego

---