Katedra Mechaniki Budowli

Wykład

Mechanika Budowli 1 [C16]

Politechnika Gdańska

2006

Marek Krzysztof Jasina

http://www.okno.pg.gda.pl –

33

–

[e-mail]

8.

Twierdzenie o wzajemności prac
i twierdzenia z niego wynikające

8.1. Oznaczenia

ij

∆ - przemieszczenie w miejscu i na kierunku ( ) wywołane przyczyną

,

i

( )

j

ij

δ

- przemieszczenie w miejscu i na kierunku ( ) wywołane jednostko-

wym obciążeniem działającym w miejscu i na kierunku

,

i

( )

j

ij

δ

′ - przemieszczenie w miejscu i na kierunku ( ) wywołane jednostko-

wym przemieszczeniem zadanym w miejscu i na kierunku

,

i

( )

j

ij

R

- reakcja w miejscu i na kierunku

wywołana przyczyną

,

( )

i

( )

j

ij

r

- reakcja w miejscu i na kierunku

wywołana jednostkowym obcią-

żeniem działającym w miejscu i na kierunku ( ,

( )

i

)

j

ij

r′

- reakcja w miejscu i na kierunku

wywołana jednostkowym prze-

mieszczeniem zadanym w miejscu i na kierunku

,

( )

i

( )

j

Miejsce i kierunek

, w którym definiowane jest przemieszczenie lub reakcja

może oznaczać określone miejsce i kierunek albo sumę określonych przemiesz-
czeń i reakcji(zob.

na Rys. 8.1)

( )

i

ij

∆

(8.1)

1

2

ij

j

j

∆ = ∆ + ∆

Rys. 8.1

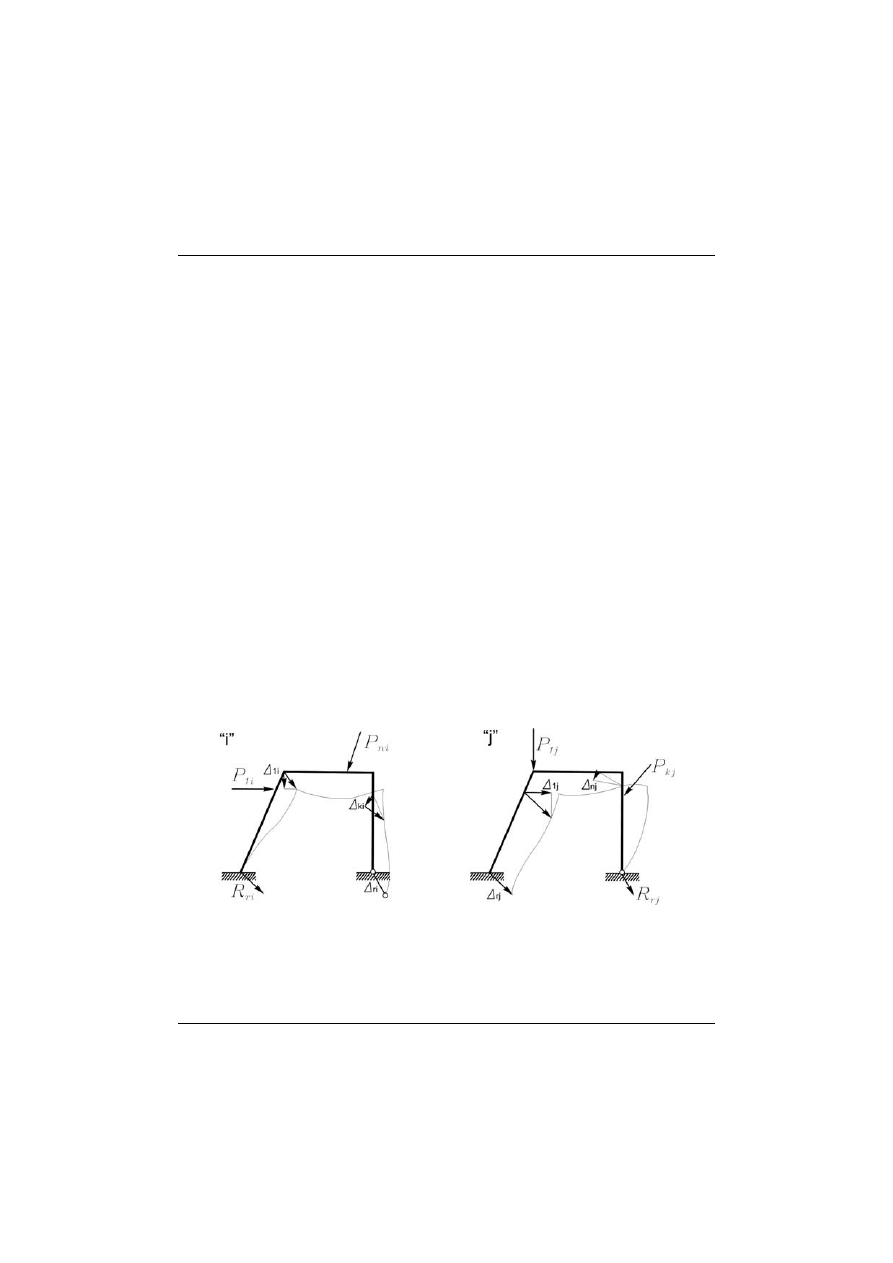
Katedra Mechaniki Budowli

Wykład

Mechanika Budowli 1 [C16]

Politechnika Gdańska

2006

Marek Krzysztof Jasina

http://www.okno.pg.gda.pl –

34

–

[e-mail]

8.2. Twierdzenie o wzajemności prac (E. Betti 1872).
Podstawowym twierdzeniem o wzajemności, z którego bezpośrednio wynikają
wszystkie dalsze, jest twierdzenie o wzajemności prac zwane twierdzeniem
Bettiego.

Rozpatrujemy dwa stany obciążeń działających na układ.

Pierwszy stan oraz wszystkie wielkości statyczne i geometryczne towarzy-

szące pierwszemu stanowi oznaczymy indeksem ( ) .

i

Odpowiednio indeksem ( oznaczymy wielkości towarzyszące drugiemu

stanowi.

)

j

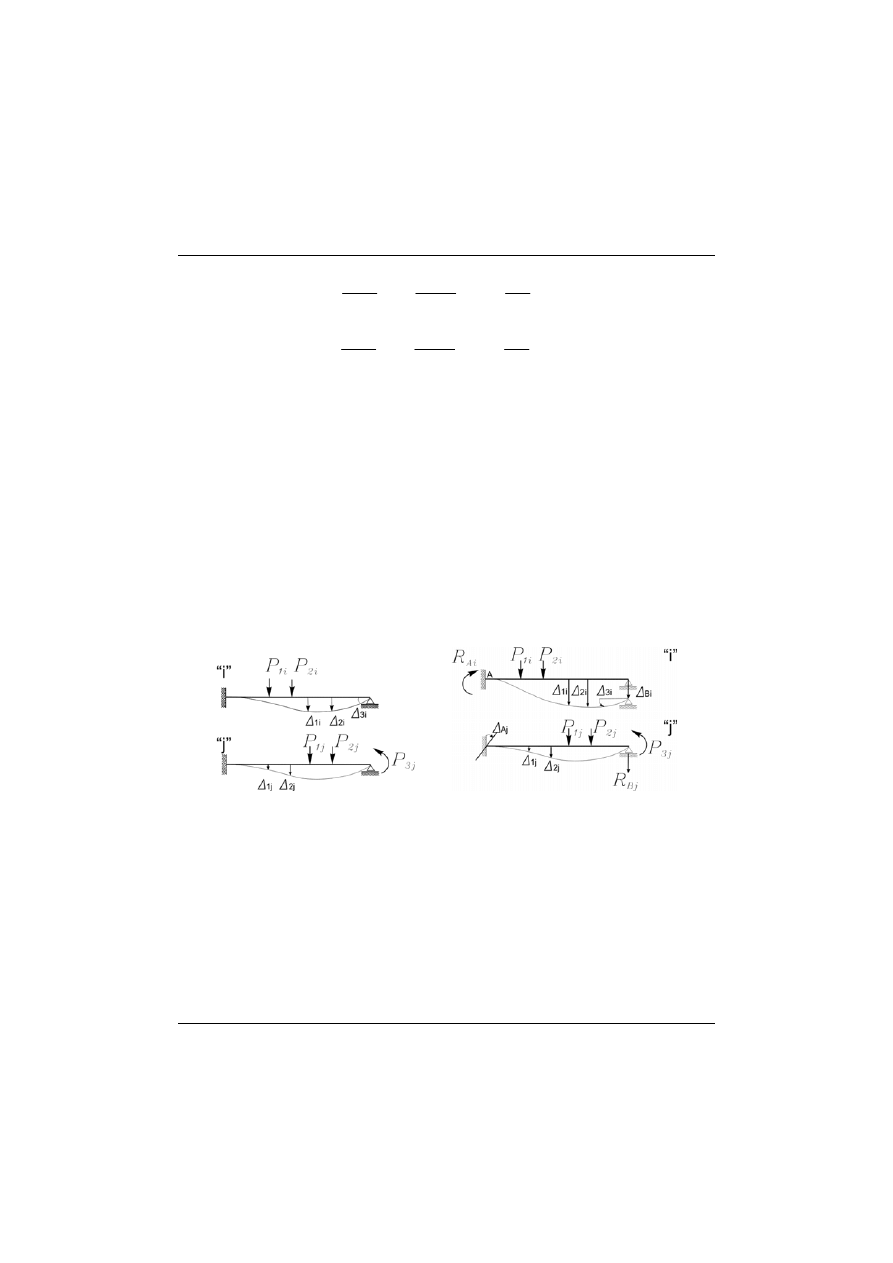
W związku z powyższym, stosując zapis z dwoma indeksami, w którym

pierwszy indeks oznacza miejsce a drugi przyczynę możemy przyjąć następują-
ce oznaczenia (zob. rys 8.2).

ni

P

i

to obciążenia (siły obciążające) i reakcje w działające „w układzie

” (to znaczy od przyczyny

);

ri

R

( )

i

( )

i

i

i

N

, M , oraz ∆

,

i

T

i

ds

ϕ

∆

i

d

, ∆

i

dh

ri

∆

)

j

oznaczają powstałe w wyniku ich działa-

nia siły przekrojowe (wewnętrzne) i odpowiadające im odkształcenia;
zaś symbolami

i

oznaczamy przemieszczenia występujące odpowied-

nio w miejscu i kierunku sił oraz reakcji.

ni

∆

Analogicznie możemy oznaczyć siły, reakcje, siły wewnętrzne, odkształcenia,
oraz przemieszczenia „w układzie ( ” (to znaczy od przyczyny ( );

)

j

Rys. 8.2

Ponieważ obciążenia i reakcje działające w obu układach a także odpowiadające
im przemieszczenia są rzeczywiste to mogą być one traktowane jako wirtualne.

Katedra Mechaniki Budowli

Wykład

Mechanika Budowli 1 [C16]

Politechnika Gdańska

2006

Marek Krzysztof Jasina

http://www.okno.pg.gda.pl –

35

–

[e-mail]

Czyli obciążenia wraz z odpowiadającymi im reakcjami obu układów mogą być
traktowane jako wirtualne. Podobnie można traktować przemieszczenia.

W związku z powyższym i dla prostoty zapisu w dalszej części wywodu pomi-
ja się w zapisie górną kreskę nad danymi oznaczeniami wielkości (np. P ,

δ

zamiast P , ).

δ

Traktując układ sił i przemieszczeń w stanie ( ) jako obciążenia i przemiesz-
czenia wirtualne dla układu ( z zasady prac wirtualnych otrzymujemy

i

)

j

dh

dh

( )

j

( )

i

( )

j

(8.2)

ni

nj

ri

rj

i

j

i

j

i

j

n

r

l

l

l

P

R

N

ds

M

d

T

ϕ

∆ +

∆ =

∆

+

∆

+

∆

∑

∑

∫

∫

∫

oraz

. (8.3)

kj

ki

rj

ri

j

i

j

i

j

i

k

r

l

l

l

P

R

N

ds

M

d

T

ϕ

∆ +

∆ =

∆

+

∆

+

∆

∑

∑

∫

∫

∫

Równanie (8.2) można traktować jako reprezentujące pracę wirtualnych obcią-
żeń i sił przekrojowych układu

na rzeczywistych przemieszczeniach układu

(porównaj 2) postać zasady prac wirtualnych opisana równaniem (7.5)).

( )

i

Analogicznie równanie (8.3) można traktować jako reprezentujące pracę rze-
czywistych obciążeń i sił przekrojowych układu

na wirtualnych przemiesz-

czeniach układu

(porównaj 1) postać zasady prac wirtualnych opisana rów-

naniem (7.4)).

( )

j

( )

i

Biorąc pod uwagę zależności (6.17) – (6.19), zapisane dla stanu

oraz dla

stanu

:

∆

=

i

i

N

ds

ds

EA

ϕ

∆

=

i

i

M

d

ds

EI

κ

∆

=

i

i

T

dh

ds

GA

,

,

, (8.4)

∆

=

j

j

N

ds

EA

ϕ

∆

=

j

j

M

d

ds

EI

κ

∆

=

j

j

T

dh

ds

GA

,

,

, (8.5)

ds

równania (8.2) i (8.3) przyjmują postać:

Katedra Mechaniki Budowli

Wykład

Mechanika Budowli 1 [C16]

Politechnika Gdańska

2006

Marek Krzysztof Jasina

http://www.okno.pg.gda.pl –

36

–

[e-mail]

i

j

i

j

i

j

ni

nj

ri

rj

n

r

l

l

l

N N

M M

T T

P

R

ds

ds

ds

EA

EI

GA

κ

∆ +

∆ =

+

+

∑

∑

∫

∫

∫

, (8.6)

j

i

j

i

j i

kj

ki

rj

ri

k

r

l

l

l

N N

M M

T T

P

R

ds

ds

ds

EA

EI

GA

κ

∆ +

∆ =

+

+

∑

∑

∫

∫

∫

. (8.7)

Łatwo można zauważyć, że prawe strony w powyższych równaniach są sobie
równe.
Przyrównując zatem do siebie lewe strony równań (8.6) i (8.7) otrzymujemy
twierdzenie Bettiego o wzajemności prac.

Twierdzenie
Jeżeli na ustrój sprężysty działają dwa niezależne od siebie układy obciążeń
(układy sił), spełniające warunki równowagi, to praca obciążeń pierwszego
układu wykonywana na przemieszczeniach wywołanych drugim układem
obciążeń równa jest pracy obciążeń drugiego układu wykonywanej na prze-
mieszczeniach wywołanych pierwszym układem obciążeń.

. (8.8)

ni

nj

ri

rj

kj

ki

rj

ri

n

r

k

r

P

R

P

R

∆ +

∆ =

∆ +

∆

∑

∑

∑

∑

Rys. 8.3 Rys. 8.4

. (8.9)

2

3

1

1

ni

nj

kj

ki

n

k

P

P

=

=

∆ =

∆

∑

∑

2

3

1

1

ni

nj

Ai

Aj

kj

ki

Bj

Bi

n

k

P

R

P

=

=

∆ +

∆ =

∆ +

∑

∑

. (8.10)

R

∆

Katedra Mechaniki Budowli

Wykład

Mechanika Budowli 1 [C16]

Politechnika Gdańska

2006

Marek Krzysztof Jasina

http://www.okno.pg.gda.pl –

37

–

[e-mail]

8.3. Twierdzenie o wzajemności przemieszczeń (E. Betti – J.C. Maxwell)
Z twierdzenia Bettiego (równanie (8.8)) wynika wprost twierdzenie o wzajem-
ności przemieszczeń.

Jeżeli założymy, że zarówno w stanie

jak i ( podpory rozważanego ukła-

du nie ulegają przemieszczeniom, czyli

( )

i

)

j

( )

r

1

=

kj

kj

P

(8.11)

0

∆ = ∆ =

ri

rj

dla wszystkich

,

przyjmując równocześnie, że w obu stanach działają jedynie siły jednostkowe

,

, (8.12)

1

=

ni

ni

P

wówczas z twierdzenia Bettiego otrzymujemy

1

1

δ

δ

=

∑

∑

ni

nj

kj

ki

n

k

, (

δ

– od obciążenia jednostkowego).

(8.13)

Lewa strona powyższej zależności reprezentuje sumę przemieszczeń w miejscu
sił układu ( ) wywołane jednostkowymi obciążeniami ze stanu (

i

)

j

1

δ

δ

=

ni

nj

ij

∑

n

1

2

j

j

ij

. (8.14)

δ

δ

δ

+

=

( )

j

1

(por. Rys. 8.3).

Analogicznie prawa strona równania (8.13) reprezentuje sumę przemieszczeń w
miejscu sił układu

wywołane jednostkowymi obciążeniami ze stanu ( )

i

δ

δ

ji

=

∑

kj

ki

k

1

2

3

i

i

i

ji

. (8.15)

δ

δ

δ

δ

+

+

=

(por. Rys. 8.4).

Po uwzględnieniu (8.14) i (8.15), równanie (8.13) można zapisać w postaci

. (8.16)

δ

δ

=

ij

ji

Powyższa zależność opisuje twierdzenie Betti-Maxwella o wzajemności prze-
mieszczeń.

Katedra Mechaniki Budowli

Wykład

Mechanika Budowli 1 [C16]

Politechnika Gdańska

2006

Marek Krzysztof Jasina

http://www.okno.pg.gda.pl –

38

–

[e-mail]

Twierdzenie
Przemieszczenie w miejscu

wywołane jednostkowym obciążeniem

działającym w miejscu

jest równe przemieszczeniu w miejscu ( wy-

wołane jednostkowym obciążeniem

działającym w miejscu

.

( )

i

(1 )

j

( )

j

)

j

(1 )

i

( )

i

Można założyć, że w każdym z rozpatrywanych poniżej stanów obciążenia
działa tylko jedna obciążająca siła uogólniona.

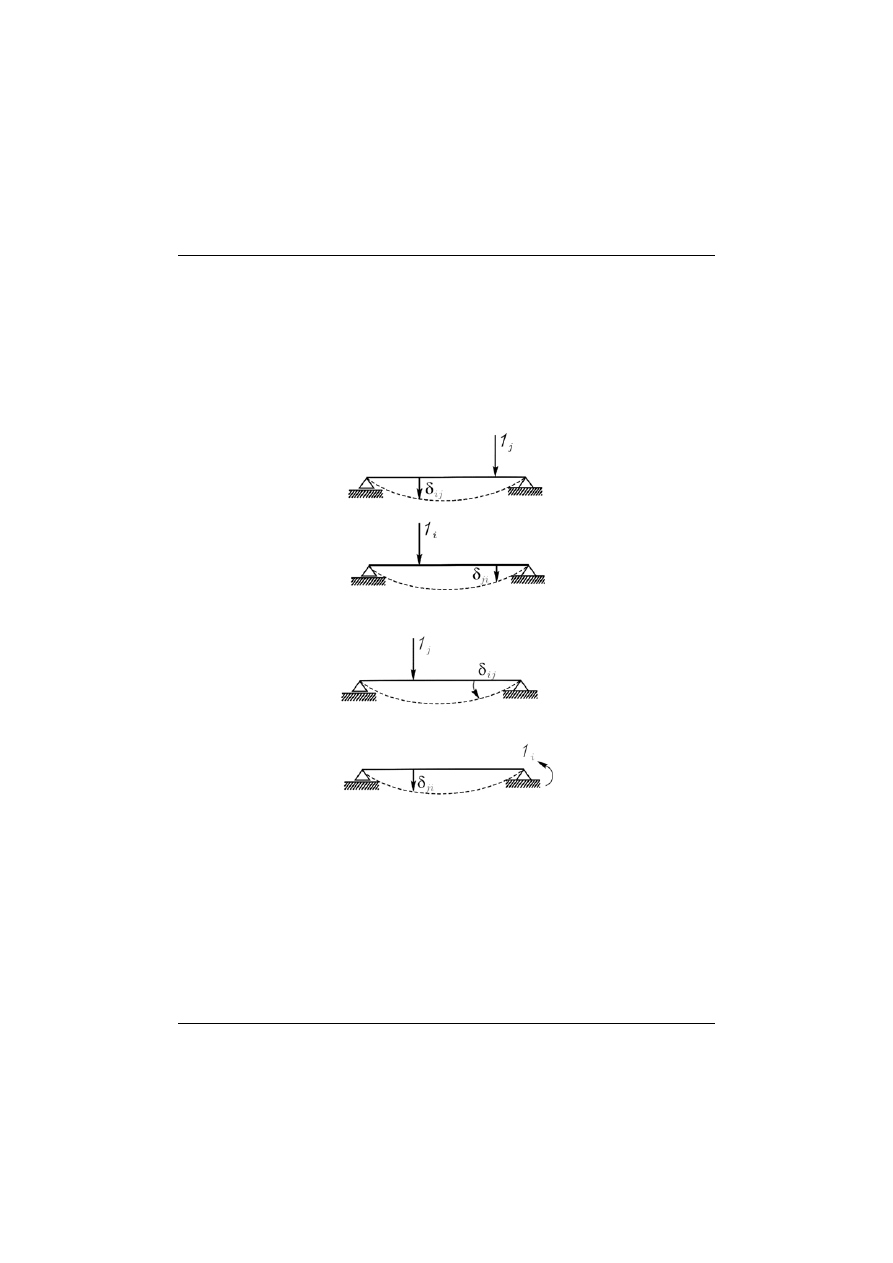
Rys. 8.5

Rys. 8.6

Ad. Rys 8.5, Rys 8.6

1

1

δ

δ

δ

δ

=

⇒

=

j

ji

ij

ji

(8.17)

i

ij

Uwaga: zaznaczone na rys 8.6 przemieszczenie

jest równe kątowi

δ

ij

δ

ji

i

, co

oznacza, że praca jednostkowej siły 1 na przemieszczeniu

δ

ij

j

jest równa pracy

momentu 1 na kącie obrotu

.

δ

ji

Katedra Mechaniki Budowli

Wykład

Mechanika Budowli 1 [C16]

Politechnika Gdańska

2006

Marek Krzysztof Jasina

http://www.okno.pg.gda.pl –

39

–

[e-mail]

Rys. 8.7

Ad. Rys 8.7

1

2

δ

δ

δ

δ

+

=

=

j

j

ij

ji

(porównaj ze wzorem (8.1)).

(8.18)

8.4. Twierdzenie o wzajemności reakcji (J.W. Rayleigh)
Podobnie, z twierdzenia Bettiego (równanie (8.8)) wynika wprost twierdzenie o
wzajemności reakcji.

Jeżeli założymy, że zarówno w stanie

jak i

siły obciążające są równe

zeru, czyli

( )

i

( )

j

0

=

=

ni

kj

P

P

)

n

1

∆ =

ri

ri

1

∆ =

rj

rj

( )

r

1

1

ri

rj

rj

ri

r

r

r

r

=

∑

∑

ij

ji

r

r

=

, (8.19)

dla wszystkich ( oraz ( , przyjmując równocześnie, że w obu stanach ob-
ciążenia stanowią jedynie jednostkowe przemieszczenia podpór

)

k

,

(8.20)

przynajmniej dla niektórych

w każdym stanie, wówczas z twierdzenia

Bettiego otrzymujemy

. (8.21)

Zgodnie z przyjętymi wcześniej oznaczeniami równanie (8.21) można zapisać w
postaci

. (8.22)

Powyższa zależność opisuje twierdzenie Rayleigha o wzajemności reakcji.

Katedra Mechaniki Budowli

Wykład

Mechanika Budowli 1 [C16]

Politechnika Gdańska

2006

Marek Krzysztof Jasina

http://www.okno.pg.gda.pl –

40

–

[e-mail]

Twierdzenie
Reakcja w miejscu i na kierunku

wywołana jednostkowym przemieszcze-

niem

zadanym w miejscu i na kierunku ( jest równa reakcji w miejscu i

na kierunku

wywołanej jednostkowym przemieszczeniem (1 zadanym w

miejscu i na kierunku

.

( )

i

(1 )

j

)

j

( )

j

)

i

( )

i

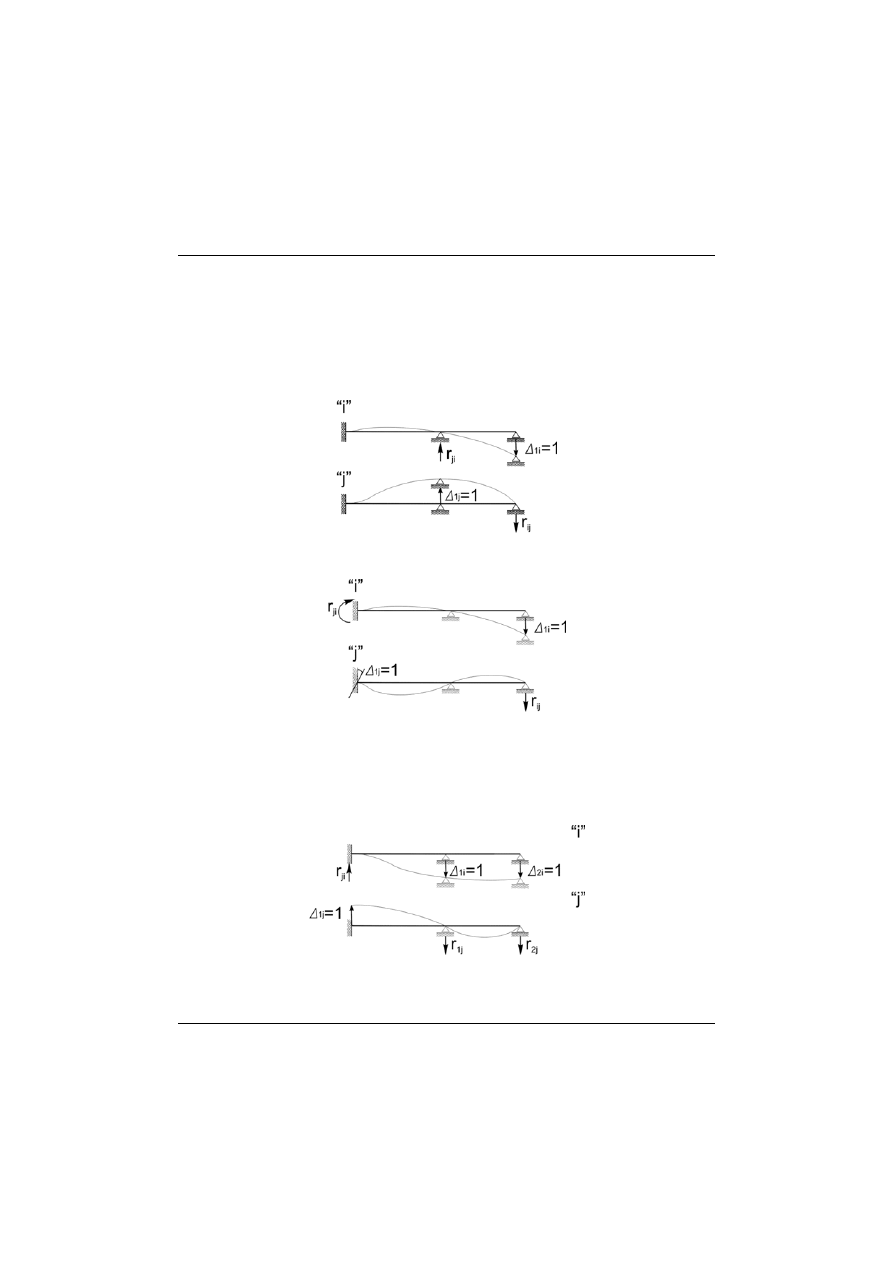
Rys. 8.8

Rys. 8.9

Ad. Rys 8.8, Rys 8.9

. (8.23)

ij

ji

r

r

=

Rys. 8.10

Katedra Mechaniki Budowli

Wykład

Mechanika Budowli 1 [C16]

Politechnika Gdańska

2006

Marek Krzysztof Jasina

http://www.okno.pg.gda.pl –

41

–

[e-mail]

Ad. Rys. 8.10

. (8.24)

1

2

ij

j

j

ji

r

r

r

r

=

+

=

8.5. Twierdzenie o wzajemności reakcji i przemieszczeń (Müller-Breslau)
Z podanego na wstępie twierdzenia Bettiego (równanie (8.8)) wynika również
twierdzenie o wzajemności reakcji i przemieszczeń.

Jeżeli założymy, że w stanie

obciążenie stanowią jedynie siły jednostkowe

( )

i

(8.25)

1

=

ni

ni

P

( )

r

( )

j

1

∆ =

rj

0

=

ki

P

1

1

0

ri

rj

n

r

r

δ

′

′

+

=

∑

∑

ij

ji

r

przynajmniej dla jednego ( ,

)

n

a podpory rozważanego układu nie ulegają przemieszczeniom, czyli

(8.26)

0

∆ =

ri

dla wszystkich

,

zaś w stanie

obciążenie stanowią jedynie jednostkowe przemieszczenia

(8.27)

przynajmniej dla jednego ( ,

)

r

a wszystkie siły równe są zeru

(8.28)

to wówczas z twierdzenia Bettiego otrzymujemy

. (8.29)

ni

nj

Zgodnie z przyjętymi oznaczeniami równanie (8.29) można zapisać w postaci

δ

′

′

= −

(1 )

j

)

j

. (8.30)

Powyższa zależność opisuje twierdzenie Müllera-Breslaua o wzajemności
przemieszczeń i reakcji.

Twierdzenie
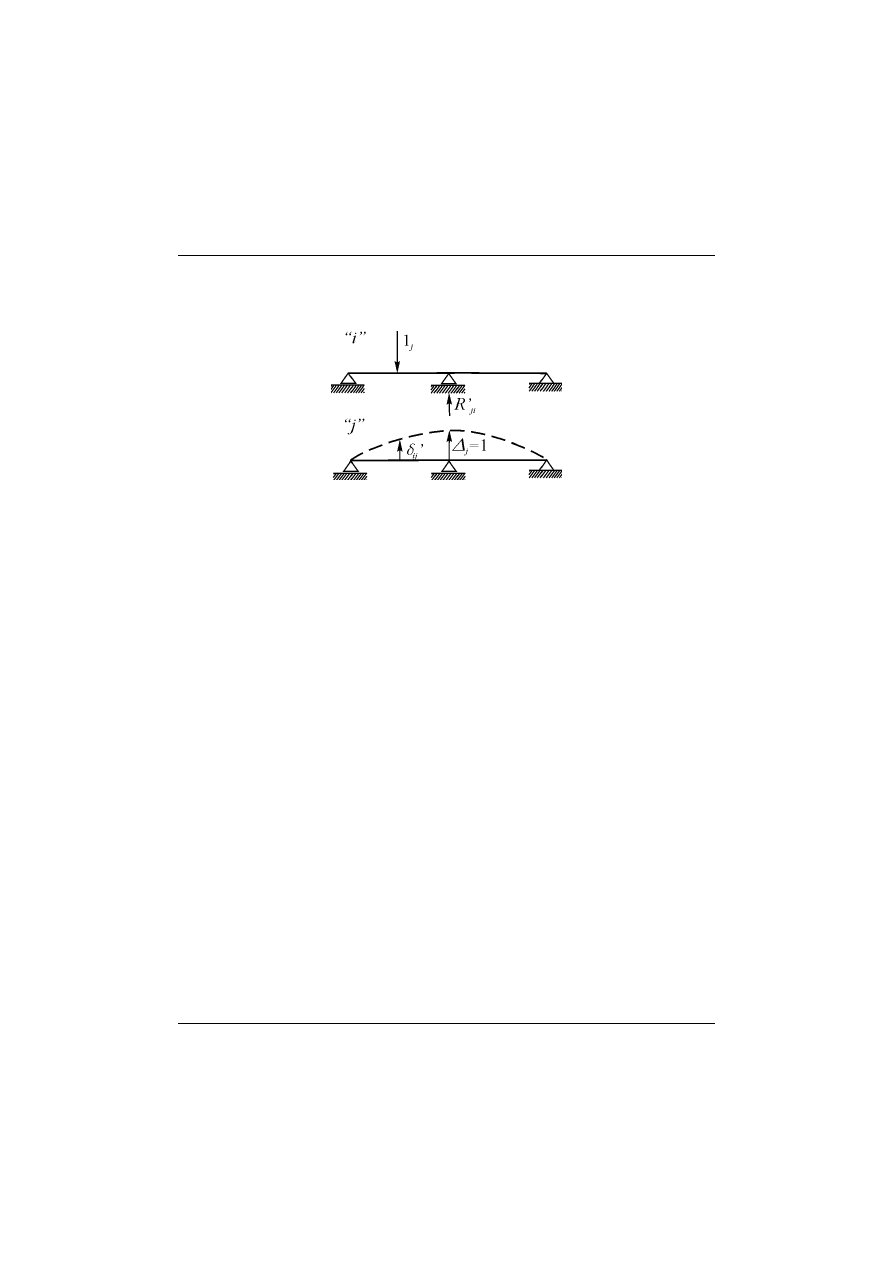
Przemieszczenie w miejscu i na kierunku

wywołane jednostkowym prze-

mieszczeniem

zadanym w miejscu i na kierunku ( jest równe, ze zna-

( )

i

Katedra Mechaniki Budowli

Wykład

Mechanika Budowli 1 [C16]

Politechnika Gdańska

2006

Marek Krzysztof Jasina

http://www.okno.pg.gda.pl –

42

–

[e-mail]

kiem przeciwnym, reakcji w miejscu i na kierunku ( wywołanej jednostko-
wym obciążeniem

działającym w miejscu

.

)

j

(1 )

i

( )

i

Rys. 8.11

ij

ji

r

δ

′ = − ′ . (8.31)