Skrypt z logiki

Dla studentów anglistyki

2008/2009

cz. II

I. Rachunek zdań

1. Zdania i wartości logiczne
Zdanie jest to wyrażenie, za pomocą którego wyraża się przekonania.

Zdania, które nie mają jako członu żadnego zdania – to zdania proste. Zdania,
które posiadają inne zdania jako swoje człony – to zdania złożone.

(1)Śnieg jest biały.
(2) Nieprawda, że śnieg jest biały.
(3) Śnieg jest biały lub trawa jest niebieska.

Spośród zdań (1)-(3) tylko zdanie (1) jest zdaniem prostym. Zdanie (2) jest
zdaniem złożonym, gdyż zawiera jedno zdanie jako człon (mianowicie zdanie
„Śnieg jest biały”), a zdanie (3) jest złożone, gdyż zawiera dwa zdania jako
swoje człony, mianowicie zdanie „Śnieg jest biały” oraz zdanie „Trawa jest
niebieska”.

Przekonania wyrażane w zdaniach – i same te zdania – bywają zgodne lub

niezgodne z rzeczywistością. Zdanie jest prawdziwe, gdy stwierdza zachodzenie
stanu rzeczy, który zachodzi. Zdanie jest fałszywe, gdy stwierdza zachodzenie
stanu rzeczy, który nie zachodzi.

Zdanie „Śnieg jest biały” jest zdaniem prawdziwym, gdyż śnieg jest biały.

Zdanie „Trawa jest niebieska” jest zdaniem fałszywym, gdyż trawa nie jest
niebieska.

Prawdziwość i fałszywość – to tzw. wartości logiczne. Symbolicznie

oznacza się je przez „1” (zdanie prawdziwe) i „0” (zdanie fałszywe).

2. Spójniki zdaniowe

Wyrażenia, które tworzą zdania złożone przez dołączenie do nich zdań

prostszych – to spójniki zdaniowe. W zdaniach:

(2) Nieprawda, że śnieg jest biały.

(4) Uważam, że śnieg jest biały.

spójnikami są wyrażenia „nieprawda, że” (2) i „uważam, że”. Są to spójniki
jednoargumentowe, gdyż tworzą zdania złożone przez dodanie do nich jednego
zdania.

W zdaniach:

(3) Śnieg jest biały lub trawa jest niebieska

(5) Jeżeli śnieg nie jest biały, to trawa jest niebieska

2

spójnikami są wyrażenia „lub” oraz „jeżeli... to”. Są to spójniki
dwuargumentowe, gdyż zdanie złożone powstaje przez dołączenie do nich
dwóch zdań.

3. Spójniki ekstensjonalne i intensjonalne

Spójnik zdaniowy jest ekstensjonalny, gdy wartość logiczna zdania, które

powstaje przez dołączenie do tego spójnika argumentów, zależy tylko od
wartości logicznej zdań dołączanych. Spójnik zdaniowy jest intensjonalny, gdy
nie jest ekstensjonalny.

Rozważmy zdania:

(2) Nieprawda, że śnieg jest biały

(6) Anna wie, że śnieg jest biały.

Spójnik „nieprawda, że” jest ekstensjonalny. Wartość logiczna zdania (2) zależy
bowiem tylko od wartości logicznej argumentu tego spójnika. Ponieważ zdanie
„Śnieg jest biały” – to zdanie prawdziwe, całe zdanie „nieprawda, że śnieg jest
biały” jest fałszywe. Jeśli zamiast zdania „śnieg jest biały” dołączymy do
spójnika „nieprawda, że” dowolne inne zdanie prawdziwe (np. „Trawa jest
zielona”), to wartość logiczna całości zawsze będzie równa 0.

Spójnik „Anna wie, że” jest intensjonalny. Wartość logiczna zdania (6)

nie zależy bowiem tylko od wartości logicznej zdania dołączonego do tego
spójnika. Załóżmy, że Ania wie, że śnieg jest biały, a więc zdanie „Anna wie, że
ś

nieg jest biały” jest prawdziwe. Prawdziwe jest też zdanie „śnieg jest biały”. Są

jednak zdania prawdziwe, które dołączone do spójnika „Anna wie, że” tworzą
zdanie fałszywe. Załóżmy, że Anna nie wie, ile wynosi obwód ziemi. Zdanie
„Anna wie, że obwód Ziemi wynosi ok. 40.000 km” jest fałszywe, choć zdanie
„Obwód Ziemi wynosi ok. 40 000 km” jest prawdziwe.

4. Klasyczny rachunek zdań
Klasyczny rachunek zdań – to teoria ekstensjonalnych spójników

zdaniowych.

Wśród wszystkich spójników zdaniowych, których dotyczy tej rachunek,

wyróżnia się pięć spójników, które wykorzystywane są najczęściej, m.in.
dlatego, że ich sens zbliżony jest do spójników języka potocznego.

Są to:
- negacja (oznaczana za pomocą symbolu „~” czytanego „nieprawda, że”)
- koniunkcja (oznaczana za pomocą symbolu „

∧” czytanego „i”)

- alternatywa (oznaczana za pomocą symbolu „

∨” czytanego „lub”)

- implikacja (oznaczana za pomocą symbolu „

→” czytanego „jeśli...to”)

- równoważność (oznaczana za pomocą symbolu „↔” czytanego

„gdy”).

Oprócz symboli spójników w rachunku zdań używa się symboli tzw.

zmiennych zdaniowych, (najczęściej liter p, q, r, ...) oraz nawiasów.

3

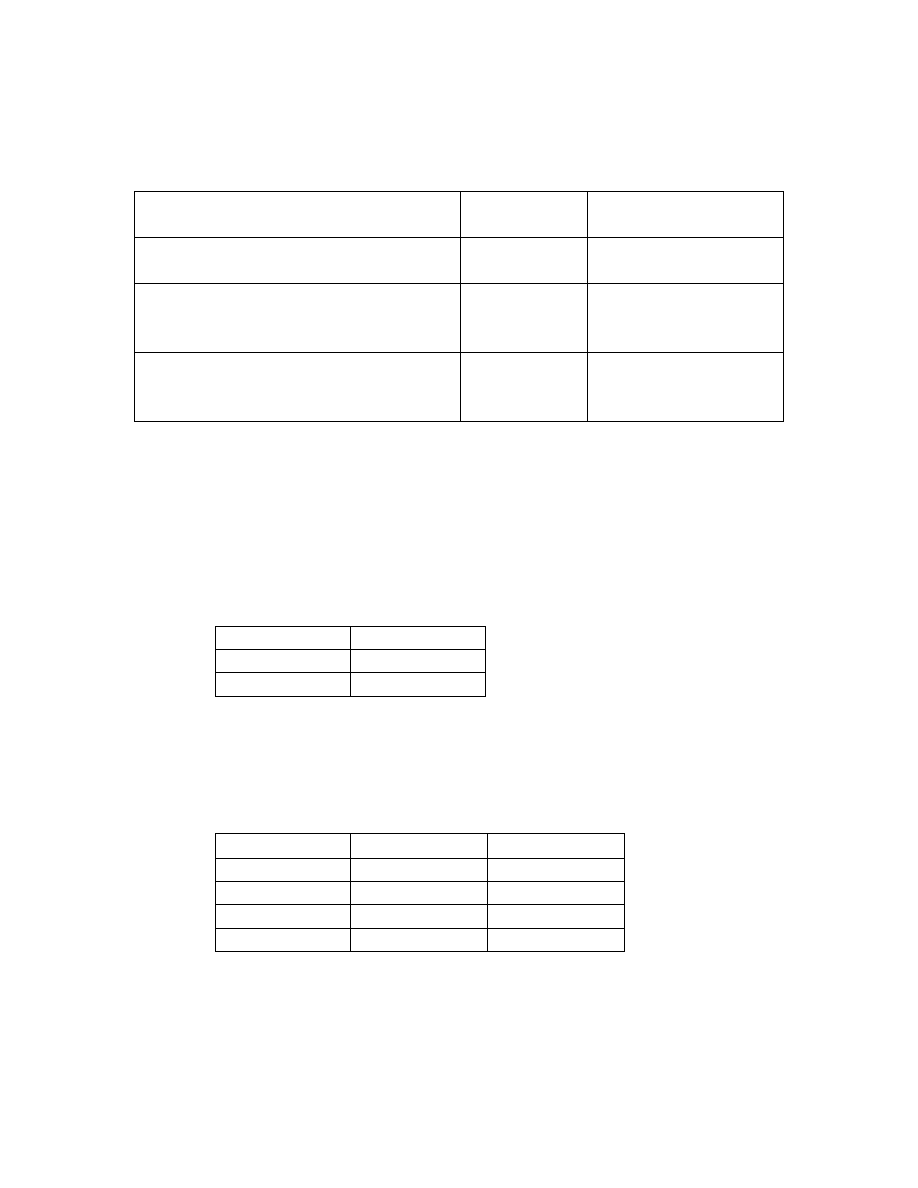
Ciągi symboli zapisane poprawnie przy użyciu wymienionych symboli –

to formuły (resp. schematy) rachunku zdań. Oto przykłady formuł wraz ze
sposobem ich odczytania:

Zapis

symboliczny

Sposób odczytania

Implikacja o poprzedniku „p” i
następniku „q”

p

→

q

„Jeżeli p, to q.”

Koniunkcja,

której

pierwszym

argumentem

jest

negacja

p

,

a

następnikiem alternatywa q i r.

~p

∧ (q ∨ r)

„Nieprawda, że p i (q
lub r)”

Implikacja, której poprzednikiem jest
równoważność p i q, a następnikiem
negacja koniunkcji q i negacji r.

(p ↔ q) →
~(q

∧ ~r)

„Jeżeli p gdy q, to
nieprawda, że q i
nieprawda, że r.”

5. Tabelki prawdziwościowe dla spójników rachunku zdań
Przyporządkowania wartości logicznych zdań z wymienionymi

spójnikami w zależności od wartości logicznej argumentów – ujmuje się w
tabelach.

(A) Negacja

p

~p

1

0

0

1

Z tabelki odczytujemy, że jeśli p ma wartość logiczną 1, to jego negacja
przyjmuje wartość logiczną 0, a jeśli p ma wartość logiczną 0, to jego negacja
przyjmuje wartość logiczną 0.

(B) Koniunkcja

p

q

p

∧q

1

1

1

1

0

0

0

1

0

0

0

0

Z tabelki odczytujemy, że koniunkcja przyjmuje wartość 1, gdy oba jej
argumenty mają wartość logiczną 1, a przyjmuje wartość logiczną 0, gdy choć
jeden z argumentów ma wartość logiczną 0.

(C) Alternatywa

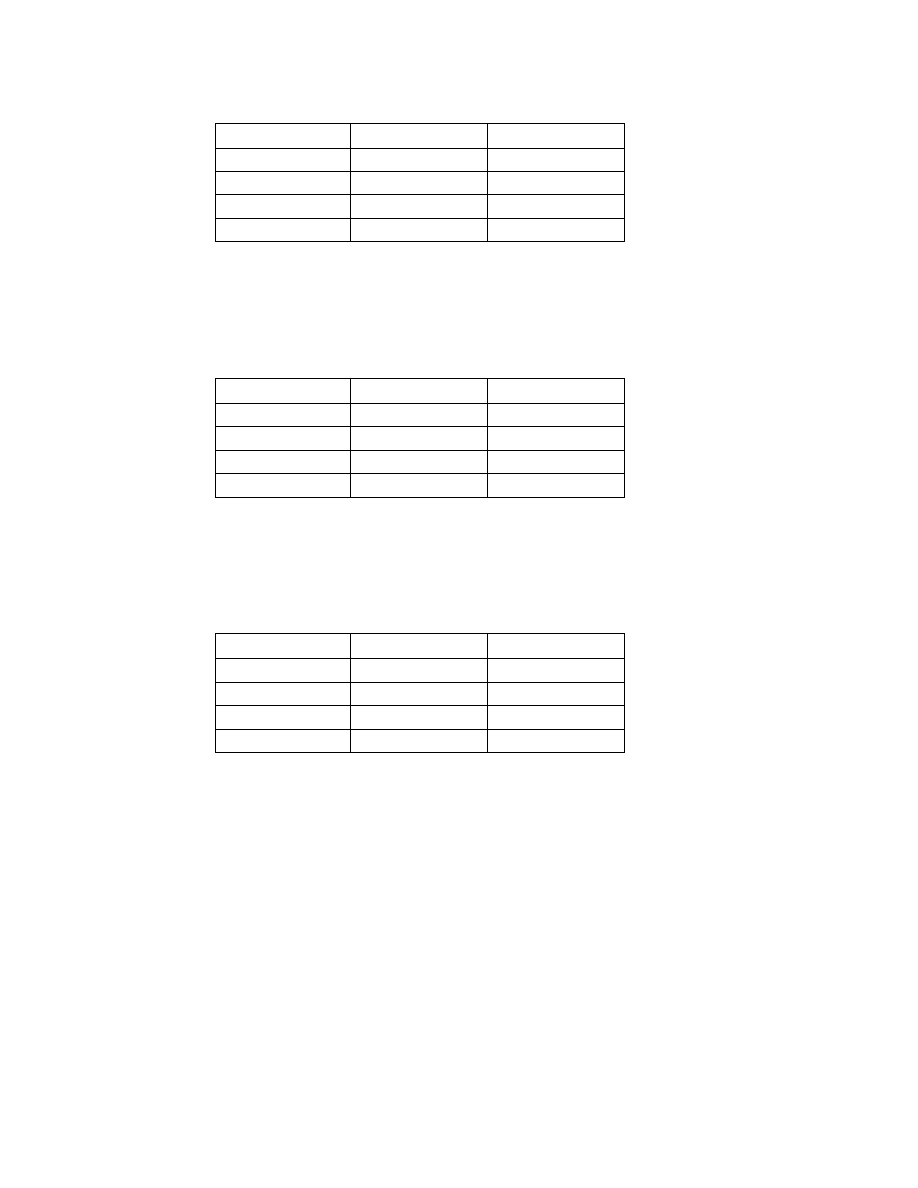
4

p

q

p

∨ q

1

1

1

1

0

1

0

1

1

0

0

0

Alternatywa przyjmuje wartość 1, gdy co najmniej jeden jej argument ma
wartość logiczną 1, a przyjmuje wartość logiczną 0, tylko gdy oba jej argumenty
mają wartość logiczną 0.

(D) Implikacja

p

q

p

→q

1

1

1

1

0

0

0

1

1

0

0

1

Implikacja przyjmuje wartość 1, gdy jej poprzednik jest fałszywy lub jej
następnik jest prawdziwy, a przyjmuje wartość logiczną 0, tylko gdy jej
poprzednik jest prawdziwy, a następnik – fałszywy.

(E) Równoważność

p

q

p

↔q

1

1

1

1

0

0

0

1

0

0

0

1

Równoważność przyjmuje wartość 1, gdy oba jej argumenty mają tę samą
wartość logiczną, a przyjmuje wartość logiczną 0, gdy jej argumenty mają różną
wartość logiczną.

6. Spójniki klasycznego rachunku zdań a spójniki języka potocznego

Spójniki charakteryzowane w klasycznym rachunku zdań tylko częściowo

odpowiadają spójnikom języka potocznego.

Rozważmy zdania:

(7) J. Kaczyński zostanie prezydentem lub L. Kaczyński zostanie

premierem.

(8) Prezydent zatwierdził uchwaloną przez sejm uchwałę i sejm uchwalił

ustawę.

(9) Jeśli trawa jest niebieska, to trawa jest fioletowa.

5

Zdanie (7) byłoby prawdziwe logicznie, nawet gdyby prawdziwe były oba
człony alternatywy, tj. nawet gdyby i J. Kaczyński został prezydentem, i L.
Kaczyński został premierem. W języku potocznym uznajemy za prawdziwe
zdania z wyrażeniem „lub” na ogół wtedy, gdy prawdziwy jest tylko jeden z
argumentów tego spójnika.
Zdanie (8) wydaje się «nienaturalne», gdyż w języku potocznym jeśli łączymy
spójnikiem „i” zdania stwierdzające fakty następujące po sobie, to zachowujemy
porządek czasowy.
Zdanie (9) jest prawdziwe, gdyż ma fałszywy poprzednik (a każda implikacja o
fałszywym poprzedniku jest prawdziwa). Zazwyczaj nie jesteśmy jednak
skłonni uznać za prawdziwe zdania o fałszywym poprzedniku.

7. Tautologie klasycznego rachunku zdań

Prawami klasycznego rachunku zdań są tautologie, czyli takie schematy

zdań złożonych, które przekształcają się w zdania prawdziwe przy dowolnym
wartościowaniu zmiennych i przy podstawieniu zdań o dowolnej wartości
logicznej. Tautologie odgrywają w logice kluczową rolę – nazywa się je także
„prawami logiki”.

Oto kilka najważniejszych tautologii rachunku zdań:

p

∨ ~p

(zasada wyłączonego środka)

p

↔ p

(zasada tożsamości)

~~p

→ p

(zasada podwójnej negacji)

(p

∧ q) → p

(symplifikacja koniunkcji)

p

→ (p ∨ q)

(addycja)

[(p

→ q) ∧ p]→ q

(modus ponendo ponens)

[(p

→ q)∧ ~q]→ ~p

(modus tollendo tollens)

Formuła, która przy każdym wartościowaniu zmiennych przyjmuje

wartość logiczną 0 – to kontrtautologia. Formuła, która przy niektórych
wartościowaniach przyjmuje wartość logiczną 1, a przy innych 0 – to formuła
spełnialna. Nie jest to ani tautologia, ani kontrtautologia.

8. Sprawdzenie tautologiczności
Są dwie efektywne metody sprawdzania, czy dana formuła rachunku zdań

jest tautologia klasycznego rachunku zdań. Pierwsza polega na sprawdzaniu,
jaka wartość logiczna przyjmuje cała formuła przy wszystkich możliwych
kombinacjach wartościowania zmiennych. Do metody tej dobrze zastosować
tabelę. W pierwszym wierszu tabeli wypisujemy wszystkie zmienne danej
formuły, a następnie coraz bardziej skomplikowane fragmenty tej formuły (tzw.
podformuły), w ostatniej kolumnie pierwszego wiersza – znajduje się cała
badana formuła.

Na przykład dla formuły:

6

[(p

→~q) ∧ q] → ~p

tabela wygląda następująco:
p

q

~p ~q p→~q

(p

→~q) ∧ q

[(p

→~q) ∧ q] → ~p

1

1

1

0

0

1

0

0

Następnie obliczamy wartości wszystkich podformuł przy wszystkich

kombinacjach wartości zmiennych.

p

q

~p ~q p→~q

(p

→~q) ∧ q

[(p

→~q) ∧ q] → ~p

1

1

0

0

0

0

1

1

0

0

1

1

0

1

0

1

1

0

1

0

1

0

0

1

1

1

0

1

Jeżeli w ostatniej kolumnie – wszystkie wartości wynoszą 1, to znaczy, że

badana formuła jest tautologią (jak w powyższym przykładzie). Jeżeli w
ostatniej kolumnie wszystkie wartości wynoszą 0, to znaczy, że formuła jest
kontrtautologią. Jeżeli w ostatniej kolumnie wartości są różne, to formuła nie
jest ani tautologią, ani kontrtautologią – jest to formuła spełnialna.

Druga metoda sprawdzania polega na założeniu, że przy pewnym

wartościowaniu

formuła

przyjmuje

wartość

logiczną

fałszu

i

na

przeprowadzeniu (na podstawie tego założenia) rozumowania zwanego
„redukcja do absurdu”. W metodzie tej:

(1) Zakładamy nie wprost, że badania formuła F nie jest tautologią, czyli

ż

e przy pewnym wartościowaniu przyjmuje wartość logiczną 0.

(2) Próbujemy dopasować wartości zmiennych w tak, aby cała formuła F

przyjęła wartość logiczną 0.

(3) Jeśli postępowanie (2) doprowadzi do sprzeczności, to znaczy, że

formuła F jest tautologią – nie może bowiem przyjąć wartości 0.

(4) Jeżeli postępowanie (2) się powiedzie, to znaczy, że formuła F nie jest

tautologią – gdyż udało się znaleźć wartościowanie, przy którym F przyjmuje
wartość logiczną 0.

II. Pojęcie konsekwencji i wnioskowania

1. Prawdy logiczne i pojęcie wynikania

Zdanie, którego schemat jest tautologią – to prawda logiczna. Aby

sprawdzić, czy dane zdanie (naturalnojęzykowe) Z jest prawdą logiczną,
budujemy schemat tego zdania w języku rachunku zdań i sprawdzamy (dowolną

7

metodą), czy schemat ten jest tautologią. Jeśli jest tautologią – to Z jest prawdą
logiczną.

Wśród prawd logicznych szczególną rolę odgrywają te, w których

głównym spójnikiem jest implikacja. O następniku takiej prawdy logicznej
powiemy, że wynika logicznie z poprzednika: jeżeli prawda logiczna ma postać
α→β, to β wynika logicznie z α. Aby więc sprawdzić, czy zdanie β wynika ze
zdania

α, tworzymy implikację o postaci α→β - i sprawdzamy, czy jest to

tautologia.

Niekiedy chcemy sprawdzić, czy zdanie β wynika ze zbioru zdań {α

1

, α

2

,

α

3

,…,

α

k

}. Powiemy, że zdanie

β wynika ze zbioru zdań {α

1

,

α

2

,

α

3

,…,

α

k

},

gdy zdanie o postaci „

α

1

∧ α

2

∧ α

3

∧…∧ α

k

→β” jest prawdą logiczną.

3. Wnioskowania i błędy we wnioskowaniach

Co najmniej niektóre myśli da się wyrazić w zdaniach, można więc

mówić (metonimiczne), że i pomiędzy treścią myśli zachodzą niekiedy relacje
wynikania. Kiedy rozumujemy – przechodzimy od myśli do myśli, starając się
drugą myśl dobrać tak, aby wynikała z pierwszej (pierwszych) lub – aby z niej
wynikała pierwsza. Jeśli poruszamy się zgodnie z kierunkiem wynikania – to
dokonujemy rozumowania progresywnego (resp. wnioskowania). Jeśli nasze
myśli poruszają się w przeciwnym kierunku – to rozumujemy regresywnie
(wyjaśniamy).

Przyjrzyjmy się rozumowaniom progresywnym.

Załóżmy, że ktoś rozumuje tak:

Jeżeli się pouczę, to zaliczę test. Jeżeli zaliczę test, to będę miał spokój

przez całe ferie. A zatem – jeżeli się pouczę, to będę miał spokój przez całe
ferie.

Termin „a zatem” sygnalizuje, że osoba przeprowadzająca rozumowanie

przechodzi od przesłanek – do wniosków, czyli sygnalizuje, że myśl wyrażana
w zdaniu będącym wnioskiem wynika ze zdań poprzednich (przesłanek).

Powiemy, że osoba O wnioskuje w sposób niezawodny, gdy wniosek jej

rozumowania rzeczywiście z przesłanek wynika. Wnioskowanie niezawodne
jest gwarancją dojścia do prawdziwych wniosków – pod warunkiem, że także
przesłanki są prawdziwe.

Powiemy, że osoba O wnioskuje w sposób zawodny, gdy wniosek jej

rozumowania nie wynika z przesłanek. Takie przejście myślowe nie gwarantuje
prawdziwości wniosku, mimo prawdziwości przesłanek.

O osobie, która wnioskuje w sposób zawodny – powiemy, że popełnia

błąd formalny we wnioskowaniu. Z kolei osoba, która uznaje fałszywą
przesłankę – popełnia błąd materialny we wnioskowaniu.

8

3. Klasyfikacje

3.1. Pojęcie klasyfikacji

Klasyfikacja zbioru Z jest to wydzielenie w zbiorze Z co najmniej dwóch

podzbiorów.

Zbiór, w którym wydziela się podzbiory – to

całość dzielona

.

Podzbiory wydzielane w klasyfikowanym zbiorze – to

człony podziału

.

Podzielmy wszystkich kompozytorów na kompozytorów pochodzenia

polskiego i kompozytorów pochodzenia niepolskiego. Całością dzieloną jest
zbiór wszystkich kompozytorów, a dwoma członami tego podziału – zbiór
kompozytorów

pochodzenia

polskiego

i

kompozytorów

pochodzenia

niepolskiego.

Wyodrębnia się różne rodzaje klasyfikacji ze względu na liczbę członów

podziału i ze względu na liczbę stopni podziału.

I tak – klasyfikacja dwuczłonowa jest to klasyfikacja o dokładnie dwóch

członach, a klasyfikacja wieloczłonowa jest to klasyfikacja o więcej niż dwu
członach.

Klasyfikacją wieloczłonową (a dokładniej – trójczłonową) zbioru

kompozytorów jest np. podział kompozytorów na kompozytorów wybitnych,
kompozytorów pochodzących z Polski i kompozytorów muzyki organowej.

Z kolei – klasyfikacja jednostopniowa jest to klasyfikacja o jednej całości

dzielonej, a klasyfikacja wielostopniowa jest to klasyfikacja o co najmniej
dwóch całościach dzielonych, które (z wyjątkiem jednej) są zarazem członami
podziału niższego stopnia. Klasyfikacja kompozytorów na kompozytorów
pochodzenia polskiego i kompozytorów pochodzenia niepolskiego, a następnie
podział

kompozytorów

pochodzenia

polskiego

na

kompozytorów

ś

redniowiecznych, renesansowych, barokowych, klasycznych, romantycznych i

współczesnych – to klasyfikacja wielostopniowa (a dokładniej –
dwustopniowa).

3.2. Poprawność klasyfikacji ze względu na dystrybucję całości

dzielonej

Klasyfikacja jednostopniowa jest poprawna, gdy spełnia zarazem

warunki: pełności, rozłączności i nasycenia.

Klasyfikacja jest pełna, gdy każdy element całości dzielonej należy do

jakiegoś członu podziału. Klasyfikacja jest rozłączna, gdy każdy element całości
dzielonej należy tylko do jednego członu podziału. Klasyfikacja jest nasycona,
gdy żaden z członów podziału nie jest pusty.

Rozważmy klasyfikację zbioru Z = {A, B, C, D} na trzy człony: Z

1

= {A,

B

}, Z

2

= {B, D} i Z

3

=

∅. Nie jest to klasyfikacja ani pełna (gdyż element C nie

znalazł się w żadnym członie podziału), ani nasycona (gdyż ostatni z
wymienionych członów jest pusty), ani rozłączna (gdyż element B należy do
dwóch członów podziału). Klasyfikacją poprawną zbioru Z ze względu na
dystrybucję elementów byłby podział na człony {A, B} i {C, D}.

9

Rozważmy z kolei klasyfikację zbioru kompozycji Fryderyka Chopina trzy

zbiory:

A

= zbór kompozycji napisanych przed 1840 rokiem;

B

= zbiór polonezów;

C

= zbiór kompozycji na harfę i klawesyn.

Nie jest ona ani pełna (gdyż np. Barkarola Fis nie znalazła się w żadnym
członie podziału), ani nasycona (gdyż zbiór C jest zbiorem pustym) ani
rozłączna (gdyż są utwory Chopina, które zostały skomponowane przed 1840
rokiem i są polonezami, czyli należą i do zbioru A, i do zbioru C).

3.3. Zasada klasyfikacji

Zasada klasyfikacji – to własności, ze względu na które wydzielane są

człony klasyfikacji.

Zasada klasyfikacji bywa dyskrepancyjna, specyfikacyjkna lub mieszana.

Zasada dyskrepancyjna – to para własności sprzecznych, czyli takich, że
element klasy dzielonej egzemplifikuje dokładnie jedną z nich. Klasyfikacja
dokonana według zasady dyskrepancyjnej jest więc zawsze dwuczłonowa.

Klasyfikacja utworów Fryderyka Chopina na kompozycje, które są w

tonacji mollowej, i kompozycje, które nie są w tonacji mollowej, jest
klasyfikacją dokonaną według zasady dyskrepancyjnej.

Zasada specyfikacyjna – to własność, która jest aspektem, czyli posiada

co najmniej dwie odmiany. Aspektem jest np. barwa (odmiany tego aspektu –
to czerwień, czerń, biel etc.), wzrost (odmiany tego aspektu – to poszczególne
«stopnie» wzrostu), rok powstania czegoś (odmiany tego aspektu – to
poszczególne lata). Klasyfikacja dokonana według zasady specyfikacyjnej Z to
klasyfikacja taka, że każdy z członów klasyfikacji jest klasą wyznaczoną przez
jedną odmianę zasady Z. Liczba członów klasyfikacji dokonanej według zasady
specyfikacyjnej jest więc różna – w zależności od tego, ile odmian danej
własności bierzemy pod uwagę.

Klasyfikacja utworów Fryderyka Chopina ze względu na rok

skomponowania jest klasyfikacją według zasady specyfikacyjnej. Każda
kompozycja powstała (a ściślej – została ukończona) w którymś roku –
przysługuje więc jej pewna odmiana własności bycia-kiedyś-skomponowaną.

Zasada mieszana – to zasada, która nie jest ani dyskrepancyjna, ani

specyfikacyjna. Rozważmy klasyfikację zbioru kompozycji Fryderyka Chopina
na trzy podklasy:

A

= kompozycji w tonacjach mollowych;

B

= kompozycji napisanych przed 1840 rokiem;

C

= kompozycji o charakterze tanecznym.

Klasyfikacja ta została dokonana według zasady mieszanej.

3.4. Poprawność klasyfikacji ze względu na zasadę

Na klasyfikacje nakłada się warunki homogeniczności i zupełności

10

specyfikacyjnej.

Klasyfikacja jest homogeniczna, gdy została dokonana według zasady

dyskrepancyjnej lub specyfikacyjnej. Klasyfikacja niehomogeniczna – to
klasyfikacja dokonana według zasady mieszanej. Od klasyfikacji żąda się
homogeniczności oprócz wymogów stawianych podziałom. Może się bowiem
zdarzyć, że jakaś klasyfikacja jest pełnym, rozłącznym i nasyconym podziałem,
choć jest dokonana według zasady niehomogenicznej. Na przykład można
sklasyfikować ballady Fryderyka Chopina na ballady w tonacji durowej,
ballady, których numer opusowy jest mniejszy niż 30 i na ballady powstałe po
1841 roku. Klasyfikacja ta jest pełna, rozłączna i nasycona, choć oczywiście nie
jest homogeniczna.

Zgodnie z postulatem zupełności specyfikacyjnej

− klasyfikacja logiczna

powinna wyróżniać tyle podzbiorów całości dzielonej, ile elementów zawiera
aspekt, według którego się dokonuje tej klasyfikacji, a do każdego członu należą
obiekty egzemplifikujące jeden z elementów spektrum. Klasyfikacja utworów
Fryderyka Chopina ze względu na rok powstania powinna mieć tyle członów, ile
było lat, w których Chopin tworzył lub wyróżniać człony klasyfikacji ze
względu na takie przedziały czasowe, aby każdy skomponowany przez Chopina
utwór znalazł się w jakimś przedziale.

5.5. Krzyżowanie i zależność klasyfikacji

Ażeby skrzyżować dwie klasyfikacje – tworzymy iloczyny każdego

członu pierwszej klasyfikacji przez każdy człon drugiej. Skrzyżowanie dwóch
klasyfikacji k

1

i k

2

jest to więc klasyfikacja k

3

taka, że każdy człon klasyfikacji

k

3

jest iloczynem

jednego z członów klasyfikacji k

1

przez jeden z członów

klasyfikacji k

2

i każdy taki iloczyn jest członem klasyfikacji k

3

.

Niech klasyfikacja k

1

będzie klasyfikacją utworów Fryderyka Chopina na

utwory na fortepian solo i utwory na fortepian towarzyszeniem orkiestry. Niech
klasyfikacja k

2

będzie klasyfikacją utworów Fryderyka Chopina na kompozycje

napisane przed 1845 rokiem i na kompozycje napisane w roku 1845 i później.

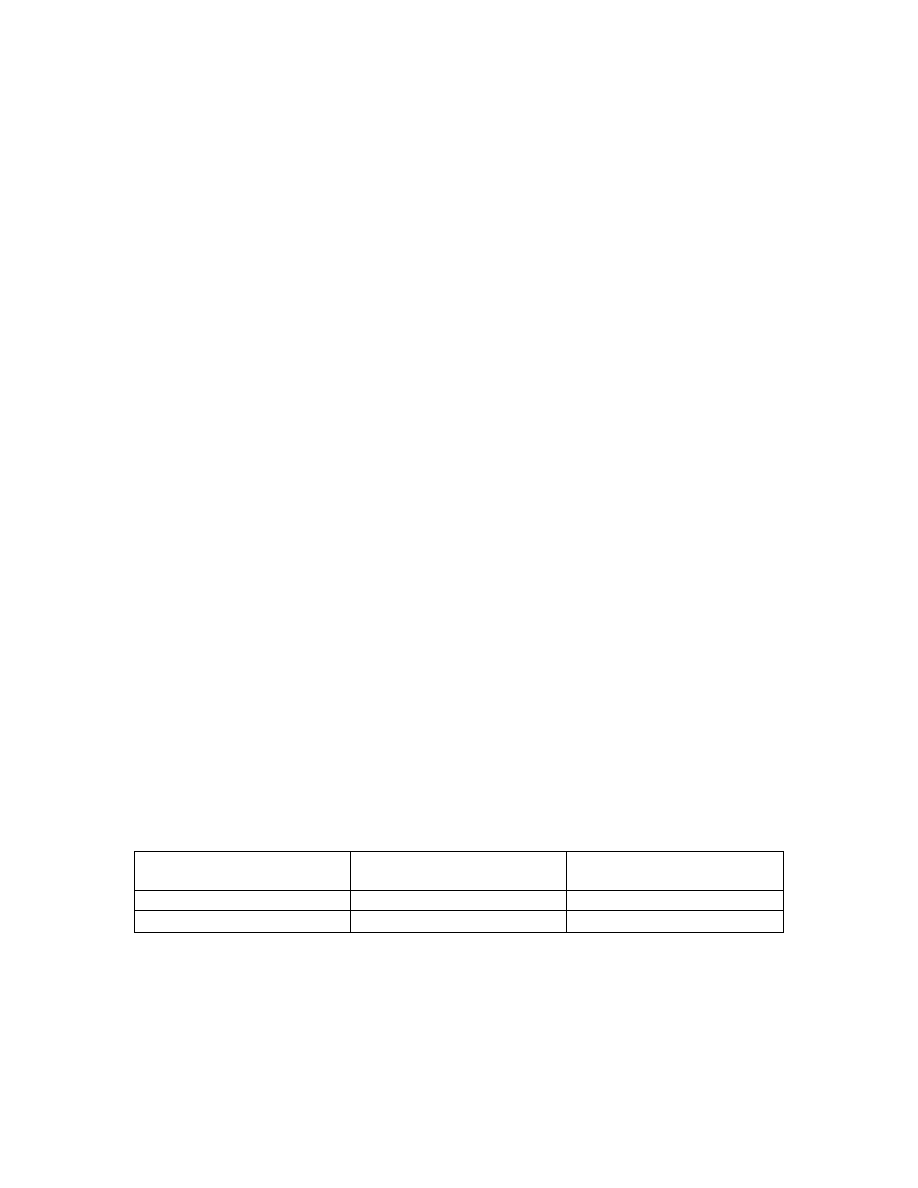
Poniższa tabela przedstawia schematycznie iloczyny członów klasyfikacji

k

1

przez człony klasyfikacji k

2

:

Utwory Fryderyka Chopina

na fortepian solo

na fortepian z

towarzyszeniem orkiestry

napisane przed 1845 rokiem Np. Ballada g-moll

Np. Koncert f-moll

napisane w 1845 lub później

Np. Barkarola Fis

∅

Jak widać, iloczyn zbiorów utworów Fryderyka Chopina na fortepian z

towarzyszeniem orkiestry i utworów napisanych po 1845 roku jest zbiorem
pustym. O takich klasyfikacjach, które po skrzyżowaniu generują zbiór pusty –
mówimy, że są

klasyfikacjami zależnymi

.

Dwie klasyfikacje są zatem względem siebie zależne, gdy chociaż jeden

11

człon ich skrzyżowania jest zbiorem pustym.

Stwierdzenie zależności między dwiema klasyfikacjami pozwala na

sformułowanie pewnych praw dotyczących elementów całości dzielonych.
Odpowiednie do omawianej klasyfikacji prawo brzmiałoby: Żaden utwór
Fryderyka Chopina na fortepian z towarzyszeniem orkiestry nie został
skomponowany po 1845 roku.