ELEMENTY RACHUNKOWOŚCI ZARZĄDCZEJ
CZ. II
KOSZTY ZMIENNE I KOSZTY STAŁE
2. METODY WYODRĘBNIANIA KOSZTÓW
3. PRÓG RENTOWNOŚCI
4. ROZSZERZENIE MODELU „PRODUKCJA-KOSZTY-ZYSK” O PRZEPŁYWY PIENIĘŻNE
5. STRUKTURA KOSZTÓW
6. DŻWIGNIA OPERACYJNA
KOSZTY ZMIENNE I KOSZTY STAŁE
Koszty stałe są to te, których wysokość nie zależy od rozmiarów sprzedaż (koszty dzierżawy, wynagrodzenia pracowników opłacanych za czas pracy, koszty administracyjne, amortyzacja). Wszystkie one zależą nie od rozmiarów sprzedaży, lecz od upływu czasu. Dlatego mówi się o nich, że są to koszty okresu.
Koszty stałe mogą mieć charakter kosztów :
- bezwzględnie stałych
- względnie stałych.
Kosztów bezwzględnie stałych, szczególnie w dłuższych przedziałach czasu, jest w praktyce stosunkowo niewiele.
Koszty względnie stałe to koszty stałe w pewnym przedziale wielkości produkcji, po przekroczeniu którego następuje ich skok na wyższy poziom. Takie koszty mogą być rozumiane jako krótkookresowe koszty zdolności produkcyjnej, potrzebnej do wykonania określonej wielkości produkcji. Jeśli chcemy tę produkcję zwiększyć, musimy również zwiększyć zdolność produkcyjną, co spowoduje wzrost poziomu kosztów stałych /amortyzacji/. Innym przykładem tego typu kosztów może być wynagrodzenie za wykonanie określonej pracy obliczone nie od liczby jednostek, lecz od grupy jednostek.
Jeżeli „skoki” kosztów stałych są częste i nieduże , koszty te upodabniają się do kosztów zmiennych. Jeśli natomiast „skoki” takie są rzadkie i wartościowo znaczne, koszty takie traktuje się jako stałe.
Rozróżnia się poza tym dwa typy kosztów stałych:
- koszty, które wynikają głównie z wcześniejszych decyzji w zakresie wydatków kapitałowych lub też z umów długoterminowych. Koszty te są nie do uniknięcia, gdyż wydatki albo już zostały dokonane albo wynikają z obowiązujących umów lub przepisów , np. amortyzacja, podatek własnościowy, płace nadzoru,
- koszty, które wynikają z decyzji krótkookresowych i są zależne od uznania , np. koszty ogłoszeń, badań, konserwacji majątku.
Koszty na ogół stałe to:
amortyzacja majtku trwałego, wydziałowe i ogólnozakładowe koszty administracji i zarządu.
Koszty stałe w ujęciu jednostkowym przy wzroście rozmiarów produkcji zmniejszają się. Zjawisko to nosi nazwę korzyści skali.
W rachunkach decyzyjnych przyjmuje się zwykle, że łączne koszty stałe nie zmieniają się przy zmianie rozmiaru działalności, należy jednak uwzględniać zmiany tych kosztów przy zmianie innych czynników. Upływ czasu ponad wyznaczony okres, inflacja, zbyt małe lub zbyt duże wykorzystanie zdolności wytwórczych powodują zmiany kosztów stałych.
Koszty zmienne to takie koszty, które zmieniają się wraz ze zmianami rozmiarów produkcji; koszty stałe natomiast - nie reagują na te zmiany. Do typowych kosztów zmiennych zalicza się: materiały bezpośrednie, robociznę bezpośrednią część pośrednich kosztów wytwarzania(np. zużycie energii technologicznej), część kosztów sprzedaży.
Trudno przesądzić jednoznacznie które rodzaje kosztów są zmienne a które stałe nie przeprowadzając stosownych badań, w wyniku których dochodzi ,zwykle do pogłębienia tej ogólnej klasyfikacji. Koszty zmienne dzieli się na:
proporcjonalne - zmieniające się w takim samym stopniu, w jakim zmienia się wielkość produkcji,
- progresywne - zmieniające się szybciej niż rozmiary produkcji.
degresywne - zmieniające się wolniej w stosunku do zmian wielkości produkcji,
Do kosztów zmieniających się proporcjonalnie należą głównie koszty bezpośrednio związane z wytwarzanymi produktami, usługami czy robotami (koszt materiałów bezpośrednich, wynagrodzenia w systemie akordu prostego). Są one w ujęciu jednostkowym stałe.
Koszty progresywne są zjawiskiem negatywnym i ich występowanie może być akceptowane tylko w wyjątkowych przypadkach np. wynagrodzenia w systemie akordu progresywnego. W ujęciu jednostkowym są one bowiem rosnące przy wzroście sprzedaży.
Koszty o zmienności degresywnej są to koszty mieszane: częściowo stałe, częściowo zmienne proporcjonalne. Jako jednostkowe maleją w przypadku wzrostu sprzedaży. Na przykład koszty rozmów telefonicznych składają się z opłaty stałej plus określona stawka za każdą jednostkę licznikową. Wynagrodzenia pracowników, jeśli prowadzona działalność ma charakter sezonowy. W przypadku, gdy 20-procentowy wzrost sprzedaży powoduje 10-procentowy wzrost takiego kosztu, możemy stwierdzić, że 50% z tych kosztów stanowiły koszty zmienne, a 50% koszty stałe. Dlatego, gdy sprzedaż wzrośnie z 1000 zł do 1400 zł, czyli o 40 %, a koszty mieszane wzrosną ze 100 zł do 110 zł, czyli o 10%, to oznacza, że tylko 25% kosztów mieszanych stanowią koszty zmienne, a 75% koszty stałe.
Przykładem kosztów mieszanych są całkowite koszty działalności operacyjnej przedsiębiorstwa. Składają się one z kosztów stałych oraz kosztów zmiennych proporcjonalnych. Można zapisać je następująco:
KC = KS + kz * x
gdzie:
KC - całkowite koszty operacyjne
KS - całkowite koszty stałe
kz - jednostkowe koszty zmienne proporcjonalnie
x - rozmiary sprzedaży
Zmienność kosztów charakteryzują wskaźniki zmienności (elastyczności), które wyrażają stosunek względnej zmiany danego kosztu do względnej zmiany rozmiaru działalności.
Wzk = Δy Δx
gdzie: y-koszt, y x
x- rozmiary działalności
5 %
Jeżeli Δx wynosi np. 10%, a Δy = 5%, to Wz = ---- =0,5
x y 10
Oznacz to, że badany koszt zmienia się o połowę wolniej niż rozmiary działalności.
Dla kosztów zmiennych proporcjonalnych Wzk =1, dla kosztów degresywnych zawarty jest pomiędzy 0 i 1, a dla kosztów progresywnych jest wyższy od 1.
Z kosztami zmiennymi związane jest pojęcie kosztu krańcowego. Koszt krańcowy to przyrost kosztu całkowitego, wynikający z przyrostu jednej jednostki produkcji (sprzedaży). Koszty krańcowe odzwierciedlają zmianę w wysokości kosztów zmiennych.
Kształtowanie się kosztów stałych całkowitych i jednostkowych przedstawiają poniższe wykresy.
Wykres: Koszty stałe
Całkowity koszt stały Jednostkowy koszt stały
koszt stały |
|
Jednostkowy koszt stały |
|
|
Wielkość produkcji Wielkość produkcji
Źródło: C. Drury, Rachunek kosztów, Wydawnictwo Naukowe PWN, Warszawa 1995, s. 46.
Wykres: Koszty częściowo stałe
|
Koszty częściowo stałe traktowane jako koszty skokowo rosnące |
|
Koszty częściowo stałe zbliżone do kosztu zmiennego |
|
Koszty częściowo stałe zbliżone do kosztu stałego |
|
,
Koszty częściowo stałe
|
|
Koszty częściowo stałe zbliżone do kosztu zmiennego
|
|
Koszty częściowo stałe zbliżone do kosztu stałego
|
|
Wielkość produkcji Wielkość produkcji Wielkość produkcji
Źródło: C. Drury, op. cit., s. 46.
Wykres: Funkcja kosztów skokowo stałych
Całkowity koszt stały Jednostkowy koszt stały
koszt stały |
|
Jednostkowy koszt stały |
|
|
Wielkość produkcji Wielkość produkcji
Źródło: C. Drury, op. cit., s. 46.
Wykres: Koszty zmienne proporcjonalne
Koszt całkowity |
|
Koszt jednostkowy |
|
|
Wielkość produkcji Wielkość produkcji
Źródło: S. Sojak, op. cit., s. 46.
Wykres: Koszty zmienne progresywne
Koszt całkowity |
|
Koszt jednostkowy |
|
|
Wielkość produkcji Wielkość produkcji
Źródło: S. Sojak, op. cit., s. 46.
Wykres: Koszty zmienne degresywne
Koszt całkowity |
|
Koszt jednostkowy |
|
|
Wielkość produkcji Wielkość produkcji
Źródło: S. Sojak, op. cit., s. 46.
Metody wyodrębniania kosztów stałych i zmiennych
Zastosowanie rachunku kosztów zmiennych wymaga wcześniejszego dokonania podziału kosztów na koszty stałe i koszty zmienne.
Do najczęściej stosowanych metod podziału kosztów na koszty stałe i koszty zmienne należą:
metoda analizy księgowej
metoda pomiaru inżynierskiego
metody statystyczno - matematyczne
Księgowa metoda wyodrębniania kosztów - polega na tym, że pracownik działu księgowości w porozumieniu z pracownikami innych działów, kwalifikuje poszczególne, zarejestrowane pozycje kosztów jako stałe lub zmienne. Kwalifikacja odbywa się na podstawie obserwacji zachowania się kosztów pod wpływem zmian stopnia wykorzystania zdolności produkcyjnych. Wykorzystuje się tu doświadczenie i rozsądny osąd pracowników księgowości którzy kwalifikują poszczególne rodzaje na koszty stałe i koszty zmienne. Koszty zmienne degresywne należy - poprzez dalszą analizę - rozłożyć na element stały i zmienny proporcjonalnie.
Największą zaletą metody analizy księgowej jest jej prosta i stosunkowa mała pracochłonność. Natomiast podstawową jej wadą jest pewna subiektywność w kwalifikowaniu kosztów. Dlatego metoda ta może mieć zastosowanie w przedsiębiorstwach małych o stosunkowo prostym profilu produkcji.
POMIAR INŻYNIERYJNY
Metoda pomiaru inżynierskiego polega na ustaleniu wielkości zużycia czynników produkcji na podstawie szczegółowej analizy produktu i procesu technologicznego. Zużycie materiałów (normy zużycia) ustala się z dokumentacji projektowej lub analizy konstrukcji i receptury produktu
Ustalenia inżynierów są ważne, lecz z reguły pracochłonne i kosztowne. Mogą być jednak pomocne dla "kosztowców" w ustaleniu poszczególnych składników kosztów stałych i kosztów zmiennych.
Statystyczne metody wyodrębniania kosztów
Metody te opierają się na założeniu, że koszty całkowite są w sposób liniowy zależne od wielkości produkcji. Zależność tę można zapisać:
Zależności te są wyrażane za pomocą funkcji liniowej.
gdzie:
Kc - koszty całkowite,
Ks - koszty stałe,
kzj - koszty zmienne jednostkowe,
x - wielkość produkcji.
Problem sprowadza się do znalezienia takich wartości parametrów jednostkowego kosztu zmiennego i kosztów stałych, aby linia prosta była jak najlepiej dopasowana do danych empirycznych. Można tego dokonać stosując:
metodę wizualną,
metodę dwóch punktów (wielkości ekstremalnych),
metodę regresji liniowej.
Metoda wizualna
Metoda wizualna polega na narysowaniu linii prostej tak, aby była najlepiej dopasowana do danych wyjściowych, rozpoczynając jej kreślenie z punktu charakteryzującego najwyższy poziom kosztów. Następnie znajdujemy punkt przecięcia linii z osią pionową - wysokość kosztów stałych. Wyliczamy koszty zmienne dla produkcji przynoszącej najwyższe koszty. Różnica między kosztami całkowitymi a kosztami stałymi dla tej wielkości produkcji oznacza wysokość kosztów zmiennych.
Metoda ta, podobnie jak poprzednia opiera się na idei kosztów krańcowych. W porównaniu z wcześniej prezentowaną uwzględnia jednak wszystkie obserwacje, nie tylko dwie skrajne. Jest ona jednak bardzo subiektywna.
Wykres 2: Oszacowanie kosztów całkowitych metodą wizualną
![]()
Źródło: S. Sojak, op. cit., s. 96.
Metoda wielkości krańcowych
Stosunkowo prosta jest metoda dwóch punktów, natomiast bardziej złożona metoda regresji. W rachunkowości zarządczej jest szeroko stosowana metoda dwóch punktów krańcowych (metoda wielkości krańcowych). Polega ona na wybraniu z szeregów liczbowych dwóch okresów o najniższej i najwyższej wielkości produkcji i odpowiadających im kosztów. Jeśli koszty zmienne będą stałe na jednostkę i koszty stałe pozostaną nie zmienione, to wzrost kosztów całkowitych będzie spowodowany wyłącznie wzrostem kosztów zmiennych. Koszt zmienny na jednostkę obliczamy w następujący sposób:
Wykres: Oszacowanie kosztów całkowitych metodą dwóch punktów
Źródło: J. Wermut, Rachunkowość zarządcza, ODDK, Gdańsk 1994, s. 22.
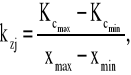
Poziom kosztów stałych ustala się, wykorzystując informacje o krańcowych wielkościach produkcji i odpowiadających im kosztach, odejmując od kosztów przy najwyższych lub najniższych rozmiarach produkcji iloczyn ustalonych wcześniej kosztów zmiennych jednostkowych i najwyższych lub najniższych rozmiarów produkcji.
![]()
gdzie:
Kcmax - koszty całkowite najwyższe spośród rozpatrywanych okresów,
Kcmin - koszty całkowite najniższe spośród rozpatrywanych okresów,
xmax - maksymalna produkcja spośród rozpatrywanych okresów,
xmin - maksymalna produkcja spośród rozpatrywanych okresów.
Sposób wyodrębnienia kosztów stałych i zmiennych przy wykorzystaniu dwóch punktów krańcowych ilustrujemy poniższym przykładem.
Przykład
Wielkość produkcji i koszty całkowite w pięciu kolejnych miesiącach kształtowały się następująco:
Miesiąc |
Produkcja (w szt.) |
Koszty całkowite (w zł) |
styczeń Luty Marzec Kwiecień Maj Czerwiec |
105 100 110 115 120 119 |
207 900 200 000 214 500 220 800 222 000 221 500 |
Na podstawie powyższych danych należy policzyć:
koszty zmienne jednostkowe,
całkowite koszty stałe,
koszty całkowite przy produkcji 150 szt. wyrobów.
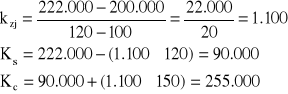
Aby wyeliminować wpływ na wielkości krańcowe przypadkowych zdarzeń metodę wielkości krańcowych zastępuje się dokładniejszą metodą zwaną metodą średnich podokresów. Polega ona na:
uporządkowaniu szeregów liczbowych od najniższych do najwyższych rozmiarów produkcji i podzieleniu go na dwie równe grupy,
obliczeniu średnich rozmiarów produkcji i kosztów dla tych dwóch grup,
wykorzystaniu wyżej wymienionych średnich do ustalenia kosztów zmiennych jednostkowych i kosztów stałych postępując identycznie jak w metodzie wielkości krańcowych, z tym że wielkości krańcowe zastępujemy średnimi.
Metoda regresji liniowej - metoda najmniejszych kwadratów(MNK)
Analiza regresji liniowej jest pozbawiona wad prezentowanych poprzednio metod. Polega ona na jak najlepszym dopasowaniu linii kosztów do wszystkich obserwacji oraz określeniu stopnia dopasowania tej linii do tych obserwacji. Wykorzystujemy do tego metodę najmniejszych kwadratów (MNK) - poszukujemy naszych zmiennych obrazujących wysokość kosztów stałych i jednostkowych kosztów zmiennych, rozwiązując dwa równania z dwiema niewiadomymi:
![]()
KC = nKS + kz ![]()
x
![]()
xKC = KS ![]()
x +k z ![]()
x2
gdzie:
n - liczba obserwacji, ; KS - koszty stałe,
![]()
x - suma obserwacji wielkości produkcji; ![]()
KC - suma obserwacji kosztów całkowitych,
![]()
x2 - suma kwadratów obserwacji wielkości produkcji; kz - jednostkowe koszty zmienne,
![]()
xK C- suma iloczynów wielkości produkcji i kosztów całkowitych.
Po obliczeniu jednostkowych kosztów zmiennych z i kosztów stałych S możemy wyznaczyć równanie linii:
Miesiąc |
Wielkość produkcji (X) |
Koszty całkowite (KC) |
X x KC |
X2 |
Lipiec |
80 |
10 200 |
816 000 |
6 400 |
Sierpień |
90 |
10 900 |
981 000 |
8 100 |
Wrzesień |
100 |
12 100 |
1 210 000 |
10 000 |
Październik |
80 |
10 800 |
864 000 |
6 400 |
Listopad |
120 |
13 700 |
1 644 000 |
14 400 |
Grudzień |
110 |
12 500 |
1 375 000 |
12 100 |
Razem |
580 |
70 200 |
6 890 000 |
57 400 |
Podstawiając wielkości do równań otrzymujemy:
Teoretyczny poziom kosztów całkowitych (równanie linii) wynosi:
KC = 78 x X + 4 160
Przeprowadzenie badań kosztów wymaga odpowiedniego przygotowania szeregów liczbowych, na podstawie których dokonuje się oszacowania funkcji. Wymaga to przemyślenia wielu kwestii:
Zakres badanych kosztów - czy badać koszty całej działalności, czy poszczególnych produktów lub usług, czy też wyodrębnionych komórek.
Wybór odpowiedniej miary produkcji - miara ta powinna wyrażać logiczny związek przyczynowo - skutkowy z badanymi kosztami (liczba produktów, czas pracy ludzi, maszyn).
Okres objęty badaniem - elementy dynamiczne (wielkość zdolności produkcyjnej, technologia i organizacja produkcji) zakłócające porównywalność danych nie powinny występować w badanym okresie.
Jednostki czasowe obserwacji - powinny nimi być najkrótsze okresy, które gwarantują kompleksowość informacji (najczęściej miesiące).
2. PRÓG RENTOWNOŚCI
W zarządzaniu przedsiębiorstwem szczególnie ważna jest odpowiedz na pytanie: kiedy sprzedaż zacznie przynosić zysk. Jak wiadomo nie każda sprzedaż przynosi zysk automatycznie. Z tej racji, iż koszty są kategorią pierwotną względem przychodów, sprzedaż wyrobów do określonej wysokości nie przynosi zysku. Służy jedynie pokrywaniu wcześniej poniesionych kosztów. Dopiero po przekroczeniu pewnej wielkości sprzedaży możliwe staje się osiąganie zysku. Wobec tego, z punktu widzenia istnienia i rozwoju przedsiębiorstwa, niezwykle ważne jest wyznaczenie minimalnej wielkości produkcji, której sprzedaż pozwoli zrównoważyć poniesione koszty. Wielkość sprzedaży równoważąca poniesione koszty jest określona mianem progu rentowności albo punktu krytycznego (break- even- point).
Wzrost przychodów ze sprzedaży jest funkcją wielkości sprzedaży i cen. Natomiast na zmianę kosztów całkowitych mogą mieć wpływ zarówno koszty stałe jak i zmienne. Jeżeli nastąpi wzrost kosztów stałych, to prosta tych kosztów przesuwa się w górę, podnosząc prostą kosztu łącznego i podwyższając tym samym próg rentowności. Ale pomiędzy kosztami stałymi i kosztami zmiennymi może wystąpić efekt substytucji. Wzrostowi kosztów stałych np. z tytułu zainstalowania nowych maszyn, mogą odpowiadać niższe koszty zmienne, np. z powodu mniejszego zużycia czynników produkcji. Wówczas wprawdzie prosta kosztów stałych przesunie się w górę, lecz krzywa kosztów zmiennych będzie mniej stroma ze względu na niższy poziom kosztów zmiennych i koszty całkowite mogą nie ulegać istotnej zmianie.
Próg rentowności dla produkcji jednoasortymentowej
Do liczenia progu rentowności warto znać pojęcie marży brutto.
Schemat rachunku jest następujący:
Przychody
Koszty zmienne
= Marża brutto (MB)
Koszty stałe
= Zysk operacyjny
Z definicji progu rentowności i marży brutto wynika, że w progu rentowności MB=KS.
Zaprezentowany poniżej wzór na ilościowy próg rentowności oznacza, że w liczniku tego wzoru koszty stałe należy traktować jako wymaganą marżę brutto a mianownik jako jednostkową marżę brutto.
Próg rentowności wyraża się ilością produkcji:
Ks
xpr = -----
c-kz
lPróg rentowności wartościowy:
Ks
c xpr = --------
1- kz/c
W analizie zależności „produkcja- koszty- zysk” występują istotne dla tej analizy, wskaźniki:
WSKAZNIK POKRYCIA
Wpo = 1 − kz/c lub Wpo = 1 − Kz/P lub Wpo = P-Kz
P
Wskaźnik ten informuje jaka część przychodu (ceny jednostkowej) pozostaje po odjęciu kosztów zmiennych (jednostkowego kosztu zmiennego) sprzedanej produkcji na pokrycie kosztów stałych okresu (przed progiem rentowności) i na zysk (za progiem rentowności). Na przykład Wpo= o,3 oznacza ,że 30% przychodu pozostanie po pokryciu kosztów zmiennych na pokrycie kosztów stałych i ewentualny zysk.
Wskaźnik pokrycia pomnożony przez przychód ze sprzedaży daje kwotę pokrycia ,z której pokrywa się koszty stałe i która zapewnia zysk. Tę samą kwotę pokrycia można ustalić mnożąc jednostkową nadwyżkę cenową (c-kz) przez liczbę sprzedanych produktów.
Znając próg rentowności możemy dowiedzieć się o ile możemy obniżyć sprzedaż nie ponosząc strat Mówi nam o tym marża bezpieczeństwa, którą obliczamy następująco:
Mbe = Xrz - Xpr
WSKAŹNIK PEWNOŚCI (BEZPIECZEŃSTWA)
Wpe = 1 − Xpr/Xrz lub Wpe = Xrz - Xpr/Xrz * 100
gdzie: Xpr- rozmiary produkcji w progu rentowności
X rz - rozmiary produkcji maksymalne lub normalne.
Wskaźnik ten informuje o jaką część można zmniejszyć maksymalne lub normalne rozmiary produkcji pozostając nadal w strefie zysków.
Wskaźnik ten informuje o jaką część można zmniejszyć maksymalne lub normalne rozmiary produkcji pozostając nadal w strefie zysków. Na przykład Wpe = 0,2 mówi ,że można o 20% zmniejszyć produkcję, poczynając od jej maksymalnych rozmiarów, zanim jednostka gospodarcza zacznie ponosić straty. Wskaźnik pewności można też rozpatrywać w stosunku do produkcji aktualnie realizowanej. Bada się wówczas w jakim stopniu można tę produkcję ograniczyć, nadal osiągając zysk.
Koszty
Przychody
Przychody
pole zysków
Koszty całkowite
Pole Koszty stałe
strat
Próg Produkcja x
rentowności
Wykres -Próg rentowności (postać I).
1. Oś pozioma x reprezentuje rozmiary produkcji = sprzedaży
2. Oś pionowa y wyraża koszty i przychody
3. Linia równoległa do osi x wyraża koszty stałe.
4. Linia biorąca swój początek w punkcie przecięcia linii kosztów stałych z osią y reprezentuje koszty całkowite (po dołożeniu kosztów zmiennych do kosztów stałych).
5. Linia wychodząca z punktu 0 jest linią przychodu ze sprzedaży.
6. Linia przychodu przecina linię kosztów całkowitych w punkcie progu rentowności, którego wielkość odczytuje się na osi x.
7. Pole na lewo od progu rentowności pomiędzy linią kosztów całkowitych a linią przychodu ze sprzedaży jest polem strat - nie pokryte koszty , pole na prawo, do sprzedaży możliwej do zrealizowania - polem zysków (nadwyżka przychodów nad kosztami).
y Przychody Koszty
całkowite
pole zysków
Koszty zmienne
Pole
strat
Próg x
rentowności
Wykres- próg rentowności (postać II).
Wykres progu rentowności II różni się od wykresu progu rentowności I jedynie kolejnością wykreślania kosztów. Na wykresie tym najpierw pokazane są koszty zmienne, a do nich dołożone koszty stałe, tworząc razem koszty całkowite. Pole strat jest tutaj równe kosztom stałym, nie pokrytym przychodem. Idea tego wykresu jest zgodna z rachunkiem kosztów zmiennych, gdzie od przychodów najpierw odejmuje się koszty zmienne ustalają nadwyżkę cenową , a z niej pokrywa koszty stałe.
Próg
rentowności
przychody
koszty Marża brutto
zysk pole
zysków
produkcja
pole (sprzedaż)
Koszty strat
stałe
strefa pewności
Wykres - Próg rentowności (postać III).
Na wykresie tym przedstawiona jest kwota pokrycia, to jest kwota, która pozostaje po pomniejszeniu przychodów o koszty zmienne. Początek linii kwoty pokrycia wyznaczony jest na osi y poziomem kosztów stałych, zaś miejsce przecięcia z osią x określa wielkość progu rentowności.. Wykres ten zawiera mniej informacji w stosunku do poprzednich, jest natomiast bardzo prosty i przejrzysty. Przydatny jest szczególnie w sytuacji rozpatrywania wpływu licznych zmian w cenach.
Uwzględnianie podatku dochodowego w analizie progu rentowności
Zakładając, że zysk operacyjny przed opodatkowaniem i do opodatkowania jest taki sam, wówczas możemy do analizy progu rentowności można włączyć wysokość podatku.
Zn = Zo * (1-p)
gdzie:
Zn - zysko operacyjny po opodatkowaniu,
p - stopa podatku dochodowego.
Zn = [(c-kz)x - KS] * (1-p)
Próg rentowności gwarantujący osiągnięcie planowanego zysku po opodatkowaniu obliczymy następująco:
albo
Próg rentowności dla produkcji wieloasortymentowej
Próg rentowności dla produkcji złożonej z wielu asortymentów nie jest punktem, tak jak w przypadku produkcji jednego rodzaju wyrobu, lecz zbiorem wielu punktów. Zrównanie przychodów i kosztów przedsiębiorstwo może osiągnąć przy wielu różnych kombinacjach struktury asortymentowej. Gdy wytwarza się 2 produkty, wówczas możliwe progi rentowności wyznacza prosta, jak na poniższym rysunku, na której znajdują się różne struktury ilościowe produkcji zapewniające znalezienie się w progu rentowności. Równanie progu rentowności przyjmuje wówczas postać:
x1* c1 + x2* c2 = x1* kzj1 + x2* kzj2 + KS
x1 ( c1 - kzj1 ) + x2 ( c2 - kzj2 ) - KS = 0
Liczba M `
400
STREFA
ZYSKU
STREFA
STRAT
600 liczba K
Formuła matematyczna progu rentowności produkcji złożonej z różnych asortymentów w ujęciu wartościowym ma następującą postać:
Prw = KS
∑ni =1 kzi * xi
∑ ni=1 ci * xi
Ustalona według powyższego wzoru „krytyczna” wartość sprzedaży odnosi się jedynie do założonej struktury produkcji. Mianownik wzoru wyraża średni wskaźnik pokrycia dla tej struktury. Informuje on jaka część przychodu ze sprzedaży pozostanie po pokryciu kosztów zmiennych w odniesieniu do wszystkich rodzajów produktów, przy określonym udziale tych produktów w tym przychodzie. Wówczas próg rentowności można obliczyć następująco:
Prw = KS
Wp
Gdzie:
Wp - wskaźnik pokrycia (MB/Sprzedaż)
Wartość sprzedaży (przychody) w progu rentowności można przeliczyć na liczbę produktów poszczególnych asortymentów wykorzystując informacje o udziale tych asortymentów w przychodzie oraz o ich cenach.
Wpływ na wielkość progu rentowności produkcji wieloasortymentowej mają te same czynniki, które wyznaczają próg dla produkcji jednorodnej, a więc :
- koszty zmienne jednostkowe poszczególnych asortymentów,
- ceny sprzedaży poszczególnych asortymentów,
- koszty stałe okresu.
Im większy będzie udział produkcji z wyższym wskaźnikiem pokrycia niż przeciętny, tym szybciej osiągnie się punkt krytyczny, to jest przy niższym przychodzie za sprzedaży. Może się bowiem zdarzyć, że produkt o wysokim wskaźniku pokrycia angażuje więcej zdolności produkcyjnych niż produkt o niskim wskaźniku. Okaże się wówczas, że łączna kwota pokrycia będzie korzystniejsza (większa) dzięki produkcji wyrobów o niższym wskaźniku pokrycia lecz dużej ich liczbie. Należy jednak zauważyć, że produkt, który w porównaniu z innymi zapewnia pokrycie kosztów niższym przychodem ze sprzedaży angażuje mniej środków pieniężnych w momencie osiągnięcia progu rentowności. W sytuacji ograniczonej podaży środków pieniężnych może to zadecydować o wyborze asortymentu produkcji.
Analiza progu rentowności pozwala na ustalenie korzyści płynących z rozszerzenia wielkości sprzedaży, zmiany cen i kosztów. Błędne byłoby jednak założenie, iż przekroczenie progu rentowności będzie oznaczać nieskończone możliwości maksymalizowania zysku. Założenie takie jest słuszne tylko wtedy, kiedy mamy do czynienia ze stosunkowo niewielkim przyrostem sprzedaży i w stosunkowo krótkim czasie. Przy znacznym wzroście wielkości produkcji, spowodowanym np. oddaniem do eksploatacji nowego zakładu produkcyjnego, założenie o liniowym przyroście kosztów należy odrzucić. Funkcja kosztów całkowitych przybiera raczej postać krzywej niż prostej. Obserwacje empiryczne dowodzą iż wraz ze wzrostem produkcji jednostkowe koszty zmienne maleją tylko do pewnej wielkości, po czym zaczynają rosnąć. W rezultacie krzywa kosztu całkowitego początkowo obniża się po czym zaczyna rosnąć w coraz szybszym tempie. Podobnie w warunkach konkurencji, nieliniowo zachowują się przychody ze sprzedaży. Funkcja przychodów przypomina również krzywą a nie prostą. Wynika to stąd, iż przy dużych rozmiarach sprzedaży następuje z reguły spadek ceny. W efekcie mogą wystąpić dwa progi rentowności, a mianowicie próg rentowności minimum i próg rentowności maksimum.
3. ROZSZERZENIE MODELU ZALEŻNOŚCI „PRODUKCJA- KOSZTY- ZYSK” O
PRZEPŁYWY PIENIĘŻNE
W praktyce występują sytuacje, w których decydenci zainteresowani są w większym stopniu wpływem rozmiarów produkcji na przepływy pieniężne niż na zysk. Powstaje pytanie czy możliwe jest prowadzenie działalności z rachunkową stratą , ale z nadwyżką wpływów pieniężnych nad wydatkami . Praktyka dowodzi, że w , krótkich przedziałach czasu można zaakceptować sytuację , w której ważniejszy jest dopływ pieniądza i kontynuacja działalności dla której wykazuje się rachunkową stratę . Strumienie pieniężne wpływów i wydatków nie muszą ,pokrywać się ze strumieniami przychodów i kosztów ( np. amortyzacja, będąc kosztem danego okresu, nie łączy się z wydatkami w tym okresie). Stąd też niekiedy wyznacza się tzw. pieniężny próg rentowności według formuły:
Próg pieniężny = Ks pokrywający się z wydatkami w danym okresie
nc pokrywająca się z nadwyżką pieniężną
gdzie: nc - jednostkowa nadwyżka cenowa.
Kwota pokrycia bez amortyzacji
zysk
Kwota pokrycia z amortyzacją
Produkcja
PR1 PR2
strata
Wykres- Próg rentowności „kosztowny” i „pieniężny”.
Wykres powyższy oparty jest na założeniu, że wpływy równe są przychodom, natomiast wydaki są mniejsze od kosztów o kwotę amortyzacji.
Jak widać na wykresie wyznaczone zostały dwa progi rentowności:
PR1- pieniężny próg rentowności, który pokazuje przy jakiej wielkości produkcji (sprzedaży) uzyskane w danym okresie wpływy pieniężne pokryją konieczne wydatki,
PR2- kosztowny próg rentowności informujący jaka wielkość sprzedaży zapewni pokrycie wszystkich kosztów z uzyskanych przychodów w danym przedziale czasu.
Praktyczne znaczenie modelu progu rentowności polega na tym, że:
- przedstawia on komunikatywnie rozmiary produkcji zapewniające osiągnięcie zysku oraz wpływ zmian w kosztach, cenach, rozmiarach i strukturze produkcji na ten zysk,
- pomaga w ustalaniu cen produktów w krótkich okresach,
- mierzy czynnik ryzyka za pomocą strefy i wskaźnika pewności.
Przedstawiony model ze względu na założenia traktowany jest jako model księgowy. Do założeń tych należą:
- stałość jednostkowego kosztu zmiennego,
- stałość cen sprzedaży.
W teorii ekonomii twierdzi się, że koszty zmienne jednostkowe nie zmieniają się liniowo w stosunku do wielkości produkcji, np. materiały bezpośrednie przy dużej liczbie można lepiej wykorzystać, duże partie materiałów można nabyć z rabatem. To samo dotyczy cen sprzedaży, które często muszą być obniżone w celu osiągnięcia większej sprzedaży (elastyczność cenowa popytu).
Względy praktyczne (wysokie koszty pozyskania dodatkowych informacji) pozwalają zaakceptować uproszczone rozumowanie, tym bardziej, że jak się okazuje jednostkowy koszt zmienny jest w przybliżeniu funkcją liniową w ramach przedziału tzw. znaczącego, czyli przedziału, który wyznaczony jest przez poziomy wykorzystania mocy wytwórczych w przeszłości i dla których dostępna jest informacja o kosztach.
4. STRUKTURA KOSZTÓW
Struktura kosztów odnosi się do odpowiednich proporcji między kosztami zmiennymi i stałymi w przedsiębiorstwie. Organizacja często posiada pewien zakres swobody w kształtowaniu struktury kosztów, np. poprzez automatyzację linii technologicznych zamiast zatrudniania siły roboczej.
Jeżeli zarządzający ma swobodę w zmienianiu struktury kosztów, to jaka jest lepsza- wysoki koszt zmienny i niski stały czy odwrotnie? Brak jednoznacznej odpowiedzi na to pytanie, możemy tylko stwierdzić, że oba rozwiązania mają swoje zalety i wady, w zależności od okoliczności. Aby stwierdzić, co to oznacza, należy zapoznać się z poniższym przykładem, w którym przedstawione są rachunki wyników firm X i Y. Należy zwrócić uwagę na rożną strukturę kosztów obu firm - firma X ma wysokie koszty zmienne i niskie stałe, a firma Y odwrotnie.
Firma X Firma Y
Liczby % Liczby %
Sprzedaż 100.000 100 100.000 100
minus koszty 60.000 60 30.000 30
zmienne
Marża na 40.000 40 70.000 70
pokrycie
Minus koszty 30.000 x 60.000
stałe
Zysk 10.000 x 10.000
operacyjny
Odpowiedz na pytanie, która z firm ma lepszą strukturę kosztów zależy od wielu czynników, włączając w to długofalowe trendy w sprzedaży, zmiany w sprzedaży w okresach rocznych, nastawienie zarządu do podejmowania ryzykownych decyzji. Jeśli oczekujemy, że trend sprzedaży będzie wznoszący w następnych latach, to firma Y ma lepszą strukturę kosztów ze względu na wyższy wskaźnik marży na pokrycie /WMNP/. Przy wzroście sprzedaży o taką samą ilość w obu firmach, firma Y osiągnie wyższy zysk operacyjny.
Aby to zilustrować załóżmy, że firmy osiągnęły wzrost sprzedaży o 10%. Nowy rachunek wyników będzie wyglądał następująco:
Firma X Firma Y
Liczby % Liczby %
Sprzedaż 110.000 100 110.000 100
minus koszty 66.000 60 33.000 30
zmienne
Marża na 44.000 40 77.000 70
pokrycie
Minus koszty 30.000 x 60.000
stałe
Zysk 14.000 x 17.000
operacyjny
Tak, jak oczekiwaliśmy firma Y, przy tym samym wzroście sprzedaży, miała największy wzrost zysku , dzięki wyższemu wskaźnikowi marży na pokrycie /70%/.
Załóżmy teraz inną sytuację - 100.000 j.p jest maksymalnym przychodem ze sprzedaży dla obu firm, a można też oczekiwać, że w pewnych okresach przychód ten spada. W tych okolicznościach lepszą strukturę kosztów posiada firma X . Dwie przesłanki potwierdzają taką ocenę. Dzięki niższemu WMNP firma X nie doświadczy tak gwałtownego spadku marży na pokrycie jak firma Y w momencie spadku sprzedaży i zysk będzie się zachowywał bardziej stabilnie. Po drugie firma X ma mniejsze koszty stałe, co powoduje, że w przypadku gwałtownego spadku sprzedaży strata nastąpi później.
Jeśli sprzedaż w obu firmach będzie oscylowała wokół 100.000 j.p to trudno stwierdzić , która z firm ma lepszą strukturę kosztów.
Podsumowując , można stwierdzić ,że w momencie zmian sprzedaży firma Y doświadczy gwałtowniejszych fluktuacji w wyniku finansowego, osiągając większe zyski w przypadku wzrostu sprzedaży. Zysk firmy X zachowywać się będzie bardziej stabilnie, ale firma narażona jest na utratę części korzyści w przypadku długofalowego trendu wzrostu sprzedaży.
5. DŻWIGNIA OPERACYJNA
Z fizycznego punktu widzenia mechanizm dźwigni wyjaśnia, jak przy użyciu małej siły można podnieść wielki ciężar. W ekonomii mechanizm dźwigni operacyjnej pomaga przedsiębiorstwu uzyskać procentowo większy wzrost zysków, przy mniejszym procentowym wzroście sprzedaży.
Przychody |
100 |
110 |
Koszty zmienne |
60 |
66 |
Marża brutto |
40 |
44 |
Koszty stałe |
30 |
30 |
Zysk operacyjny |
10 |
14 |
SDO = %przyrost zysku operacyjnego
% przyrost rozmiarów sprzedaży
SDO = 40% = 4
10%
Przyczyną dźwigni operacyjnej są koszty stałe. Powodują one, że koszty rozpatrywane łącznie, czyli koszty całkowite (koszty stałe i zmienne) są kosztami degresywnymi. Oznacza to, że rosną wolniej od sprzedaży, co powoduje, że zysk jako wielkość wynikowa musi rosnąć szybciej niż sprzedaż. Można te koszty rozpatrywać w ujęciu jednostkowym. Wówczas koszt jednostkowy jako koszt degresywny będzie się zmniejszał w miarę wzrostu sprzedaży a to oznacza, że zysk w ujęciu całkowitym będzie rósł szybciej niż sprzedaż (przy stałym koszcie jednostkowym zysk całkowity rósł by proporcjonalnie do sprzedaży). Wynika z tego, że nie uwzględnia się wpływu cen na przychody i koszty.
Tak więc dźwignia operacyjna jest miarą wagi kosztów stałych w ogólnej strukturze kosztów przedsiębiorstwa. Jest wyższa w firmach mający większy udział kosztów stałych w stosunku do kosztów zmiennych.
Jeśli firma ma wysoką dźwignię operacyjną, wtedy jej zyski będę bardziej wyczulone na zmiany przychodów ze sprzedaży. Minimalny odsetek wzrostu lub spadku sprzedaży może spowodować dużo większy wzrost lub spadek zysków. Dlatego SDO wskazuje na ryzyko operacyjne danego przedsiębiorstwa.
Dźwignia operacyjna będzie zilustrowana danymi z poprzedniego przykładu. Przy sprzedaży całkowitej 100.000 j.p. obie firmy mają takie same koszty całkowite /90.000 j.p./. Firma Y ma jednak większy odsetek kosztów stałych niż firma X. Przy wzroście sprzedaży w obu firmach o 10%, firma Y osiągnie wzrost zysku o 70% /z 10.000 j.p. do 17.000 j.p./, a firma X osiągnie wzrost zysku o 40 % /z 10.000 j.p. do 14.000 j.p./. Przyczyną różnicy we wzroście zysku w obu firmach jest wyższa dźwignia operacyjna firmy Y.
Stopień dźwigni operacyjnej w danej firmie, przy danym dochodzie ze sprzedaży, jest mierzony następującym wzorem:
stopień marża na pokrycie
dźwigni =
operacyjnej zysk operacyjny
Stopień dźwigni operacyjnej jest miarą mówiącą, jak przy danym poziomie sprzedaży, wpłynie na zysk procentowa zmiana przychodów ze sprzedaży. Na przykład stopień dźwigni operacyjnej w firmie X i Y, przy poziomie sprzedaży 100.000 j.p. wyniesie:
firma X 40.000/10.000 = 4
firma Y 70.000/10.000 = 7
Interpretując te wyniki, możemy stwierdzić, że przy zmianie sprzedaży o 1% możemy oczekiwać w firmie Y zmiany zysku operacyjnego o 7%, a w firmie X- o 4%. Przy wzroście sprzedaży o 10% firma Y uzyskała wzrost zysku operacyjnego w wysokości 70%, a firma X- o 40%.
%-owy wzrost zysku = %owy wzrost sprzedaży ∗ stopień dźwigni operacyjnej
Stopień dźwigni operacyjnej jest największy w przedsiębiorstwie na poziomie sprzedaży w pobliżu progu rentowności i maleje zarówno ze spadkiem, jak i ze wzrostem sprzedaży i zysku. Można ten efekt zobaczyć w tabeli poniżej, która pokazuje stopień dźwigni operacyjnej dla firmy Z, przy różnych poziomach dochodu ze sprzedaży.
Sprzedaż 75.000 80.000 100.000 150.000 225.000
Koszty zmienne 45.000 48.000 60.000 90.000 135.000
Marża na pokrycie /a/ 30.000 32.000 40.000 60.000 90.000
Koszty stałe 30.000 30.000 30.000 30.000 30.000
Zysk operacyjny /b/ 0 2.000 10.000 30.000 60.000
Stopień dźwigni oo 16 4 2 1,5
operacyjnej (a/b)
Kolejny wzrost sprzedaży o 10% przy poziomie sprzedaży 225, zwiększyłby zysk tylko o 15% (10%∗1,5 ); natomiast przy poziomie sprzedaży 100 zysk wzrasta o 40%. Stopień dźwigni operacyjnej zmniejsza się wraz z oddalaniem się przychodu ze sprzedaży od punktu krytycznego. przy progu rentowności stopień dźwigni operacyjnej zmierza do nieskończoności (30/0).
Dźwignia operacyjna jest narzędziem pozwalającym zarządowi szybko określić, jaki wpływ na zyski będą miały zmiany w wielkości sprzedaży, bez konieczności przygotowywania szczegółowych rachunków wyników. Jak pokazały przykłady wpływ dźwigni operacyjnej na zysk może być znaczny, szczególnie w pobliżu progu rentowności.
Dźwignia operacyjna jako miara kosztów stałych w strukturze kosztów informuje o skali ryzyka operacyjnego. Wysoki stopień dźwigni operacyjnej oznacza, iż zakres zmian zysku operacyjnego będzie duży a to z kolei jest miarą ryzyka prowadzonej działalności.
A. Jarugowa, A. Szychta, Zaawansowana rachunkowość zarządcza, Fundacja Rozwoju Rachunkowości, Warszawa 1994, s. 38.
Tamże, s. 83.
S. Sojak, op. cit., s. 97.
Rachunkowość zarządcza, praca pod red. G. K. Świderskiej, ..., s. 85-86.
J. Wermut, Rachunkowość zarządcza, ODDK, Gdańsk 1994, s. 26.
S. Sojak, op. cit., s. 97- 98.
47 J. Wermut, op. cit., s. 28- 29.
Rachunkowość zarządcza, praca pod red. G. K. Świderskiej, ... , s. 86-87.
J. Wermut, op. cit., s. 30.
J.Wermut, Rachunkowośc zarządcza. Rachunek kosztów i wyników w podejmowaniu decyzji, Ośrodek Doradztwa i Doskonalenia Kadr, Gdańsk 1997.
25
dr Krzysztof Postrach Wydział Zarządzania i Ekonomii Politechniki Gdańskiej
25
Teoretyczny poziom kosztów całkowitych
=
Jednostk. koszty
zmienne
x
Wielkość prod. prod.prdukcji
+
K. stałe ststałe
stałe
![]()
![]()
S
S - koszty stałe
Różnica w rozmiarach
produkcji
Różnica w kosztach
zmiennych
Wielkość produkcji
Koszty całkowite
Koszty całkowite
Wielkość prod. prodprod.prod.odukcji
Różnica w kosztach
całkowitych
Różnica w
rozmiarach
produkcji
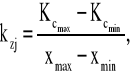
![]()
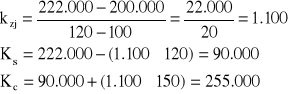
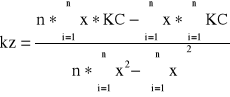
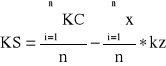
Teoretyczny poziom kosztów całkowitych
=
Jednostkowe
koszty
zmienne
x
Wielkość produkcji
+
Koszty stałe
![]()
![]()
![]()
![]()
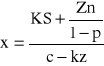
Wyszukiwarka
Podobne podstrony:
RZ cz.I-internet, Studia, STUDIA PRACE ŚCIĄGI SKRYPTY
RZ cz.III-internet, Studia, STUDIA PRACE ŚCIĄGI SKRYPTY
zj-II-z, Studia, STUDIA PRACE ŚCIĄGI SKRYPTY
Teoria konsumenta, Studia, STUDIA PRACE ŚCIĄGI SKRYPTY
17, Studia, STUDIA PRACE ŚCIĄGI SKRYPTY
pomoc publiczna, Studia, STUDIA PRACE ŚCIĄGI SKRYPTY
konsorcjum gospodarcze, Studia, STUDIA PRACE ŚCIĄGI SKRYPTY
Ś z integracji europejskiej, Studia, STUDIA PRACE ŚCIĄGI SKRYPTY
Logistyka, Studia, STUDIA PRACE ŚCIĄGI SKRYPTY
Egzaminu przedmiotu Normalizacja, Studia, STUDIA PRACE ŚCIĄGI SKRYPTY
Folie do tematow 1-2, Studia, STUDIA PRACE ŚCIĄGI SKRYPTY
44, Studia, STUDIA PRACE ŚCIĄGI SKRYPTY
Przykadowy egzamin, Studia, STUDIA PRACE ŚCIĄGI SKRYPTY
więcej podobnych podstron