1

Wykłady uzupełniające,

Budownictwo, I rok, studia magisterskie

Wykład 1

1.

Wektory

Wektor – uporządkowana para punktów.
Trzy wielkości, charakteryzujące:

•

Zwrot

•

kierunek

•

Wartość (długość – moduł wektora)

Rodzaje wektorów:

a)

Swobodne;

b)

W układzie współrzędnych

Działania na wektorach:

1.

Mnożenie przez liczbę,

2.

Dodawanie wektorów,

3.

Mnożenie wektorów;

a)

Skalarne;

b)

Wektorowe;

4.

Normalizacja wektora

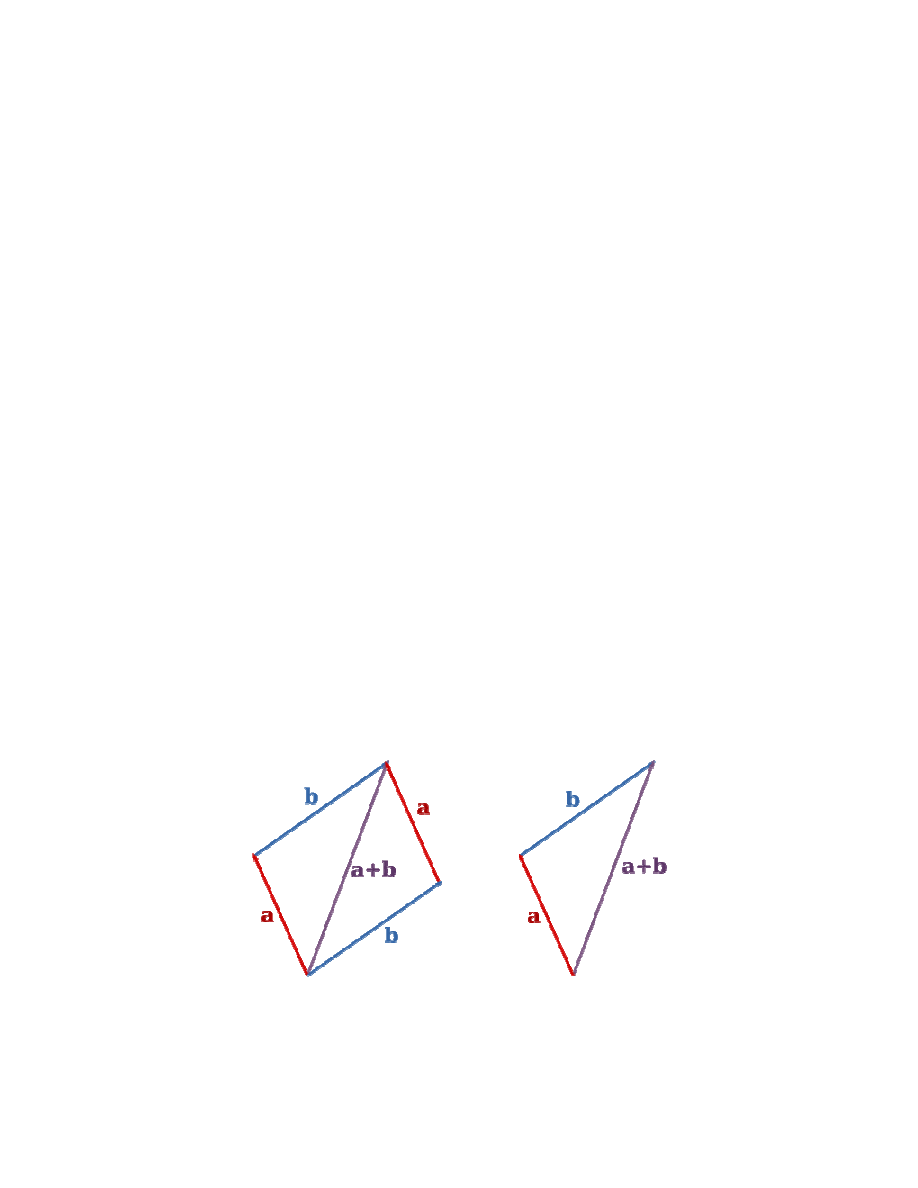
Dodawanie wektorów

Graficzne dodawanie wektorów swobodnych

Rys. 1. Dodawanie wektorów

2

]

,

,

[

ˆ

ˆ

ˆ

z

y

x

z

z

y

y

x

x

a

a

a

e

a

e

a

e

a

a

=

⋅

+

⋅

+

⋅

=

r

]

,

,

[

ˆ

ˆ

ˆ

z

y

x

z

z

y

y

x

x

b

b

b

e

b

e

b

e

b

b

=

⋅

+

⋅

+

⋅

=

r

Suma wektorów:

]

,

,

[

z

z

y

y

x

x

b

a

b

a

b

a

b

a

+

+

+

=

+

r

r

Iloczyn skalarny wektorów

)

,

cos(

b

a

b

a

b

a

r

r

r

r

∠

⋅

⋅

=

⋅

z

z

y

y

x

x

b

a

b

a

b

a

b

a

⋅

+

⋅

+

⋅

=

⋅

r

r

Własności

a)

przemienny

b)

pole powierzchni

c)

równy zero dla wektorów prostopadłych

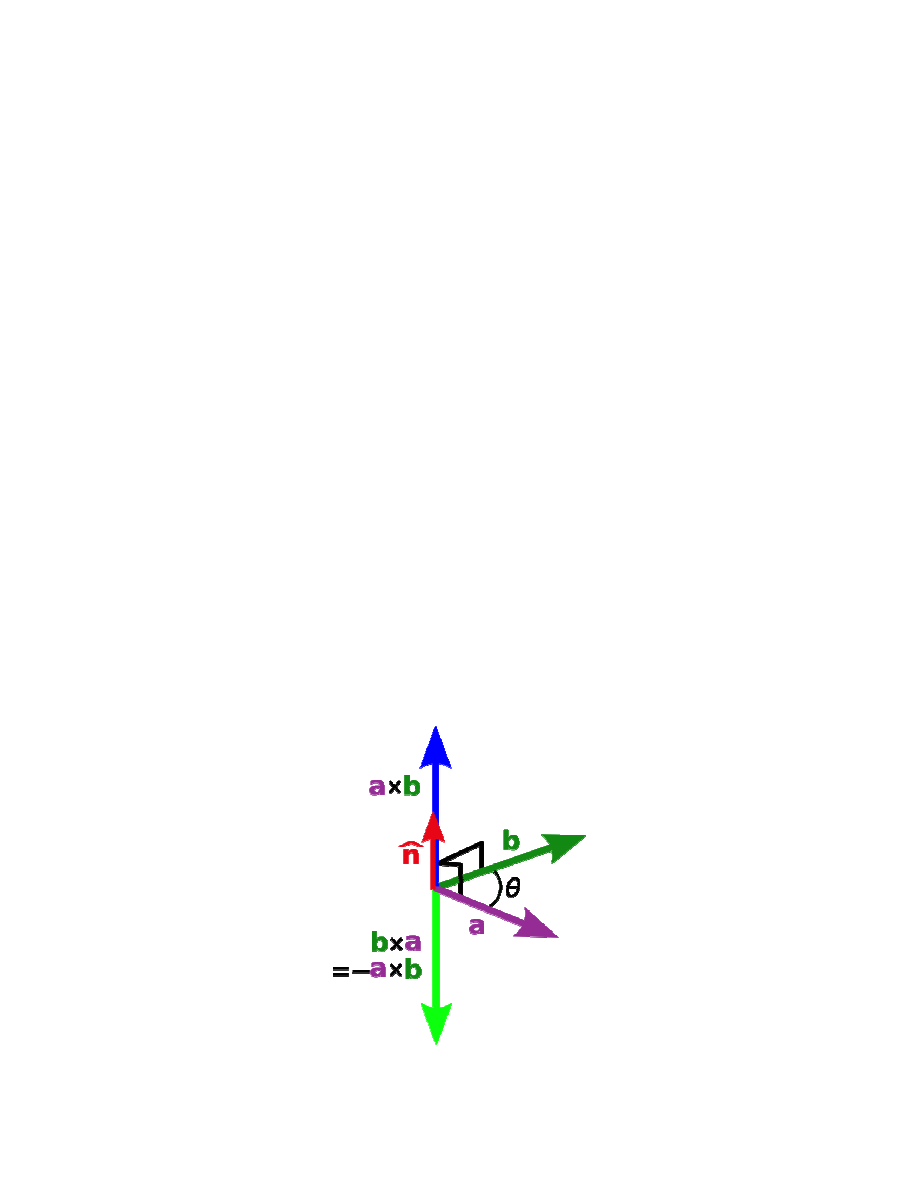
Iloczyn wektorowy
Własności wektora (do wyznaczenia)

a)

kierunek,

b)

zwrot

c)

wartość, długość wektora

Rys. 2. Iloczyn wektorowy

3

Długość iloczynu wektorowego:

)

,

sin(

b

a

b

a

b

a

r

r

r

r

∠

⋅

⋅

=

×

)

(

ˆ

)

(

ˆ

)

(

ˆ

ˆ

ˆ

ˆ

x

y

y

x

z

z

x

x

z

y

y

z

z

y

x

z

y

x

z

y

x

z

y

x

b

a

b

a

e

b

a

b

a

e

b

a

b

a

e

b

b

b

a

a

a

e

e

e

b

a

−

+

−

+

−

=

=

=

×

r

r

Własności iloczynu wektorowego:

a)

nieprzemienny,

b)

równy zero dla wektorów równoległych

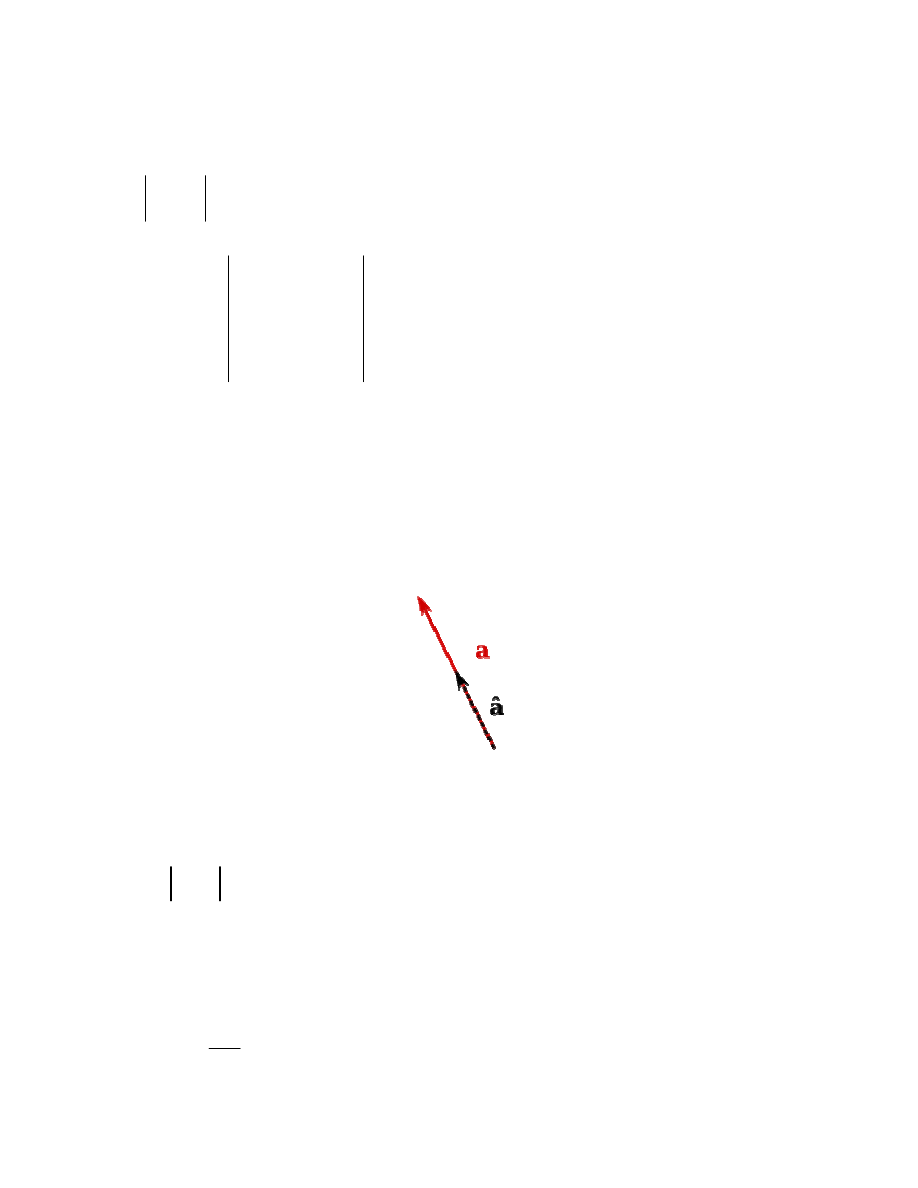
Wektor jednostkowy, normalizacja wektora

Rys. 3. Normalizacja wektora

Wektor i wersor.

1

)

(

ˆ

)

(

ˆ

lub

1

)

(

ˆ

)

(

ˆ

)

(

)

(

=

⋅

=

⋅

=

t

a

t

a

t

a

t

a

t

a

t

a

r

4.

Pochodna wektora

;

t

d

r

d

v

r

r

=

4

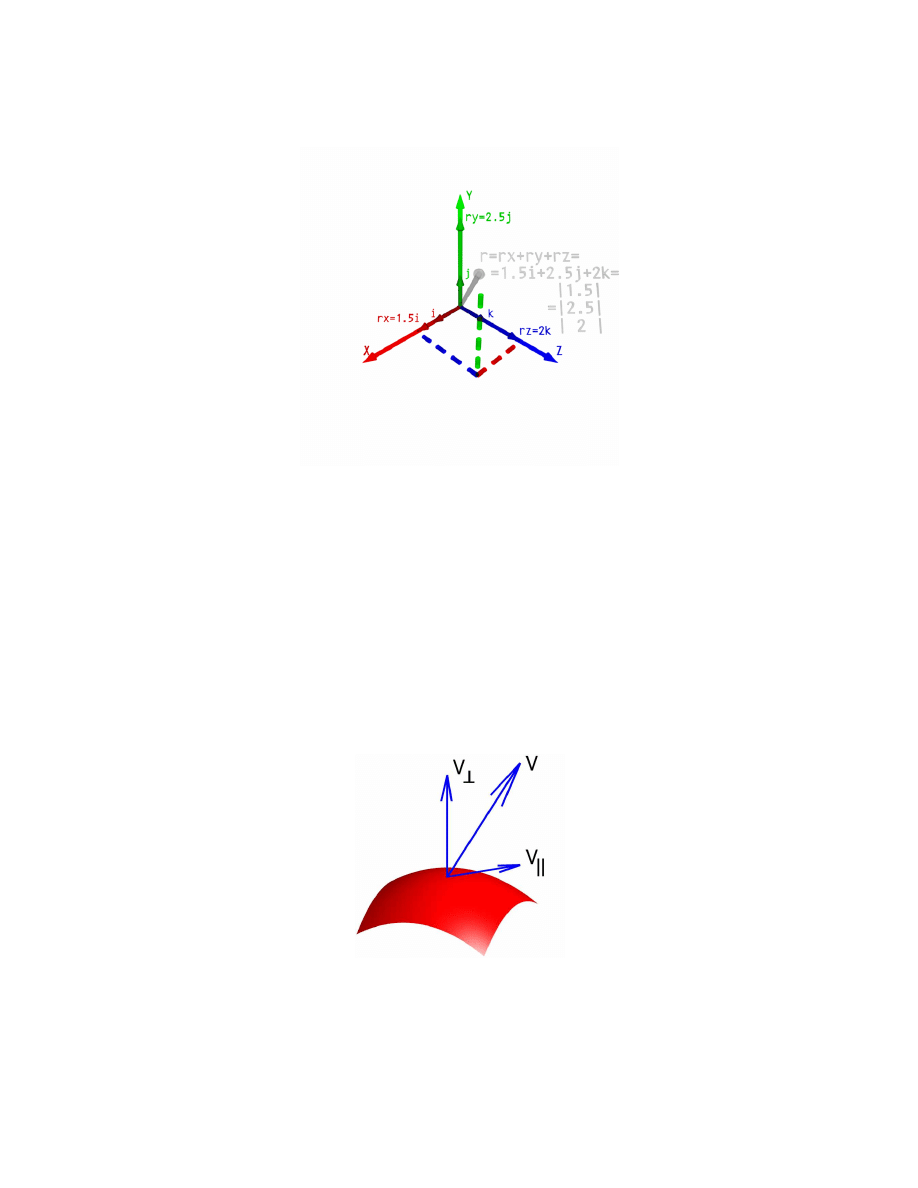
Wektor w kartezjańskim układzie współrzędnych

Rys. 4. Układ kartezjański i wektory w układzie współrzędnych

Użyteczne tożsamości wektorowe:

)

(

)

(

)

(

)

(

)

(

)

(

)

(

)

(

)

(

)

(

ˆ

)

(

ˆ

)

(

ˆ

;

a

c

b

b

a

c

c

b

a

c

a

b

b

c

a

c

b

a

a

c

b

b

c

a

c

b

a

b

a

b

a

e

b

a

b

a

e

b

a

b

a

e

b

a

b

a

b

a

b

a

b

a

x

y

y

x

z

z

x

x

z

y

y

z

z

y

x

z

z

y

y

x

x

r

r

r

r

r

r

r

r

r

r

r

r

r

r

r

r

r

r

r

r

r

r

r

r

r

r

r

r

r

r

r

×

⋅

=

×

⋅

=

×

⋅

⋅

⋅

−

⋅

⋅

=

×

×

⋅

⋅

−

⋅

⋅

=

×

×

−

+

−

+

−

=

×

+

+

=

⋅

Rys. 5. Składowe wektora: normalna i styczna do powierzchni

5

Zadanie 1
Dane są dwa wektory:

]

5

,

4

,

3

[

ˆ

5

ˆ

4

ˆ

3

=

⋅

+

⋅

+

⋅

=

z

y

x

e

e

e

a

r

]

1

,

0

,

1

[

ˆ

1

ˆ

1

−

=

⋅

+

⋅

−

=

z

x

e

e

b

r

Obliczyć:

a)

długość każdego z wektorów,

b)

iloczyn skalarny

b

a

r

r

⋅

c)

iloczyn wektorowy

b

a

r

r

×

,

d)

kąt zawarty między wektorami

Zadanie 2
Równania ruchu dwóch punktów w pewnym określonym układzie
współrzędnych są następujące:

]

2

,

3

,

4

[

ˆ

2

ˆ

3

ˆ

4

1

−

=

⋅

+

⋅

−

⋅

=

z

y

x

e

e

e

r

r

]

1

,

2

,

1

[

ˆ

1

ˆ

2

ˆ

1

2

=

⋅

+

⋅

+

⋅

=

z

y

x

e

e

e

r

r

Obliczyć:

a)

długości obydwu wektorów,

b)

przemieszczenie drugiego punktu względem pierwszego

12

r

r

,

c)

kąty między tymi trzema wektorami,

d)

rzut wektora

12

r

r

na

1

r

r

,

e)

iloczyn wektorowy

2

1

r

r

r

r

×

Zadanie 3
Równania ruchu dwóch punktów w określonym układzie współrzędnych są
następujące:

[

]

2

1

]

0

,

1

,

1

[

]

2

,

1

,

3

[

0

,

2

,

0

t

t

r

⋅

+

⋅

+

=

r

[ ]

t

r

⋅

+

=

]

1

,

2

,

0

[

1

,

0

,

1

2

r

Obliczyć:

a)

prędkość v

r

drugiego punktu względem pierwszego

b)

przyśpieszenie a

r

drugiego punktu względem pierwszego.

6

Zadanie 4
Punkty A i B poruszają się wzdłuż osi OX i OY z prędkościami

]

0

,

2

[

=

A

v

[m/s]

i

]

3

,

0

[

=

B

v

[m/s]. W chwili początkowej

0

=

t

znajdują się w punktach

]

0

,

3

[

−

=

A

r

[m],

]

3

,

0

[

−

=

B

r

[m]. Obliczyć

B

A

AB

r

r

r

r

r

r

−

=

, położenie punktu B

względem A. Kiedy te punkty znajdą się najbliżej siebie i w jakiej odległości?

Zadanie 5
Sprawdzić poprawność tożsamości:

)

(

)

(

)

(

a

b

c

c

a

b

c

b

a

r

r

r

r

r

r

r

r

r

⋅

⋅

−

⋅

⋅

=

×

×