Strickland Finite Subgroups of Formal Groups (1996) [sharethefiles com]

Finite Subgroups of Formal Groups

Neil

Stric

kland

Trinity College, Cambridge CB2 1TQ, England

Abstract

We discuss various moduli problems involving the classi cation of nite subgroups

or related structures on formal groups of nite height

. We show that many moduli

schemes are smooth or at least Cohen-Macaulay. Moreover, many maps between

such schemes are nite and at, and their degrees can be predicted by thinking of

(

)

as a \discrete model" for the formal group.

1 Introduction

In this paper we discuss various moduli problems involving the classi cation

of nite subgroups or related structures on formal groups of nite height.

Analogous problems for elliptic curves have of course been widely studied 9].

The moduli spaces which we consider turn out to be surprisingly well-behaved.

They are all Cohen-Macaulay, and most of them are smooth. The original

motivation for this work came from algebraic topology, in particular the study

of power operations in certain homology theories constructed by Morava. I

learnt most of what I know about these questions from Mike Hopkins, and a

great deal of the theory presented here was developed in discussions with him.

See Section 14 for a brief discussion of how moduli problems arise in algebraic

topology, and 15] for more details. Some readers may prefer a version of this

paper containing rather more exposition of standard algebraic material, which

is available from the author.

1.1 Synopsis

In Section 2 we set up our technical context by recalling various results about

complete local rings, interpreted in a geometric manner. In Sections 3 and 4,

partially supported by the N.S.F.

Preprint submitted to Elsevier Science

3 September 1996

we establish some basic facts about formal groups and divisors. In Section 5

we show that the quotient of a formal group by a nite subgroup is again a

formal group. In Section 6 we reformulate the Lubin-Tate deformation theory

of formal groups in a coordinate-free way.
For the rest of this synopsis, we consider a formal group

of nite height

over a eld of positive characteristic, and let

be its universal deformation.

The content of subsequent sections is as follows.

Section 7:

We de ne level-

structures on

(where

is a nite Abelian group). We prove

that the moduli space Level(

) is smooth, and that the map Level(

)

;

is nite and at.

Section 8:

We investigate maps of schemes over

between the schemes Level(

) they

all arise (contravariantly) from monomorphisms of nite Abelian groups, and

are nite and at.

Section 9:

We show how an epimorphism

;

gives rise to a nite at map

Level(

)

;

Level(

), for a dierent group

Section 10:

We show that the subgroups of

of degree

are classi ed by a scheme

Sub

(

) which is nite and at over

Section 11:

We consider ags 0 =

< K

< ::: < K

(1), where

(1) is the kernel

of multiplication by

and

has given degree

. We show that such

ags are classi ed by a smooth scheme Flag(

), and that there are nite at

maps Level(1

)

;

Flag(

)

;

, the rst of which is a Galois covering.

Section 12:

We consider the orbit scheme Type(

) = Level(

)

Aut(

) (suitably in-

terpreted). We show that Type(

) is smooth and the maps Level(

)

;

Type(

)

;

are nite and at. We also show that the normalisation

of Sub

(

) is a disjoint union of schemes of the form Type(

). More-

over, if the height of

is at most two (but not in general), then the maps

Type(

)

;

Sub

(

) are closed embeddings.

Section 13:

We consider the problem of classifying deformations of a given isogeny of

formal groups over a eld.

Section 14:

We sketch the way in which the problems discussed above arise in algebraic

topology.

Section 15:

We derive some formulae which help one to construct and compute with formal

groups.

Section 16:

We present some detailed examples.

2 Geometry of Complete Local Rings

For brevity, a scheme will mean a formal scheme of the form spf(

), where

is a nite product of complete Noetherian local rings of residue characteristic

p >

0. We shall often assume that

is local, leaving trivial modi cations

for the semi-local case to the reader. We shall primarily think of schemes as

representable functors from the category of complete Noetherian local rings

and local homomorphisms to sets, via the de nition

spf(

)(

) = Hom(

)

= spf(

) we write

for

. Given schemes

over a base scheme

(which is usually to be understood from the context), a point of

dened

over

will mean a map

;

of schemes over

. We write ;(

) for

the set of such points. If

then we write

(

) for

is connected (i.e.

is local) we write

for the residue

eld. We also write

= spf(

) and refer to this as the special bre of

We write dim(

) for the Krull dimension of

and embdim(

) for the em-

bedding dimension, that is

embdim(

) = dim

(

2
X

)

We shall say that

is integral if

is an integral domain, and smooth if

is a regular local ring. If

is integral we write

for the eld of fractions

. Suppose we have a map of schemes

;

, and thus a map

;

, using which we consider

as a module over

. As usual,

we say that

is at (resp. nite ) if

is a at (resp. nitely generated)

-module. We also say that

is dominant (resp. epi) if the kernel of

nilpotent (resp. zero).
If

is nite and

is connected we de ne the degree of

to be deg(

) =

dim

(

). In our context, if

is also at then

is actually a free

module over

(see 11, Theorem 7.10]).

We next state in this language some standard facts from commutative algebra.

Lemma 1

A nite dominant map of smooth schemes is at.

Lemma 2

Let

and

be integral schemes of the same dimension

, with

maps

;

. If

is nite and dominant, then the same is true of

and

Lemma 3

is smooth and

;

is nite and at then

is smooth.

Proof.

Use the homological criterion 11, Theorem 19.2].

Let

be a scheme with an action of a nite group ;. We shall write

; for

the scheme spf(

). This is of course not a very good construction in general,

but it will turn out to be well-behaved in the cases we consider.

Denition 4

A nite extension

;

of integral domains is

Galois if

is the xed subring for the action of

Aut

(

) on

and

is free over

. I

am not sure whether this denition is standard. Similarly, we say that a map

;

of integral schemes is a

Galois covering if

;

is Galois.

The next two lemmas follow easily from the Galois theory of elds and the

fact that regular local rings are integrally closed.

Lemma 5

;

is Galois then

is Galois over

and

deg(

) =

] =

Aut

(

)

Aut

(

)

Lemma 6

A nite dominant map

;

of smooth schemes is a Galois

covering if and only if the extension of function elds

;

is Galois.

Lemma 7

Let

be a smooth scheme with a faithful action of a nite group

;. Suppose that

;

is a nite at map of degree

;

, such that

for all

;. Then

is smooth,

is Galois, and the induced map

;

is iso.

Proof.

By Lemma 3, we see that

is smooth. Because

] =

;

and

, Galois theory tells us that

and thus

;

is Galois.

The claim now follows from Lemma 6.

We next record a few basic facts about norms. Suppose that

;

a nite at map of degree

. We can then de ne a (nonadditive) norm map

X=Y

;

, by letting

(

) be the determinant of multiplication

, considered as an

-linear endomorphism of

Lemma 8

Suppose we have a pullback diagram

is a nite free map then so is

, and

Proof.

For the square to be a pullback means that

, and

with this identi cation we have

= 1

and

1. The claim follows

easily by choosing bases.

Lemma 9

Suppose that

;

is a section of

, and that

= 0. Then

(

) = 0.

Proof.

We can write

, where

= ker(

). As

, the image

of multiplication by

lies in the proper summand

, so the determinant

is zero.

3 Formal Groups

Let

= spf(

) be a scheme, and

a one-dimensional commutative formal

group over

. In more detail, we have

= spf(

) where

is isomorphic to

]] as an augmented

-algebra, and we are given a commutative group law

;

(which we shall write additively). In future, we shall simply

say \formal group" instead of \commutative one-dimensional formal group". A

coordinate

on a formal group

is a choice of generator

ker(0

;

)

such that

]]. (Here 0

is the map induced by the zero-section

;

A homomorphism (

): (

)

;

(

) of formal groups consists of maps

as follows, which make the obvious diagrams commute.

We shall say that (

) (or just

) is a brewise isomorphism if the diagram

above is a pullback.
Let

be a coordinate on

, and let

be obtained by pulling back

along the two projections

;

. Then

]], so we

can write

(

) for a unique power series

over

. Equivalently,

for any two points

;

we have

(

) =

(

)

(

)). This series

is called the formal group law associated to

and

. It is easily seen to have

the following properties:

(

(mod

)

(

)

(

)

(

))

We also write

for

(

). Much of the literature on formal groups

is written in terms of formal group laws 6] 14, Appendix 2] 7]. However,

we shall nd it conceptually clearer to take a coordinate-free de nition the

primary one.
Let

= spf(

) be the special bre, and put

. This is a

formal group over

The following lemma is well-known.

Lemma 10

Let

;

be a nonzero homomorphism of formal groups

over a base

, and let

and

be coordinates on

and

. Then there exist

and

such that

= 0 and

(mod

Denition 11

We shall call the integer

described above the

strict height of

, and dene the

height of

to be the strict height of

;

. We also

dene the (strict) height of

to be the (strict) height of the endomorphism

;

, which is just

times the identity map.

From now on, we shall take

to be a formal group of nite height

over a

connected base scheme

Proposition 12

;

is nonzero, then

= height(

) is nite and

is at of degree

. Moreover,

height(

) = height(

Proof.

This is essentially standard. If

has in nite height then

= 0 this

is an easy generalisation of 6, p. 99] (in which

is assumed to be a DVR).

If there is a nonzero map

;

then height(

) = height(

) | this

is proved as a corollary of the last reference. The Weierstrass preparation

Theorem 6, Chapter 1] implies that

is freely generated over

x::: x

;

. It is not hard to conclude that these elements also form a

basis for

over

4 Divisors

By a divisor on

we shall mean a closed subscheme

which is nite

and at over

. We briey record how things work out in our context. The

proofs are either easy or parallel to 9, Section 1.1] (for example).

Proposition 13

is a divisor of degree

and

is a coordinate,

then there is a unique monic polynomial

(

) of degree

such that

(

). Moreover,

(

) is the characteristic polynomial of the

-linear

endomorphism of

given by multiplication by

, and

(

) =

(mod

Denition 14

The

equation of a divisor

(with respect to a given coordinate

) is the polynomial

(

) as above. If

(

) =

dk=0

(with

= 1) then

the

parameters of

are the coecients

::: c

;

More generally, given a scheme

over

, a divisor on

over

will just mean

a divisor on the pulled-back group

Because we are assuming that

has nite height

, the subscheme

(

) = ker(

;

) = spf(

(

)

is a divisor of degree

is a section of

then we write

] for the associated divisor, which has

(

) =

;

(

). The following lemma provides a useful alternative repre-

sentation:

Lemma 15

For any formal group law over any ring

, the power series

;

is a unit multiple of

;

]].

Proof.

;

clearly vanishes mod (

;

). By considering the rst few terms,

it is easy to see that (

;

)

(

;

) must be 1 modulo (

), so it is a unit.

The functor from schemes over

to sets de ned by

divisors of degree

over

is represented by a scheme Div

(

) =

. If

is a coordinate on

then

the ring of functions on this scheme is just the symmetric subring

Div

(

)

:::

]]

::: x

]] =

(where

is the

'th elementary symmetric function in the variables

). The

equation of the universal divisor over this ring is

(

) =

(

;

) =

k=0

(

;

The following proposition (taken from 9]) will help us to construct various

moduli schemes:

Proposition 16

Let

be two divisors on

over

. There is then a

closed subscheme

such that for any map

;

we have

;(

Div(

)) if and only if

factors through

Proof.

Choose a coordinate

, and let

be the degree of

. Then there

are unique elements

such that

(

) =

;

k=0

(mod

(

))

Put

= spf(

(

::: b

;

)), and check that this works.

5 Subgroups and Quotient Groups

By a nite subgroup of

we shall simply mean a divisor

K <

which is also

a subgroup scheme.

Proposition 17

is a nite subgroup of

then the degree of

is a power

Proof.

It is enough to prove the proposition when

= spec(

), so that

(

) =

. It then follows from the general theory of nite group schemes

over a eld, but we shall give a direct proof. Let

be the formal group law

, so that

(

) =

(mod

). Because

is a subgroup, we have

(

)) = 0 (mod

(

)

(

)). Reading this modulo (

)

d+1

, we see

that the binomial coecient (

) is divisible by

when 0

< k < d

. As in

Lemma 10, this implies that

is a power of

Proposition 18

is a nite subgroup of

of degree

then

= 0 and

thus

(

) = ker(

Proof.

This is a special case of a result of Deligne | see 16]. A key point

is that one can give a purely equational proof that any element

of a nite

Abelian group

of order

has

= 1. Indeed,

Let

be a nite subgroup of

of degree

. We would like to be able to

construct a quotient group

. To do this, write

for the addition map

;

(or any of its restrictions) and

;

for the

projection. Let

be the equaliser

Let

be a coordinate on

, so that

Theorem 19

With

and

as above, we have

(i)

(mod

(ii)

]].

(iii)

has a natural structure as a formal group.

(iv) The projection

;

is the categorical cokernel of

;

(v) For any map

;

we have

(

Proof.

First, there is a map

;

de ned on points by

(

) = (

;

). This is an automorphism and satis es

. We know

that

is a nite at map, so we conclude that the same is true of

. Next, let

;

be the projection on the rst two factors, and

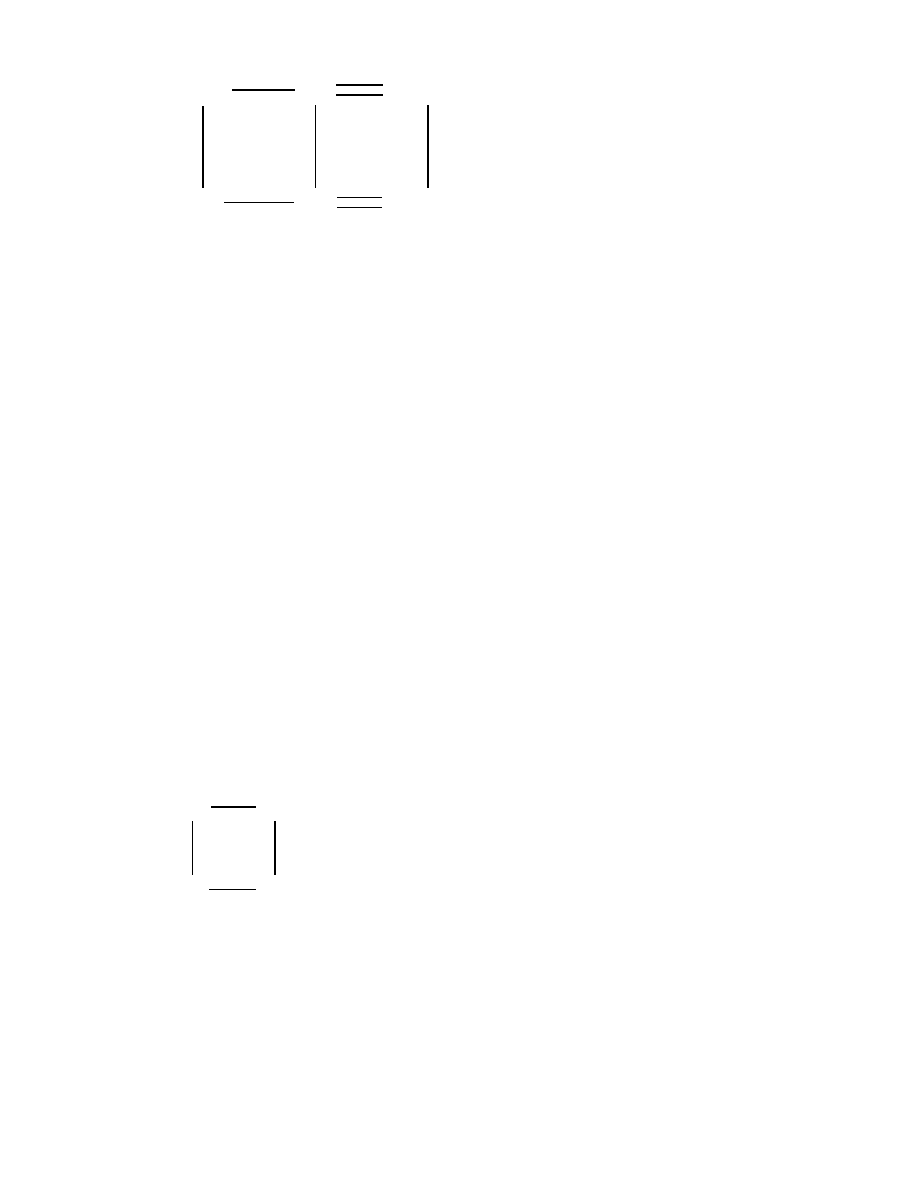
consider the following commutative squares:

A diagram chase shows that they are both pullbacks. It follows that all the

maps involved are nite at maps, and that

)

(

Combining this with the fact that

) =

(

1), we see that

actually lies in

as claimed. The argument so far follows 3].

Next, write

;

for the inclusion. I claim that

= 0. To see this, let

;

be the map

), so that

= 0 and

. Thus

= 0

. Next consider the diagram

Using Lemma 8 we see that 0

K=X

. The claim now

follows from Lemma 9, using the zero section

;

Let

be the equation of the divisor

, so that

is a monic polynomial of

degree

and ker(

) = (

(

)). It thus follows that

is divisible by

(

From Proposition 13 we know that

]]

, so that

]]

As working mod

is the same as restricting to

, we see that the image of

in this ring agrees with

mod

. Using the basis

z::: z

;

, we

conclude that the norm of

is just

. However, this norm is just the

image of

, which gives part (1) of the theorem. It follows easily

from this that

is a unit multiple of

(

It is not hard to see that there is a commutative diagram

Suppose

. By the above diagram,

(

;

(0)) = 0. By the

last paragraph, we see that

;

(0) is divisible by

, say

(0) +

with

. Using the Weierstrass factorisation, we see that

is not a zero

divisor in

. Using this, we can check that

. Extending this

inductively, we conclude that

]], giving part (2) of the theorem.

For part (3), a diagram chase now shows that

;

factors

;

for a unique map

, which makes

into a formal group with coordinate

. It is easy to see from the de nition of

that

is the categorical cokernel of

, in other words that a map

;

of formal groups factors through

if and only if

= 0 this is

part (4). Finally, our construction of

clearly commutes with base change. It

follows that

(

) =

for any map

;

, as claimed in (5).

6 The Universal Deformation

Suppose that

is a scheme of the form spf(

) (where

is a eld of character-

istic

), and that

is a formal group over

of nite height

. A deformation

consists of a formal group

over a scheme

together with a pullback

diagram as follows, exhibiting the restriction of

to the special bre of

a pullback of

Of course, if we start with a group

over

and de ne

to be the special

bre of

and

to be the restriction of

, then

is a deformation of

in a tautological way.

A morphism of deformations is a pullback square as follows, which is compat-

ible in the obvious sense with the given maps

;

Recall that the pullback condition means (by de nition) that the map

;

is a brewise isomorphism.
In 10] Lubin and Tate construct universal deformations of formal group laws.

The following proposition is a simple translation of their result into coordinate-

free language.

Proposition 20

The category of deformations of

has a terminal object

. Moreover, coordinates can be chosen such that

::: u

;

]]

(where

is the Witt ring of

) and

(mod

::: u

;

)

(where

). Note that

is a smooth scheme of dimension

, and

the special bre of

. We refer to

as the deformation space of

, and

as the universal deformation.
Suppose we start with a group

, de ne

to be the special bre

and

the restriction of

over

. Let

be the universal

deformation of

. There is then a unique map

;

such that

. We shall often use only the much weaker corollary that

obtained by pulling back a group over a smooth scheme.

7 Level Structures

Let

be a nite Abelian

-group. It is not hard to see that the functor from

schemes over

to sets given by

Hom(

;(

))

is represented by a scheme Hom(

) over

. Indeed, we may write

in the

form

;

k=0

, and then Hom(

) is isomorphic to the closed subscheme

(

) of

(where

(

) = ker(

) as usual). If

is a coordinate on

then

Hom(

)

::: x

;

]]

(

](

)

:::

](

;

))

By Proposition 12, this is a nite free module over

, in other words the

map Hom(

)

;

is nite and at. The degree is

were a discrete group, it would be natural to write

Hom(

) =

Mon(

A=B

)

(where Mon denotes monomorphisms). However, except in trivial cases, there

is no scheme Mon(

) over

such that

Mon(

;(

)) = ;(

Mon(

))

Indeed, by considering the inclusion

;

we see that the left hand side

is not even a functor of

. The object of the theory of level structures is to

approximate the above decomposition as well as possible. The key idea is due

to Drinfel'd 5], and some of our results below are parallel to results in 9,

Section 1.6].
We write

(

) = ker(

;

). For any map

;

;(

) we write

] for the divisor

(

)]. We also put = (

)

, so that (

) =

(

)

. Note that

Hom(

)

, which is the same as the degree

of Hom(

)

;

. This is the rst of many cases in which serves as a

\discrete approximation" to

Denition 21

level-

structure on

over an

-scheme

is a map

;

;(

) such that

(1)]

(1) as divisors. A level-

structure

means a level-

(

) structure.

The following is very similar to 9, Proposition 1.6.2].

Proposition 22

The functor from schemes over

to sets given by

level-

structures on

over

is represented by a scheme Level

(

) over

. (We will write Level

(

) =

Level

((

)

)).

Proof.

We can consider

Hom(

) as a formal group over Hom(

On this group we have a tautological map

;

;(Hom(

)

) and

thus a divisor

(1)]

;(Hom(

)

Div(

)). Applying Proposition 16 to

this divisor and the divisor

(1)

Hom(

), we get a closed subscheme

Level(

)

Hom(

). It is easy to see that this does the job.

Suppose that

;

is mono, and that

;

;(

) is a level struc-

ture. Then

is clearly a level-

structure, and is thus classi ed by a

map

;

Level(

). Applying this in the universal case, we obtain a map

: Level(

)

;

Level(

). This construction is contravariantly functo-

rial.

Theorem 23

Level

(

)

;

is a nite at map. If

is the universal

deformation of

then Level

(

) is smooth and has dimension

Theorem 24

;

is a level structure then

] is a subgroup of

and

(

)]

(

) for all

. If

= (

) then

] =

(

The proofs of these two theorems will follow after a number of intermediate

propositions. Similar results are proved in 5] and 9].

Notation

(

) is the Weierstrass polynomial (of degree

) which is a

unit multiple of

(

)

(

Lemma 25

If rank

(

)

> n

then Level

(

) =

Proof.

In this case

(1)] has degree greater than that of

(1), so we can

never have

(1)]

(1).

From now on, we will always assume that

has rank at most

Proposition 26

is an integral domain of characteristic zero, then a

map

;

;(

) is a level structure if and only if it is injective.

Proof.

Observe that

is injective if and only if ker(

)

(1) = 0, so we may

assume that

(1). Write

(

)) and

(

) =

(

;

)

Suppose that

is a level structure. Then for

0 we have divisibility

relations:

(

;

)

+ higher terms

= 0 in

, we must have

= 0 and thus

(

)

= 0, as required. Con-

versely, suppose

is injective. The values

runs over

are distinct

roots of the Weierstrass polynomial

(

) de ned above. By the usual theory

of factorisation over a domain, the product

(

;

)

divides

(

), so we have a level structure.

Proposition 27

Suppose that

is integral. Then there is a prime ideal

evel

(

)

with

= 0.

Proof.

Let

be large enough that

= 0. Let

be the eld of fractions

the splitting eld of

over

, and

the subring of

generated

over

by the roots of

. These roots are the same as the zeros of (

)

, so

they form a group

under the operation +

. If we identify a map

;

over

with the element

(

) =

(

)

, then

= ;(

(

)).

Write

= (

)

. Note that

(mod

), and

= 0 in

, so

vanishes

only to rst order at 0. Suppose that

are points of

and

= 0. Then

(

) =

(

) =

(

). It follows that

vanishes only to rst order

. Thus, all the roots of

are distinct.

Clearly

(1) is the set of roots of

, and thus has order

. Moreover,

0 and

. It follows by the structure theory of nite Abelian groups

that

(

)

, and thus that we can choose an embedding

;

. By

Proposition 26, this is a level structure on

over

. It is therefore classi ed

by a map

;

Level(

) of schemes over

. We can take

to be the

kernel of

Level(

)

;

Remark 28

In geometric language, this says that there is an irreducible com-

ponent

of Level

(

) such that

;

is nite and dominant. We shall

see shortly that

= Level(

Corollary 29

is integral then

dim(Level(

))

dim(

)

Proposition 30

is the universal deformation of

then Level

(

) is

a smooth scheme of dimension

Proof.

Write

::: u

;

]] (as in Section 6), and

Level(

)

. Suppose that

has rank

, say

::: a

;

. Write

(

))

. By the proof of Proposition 22, we know that these elements

topologically generate

over

, so that the

's and

's generate

. We

also put

= (

::: x

;

::: u

;

)

It is enough to show that

, for then

embdimLevel(

)

= dim

dimLevel(

)

Write

= spf(

). The map

;

;(

) sends the generators to zero,

so it is zero. Thus,

(

) =

A(1)]

(

) =

in (

)

]. Because

is a level

structure, this divides

. Using the fact (see Section 6) that

(mod

::: u

;

)

we nd that

::: u

;

vanish in

. Of course, the rest of the

's also

vanish by de nition of

. As the

's and

's generate

, this implies that

as claimed.

Proposition 31

For any

, the projection Level

(

)

;

is a nite at

map.

Proof.

We may assume that

is the universal deformation of

, as the

general case is easily recovered by base change. As Level(

) is a closed

subscheme of Hom(

) and Hom(

)

;

is a nite at map, we see

that Level(

)

;

is nite. By propositions 27 and 30, we see that it is

also dominant. A nite dominant map of smooth schemes is at (Lemma 1).

Proposition 32

is a level structure then

(

)] is a subgroup scheme

contained in

(

Proof.

We may assume that

(

), so that

= 0. Suppose for the mo-

ment that the base scheme

is integral. As in the proof of Proposition 27, we

see that the Weierstrass polynomial

has distinct roots. By Proposition 26,

is injective, so the polynomials

;

for

are distinct factors of

(

It follows that

(

;

) divides

(

), so that

]

(

) as claimed.

Next, write

(

;

) = (unit)

(

;

)

In other words, for any point

we have

(

) =

(

;

(

))

Write

= spf(

]]), so

is a quotient scheme of

. By the Weierstrass

preparation theorem, we see that

;

is at, of degree

We can let

act on

, with

acting as translation by

(

). This action

is faithful, because

is injective. The map

;

clearly factors through

. It follows from Lemma 7 that

and that

is Galois. Similarly,

we nd that (

)

(

) =

. Using these descriptions, it is

easy to construct a (unique) multiplication on

such that

is an isogeny of

formal groups. The kernel of

is just spf(

) =

], so

] is a subgroup

scheme as claimed.
Now suppose that

is not integral. Let

be the universal deforma-

tion of

, and

the universal level structure de ned over Level(

). By

Proposition 30, we know that Level(

) is integral, so the above tells us

that

(

)] is a subgroup scheme contained in

(

). Using the de ning

properties of

and Level(

), we construct a map

;

Level(

)

such that the pullback of

and the pullback of

. It follows that

(

)] =

(

)] is a subgroup scheme of

(

), as claimed.

Corollary 33

It follows from the above proof that

(

;

) is a

coordinate on the quotient group

8 Galois Theory of Level Structures

In this section, we assume that

is the universal deformation of

. We write

Level(

)

Level(

)

= eld of fractions of

Theorem 34

Let

and

be nite Abelian

-groups of rank at most

, and

;

a monomorphism. Then:

(i)

Hom

(

) = Hom

(

) = Mon(

(ii) The map

: Level(

)

;

Level

(

) (which sends

) is nite

and at.

(iii) If

(

) then

is a Galois covering.

(iv) The torsion subgroup of

;(Level(

)

) is

The proof will follow after a number of lemmas.

Lemma 35

Hom

(

) = Hom

(

) = Mon(

;(

))

Proof.

By applying Lemma 2 to a sequence of maps

Level(

)

;

Level(

)

;

we see that every

-algebra map

;

is a monomorphism, and thus

induces a map

;

of the elds of fractions. Conversely, consider a

-algebra map

;

. The image of

is integral over

, hence over

. As

is a unique factorisation domain (by Theorem 23), it is integrally

closed in its eld of fractions. Thus, the image of

is contained in

It follows that Hom

(

) = Hom

(

). On the other hand, the

de ning property of

implies that

Hom

(

) =

level-

structures on

over

By Proposition 26, this is just Mon(

;(

)).

Lemma 36

Aut((

)) acts transitively on Mon(

(

)).

Proof.

Without loss of generality, we may assume that there is a monomor-

phism

;

(

), and thus think of

as a subgroup of (

). Suppose that

;

(

) is a mononomorphism other than the inclusion. Our task is

then to nd an automorphism

of (

) extending

. By elementary linear

algebra over

, the map

(1)

;

(1) extends to an automorphism of

(1). This patches with

to give a map

+ (1)

;

(

)

. As is

a divisible group, it is injective, so

extends to a map

: (

)

;

. The

image must be killed by

, so we actually have

: (

)

;

(

). This is iso

on (1), so the kernel of

contains no points of order

, so

itself is mono.

By counting,

must be iso. Thus

Aut((

)) and

as required.

Lemma 37

Let

be a subgroup of

(

), and set

; =

Aut((

)) such that

= 1

Then the group of xed points of

; is just

Proof.

Suppose that

. We need to construct

; with

(

)

Suppose that

generates a cyclic subgroup

of order

, and that

is generated by

and so has order

;

< p

. We can then construct an

automorphism

by de ning

(

) =

+ (1 +

;

)

when

and

(it is not hard to check that this is well-de ned). This

in turn extends to an automorphism of (

) by Lemma 36. It sends

(1 +

;

)

Note that

is generated over

by roots of the Weierstrass polynomial

which splits completely over

. Thus

is the splitting eld of

, and so

is Galois over

. We can also see that (

) is the full group of points of order

in ;(

), as

can only have deg(

) =

(

)

roots. It follows

using Lemma 35 that Gal(

) = Aut

(

) = Aut((

)). Moreover, if

= 0 then

is generated by a subset of the roots of

, so that

contains a normal closure of

. The degree of the extension

;

is just

the number of embeddings of

in the normal closure, so

] =

Hom

(

)

Mon(

(

))

Lemma 38

Hom

(

) = Mon(

)

Proof.

The extension

is Galois as

is. Moreover, the subgroup

of Gal(

) xing

is just the group ;

Aut((

)) of Lemma 37. By

the fundamental theorem of Galois theory, the xed eld of ; is just

. Thus

Hom

(

) = Hom

(

)

;

= Mon(

(

))

;

= Mon(

)

the last equality coming from Lemma 37.

Corollary 39

The torsion subgroup of

;(

) is

Proof.

This follows easily by comparing Lemma 38 with Lemma 35

Proof of Theorem 34

Part (1) follows immediately from lemmas 35 and 38.

It follows that all the maps

: Level(

)

;

Level(

) are dominant. Both

the source and target are smooth by Theorem 23, so

is at by Lemma 1.

This gives (2). Now suppose that

(

), so without loss of generality

= (

). We have seen above that

is Galois, so Lemma 6 tells

us that

is a Galois covering. This gives (3). Finally, (4) is Corollary 39.

We can use the above theory to understand the structure of

more ex-

plicitly. For simplicity, assume that

, with

(the ex-

tension to groups of larger rank is evident). It is clear that

(

) is divisible

;

(

), say

(

) =

;

(

)

(

) for some Weierstrass polynomial

degree

;

n(k

;

. Let

be the subring of

generated over

by the

root

(

)) of

(

). Over

, the series

(

) has

;

roots,

(

;

)

< j < p

= 0 (mod

)

. After dividing out the cor-

responding linear factors, we obtain a Weierstrass polynomial

(

) of degree

;

n(l

;

. The ring

is generated over

by a root

(

))

of this polynomial. It is not hard to see that the product of the degrees of

and

is the same as the rank

Mon(

)

over

. It follows that

]]

(

)

(

)).

9 Quotients by Level Structures

Let

be a formal group of height

over

= spec(

). For every

, the

divisor

0] is a subgroup of

. We write

for the quotient group

0], and

;

for the universal deformation of

;

Note that

(1) = ker(

;

) =

It follows that

induces an isomorphism

;

. We use this

to identify

with

and

with

Proposition 40

Let

;

be an epimorphism of nite Abelian

-groups,

with

ker(

)

say. Then

induces a map

: Level(

)

;

Level

(

)

Proof.

Let

be the universal level-

structure on

, which is de ned

over the scheme

= Level(

). Write

ker(

)]. This is a subgroup

divisor on

, whose restriction to the special bre of

0]. It

follows that

is a deformation of

. The composite

ker(

)

;

;(

)

;

;(

)

is clearly zero. This gives a map

;

;(

)

I claim that this is a level structure. As

is an integral domain of character-

istic zero, it is enough to show that

is injective (Proposition 26). Suppose

ker(

), and let

be a coordinate on

. In view of Corollary 33,

we need only check that that the following product does not vanish:

(

) =

ker(

(

;

) =

ker(

(

;

))

Because

is a level structure,

;

= 0, and

is an integral domain, we

conclude that

(

;

))

= 0. It follows that

(

))

= 0 as required.

The level structure

is classi ed by a map Level(

)

;

Level(

), which we take to be

In particular, if

then the maps 0

;

0 induce maps

: Level(

)

;

Level(0

) =

: Level(

)

;

Level(0

) =

The rst of these is just the usual projection.

Theorem 41

(1)

is a covariant functor of

(2)

is a nite at map.

(3) The maps

;

(

)

;

0 give the same map

= 0

: Level(

)

;

(4) Consider a commutative square as follows.

This is a pullback if and only if it is a pushout. If so, then

: Level(

)

;

Level

(

)

(where

ker(

)

ker(

)

(5) If

is iso then

= (

)

;

= (

;

)

(6) If

(

) then

is a Galois covering, with Galois group

; =

Aut(

)

(7) The maps

: Level(

)

;

and

: Level(

)

;

have the same degree.

Proof.

We can take

= 0 without loss of generality, and assume that

the universal deformation of

(1) This is clear.

(2) This will be proved after (3).

(3) The map 0

: Level(

)

;

is just the originally given projection, so

the group over Level(

) with which we implicitly start is just (0

)

We have a universal level structure

: (

)

;

)

. By Theorem 24,

we have

(

)] =

(

). By the de nition of the map 0

, we have an

isomorphism

)

(

) = (0

)

(

)]

;

whose restriction to the special bre is just the identity map of

0].

After using our standard identi cation of

with

, we get an iso-

morphism

)

(

)

;

whose restriction to the special bre is the map

;

Because

is the universal deformation of

, the map 0

is uniquely

characterised by the existence of such an isomorphism. On the other

hand, we have an isomorphism

: (0

)

(

)

;

)

which has the same eect on the special bre. It follows that 0

= 0

(2) Choose an epimorphism

: (

)

;

(for some large

). We thus have a

chain of epimorphisms

(

)

;

This gives maps as follows, where the

's refer to various integers:

Level(

)

;

Level(

)

;

Level(

)

;

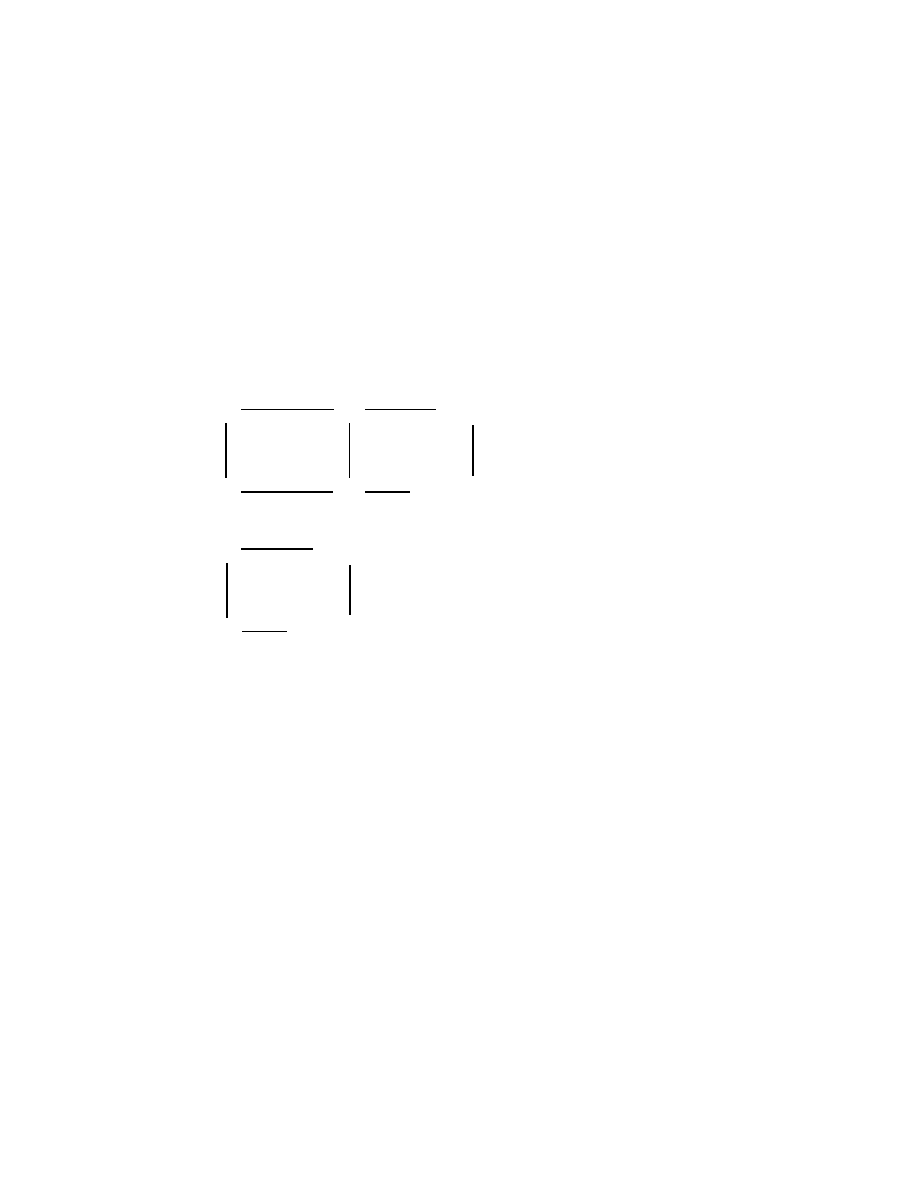
By (3), we know that the full composite 0

is nite and dominant. All

the schemes involved are smooth (and thus integral) and have dimension

. Applying Lemma 2 twice, we see that

is nite and dominant. It is

therefore at, by Lemma 1.

(4) Consider the following sequence

(

)

;

(

;

The left hand map is mono (because

is), the right hand map is epi

(because

is) and the composite is zero (because the diagram commutes).

It is easy to see from this that the sequence is exact if and only if the

square is a pushout, if and only if the square is a pullback. If so, we write

= ker(

) and observe that

ker(

). Write

= Level(

), so

we have a level structure

;

;(

). We de ne maps

and

requiring that the following diagrams commute:

;(

)

;(

])

;(

)

;(

])

The two maps

and

from

to Level(

) classify the two level

structures

and

]. On the other hand, it is clear from

the above diagrams that these level structures are the same.

(5) Apply (4) with

;

and

= 1.

(6) By (3) and Theorem 34, we know that the composite Level(

)

;

Level(

)

;

is a Galois covering. Using Lemma 6 to reduce

to the case of eld extensions, we see that

is Galois. Referring again

to Theorem 34, we see that the Galois group is

; =

Aut(

)

Using (5) and the fact that level structures over integral domains in char-

acterstic zero are injective, we conclude that

; =

Aut(

)

(7) Choose an epimorphism

= (

)

;

, and let ; be as above. By

the Pontrjagin dual of Lemma 36, we see that

deg(0

) =

Aut(

)

;

Mon(

(

)

Epi((

)

(where

= Hom(

) etc.). As there are (unnatural) isomorphisms

and (

)

(

)

, we see that

deg(0

) =

Mon(

(

))

Mon(

)

By Theorem 34, this is the same as the degree of deg(0

10 Classication of Subgroups

We now x

0 and study the classi cation of subgroups of

of degree

Theorem 42

The functor from schemes over

to sets given by

subgroups of

of degree

is represented by a scheme Sub

(

) over

. Moreover, for any map

;

we have

Sub

(

) = Sub

(

)

The projection Sub

(

)

;

is a nite at map, of degree

Sub

()

= number of subgroups of of order

Formulae for

will be given later. The scheme Sub

(

) is Gorenstein.

The rest of this section will constitute the proof. The existence and behaviour

under pullback of Sub

(

) is given by 9, Corollary 1.3.7]. In Subsection 10.1,

we prove some combinatorial formulae. In 10.2, we apply these formulae in an

argument inspired by the theory of Gr obner bases to give an upper bound for

the degree of the map Sub

(

)

;

. In 10.3, we analyse what happens when

we invert

and thus make all nite subgroups !etale (cf. 9, Corollary 3.7.2]).

In 10.4, we assemble these results to prove the theorem, except for the fact

that Sub

(

) is Gorenstein, which is proved in 10.5.

10.1 Combinatorics

We write

= Hom(

) =

. Note that

(

) is also the number of

lattices

of index

. Any lattice

has the form

for some

matrix

(

) with det(

)

= 0, and two matrices give the same lattice

if and only if they are related by reversible column operations.

Notation

Given a sequence

(

k+1

:::

;

) we write

= 1 we allow the empty sequence, with

= 0.

Lemma 43

Every matrix in

(

) with det(

)

= 0 can be reduced

by reversible column operations to a unique matrix of the following form (we

show the case

= 4, but the generalisation is evident). Equivalently, any

lattice

has a unique basis given by the columns of such a matrix.

0 0 0

0 0

< p

The index of such a lattice is

Proof.

We nd an element of minimal valuation in the top row and move the

corresponding column to the left hand end. We then multiply this column by

a unit to get

at the top left, and then perform column operations to clear

the rest of the top row. By induction, we can reduce the (

;

(

;

submatrix at the bottom right to the desired form. A few more evident column

operations put the entries in the rst column into the stated range. It is now

not hard to see that

is the minimal valuation of

among vectors of the

form (0

:::

::: b

;

) in the lattice

. Moreover, the (

+1)'th

column above is the unique such vector with

and 0

< p

for

l > k

. This gives uniqueness. It is not hard to see that the vectors

with

< p

form a transversal for

, so that

Corollary 44

runs over sequences

(

:::

;

) with

then

(

) =

It follows that

(

) =

(

)

;

k=0

;

Proof.

The rst statement follows by counting the possible matrices in the

lemma in the obvious way. Next, write

;

)

;

The second claim follows by expanding out the product.

We can also give a somewhat more explicit formula for

(

). First, we recall

the de nition of the Gaussian binomial coecients:

;

m=0

;

m=1

;

l+m

;

This can also be interpreted as the number of

-dimensional subspaces of a

-dimensional vector space over

Lemma 45

The Gaussian binomial coecients satisfy

;

and

;

Proof.

Suppose dim

. There is an obvious bijection

ann(

)

between

-dimensional subspaces of

and (

;

)-dimensional subspaces of

, which gives the rst statement. Now write

with dim

= 1.

Let

have dimension

. If

contains

then it has the form

for a unique (

;

1)-dimensional subspace of

there are

;

such

's.

does not contain

then it is the graph of a unique linear map

;

for a unique

-dimensional subspace

this occurs

;

times.

The second claim follows.

Lemma 46

(

) =

;

Proof.

We know that

(

) =

(

)

;

k=0

;

We want to show that this is the same as

(

) =

;

It is enough to show that

(

) =

(

) (which is immediate) and that

;

)

(

) =

;

(

)

This follows easily from the equation

;

which follows in turn from Lemma 45.

We shall need another auxiliary numerical function. Fix

and

. For 0

and 0

we de ne

(

) =

where

= (

:::

;

) and

Of course, we have

1) =

(

). If

we again allow

to be the

empty sequence, with

= 0. Thus

(

) = 1 provided that

Lemma 47

(

) is the unique function with the properties

(

) = 1

(

) = 0

k > m

(

) =

(

+ 1) +

(

+ 1

) if

l < n:

Proof.

It is clear that

(

) has the rst two properties. For the third, recall

that

(

) =

= (

:::

;

) and

The sum of the terms with

= 0 is just

(

+ 1). If

0 then we can

write

;

1 and

for

j > l

. Then

= 1+

and

The sum of the terms with

0 is thus

= (

:::

;

) and

+ 1 +

This is just

(

+ 1

). It is easy to see that these properties characterise

uniquely.

10.2 Innitesimal Theory

In this section, we study the scheme Sub

(

) (which is the same as

Sub

(

)). We rst give a lemma which is slightly more general than what we

need in this section, but the extra generality will be useful later.

Lemma 48

Let

be a nite-dimensional

-algebra, and suppose that ele-

ments

::: b

satisfy

= 0 with

0 for all

. Then

dim

B=b

Proof.

Write

i>0

(so that

= 0). For 0

j < n

, the space

=Bb

j+1

is a cyclic module over

B=b

. Moreover,

is a cyclic module

for

B=b

. It follows that

dim

B=b

+ dim

B=b

By induction on

, we nd that

dim

B=b

i>0

dim

(

) =

i>0

dim

B=b

The claim follows.

Proposition 49

deg Sub

(

)

;

]

(

Proof.

Write

= Sub

(

) and

and

. Note that

has strict height

. We have a universal subgroup

K <

of degree

and a

quotient map

;

. Note that

has height

and

has height

. Let

(

) be the closed subscheme of

on which

has strict height at

least

and

has strict height at least

, and write

(

) =

Y (kl)

(

) = dim

(

)

Because

= 0 in

we have

1). Clearly also

(

) =

and

(

) = 0 if

k > m

Next, recall that

= Sub

(

) is a closed subscheme of Div

(

). To see

what this means more explicitly, choose coordinates

and

By the Weierstrass preparation theorem, we can write

(

)

(

) with

monic polynomial of degree

congruent to

modulo

, and

invertible.

It follows that

is just the monic polynomial

classifying the divisor

, and

thus that the coecients of

(excluding the top one) generate the maximal

ideal of

. Over

(

) we have

= 0 (mod

) from which we see that

(

) =

. It follows that the maximal ideal of

(

) is zero, so that

(

)

Next, I claim that

(

)

(

+1)+

(

) when

l < n

. To see this,

we work temporarily over

(

). There are elements

uva

(

) with

invertible such that

Note that

(

)

(

+ 1

) and

(

)

(

+ 1). The relation

gives

Because we assume that

l < n

, we nd that

= 0. The claim now follows

from Lemma 48.
We next consider the analogous situation with

and

k < m

, so that

lies

in the maximal ideal of

. By the same argument, we nd that

so that

;

) = 0

The term in parentheses is a unit, so

= 0. This shows that

(

) =

(

+ 1

). By induction, we see that

(

) =

(

), so that

(

) =

(

)

From the above and Lemma 47 we see that

(

)

(

). In particular,

dim(

) =

1) =

(

) as claimed.

10.3 Rational Theory

In this section, we shall assume that

is an integral domain in which

= 0,

that

is a subgroup of

of degree

, and that we are given a level-

structure

: (

)

;

. For

(

) we write

(

))

For any subgroup

of order

of (equivalently, of (

)), we have a

subgroup-scheme

] of

, with degree

. This corresponds to a section

;

Sub

(

). Putting these together, we get a map

Sub

()

;

Sub

(

)

or equivalently

Sub

(

)

;

(Sub

()

)

(The target ring

(Sub

()

) is the ring of functions from the nite set

Sub

() to the ring

, with pointwise operations.)

Proposition 50

The resulting map

Sub

(

)

]

;

(Sub

()

])

is surjective with nilpotent kernel.
The proof will be given after some intermediate results. We write

if and

only if

is a unit multiple of

Firstly, recall from Theorem 24 that

(

)] =

(

), and hence that

(

)

(

;

)

On the other hand, for any formal group we have (

)

(mod

). It

follows that

Consider the discriminant

" =

(

;

)

Write

(

)

. It follows easily from the above and Lemma 15 that

;

In particular, " becomes invertible when we invert

Now write

Sub

(

)

, and

= ker(

)

. Note that

Lemma 51

then

is nilpotent mod

Proof.

We may suppose that there exists

. Modulo

we have

(

) =

(

;

), and modulo

we have

(

) = 0. Thus, using

Lemma 15 we get

0 =

(

) =

(

;

)

;

(mod

)

Each term in the product

(

;

) divides " and thus divides a power

. Thus

is nilpotent mod

as claimed.

Lemma 52

is a prime ideal in

and

then

for some

Proof.

We know that

(

), so

(

) divides

(

) =

(

;

). Now work over the integral domain

. We know that the discriminant

(

is nonzero, so the roots are distinct. We must therefore have

(

) =

(

;

) for some uniquely determined subset

(

). As

is a

subgroup scheme of

, it must be invariant under translation by any of its

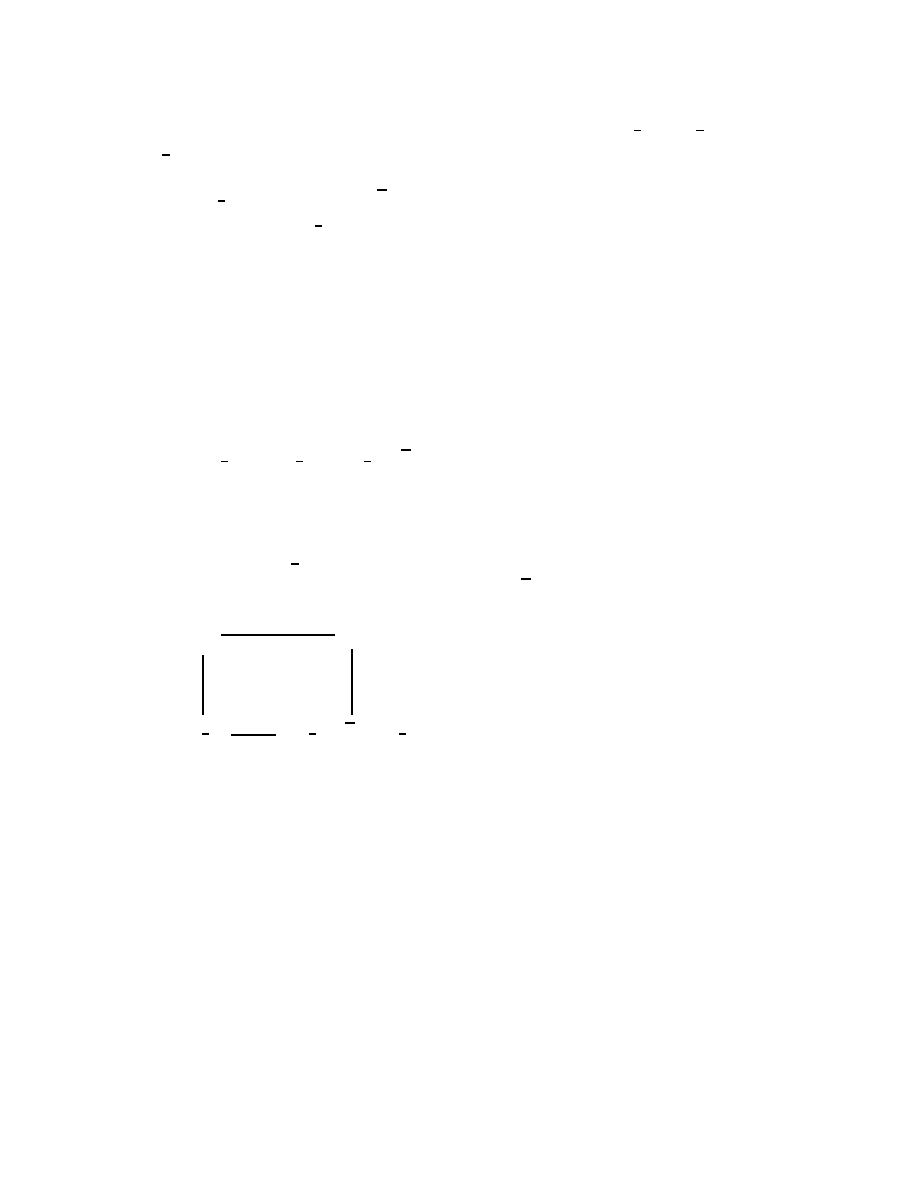
points. From this, it follows easily that

is a subgroup of (

), and that

Proof of Proposition 50

The last two lemmas show that

] +

] =

] and

] =

spec

1p]

The proposition follows by the Chinese remainder theorem.

Corollary 53

The map Sub

(

)

;

is at, with degree

(

Proof.

Write

and

(

). By Proposition 49 we know that

there is an

-linear epimorphism

;

. It follows that the induced map

]

;

]

;

]

is epi. By Proposition 50, this is an epimorphism between two free modules of

the same rank, so it is iso. By assumption

is an integral domain in which

= 0, so

;

]

is mono. By considering the following square, we see

that

is mono and thus iso (and thus that 0 =

]

10.4 General Theory

We can now prove Theorem 42, except for the Gorenstein property, which is

treated in the next subsection. Let

be a formal group of height

over an

arbitrary connected base

. Let

be the universal deformation of

and let

be the pullback of

to Level(

). We can apply Corollary 53

to conclude that the projection

Sub

(

) = Level(

)

Sub

(

)

;

Level(

)

is at, with degree

(

). As Level(

)

;

is faithfully at, it is not

hard to conclde that Sub

(

)

;

is also at, with degree

(

). As

Sub

(

) =

Sub

(

), we see that Sub

(

)

;

is again at, with

the required degree.

10.5 The Gorenstein property

We next show that the scheme Sub

(

) is Gorenstein (I do not know whether

it is a complete intersection). We rst recall the de nition and basic facts about

Gorenstein rings.

Denition 54

A Noetherian local ring

Gorenstein if the

-module

admits a nite resolution by injective

-modules.

Proposition 55

(a) Let

be a Noetherian local ring, and

(

::: x

) a regular sequence in

generating an ideal

. Then

is Gorenstein if and only if

R=I

Gorenstein.

(b) A regular Noetherian local ring is Gorenstein.

is Gorenstein if and only if the socle

soc(

) =

= 0

has dimension one over

Proof.

Part (a) is 2, Proposition 3.1.19(b)]. As a eld is visibly Gorenstein,

part (b) follows. Part (c) is essentially 2, Theorem 3.2.10].

Recall the notation used in the proof of Proposition 49. We write

for the

scheme Sub

(

) and put

. We have a universal subgroup

K <

of degree

and a quotient map

;

. We choose coordinates

and

. There is thus an element

such that

(mod

). We can also consider the equation

(

) of the divisor

, which is

a unit multiple of

]]. Thus

(

) =

(mod

) for some element

, which is a unit multiple of

Proposition 56

The ring

Sub

(

)

is Gorenstein. The socle of the quotient

ring

Sub

(

)

is generated by the element

(

:::

;

) (where

means

). It is also generated by

(

:::

;

Proof.

First, recall that

Sub

(

)

Sub

(

)

, which is obtained from

Sub

(

)

by killing the sequence (

::: u

;

). This sequence is regular (be-

cause Sub

(

)

;

is at). Thus, by part (a) of Proposition 55, it is enough

to show that

Sub

(

)

is Gorenstein. Moreover, by part (c) of Proposition 55,

it is enough to show that the socle is generated by

(

:::

;

To do this, we reuse the notation and ideas of the proof of Proposition 49. It

was shown there that

(

)

(

+ 1) +

(

+ 1

)

(

l < n

)

There is a similar relation for the numbers

(

), with the inequality replaced

by an equality. Moreover, we have

(

)

1 =

(

)

(

)

(

) = 0 =

(

)

(

k > m

)

Finally, Theorem 42 implies that

1) =

(

) =

1). It follows eas-

ily that

(

) =

(

) when

and

, and thus that

(

) =

(

+ 1) +

(

+ 1

) when

l < n

. In particular, we have

) =

+1)+

). Recall that the corresponding inequality was derived from

the relation

= 0, with

)

) and

)

+ 1).

Because we are considering the case

= 0, the element

here is the same as

that in the statement of the proposition. Using Lemma 57 below, we nd that

multiplication by

gives an isomorphism soc(

+ 1))

soc(

)).

It follows that multiplication by

(

:::

;

) gives an isomor-

phism soc(

))

soc(

1)). As

) =

) = 1, we see that

) =

and thus that soc(

)) =

. Moreover,

1) =

Sub

(

)

It follows that soc(

Sub

(

)

) is generated by

, as claimed. The last statement

of the proposition is trivial.

We still owe the reader the following lemma.

Lemma 57

Let

be a nite-dimensional local algebra over a eld

, with

maximal ideal

. Suppose that

satisfy

= 0 (for some

) and

dim(

) = dim(

R=v

) +

dim(

R=a

). Then multiplication by

is a monomor-

phism

R=v

;

, whose image is the annihilator of

. Moreover, this map

induces an isomorphism

soc(

R=v

)

soc(

Proof.

As in the proof of Lemma 48, we lter

by the ideals

(where 0

). The quotients are cyclic modules over

R=a

, and the last ideal

is a

cyclic module over

R=v

, so that dim(

=Ra

i+1

)

dim(

R=a

) and dim(

)

dim(

R=v

). On adding up these inequalities, we obtain the inequality dim(

)

dim(

R=v

dim(

R=a

), which is by assumption an equality. It follows that all

our inequalities are actually equalities, and thus that all our cyclic modules

are actually free of rank one. This means that multiplication by

gives a

monomorphism

R=v

;

Let

be the annihilator of

, so that the image of the above map is clearly

contained in

. On the other hand, we have short exact sequences

;

R=v

which imply that dim(

) = dim(

R=v

). It follows that our monomorphism

R=v

;

is actually an isomorphism.

It is immediate that

soc(

R=v

)

soc(

). Conversely, suppose that

soc(

). As

, we have

= 0, so that

. It follows that

for some

R=v

. Suppose that

. Then

(

) =

= 0 because

soc(

). As multiplication by

is a monomorphism, we see that

0 in

R=v

. Thus

soc(

R=v

). This means that

gives an isomorphism

soc(

R=v

)

soc(

), as claimed.

11 Flags

Consider a sequence

= (

= 0

< ::: <

). A ag of type

will mean a sequence of subgroup divisors 0 =

< K

< ::: < K

(1)

such that

has degree

. Using Proposition 16 and Theorem 42, we see

that the functor from schemes over

to sets given by

ags of type

is represented by a scheme Flag(

) over

. This is in fact a closed sub-

scheme of

Sub

(

) and thus is nite over

Similarly, we let Flag(

) be the set of sequences 0 =

< A

< ::: < A

(1) such that

. Let

::: a

;

be the standard basis of (1) =

(

)

. Write

i <

, so that = (

:::

)

Flag(

Write ; = Aut((1)) and let ;(

) be the subgroup which preserves . Clearly

Flag(

)

;

;(

: (1)

;

;(

) is a level structure then by putting

] we

obtain a ag of type

. This construction gives rise to a map Level(1

)

;

Flag(

Theorem 58

The maps

Level

)

;

Flag

(

)

;

are at of degree

;(

)

and

Flag

(

)

respectively. If

is the universal

deformation of

then Flag

(

) is a smooth scheme and Level(1

)

;

Flag

(

) is Galois.

We will prove this theorem at the end of this section.
First, observe that whenever we have a ag of type

we have isogenies

;

:::

;

At the last stage, we have identi ed

(1) with

via the isomor-

phism

(1)

. With this convention, we have

;

Moreover,

has height

;

11.1 Combinatorics

Consider a sequence

= (0 =

:::

). Choose linearly

independent subspaces

(1) of dimension

;

and put

kj=1

and

mj=k+1

Denition 59

(

) is the number of ags of type

such that

for

. This is clearly independent of the choices made. Note that

:::

0) =

Flag

(

)

, that

(

) = 0 unless

k+1

;

k+1

;

for

k < m

, and that

(

) = 1 if

for

k < m

Denition 60

< n

and

< k

write

= (

:::

;

+ 1

:::

+ 1)

Lemma 61

< n

then

(

) =

k=1

;

(

)

Proof.

Choose

(1) with dim

= 1 and

= 0. Let

be a ag

of type

such that

for all

. There is an exact sequence

;

(

)

;

Note that

is epi. Let

be the least value of

for which

is epi (or

equivalently, nonzero). For

j < k

we have

(

) =

. For

there is a unique map

;

such that

(

) =

(

) =

graph(

)

Moreover,

j+1

is just the composite

;

j+1

;

j+1

It follows that all the

are determined by

Hom(

). Moreover, any

homomorphism

;

can arise in this way. It follows that the number of

's with a given value of

Hom(

)

(

) =

;

(

). The claim

follows.

11.2 Innitesimal Theory

We next study the scheme

Flag(

). Consider a sequence

above. Write

(

) for the closed subscheme of

on which

has strict height

at least

;

for all

. Put

(

) =

Y ()

and

(

) = dim

(

). Note

that

:::

0) = dim

. Recall that we have isogenies

;

with

;

Proposition 62

deg Flag(

)

;

] = dim

Flag

(

)

Proof.

Note that

:::

0) = dim

= deg Flag(

)

;

]

and that

:::

0) =

Flag(

)

so it is enough to prove that

(

)

(

) for all

. It is clear that

(

) = 0

unless

k+1

;

k+1

;

for 0

k < m

. Next, suppose that

for

k < m

. It follows that over

(

) we have

0] for 0

k < m

. By

construction, the ring

is generated over

by the parameters of the divisors

, so this implies that

;

(

) is epi and

(

)

1. We now need only

prove that when

< n

we have

(

)

k=1

(

)

To see this, we work temporarily over

(

). We shall write

for

where typographically convenient. Choose coordinates

on the formal groups

. There are elements

(

) such that

(

;

(

;

)) + higher terms

Note that

(

)

(

). We also have

:::q

= (

)

k=1

(

;

) + higher terms

On the other hand,

:::q

, and this is divisible by

(because

lies over

). By assumption

< n

, so we have

k=1

(

;

) = 0

It follows by Lemma 48 that

dim

(

)

;

dim

(

)

;

dim

(

)

In other words,

(

)

k=1

(

)

as required.

11.3 Galois Theory

In this subsection we assume that

is the universal deformation of

. As

mentioned earlier, there is a map Level(1

)

;

Flag(

), classifying the

]

< ::: <

] this clearly factors through Level(1

)

;(

Given a subset

(1), we have a divisor

] =

(

)] on

over

Level(1

). Suppose we have maps Level(1

)

;

such that

epi and

is the usual map. We shall say that

is de ned over

(or over

) if and only if there is a (unique) divisor

such that

] =

or equivalently if and only if the polynomial

(

;

) lies in the subring

]

Level(1

)

For example, if

is invariant under the action of ;(

) then

is de ned over

the quotient scheme Level(1

)

;(

). The following facts are evident:

(i) If

and

are de ned over

then so is

(ii) If

and

are de ned over

then so is

(iii) If the point

and the divisor

are de ned over

then so is the translate

Lemma 63

Suppose we have epimorphisms Level

)

;

Suppose that

, that

is dened over

, and that

is generated

over

. Then

deg(

)

Proof.

Consider the polynomial

(

) =

(

;

)

], which is monic

and has degree

. Clearly

(

) = 0 so

is a quotient of

]

(

) and

thus needs at most

generators over

Remark 64

Geometrically, this means that

embeds as a closed subscheme

of the divisor

] over

Proposition 65

deg Level(1

)

;

Flag

(

)]

;(

)

Proof.

We again write

::: a

;

for the standard basis of (1), so that

i <

. Put

;

;(

)

(

) =

for

i < k

Clearly

;(

)

;

k=0

;

k+1

k=1

;

Suppose that

k <

j+1

. A little linear algebra shows that

;

j+1

i < k

Write

= spf(

) = image(Level(1

)

;(

)

;

Flag(

)

(

))

Level(1

)

j < k

]

= spf(

)

We thus have maps

Level(1

) =

;

:::

;

Flag(

)

the last of which is a closed embedding.
The map Level(1

)

;

Flag(

) is de ned so that the pullback of the

divisor

is precisely

]. It follows that

is de ned over

for all

The point

over

is actually de ned over

k+1

. Using our description

of ;

above, we see that ;

is de ned over

. Applying Lemma 63, we

see that deg

k+1

;

]

;

k+1

. It follows that

deg Level(1

)

;

Flag(

)]

;

k+1

;(

)

Proof of Theorem 58

We may assume that

is the universal deformation

. Write

;(

)

and

Flag(

)

, and note that

;

. Consider

the maps

Level(1

)

;

Level(1

)

;(

)

;

Flag(

)

;

By propositions 62 and 65 we know that deg(

)

and deg(

)

by Theorem 23 we know that

gfh

is at of degree

and it is clear that

deg(

gfh

)

deg(

)deg(

). It follows that deg(

) =

and deg(

) =

Lemma 7 now tells us that Flag(

) is smooth,

is Galois and

is iso.

Finally, lemmas 2 and 1 tell us that

is at.

12 Typed Subgroups

Let

be a nite Abelian

-group of order

and rank at most

. We write

Type(

subgroups of isomorphic to

Mon(

)

Aut(

)

Sub

()

In this section, we investigate what it would mean to replace with

. We

shall de ne a scheme Type(

) of \ nite subgroups of

of type

Remark 66

This description is somewhat misleading, because it suggests that

Type

(

) should be a subscheme of Sub

(

). There is a natural map

Type

(

)

;

Sub

(

)

but it is not usually an embedding. The smallest case where it fails to be an

embedding is

= 3,

2 | I have proved this by elaborate calcula-

tion. See also Theorem 70 below, and the example at the end of Section 16. It

would be interesting to have a compelling moduli interpretation of Type

(

but I cannot at present oer one.

Denition 67

is the universal deformation of

, then we take

Type

(

) = Level(

)

Aut(

)

In the general case, we let

be the universal deformation of

and

take

Type

(

) = Type(

)

Over the course of this section, we shall prove the following theorem.

Theorem 68

The maps

Level

(

)

;

Type

(

)

;

are at, of degree

Aut(

)

and

Type

(

)

respectively. If

is the universal

deformation of

then Type

(

) is smooth.

We next consider the scheme

(

Type(

), where the coproduct runs over

the isomorphism classes of Abelian groups

of order

and rank at most

Theorem 69

Let

be the evident map

(

Type

(

)

;

Sub

(

)

Suppose that

is the universal deformation of

. Then the induced map

of rings is injective, and becomes iso after inverting

Theorem 70

Suppose that

has the form

m+l

(

)

;

. Then

Type

(

)

;

Sub

m+nl

(

)

is a closed embedding. In particular, when

= 2 (the case arising from a

deformation of a supersingular elliptic curve), this holds for all

We now start work on the proofs.
Let

be a nite Abelian

-group. De ne

(

)

;

(

)

(

)

(

)

(

)

Note that

and

are additive functors, and that if

is a cyclic

group then

(

) =

A=p

otherwise

Now choose an isomorphism

Write

(with 0

l < m

) for the generators of the cyclic summands. We

shall order the pairs (

) as follows:

(

)

(

) i

i > k

or (

and

j < l

)

Note that the ordering on the rst index is reversed, so that the generators

of the largest cyclic summands come rst in the ordering.

For 0

l < m

we de ne

(

) =

::: a

;

(

)

(

)

(

) =

(

)

(

)

(

)

and

(

) =

(

)

(

)

(

0) =

(

)

We also write

; = Aut(

)

and

;(

) =

;

(

) =

if (

)

(

)

;(

) = ;(

;

and

;(

)

;(

+ 1)

;(

)

Lemma 71

;(

)

(

) and

;

(

)

Proof.

As ;(

)

;(

+ 1)

;(

)

, the second statement will follow

easily from the rst.
Any

; preserves

(

) and induces an automorphism of

(

). If

;(

) then it is easy to see that

(

)

(

), lest the induced endomor-

phism of

(

) fail to be iso. Conversely, suppose

(

). Write

= (

)

(

)

Let

and

be the components of

and

. By linear algebra over

we can nd an automorphism

(

) =

with

(

) =

for

j < l

and

(

) =

(mod

). We can then lift this to get an automorphism

with

(

) =

for

j < l

and

(

) =

. Finally, we de ne an

endomorphism

, with components as follows:

;

other generators

;

identity

It is easy to check that this is iso, and

(

) =

. Thus

;(

)

(

)

Remark 72

It is neither hard nor apparently helpful to write explicit formulae

for

(

)

and

;

We assume until further notice that

is the universal deformation of

. As

in Subsection 11.3, we shall say that a subset

is de ned over a quotient

scheme

of Level(

) if there is a divisor

over

whose pullback

Proof of Theorem 68

We now write

Level(

)

and

Type(

)

. De ne

(

))

(

) =

(

)

(

)]

(

) = spf(

(

))

Note that

(

) =

(

;

0) and that we have maps

Level(

)

;

(

+ 1)

;

(

)

;

Type(

)

Because

(

) and

::: a

;

are de ned over

(

), we see that

(

)

is de ned over

(

). Moreover,

(

) and

(

+1) is generated over

(

) by

. It follows by Lemma 63 that

deg

(

+ 1)

;

(

)]

(

)

Combining this with Lemma 71, we see that

deg Level(

)

;

Type(

)]

;

It follows from Lemma 7 that Level(

)

;

Type(

) is Galois and that

Type(

) is smooth. Lemmas 2 and 1 now tell us that Type(

)

;

at. As deg Level(

)

;

] =

Mon(

)

, we see that

deg Type(

)

;

] =

Mon(

)

;

Type(

)

Proof of Theorem 69

Write

Sub

(

)

. In Subsection 10.3, we con-

structed a map

;

(Sub

()

)

We proved there that after inverting

becomes epi with nilpotent kernel.

In the light of Theorem 42, we conclude that

is mono, and becomes iso after

inverting

. We now put ; = Aut((

)), and note that

is equivariant for

the evident actions of ;. Passing to xed points, we obtain a map

;

: (

)

;

(Sub

()

)

;

which is again mono, and becomes iso after inverting

By Theorem 34, we know that

. Because

is free over

, we conclude

that (

)

;

. Next, for each isomorphism class of Abelian

-groups

of order

and rank at most

, choose a representative subgroup

(

Write

for the set of chosen representatives. For

write ;

;

(

) =

. We have an isomorphism of ;-sets

Sub

()

;

It is not hard to conclude that

(Sub

()

)

;

Lemma 36 implies that ;

;

Aut(

) is epi write ;

for the kernel. Using

Theorem 34 we nd that

;

= (

;

)

Aut(

Thus,

;

is a map

;

One can check that this is the same map as that described in the statement

of the theorem.

Denition 73

Let

be the universal subgroup over Sub

(

). We write

;

for the kernel of the composite

;

=K:

Thus

;

is a subgroup divisor of degree

m+nr

dened over Sub

(

), and

its equation

;

(

) is a unit multiple of

((

)

). The subgroup

;

classied by a map

;

: Sub

(

)

;

Sub

m+nr

(

)

Lemma 74

The map

;

: Sub

(

)

;

Sub

m+nr

(

) is a closed embedding,

and identies Sub

(

) with the scheme of subgroups of degree

which

contain

(

Proof.

Over Sub

m+nr

(

), we have an exact sequence of formal groups

(

)

;

We know by Proposition 16 that there is a closed subscheme

Sub

m+nr

(

)

which is universal for subgroups containing

(

). Let

be the universal

subgroup over

and

;

the projection. Then the composite

(

)

;

is zero so there is a map (of formal groups over

)

;

with

. The kernel

therefore has degree

, and is classi ed by a map

;

Sub

(

). Clearly

;

: Sub

(

)

;

Sub

m+nr

(

) factors through

, and the maps

;

Sub

(

)

;

are

mutually inverse.

Proposition 75

Suppose that

is such that

(

)

(

) (so that

has

rank

and every cyclic factor has length at least

). Write

A=A

(

) and

. Then there is a canonical isomorphism Type

(

)

Type

(

and the following diagram commutes:

Type

(

)

Sub

m+nr

(

)

Type

(

)

Sub

(

)

;

Proof.

It is easy to see that multiplication by

induces a bijection between

Type(

) and Type(

). Thus

Epi(

)

Aut(

)

Type(

)

Type(

)

Epi(

)

Aut(

)

Let

;

be the projection. Any automorphism

induces an

automorphism

, with

. It follows easily that there is a map

making the following diagram commute:

Level(

)

Type(

)

Level(

)

Type(

)

By Theorem 41, we know that

is a nite at map of degree

Epi(

)

Epi(

)

On the other hand,

and

are nite at maps of degree

Aut(

)

and

Aut(

)

respectively. It follows (using lemmas 2 and 1) that

is a nite at

map of degree

Epi(

)

Epi(

)

Aut(

)

Aut(

)

= 1

In other words,

is iso as claimed. It is not hard to see that the diagram

commutes.

Proof of Theorem 70

We may as usual assume that

is the universal

deformation. First, suppose that

is cyclic, say

generated by

We need to prove that

is generated by the parameters of the divisor

As discussed at the end of Section 8, we can write (

)

(

)(

;

)

for a

series

(

)

]] of Weierstrass degree

;

n(m

;

. Thus,

(

) is a unit

multiple of a monic polynomial

(

) of degree

with

(

) =

(mod

Moreover,

]

(

), where

(

)). Write

and

, so that

is just

]

. We shall say that an element of

has valuation

if it is divisible by

but not by

t+1

. For

we have

(

)) =

(mod

), so this has valuation 1 if

= 0 (mod

) and

valuation greater than 1 otherwise. Now write

;

(which divides

)

and let

be the

'th symmetric polynomial in

j < p

. This is

the

'th parameter of the divisor

], so it lies in the image of

Sub

(

)

;

Let

be the image of

. If we write

in the usual way as a sum of

-fold products, then there is one term

= 0 (mod

)

of valuation

, and the other terms have higher valuation. Thus

itself has valuation

and the subring of

generated by

has dimension

s=r

as a vector space

over

. On the other hand, one can see that

s=r

Type(

)

Consider the maps

s=r

u::: u

s=r

;

and the resulting maps

s=r

:::

(

)

s=r

;

We have just seen that

is mono, so

is mono. By dimension count,

iso. It follows that

is epi, and thus that

Sub

(

)

;

is epi as claimed.

Now suppose that

r+m

(

)

;

. Then

A=A

(

) is cyclic.

Proposition 75 gives a commutative diagram as follows:

Type(

)

Sub

m+nr

(

)

Type(

)

Sub

(

)

;

We have just shown that the bottom map is a closed embedding. The map

;

is a closed embedding by Lemma 74. It follows that the top map is also a

closed embedding, as claimed.

13 Deformation of Isogenies

Consider two schemes

and

, each of which is spec of a eld of charac-

teristic

. Suppose we have a morphism of formal groups as follows:

We shall suppose that the induced map

;

is an isogeny of degree

. We would lose little generality by requiring

to be the identity, but in

algebraic topology we naturally encounter the case in which

is a power of

Frobenius. By a deformation of

we shall mean a morphism

;

formal groups over a scheme

, where

and

are deformations of

and

respectively, and the restriction of

over

is compatible with

. In more

detail, we de ne

and

to be the restrictions of

and

, and we

require a commutative diagram as follows:

]

The diagram contains three parallel vertical squares. The middle one is by

de nition the restriction of the left-hand one over the special bre

The back face of the right hand cube is required to be a pullback square,

making

into a deformation of

. Similarly for the front face of the right

hand cube. This forces

to be an isogeny of degree

Our next task is to classify such deformations. First, let

be the universal

deformation of

. Let

: Sub

(

)

;

be the usual projection, and let

K < a

be the universal example of a subgroup of degree

. As Sub

(

) is

a closed subscheme of Div

(

) and Div

(

)

, we see that Sub

(

)

. There is a unique subgroup of order

de ned over

, viz. the

divisor

0] = spf(

). In particular,

0] = ker(

). It follows

that there is a pullback diagram as shown below.

(

)

Sub

(

)

Using this, we can consider the projection

;

as a deformation

. It is not hard to check that it is the terminal object in the category of

deformations.
Now let

be the universal deformation of

. The above construction

also exhibits

as a deformation of

. It is therefore classi ed by a map

: Sub

(

)

;

extending the map

: Sub

(

)

;

Proposition 76

is a nite at map, of degree

Sub

()

Proof.

Recall from Theorem 69 that we have a dominant map

(

Type(

)

;

Sub

(

)

(where

runs over isomorphism types of nite Abelian

-groups of order

and rank at most

). Moreover,

becomes iso when we invert

. It is easy to

see that the composite

Level(

)

;

Type(

)

;

Sub

(

)

;

can be identi ed with the map 0

of Section 9. By part (7) of Theorem 41, this

map is at and has degree

Mon(

)

. Moreover, Level(

)

;

Type(

)

is a Galois covering with Galois group Aut(

). Using lemmas 2 and 1, we see

that Type(

)

;

is at. The degree is clearly

Mon(

)

Aut(

)

Type(

)

. It follows that

is a at map of degree

Type(

)

Sub

()

, and thus that

Sub

(

)

] is free of this rank over

We next let

Y <

Sub

(

) be the preimage of

under

, and write

and

. I claim that dim

Sub

()

. The proof is similar to

that in Subsection 10.2. To recall some notation from there: Given a sequence

(

k+1

:::

;

) we write

runs over sequences (

:::

;

) with

then

(

) =

Note, however, that

and

have dierent meanings here from those used

in Subsection 10.2. We write

for the restriction of

, and

for the

evident subgroup of

, so that

is a pullback of

and thus has strict

height

. Let

be the projection

;

. Choose coordinates

and

. Let

(

) be the largest closed subscheme of

over which

has strict height at least

and

has strict height at least

, and write

(

) =

Y (kl)

and

(

) = dim

(

). Working over

(

) we see

that there are elements

uva

(with

invertible) such that

Thus

(

+ 1

) =

(

)

and

(

+ 1) =

(

)

. Reading the

relation

to lowest order, we nd that

k < n

then we conclude that

= 0, and then Lemma 48 tells us that

(

)

(

+ 1) +

(

+ 1

). If

then

is invertible and we have

(

;

) = 0. If also

l < n

then

is topologically nilpotent so

;

is invertible so

= 0, which shows that

(

) =

(

+ 1) =

(

From the construction of Sub

(

) one can see that

;

(

) is epi, and

that

(

) = 0 if

k > n

l > m

. To summarise, we have

(

)

(

+ 1) +

(

+ 1

) if (

k < n

)

(

)

(

) = 0

if (

l > m

)

We next de ne a function

(

) for 0

and 0

(

) =

= (

:::

;

)

;

We make the usual convention that

(

) = 1 for

and

(

) = 0 for

l > m

. I claim that

(

)

(

+ 1) +

(

+ 1

) when

k < n:

To see this, consider the sum which de nes

(

). The sum of the terms with

;

> l

(

+ 1). If

;

, we de ne

= (

:::

;

)

Note that

, that

;

(

k+1)

, and that

. Using this

construction, we see that the sum of

for these

's is

(

+ 1

), as

required. It follows that

(

)

(

), and in particular that

dim

(

) =

0) =

(

) =

Sub

()

By an argument very similar to that of Subsection 10.4, we conclude that the

map

: Sub

(

)

;

is at and has degree

(

14 The Connection with Algebraic Topology

In this section, we make a few brief remarks about how formal groups and

moduli problems arise in algebraic topology. Good general references are 1]

and 14]. However, they are not written from an algebro-geometric point of

view, which was rst introduced by Morava 12,13]. This philosophy is de-

veloped in 15]. In the discussion below, we shall take a few liberties with

technical details.
Let

be a topological space. A geometric chain in

is a smooth manifold

(possibly with boundary)

equipped with a map

;

. Geometric chains

form a graded Abelian monoid GC

under disjoint union. Restriction to the

boundary gives a dierential

: GC

;

. The homology of this

complex is a graded Abelian group

. If we require that all manifolds

have a given complex structure on the stable normal bundle, we obtain a

dierent group

, the complex bordism group of

. We write

for

(point), which is a ring under cartesian product. By a related geometric

procedure, we can de ne a group

(which is often but not always the

-dual of

). In fact

has a natural ring structure. It can be

thought of as an analogue of the Chow ring, which some readers may nd

more familiar. The functor

has a number of formal properties

(Mayer-Vietoris sequences etc.), which can be summarised by saying that it is

a multiplicative generalised cohomology theory. It is the most powerful such

theory which one has any reasonable chance of computing for popular spaces

. See 4] for some justi cation of this claim.

Let

denote the colimit of the nite-dimensional complex projective

spaces

, or equivalently the classifying space of the circle group. This

is itself (homotopy equivalent to) a topological Abelian group. Moreover,

is isomorphic to

]]. The group structure on

gives rise

to a coproduct on

and hence a formal group law over

. Lazard

showed that there is a universal example of a ring

equipped with a formal

group law

, and that

is a polynomial algebra over

on countably many

generators. Quillen proved the fundamental theorem that the classifying map

;

is an isomorphism. This is the source of all connections between

algebraic topology and formal group theory. If we consider instead manifolds

with a splitting of the stable normal bundle as a sum of two complex bundles,

we obtain a ring (

)

. If we take

to be a point, this is the univer-

sal example of a ring with two formal group laws and an isomorphism between

them. Using these ideas, we can construct descent data making

into a

sheaf over the stack of formal groups. The cohomology of the dual sheaf

is the

term of the Adams-Novikov spectral sequence, which converges to

the stable homotopy groups of

A formal group

over a scheme

= spf(

) gives rise to a map from

this stack. By pulling back

, we obtain an algebra

over

, and thus

a scheme

= spf(

) over

. If the map from

to the stack of formal

groups is at, then the functor

de nes a generalised cohomology

theory. This atness condition is called Landweber exactness in the topological

literature. It holds in particular if

is the universal deformation of a formal

group of nite height over a eld. If

is a nite Abelian group and

is the

classifying space of its dual then (

)

= Hom(

). For nite non-Abelian

groups

, the generalised character theory of 8] establishes a connection

between

and schemes of the form Level(

). There is also a map from

a certain closed subscheme spf(

) of (

)

to Sub

(

), which turns out to

be an isomorphism. Theorem 42 is half of the proof of this fact, the other half

is topology. A topological calculation shows that the socle element is not in

the kernel of the map

Sub

(

)

;

as the source is a Gorenstein ring

of dimension zero, we conclude that the map is injective. Another elaborate

topological argument computes the dimension of

, showing that it

coincides with the dimension of

Sub

(

)

given by Theorem 42.

Using this fact, we obtain extra structure on

. Suppose that

are two

points of

, that

and

are the bres of

over

and

, and that

;

is an isogeny. A certain topological construction then gives rise

to a map (

)

;

(

)

, which is functorial in

and natural in

. This gives

powerful information about the schemes

. It can be reformulated as saying

that a certain kind of generalised Hecke algebra acts on

, and on certain

other topologically de ned rings. Certain

Ext

groups over this algebra form

the input to spectral sequences that compute homotopy groups of spaces of

maps of strictly commutative ring spectra, for example. A conjecture of Mike

Hopkins (inspired but not implied by the theory of the Bruhat-Tits building)

would mean that this Hecke algebra has nite global dimension this would be

very helpful for the applications. It should be possible to prove the conjecture

using the results and methods of this paper.

15 Explicit Formulae

Many of the above results were suggested by computer-assisted calculations

using explicit examples of formal group laws. In this section, we record some

useful formulae which will help the reader to carry out such experiments for

herself. We shall assume that

n >

1 and

p >

2 some small modi cations are

needed when in the exceptional cases, but they generally make things easier.

We write

for

(mod

We rst de ne

(

) =

(

) =

;

(

)

( so

(

)) =

)

Note that

(

)

]], and in fact

(

)

(mod

)

The composition inverse of this series is

(

)

, so

(

)

(mod

)

We de ne a formal group law

over

(

) =

(

)

(

))

It is shown in 7] (for example) that this is actually de ned over

(or even

but this is irrelevant for us). We write

(

) for the resulting formal group

over

. It is known that any formal group law of height

over a separably

closed eld of characteristic

is isomorphic to

(see 6, p. 72]).

For any

we write

](

) =

(

))

In other words, if

is the formal group de ned by

we have

](

) =

By applying

one checks that

](

) =

(

) +

We next de ne

(

) = (

;

(

)

=p:

Lemma 77

(

)

;

k=1

(

;

)

;

Proof.

This follows easily from Wilson's Theorem (that (

;

1)!

;

1), the

equation

(

;

)! =

;

l=k

(

;

)

(

;

(

;

1)!

(

;

1)!

and the binomial expansion of (

)

Lemma 78

(

)

(

q=p

)

Proof.

We have

q=p

= (

)

q=p

for some

. Raising this to the

'th power, we nd that (

q=p

)

= (

)

(mod

). We also have

= (

)

(

)

= (

q=p

)

(

q=p

)

Subtracting these, we obtain

(

) =

(

q=p

) (mod

)

The claim follows.

Note that

divides

(

), so that

q=p

divides

(

) mod

We write

(

) for the

-adic valuation of

Lemma 79

< l < q

then

;

(

)

Proof.

We can write

;

j=1

;

j :

The terms in the product are clearly

-adic units the claim follows.

Lemma 80

(

q=p

) (mod (

)

Proof.

It is enough to prove this mod

, for then by symmetry and unique

factorisation it will hold mod (

)

. For the rest of the proof, we put

= 0.

For some

]] we have

(

) =

yw:

Applying

, we obtain

(

) +

(

) =

(

) =

(

) +

;

j=1

(

)(

)

Because

= 0, we have

(

) =

. We conclude that

;

j=1

(

)(

)

Lemma 79 implies that the series

(

)

! for 0

< j < q

are all integral, and

moreover that

(

)

;

< j < q

)

(

)

1 + 1

;

This implies that

;

j=1

;

(

xyw

)

;

(

q=p

(

)

q=p

)

Now de ne

(

q=p

) +

Note that

q=p

divides

(

q=p

). As

2, we nd that

= 0 it

follows that

(

q=p

)

q=p

= 0, and thus that (

)

q=p

. Feeding

this back into our previous equation, we nd

(

q=p

) +

;

(

q=p

)

(

q=p

)

;

(

q=p

)

It follows easily that

q=p

divides

mod

. On the other hand, the de nition

implies that

divides

, and thus that

is nilpotent. As

is nilpotent

and

q=p

divides

, we see that

= 0. The claim follows.

Corollary 81

There is a power series

over

such that

(

) =

(

q=p

)

Proof.

Work in

xyz

]]

q=p

. Let

be an integer, and write

with

0. We then have

(

)

= (

)

;

It follows that (

)

q=p

divides

. Next, write

(

) =

k>0

(

)

The associativity law says that

(

)) =

(

)

By the previous lemma, we have

(

) =

for all

. It follows that

(

) =

(

) +

k>0

(

)(

)

k>0

(

)

We conclude that

(

) = 0 unless

q=p

divides

, so that

(

)

;

is a

function of

q=p

. By symmetry, it is also a function of

q=p

. The claim follows.

Next, we write

for the Witt ring of

. Recall that for each

there is a unique element ^

(the Teichm uller representative) such

that ^

= ^

and ^

. Any element

can be written uniquely as

, with

. There is a Frobenius automorphism

de ned

(

) =

For any

we have

) = ^

(

)

It follows easily that

) = ^

(

)

) = ^

(

)

If we write

(

) =

(

) =

then we can conclude that

= 0 unless

= 1 (mod

;

1), and similarly

for

(

) etc.

Now suppose that

is arbitrary. We de ne

](

) =

(

))

By expressing

in the form

, we can show that this lies in

]]. The

map

](

) gives a ring homomorphism

;

End(

We next put

::: u

;

]]

p u

= 1

We also let

denote the endomorphism of

which is the Frobenius on

and sends

for 0

< k < n

, so that

(mod

) for all

Over

] we have a formal power series log

(

) =

(

) characterised

uniquely by either of the two following equations:

log

(

) =

+ 1

k=1

log

(

)

log

(

) =

+ 1

k=1

log

(

)

From either of these equations, one can see that

(mod

::: u

;

The following more explicit formulae are given in 14, Section 4.3]. Consider

a (possibly empty) sequence

= (

::: i

) with 0

< i

for all

. Write

and

l<k

. Finally, put

We then have

log

(

) =

We write exp

(

) for the inverse of log

(

) (under composition) and set

(

) =

= exp

(log

(

) + log

(

))

One can show that this lies in

]] (rather that

]

]]), so it de nes a

formal group law over

By applying log

, one can check that

]

(

) = exp

(

) +

;

Lemma 82

k >

0 then

(

)

mod (

::: u

;

) + (

)

Proof.

We work mod (

)

and (

::: u

;

). This leaves us with a

torsion-free ring, so we can still use the logarithm. In this setting, for

(

)

we have log

(

) =

and

(

) = 0. For some

(

) we

have

(

) =

(

) +

Applying log

, we get

log

(

) + log

(

) = log

(

) +

)

(

) +

(

)

(

)

;

(

)

=p:

Thus

(

xyz

)

= (

)

. As the ideal (

) is nilpotent, we have

= 0 as

claimed.

It follows from this (see 10]) that

is the universal deformation of

Lemma 83

(

) =

mod

(

) or mod (

q=p

y::: u

;

Proof.

The rst statement holds for any formal group law. Now work mod

the second ideal. By the rst statement,

(

)

;

(

) is divisible by

From the de nitions, all the coecients also lie in the ideal

= (

::: u

;

Because

= 0, we see that

(

) =

(

). Now consider

(

)

;

Using Lemma 80, we see that every term is divisible either by

or by

q=p

both of which are zero. Thus

(

) =

as required.

Next, observe that (

)

. It follows that (

)

;

(

) is divisible by

. Thus, there are unique series

(

)

]]

such that

(

)

(

)

Lemma 84

(

) =

(

)

;

k=1

(

) mod (

::: u

;

)

Proof.

Write

= (

::: u

;

) and

= (

) +

. For the moment, we work

mod

. In this setting we have

log

(

) =

k=1

(

)

(

) +

;

k=1

(

)

=p:

Next, observe that

;

(

) vanishes mod

, so there are unique

series

(

)

]] such that

;

(

) =

;

k=1

(

) (mod

)

By Lemma 83 we can rewrite the right hand side as a formal sum. Thus

= (

) +

(

) +

;

(

)

We now apply log

to this equation. The left hand side becomes

(

) +

(

) +

;

k=1

(

) +

(

))

The right hand side becomes

(

) +

p l

((

)

) +

(

)

Recall that

(

) =

(

) +

(

) and

((

)

) =

(

) +

(

) +

(

))

Using this to simplify the right hand side further, and rearranging, we conclude

that

(

) +

p l

(

)) = 0

Finally, we recall that

(

)

(mod

). This implies that

(

) =

;

(

) (mod

), which proves the lemma.

16 Examples

In this section we let

be the formal group over

with logarithm log

(

) =

, so that

is a formal group of height 2 over

. Computer

calculations give results as follows.

(i) Let

2 be generated by

. Given a level-

structure

, we shall

identify

with

(

)). We then have

Level(

) = spf(

]

)

A coordinate on the quotient group

] is given by

The associated formal group law is

ayz

(

) +

(

) +

(ii) Now take

(

, with generators

and

. Then

Level(

) = spf(

]

(

))

Because

= (1), the corresponding subgroup divisor is just

(1), and

a coordinate on the quotient group is just given by 2](

) =

(iii) Take

4 generated by

. Then

Level(

) = spf(

]

)

Type(

) = spf(

]

)

The equation of the subgroup divisor is

(

;

) =

(iv)

Sub

(

) = spf(

]

)

The equation of the subgroup divisor is

+ (

)

The map of rings induced by Type(

)

;

Sub

(

) just sends

Now let

be the standard height 3 formal group over

, with logarithm

log

(

) =

. Let

2 be generated by

and

. Then

Level(

) = spf(

]

(

))

Type(

) = spf(

]

(

))

where

The equation of the group divisor is

(

)

(

)

(

)

(

)

Note that

(

) =

(mod

) it follows that

does not lie in the subring

generated by the coecients of

, which shows that the map Type(

)

;

Sub

(

) is not a closed embedding.

References

1] J. F. Adams. Stable Homotopy and Generalised Homology. University of

Chicago Press, Chicago, 1974.

2] W. Bruns and J. Herzog. Cohen-Macaulay Rings, volume 39 of Cambridge

Studies in Advanced Mathematics

. Cambridge University Press, 1993.

3] M. Demazure and P. Gabriel. Groupes Algebriques. North-Holland, 1970.
4] E. S. Devinatz, M. J. Hopkins, and J. H. Smith. Nilpotence and stable

homotopy theory I. Annals of Mathematics, 128:207{242, 1988.

5] V. G. Drinfel'd. Elliptic modules. Math. USSR Sb., 23:561{592, 1974.
6] A. Frolich. Formal Groups, volume 74 of Lecture Notes in Mathematics.

Springer{Verlag, 1968.

7] M. Hazewinkel. Formal Groups and Applications. Academic Press, 1978.
8] M. J. Hopkins, N. J. Kuhn, and D. C. Ravenel. Generalised group characters

and complex oriented cohomology theories. To appear.

9] N. M. Katz and B. Mazur. Arithmetic Moduli of Elliptic Curves, volume 108

of Annals of Mathematics Studies. Princeton University Press, 1985.

10] J. Lubin and J. Tate. Formal moduli for one parameter formal lie groups. Bull.

Soc. Math. France

, 94:49{60, 1966.

11] H. Matsumura. Commutative Ring Theory, volume 8 of Cambridge Studies in

Advanced Mathematics

. Cambridge University Press, 1986.

12] J. Morava. Completions of complex cobordism. Lecture Notes in Mathematics,

658:349{361, 1978.

13] J. Morava. Noetherian localisations of categories of cobordism comodules.

Annals of Mathematics

, 121:1{39, 1985.

14] D. C. Ravenel. Complex Cobordism and Stable Homotopy Groups of Spheres.

Academic Press, 1986.

15] N. P. Strickland. Functorial philosophy for formal phenomena. in preparation,

1994.

16] J. Tate and F. Oort. Group schemes of prime order. Ann. scient. Ecoles Norm.

Sup.

, 3:1{21, 1970.