Wprowadzenie do mechaniki analitycznej

Wprowadzenie do mechaniki analitycznej.

##################################################################################
Autor : R. Waligóra ; data powstania dokumentu : 2009-08-24
; ostatnie poprawki z dnia: 2009-12-02
##################################################################################

I. Wprowadzenie.

Mechanika, (klasyczna, newtonowska ) (skrót -MK) w ogólności zajmuje się badaniem ruchu punktu materialnego lub
układów takich punktów, w szczególności rozumianych jako model tzw. ciała sztywnego (bryły sztywnej – bryłą sztywną,
doskonałą, nazywamy skończony, układ punktów materialnych w którym odległości wzajemne między poszczególnymi
punktami są niezmienne ) w dalszej kolejności rozszerzając takie układy na ośrodki ciągłe m.in. płyny : gazy i ciecze.
Podstawowym działem mechaniki jest dynamika, bada ona zależność ruchu od działających na zadany układ materialny
sił. Centralnym prawem dynamiki jest równanie wektorowe zwane II prawem Newtona ( II prawem ruchu , II prawem
dynamiki lub po prostu prawem ruchu ) :

F = ma

≡

F = dp/dt

≡

Fi = pi

•

; i = 1, .. ,n (dla układów n-punktów materialnych )

; kropka zgodnie z tradycją oznacza różniczkowanie względem czasu tj. p

•

= dp/dt

; czcionką pogrubioną oznaczono wielkości wektorowe

Dla szczególnych układów w których działają siły posiadające potencjał skalarny ( siły potencjale ) mamy :
F = - grad U ; U = U (x, y, z) – funkcja potencjalna.

•

∇

U ; operator

∇

∂

x i +

∂

y j +

∂

z k

Prawo to wraz z innymi, szczegółowo zdefiniowanymi pojęciami kinetycznymi ( pamiętamy oczywiście o zakresie ich
stosowania ) pozwala ułożyć równania ruchu dowolnego układu materialnego ( o naturze dyskretnej lub ciągłej )
Dla takiego podejścia charakterystyczne są określenie wektorowego pola siły ( sił) oraz poprawne określenie równania
wektorowego ruchu, sprowadzającego się do układu równań różniczkowych zwyczajnych (rrz) ( w szczególnych
przypadkach równań o pochodnych cząstkowych ) (rrc). Poprawne określenie takiego układu zawiera określenie jego
warunków brzegowych oraz określenie stabilności jego rozwiązań. [ zobacz 5, 6, 9 – literatury dodatkowej ].
W konsekwencji takiego sformułowania, można było by rozpatrywać mechanikę jako pewien rozdział teorii równań
różniczkowych.
Warto nadto podkreślić centralną rolę pojęcia siły w „podejściu” newtonowskim. Jak przekonamy się dalej możliwe jest
zastąpienie tego pojęcia ( wielkości fizycznej ) inną wielkością fizyczną np. energią i równoważne wyprowadzenie z niego
podstaw mechaniki.
Poglądowość i długa tradycja stanowi o utrwaleniu „newtonowskiego” spojrzenia na mechanikę, jednakże w ogólności
spojrzenie to nie jest ani bardzo głębokie ani bardzo płodne tj. posiada ograniczony zakres zastosowania i trudno powiązać
go z np. grupami symetrii. Dla układów bardziej złożonych okazuje się, że wyprowadzone z prawa Newtona równania,
okazują się bardzo skomplikowane i przez to trudne do analitycznego rozwiązania. Trudno również w oparciu o to
klasyczne podejście przejść do mechaniki kwantowej lub relatywistycznej.
W ciągu kilku wieków rozwoju fizyki wypracowano szereg bardzo eleganckich matematycznie metod, pozwalających na
syntetyczne i głębokie ujęcie dynamiki układów mechanicznych. Metody te zazwyczaj grupuje się pod jednolitym
terminem „mechanika analityczna” ( analytical mechanics ) ( Zainteresowanego historią rozwoju mechaniki odsyłam do
[ 4, od str. 205 ] )
Mechanika analityczna ( MA) – w obecnym czasie jest terminem obejmującym klasyczne już podejście Lagrange’a i
Hamiltona zwane ( ogólnie ) aparatem kanonicznym ( „analityczność” tej mechaniki związana jest z wykorzystaniem w
szerszym zakresie metod analizy matematycznej funkcji jednej i wielu zmiennych, metod wariacyjnych oraz metod analizy
funkcjonalnej ). W związku z ogromną siłą eksplanacyjną tego aparatu wielokrotnie mechanikę analityczna kojarzy się z
całością mechaniki teoretycznej - zobacz wstęp [ 15 ].
Mechanika analityczna organicznie związana jest z tzw. zasadami wariacyjnymi ( różniczkowymi i/lub całkowymi )
Istnieje kilka „podstawowych” zasad wariacyjnych. Wybór konkretnej zasady z której akurat korzystamy, zazwyczaj
podyktowany jest względami ekonomiki zapisu tj. łatwością ujęcia i rozwiązania danego zagadnienia fizycznego.
Istnieje właściwie prawie dowolna „ścieżka” prowadząca do sformułowania praw mechaniki, ( jak wiadomo prawie każdy
dział fizyki czy to np. mechanikę kwantowa ( MQ ) czy np. termodynamika, może być sformułowana z wykorzystaniem
różnych narzędzi matematycznych np. MQ może być sformułowana poprzez język operatorów działających w przestrzeni
Hilberta lub w języku C*-algebry. ( o sformułowaniach MQ można przeczyta np. w Michał Heller „Mechanika kwantowa
dla filozofów” OBI str. 77 ). Weryfikacja poprawności danego sformułowania zawsze jest sprawą zgodności
teoria-empiria lub odpowiedniości „teoria nowa”

≡

lub

≈

„teoria stara” tj. teoria już sprawdzona empirycznie.

W przypadku mechaniki weryfikacja zazwyczaj sprowadza się do sprawdzenia zgodności wyników „nowej teorii” z teorią
Newtona. Ogólnie możemy powiedzieć , że „wykład” mechaniki analitycznej polega na wyprowadzeniu z pewnych
ogólnych zasad lub zasady, sposobem analitycznym równań ruchu lub pewnych równań charakteryzujących układ
mechaniczny.

Do podstawowych pojęć MA należą m.in. : więzy, współrzędne uogólnione – wielkości uogólnione, zasada wariacyjna,
równania kanoniczne, lagranżajn, hamiltonian, transformacja kanoniczna, przestrzeń fazowa lub konfiguracyjna itp.

W całym tekście przyjmuje znajomość podstawowych pojęć mechaniki klasycznej tj. przynajmniej ogólne zapoznanie się z
[1, 2, 3], oraz znajomość podstaw teorii rrz i rachunku wariacyjnego.
W prezentowanym tekście skłaniam się w istocie do prymatu mechaniki analitycznej tj. stwierdzenia, że MA jest
kwintesencją mechaniki w ogólności. Można powiedzie nawet więcej, MA jest filarem na którym opiera się cała fizyka
teoretyczna. Należy również podkreślić, że materiał wyłożony w dalszych rozdziałach ujawnia specyficzne preferencja
autora, który patrzy na MA poprzez pryzmat jej dalszego zastosowania w innych działach fizyki teoretycznej zwłaszcza
MQ, QTP ( kwantowej teorii pola ) i dynamice chaotycznej. ( w szczególności tekst nie zawiera rozwinięcia zastosowania
MA np. do mechaniki technicznej )
Uwaga ! Wspominam o prymacie MA np. nad mechaniką kwantową, chociaż wiadomo, że z ontologicznego punktu
widzenia to właśnie prawa kwantowe są „pierwotniejsze” od mikroskopowych praw mechaniki klasycznej. Prymat polega
jedynie na tym, że metody i prawa MA jako wcześniej odkryte i bardziej „oczywiste” dla ludzkiej percepcji zostają
przystosowane dla potrzeb innych działów fizyki teoretycznej.

Podstawowe pojęcia MA.

II. Więzy ( constraints ).

Definicja 2.1 Układem materialnym nazywamy zbiór punktów materialnych tj. punktów o niezerowej masie, których
położenie (ruch ) jest dane (zadany) w układzie ortokartezjańskim Oxyz. Układ ten będziemy traktowali jako IUO.
( układ materialny będziemy również nazywa układem mechanicznym )

Wybór akurat takiego układu jest jedynie kwestią poglądowości, w każdej chwili możemy przejść do dowolnego innego
układu współrzędnych nie wyłączając współrzędnych krzywoliniowych.
Możemy rozważać zbiór n-punktów materialnych ( obecnie ograniczymy się do zbioru przeliczalnego ). Nie istnieje
również problem ilości wymiarów ( ilości zmiennych niezależnych ), w każdej chwili ( o ile jest to oczywiście
uzasadnione, matematycznie i fizycznie ) możemy rozważać wielowymiarowy układ współrzędnych.

Definicja 2.2 Ruch swobodny układu materialnego to ruch spowodowany jedynie przez siły dane (zadane ) :
Fi = Fi (x, y, z, t )

≡

Fi (ri, t ) lub Fi = Fi (x, y, z, t, v ) ; i = 1, ... , k

ri – wektor wodzący i-tego punktu materialnego.
Ruch nieswobodny układu materialnego jest to ruch swobodny na który nałożono pewne ograniczenia, zwane więzami.
Więzy wyrażamy w postaci analitycznej przy pomocy równań lub nierówności o przykładowej postaci :
Gj ( ri, t ) = 0 - więzy dwustronne (utrzymujące ) (2.1)
Gj ( ri, t )

≤

0 - więzy jednostronne. ( nieutrzymujące ) (2.2)

Ogólnie układ, który może zajmować dowolne położenie oraz może poruszać się z dowolną prędkością nazywamy
układem swobodnym.
Przykładem układu nieswobodnego z nałożonymi więzami utrzymującymi jest koralik nanizany na nitkę, przykładem
układu z więzami nieutrzymującymi jest bila poruszająca się po stole bilardowym tak na marginesie jest to przykład układu
nieholonomicznego.
Jeżeli do zadanych równań więzów (2.1) lub (2.2) czas nie wchodzi w sposób jawny to więzy nazywamy
„skleronomicznymi” (stacjonarne ) w przypadku jawnej zależności od czasu więzy nazywamy „reonomicznymi”.
Można pokazać, że ruch układu podlegającego więzom jednostronnym zawsze możemy sprowadzić do ruchu swobodnego
i ruchu z więzami dwustronnymi – z tego względu można ograniczyć się do analizy tylko układów z więzami
dwustronnymi.
Jeżeli w równaniach więzów nie występują prędkości poszczególnych punktów to więzy nazywamy „skończonymi” lub
„geometrycznymi”. Jeżeli choć jedna z funkcji jest zależna od prędkości to więzy nazywamy „różniczkowymi” lub
„kinematycznymi” . Mogą występowa więzy czysto geometryczne lub czysto różniczkowe.
Każde więzy geometryczne reonomiczne powodują występowanie więzów różniczkowych , których równanie
otrzymujemy przez różniczkowanie (2.1) :
n

ΣΣΣΣ

(

∂

G /

∂

ri ) ri

•

∂

Gi/

∂

t = 0 (2.3)

i=1
Oczywiście dla więzów skleronomicznych mamy :
n

ΣΣΣΣ

(

∂

G /

∂

ri ) ri

•

= 0 (2.3a)

i=1
Więzy to ograniczenia ruchu związane z pewnymi warunkami dodatkowymi nakładanymi na możliwości ruchu układu
materialnego np. : układ materialny umieszczono w pojemniku o zadanej geometrii, układ może poruszać się jedynie z
ograniczona prędkością, układ porusza się po zadanej płaszczyźnie.

Przykładowo więzy postaci G(x, y, z ) = 0 możemy interpretować jako nieruchomą powierzchnię na której musi
pozostawać układ materialny podczas całego czasu ruchu.
W przypadku układu nieswobodnego (skrępowanego ) równania ruchu muszą by zgodne z narzuconymi równaniami
więzów. W przypadku więzów ograniczających „geometrię” układu materialnego, mówimy, że układ materialny może
przemieszcza się zgodnie z narzuconymi więzami, wtedy mówimy o przemieszczeniu możliwym.
Więzy tj. ich równania zazwyczaj definiujemy w układzie odniesienia związanym z rozpatrywanym układem materialnym.

Zauważmy , że :

∂

G /

∂

ri = grad i Gi

jest to wektor ( normalny do powierzchni więzów ), nazywamy go „gradientem więzów” lub „parametrem różniczkowym
więzów” .
Warunek (2.3) oznacza, że składowe styczne prędkości do powierzchni więzów są dowolne, składowe normalne podlegają
ograniczeniu.
Jeżeli równania różniczkowe przedstawiające więzy kinematyczne (2.3) możemy scałkować to mówimy , że więzy
kinematyczne są całkowalne.
Definicja 2.3 Nieswobodny układ materialny nazywamy układem holonomicznym jeżeli nałożone na niego więzy są
całkowalne. Jeżeli układ podlega niecałkowalnym więzom różniczkowym to nazywamy go układem nieholonomicznym.
( Warunki konieczne i wystarczające całkowalności więzów kinematycznych przedstawiono w pracy :
Ju. Nejmark, I. A. Fufajew „Dynamika układów nieholonomicznych” PWN )
Klasycznym przykładem układu nieholonomicznego jest tocząca się po zadanej powierzchni, bez poślizgu obręcz lub
tarcza.

Rozpatrując układ mechaniczny złożony z n-punktów materialnych aby jednoznacznie określić jego konfiguracje, należy
podać 3n współrzędnych. Mówimy wtedy, że układ posiada 3n stopni swobody. Układ nieswobodny posiada 3n-m
stopni swobody ; m – liczba niezależnych równań więzów ograniczających swobodę układu, oczywiście m

≤

S = 3n – m ; S – liczba stopni swobody układu mechanicznego.
Gj ( ri, t ) = 0 ; j = 1, ... ,m ; i = 1, ... ,n - równania więzów.
Swobodny punkt materialny w przestrzeni n-wymiarowej posiada n stopni swobody. Swobodny układ materialny złożony
z k punktów w przestrzeni n wymiarowej posiada kn stopni swobody.
Jak wiadomo do określenia położenia bryły sztywnej w przestrzeni n-wymiarowej, potrzeba n współrzędnych
( niekomhiperplanarnych tj. nie należących do jednej hiperpłaszczyzny )
Wahadło sferyczne posiada dwa stopnie swobody, wahadło płaskie jeden a wahadło płaskie podwójne dwa stopnie
swobody. Są to przykłady układów o skończonej liczbie swobody.

Definicja 2.4 Układ materialny nazywamy układem o skończonej liczbie stopni swobody jeżeli można wprowadzi taką

skończenie wymiarową przestrzeń wektorową Rn i taki zbiór punktów M

∈

Rn , że między wszystkimi możliwymi

położeniami tego układu i wszystkimi punktami M istnieje odpowiedniość wzajemnie jednoznaczna.

III. Współrzędne uogólnione ( generalized coordinates ). Przestrzeń konfiguracyjna.

Definicja 3.1 Niezależne współrzędne, których liczba jest najmniejszą potrzebną do określenia stanu układu materialnego
( w szczególności jego położenia ) nazywamy „współrzędnymi uogólnionymi”. ( WO )

Liczba współrzędnych uogólnionych równa jest liczbie stopni swobody. Współrzędne uogólnione będziemy, kierując się
tradycją oznaczać jako : q1 , ... ,qn ; n = 1, ... ,S
Jako współrzędne uogólnione możemy wybrać standardowe współrzędne kartezjańskie, współrzędne krzywoliniowe lub
dowolne inne charakteryzujące stan układu materialnego, WO nie koniecznie muszą mieć wspólne miano, mogą to być np.
współrzędne postaci : długość-kąt ; długość – pole. Zazwyczaj konkretny wybór WO podyktowany jest względami
prostoty rachunkowej.

Przykład 3.1 Niech punkt M porusza się po powierzchni sfery o promieniu R o środku w początku układu współrzędnych.
Dla tego przypadku więzy będą więzami holonomicznymi, stacjonarnymi i układzie współrzędnych kartezjańskich mają
postać :

x2 + y2 + z2 - R2 = 0
Położenie punktu określić możemy jednak jednoznacznie podając dwie współrzędne ( zatem układ ma 2 stopnie swobody )
Najlepszy wybór dla współrzędnych uogólnionych ( podyktowany symetrią sferyczna zagadnienia ) to współrzędne
sferyczne – q1= kąt długości φ ; q2 = kąt szerokości

Współrzędne kartezjańskie powinny by funkcjami WO postaci :
xi = xi(t, q1, ... ,qn ) (3.1)
yi = yi(t, q1, ... ,qn )
zi = zi(t, q1, ... ,qn )

Zależności te są równaniami parametrycznymi n-wymiarowej hiperpowierzchni więzów tzw. rozmaitości konfiguracyjnej.
WO są więc pewnymi współrzędnymi krzywoliniowymi na n-wymiarowej na tej powierzchni. I bywają nazywany
„WO zgodnymi z więzami”.
Role WO podkreśla Lanczos : “Mechanika analityczna jest czysto matematyczną nauką. Wszystko w niej sprowadza się
do obliczeń w abstrakcyjnej przestrzeni wielkości matematycznych. Świat fizyczny tłumaczymy na język zależności
matematycznych, a tłumaczenia tego dokonujemy za pomocą współrzędnych. Współrzędne ustanawiają jednoznaczną
zależność między punktami świata fizycznego i liczbami. Po ustanowieniu takiej zależności możemy posługiwać się
współrzędnymi jako wielkościami algebraicznymi zapominając o ich fizycznym znaczeniu. Końcowy wynik takich
obliczeń przekształcamy następnie, odwrotnie na świat fizycznych realiów. „ [ 2- literatury w języku angielskim , str. 29 ]

Funkcje (3.1) powinny być ciągłe, różniczkowalne, jednoznaczne i nieosobliwe ( warunki te mogą by naruszone co
najwyżej w przeliczalnej liczbie punktów, które powinniśmy wyłączy z ich dziedziny ). Warunki takie gwarantują istnienie
transformacji między różnymi stosowanymi współrzędnymi.

Ruch n-punktów materialnych możemy rozpatrywać jako ruch n-wektorów w przestrzeni współrzędnych kartezjańskich.
Można jednak do tego zagadnienia podejść inaczej – rozpatrując ruch jednego wektora w abstrakcyjnej przestrzeni położeń

R3n – przestrzeń taką nazywamy „przestrzenią konfiguracyjną” układu n-punktów.

Definicja 3.2 zbiór M

⊂

Rn nazywamy „rozmaitością konfiguracyjną” układu materialnego jeżeli odwzorowanie

zdefiniowane w definicji 2.4 jest odwzorowaniem dyfeomorficznym ( różniczkowalnym i wzajemnie jednoznacznym )

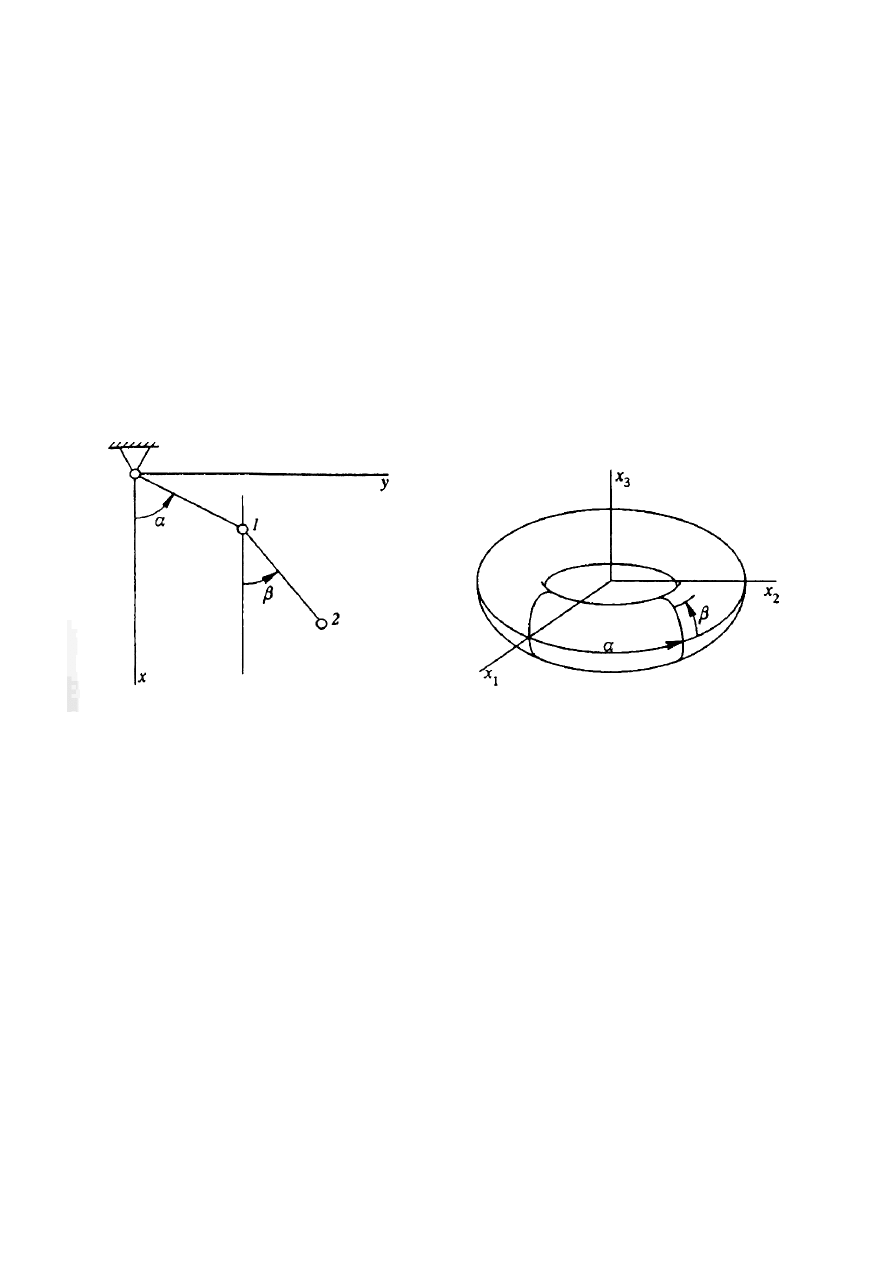
Przykład 3.2 Przestrzenią konfiguracyjną wahadła podwójnego jest torusem.

Rys. 1 Wahadło płaskie podwójne i jego przestrzeń konfiguracyjna.

Teraz można stwierdzić, że liczba stopni swobody jest wymiarem przestrzeni konfiguracyjnej.

IV. Prędkości i przyspieszenia uogólnione.

Definicja 4.1 Prędkościami uogólnionymi nazywamy pierwsze pochodne względem czasu współrzędnych uogólnionych.
Jeżeli : q1= q1(t) , ... , qn= qn(t) ,to otrzymujemy następujące prędkości uogólnione :

v1= dq1(t) /dt

≡

•

, ... , vn= dqn(t) /dt

≡

•

(4.1)

Oczywiście, ponieważ WO mają różne jednostki, prędkości uogólnione będą również miały różne jednostki np.

rad/s –prędkość kątowa, m2/s – prędkość polowa
Dla układu kartezjańskiego mamy :
n

•

ΣΣΣΣ

(

∂

xi/

∂

qj ) qj

•

∂

xi/

∂

t (4.2a)

j=1
n

•

ΣΣΣΣ

(

∂

yi/

∂

qj ) qj

•

∂

yi/

∂

t (4.2b)

j=1

n

•

ΣΣΣΣ

(

∂

zi/

∂

qj ) qj

•

∂

zi/

∂

t (4.2c)

j=1
Skąd otrzymujemy :

∂

•

∂

•

∂

xi/

∂

qj ;

∂

•

∂

•

∂

yi/

∂

qj ;

∂

•

∂

•

∂

zi/

∂

qj (4.3)

Przy zmianie czasu o dt układ pod działaniem przyłożonych sił przemieszcza się do nowego położenia. W przypadku
więzów niestacjonarnych nieskończenie małe przemieszczenia maja postać :
n

dxi =

ΣΣΣΣ

(

∂

xi/

∂

qj ) dqj + (

∂

xi/

∂

t) dt (4.4a)

j=1
n

dyi =

ΣΣΣΣ

(

∂

yi/

∂

qj ) dqj + (

∂

yi/

∂

t) dt (4.4b)

j=1
n

dzi =

ΣΣΣΣ

(

∂

zi/

∂

qj ) dqj + (

∂

zi/

∂

t) dt (4.4c)

j=1
Dla więzów stacjonarnych wyrażenia te upraszczają się. ( odrzucamy ostanie człon równania )

Definicja 4.2 Przyspieszeniami uogólnionymi nazywamy drugie pochodne względem czasu współrzędnych uogólnionych.

w1= d

1(t) /dt

≡

••

, ... , wn= d

n(t) /dt

≡

••

(4.5)

Dla współrzędnych kartezjańskich otrzymujemy :
n n n

••

ΣΣΣΣ

(

∂

xi/

∂

qj ) qj

••

ΣΣΣΣ

(

∂

qν

∂

qj ) qν

•

+ (

∂

t2 ) (4.6a)

j=1 ν=1j=1
(wzory dla współrzędnych y , z są analogiczne )

Różniczkowe zasady wariacyjne MA.

V. Przesunięcia przygotowane ( wirtualne ).

Rozważmy układ materialny złożony z n punktów skrępowany więzami geometrycznymi niestacjonarnymi całkowalnymi
postaci :
Gi (qj, t ) = 0 ; i = 1, .. , α ; j = 1, ... ,3n

Definicja 5.1 Przesunięciem przygotowanym, wirtualnym lub możliwym, układu mechanicznego nazywamy nieskończenie
małe przesunięcie zgodne z więzami pozwalające przejść z jednego punktu przestrzeni konfiguracyjnej do drugiego punktu
tej przestrzeni bez uwzględnienia upływu czasu tj. w tej samej chwili czasu.
Innymi słowy ( bez rozróżnienia szczegółowo pojęć ) przesunięcie wirtualne to przesunięcie zgodne z więzami i nie
związane z działającymi siłami ani czasem.
Wektor przesunięcia wirtualnego oznaczmy jako δr , zatem słuszny jest następujący wzór :

ΣΣΣΣ

δri

∇

Gi = 0 (5.1)

( symbol δ przypomina, nie przypadkowo symbol wariacji – jest to istotnie wariacja izochroniczna tj. wariacja bez wariacji
czasu δt = 0 )
Oczywiście dla WO mamy zależność postaci :

δri =

ΣΣΣΣ

(

∂

ri/

∂

qν) δqν ; ν = 1, … , n (5.2)

Należy rozróżniać pojęcia : przesunięcia wirtualnego δri i przesunięcia infinitezymalnego dri , to ostatnie jest nazywane
„przesunięciem nieskończenie małym rzeczywistym” i jest wywołane działającymi siłami rzeczywistymi i zachodzi w
czasie infinitezymalnym dt. I oczywiście mamy : dri = ri dt.
Dla więzów skleronomicznych przesunięcie rzeczywiste jest jednym z przesunięć możliwych. W przypadku więzów
reonomicznych powierzchnia więzów może przemieszczać się w czasie „unosząc” ze sobą układ mechaniczny.

VI. Siły reakcji więzów. Więzy doskonałe.

Nałożenie więzów możemy traktować jako pojawienie się dodatkowych sił zwanych siłami reakcji więzów.

Rys. 2 Ruch punktu nieswobodnego i pojawienie się siły reakcji więzów R.

Stwierdzenie : każdy układ nieswobodny może być traktowany jako układ swobodny jeżeli odrzucimy więzy i zastąpimy
ich działanie odpowiednio dobranymi siłami reakcji więzów, nazywamy „postulatem oswobodzenia od więzów”.
Oznaczmy siły reakcji więzów jako Ri , siły takie możemy zawsze rozłożyć na składowe : normalną R

⊥

i styczną R|| do

toru punktu. Składową styczną nazywamy siłą tarcia i zazwyczaj oznaczamy : T = µN ; µ – współczynnik tarcia.
Składową normalną możemy zapisać następująco :
R

⊥

= λi grad Gi ; λi – pewne współczynniki

Jeżeli więzy są tego rodzaju, że składowa styczna siły reakcji znika w każdym punkcie toru , to linię lub powierzchnie
więzów nazywamy gładką. W dalszym ciągu ograniczymy się do rozważania powierzchni gładkich.
Równanie ruchu punktu materialnego ma teraz postać :

•

= F + R lub pi

•

= Fi + Ri

(6.1)

W odróżnieniu od sił reakcji siły

Fi nazywamy siłami aktywnymi. Podstawowe zagadnienie dynamiki układu

nieswobodnego jest zatem następujące :
Dane są siły aktywne, równania więzów oraz zgodne z tymi więzami położenia początkowe i prędkości początkowe
punktów rozważanego układu mechanicznego. Na podstawie tych danych należy wyznaczyć ruch tego układu i siły reakcji
więzów. Takie zadanie jest zadaniem nieoznaczonym ( liczba zmiennych jest większa niż liczba równań ) i dlatego
konieczne jest pewne dodatkowe założenie.
W mechanice wyróżniamy pewną szczególną klasę więzów zwanych więzami idealnymi ( doskonałymi).
Jeżeli na punkt materialny działa siła F to przesuwając wirtualnie ten punkt o wektor δr wykonamy pracę elementarną :
δW = F δr (6.2)
Pracę elementarną siły aktywnej na przesunięciu przygotowanym nazywamy „pracą przygotowaną”.
Uwaga ! Przypominam, że praca dWi sił Fi na przemieszczeniu dri definiowana jest jako iloczyn skalarny :
dWi = Fi

•

dri

Definicja 6.1 Więzami idealnymi nazywamy więzy przy których praca sił reakcji na przesunięciu wirtualnym jest równa
zeru.

δWi =

ΣΣΣΣ

Ri δri = 0 (6.3)

Przykładem więzów idealnych są więzy gładkie.

VII. Zasada prac przygotowanych.

W dalszym ciągu rozważamy układ n-punktów materialnych na który działają siły aktywne Fi , skrępowany więzami
holonomicznymi, skleronomicznymi dwustronnymi, idealnymi.
Warunkiem koniecznym i wystarczającym równowagi układu jest aby praca sił aktywnych Fi na przesunięciach
przygotowanych δri była równa zeru, tj. aby :

δWi =

ΣΣΣΣ

Fi δri = 0 (7.1)

Zasadę prac przygotowanych uważamy za zasadę wariacyjną ponieważ zawiera ona w swej treści przesunięcia
przygotowane tj. bierzemy pod uwagę zbiór różnych konfiguracji otrzymanych w wyniku przesunięć wirtualnych.

Do zalet zasady prac przygotowanych zaliczamy to, że wszystkie warunki równowagi można wyrazić za pomocą jednego
równania, nie wchodząc w szczegóły więzów nałożonych na punkty układu. [14, str. 91 ]
Rozkładając równanie (7.1) na składowe otrzymamy :

ΣΣΣΣ

( Xi δxi + Yi δyi + Zi δzi ) = 0 (7.2)

Xi , Yi , Zi – rzuty wektorów sił Fi na osie układu kartezjańskiego.
δxi , δyi , δzi – rzuty wektorów przemieszczeń wirtualnych δri na osie układu kartezjańskiego.
Równanie (7.2) nazywane jest ogólnym równaniem statyki. Dowód zasady prac przygotowanych można znaleźć w
[ 14, 89; 1-literatury w języku rosyjskim str. 31 ]
Aby wyrazić omawianą zasadę we współrzędnych uogólnionych wprowadzimy najpierw pojęcie siły uogólnionej ,
zdefiniowanej zależnością :
n

Qi =

ΣΣΣΣ

[ Xi (

∂

xi /

∂

qj ) + Yi (

∂

yi /

∂

qj ) + Zi (

∂

zi /

∂

qj ) ] (7.3)

i=1
Zasada prac przygotowanych we współrzędnych uogólnionych ma teraz postać :

ΣΣΣΣ

Qi δqi = 0 (7.4)

Równość ta oznacza, że warunkiem koniecznym i dostatecznym, równowagi rozważanego układu mechanicznego jest
równość zeru sił uogólnionych Qi odpowiadającym zmiennym niezależnym qi.

VIII. Siły potencjalne.

Jeżeli układ znajduje się pod działaniem sił o potencjale skalarnym U = U(xi , yi, zi ) to suma prac przygotowanych będzie
różniczka zupełną funkcji U. W tym przypadku otrzymujemy :

dU =

ΣΣΣΣ

( Xi dxi + Yi dyi + Zi dzi ) (8.1)

Stąd wynika , że :
Xi =

∂

U/dxi ; Yi =

∂

U/dyi ; Zi =

∂

U/dzi (8.2)

A zatem wyrażenie dla sił uogólnionych ma postać :
Qi =

∂

U/dqi (8.3)

Energia potencjalna V = V(x, y, z) określona jest jako praca, którą powinny wykonać siły pola aby przeprowadzi układ z
położenia ( xi , yi , zi ) do nowego położenia ( xi0 , yi0 , zi0 ) ( droga na której dokonywane jest to przemieszczenie jest
dowolna ). Otrzymujemy zatem :
n ( xi0 , yi0 , zi0 )

V( xi , yi , zi ) =

ΣΣΣΣ

∫

( Xi dxi + Yi dyi + Zi dzi ) (8.4)

i=1 ( xi , yi , zi )
Zatem :
( xi0 , yi0 , zi0 )

V( xi , yi , zi ) =

∫

dU (8.5)

( xi , yi , zi )
Po scałkowaniu trzymujemy :
V( xi , yi , zi ) =

U ( xi0 , yi0 , zi0 ) -

U( xi , yi , zi )

Tj. energia potencjalna V z dokładnością do stałej addytywnej jest równa minus potencjałowi.
V( xi , yi , zi ) = -

U( xi , yi , zi ) (8.6)

Uwaga ! Widać tu zatem różnicę między potencjałem a energią potencjalną, które to wielkości bywają wielokrotnie
niesłusznie utożsamiane. Warto również na marginesie zauważyć, że w MA przyjmuje się zamienność operatora
różniczkowania d i operatora wariacji δ tj. dδF = δdF ( zobacz dokładnie [14 str. 73 ]
Zasada prac przygotowanych może być teraz wyrażona za pomocą energii potencjalnej V :
δV = 0 (8.7)
tzn. warunkiem koniecznym i wystarczającym równowagi układu jest aby, pierwsza wariacja energii potencjalnej była
równa zeru. Z rachunku wariacyjnego wiemy, że jest to warunek stacjonarności.

IX. Zasada d’Alemberta (d’Alembert’s principle ) .

Rozważmy ruch skrępowanego układu n-punktów pod wpływem sił aktywnych Fi, oraz sił reakcji Ri , równanie ruchu ma
postać :
mi ai = Fi + Ri (9.1)
Wprowadźmy następnie wektor : Ji = - mi ai zwany siłą bezwładności d’Alemberta. Równanie (9.1) możemy teraz
przepisać w postaci :

Ji + Fi + Ri = 0 (9.2)
D’Alembert podstawił wyrażenie (9.2) do wzoru na pracę przygotowaną :

ΣΣΣΣ

( Ji + Fi + Ri ) δri = 0 (9.3)

Jeżeli więzy są idealne to wyrażenie (9.3) upraszcza się do formy :

ΣΣΣΣ

( Ji + Fi ) δri = 0 (9.4)

Wzór (9.4) wyraża analitycznie zasadę d’Alemberta będącej podstawą dynamiki układów nieswobodnych. Zależność ta
bywa również nazywana „ogólnym równaniem dynamiki”.
Zasada D’Alemberta. Jeżeli układ mechaniczny jest skrępowany więzami holonomicznymi
( a nawet nieholonomicznymi ) dwustronnymi i doskonałymi , to praca sił aktywnych i sił bezwładności na przesunięciach
przygotowanych jest równa zeru.
Równanie (9.4) możemy rozpisać na składowe :

ΣΣΣΣ

{ [ Xi + mi (d

xi/dt

2 )] δx

i + [ Yi + mi (d

yi/dt

2 )] δy

i + [ Zi + mi (d

zi/dt

2 )] δz

i } = 0 (9.5)

Z równania ( wariacyjnego ) (9.4) możemy wyprowadzić równania ruchu jak również wszystkie twierdzenia dynamiki,
możemy go zatem przyjąć jako równanie definiujące pewną zasadę leżącą u podstaw mechaniki.
Dla sił potencjalnych równanie (9.5) przyjmuje postać :

ΣΣΣΣ

[ mi (d

xi/dt

2 ) δx

i + mi (d

yi/dt

2 ) δy

i + mi (d

zi/dt

2 ) δz

i ] = δU (9.6)

X. Równania Lagrange’a I rodzaju.

Znajdziemy teraz, opierając się na zasadzie d’Alemberta, równania ruchu układu nieswobodnego, wyrażając siły reakcji w
ten sposób aby spełnić równania więzów. Równania te pozwolą wyznaczyć zarówno ruch układu jak i siły reakcji, które to
nie są wiadome. Powróćmy w tym celu do równania (9.5) i rozpiszmy je na składowe :

Xi + mi (d

i/dt

2 ) = 0 ; Y

i + mi (d

i/dt

2 ) = 0 ; Z

i + mi (d

i/dt

2 ) = 0

Są to równania układu swobodnego. Jeżeli nałożymy więzy postaci :
Gi (qj, t ) = 0 ; i = 1, .. , α ; j = 1, ... ,3n
To wariacje współrzędnych δxi , δyi , δzi nie będą już niezależne ponieważ powinny spełniać α równań różniczkowych
postaci :

ΣΣΣΣ

[ (

∂

Gj /

∂

xi ) δxi + (

∂

Gj /

∂

yi ) δxi (

∂

Gj /

∂

zi ) δxi ] = 0 ; j = 1, ..., α (10.1)

Równanie to oczywiście można zapisać następująco :

ΣΣΣΣ

gradi Gj δri = 0 ; j = 1, ..., α (10.2)

Mnożąc równanie (10.1) przez nieznane współczynniki λi tj. stosując metodę mnożników Lagrange’a , a następnie dodając
odpowiednie człony do równania (9.5) otrzymujemy :
n k

ΣΣΣΣ

{ [ Xi - mi (d

xi/dt

2 ) +

ΣΣΣΣ

λi (

∂

Gj /

∂

xi ) ] δxi + [ Yi - mi (d

yi/dt

2 ) +

ΣΣΣΣ

λi (

∂

Gj /

∂

yi ) ] δyi +

i=1 j=1 j=1

+ [ Zi - mi (d

zi/dt

2 ) +

ΣΣΣΣ

λi (

∂

Gj /

∂

zi ) ] δzi } = 0 (10.3)

Wybierzemy teraz współczynniki λi tak aby wyrażenia stojące w nawiasach przy wariacjach były równe zeru. Wtedy :

Xi - mi (d

xi/dt

2 ) +

ΣΣΣΣ

λi (

∂

Gj /

∂

xi ) = 0 (10.4)

Yi - mi (d

yi/dt

2 ) +

ΣΣΣΣ

λi (

∂

Gj /

∂

yi ) = 0

Zi - mi (d

zi/dt

2 ) +

ΣΣΣΣ

λi (

∂

Gj /

∂

zi ) = 0

Równania (10.4), jest ich 3n, są to równania układu nieswobodnego i nazywamy je równaniami Lagrange’a I rodzaju.
( Równania te wyprowadził Lagrange w znamienitym dziele pt. „Mecanique analytique” 1788 )
Równania te wraz z α równaniami więzów wystarczają aby znaleźć 3n współrzędnych xi , yi , zi oraz α nieznanych
mnożników Lagrange’a λi. Równania te są, oczywiście równoważne zasadzie D’Alemberta.
Równania (10.4) możemy przepisać do postaci :

mi (d

ri /dt

2 ) - F

i - λi grad Gi = 0 (10.5)

XI. Zasada Gaussa.

Zasada Gaussa w odróżnieniu od zasady d’Alemberta polega na tym, że zamiast przesunięć przygotowanych δri , we
wzorze (9.4), wprowadza się przyspieszenia przygotowane δai, przy założeniu że : δri = δvi = 0. Wyrażenia δai noszą
nazwę wariacji Gaussa. Zasada Gaussa ma zatem postać :

ΣΣΣΣ

( Ji + Fi ) δai = 0 (11.1)

Ponieważ siły Fi są danymi funkcjami współrzędnych, prędkości i czasu, więc zgodnie z uczynionym założeniem :
δri = δvi = 0. oraz δt = 0 zatem również δFi = 0. Możemy zapisać wzór (11.1) następująco :

ΣΣΣΣ

mi [ (Fi /mi ) - ai ] [ δai (1/mi )δFi ] = 0 (11.2)

I dalej, po przekształceniach :

δ ½

ΣΣΣΣ

mi [ ai - (Fi /mi )] [ ai - (Fi /mi )] = δ ½

ΣΣΣΣ

mi [ ai - (Fi /mi )]

2 = 0 (11.3)

Wyrażenie :

Z = ½

ΣΣΣΣ

mi [ ai - (Fi /mi )]

2 (11.4)

Nazywamy „skrępowaniem” lub „przymusem” układu. Za pomocą tej wielkości możemy zasadę Gaussa wyrazić wzorem :
δZ = 0 (11.5)
To znaczy : wariacja przymusu jest równa zeru tj. przymus w ruchu rzeczywistym ma wartość ekstremalną. Można
pokazać, że w ruchu rzeczywistym przymus przybiera wartość minimalną, z tego powodu zasada Gaussa nazywa się
również „zasadą najmniejszego przymusu” lub „zasadą najmniejszego skrępowania” . [ 14, od str. 107 ].

Oprócz zasady Gaussa możemy wprowadzi inne różniczkowe zasady wariacyjne np. zasadę Hertza – najprostszego toru,
zasadę Jourdaina, można również wykazać iż wszystkie te zasady są równoważne tj. jak należy się tego spodziewać, w
finale prowadza do tych samych równań dynamiki układów mechanicznych. Mimo wszystko należy pamiętać, że zasada
d’Alemberta jest podstawową różniczkową zasadą wariacyjną MA. Zacytujmy ponownie Lanczosa :
„Zasada d’Alemberta pozwala rozwiązywać zadania mechaniki w sposób zupełny. Wszystkie pozostałe zasady mechaniki
– są to, prostu matematycznie inne sformułowania zasady d’Alemberta. Najbardziej rozwinięta wariacyjna zasada
mechaniki, zasada Hamiltona, może być otrzymana z zasady d’Alemberta na drodze pewnego matematycznego
przekształcenia. W tych przypadkach, kiedy stosowalne są obie zasady, są one równoważne. Jednak zasada Hamiltona
odnosi się tylko do układów holonomicznych, podczas gdy zasada d’Alemberta może być stosowana zarówno do układów
holonomicznych jak i nieholonomicznych.
Zasada d’Alemberta jest bardziej elementarna w porównaniu z pozostałymi zasadami wariacyjnymi , ponieważ nie
wymaga ona całkowania względem czasu. Niedostatkiem tej zasady jest to ,że praca wirtualna sił bezwładności jest
wielkością niesprowadzalną do jednej funkcji skalarnej. To powoduje niewygodę przy wykorzystywaniu współrzędnych
krzywoliniowych”. [ 2- literatury w języku angielskim , str. 116 ]

XII. Równania Lagrange’a II rodzaju. Pojęcie lagranżjanu.

Zdefiniujmy teraz pewne wielkości. Wielkość określona zależnością :
n n

T = ½

ΣΣΣΣ

mi vi

2 =

ΣΣΣΣ

mi vi

•

vi (12.1)

i=1 i=1
nazywa się „energią kinetyczną“ układu n-punktów materialnych.
Wielkości :
n

pi =

ΣΣΣΣ

mi vi

(

∂

rj/

∂

qj ) ; j = 1, ... , k (12.2)

i=1

nazywamy „pędami uogólnionymi”. Na mocy równości :

∂

rj/

∂

qj =

∂

vj/

∂

•

otrzymujemy :

pi =

∂

•

ΣΣΣΣ

mi vi

•

vi (12.3)

i=1
Zatem :

pi =

∂

•

(12.4)

Jak widać pęd uogólniony jest pochodną energii kinetycznej względem prędkości uogólnionej. Zasadę d’Alemberta
możemy zapisać wykorzystując energię kinetyczną. Ale można również pokazać, że :

T = ½

ΣΣΣΣ

pi qi

•

(12.4a)

Rozpatrzmy teraz zasadę d’Alemberta.

ΣΣΣΣ

(Fi - ai mi ) δri = 0 ⇒ d/dt

ΣΣΣΣ

mi vi δri = δ ½

ΣΣΣΣ

mi vi

2 +

ΣΣΣΣ

Fi δri

--- T ---- ---δW---
δW – praca przygotowana sił aktywnych na przesunięciach przygotowanych.
Zatem :

d/dt

ΣΣΣΣ

mi vi δri = δ T + δW (12.5)

Związek określony wzorem (12.5) nazywa się „centralnym równaniem Lagrange’a” [ 14, str. 103 ]. Ponieważ :

ΣΣΣΣ

mi vi δri =

ΣΣΣΣ

pi δqi , zatem :

d/dt

ΣΣΣΣ

pi δqi = δ T + δW (12.6)

Oczywiście: δW =

ΣΣΣΣ

Qi δqi , zatem centralne równanie Lagrange’a dla współrzędnych uogólnionych będzie miało postać :

d/dt

ΣΣΣΣ

pi δqi = δ T +

ΣΣΣΣ

Qi δqi (12.7)

Ale : δT =

ΣΣΣΣ

[ (

∂

qi ) δqi + (

∂

•

) δqi

•

], zatem wzór (12.6) przybiera postać :

d/dt

ΣΣΣΣ

(

∂

•

) δqi

ΣΣΣΣ

[ (

∂

qi ) δqi + (

∂

•

) δqi

•

+ Q

i δqi ] (12.8)

Po przekształceniu :

ΣΣΣΣ

[ d/dt (

∂

•

) – (

∂

) - Q

i ] δqi = 0 (12.9)

Ponieważ więzy są holonomiczne a współrzędne qi

niezależne, więc δq

są również niezależne, zatem :

d/dt (

∂

•

) – (

∂

) = Q

i (12.10)

Równania (12.10) nazywamy równaniami Lagrange’a II rodzaju we współrzędnych uogólnionych. Są to rrz drugiego
rzędu, ich liczba jest równa stopniowi swobody układu. Równania te nie zawierają sił reakcji ( w przeciwieństwie do
równań Lagrange’a I rodzaju ), zatem nie pozwalają one na wyznaczenie ich wartości.

Określmy teraz jedno z ważniejszych pojęć MA – funkcje Lagrange’a ( zwaną lagranżjanem - układu mechanicznego, jak
również potencjałem kinetycznym )

L = L ( t, qi , ... , qn , q1

•

, ... , qn

•

) = T – V

Warto podkreślić, że lagranżjan jest zależny jedynie od prędkości tj. od pierwszej pochodnej współrzędnych uogólnionych,
jest to formalnym odpowiednikiem stwierdzenia, że stan układu mechanicznego jest określony całkowicie przez
współrzędne i prędkości.
Można pokazać , że spełnione są następujące równania :

∂

•

∂

•

= pi

(12.10a)

∂

qi = (

∂

qi ) - (

∂

qi ) (12.10b)

∂

t = - d/dt [

ΣΣΣΣ

(

∂

•

) qi

•

– L ] (12.10c)

Można pokazać również, że w przypadku sił potencjalnych równanie (12.6) możemy zapisać następująco :

d/dt

ΣΣΣΣ

pi δqi = δ L (12.11)

Zauważmy następnie, że :

Fi = d/dt (

∂

•

)

Jeżeli mamy do czynienia z siłami potencjalnymi to równanie (12.10) możemy zapisać w postaci :

d/dt (

∂

•

) – (

∂

) = -

∂

qi (12.12)

Ponieważ

∂

•

= 0 otrzymujemy :

d/dt (

∂

•

) – (

∂

) = 0 (12.13)

Można dowieść, że równania Lagrange’a II rodzaju równoważne są zasadzie d’Alemberta.

Wzór (7.3) dla sił uogólnionych możemy zapisać również w postaci :

Qi =

ΣΣΣΣ

Fj (

∂

xj /

∂

qi ) (12.8)

j
dla układów zachowawczych :

Qi =

ΣΣΣΣ

(

∂

xj ) (

∂

xj /

∂

qi ) = -

∂

qi (12.9)

J
Sił wyrażające się wzorem :

Qi =

ΣΣΣΣ

(

∂

xi ) + d/dt (

∂

•

) (12.9a)

Nazywamy siłami o potencjale uogólnionym. Przykładem siły mającej potencjał uogólniony jest siła Lorentza.
Można pokazać , że :
Qi =

∂

Energia kinetyczna układu mechanicznego wyrażona we współrzędnych uogólnionych.

Rozpatrzmy teraz nieco dokładniej strukturę równania dla energii kinetycznej, zapisując je we współrzędnych
uogólnionych.

dri/dt = (

∂

ri/

∂

qj ) qj

•

+ (

∂

ri/

∂

t ) - dla układu reonomicznego

dri/dt = (

∂

ri/

∂

qj ) qj

•

- dla układu skleronomicznego

Zatem dla układu skleronomicznego

∂

ri/

∂

t = 0, zatem :

T = ½

ΣΣΣΣ

(

∂

ri/

∂

qj ) (

∂

ri/

∂

qk ) qj

•

(12.10)

I dalej :

T = ½

ΣΣΣΣ

mi aik qi

•

(12.11)

Gdzie aik =

ΣΣΣΣ

(

∂

ri/

∂

qj ) (

∂

ri/

∂

qk ) – jest dodatnio określoną formą kwadratową prędkości uogólnionych

Dla układu reonomicznego otrzymamy :

T = ½

ΣΣΣΣ

mi {

ΣΣΣΣ

[ (

∂

ri/

∂

qj ) qj

•

+ (

∂

ri/

∂

t) ] }2 = ½

ΣΣΣΣ

mi aik qi

•

ΣΣΣΣ

mi ai qi

•

+ a0 (12.12)

Równanie to zapisuje się zazwyczaj następująco :
T = T0 + T1 + T2

T0 = a0 ; T1 =

ΣΣΣΣ

mi ai qi

•

; T2 = ½

ΣΣΣΣ

mi aik qi

•

Gdzie : ai = (

∂

ri/

∂

qj ) (

∂

ri/

∂

t ) ; a0 = ½

ΣΣΣΣ

mi (

∂

ri/

∂

t) 2

Widać więc , że w ogólnym przypadku energia kinetyczna składa się z trzech członów : kwadratowego T2, liniowego Ti i
formy zerowej T0.
[ dokładnie zobacz 15, str. 41 ]

Przykład 12.1 Znaleźć wyrażenie dla energii kinetycznej punktu materialnego mogącego poruszać się po prostej
obracającej się w płaszczyźnie xy z prędkością kątową ω.
Składowe kartezjańskie położenia punktu są dane :
x = r cos(ωt) ; y = r sin(ωt)

•

= r

•

cos(ωt) – r ω sin(ωt) ; y

•

= r

•

sin(ωt) + r ω sin(ωt) ;

Zatem :

T = ½ m ( x

•

2 + y

•

2 ) = ½ mr

•

2 + ½ m r2 ω2

--- T1--- --- T0---
W ogólnym przypadku :

T = T( q1 , ... , qm , q1

•

, ... , qm

•

, t )

Zatem pochodna po czasie energii kinetycznej jest dana wzorem:
m m

dT/dt =

ΣΣΣΣ

(

∂

qi) qi

•

ΣΣΣΣ

(

∂

•

) qi

•

+ (

∂

t )

i i
Ale można pokazać, że :
dT/dt = P + d/dt ( 2T0 + T1 ) - (

∂

t ) (12.13)

P =

ΣΣΣΣ

Qi qi

•

- moc sił uogólnionych.

Dla więzów skleronomicznych równanie (12.13) przyjmuje postać :
dT/dt = P
co jest wyrazem zasady zachowania energii. Dla sił potencjalnych mamy : P = dV/dt

Całki pierwsze równań Lagrange’a II rodzaju.

Dla omawianych równań wielokrotnie możemy znaleźć pewne ich całki pierwsze. Zapiszmy te równania w równoważnych
postaciach :

d/dt (

∂

•

) – (

∂

) = 0

d/dt (

∂

•

) – (

∂

) = Q

d/dt (

∂

•

) = (

∂

) + (

∂

)

Oczywiście na mocy wprowadzonych wzorów mamy :

•

– (

∂

) = 0 (12.13)

Jak wiadomo znajomość całek pierwszych równań ruchu jest bardzo pożyteczna gdyż ułatwia ona dalsze ich
rozwiązywanie. Niezależnie od pożytku matematycznego z nich płynącego, całki pierwsze mają wielokrotnie interpretacje
fizyczna o podstawowym znaczeniu. W mechanice do całek pierwszych należy m.in. całka energii i całka pędu.

Przypomnijmy pewne wiadomości z matematyki :
Definicja 12.1 Rozpatrzmy autonomiczny układ równań różniczkowych postaci :

•

= Fi (x1 , ... , xn )

Prawa storna tego równania tj. układ funkcji Fi , niech będzie określona w pewnym obszarze D

⊂

Rn.

Funkcja skalarna Gi (x1 , ... , xn ) nie równa tożsamościowo stałej liczbie, określona w obszarze D , nazywa się „całką
pierwszą” rozpatrywanego układu jeżeli pozostaje ona stała wzdłuż dowolnej linii całkowej układu rr

Określenie całki pierwszej dla układu nieautonomicznego :

•

= Fi (t, x1 , ... , xn )

sprowadza się do formalnego sprowadzenia tego układu do postaci autonomicznej poprzez dopisanie jeszcze jednego
równania postaci dt/dt = 1
Układ mechaniczny nazywa się układem całkowalnym , jeżeli posiada chociaż jedną całkę pierwszą.

Definicja 12.2 Jeżeli funkcja Lagrange’a nie zależy jawnie od pewnej współrzędnej uogólnionej qα

, to taką współrzędną

nazywamy „cykliczną”.
Uwaga ! Należy zaznaczyć, że jeśli współrzędna jest cykliczna to wcale nie oznacza, że lagranżjan nie może zależeć od jej
pochodnej. Nazwa „cykliczna” bierze się z stąd, że często taką współrzędną uogólnioną jest kąt – „cyklicznie” zmieniający
się od 0 do 2π

Dla takiej współrzędnej równanie (12.13) sprowadza się do zależności :

pα

•

= 0 ⇒ pα = const.

Zatem pęd uogólniony pα , odpowiadające współrzędnej cyklicznej qα jest stały tj. jest zachowany podczas ruchu układu
mechanicznego. Szczególnymi przypadkami tego faktu są zasady zachowania pędu i momentu pędu.

Pomnóżmy teraz równanie (12.13) przez qm

•

a następnie zsumujmy po wszystkich m :

ΣΣΣΣ

[ pm

•

- (

∂

qm ) qm

•

] = 0 (12.14)

Przekształcając otrzymujemy :

d/dt

ΣΣΣΣ

( pm qm

•

- L ) = 0 (12.15)

Wprowadzając wielkość zdefiniowaną zależnością :

H =

ΣΣΣΣ

pm qm

•

- L (12.16)

Którą w dalszej kolejności nazwiemy “funkcją Hamiltona”, możemy zapisać :

•

= -

∂

Z równania tego wnioskujemy, że jeżeli czas jest zmienną cykliczną to : G = const.
Można pokazać, że jeżeli funkcje transformujące xi

→

qj nie zawierają czasu w sposób jawny a na układ mechaniczny

działają tylko siły potencjalne to :
G = T + V
Zatem możemy stwierdzić : jeżeli lagranżjan układu mechanicznego nie jest zależny jawnie od czasu to energia całkowita
tego układu jest zachowana. Całka pierwsza postaci G = const. jest więc dla tego przypadku całką energii. [2, str. 184]
Układ mechaniczny nazywa się układem konserwatywnym jeżeli spełnione są następujące warunki :

a) układ jest reonomiczny
b) działające siły są potencjalne
c) potencjał nie zależy

Dla układu zachowawczego, człony energii kinetycznej : T1 = T0 = 0

Niezmienniczość równań Lagrange’a II rodzaju.

Rozważmy układ holonomiczny, którego konfiguracja w każdej chwili t jest określona k współrzędnymi uogólnionymi
qi . Ruch układu możemy reprezentować jako ruch punktu M w k-wymiarowej przestrzeni konfiguracyjnej. Jeżeli
wprowadzimy teraz nowe współrzędne ūi związane ze starymi zmiennymi związkami :
ūi = fi (qi ) (12.17)
Zakładamy, że jakobian przekształcenia (12.17) jest różny od zera. Istnieje wtedy przekształcenie odwrotne :
qi = φi ( ūi ) (12.18)
Ruch układu możemy wtedy traktować również jako ruch punktu N w przestrzeni konfiguracyjnej ūi
Przekształcenie (12.17) traktowa możemy jako odwzorowanie punktów jednej przestrzeni na punkty drugiej przestrzeni.
Z tego względu przekształcenia te nazywamy „przekształceniami punktowymi”.
Można wykazać, że równania Lagrange’a II rodzaju są niezmiennicze względem przekształceń punktowych (12.17)

Całkowe zasady wariacyjne MA.

XIII. Zasada Hamiltona.

Rozważane dotychczas zasady i wynikające z nich równania ( głównie zasada d’Alemberta oraz równania Lagrange’a I
rodzaju ), wiążą ze sobą zdarzenia czasoprzestrzenne w infinitezymalnie sąsiadujących ze sobą punktach przestrzeni
konfiguracyjnej i o infinitzymalnym interwale czasowym. Wynika to z ich różniczkowego charakteru – rozpatrujemy
równania zawierające pochodne współrzędnych punktów układu mechanicznego względem czasu. Wiążą one konfiguracje
tego układu w chwili t z konfiguracją układu w chwili t + dt. W tym kontekście mówimy o przyczynowym ujmowaniu
zjawisk przyrody. ( kazualistycznym )
Wprowadzone dalej zasady całkowe, w przeciwieństwie do poprzednio omówionych, charakteryzują ruch w całym,
skończonym przedziale czasu, żądając zwykle aby pewne całki ( w rozpatrywanym przedziale czasu ) miały dla ruchu
rzeczywistego ekstrema ( najczęściej minima ) w porównaniu z wartościami dla pewnej klasy ruchów porównawczych.
Wśród zasad całkowych największa rolę odgrywają tzw. „zasady najmniejszego ( poprawniej - stacjonarnego ) działania”.

Rozważmy dalej ruch układu materialnego skrępowanego więzami holonomicznymi o k stopniach swobody, opisywanego
w przestrzeni konfiguracyjnej przez współrzędne uogólnione : qi , ... , qk. Ruch ten będziemy geometrycznie badali w
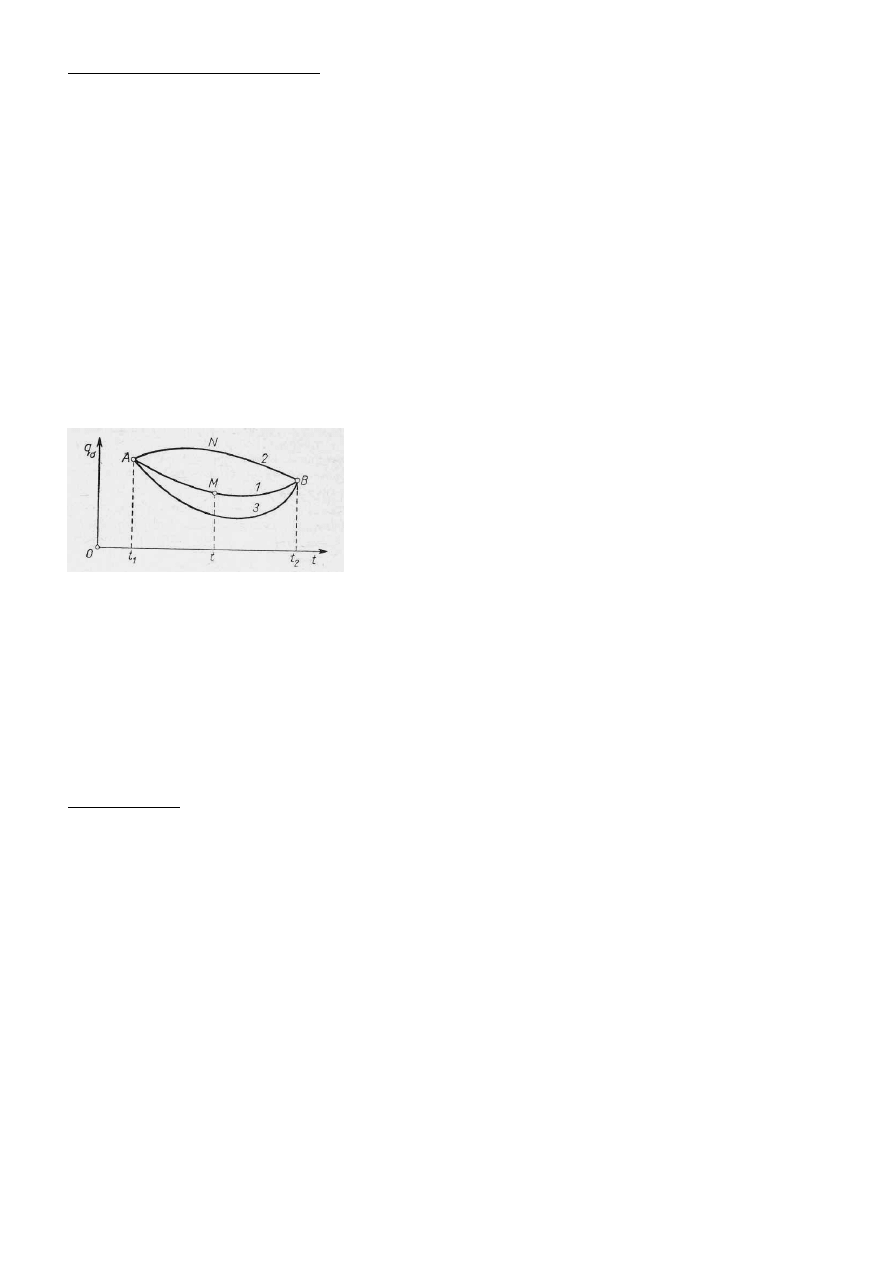
przestrzeni zdarzeń k+1 wymiarowej. Rozważmy chwile t1 i t2 dla których położenie układu określone jest
współrzędnymi q1 i q2 ( ze względów poglądowych nie tracąc na ogólności, rozpatrywać będziemy przestrzeń zdarzeń
dwuwymiarową ). Niech chwilom t1 i t2 w rozpatrywanej przestrzeni odpowiadają dwa różne punkty :
A(t1, q1 ) i B( t2 , q2 ).

Rys. 3 Trajektorie w przestrzeni zdarzeń.

Podczas ruchu rzeczywistego układ przemieści się z punktu A do B wzdłuż pewnej trajektorii , niech będzie to krzywa M.
( trajektoria bezpośrednia ). Możemy jednak rozpatrywać również inne trajektorie ( zgodne z nałożonymi więzami ) np.
krzywe 2, 3 ( trajektorie wariacyjne ). Wprowadzimy teraz kryterium pozwalające wyróżnić właśnie ta krzywą M po której
układ porusza się w ruchu rzeczywistym. Aby go wyprowadzić zdefiniujmy funkcjonał o postaci :
t2

S [ qi, qi

•

, t ] =

∫

L dt (13.1)

t1
Funkcjonał ten nazywamy „działaniem w sensie Hamiltona” ; L = T – V – funkcja Lagrange’a ;

zmienne : ( qi, qi

•

, t ) – to zmienne Lagrange’a.

Zasada Hamiltona. Rzeczywisty ruch układu mechanicznego w polu sił potencjalnych , przy przejściu z punktu A do B
przebiega w taki sposób, że działanie S, obliczone wzdłuż trajektorii tego ruchu ma wartość stacjonarną w porównaniu z
wartościami które przybiera działanie S wzdłuż dróg wariacyjnych.
Zatem dla trajektorii bezpośredniej spełnione jest równanie wariacyjne δS = 0.
Zasada sformułowana w ten sposób została wyprowadzona w oparciu o zasadę d’Alemberta przyjętą jako postulat. Można
jednak postąpić odwrotnie. Zaleta zasady Hamiltona jest jej niezmienniczość względem wyboru układu odniesienia ( w
szczególności od wyboru układu współrzędnych ). Ponadto pozwala ona formułować w sposób jednolity prawa odnoszące
się do rozmaitych dziedzin fizyki np. elektrodynamiki, hydrodynamiki, optyki i tym samym stwarza możliwość rozwijania
wielu analogii i uogólnień.
Można pokazać, że dla dostatecznie małego przedziału czasu

∆

t = t2 – t1 funkcjonał S przybiera na trajektorii

bezpośredniej wartość minimalną, stad zasada Hamiltona bywa nazywana „zasadą najmniejszego działania”
( zobacz pewne komentarze dotyczące minimum funkcjonału w tekście pt. „Podstawy rachunku wariacyjnego” )

Uwaga ! Warunek minimalności nie jest oczywiście spełniony na każdej drodze. Dla przykładu rozpatrzmy ruch
bezwładny na powierzchni kuli. Jeżeli łączymy ze sobą dwa bliskie punkty M i N to możemy wyznaczyć najkrótsza drogę
po linii geodezyjnej . Jeżeli jednak rozpatrywać będziemy ruch między dwoma symetrycznymi punktami A i B, to każdy
południk może być torem bezpośrednim i nie można wyznaczyć minimalnej wartości działania.
Takie położenie, które możemy osiągnąć nieskończenie bliskimi sobie drogami bezpośrednimi, nazywamy „ sprzężonymi
ogniskami kinetycznymi”. Można wykazać, że warunek minimalności działania jest przy więzach niezależnych od czasu

spełniony jeżeli położenia końcowe jest od początkowego oddalone nie bardziej niż najbliższe ognisko kinetyczne
sprzężone z położeniem końcowym. [ 7, str. 317 ]

rys. 4 Tory ruchu na powierzchni kuli.

W tym przypadku : δ2S

≥

0 zatem funkcjonał posiada minimum. [ 1- literatury w języku rosyjskim , str. 61 ]

Jak wiadomo odpowiednie równanie Eulera ( w tym przypadku zwane równaniem Eulera –Lagrange’a ) dla funkcjonału
postaci (13.1) ma postać :

d/dt (

∂

•

) - (

∂

qi ) = 0 ; i = 1, .. ,n (13.2)

d/dt (

∂

•

) = (

∂

qi ) ; i = 1, .. ,n (13.2a)

Jak widać równanie to jest niczym innym jak równaniem Lagrange’a II rodzaju. Zasadę Hamiltona można więc
wyprowadzi z tych ostatnich. Warto zauważyć, że równanie (13.2a) ma strukturę :
Szybkość zmian pędu uogólnionego = uogólniona siła.

W przypadku kiedy mamy do czynienia z układem swobodnym wtedy : L ( qi, qi

•

, t )

= T ( qi, qi

•

, t )

δS = δ

∫

T dt = δ

∫

ΣΣΣΣ

mi aik qi

•

Można pokazać, że zarówno równania Lagrange’a II rodzaju jak i równania Eulera-Lagrange’a pozostaną niezmienione
jeżeli do lagranżjanu dodamy pochodną zupełną d

/dt , dowolnej funkcji

(q, t) – mającej ciągłe drugie pochodne tj.

wspomniane równania są niezmiennicze wobec transformacji :
L’

→

L + d

/dt

XIV. Zasada Maupertuisa-Lagrange’a. ( M-L )

W zasadzie Hamiltona porównuje się ruch rzeczywisty z ruchami porównawczymi ( wariacyjnymi) w tych samych
chwilach czasu, mówimy wtedy o wariacji synchronicznej tj. wariacji bez wariacji czasu. W zasadzie M-L porównuje ruch
rzeczywisty z ruchami porównawczymi w różnych chwilach czasu. Zasadę ta wykorzystujemy w układach
holonomicznych, skleronomicznych dla sił zachowawczych spełniających zasadę energii mechanicznej :
T + V = h = const
Warunek ten nakłada pewne ograniczenia na prędkości punktów układu mechanicznego, więc czas przejścia od punktu A
do B ( rys. 3 ) po różnych drogach jest różny. Chcąc zastosować metodę wariacyjną do tego przypadku należy stosować
wariację asynchroniczną tj. wariację z wariacją czasu.
Zacznijmy od centralnego równania Lagrange’a dla sił potencjalnych :

d/dt

ΣΣΣΣ

pi δqi = δ L = δT – δV (14.1)

ponieważ δV = δh – δT więc δV = - δT , zatem :

d/dt

ΣΣΣΣ

pi δqi = 2δT (14.2)

Po dalszych przekształceniach [ 14, str 136-138 ] możemy otrzymać zależność :
t2 t2

δ*

∫

2T dt =

∫

[ δ* 2T + 2T (δt)

•

) ] dt = 0 (14.3)

δ* - wariacja asynchroniczna
Wprowadźmy wielkość :
t2

W =

∫

2T dt (14.4)

t1
którą nazywamy „działaniem w sensie M-L“. Możemy zatem zapisać :
δ*W = 0
Zasada M-L. Działanie w sensie M-L między dwoma ustalonymi położeniami układu w przestrzeni konfiguracyjnej ma
wartość stacjonarną w ruchu rzeczywistym w porównaniu z ruchami wariacyjnym, przy założeniu , że wzdłuż trajektorii

bezpośredniej i trajektorii wariacyjnych ma miejsce zachowanie całkowitej energii mechanicznej o tej samej stałej
wartości.
Zasadę tę wprowadził Maupertius bez uzasadniania matematycznego ( i odwołując się do niejasnych założeń ), jej dowód
matematyczny podał Lagrange.

XV. Zasada Jakobiego.

Zasadę Jakobiego otrzymujemy w wyniku pewnego przekształcenia zasady M-L do postaci, w której nie występuje czas t.
Czas eliminujemy korzystając z równania : T + V = h = const.
Zapiszmy wzór (14.4) następująco :
t2

W =

∫

sqrt(T)sqrt(T) dt (15.1)

t1
Następnie :
2T = 2 ( h – T)

2T =

ΣΣΣΣ

mi vi

2 =

ΣΣΣΣ

( dri/dt ) (drj/dt ) =

ΣΣΣΣ

( dsi/dt )

2 (15.2)

Zatem :
t2

W =

∫

sqrt[ 2 (h – V)] sqrt [

ΣΣΣΣ

( dsi/dt )

2 ] dt (15.3)

t1
Wzór (15.3) przedstawia działanie w postaci Jakobiego. Działanie to przybiera wartość stacjonarną dla ruchu
rzeczywistego. Ponieważ nie występuje w niej czas w postaci jawnej możemy ten fakt zapisać korzystając z wariacji
synchronicznej δ, zatem :
δW = 0
Przykładowo dla jednego punktu poruszającego się po pewnej krzywej łączącej A i B, przy zadanej wartości energii
całkowitej h, otrzymujemy :
t2

∫

sqrt[ 2m (h – V)] ds =0 (15.4)

t1
Wyrażenie to przedstawia przypadek szczególny ( ale często wykorzystywany ) zasady Jakobiego. Możemy zatem
powiedzieć :
Rzeczywista droga układu miedzy punktami A i B , przy zadanej wartości energii całkowitej jest drogą, dla której działanie
w sensie Jakobiego przyjmuje wartość stacjonarną.
Dla bardziej szczególnego przypadku kiedy na punkt nie działają żadne siły i porusza się on po zadanej powierzchni
niezależnej od czasu otrzymamy :

∫

ds =0 (15.5)

krzywe spełniające równanie (15.5) to jak wiadomo linie geodezyjne.

XVI. Siły żyroskopowe i siły dyssypacyjne (rozpraszające).

Siły żyroskopowe to siły nie wykonujące pracy.
Jeżeli

i są siłami żyroskopowymi to :

P =

ΣΣΣΣ

i qi

•

= 0

Inna równoważna definicja sił żyroskopowych mówi, że są to siły o mocy równej zeru.
Najprostszym przykładem sił żyroskopowych są siły uogólnione będące liniowymi funkcjami prędkości uogólnionych :

i =

ΣΣΣΣ

γij

•

(16.1)

gdzie γij (t, q1, ..., qk ) = - γji (t, q1, ..., qk ) – warunek antysymetrii macierzy współczynników γji jest nie tylko
warunkiem koniecznym ale i wystarczającym na to by siły były żyroskopowe [ 15, str. 47 ]

Ogólnie siły liniowo zależne do prędkości uogólnionych nazywa się wiskotycznymi.

Można pokazać, że jeżeli na układ mechaniczny oprócz sił potencjalnych działają siły żyroskopowe to zasada zachowania
energii całkowitej pozostaje nadal spełniona. Przykładem siły żyroskopowej jest siła Coriolisa i siła Lorentza.

Siły dyssypacyjne ( inna nazwa : dyssypatywne ) to siły wywołujące ubytek energii mechanicznej układu.
Inna równoważna definicja sił dysypatywnych mówi, że są to siły o mocy niewiększej od zera.

P =

ΣΣΣΣ

Qi qi

•

≤

Najbardziej charakterystycznym przykładem siły dysypatywnej jest siła oporu ( tarcia )

Siły dyssypatywne są siłami wiskotycznymi które możemy określi za pomocą tzw. dyssypacyjnej funkcji Rayleigha.
( czytaj : Releja )

R = ½

ΣΣΣΣ

βij qi

•

(16.2)

βij = βji - jednorodna symetryczna forma kwadratowa prędkości uogólnionych.
Siły dyssypatywne określimy następująco :

Q*i = -

ΣΣΣΣ

βi qi

•

(16.3)

Zatem siła dyssypatywna może by przedstawiona jako :

Q*i = -

∂

•

(16.4)

Fizyczny sens funkcji Rayleigha to prędkość zmniejszania się całkowitej energii mechanicznej h, układu materialnego :
dh/dt = R
Siły dyssypatywne możemy uwzględni w równaniach Lagrange’a drugiego rodzaju następująco :

d/dt (

∂

•

) – (

∂

) = Q

i + Q*i

Równania ruchu układów holonomicznych w zmiennych kanonicznych.

XVII. Równania kanoniczne Hamiltona.

Metoda Lagrange’a pozwala sprowadzić problem ruchu do zagadnienia całkowania układu k ( k- liczba stopni swobody )
rrz drugiego rzędu. Hamilton wskazał drugi sposób rozwiązywania zagadnień dynamicznych , który prowadzi do
całkowania układu 2k równań rrz pierwszego rzędu. Równania te dzięki swojej prostocie i symetrii zostały nazwane
„równaniami kanonicznymi”. Formalizm Lagrange’a i formalizm Hamiltona stanowią podstawę dla formułowania prawie
wszystkich równań fizyki teoretycznej. Nie można twierdzić, że formalizm Lagrange’a jest dogodniejszy od formalizmu
Hamiltona lub odwrotnie, konkretne wykorzystanie zależy bowiem od rodzaju rozwiązywanego problemu ruchu.

Zmienne ( t, qi

, p

) – nazywamy „zmiennymi kanonicznymi” ( lub zmienne Hamiltona )

Zmienne ( t, qi

, q

•

) – nazywamy „zmiennymi Lagrange’a”

Przestrzeń zmiennych ( t, qi

) nazywamy „przestrzenią zdarzeń”

Przestrzeń zmiennych ( qi

) nazywamy „przestrzenią konfiguracyjną”

Przestrzeń zmiennych ( t, qi

, p

) nazywamy „przestrzenią stanów”

Przestrzeń zmiennych ( qi

, p

) nazywamy „przestrzenią fazową”

Wprowadźmy teraz funkcje K (t, qi , pi ), określoną zależnością :

K =

ΣΣΣΣ

pi qi

•

- T (17.1)

Przekształcającą zmienne Lagrange’a do zmiennych kanonicznych.
Jeżeli rozpatrujemy siły potencjalne to możemy wprowadzić funkcję Hamiltona zwaną hamiltonianem
( zobacz równanie (12.16) )

H = K + V =

ΣΣΣΣ

pi qi

•

- T + V (17.2)

Jak pamiętamy :

∂

qi = d/dt (

∂

•

) = pi

•

(17.3)

Zatem :

H =

ΣΣΣΣ

(

∂

•

)

•

- L (17.4)

Należy podkreślić, że funkcja Hamiltona zależy od współrzędnych uogólnionych, pędów uogólnionych i czasu.
Powróćmy do wzoru (12.10c) :

∂

t = - d/dt [

ΣΣΣΣ

(

∂

•

) qi

•

– L ]

---- H ----
Zatem :

∂

t = -

∂

t (17.5)

Jeśli lagranżjan nie zależy jawnie od czasu wtedy :

∂

t = 0

→

∂

t = 0 ⇒ H = const.

W przypadku : ri = ri ( q1, ... , qk ) ; V = V ( q1, ... , qk )
H = T + V
Zatem funkcja Hamiltona ma dla tego przypadku sens fizyczny całkowitej energii mechanicznej układu : T + V = const.

Przykład 17.1 Funkcja Hamiltona dla swobodnego punktu materialnego poruszającego się w polu siły zachowawczej
zapisana w układzie kartezjańskim ma postać :

H = ½ m v2 + V(x, y, z)

A lagranżjan :

L = ½ m v2 - V(x, y, z)

Można dowieść słuszności następujących zależności [ 14, str. 202 ; 1-literatury w języku rosyjskim , str. 164 ]:

dqi/dt =

∂

pi lub qi

•

∂

pi (17.6)

dpi/dt = -

∂

qi lub pi

•

= -

∂

qi (17.7)

oraz :
dH/dt =

∂

t (17.8)

Zależności te nazywamy „kanonicznymi równaniami ruchu Hamiltona”. Równania te możemy wyprowadzić korzystając
albo z równań Lagrange’a II rodzaju lub z zasady Hamiltona lub z centralnego równania Lagrange’a.
(i są im równoważne )
Obowiązują one dla układów mechanicznych o więzach holonomicznych, dwustronnych przy istnieniu potencjału
kinetycznego.
Jeżeli współrzędna uogólniona jest cykliczna jest również cykliczna dla funkcji Hamiltona ( i odwrotnie ).
W związku z równaniami kanonicznymi o zmiennych pi i qi mówimy , że są kanonicznie sprzężone.
Reasumując : równania Hamiltona otrzymujemy zazwyczaj wykorzystując równania Eulera-Lagrange’a,

wiążą się one z przejściem zmiennych postaci ( t, qi

, q

•

)

→

( t, qi

, p

) w oparciu o zależności (17.4) , które to są

szczególnym przypadkiem przekształcenia Legendre’a ( służy ono do zastępowania w równaniach różniczkowych
pewnego układu zmiennych przez inny i jest bardzo często wykorzystywane w fizyce ). Za pomocą odwrotnego

przekształcenia Legendre’a możemy dokona przejścia ( t, qi

, p

)

→

( t, qi

, q

•

Całki pierwsze równań kanonicznych Hamiltona.

Z równań kanonicznych Hamiltona bardzo często możemy, w prosty sposób otrzymać pewne ich całki pierwsze.
Analogicznie jak dla przypadku równań Lagrange’a II rodzaju jeżeli współrzędna qα lub qα nie występuje w sposób jawny
w funkcji Hamiltona tj. jest współrzędną cykliczną wnioskujemy , że :

pα

•

= -

∂

qα = 0 lub qα

•

∂

pα = 0

czyli :
pα = const. lub qα = const.
jest całką pierwszą równań ruchu.

XVIII. Nawiasy Poissona ( Poisson bracket ) .

( zobacz również tekst pt. „Podstawy rachunku wariacyjnego” )
Równania kanoniczne możemy zapisać w bardzo elegancki sposób za pomocą nawiasów Poissona. Nawiasy Poissona
odgrywają kluczowa rolę przy przejściu od mechaniki klasycznej do mechaniki kwantowej (równania ruchu MK zapisane
przy użyciu tych nawiasów odpowiednio zinterpretowane stają się równaniami ruchu MQ ).

Definicja 18.1 Niech będą dane dwie funkcje różniczkowalne ( o pochodnych cząstkowych odpowiedniego rzędu )
zmiennych kanonicznych :

( t, qi

, p

)

;

( t, qi

, p

). Nawiasem Poissona tych funkcji nazywamy wyrażenie :

[

] =

ΣΣΣΣ

[ (

∂Φ

∂

qi ) (d

∂

pi ) - (

∂Φ

∂

pi ) (d

∂

qi ) ] (18.1)

i=1

Można dowieść następujących własności nawiasu Poissona :
[

] = - [

] - relacja antykomutacji. (18.2a)

[

] = [

] = 0 (18.2b)

[

1 +

2 ,

] = [

] + [

2 ,

]

(18.2c)

[ α

] = α [

] ; α – dowolna liczba rzeczywista.

(18.2d)

[

2 ,

] =

1 [

2 ,

] +

2 [

]

(18.2e)

∂

] = [

∂Φ

∂

t ,

] + [

∂Ψ

∂

t ]

(18.2f)

[

, qi ] = -

∂Φ

∂

pi ; [

, pi ] = -

∂Φ

∂

(18.2g)

[ qi , qj ] = [ pi , pj ] = 0 ; [ qi , pj ] = δ

j - analogia komutatorów Heisenberga.

[

2 ,

] = 2

[

]

(18.2h)

Dla trzech funkcji zmiennych kanonicznych możemy utworzyć podwójny nawias Poissona :
[

, [

] ]

przy czym ma miejsce następująca tożsamość Poissona-Jakobiego :

[

, [

] ] + [

, [

]] + [

, [

, ] ] = 0 (18.3)

Rozważmy teraz związek nawiasów Poissona z równaniami ruchu układu materialnego. W tym celu obliczmy pochodną
zupełną względem czasu funkcji zmiennych kanonicznych

/dt =

ΣΣΣΣ

[ (

∂Φ

∂

qi )qi

•

+ (d

∂

pi )pi

•

] + (

∂Φ

∂

t) (18.4)

Jeżeli podstawimy : pi

•

= -

∂

qi ; qi

•

∂

pi , to otrzymamy :

/dt =

ΣΣΣΣ

[ (

∂Φ

∂

qi )(

∂

pi ) - (d

∂

pi )(

∂

qi ) ] + (

∂Φ

∂

t) (18.5)

Zatem :
d

/dt = [

, H ] + (

∂Φ

∂

t) (18.6)

tzn. pochodna zupełna dowolnej funkcji zmiennych kanonicznych względem czasu jest równa nawiasowi Poissona tej
funkcji i funkcji Hamiltona plus pochodna cząstkowa tej funkcji po czasie.
Jeżeli funkcja

nie zależy jawnie od czasu, to :

/dt = [

, H ] (18.7)

W mechanice kwantowej odpowiednik równania (18.6) nazywa się równaniem Heisenberga.
Z równania (18.7) wynika, że funkcja

jest stałą ruchu wtedy i tylko wtedy jeśli :

[

, H ] = 0 tj.

= const

⇔

[

, H ] = 0 (18.8)

Z tego faktu możemy skorzystać w celu wyznaczenia całek pierwszych równań ruchu.

Za pomocą wzoru (18.6) możemy zapisać kanoniczne równania ruchu Hamiltona. Przyjmując kolejno za współrzędne
uogólnione qi i pędy uogólnione pi , funkcję

otrzymujemy :

dqi/dt = [ qi, H ] ; dpi/dt = [ pi, H ] ; i = 1, ... , k (18.9)
Jest to forma zapisu równań ruchu za pomocą nawiasów Poissona

Twierdzenie 18.1 ( twierdzenie Poissona ) Jeżeli dwie funkcje

( t, qi

, p

)

;

( t, qi

, p

), są całkami układu

kanonicznego Hamiltona , to ich nawias Poissona jest również całką tego układu.

Mając zatem dwie całki pierwsze możemy utworzyć trzecią całkę pierwszą itd. Ta nowa całka może jednak w pewnych
okolicznościach by równa tożsamościowo zeru lub by zależna od dwóch poprzednich.

Przykład 18.1 Obliczyć nawiasy Poissona dla składowych kartezjańskich wektora momentu pędu punktu materialnego.
r = r(x, y, z ) p = ( px , py , pz )
Składowe kartezjańskie wektora momentu pędu są równe :

Jx = m(yz

•

- zy

•

) = ypz - zpy

Jy = m(zx

•

- xz

•

) = zpx - xpz

Jz = m(xy

•

- yx

•

) = xpy - ypx

Obliczmy nawias Poissona :
3

[ Jx , Jy ] =

ΣΣΣΣ

[ (

∂

Jx/

∂

ri )(

∂

Jy/

∂

pi ) (dJx/

∂

pi )(

∂

Jy/

∂

ri ) ] = (

∂

Jx/

∂

x )(

∂

Jy/

∂

px ) - (dJx/

∂

px )(

∂

Jy/

∂

x ) +

i=1 = 0 = 0
+ (

∂

Jx/

∂

y )(

∂

Jy/

∂

py ) - (dJx/

∂

py )(

∂

Jy/

∂

y ) + (

∂

Jx/

∂

z )(

∂

Jy/

∂

pz ) - (dJx/

∂

pz )(

∂

Jy/

∂

z ) = (-py) (-x ) – ypx = Jz

= 0 = 0
Przez cykliczną zmianę wskaźników x

→

x dostajemy następne nawiasy Poissona :

[ Jy , Jz ] = Jx ; [ Jz , Jx ] = Jy
Można pokazać na podstawie wzoru (18.2h), że :

[ J2 , J ] = 0 tj. nawias Poissona wektora momentu pędu z jego własnym kwadratem jest równy zeru.
( relacja ta przyda się w mechanice kwantowej )

Można spotkać się czasami ze stwierdzeniem, że dwie funkcje znajdują się w inwolucji lub komutują ze sobą jeśli ich
Nawias Poissona jest równy zeru.

Uogólniony nawias Poissona.

Niech A(z), B(z) będą dwiema dowolnymi funkcjami zmiennej z ( wektora zmiennych ). Uogólnieniem nawiasu Poissona
funkcji A, B jest wyrażenie :

[A, B] =

ΣΣΣΣ

gik (

∂

zi )(

∂

zk ) ; gik= gik (z) – pewien tensor ( najczęściej tensor metryczny )

i,k =1
Tensor gik możemy zapisać następująco : gik= [ zi , zk] , a nawias Poissona możemy przepisać do postaci :
2n

[A, B] =

ΣΣΣΣ

(

∂

zi )(

∂

zk )[ zi , zk]

i,k =1
Uogólnionym układem hamiltonowskim nazywamy układ opisywany następującym równaniem ruchu :

•

= [ z

, H ] ; i = 1,2, ... , 2n (18.10)

Jeżeli w szczególności tensor gik jest tensorem skośnie symetrycznym o postaci :
gik= ( 0 1 )
( -1 0 )
to przy n =1, z1 = q , z2 = p równania (18.10) są równoważne równaniom Hamiltona.
Dla układu o dowolnym wymiarze równoważność równań (18.10) zapewniona jest przy :
gik= ( 0 I ) ; I - macierz jednostkowa
( -I 0 )
( z1, ... , zN ) = ( q1, ... , qN ) ; ( zN+1, ... , z2N ) = ( p1, ... , pN ) ;

XIX. Równania Routha.

Routh zaproponował wziąć jako podstawowe zmienne, charakteryzujące stan układu mechanicznego w chwili t, część
zmiennych Lagrange’a i część zmiennych Hamiltona. Zmiennymi Routha nazywamy zmienne :

t, qi , qβ, qi

•

, pβ

•

; i = 1, ... m ; β = m+1, ... , k

Funkcje Routha definiujemy jako wielkość pośrednią pomiędzy funkcją Lagrange’a i Hamiltona :
k

R =

ΣΣΣΣ

pβ qβ

•

- L (19.1)

β = m+1
Sumowanie we wzorze (19.1) odbywa się nie po wszystkich współrzędnych uogólnionych , ale tylko po współrzędnych
cyklicznych, od których funkcja Lagrange’a nie zależy. Funkcja Routha zależy wtedy tylko od pozostałych, niecyklicznych
współrzędnych i prędkości uogólnionych oraz od stałych ruchu pi

i = 1, ... , s

związanych ze współrzędnymi cyklicznymi.

R = R(p1 = const. , …,ps = const. , qs+1 ,qs+1

•

… ,

qk,

•

)

Przy pomocy funkcji Routha z równań ruchu można wyeliminować zupełnie stopnie swobody związane ze współrzędnymi
cyklicznymi i zastąpić je przez s całek ruchu. Dla współrzędnych cyklicznych równaniami ruchu są równania Hamiltona :

∂

ps = qs

•

= const.

;

∂

qs = -ps

•

= 0

; s = m+1 , … , k (19.2)

Równania (19.1) składają się z 2(k- m) równań różniczkowych pierwszego rzędu typu Hamiltona.
Dla pozostałych współrzędnych niecyklicznych obowiązują równania Lagrange’a ( równania drugiego rzędu ) :

d/dt (

∂

•

) - (

∂

) = 0 ; i = m+1 , .. , k (19.3)

O równaniach (19.2) i (19.3) mówi się „równania Routha”. Funkcja Rutha odgrywa zatem odpowiednio rolę funkcji
Lagrange’a i Hamiltona.

XX. Metoda Hamiltona-Jakobiego.

Metody całkowania równań ruchu w sposób istotny zależy od postaci rozważanego układu równań. Równaniom tym
możemy nadać różną formę, różną – zależną od wyboru funkcji charakterystycznej, za pomocą której zostały one
zbudowane.
Do tej pory rozpatrywaliśmy dwie metody : metodę Lagrange’a i metodę Hamiltona. W dalszej kolejności rozpatrzymy
trzecią metodę, znana jako metodę Hamiltona-Jakobiego ( H-J). Za pomocą tej metody zagadnienie mechaniczne
sprowadza się do całkowania jednego równania różniczkowego o pochodnych cząstkowych , postaci :
(

∂

t) + H(t, qi ,

∂

qi ) = 0

gdzie : H – funkcja Hamiltona, S – główna funkcja Hamiltona.

Główna funkcja Hamiltona

Rozpatrzmy ruch układu holonomicznego o k stopniach swobody, którego stan określony jest w każdej chwili t przez
współrzędne uogólnione qi ; i= 1, ... ,k . Rozpatrzmy dwa stany układu mechanicznego odpowiadające dwóm różnym
chwilom czasu t1 i t2 i niech tym dwóm stanom w przestrzeni konfiguracyjnej odpowiadają dwa punkty A i B.
Rozważmy działanie w sensie Hamiltona :

S =

∫

L(t, qi , qi

•

) dt (20.1)

t1
Wartość tego funkcjonału możemy obliczy np. z równania Lagrange’a II rodzaju, dostaniemy wtedy pewne funkcje :

qi = qi ( t, C1, ... , C2k ) ; qi

•

= qi

•

( t, C1, ... , C2k )

Podstawiając te funkcje do wzoru (20.1) otrzymamy po scałkowaniu :
S = S( t1, t2, C1, ... , C2k )
Mając do dyspozycji zadane współrzędne punktów A i B wyznaczamy wartości stałych C1, ... , C2k . Mamy zatem :
S* = S*( t1, t2, q1

A, ... , q

A, q

B, … , q

B )

Gdzie q1

A, ... , q

A – współrzędne punktu A ; q

B, ... , q

B – współrzędne punktu B

Teraz osłabimy warunki nałożone na trajektorię bezpośrednią i wariacyjne przyjmując , że chwila końcowa t2 nie jest
ustalona ale zmienna .
Zatem :
t

S =

∫

L(t, qi , qi

•

) dt = S [ t, q1(t), ... , qk(t), t1, q1

A, ... , q

A ] (20.2)

t1
tj. rozpatrujemy funkcjonał zmiennych t, zmiennych q1(t), ... , qk(t) oraz pewnych stałych parametrów t1, q1

A, ... , q

Wielkość określona wzorem (20.2) nazywamy „główną funkcją Hamiltona”.

Równanie różniczkowe Hamiltona-Jakobiego.

Obliczmy teraz pochodną zupełną po czasie :

dS/dt = d/dt

∫

L(t, qi , qi

•

) dt = L

ale jest jednocześnie, jeśli działanie rozpatrywać w formie funkcji Hamiltona postaci :

S [ t, q1(t), ... , qk(t), t1, q1

A, ... , q

A ]

dS/dt =

∂

t +

ΣΣΣΣ

(

∂

qi)qi

•

(20.3)

( czas t wchodzi do funkcjonału (20.2) zarówno w formie jawnej jak i nie jawnej poprzez współrzędne uogólnione
qi = qi(t) )
Zatem :

L =

∂

t +

ΣΣΣΣ

(

∂

qi)qi

•

(20.4)

Ze wzoru tego wynika bezpośredni związek :

Pi =

∂

•

∂

qi (20.5)

Zatem możemy napisać :

∂

t +

ΣΣΣΣ

pi qi

•

- L = 0 (20.6)

ale

H =

ΣΣΣΣ

pi qi

•

- L

Zatem :

∂

t + H = 0 (20.7)

Jest to szukane równanie różniczkowe H-L, o pochodnych cząstkowych pierwszego rzędu, nieliniowe. Funkcją
niewiadomą jest w nim główna funkcja Hamiltona S.
Uwaga! Równanie H-L posiada nietrywialną analogię z równaniem falowym ( analogia mechanika falowa i mechanika
klasyczna ) w tym kontekście porównuje się prędkość fazową fali i prędkość „fali działania mechanicznego”.
[1-literatury w języku rosyjskim , str. 222]

Przykład 20.1 Jeśli funkcja Hamiltona układu mechanicznego jest dana przez wyrażenie postaci :

H =

ΣΣΣΣ

pxi

2 / m

i + V(x , t)

Wówczas równanie H-L ma postać :

ΣΣΣΣ

(1/2mi ) (

∂

xi ) + V(x , t) +

∂

t = 0

XXI. Przekształcenia kanoniczne.

Przekształcenia kanoniczne to ogólna procedura zmiany zmiennych kanonicznych postaci :
Ai= Ai( t, qi

, p

)

→

Bi= Bi( t, qi

, p

)

Przekształcenie zmiennych kanonicznych nazywamy “przekształceniem kanonicznym” jeśli równania Hamiltona
przepisane w nowych współrzędnych uogólnionych i nowych pędach uogólnionych zachowują swoją postać.
Podstawową rolę w teorii przekształceń kanonicznych odgrywają przekształcenia Legendre’a ( czytaj: leżandra )

Przekształcenia Legendre’a

Dla uproszczenia rozpatrzmy przypadek funkcji dwóch zmiennych : z = f(x, y). Różniczka tej funkcji jest dana :
dz = udx + vdy
gdzie : u(x,y) =

∂

x ; v(x,y) =

∂

Jeśli teraz jako zmienne niezależne weźmiemy u i v to x i y będą funkcjami zmiennych u i v :
x = φ(x, y) ; y = ρ(u, v)
Rozpatrzmy teraz funkcje Z =Z(u, v) taka , że jej różniczka zupełna jest równa :
dZ = φdu + ρdv
Funkcję z będziemy nazywali „funkcją tworząca” względem zmiennych x, y ; funkcja Z będzie funkcją tworzącą
względem zmiennych u, v. Przejście od zmiennych x, y do u, v i związane z tym przejście od funkcji tworzącej z do
funkcji tworzącej Z nazywamy „przekształceniem Legendre’a”.
W rozpatrywanym przypadku funkcji dwóch zmiennych przekształcenie Legendre’a ma postać :
Z = xu + yv – z
Gdy przechodzimy od zmiennych x, y do zmiennych x, v tj. od funkcji tworzącej z(x, y) do funkcji tworzącej Z(x, v) to
przekształcenie Legendre’a ma postać :
Z = yv – z
Dla przejścia postaci x, y

→

u, y mamy :

Z = xu – z
Przypadek rozpatrywany możemy teraz uogólnić dla funkcji większej ilości zmiennych :
z= z (x1, ... , xk , y1, ... , yk )
Różniczka zupełna tej funkcji jest równa :

dz =

ΣΣΣΣ

ui dxi +

ΣΣΣΣ

vi dyi

gdzie : ui =

∂

z/dxi ; vi =

∂

z/dyi ;

Dla przejścia postaci : xi , yi

→

ui , vi funkcja tworząca jest wyznaczona przekształceniem Legendre’a postaci :

Z =

ΣΣΣΣ

ui xi +

ΣΣΣΣ

vi yi - z

Dla przejścia postaci : xi , yi

→

xi , vi funkcja tworząca jest wyznaczona przekształceniem Legendre’a postaci :

Z =

ΣΣΣΣ

yi vi - z

Zastosujmy teraz przekształcenie Legendre’a do równań mechaniki. Rozważmy funkcje Lagrange’a 2k+1 zmiennych :

L = L (t, q1, ... , qk , qi

•

, ... , qk

•

)

Mamy zatem :

dL =

ΣΣΣΣ

(

∂

qi ) dqi +

ΣΣΣΣ

(

∂

•

)qi

•

+ (

∂

t)dt (21.1)

Wprowadzając pędy uogólnione : pi =

∂

•

mamy na mocy równań Lagrange’a II rodzaju zależność :

(

∂

•

)

•

= pi

•

∂

qi (21.2)

Zatem różniczkę zupełną dL możemy przedstawić następująco :

dL =

ΣΣΣΣ

•

dqi +

ΣΣΣΣ

pi dqi

•

+ (

∂

t)dt (21.3)

Funkcja Lagrange’a jest więc funkcją tworzącą względem 2k +1 zmiennych Lagrange’a.
Przejdźmy teraz od zmiennych Lagrange’a do zmiennych kanonicznych. Odpowiednie przekształcenia Legendre’a mają
już znajomą postać funkcji Hamiltona :

H =

ΣΣΣΣ

pi qi

•

- L

Zatem funkcja Hamiltona jest funkcją tworzącą względem 2k+1 zmiennych Hamiltona.

dH =

ΣΣΣΣ

•

dpi +

ΣΣΣΣ

pi dqi

•

- dL (21.4)

Podstawiając za dL wyrażenie (21.3) otrzymujemy :

dH = -

ΣΣΣΣ

•

dqi +

ΣΣΣΣ

•

dpi - (

∂

t)dt (21.5)

ale z drugiej strony mamy :

dH = -

ΣΣΣΣ

(

∂

qi )dqi +

ΣΣΣΣ

(

∂

pi) dpi - (

∂

t)dt (21.6)

Porównując dwie ostatnie zależności otrzymujemy :

∂

t = -

∂

•

∂

•

= -

∂

Wzory powyższe to nic innego jak równania kanoniczne Hamiltona, otrzymane jako rezultat przekształcenie Legendre’a
przy przejściu od zmiennych Lagrange’a do zmiennych Hamiltona.

Przekształcenia kanoniczne ( jako szczególny przypadek przekształceń stycznościowych )

Rozważmy teraz ogólną teorię przekształceń zmiennych qi

, p

→

, P

= ( t, q

1, ... , qk ; p1, ... , pk ) ;

= ( t, q

1, ... , qk ; p1, ... , pk ) (21.7)

Po pierwsze zakładamy, że jakobian tego przekształcenia jest różny od zera istnieje wtedy przekształcenie odwrotne.
tj. jeśli J =

∂

(Q1, ... , Qk ; P1, ... , Pk )/

∂

(q1, ... , qk ; p1, ... , pk )

≠

0 to istnieją funkcje :

= ( t, Q

1, ... , Qk ; P1, ... , Pk ) ;

= ( t, Q

1, ... , Qk ; P1, ... , Pk ) ;

Jak wspomniano będą nas interesowały tylko takie przekształcenia zmiennych które są kanoniczne. Oznacza to żądanie aby
równania ruchu w nowych zmiennych miały postać :
dQi

/dt =

∂

Pi , dPi/

∂

t = -

∂

gdzie K = K( t, Q1, ... , Qk ; P1, ... , Pk ) - jest pewną funkcją nowych zmiennych spełniająca rolę funkcji Hamiltona.

Warunkiem ( warunek Liego ) dostatecznym na to aby odwracalne przekształcenie (21.7) było kanoniczne jest aby forma
różniczkowa :

ΣΣΣΣ

i =

ΣΣΣΣ

i + H0 dt + dF (21.8)

gdzie : H0 , F – dowolne funkcje 4k+1 zmiennych ( t, q1, pi , Pi , Qi )
była spełniona tożsamościowo.
Forma (21.8) może by zapisana inaczej :

ΣΣΣΣ

i - Hdt =

ΣΣΣΣ

i - Kdt + dF (21.9)

K = H - H0
Formę tę nazywamy „formą Liego”. [ 14 , od str. 256 1-literatury w języku rosyjskim od str. 228 ]
Na koniec rozważań ( które oczywiście tylko zarysowują temat ) zacytuje fragment [ 10, str. 446 ] :
„Przekształcenia kanoniczne mają duże znaczenie zarówno z punktu widzenia pojęciowego jak i praktycznego. Okazuje się
,że każdy ruch można uważać za pewne przekształcenie kanoniczne, co pozwala na nadanie sensu fizycznego i to bardzo
bezpośredniego takim wielkościom jak funkcja tworząca przekształcenia....” I dalej :
„Co więcej, tego rodzaju interpretacja zbliża nas do kręgu pojęciowego mechaniki kwantowej.”

Warto również podkreślić iż równania H-J mogą by wyprowadzone jako konsekwencja pewnego przekształcenia
kanonicznego.

Przekształcenia kanoniczne tworzą grupę ( Liego ) przekształceń w przestrzeni fazowej, przy czym ustalonemu elementowi
tej grupy odpowiada ustalona funkcja tworząca, przy ustalonej wartości parametru .
Wynika z tego, że :

a) istnieje jednoznacznie ustalone przekształcenie tożsamościowe
b) superpozycja dwu transformacji kanonicznych jest przekształceniem kanoniczny.
c) transformacja odwrotna do dowolnej transformacji kanonicznej jest przekształceniem kanonicznym.

Ponadto możemy dowieść, że nawiasy Poissona są niezmiennikami przekształceń kanonicznych. ( co wynika m.in. z tego,
że równania Hamiltona można zapisać przy użyciu tych nawiasów ) [ 2, od str. 237 ]

Dynamika układów hamiltonowskich.

XXII. Przestrzeń fazowa i formalizm kanoniczny.

Jak już powiedziano przestrzeń zmiennych : qi, pi nazywamy „przestrzenią fazową”.
W przestrzeni tej możemy wprowadzić pojęcie wektora wodzącego opisującego ruch punktu w tej przestrzeni, nazwiemy
go „wektorem fazowym”, a wskazywany przez niego punkt nazwiemy „punktem fazowym”.
Tor ruchu punktu fazowego nazywamy „trajektorią fazową”. Zbiór możliwych trajektorii układu mechanicznego
nazywamy „portretem fazowym” tego układu.

Przykład 22.1 Jednowymiarowy oscylator harmoniczny.

Równania ruchu jednowymiarowego oscylatora harmonicznego na powierzchni więzów R1, możemy zapisać następująco :

m x

••

= - kx (22.1)

Oczywiście :

•

= - kx

;

•

= p/m

W ten sposób zamiast jednej zmiennej dynamicznej x wprowadzamy dwie zmienne x, p. Dostajemy następnie dwa
równania pierwszego rzędu które interpretujemy w przestrzeni zmiennych (x, p) tj. w przestrzeni fazowej.

Dowodzi się , że przez każdy punkt przestrzeni fazowej, dla postawionego zagadnienia ruchu układu mechanicznego,
może przechodzić tylko jedna trajektoria fazowa, odróżnia to przestrzeń fazową od przestrzeni konfiguracyjnej w której
przez każdy punkt może przechodzić nieskończenie wiele trajektorii. Zatem trajektorię fazowe nie mogą się przecinać.
Ma to, jak zobaczymy dalej nietrywialne konsekwencje ,oznacza to bowiem, że każdemu konkretnemu Hamiltonianowi
odpowiada pewne rozbicie przestrzeni fazowej na trajektorię q(t) , p(t) , w konsekwencji dynamika w przestrzeni fazowej
daje się sprowadzić do geometrii. [ 1, str. 88 ]

Jak wiadomo rozwiązaniem równania (22.1) jest funkcja o postaci :
x(t) = A sin( ωt + δ ) ; ω = sqrt ( k/m) – częstość oscylacji ; (22.2)
A, δ – parametry ( amplituda, faza początkowa ) zależne od warunków początkowych.
Aby otrzymać trajektorię fazowe ( portret fazowy ) dla tego zagadnienia należy zapisać równanie zależności pędu od czasu
p(t) = mωA cos(ωt + δ ) (22.3)
Równania (22.2) i (23.3) opisują elipsy w przestrzeni fazowej.

Rys. 5 Portret fazowy jednowymiarowego oscylatora harmonicznego.

Przekształcając te równania do postaci parametrycznej otrzymujemy równanie elipsy :

( x2 /A2 ) + (p2 / mωA2 ) = 1 (22.4)
I dalej :

( p2 /2m ) + ½ kx2 = ½ mωA2 (22.5)
-- energia całkowita --
Widać więc, że każda trajektoria fazowa związana jest z konkretną wartością energii całkowitej.
Zapiszmy teraz równania oscylatora następująco :

T = ½ m x

•

2 - energia kinetyczna oscylatora

U = ½ k x2 - energia potencjalna oscylatora.
Zatem :

p =

∂

•

= mx

•

Funkcja Hamiltona ma postać : H = T + U = ( p2 /2m ) + ½ kω2 x2

•

∂

p = p/m ; p

•

= -

∂

x = - m ω2 x

Należy podkreślić, że trajektorie fazowe ( ogólnie portrety fazowe ) pozwalają, w sytuacja kiedy analityczne rozwiązanie
równań ruchu jest bardzo trudne, na pewną jakościową analizę zachowania układu mechanicznego.

Przykład 22.2 Rozważmy teraz ruch swobodnego punktu materialnego na prostej.

Dla tego przypadku mamy : H = T = ½ mx

•

2 = p2 /2m

•

∂

p = p/m ; p

•

= -

∂

x = 0

Zatem :
p(t) = p0

const. ; x(t) = x0 + (

p0t / m)

Równania te w przestrzeni fazowej przedstawiają linię proste równoległe do osi Ox.

Rys. 6 Portret fazowy punktu materialnego poruszającego się swobodnie po prostej.

Często zdarza się, że chcemy śledzić i porównywać przebieg portretów fazowych dwóch układów mechanicznych, które
różnią się nieznacznie pewnymi warunkami początkowymi. Jeśli ruch nie jest ruchem chaotycznym , to punkty w
przestrzeni fazowej reprezentujące oba układy stale będą znajdować się blisko siebie, jeśli jednak ruch jest chaotyczny , to
oddalą się szybko od siebie. Ta technika znajduje właśnie zastosowanie w badaniu dynamiki układów chaotycznych.

Rys 6a Przykłady trajektorii ruchu w przestrzeni fazowej : a) ruch nieograniczony b) ruch ograniczony

Definicja 22.1 Potokiem fazowym nazywamy pewien operator T^ przeprowadzający układ mechaniczny z jednego stanu
( w pewnej chwili t1 ) do innego stanu ( w chwili t2 )
( q(t2), p( t2) ) = T^ ( q(t1), p( t1) )
Zwykle potok fazowy zadajemy za pomocą równań różniczkowych ruchu.
Ponieważ krzywe fazowe nie przecinają się ( z wyjątkiem co najwyżej przeliczalnej liczby punktów ), operator T^ jest
operatorem odwzorowania wzajemnie jednoznacznego przestrzeni fazowe w siebie.

Przykład 22.3 Rozważmy jednowymiarowy układ mechaniczny dla którego hamiltonian ma postać :

H = p2/2m + V(q)
Ponieważ nie zależy on jawnie od czasu, to energia tego układu E = H(p, q ) jest inwariantem ruchu. To pozwala zapisać :

p = m x

•

sqrt [ 2m ( E – V ) ]

tj. wykonać całkowania postawionego zagadnienia.
Wielokrotnie możliwe jest jakościowe zbadanie zachowania układu mechanicznego ( tj. wyznaczenie pewnych
charakterystycznych cech jego ruchu bez całkowania jego równań dynamiki ).
Dla układów potencjalnych w zależności od struktury funkcji potencjalnej V(q) możemy przedstawi odpowiedni portret
fazowy układu a na jego podstawie określić sposób jego zachowania.

Rys 6b Wykres funkcji potencjalnej V oraz odpowiadający mu portret fazowy.

Różne „obszary” zachowania układu rozdzielone są krzywymi zwanymi „separatysami” ( na rysunku 6b separatysy
przedstawiają krzywe C1, C2 )
Definicja 22.2 Krzywe fazowe oddzielające ( separujące ) obszary przestrzeni fazowej , w których ruch ma jakościowo
różny charakter nazywamy separatysami.

XXIII. Ciecz fazowa – twierdzenie Liouville’a.

Bardzo ważną własnością przestrzeni fazowej jest zachowanie objętości elementu fazowego, bez względu na deformacje
jakim może podlega ten element.
Twierdzenie Liouville’a stwierdza, że jeśli ewolucja elementu fazowego opisana jest równaniami Hamiltona to jego
objętość fazowa jest zachowana w czasie. ( dowód np. w [ 3, tom str. 98 ; 10 str. 437 ; 20 str. 68 ]

Rys. 7 Klasyczny „kotek” z książki [ 20 ] przedstawiający idee zachowania objętości elementu fazowego.

Obraz każdego układu mechanicznego w przestrzeni fazowej możemy uważać za cząstkę 2k-wymiarowej cieczy, ich a
trajektorię fazową za linie prądu. Przy takiej interpretacji ruchu układów mechanicznych w przestrzeni fazowej można
lepiej unaocznić kilka ważnych twierdzeń, odnoszących się do tego ruchu. Tka „ciecz fazowa” jest formalnie bardzo
podobna do zwykłej cieczy nielepkiej i nieściśliwej. Należy również zauważyć, że taka terminologia przybliża nas do
zagadnień mechaniki statystycznej , która w znacznym stopniu wykorzystuje wprowadzone tutaj metody.

Przykładowo w mechanice statystycznej gazu doskonałego pragniemy śledzić ruch ok. 1023 identycznych cząstek
przemieszczających się w pewnym naczyniu. Każda cząsteczka jest opisywana tym samym hamiltonianem i porusza się w
6-wymiarowej przestrzeni fazowej ( x, y, z, px , py, pz ). Aby opisać stan takiego układu w dowolnej chwili trzeba określić
położenie 1023 kropel cieczy fazowej. W miarę upływu czasu taki zbiór kropel będzie ewoluował zgodnie z równaniami
ruchu – zmieniając swój kształt ( patrz przykładowy rys. 7 )
Ogólnie rozpatruje się ruch zbioru N takich kropel ( zajmujących pewną objętość – raczej hiperobjętość ). W mechanice
statystycznej zbiór zupełnie jednakowych „egzemplarzy” układu różniących się jeden od drugiego jedynie niewielkimi

zaburzeniami stanów początkowych ( pi

0 , q

0 ) nazywamy „zespołem (ensemblem ) statystycznym”

Z twierdzenia Liouville’a możemy wnioskować, że gęstość z jaką rozmieszczone są krople cieczy fazowej w określonej
ich objętości jest niezmienna.
Własność zachowywania objętości fazowej wyróżnia określoną klasę układów mechanicznych ( ogólnie fizycznych )
zwanych układami hamiltonowskimi.
Układy dysypatywne nie spełniają omawianego twierdzenia – ich objętość maleje z czasem.

Twierdzenie Poincarego o powrocie.

Do najciekawszych wniosków wynikających z twierdzenia Liouville’a należy również twierdzenie Poincarego
„o powrocie”. Stwierdza ono, mówiąc skrótowo, że prawie każdy stan początkowy układu mechanicznego pojawia się
ponownie podczas jego ewolucji.

Twierdzenie Poincarego ( szkic ) Jeżeli spełnione są pewne ( ogólne ) warunki to prawdziwe jest stwierdzenie :
Prawie każdy punkt przestrzeni fazowej jest punktem okresowym tzn. zbiór tych punktów, do których rozpoczęty w nich
ruch nie powraca dowolnie blisko po wystarczająco długim czasie, jest zbiorem miary zero.
Innymi słowy, jeżeli dana jest pewna trajektoria fazowa oraz punkt na niej wraz z pewnym swoim dowolnie małym
otoczeniem to podczas ewolucji układu ta trajektoria znajdzie się w tym otoczeniu ( po odpowiednio długim czasie )
[ 11-literatury dodatkowej , str. 55 ; 10 str. 477 ]

Typowe własności układów hamiltonowskich – twierdzenie KAM.

Można zapytać ( w związku z twierdzeniem Poincarego ) czy ewolucja hamiltonowska w ograniczonym obszarze
przestrzeni fazowej ( PF) jest zawsze okresowa lub quasi-okresowa ?
Odpowiedź na to pytanie jest przecząca. Poszukiwanie odpowiedzi na to pytanie doprowadziło do sformułowania ogólnych
wniosków dotyczących typowych własności układów hamiltonowskich.
Wydaje się , że wśród tych układów dominują układy są niecałkowalne, jednak w pewnym obszarze przestrzeni fazowej
zachowują się zgodnie z twierdzeniem Kołmogorowa-Arnolda-Mosnera ( KAM ). Twierdzenie to mówi, że w typowym

układzie całkowalnym pod wpływem słabego ( nie określa się jak słabego ) tylko w pewnej ( nie określa się dokładnie
konstrukcji tego obszaru ) części przestrzeni fazowej ruch okresowy lub quasi-okresowy na f-wymiarowych poziomicach
Całek ruchu zostaje zaburzony. Objętość tej części PF maleje do zera wraz z wyłączaniem zaburzenia. W pozostałej części
PF ruch pozostaje quasi-okresowy, chociaż powierzchnie niezmiennicze są odkształcane w stosunku do powierzchni całek
ruchu układu niezaburzonego.
[1, str. 116 ]

XXIV. Niezmienniki całkowe ( inwarianty integralne ).

Przy przekształceniach kanonicznych ( w szczególności podczas ruchu układu mechanicznego w przestrzeni fazowej )
Kanoniczna forma równań Hamiltona zostaje zachowana, wiemy również, że zachowana jest objętość kropli fazowej.
Istnieją również inne wyrażenia analityczne które są inwariantem przekształceń kanonicznych. Takimi wyrażeniami w
szczególności są pewne całki , nazwane przez Poincarego – „niezmiennikami całkowymi”.

Całka :

J1 =

∮

ΣΣΣΣ

δq

i (24.1)

Obliczana wzdłuż linii zamkniętej C , złożonej z punktów odpowiadających jednoczesnym stanom układu mechanicznego
zachowuje wzdłuż rurki fazowej stałą wartość. Całkę tę nazywamy „względnym niezmiennikiem całkowym Poincarego
pierwszego rzędu”.
Rurką fazowa nazywamy zbiór trajektorii fazowych rozpiętych na pewnych konturach.

Rys. 8 Rurka fazowa rozpięta na konturach C1, C2.

E. Cartan pokazał, że istnieją ogólniejsze niezmienniki całkowe w których kontury rurki fazowej ( kontury całkowania) nie
koniecznie musza być krzywymi złożonymi z punktów stanów niejednoczesnych. W celu wyznaczenia tych
niezmienników wprowadza się tzw. „rozszerzona przestrzeń fazową” tj. przestrzeń ( t, qi , pi )
( przestrzeń fazowa z czasem ).
Całka :

J*1 =

∮

(

ΣΣΣΣ

δq

i – H δt ) (24.2)

Obliczana wzdłuż linii zamkniętej C, złożonej z punktów końcowych trajektorii bezpośrednich, zachowuje wzdłuż rurki
fazowej stałą wartość.
Całkę tę nazywamy „względnym niezmiennikiem całkowym Poincarego-Cartana, pierwszego rzędu”

Niezmiennik ten jest uogólnieniem niezmiennika (24.1) ( dla t = const. H δt = 0 )
Definicja 24.1 Niezmiennikami całkowymi bezwzględnymi nazywamy takie całki których niezmienniczość zostaje
zachowana przy dowolnym wyborze obszaru całkowania, w szczególności obszar ten może nie być konturem
( tj. krzywą zamkniętą )

Zasada zachowania energii-pędu wg. Cartana.

Badając własności niezmiennika (24.2) E. Cartan sformułował zasadę nazwaną przez siebie „zasadą zachowania energii-
pędu” – zasadę tę można przyjąć za podstawę MK.
Wyrażenie stojące pod znakiem całki (24.2) Cartan nazwał „tensorem energii i pędu”( ponieważ wielkości pi

związane są z

pędem układu, H związane jest z energią całkowitą )

Zasada zachowania energii-pędu wg Cartana.
Różniczkowe równania ruchu układu mechanicznego mają tę własność, że dopuszczają w charakterze niezmiennika
całkowego całkę tensora energii-pędu wziętą wzdłuż dowolnego konturu w rozszerzonej przestrzeni fazowej.

Fakt, że niezmiennik (24.1) może być podstawa MK wynika z dwóch okoliczności : po pierwsze, wychodząc z tego
niezmiennika można otrzymać równania ruchu w postaci kanonicznej, po drugie – równania te są jedynymi które mają
niezmiennik całkowy o w/w postaci. Zbudowanie mechaniki w oparciu o zasadę Cartana jest bardziej ogólne niż np. ujęcie
w oparciu o zasadę Hamiltona. Z tego względu niezmiennik (24.2) nazywany jest „podstawowym niezmiennikiem
całkowym mechaniki”. [ 15, str. 88 ]

Należy również zauważyć , że niezmiennik całkowy postaci :

J =

∫

...

∫

δp1 δq1 ... δpn δqn (22.5)

Oznacza niezmienniczość objętości w przestrzeni fazowej. ( tj. wyraża twierdzenie Liouville’a )

XXV. Mechanika w ujęciu geometrycznym.

Jak już można było się przekonać mechanikę klasyczna możemy rozwinąć (czasami równoważnie ) korzystając z różnych
przestrzeni :

przestrzeń konfiguracyjna qi

przestrzeń zdarzeń ( qi, t )

przestrzeń pędu i energii

przestrzeń fazowa ( qi, pi )

przestrzeń fazowa rozszerzona ( qi, t )

Przestrzeń konfiguracyjną możemy traktować jako pewną rozmaitość różniczkową, oznaczmy ja jako Mn.
( rozmaitość konfiguracyjna, dla układu mechanicznego o n stopniach swobody będzie to rozmaitość n wymiarowa )

W każdej chwili t, położenie układu mechanicznego reprezentowane jest przez pewien punkt q(t)

∈

Mn.

Dla lokalnego układu współrzędnych określonego na rozmaitości konfiguracyjnej położenie układu możemy opisywać

przez współrzędne uogólnione : q1(t), ... , qn(t)

∈

Mn.

Ruch układu jest znany, gdy znane jest odwzorowanie :

→

q(t)

∈

< a, b >

Doświadczenie poucza, że jednoczesna znajomość wszystkich współrzędnych i prędkości uogólnionych całkowicie określa
stan układu i ( z punktu widzenia MK ) pozwala jednoznacznie przewidzieć dalsze jego zachowanie.

Zbiór wszystkich wektorów stycznych do rozmaitości Mn, tzn. sumę przestrzeni stycznych do tej rozmaitości we
wszystkich jej punktach :

T(M) :=

∪

Tn ( M)

∈

nazywamy „wiązką styczną” do rozmaitości Mn. Zbiór T(M) w sposób naturalny wyposażony w strukturę rozmaitości
różniczkowej.
Bardzo ważne jest spostrzeżenie, że forma kwadratowa związana z energią kinetyczną T wprowadza na przestrzeni M
strukturę przestrzeni Riemanna. [ 17, str. 121 ]
Definicja 25.1 Naturalnym układem mechanicznym nazywamy trójkę ( M, T, V) ; M – rozmaitość konfiguracyjna , T-
metryka riemannowska na M ( energia kinetyczna ), V – gładka funkcja na M ( potencjał pola sił ). Ruchem układu
mechanicznego nazywamy odwzorowanie gładkie q : R

→

M, będące ekstremalami funkcjonału działania postaci (13.1).

Układy naturalne są układami odwracalnymi tj. ich lagranżjany są inwariantne względem transformacji odwrócenia czasu.
Uogólnieniem układów naturalnych są układy w których występują siły żyroskopowe.

Najważniejsza strukturą określającą przestrzeń mechaniki hamiltonowskiej jest struktura symplektyczna. Strukturę

symplektyczną na rozmaitości Mn, możemy wprowadzić na kilka sposobów.
Ważnym dla dalszych wywodów wydaje się następujące twierdzenie :
Twierdzenie 25.1 Przestrzeń fazową układu o n stopniach swobody można w naturalny sposób wyposażyć w strukturę
symplektyczną , tworząc w ten sposób 2n-wymiarową przestrzeń symplektyczną.

Niech Mn, będzie parzystowymiarową rozmaitością różniczkową, zbiór wszystkich funkcji różniczkowalnych

nieskończenie wiele razy f : Mn

→

R oznaczmy symbolem C

∝

(Mn). Strukturą symplektyczną

na Mn, nazywamy

odwzorowanie biliniowe [ . , . ] : C

∝

(Mn)

∝

(Mn)

→

∝

(Mn) , spełniające następujące warunki :

a) [ f , g ] = - [g , f ] antysymetryczność
b) [ fg, h ] = f [ g, h ] + g [f, h ]
c) [ [ f, g ] , h ] + [ [ g, h ] , f ] + [ [ h, f ] , g ] = 0
Parę ( M,

) nazywamy rozmaitością symplektyczną. ( przestrzenią symplektyczną )

W funkcji [ . , . ] rozpoznajemy znajomy nawias Poissona.

Nawias Poissona przekształca przestrzeń liniową C

∝

(Mn) w nieskończenie wymiarową algebrę Liego nad ciałem R.

Centrum tej algebry ( zbiór elementów komutujących ze wszystkimi elementami algebry ) składa się tylko z funkcji
stałych.

Niech H : Mn

→

R będzie funkcją gładką. Układem hamiltonowskim na przestrzeni symplektycznej o funkcji Hamiltona

H , nazywamy równanie różniczkowe :

•

= [ F, H ] ; F

∈

∝

(Mn) (25.1)

We współrzędnych symplektycznych ( xi

, y

i ) równanie (25.1) jest równoważne równaniom kanonicznym Hamiltona.

Powyżej określiliśmy strukturę symplektyczną za pomocą nawiasu Poissona.

Strukturę tą możemy określić wprowadzając na M2n pewną 2-formę zamkniętą

Ω

. Forma

Ω

pozwala określić izomorfizm

przestrzeni stycznej T(M) i przestrzeni kostycznej T*(M). ( przestrzeń kostyczna to przestrzeń 1-form na przestrzeni
stycznej )

Zgodnie z twierdzeniem Darboux w małym obszarze punktu p

∈

M2n we współrzędnych symplektycznych forma

Ω

przyjmuje postać

Ω

ΣΣΣΣ

∧

dxi (25.2)

Forma

Ω

( tensor antysymetryczny ) określa strukturę geometryczna rozmaitości M , podobnie jak symetryczny tensor

metryczny Riemanna określa strukturę geometryczna przestrzeni Riemanna. Między tymi przypadkami istnieją oczywiście
zasadnicze różnice spowodowane odmiennymi typami symetrii tensorowej. Istnieje jednak wspólna idea zasadnicza –
geometrię rozmaitości opisują związki w których występuje wyróżniony tensor o walencji dwa. ( jest to charakterystyczny
wyróżnik dla określenia geometrii metrycznej ). Odpowiednikiem izometrii w przestrzeni fazowej są przekształcenia
kanoniczne. Nie na każdej rozmaitości można wprowadzić strukturę przestrzeni fazowej.
Wnioskiem z określenia PF przez formę

Ω

jest parzystość wymiaru PF.

Uogólnieniem PF jest dopuszczenie osobliwości formy

Ω

[ 17, od str. 115 ; 3-literatury dodatkowej ; 8, 9-literatury w języku rosyjskim, od str. 19 , od str. 72 ]

XXVI. Zmienne kąt -działanie.

Na przykładzie układu o jednym stopniu swobody można zilustrować pewne ważne pojęcie dotyczących układów o ruchu
ograniczonym. Dla układów hamiltonowskich zmienne p, q są jak wiadomo zmiennymi kanonicznie sprzężonymi.
Możemy oczywiście wprowadzić inną parę takich zmiennych – zmienne kąt-działanie lub działanie –kąt ( I,

Dla układu o jednym stopniu swobody ( np. oscylator harmoniczny ) definiujemy je następująco :

I = (1/2π)

∮

p(q, H) dq (26.1)

( przyjmujemy założenie, że układ porusza się w PF po krzywej zamkniętej i całkujemy po konturze – chociaż możemy
wprowadzić zmienne kąt-działanie dla układów poruszających się po krzywych otwartych )

Wzór (26.1) definiuje wielkość mającą wymiar

∫

L dt i nosi nazwę „działania”. Działanie I , dla naszego przypadku

przybiera postać :
I = E/ω
i jest całka ruchu. Hamiltonian możemy przedstawi w postaci :
H(I) = ωI
Zmienną „kąt” definiujemy zależnością :

∂

S(q, I )/

∂

I ; S(q, I ) = S(q, H(I) ) =

∫

p dq (26.2)

Dla rozpatrywanego przez nas przypadku będzie ona po prosty kątem φ wychylenia.
Zmienne (I,

) – działanie-kąt spełniają rolę współrzędnych w PF. Równania ruchu dla tych zmiennych mają postać :

•

= -

∂

H(I)/

∂ϑ

;

ϑ•

= dH(I)/dI (26.3)

Dla naszego przypadku mamy :

•

= 0 ;

ϑ•

= ω(I)

Widać więc, że zmienne o tej postaci są zmiennymi sprzężonymi kanonicznie.
Dla wielu przypadków równania ruchu wyrażone poprzez takiego typu zmienne są nadzwyczaj proste.
Najważniejszą własnością zmiennej

jest jej okresowość. Zmienna działania S, zmienia się w tym okresie zgodnie ze

wzorem :

∆

S =

∮

p dq = 2π I (26.4)

Zatem :

∆ϑ

∂∆

∂

I = 2π

XXVII. Twierdzenie Liouville’a-Arnolda o całkowalności.

Twierdzenie które omówię w tym punkcie pozwala ustalić warunki całkowalności układu o n stopniach swobody.
Zagadnienie całkowalności równań dynamiki Hamiltona odpowiada analogicznemu zagadnieniu całkowania układu
równań różniczkowych.

Twierdzenie 27.1 Niech układ hamiltonowski o n stopniach swobody porusza się ruchem ograniczonym i niech ma n całek
pierwszych.
Fi = Fi ( p, q ) ; i = 1, ... , n
Liniowo niezależnych i znajdujących się w inwolucji tj. :

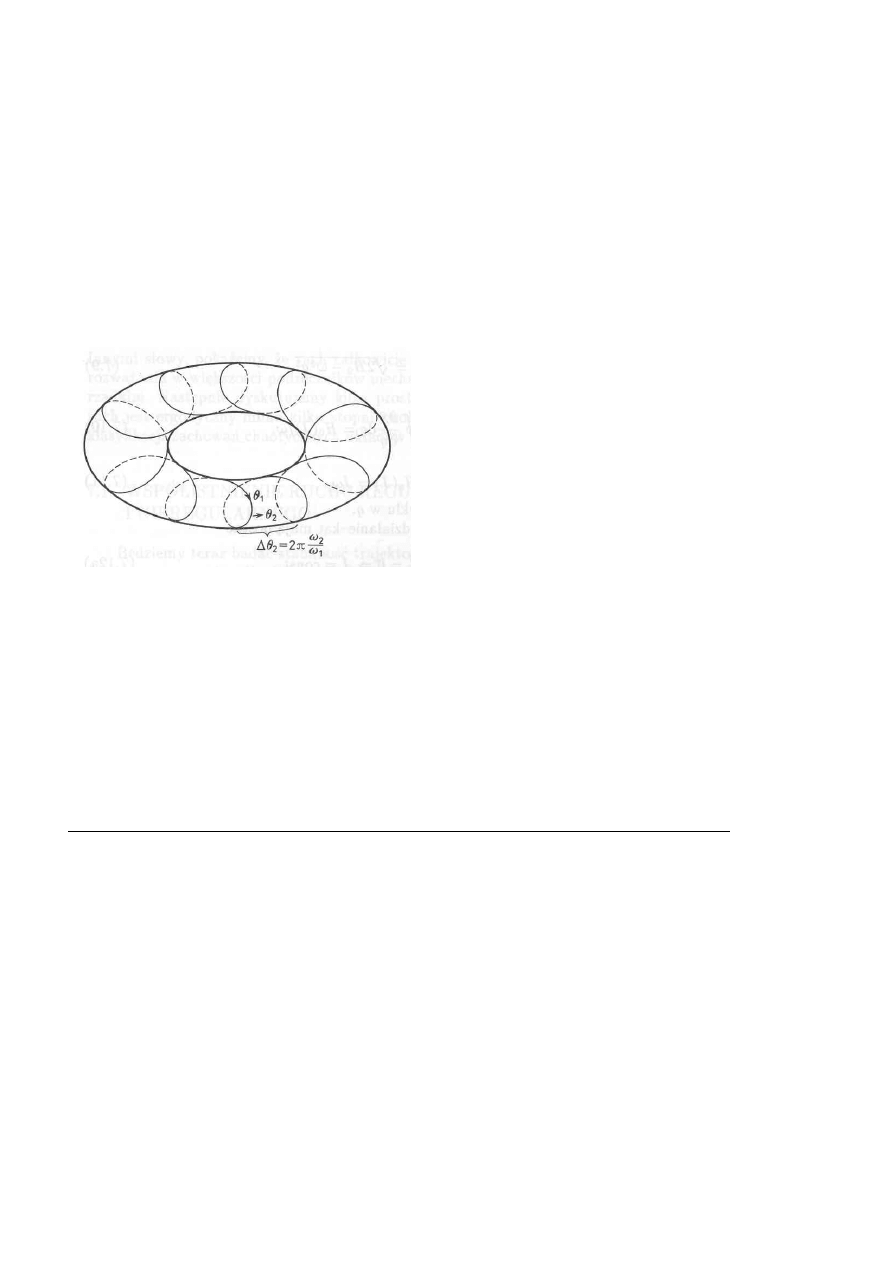
[ Fi , Fj ] = 0
Wtedy :
a) Trajektorie tego układu leżą na n-wymiarowym torusie.
b) Ruch jest quasi-periodyczny i charakteryzuje się n –toma częstościami :
ωi = ωi ( F1 , … , Fn )
c) zmienne kątowe

i charakteryzujące współrzędne na torusie spełniają równania :

ϑ•

i = ωi ( F1 , … , Fn )

Równania te możemy scałkować bezpośrednio otrzymując :

i = ωit + const.

Zatem do pełniej całkowalności układu hamiltonowskiego wystarcza znajomość n całek ruchu znajdujących się w
inwolucji. Nie trzeba dodawać, że układy całkowalne są raczej przypadkami szczególnymi w zbiorze układów
hamiltonowskich.
Podczas ruchu trajektorie pozostają cały czas na torusie dlatego mówimy o istnieniu torusów inwariantnych. Zmieniając
całki ruchu Fi , otrzymujemy zbiór inwariantnych torusów.

Rys. 9 Ruch periodyczny lub quasi-periodyczny na torusie.

Możemy teraz powiązać układy hamiltonowskie całkowalne z wprowadzonymi zmiennymi działanie-kąt.
Mówimy, że układ hamiltonowski jest całkowalny jeśli możemy znaleźć przekształcenie kanoniczne S(q, I) do zmiennych
(

, I ) :

( q, p) =

∂

S(q, I)/

∂

⇔

(

, I ) =

∂

S(q, I)/

∂

takie , że w tych nowych zmiennych hamiltonian zależy tylko od I tj. S(q, I) jest rozwiązaniem równania H-J
wtedy równania ruchu (26.3) we współrzędnych (

, I ) całkujemy bezpośrednio. [ 12- literatury dodatkowej , str. 191 ]

X. Literatura.

( tekstem podkreślonym zaznaczono pozycje z których autor korzystał najobficiej )

1) „Wstęp do mechaniki klasycznej” -- K. Stefański
WN-PWN 1999
2) „Mechanika teoretyczna” -- W. Rubinowicz, W. Królikowski
WN-PWN 1998
3) „Mechanika klasyczna” -- J. R. Taylor
tom 1, 2 WN-PWN 2006
4) “Historia fizyki” -- A. K. Wróblewski
WN-PWN 2007
5) „Od Newtona do Mandelbrota – wstęp do fizyki teoretycznej” -- D. Stauffer, H. E. Stanley
WNT1996
6) „Wstęp do fizyki współczesnej” -- J. Kociński
PWN 1977
7) „Mechanika ogólna” -- Z. Osiński
WN-PWN 2000
8) „Mechanika teoretyczna” -- P. Wilde, M. Wizmur
PWN 1984
9) „Mechanika teoretyczna” -- J. J. Olchowski
PWN 1978
10) „Mechanika klasyczna” -- G. Białkowski
PWN 1975
11) „Mechanika” -- B. Skalmierski

WN-PWN 1998
12) „Mechanika” -- S. Banach
PWN 1956
13) Metody matematyczne mechaniki klasycznej” -- W. J. Arnold
PWN 1981
14) „Mechanika analityczna” -- R. Gutowski
PWN 1971
15) „Wykłady z mechaniki analitycznej” -- F. R. Gantmacher
PWN 1972
16) „Dynamika analityczna” -- E. T. Whittaker
PWN 1959
17) „Mechanika klasyczna” -- R. S. Ingarden, A. Jamiołkowski
PWN 1980
18) „Mechanika teoretyczna” -- G. K. Susłow
PWN 1960
19) „Krótki kurs fizyki teoretycznej” -- L. D. Landau, E. M. Lifszyc
tom I – Mechanika, elektrodynamika PWN 1980
20) „Metody matematyczne mechaniki klasycznej” -- W. I. Arnold
PWN 1981

Literatura dodatkowa

1) „Wstęp do dynamiki układów chaotycznych” -- G. L. Baker, J. P. Gollub
WN-PWN 1998
2) „Chaos w układach dynamicznych” -- E. Ott
WNT 1997
3) „Geometria przestrzeni fazowych” -- J. Sławianowski
PWN 1975
4) „Czas i dynamika w równaniach różniczkowych i układach -- A. Pelczar
dynamicznych” OBI 2003
5) „Równania różniczkowe zwyczajne” -- W. I. Arnold
PWN 1975
6) „Teoria równań różniczkowych” -- W. I. Arnold
PWN 1983
7) „Matematyka w fizyce i chemii” -- H. Margenau, G. M. Murphy
PWN 1962
8) „Elementy dynamiki geometrycznej” -- J. M. Skowroński
WNT 1972
9) „Równania różniczkowe zwyczajne” -- Roman Gutowski
WNT 1971
10) „Wykłady z równań różniczkowych” -- Jerzy Ombach
Wydawnictwo UJ 1999
11) „Wprowadzenie do teorii chaosu w nierównowagowej -- J. Robert Dorfman
mechanice statystycznej” WN-PWN 2001
12) „Chaos deterministyczny – wprowadzenie” -- H. G. Schuster
WN-PWN 1995
13) „Wstęp do teorii gładkich układów dynamicznych” -- Wiesław Szlenk
PWN 1982

Literatura w języku angielskim.

1) „Classical dynamics : a contemporary approach” -- Jorge V. Jose, Eugene J. Saletan
Cambridge University Press 1998
2) “The variational principles of mechanics” -- Cornelius Lanczos
tłumaczenie rosyjskie

Moskwa Mir 1965

3) „Lectures on classical mechanics” -- John C. Baez
Louisiana State University 2005
4) “Elements of hamiltonian mechanics” -- D. ter Haar
tłumaczenie rosyjskie Moskwa Nauka 1974
5) „Classical mechanics – systems of particles and hamiltonian dynamics” -- Walter Greiner
Springer 2003
6) “Geometric mechanics” -- J. Marsden
wersja elektroniczna 1998
7) “Classical mechanics” -- J. Leech
tłumaczenie rosyjskie Moskwa 1961

8) „Dynamical systems” -- G. D. Birkhoff
tłumaczenie rosyjskie 1999
9) „Classical dynamics” -- J. L. Synge
tłumaczenie rosyjskie FizMatLit Moskwa 1963
10) „Classical mechanics” -- H. Goldstein
Addison-Wesley 1981
jest tłumaczenie rosyjskie
11) „Phase-space dynamics of particles” -- Allan J. Lichtenberg
tłumaczenie rosyjskie Moskwa Atomizdat 1972
12) „Regular and stochastic motion” -- A. J. Lichtenberg, M. A. Liberman
tłumaczenie rosyjskie Moskwa 1988

Literatura w języku rosyjskim.

1) „Wwiedjenie w analiticzeskuju mechaniku” -- I. M. Bielenkij
Moskwa Wyższa Szkoła 1964
2) „Osnowy analiticzeskoj mechaniki” -- W. W. Dobronrawow
Moskwa Wyższa Szkoła 1976
3) „Analiticzeskaja mechanika” -- A. I Lurie
FizMatLit Moskwa 1961
4) „Wariacionnyje princypy machaniki, ich razwitie i -- L. S. Polak
primienienie w fizikje” Fizmatgiz Moskwa 1960
5) „Teoreticzeskaja mechanika” -- A. P. Markeew
Iżewsk 1999
6) „Osnowy teoreticzeskoj mechaniki” -- W. F. Żurawlew
Moskwa Fizmatlit 2001
7) „Lekcii po teoreticzeskoj mechanikie” -- Ju. G. Pawlenko
Moskwa Fizmatlit 2002
8) „Symmetrii, topologia i rezonansy w gamiltonowoj mechanikie” -- W. W. Kozłow
Iżewsk 1995
9) „Haos i interrirujemost w nieliniejnoj dinamikie” -- M. Tabor

10) „Wwiedenie w nielinejnuju fizyku : ot majtnika do turbulentnosti -- G. M. Zaslawskij, R. Z. Sagdeew.
i haosa”

Literatura w języku francuskim.

1) „Geometrie differentielle et mecanique analytique” -- C. Godbillon
tłumaczenie rosyjskie Moskwa Mir 1973

Literatura w języku niemieckim.

1) „Grundprinzipen der klassischen mechanik -- E. Schmutzer
und der klassischen feldtheorie“ Berlin 1973
tłumaczenie rosyjskie Moskwa Mir 1976
dostępne tłumaczenie własne

Wyszukiwarka

Podobne podstrony:
Cwiczenie nr 03 Wprowadzenie do chemii analitycznej
3 5 Wprowadzenie do mechaniki pękania
biologia, ZANIECZYSZCZENIA WODY2, Zanieczyszczenia wód, wprowadzone do wód naturalnych organizmy żyw
Wprowadzenie do Matlaba w97, Politechnika Śląska ZiIP i inne, Mechanika
mechanika analityczna wprowadzenie
Wykład 1 inżynierskie Wprowadzenie do zarządzania operacyjnego
Wprowadzenie do medycyny rozwojowej 1
PD W1 Wprowadzenie do PD(2010 10 02) 1 1
Wprowadzenie do psychologii
Wprowadzenie do filozofii
(1) Wprowadzenie do nauki o finansach 1id 778 ppt
wprowadzenie do systemu win i podst sieci
wprowadzenie do psychologii społecznej
Wprowadzenie do cw1A
1 Wprowadzenie do psychologii pracy (14)id 10045 ppt

więcej podobnych podstron