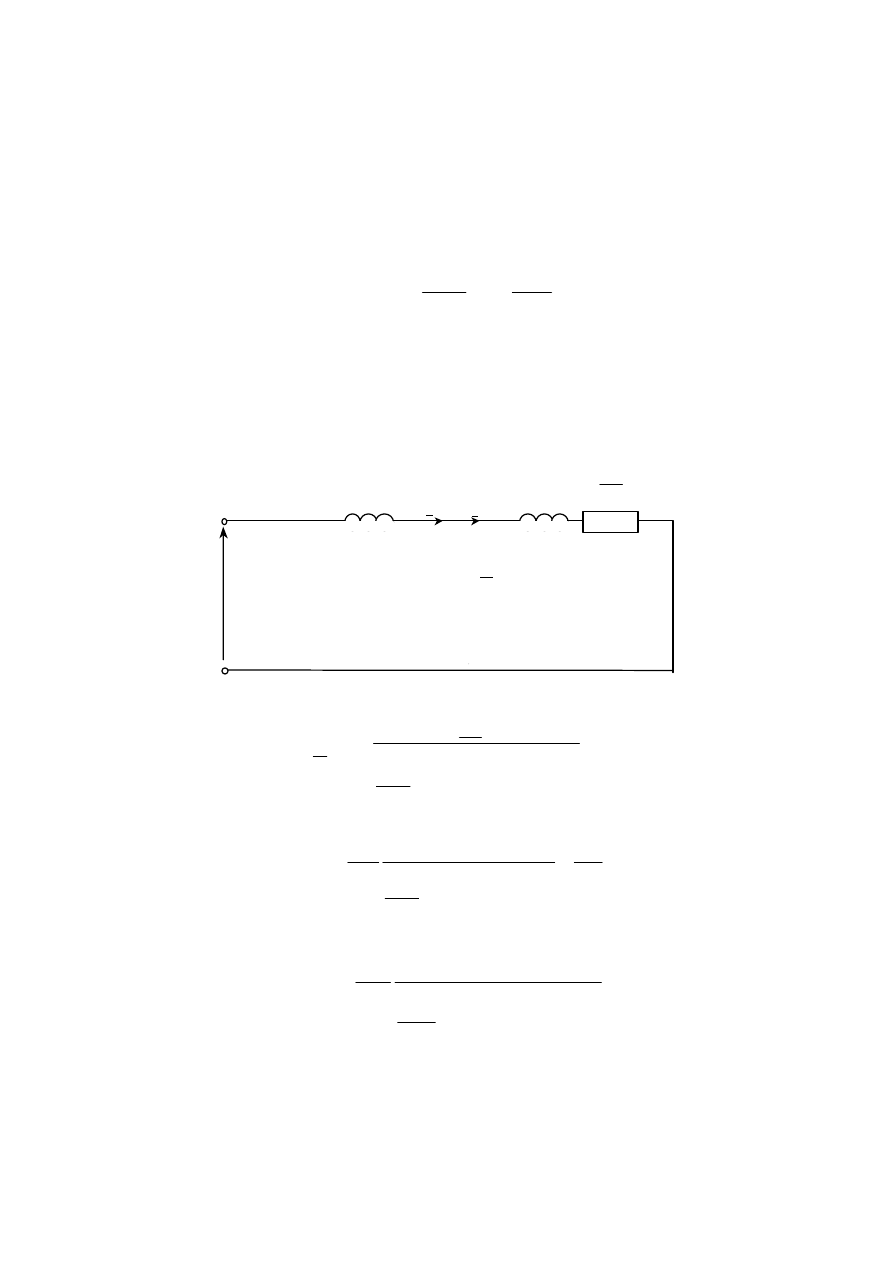
MOMENT MASZYNY ASYNCHRONICZNEJ W STANIE

USTALONYM

(wzór Klossa)

Moment elektromagnetyczny maszyny asynchronicznej można wyrazić wzorem:

s

R

I

p

M

r

e

r

'

2

'

1

3

ω

=

Na potrzeby wyznaczenia momentu uprośćmy schemat zastępczy

maszyny asynchronicznej pomijając gałąź poprzeczną (R

fe

i X

µ

) oraz przyjmują,

że:

R

r

/s>>R

s

jX

σ

s

'

r

jX

σ

s

R

r

'

U

s

I

s

I

r

’

Otrzymamy:

)

(

'

'

'

r

s

r

s

X

X

j

s

R

U

I

r

+

+

=

s

R

X

X

s

R

U

p

M

r

r

s

r

s

e

'

2

'

2

2

'

2

1

*

)

(

3

+

+

=

ω

2

'

2

'

'

2

1

)

(

3

r

s

r

r

s

e

X

X

s

s

R

R

U

p

M

+

+

=

ω

Wartość maksymalna momentu wyznaczymy z warunku:

-1-

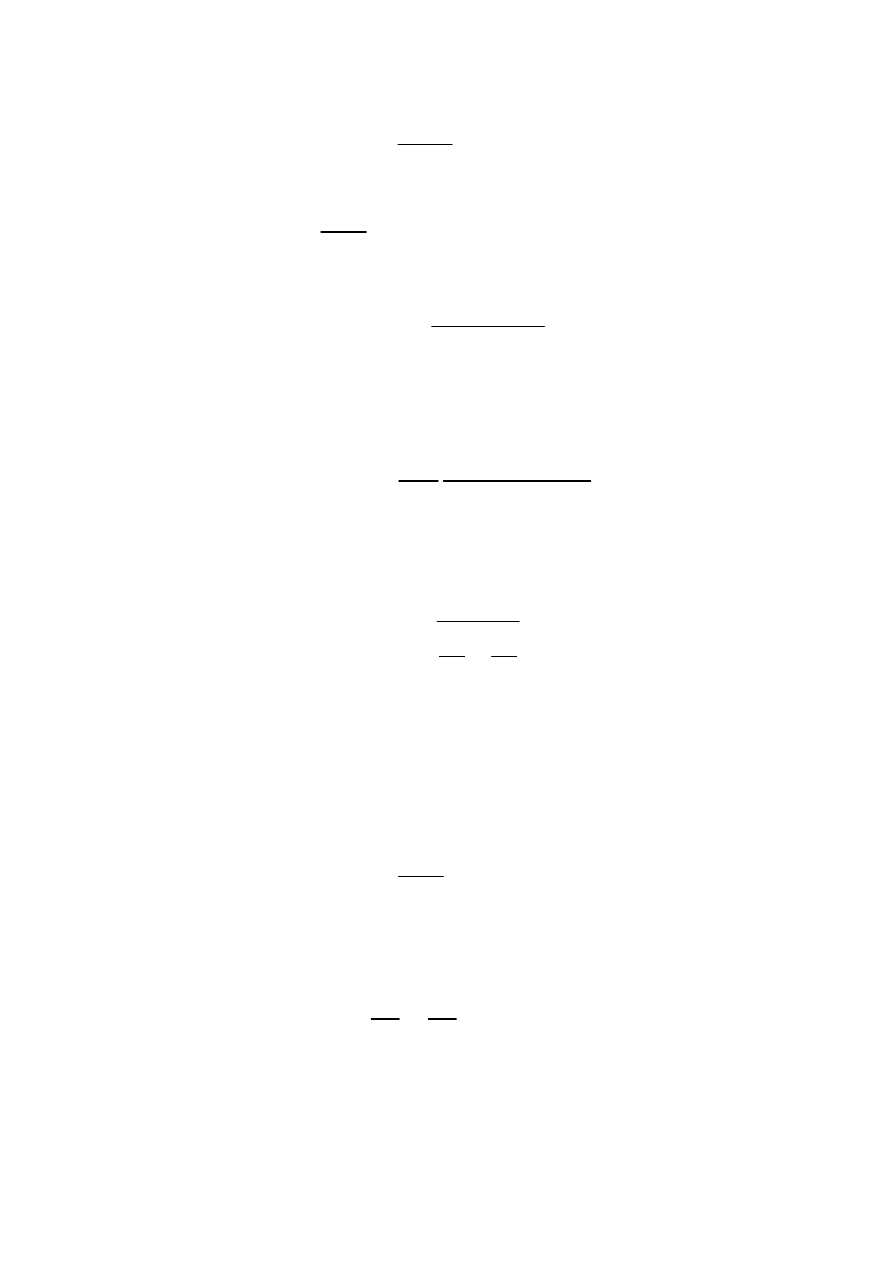
0

=

ds

dM

e

0

)

(

2

'

2

2

'

=

+

+

−

r

s

r

X

X

s

R

'

'

r

s

r

k

X

X

R

s

+

±

=

Dla takiego poślizgu, nazywanego poślizgiem krytycznym moment
jest równy:

)

(

2

3

'

2

1

r

s

s

k

X

X

U

p

M

+

±

=

ω

Jeśli wartość momentu podzielimy przez tą wartość momentu,
nazywanego momentem krytycznym, otrzymamy wzór Klossa:

s

s

s

s

M

M

k

k

k

e

+

=

2

Wzór Klossa jest bardzo wygodnym uproszczeniem

charakterystyki mechanicznej silnika asynchronicznego, stąd bardzo
często używany jest w technice napędu elektrycznego do szacowania
różnych wielkości w silniku asynchronicznym np. na podstawie
danych katalogowych. W katalogu podaje się m.in. parametr:

λ

=

n

k

M

M

Możemy szacować wartość poślizgu krytycznego ze wzoru

Klossa:

λ

2

=

+

n

k

k

n

s

s

s

s

0

2

2

2

=

+

−

n

k

n

k

s

s

s

s

λ

-2-

)

1

(

4

4

4

2

2

2

2

2

−

=

−

=

∆

λ

λ

n

n

n

s

s

s

2

)

1

(

2

2

2

−

±

=

λ

λ

n

n

k

s

s

s

)

1

(

2

−

±

=

λ

λ

n

k

s

s

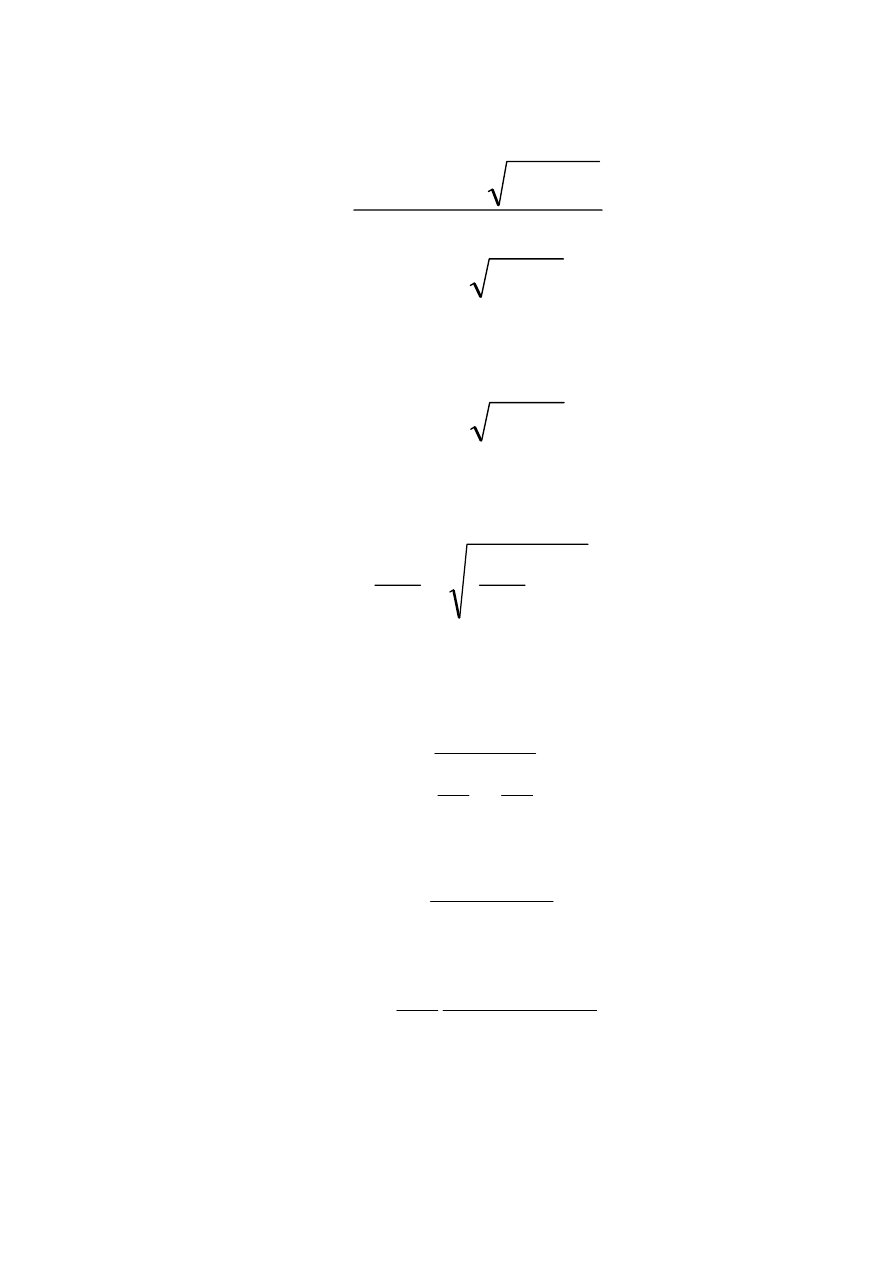
Z uwagi na symetrię względem poślizgu znamionowego i

krytycznego do obliczenia poślizgu krytycznego należy stosować

znak "+":

)

1

(

2

−

+

=

λ

λ

n

k

s

s

Analogiczne obliczenia poślizgu dla danego momentu (na części

stabilnej charakterystyki mechanicznej) należy wykonywać wg

zależności:

)

1

)

(

(

2

−

−

=

M

M

M

M

s

s

k

k

k

Postępowanie takie umożliwia szacowanie charakterystyk

momentu na podstawie danych katalogowych, także po wtrąceniu
rezystancji dodatkowej do obwodu wirnika, wówczas mamy bowiem:

s

s

s

s

M

M

k

k

k

e

+

=

2

'

'

'

r

s

d

r

k

X

X

R

R

s

+

+

±

=

)

(

2

3

'

2

1

r

s

k

X

X

U

p

M

s

+

±

=

ω

Wynikają stąd ważne wnioski dotyczące zależności momentu od

napięcia i częstotliwości:

-3-

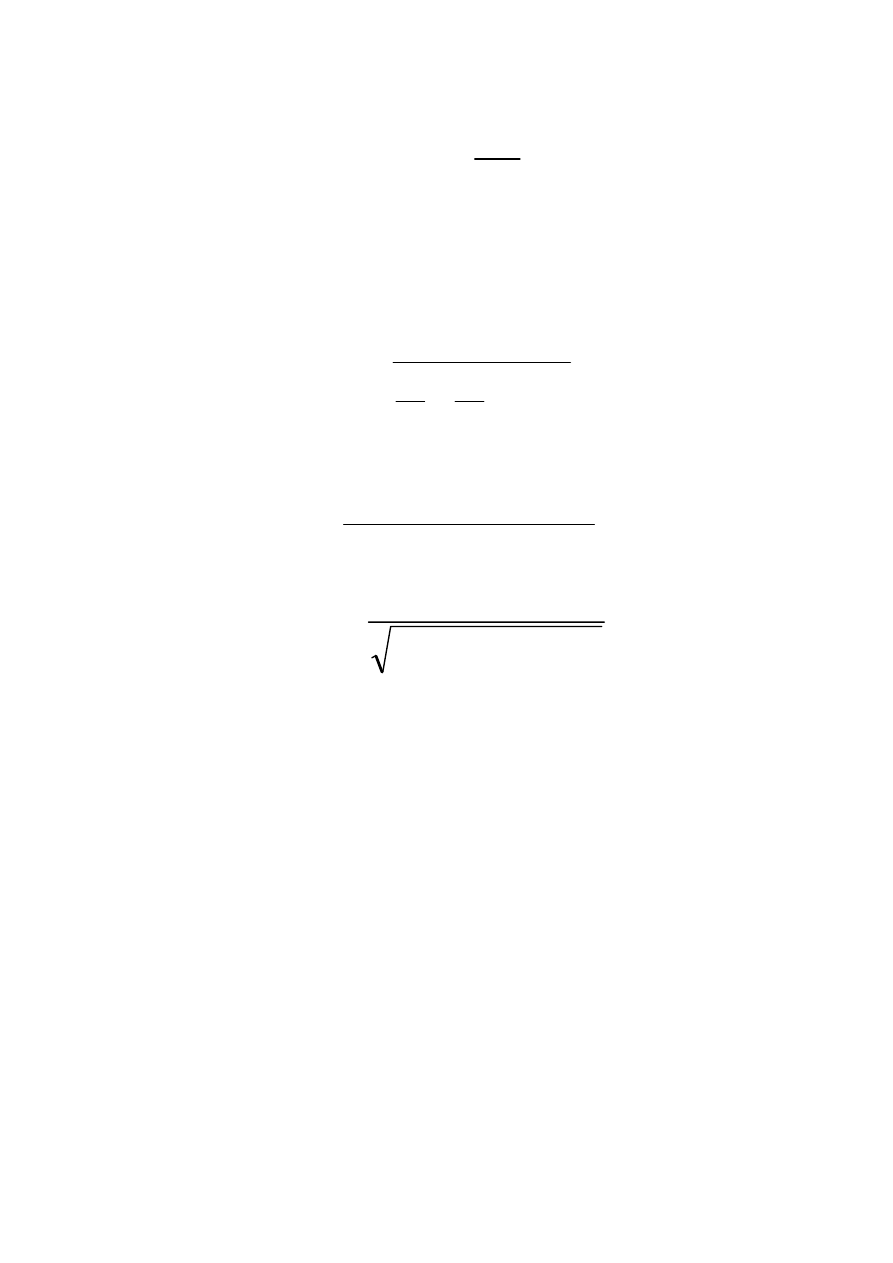
2

2

f

U

c

M

s

k

=

oraz wnioski dotyczące kształtowania momentu (np. rozruchowego)
poprzez wtrącenie do obwodu wirnika dodatkowej rezystancji

Dokładniejszą postać wzoru Klossa otrzymamy przy

uwzględnieniu R

s

oraz X

µ

. Otrzymamy wówczas:

ε

ε

k

k

k

k

k

e

s

s

s

s

s

s

M

M

2

)

1

(

2

+

+

+

=

gdzie:

)

)

(

(

2

2

'

2

s

s

r

s

X

X

R

R

X

R

+

+

=

µ

µ

ε

2

'

2

'

)

(

r

s

s

r

k

X

X

R

R

s

+

+

±

=

Rezystancję stojana pomija się zwykle dla silników o mocy większej

niż 10kW (wówczas

ε=0 oraz R

s

=0) i wówczas pełny wzór Klossa

przyjmuje postać uproszczoną.

Uwaga!

Przedstawione wyżej zależności wymagają uzupełnienia,

szczególnie w sytuacji, gdy zmieniamy częstotliwość napięcia
zasilającego. W

przypadku częstotliwości bliskich znamionowej

można stosować uproszczony wzór Klossa, natomiast obniżenie
częstotliwości powoduje, że niezbędne jest uwzględnienie rezystancji
stojana, czyli użycie pełnej zależności.

Należy też uwzględnić przypadek skrajny f=0!. Biorąc pod

uwagę analizę polegającą na sprowadzaniu wielkości wirnika na
stronę stojana otrzymamy stan gdy prąd jest wartością stałą – nie
istotne są zatem wartości reaktancji – w schemacie zastępczym (od
strony stojana) występuje jedynie rezystancja uzwojenia stojana.

-4-

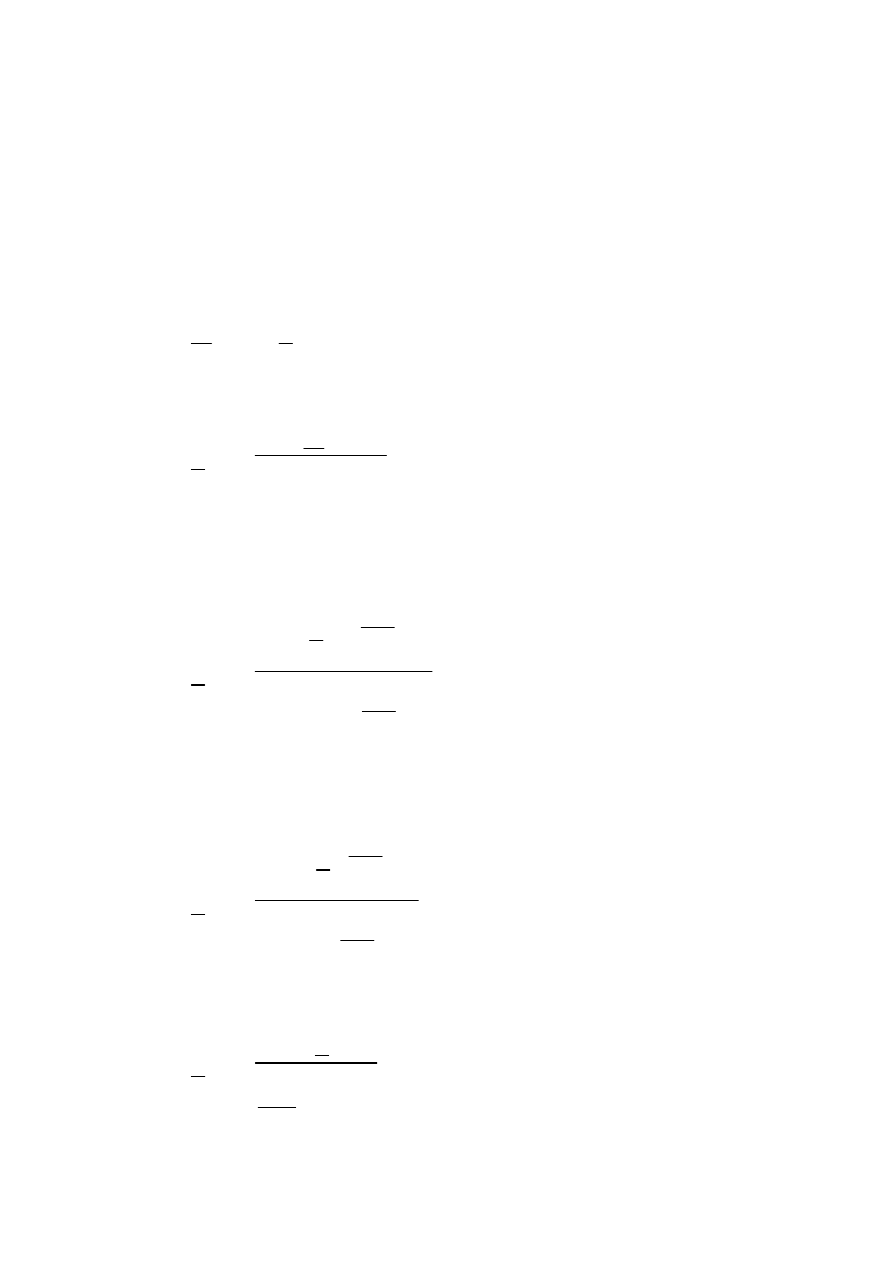
Pojawia się tu pytanie: jaki występuje tu moment obrotowy w sytuacji
wirowania wirnika? Sytuację mamy następującą:

1. prąd stały w uzwojeniach stojana wytwarza stały strumień
2. wirowanie wirnika z prędkością

ω powoduje powstanie siły

elektromotorycznej sinusoidalnej o wartości zależnej od
aktualnej prędkości i od prądu stojana o częstotliwości
wynikającej z prędkości obrotowej wirnika

ω

s

I

k

E

r

=

3. Taka wartość siły elektromotorycznej wytwarza prąd

ograniczony rezystancją i reaktancją rozproszenia:

r

r

r

L

j

R

E

I

r

ω

+

=

4. W celu stosowania parametrów dla stanu znamionowego

występujące w równaniu tym zależności przedstawić można
jako:

r

r

s

L

j

R

I

k

I

r

1

1

1

1

ω

ω

ω

ω

ω

ω

+

=

5. Biorąc pod uwagę, że

ω

1

jest pulsację przy częstotliwości

znamionowej otrzymamy:

r

r

s

X

j

R

I

k

I

r

1

1

'

ω

ω

ω

ω

+

=

6. Oznaczając względną wartość prędkości jako

σ otrzymamy:

r

r

s

jX

R

I

k

I

r

+

=

σ

'

-5-

-6-