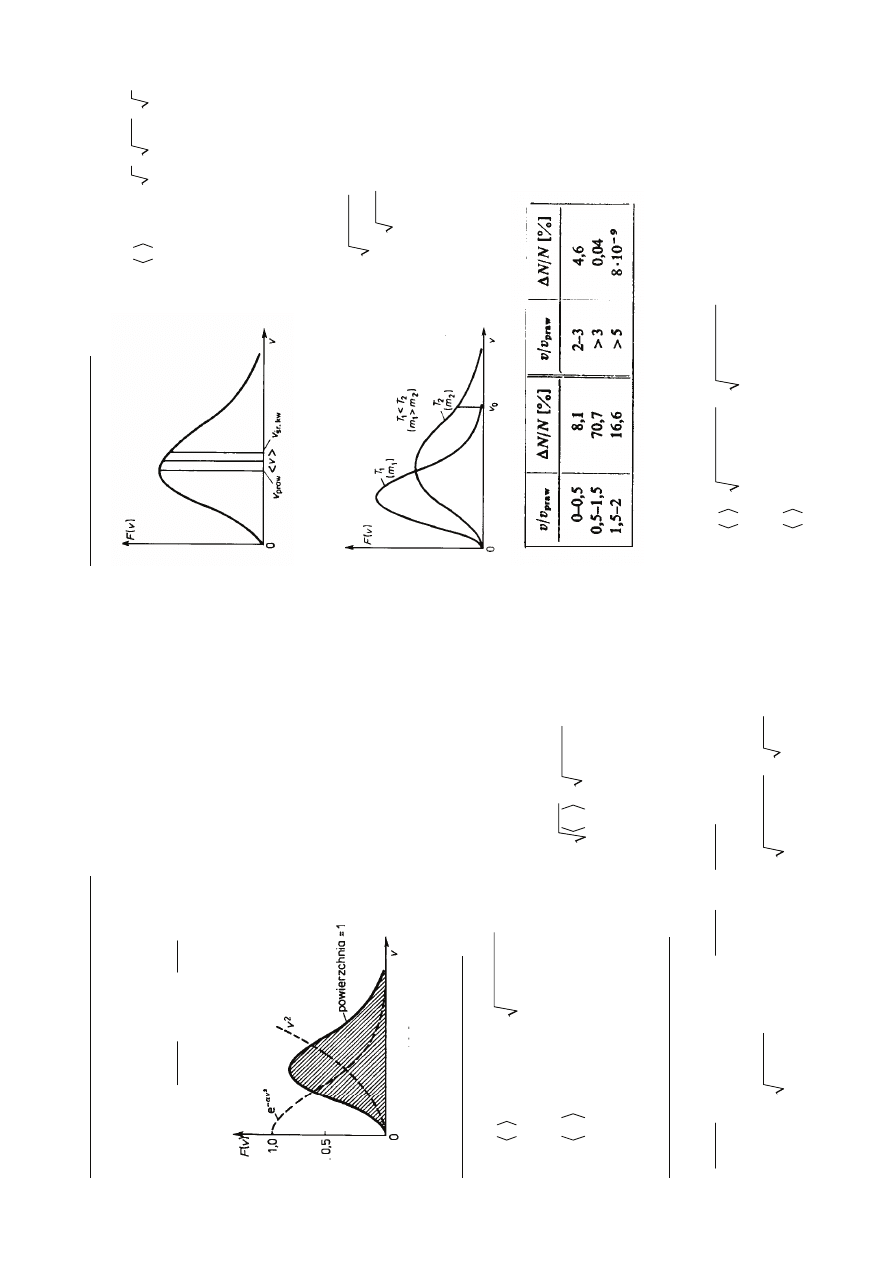
F

iz

y

k

a

s

ta

ty

s

ty

c

z

n

a

5

R

o

zk

#a

d

M

ax

w

el

la

(

ro

zk

#a

d

p

r!

d

k

o

%c

i

cz

$s

te

k

)

(

)

F

υ

-

f

u

n

k

c

ja

r

o

zk

$a

d

u

p

r%

d

k

o

#c

i

c

z&

st

ec

ze

k

g

a

zu

.

3

/2

2

2

(

)

ex

p

4

2

2

m

m

F

k

T

k

T

υ

υ

π

υ

π









=

− 















(r

o

zk

#a

d

M

ax

w

el

la

)

(

)

F

d
υ

υ

m

a

zn

ac

ze

n

ie

p

ra

w

d

o

p

o

d

o

b

ie

's

tw

a

te

g

o

,

"e

d

an

a

cz

$s

te

cz

k

a

m

a

m

o

d

u

#

p

r!

d

k

o

%c

i

za

w

ar

ty

w

p

rz

ed

zi

al

e

(

,

)
d

υ

υ

υ

+

)r

ed

n

ie

p

r!

d

k

o

%c

i

cz

$s

te

cz

ek

g

az

u

(

)

0

(

)

8

/

F

d

k

T

m

υ

υ

υ

υ

π

∞

=

=

∫

2

2

0

(

)

3

/

F

d

k

T

m

υ

υ

υ

υ

∞

=

=

∫

,

2

sr

.k

w

.

3

/

k

T

m

υ

υ

=

=

P

r!

d

k

o

%&

n

aj

b

ar

d

zi

ej

p

ra

w

d

o

p

o

d

o

b

n

a

p

ra

w

.

(

)

0

d

F

d

υ

υ

υ

υ

=





=









→

2

2

p

ra

w

.

p

ra

w

.

p

ra

w

.

ex

p

2

0

2

m

m

k

T

k

T

υ

υ

υ







−

−

=



















p

ra

w

.

2

/
k

T

m

υ

=

,

p

ra

w

.

(

)

(4

/

)

/(

2

)

/

F

e

m

k

T

m

T

υ

π

=

"

F

iz

y

k

a

s

ta

ty

s

ty

c

z

n

a

6

W

#a

%c

iw

o

%c

i

ro

zk

#a

d

u

M

ax

w

el

la

p

ra

w

.

sr

.k

w

.

:

:

2

:

8

/

:

3

(:

(,

(3

:(

,2

2

υ

υ

υ

π

=

=

p

ra

w

.

2

/
k

T

m

υ

=

p

ra

w

.

(

)

/

F

m

T

υ

"

T

le

n

(

32

g/

m

o

l,

3

00

K

T

µ

=

=

)

(

)

(

)

8

/

8

/

5

0

0

m

/s

k

T

m

R

T

υ

π

π

µ

=

=

≈

W

o

d

ó

r

(

2

g

/m

ol

,

30

0

K

T

µ

=

=

)

2

0

0

0

m

/s

υ

≈