Łukasz Chraniuk 28.09.2011

[e-mail]

NEMAR - Rozwiązania zadań z wykładu 1 (Poprawa)

Zadanie 1

Równanie ruchu ma postać

gdzie J = 10kgm² zaś M = 15Nm. W chwili t = 0 jest α = 0, ω = 100 rad/s 0. Narysować wykresy funkcji α(t) oraz ω(t) jeżeli wiadomo, że

M = 0 dla 0 ≤ t ≤ 10 s

M = - 2(t-10) Nm dla t > 10s.

Obliczenia przeprowadzić do chwili, w której ω zmniejszy się do zera.

Rozwiązanie

Dla 0 ≤ t ≤ 10s

Równanie ruchu ma postać:

dzieląc obie strony równania przez 10 otrzymujemy:

ω = dx/dt =
=
dt =

α =
dt =
dt =
+

,
- stałe całkowania

Z warunków brzegowych ( t = 0 to α = 0, ω = 100 rad/s) obliczam stałe całkowania:

Po podstawieniu stałych równania dla 0 ≤ t ≤ 10s są następujące:

ω = 100

α = 100t

Dla t > 10s

Równanie ruchu ma postać:

dzieląc obie strony równania przez 10 otrzymujemy:

ω = dx/dt =
=
dt

α =
dt =
dt =

,
- stałe całkowania

Warunki brzegowe dla t > 10s:

ω = 100

α = 100*10 = 1000

Z warunków brzegowych obliczam stałe całkowania:

Po podstawieniu stałych równania dla t > 10s są następujące:

ω =

α =

Wykresy:

Zadanie 2

Narysować wykresy obrazujące funkcje x(t) oraz dx/dt (t), które są rozwiązaniami równania

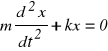
Przyjąć, że m = 5 kg zaś k = 30 kN/mm. Warunki początkowe: dla t = 0, x = -10 mm, dx/dt = 0.

Rozwiązanie:

m - masa,

k - stała sprężystości sprężyny

Przeliczam jednostki na jednostki SI:

Prawo Hooke'a:

F(x) = - kx

Równanie ruchu:

ma = F(x) = -kx

Pamiętając, że:

Otrzymuje:

Rozwiązanie ogólne zależy od dwóch stałych A, B:

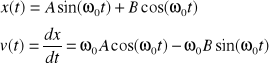
Wyznaczam stałe z warunków początkowych (dla t = 0, x = -0,01 , dx/dt = 0):

Po podstawieniu stałych równania wyglądają następująco:

Wykresy:

Zadanie 3

Obliczyć masowy moment bezwładności względem osi 0-0 elementu pokazanego poniżej.

Rozwiązanie:

Przyjmuję:

- gęstość stali

- gęstość żeliwa

Obliczam masę poszczególnych elementów:

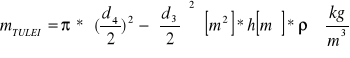
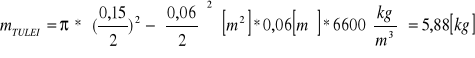
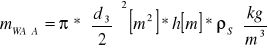
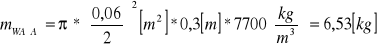
Obliczam momenty bezwładności elementów składowych względem osi 0-0

Korzystam z twierdzenia Steinera :

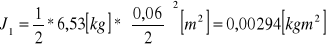
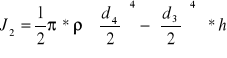
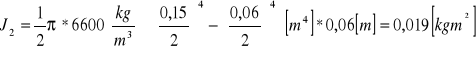
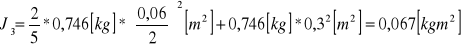
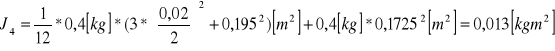
- moment bezwładności wała

- moment bezwładności tulei

- moment bezwładności kuli

- moment bezwładności pręta

Obliczam całkowity moment bezwładności względem osi 0-0:

0

8 szprych

Materiał: stal

300

Ø60

300

Materiał: żeliwo

Ø20

Ø_kuli 60

60

Ø150

0

---