___________________________________________________________________________________________________________________________

Recenzent: Prof. dr hab. inż. Andrzej Grono – Wydział Elektrotechniki i Automatyki

Politechnika Gdańska

Zeszyty Naukowe Wydziału Elektrotechniki i Automatyki Politechniki Gdańskiej

XVII Seminarium

ZASTOSOWANIE KOMPUTERÓW W NAUCE I TECHNICE’ 2007

Oddział Gdański PTETiS

Referat nr 4

SYMULATOR ROBOTA MOBILNEGO W ŚRODOWISKU MATLAB-SIMULINK

Mariusz DĄBKOWSKI

1.

Politechnika Gdańska, ul. G. Narutowicza 11/12, 80-925 Gdańsk,
tel: [phone]

fax: [phone]

e-mail: [e-mail]

Streszczenie:

Opisano

symulator

robota

mobilnego

opracowanego w środowisku MATLAB-SIMULINK. Podano
główne przesłanki do opracowania aplikacji oraz jej najważniejsze
zadania. Przedstawiono strukturę symulatora składającego się z
czterech głównych bloków. Opisano model fizycznej platformy
robota mobilnego oraz zależności matematyczne pozwalające
rozwiązać zagadnienie kinematyki i dynamiki odwrotnej ruchu
urządzenia na płaszczyźnie. Opisano sposób implementacji
układów odometrycznej realizacji pomiarów przebytej drogi oraz
prędkości ruchu urządzenia. W referacie przedstawiono również
model czujnika do pomiaru odległości – sonaru. Ponadto podano
również wyniki badań uzyskanych za pomocą opisanego
symulatora w postaci kolejnych punktów położenia robota
mobilnego na płaszczyźnie, realizującego zadanie całkowitego
pokrycia powierzchni w otoczeniu przeszkód ruchomych.
Przedyskutowano zalety oraz wady przedstawionej aplikacji,
a także zwrócono uwagę na możliwe kierunki jej rozwoju.

Słowa kluczowe: robotyka, robotyka mobilna.

1.

WSTĘP

Symulator robota mobilnego, opisany w niniejszym

artykule, został opracowany w celu przeprowadzenia badań

weryfikacyjnych

zaprojektowanego

uprzednio

behawioralnego systemu sterowania robota, pozwalającego
unikać zderzeń z przeszkodami ruchomymi podczas
wykonywania zadania całkowitego pokrycia nieznanej
powierzchni. Główną przesłanką do jego zbudowania był
brak rzeczywistego urządzenia, które pozwoliłoby na
przeprowadzenie testów układu sterowania.

Symulator robota mobilnego stanowi aplikację

komputerową opracowaną w środowisku MATLAB-
SIMULINK, w której zaimplementowano zaczerpnięte
z literatury

modele

elementów

składowych

robota

(platformy, układu napędowego, pomiarowego, a także
ś

rodowiska zewnętrznego – sceny oraz przeszkód

ruchomych). Należy podkreślić, że odzwierciedlono w niej
jedynie

niezbędne,

z

punktu

widzenia

badań

weryfikacyjnych

nad

systemem

sterowania

robota

mobilnego, cechy fizyczne. Niemniej jednak, starano się
stosować jak najmniej uproszczeń, aby symulator możliwie
wiernie odzwierciedlał rzeczywiste elementy urządzenia.
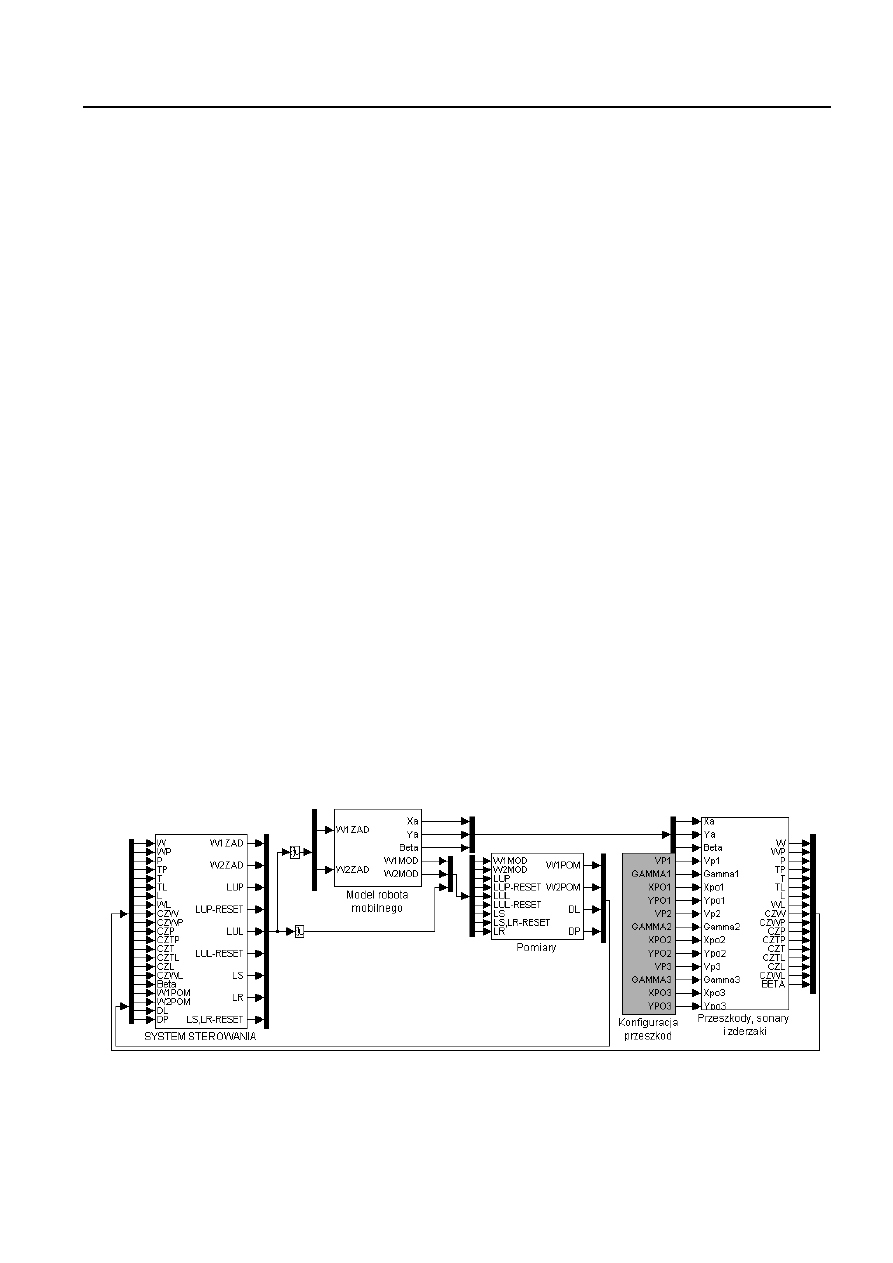
Schemat graficzny symulatora przedstawiono na rysunku 1
[1].

Rys. 1. Blokowa struktura symulatora robota mobilnego dla potrzeb rozwiązania problemu unikania kolizji z przeszkodami ruchomymi

podczas wykonywania zadania całkowitego pokrycia powierzchni terenu wraz z nadrzędnym systemem sterowania: 1 – nadrzędny

system sterowania; 2 – model kinematyki i dynamiki robota mobilnego; 3 – układ pomiaru prędkości obrotowej, przebytej drogi,

zliczania ucieczek, skrętów oraz ruchów na zadaną odległość do przodu lub do tyłu; 4 – interfejs konfiguracji parametrów początkowych

ruchu przeszkód ruchomych; 5 – modele przeszkód ruchomych, czujników zbliżeniowych i zderzeniowych [1]

1

2

3

4

5

- 24 -

W

referacie

opisano

jedynie

bloki

zawierające

implementacje modeli elementów fizycznych urządzenia
bez opisu nadrzędnego system sterowania. Wyczerpujące
informacje na temat jego budowy można znaleźć w [1].

2.

BLOK „MODEL ROBOTA MOBILNEGO”

Zaimplementowany w symulatorze model robota

wzorowany jest na budowie robota mobilnego TALRIK II.
Przyjęto, że platforma mobilna ma kształt koła, a układ
napędowy stanowią dwa koła napędzane umieszczone w
jednakowej odległości od środka robota i pracujące w
konfiguracji różnicowej. Trzecie koło jest samonastawne i
stanowi tylko punkt podparcia [1].

Blok składa się z pięciu podstawowych członów:

−

„układu ograniczania szybkości narastania sygnałów
referencyjnych” – w którym formowany jest sygnał
wejściowy, czyli wektor dwóch prędkości zadanych:
koła lewego i prawego, pochodzących z systemu
sterowania,

−

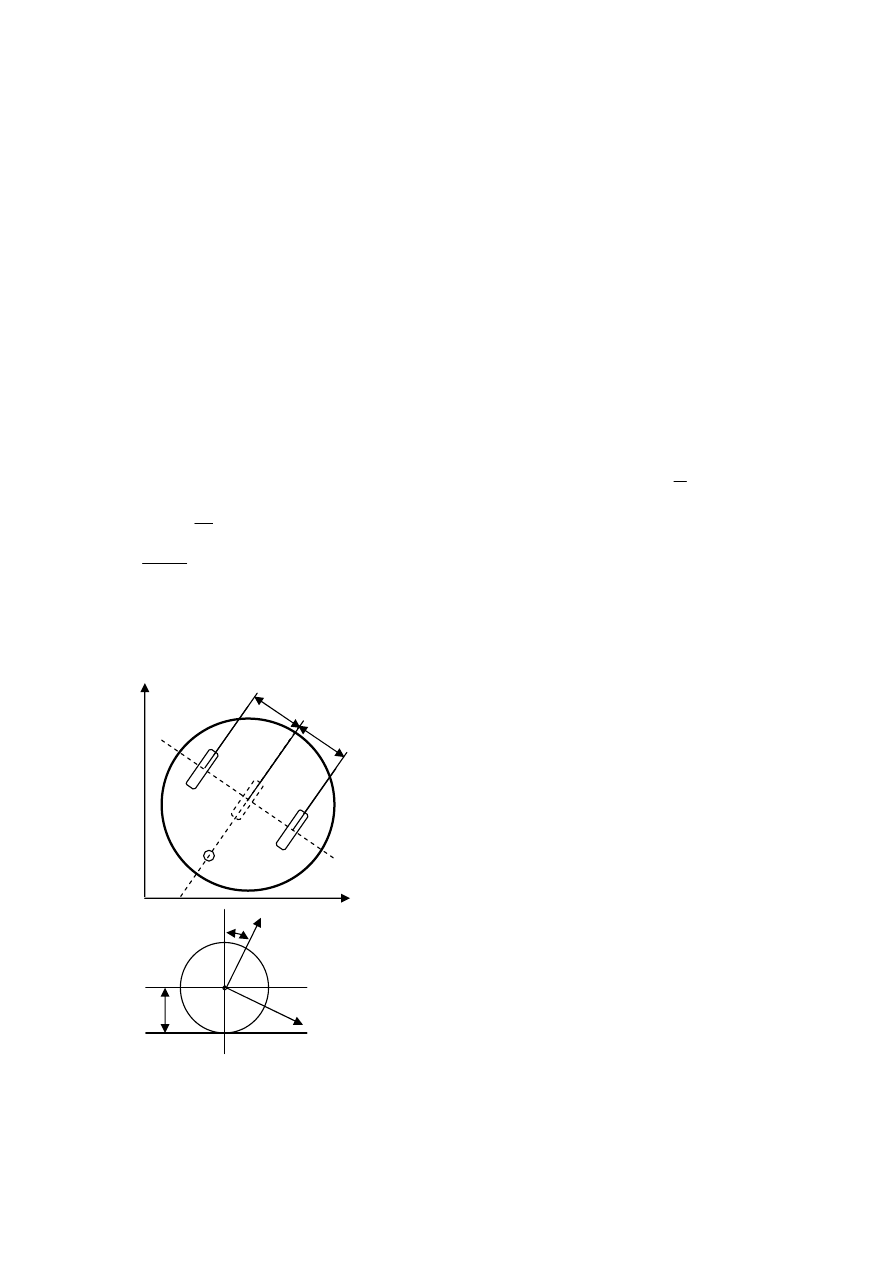
„modelu kinematyki robota” – bloku, stanowiącego
odzwierciedlenie uproszczonego zadania kinematyki
odwrotnej (rys. 2 a, b) [2]

1

1

2

2

)

(

l

r

α

α

β

&

&

&

−

=

(1)

2

2

1

α

α

α

&

&

&

+

=

(2)

gdzie:

β

& – prędkość obrotu platformy,

α

α

α

&

&

&

,

,

2

1

– prędkości

odpowiednio: koła lewego, prawego i zastępczego,

r – promień

koła,

l

1

– odległość koła od środka robota

Rys. 2. Model robota mobilnego Talrik II: a) platforma
mobilna; b) koło;1 – koło lewe; 2 – koło prawe; 1z – koło
zastępcze; A – środek ciężkości ramy oraz geometryczny
ś

rodek koła zastępczego 1z; B, C – geometryczne

ś

rodki kół 1, 2 [2]

−

układu regulacji nadążnej i modelu dynamiki” –
zawierającego implementację modelu dynamiki robota
jako

układu

nieholonomicznego

opisanego

równaniami Lagrange’a II rodzaju z mnożnikami
w formie odsprzężonej oraz układu regulacji nadążnej
z linearyzacją przez sprzężenie zwrotne [2]

(

)

(

)

1

2

2

1

1

2

1

2

1

1

1

4

2

1

1

2

2

2

h

f

N

f

N

M

M

h

I

I

I

l

m

z

x

z

+

−

−

=

=

+

+

+

β

&

&

(3)

(

)

[

]

2

2

1

1

2

1

1

2

4

1

2

2

f

N

f

N

M

M

I

r

m

m

z

−

−

+

=

=

+

+

α

&

&

(4)

gdzie:

M

1

,

M

2

– momenty napędzające koła: lewe i prawe

I

x1

=

I

x2

– zastępcze masowe momenty bezwładności kół 1 i 2

określone względem osi

x

1

i

x

2

związanymi z tymi kołami,

I

z1

=

I

z2

– zastępcze masowe momenty bezwładności kół 1 i 2

określone względem osi obrotu własnego tych kół,

m

4

– masa ramy,

I

z4

– zastępczy masowy moment bezwładności

ramy określony względem osi związanej z ramą,

N

1

,

N

2

– siły nacisku na koła odpowiednio 1 i 2,

f

1

,

f

2

–

współczynniki tarcia toczenia kół,

M

1

,

M

2

– momenty napędzające

koła,

r

1

=

r

2

=

r – promień kół, l

1

,

1

1

l

r

h

=

– odległości oraz

współczynnik wynikające z geometrii układu

−

„modelu sił tarcia” – w którym zawarto formuły
matematyczne pozwalające wyliczyć siły tarcia na
styku koła zastępczego z jezdnią podczas ruchu
robota, potrzebne do określenia maksymalnego
możliwego do uzyskania przyspieszenia urządzenia,
przy którym nie zachodzi zerwanie przyczepności [2],

−

„układu

formowania

sygnałów

wyjściowych

z modelu” – w którym odzwierciedlono wzory
matematycznych pozwalające określić położenie
robota w nieruchomym układzie współrzędnych XY
oraz prędkości poszczególnych kół.

3.

BLOK „POMIARY”

W

symulatorze

zaimplementowano

następujące

pomiary: odległości robota od przeszkód (sensory
ultradźwiękowe),

przebytej

drogi

przez

urządzenie

i prędkości

kątowej

poszczególnych

kół

(układy

odometryczne) oraz liczby zrealizowanych manewrów
(skrętów, ruchów do przodu, do tyłu i ucieczek – liczniki).

Idea działania układu odometrycznego pomiaru

przebytej drogi polega na wykorzystaniu prostej zasady
zliczania impulsów, która może być wykorzystana zarówno
do budowy układów określania długości przebytej drogi,
jak też do pomiaru prędkości [3]. Natomiast wartość
długości drogi pokonanej przez robota wyznaczana jest na
podstawie

ś

redniej

arytmetycznej

wartości

dróg

pokonanych przez poszczególne koła. Wartość średniej
prędkości liniowej ruchu robota wyliczana jest na
podstawie pomiaru wartości przebytej przez robota drogi w
danej jednostce czasu. Układy zliczające mają postać
prostych liczników.

X

.

.

.

A

C

B

.

l

1

l

1

ββββ

1

2

1z

Y

(a)

αααα

1,2

x

1,2

y

1,2

r

C

B

(b)

- 25 -

4.

BLOK „PRZESZKODY, SONARY I ZDERZAKI”

4.1.

Blok „przeszkody”

W wyniku analizy zadań do wykonania przez robota,

przyjęto, że do robota mogą zbliżać się maksymalnie trzy
obiekty dynamiczne w kształcie kół o określonych
ś

rednicach, które poruszają się ruchem jednostajnym po

linii prostej. W bloku „przeszkody” zdefiniowano ich ruch
za pomocą równań kinematyki określających współrzędne
położenia

punktów

charakterystycznych

(środków

geometrycznych) w czasie [4]. Wartości wielkości takich
jak: współrzędne punktu początkowego – x

0i

,

y

0i

, prędkość –

V

i

,, kierunek ruchu –

γ

i

są określane przez użytkownika

symulatora w bloku „konfiguracja przeszkód” (rys. 1 – blok
numer 5), który stanowi prosty interfejs użytkownika.

4.2.

Blok „sonary i zderzaki”

Blok „sonary i zderzaki” jest najważniejszy, z punktu

widzenia akwizycji wiedzy o środowisku zewnętrznym.
Zamodelowano w nim sposób działania 8 sensorów
zbliżeniowych oraz 8 zderzeniowych rozmieszczonych na
obwodzie platform mobilnej co 45

0

.

W

aplikacji

komputerowej

symulatora

zaimplementowano

model

analogowego

czujnika

ultradźwiękowego UM-30-3000A-HP firmy SELS [5]. Na
rysunku 3 zobrazowano graficznie strefy wykrywania przez
czujnik

ultradźwiękowy

przeszkód

ruchomych

i

nieruchomych.

Wartość odległość robota od przeszkody obliczana

jest na podstawie znajomości położenia środków: robota i
przeszkód oraz orientacji robota, czyli usytuowania stref
wykrywania

obiektów

poszczególnych

czujników

rozmieszczonych na obwodzie platformy względem
przeszkód w globalnym układzie współrzędnych.

Zasada działania zamodelowanych w s-funkcji

sensorów zderzeniowych polega na wykrywaniu kolizji,
które dokonywane jest na podstawie monitorowania
wartości

sygnałów

odległości

i

wystawianiu

„1”

w przypadku zderzenia (odległość od przeszkody równa 0),
a w przeciwnym – „0” [1].

Rys. 3. Układ współrzędnych związany z czujnikiem oraz funkcje

liniowe aproksymujące granice obszarów detekcji w lokalnym

układzie kartezjańskim: 1, 1’ – funkcje graniczne obszaru detekcji

przeszkód nieruchomych, 2, 2’, 3, 3’, 4, 4’ – funkcje graniczne

obszaru detekcji przeszkód ruchomych [5]

Fizyczne

granice

obszaru

roboczego

(ściany)

zdefiniowano również w s-funkcji, jako boki kwadratu
o długości 4 m [1].

5.

BADANIA WERYFIKACYJNE SYMULATORA

Badania weryfikacyjne zaprojektowanego symulatora

robota mobilnego przeprowadzono po włączeniu w jego
strukturę

behawioralnego

systemu

sterowania.

Przeprowadzono szereg symulacji połączonych aplikacji, w
wyniku których otrzymano ścieżki ruchu robota na
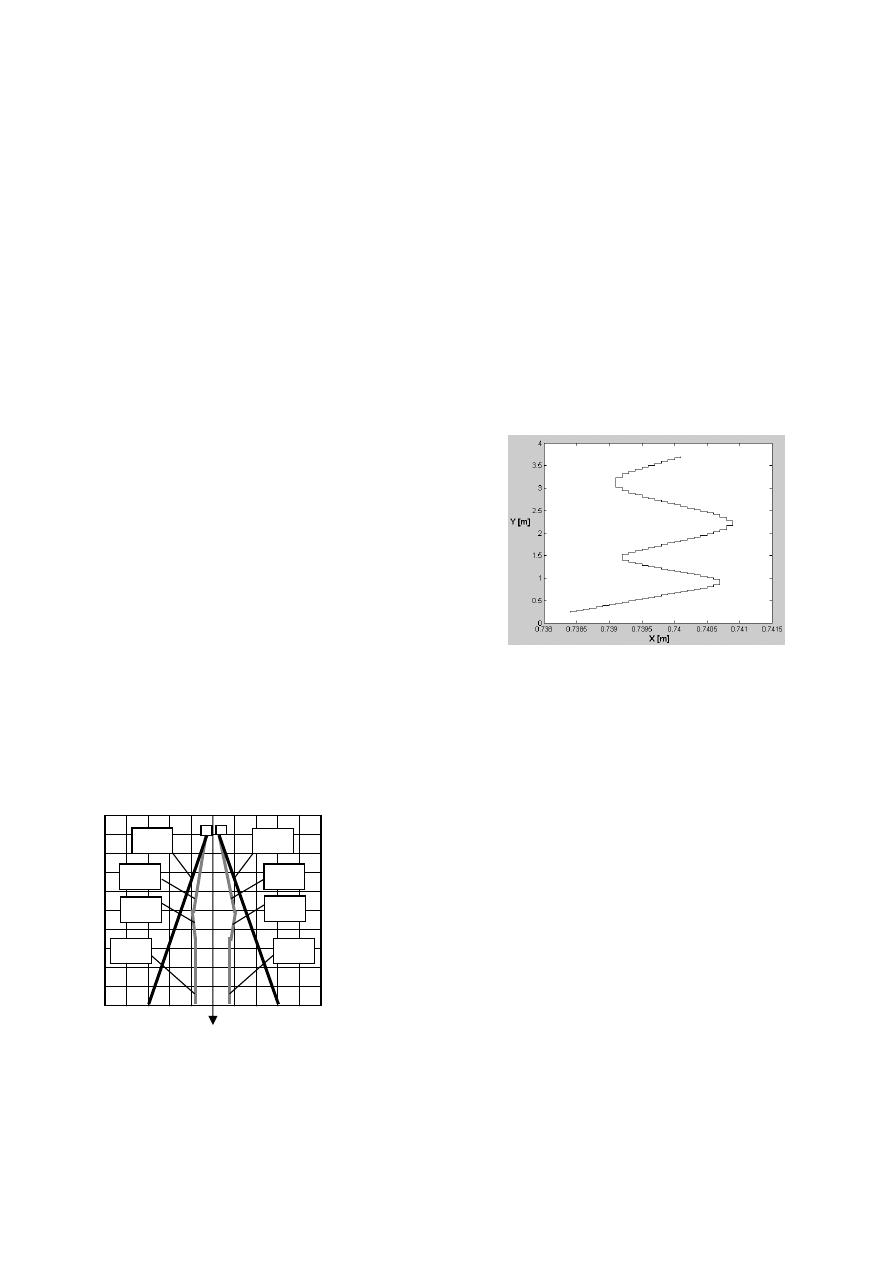
płaszczyźnie. Na rysunku 4 przedstawiono przykładowy,
graficzny zapis drogi pokonanej przez robota sterowanego
przez nadrzędny układ sterowania, a ściślej przez
zachowania ruchu do przodu oraz ruchu wzdłuż ściany.
Ś

cieżka wyznaczona została na podstawie rzutów

chwilowych punktów położenia środka platformy na
powierzchnię terenu.

Rys. 4. Graficzne przedstawienie ścieżki ruchu robota pomiędzy

nawrotami [1]

Uzyskany wynik jest zgodny z oczekiwaniami, co

pokazuje, że zarówno układ sterowania, jak i symulator
robota jest zaprojektowany poprawnie. Można stwierdzić,
ż

e symulator spełnił swoją główną funkcję, a więc

umożliwił poprawne testowanie zbudowanego układu
sterowania. Ponadto poprawny przebieg symulacji ruchu
robota pozwolił stwierdzić, że zaimplementowane modele
sensorów ultradźwiękowych umożliwiają w sposób
prawidłowy

wykrywanie

przeszkód

ruchomych

i

nieruchomych,

a

zderzeniowych

–

właściwe

sygnalizowanie kolizji. Układy odometrii z kolei poprawnie
mierzą odległość przebytą przez robota, jego orientację na
powierzchni terenu, a także prędkość.


6.

PODSUMOWANIE I WNIOSKI

W referacie przedstawiono strukturę symulatora

robota mobilnego zawierającego implementacje modeli,
niezbędnych

do

działania

urządzenia,

elementów:

platformy, układu napędowego, pomiarowego oraz świata
zewnętrznego.

Zaletą opisanego symulatora jest modułowa struktura,

która

zapewnia

dużą

elastyczność

użytkowania.

Poszczególne bloki mogą być swobodnie zastępowane
innymi (układy sterowania, modele kinematyki ruchu

- 0 cm

- 30 cm

- 60 cm

- 90 cm

- 120 cm

- 150 cm

- 180 cm

- 210 cm

- 240 cm

- 300 cm

- 270 cm

X

S

1

1’

2

2’

3’

4’

3

4

- 26 -

platformy) bądź rozbudowywane (układy pomiarowe).
Dzięki temu można badać różne typy nadrzędnych
systemów sterowania na modelach robotów o innych
konfiguracjach

napędowych (np.: trójkołowych lub

czterokołowych). Możliwe jest również wzbogacanie
układu pomiarowego o modele innego rodzaju sensorów
(np.:

podczerwieni)

lub

też

wykorzystywanie

ich

zamiennie.

Należy pamiętać, że zaimplementowane modele są

tylko

przybliżeniem

fizycznych

urządzeń,

jednak

zakładając, że niezbędne, z punktu widzenia zastosowania,
cechy elementów zostały uwzględnione, można prowadzić
przy ich użyciu wiarygodne badania bez konieczności
kupna bardzo drogiego sprzętu, jakim jest robot mobilny.
Poza tym modele poszczególnych części składowych
platformy mogą być również modyfikowane, tak by
odzwierciedlały pożądane własności fizyczne, istotne dla
użytkownika.

Opisana w referacie aplikacja ze względu na wielkie

zalety, przy świadomości jej ograniczeń, może być z
powodzeniem użyta w procesie kształcenia studentów.

7.

BIBLIOGRAFIA

1.

Dąbkowski M.: Analiza jakości wykonania pokrycia
powierzchni terenu przez autonomicznego robota
mobilnego. 2006. Rozprawa doktorska. Politechnika
Gdańska. Wydział Elektrotechniki i Automatyki.

2.

Giergiel M. J., Hendzel Z., śylski W.: Modelowanie i
sterowanie mobilnych robotów kołowych. Warszawa:
Wydawnictwa Naukowe PWN 2002.

3.

Borenstein J., Everett H. R., Feng L.: Where am I? –
sensors and methods for mobile robot positioning. The
University of Michigan.1996.

4.

Craig J.: Wprowadzenie do robotyki. Mechanika
i sterowanie. Wydawnictwo Naukowo-Techniczne.
Warszawa: 1993.

5.

Strona internetowa: http://www.sels.com.pl. - 2005

MOBILE ROBOT SIUMULATOR IN MATLAB-SIMULINK ENVIRONMENT

In paper was described the mobile robot simulator developed in MATLAB-SIMULINK environment. The main premises
and tasks of the application was given. A structure of the simulator which contained four main blocks was showed. The
phisical model of the mobile robot platform was described and mathematical equations, which permit to solve an inverse
kinematic and dynamic problem of a robot’s movement on the terrain surface, was given. The way of an implementation of
the dead reckoning system, which allowed the measurement of path’s length and robot’s speed, was described. In paper the
model of the sonar also was showed. Furthermore results of tests obtaining by the simulator was given. Advantages and
disadvantages of the simulator were discussed and pointed out possible directions of the application’s delevelopment.