Akademia Górniczo-Hutnicza w Krakowie

Imię i nazwisko:
Jan Tobijasiewicz

Laboratorium Metod Numerycznych

Wydział: EAIiE

Rok

Akad.:

2011/2012

Rok studiów: IV

Kierunek:
Elektronika i Telekomunikacja

Temat ćwiczenia:

Problem własny, diagonalizacja macierzy

i rozwiązywanie równań różniczkowych

Data wykonania:
18.06.2012

Data zaliczenia:

Ocena:

Wstęp

Na laboratorium wykonywałem ćwiczenia związane z numerycznymi operacjami

na macierzach.

Zadanie 1

Oblicz, stosuj

ąc metodę potęgową, największą wartość własną i odpowiadający jej

wektor w

łasny dla następującej macierzy:

wektor startowy x

(0)

= (1,0,0)

T

, dokładność ε=0.1.

Obliczeń dokonano dzięki zaimplementowaniu metody potęgowej:

A = [-1 -1 0,

% zadana macierz

-2 4 -2,
0 -1 1];

i = 1;
x = [1 0 0]';

% zadany wektor poczatkowy

eps = 0.1;

% zadana dokladnosc

dokladnosc = 1;

% inicjalizacja wartosci dokladnosci

while

dokladnosc > eps

if

i > 1

x(:,i) = B./lambda(i-1);

end

B = A*x(:,i);
lambda(i) = max(abs(B));

if

i>1

dokladnosc(i-1) = abs((lambda(i)-lambda(i-1))/lambda(i));

end

i = i+1;

end

Wyniki:

Kolejne przyblizenia wartosci wlasnych

lambda =

2.0000 3.0000 5.6667 4.6471 4.9241

Odpowiadajace im wektory wlasne

x =

1.0000 -0.5000 0.5000 0.0882 0.1962
0 -1.0000 -1.0000 -1.0000 -1.0000
0 0 0.3333 0.2353 0.2658

Dokladnosci kolejnych przyblizen

dokladnosc =

0.3333 0.4706 0.2194 0.0563

Wnioski

Widać jak szybko metoda zmierza do poprawnego rozwiązania, już w piątej

iteracji pojawia się satysfakcjonujący wynik. Wykonywane są tu głównie proste operacje
na macierzach, metoda powinna sprawować się szczególnie dobrze w przypadku
większych macierzy.

Zadanie 2

Dany jest uog

ólniony problem własny:

Sprowadzi

ć ten problem do postaci standardowej, a następnie obliczyć dominującą

warto

ść własną i odpowiadający jej wektor własny.

Widzimy, że macierze są symetryczne, wyrazy położone symetrycznie względem
głównej przekątnej mają takie same wartości. Można zatem skorzystać z rozkładu
Choleskyego.
Uogólniony problem własny jest zdefiniowany następująco:

C

Sprowadzamy równanie do zwykłego problemu własnego

,

gdzie: v to wektor własny a

to wartość własna

Obliczone wartości własne dla uogólnionego problemu własnego :

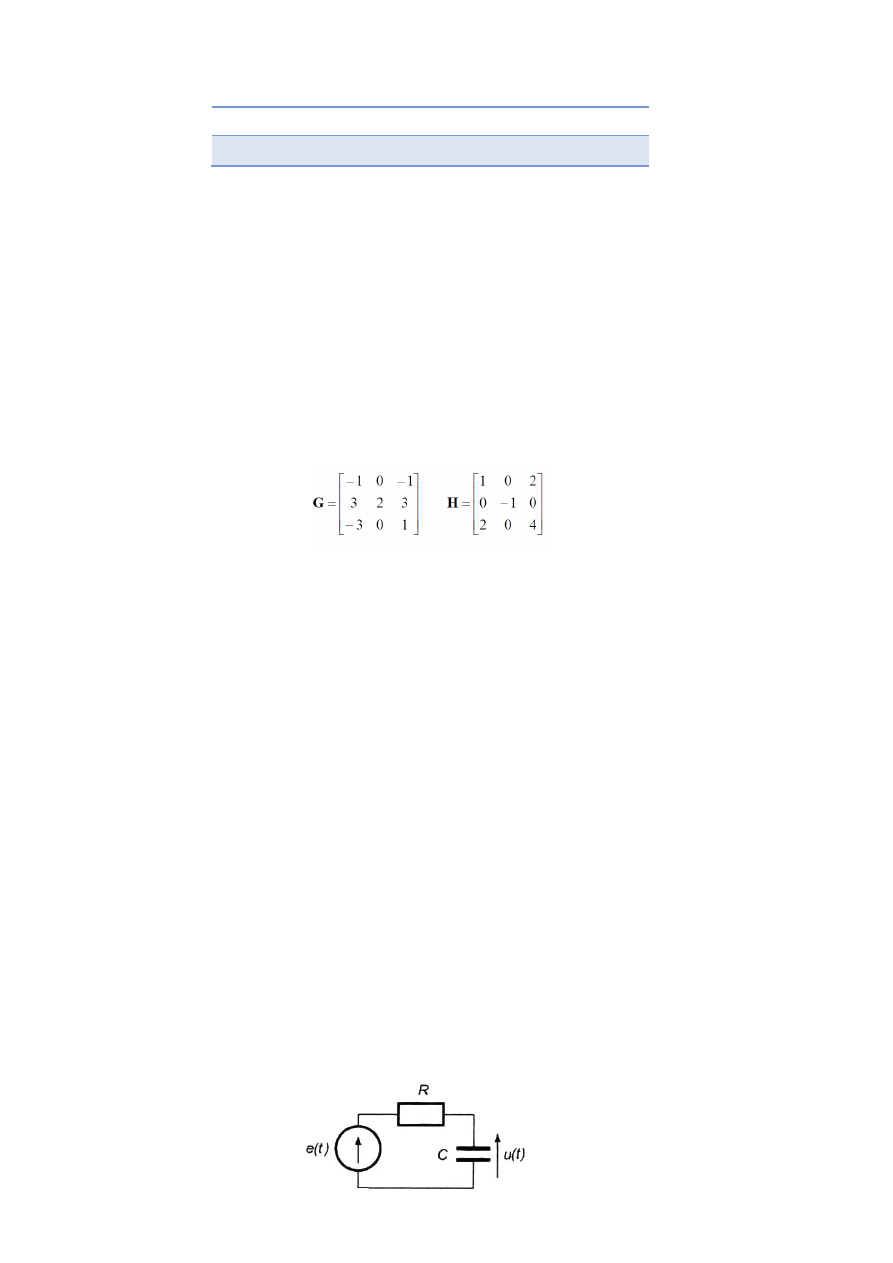
v1 = [-1; 0]

v2 = [0.3162; -0.9487]

Wnioski

W tym zadaniu szczególnie pomocny był symetryczny charakter macierzy,

problem sprowadził się dzięki temu do kilku operacji.

Zadanie 3

Sprawdzić czy macierze G i H są diagonalizowalne:

Macierz A

∈ Fn×n jest diagonalizowalna wtedy i tylko wtedy, gdy jej wielomian

charakterystyczny ma n pierwiastków w ciele F (liczonych z krotnościami)
W takim razie korzystając z funkcji wbudowanej [V,D] = eig() obliczyliśmy wartości
własne macierzy

1) Macierz G posiadała 3 wartości własne -2 i 2 z czego krotność wartości własnej 2

wynosiła 2. Wielomian charakterystyczny macierzy G posiada 3 pierwiastki, a jej
wymiar także wynosi 3. Macierz jest diagonalizowalna.

2) Macierz H posiadała 3 wartości własne -1, 0, 5. Wielomian charakterystyczny

macierzy H posiada 3 pierwiastki, a jej wymiar także wynosi 3. Macierz jest
diagonalizowalna.

Wnioski

Matlab jest dedykowany do operowania na macierzach, w przypadku tego zadania

pomogła jego wbudowana funkcja.

Zadanie 4

Porównaj dokładność rozwiązania równania różniczkowego opisującego liniowy układ

RC (pokazany na rysunku) za pomoc

ą wybranych metod całkowania: a) otwartej metody

Eulera, b) metody Heuna;

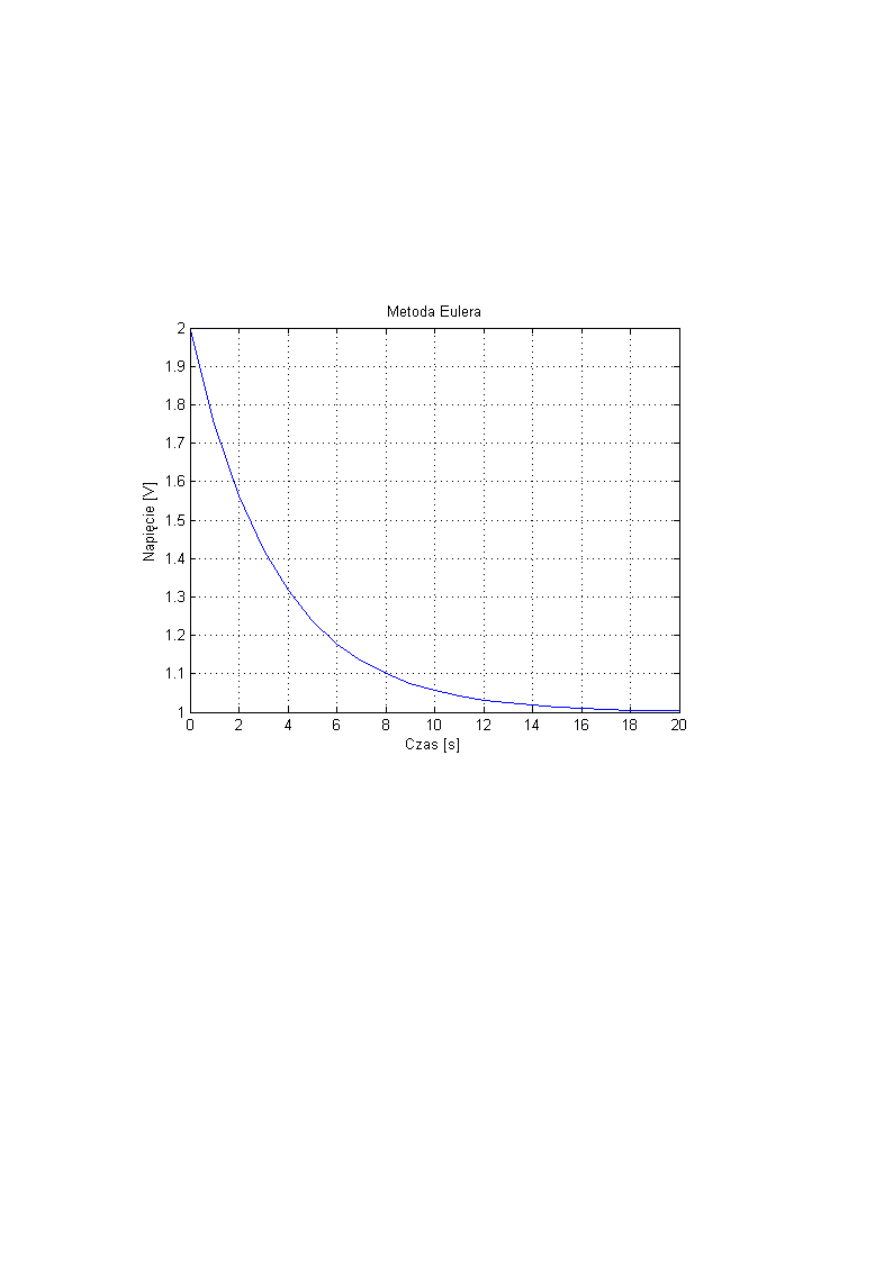
Dane do rozwiązania problemu to:
Liczba kroków czasowych: N = 20,
Napięcie początkowe na pojemności: U(t=0) = 2 V,
Wymuszenie napięciowe: e(t) = 1(t) V.

Do rozwiązania zadania wybrano wartości iloczynu rezystancji i pojemności RC

oraz wielkość kroku czasowego. W wyniku wykonania programu otrzymano następujące
przebiegi napięć na kondensatorze:

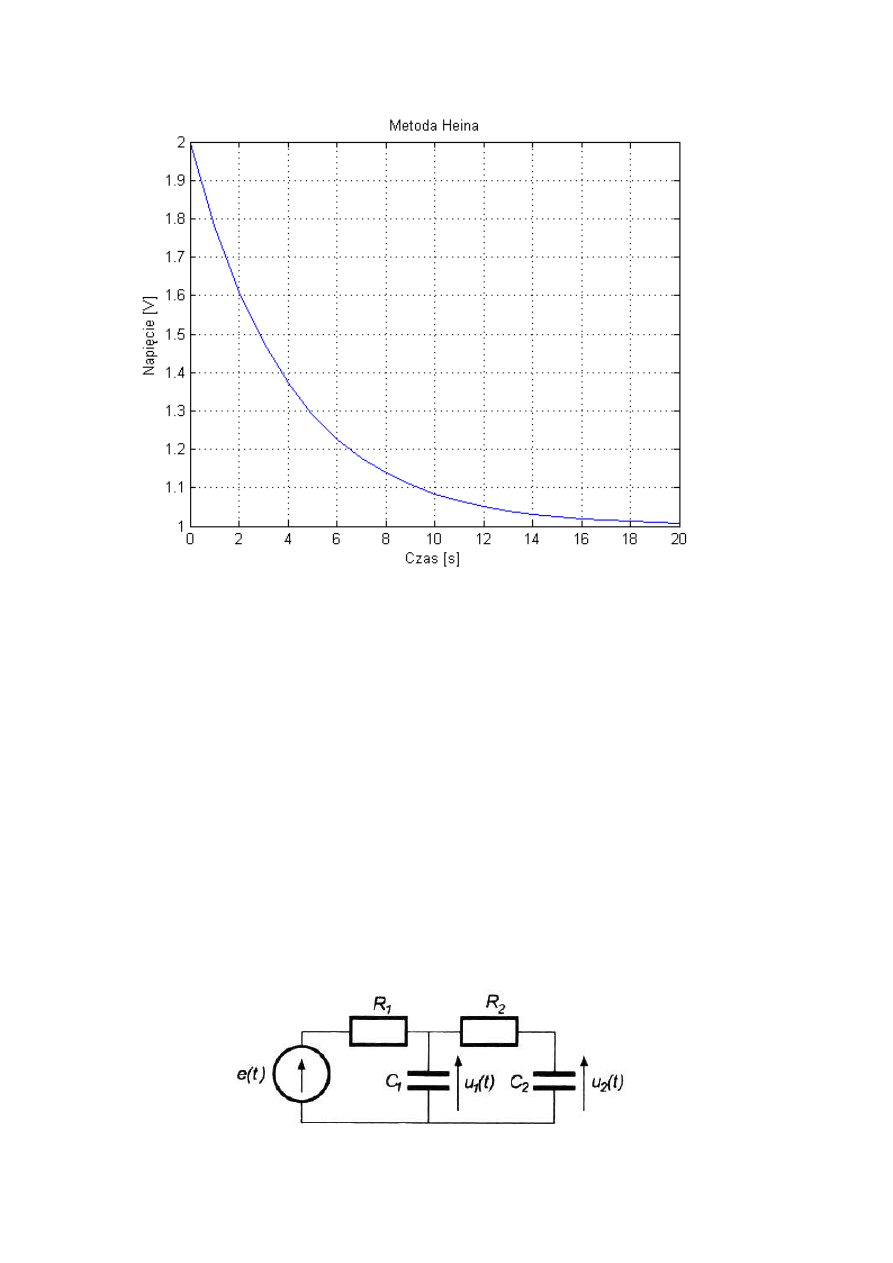
Wnioski

Wynik obliczenia różniczki metodą Eulera. Stała czasowa mówi nam po jakim

czasie napięcie spadnie do danego poziomu. Aby lepiej było widać spadek napięcia do
wartości ustalonej przyjołem, że czas trwania rozładowywania kondensatora wynosi 4s.
Jak możemy zauważyć metoda Eulera niezbyt dobrze przybliża nasze rozwiązanie,
metoda Heuna daje lepsze rezultaty.

Zadanie 5

Za pomoc

ą otwartej metody Eulera proszę wyznaczyć odpowiedź sieci

elektrycznej przedstawionej na rysunku, przyjmuj

ąc następujące wartości parametrów:

R1 = 1kOhm, R2 = 1MOhm, C1 = C2 = 1uF oraz e(t)=1(t)V. Prosz

ę przyjąć zerowe

napi

ęcia początkowe na obu pojemnościach. Podać warunek bezwzględnej stabilności

uk

ładu. Należy wykreślić dokładne przebiegi obu napięć węzłowych oraz przedstawić

odpowiednie wyniki oblicze

ń.

W celu dokonania obliczeń napisałem równanie obwodu w postaci:

Kod napisany w mat labie wyglądał następująco:

clc, clear

all

R1 = 1e3;

% rezystancja w pierwszym oczku

R2 = 1e6;

% rezystancja w drugim oczku

C1 = 1e-6;

% pojemnosc w pierwszym i drugim oczku

C2 = C1;

% pojemnosc w drugim oczku

e = 1;

% wymuszenie

u1(1) = 0;

% warunki poczatkowe

u2(1) = 0;
t(1) = 0;

N = 100;

% zalozona ilosc krokow czasowych

h = 0.0001;

% zalozona dlugosc kroku czasowego

for

i = 1:N

du2(i) = (u1(i) - u2(i)) / (R2 * C2);
du1(i) = ((e - u1(i)) / (C1 * R1)) - ((u1(i) - u2(i)) / (C1 * R2));
u1(i+1) = u1(i) + du1(i) * h;
u2(i+1) = u2(i) + du2(i) * h;
t(i+1) = t(i) + h;

end

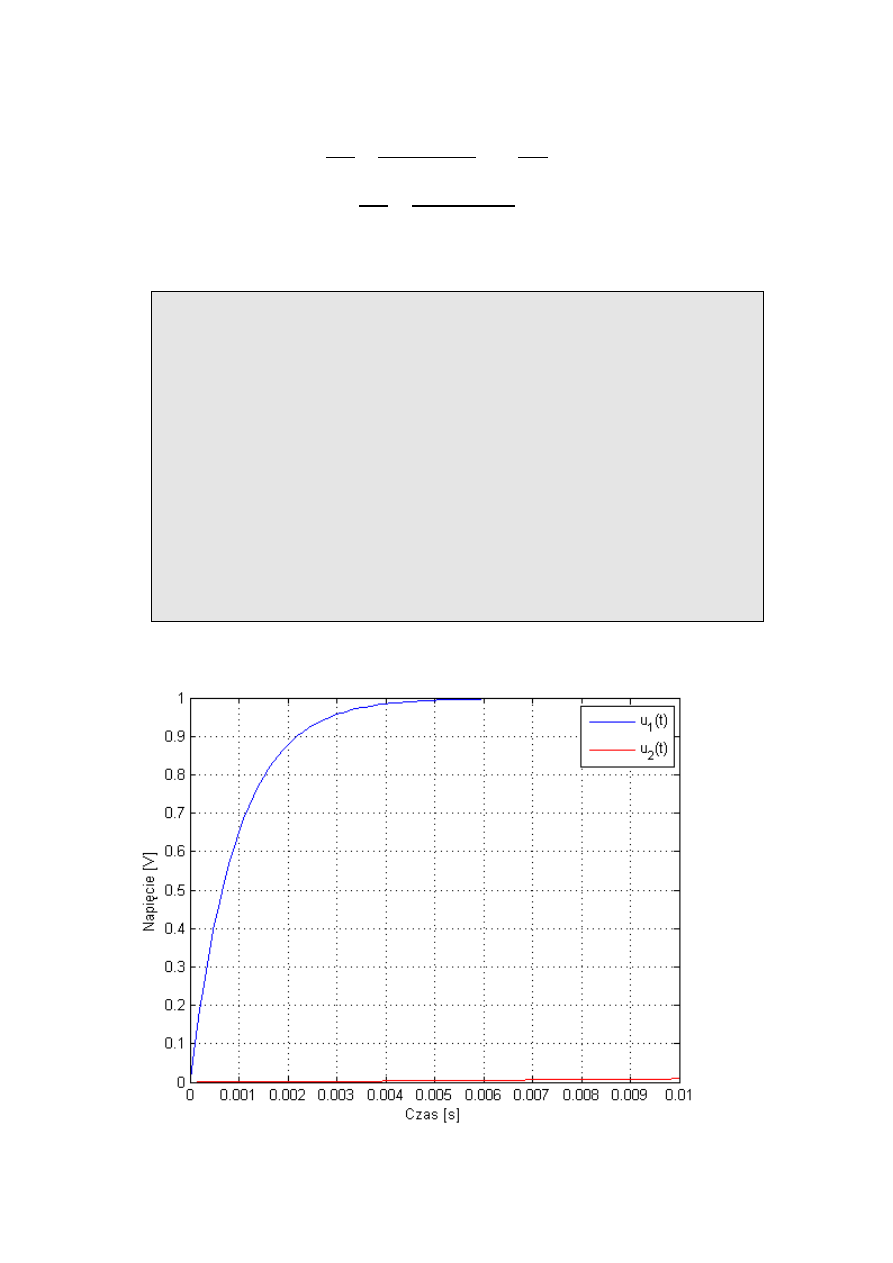
Oto otrzymane przebiegi czasowe:

Wnioski ogólne

Udało się wykonać wszystkie ćwiczenia, pokazały one jak przydatnym

środowiskiem jest matlab jeśli chodzi o operacje na macierzach. Po raz kolejny dobór
metody do zdanego zagadnienia był kluczowy w niektórych zadaniach. Zadanie 2
pokazuje jak przydatna może być znajomość własności macierzy symetrycznych, należy
o tym pamiętać by nie utrudniać sobie niepotrzebnie obliczeń.