1

Macierz -- definicja

• Definicja macierzy:

– teoretycznie: funkcja rzeczywista (lub zespolona) dwóch

zmiennych całkowitych, i oraz j:

X:=[x

ij

], i=1..M, j=1..N

– praktycznie: dwuwymiarowa tablica liczb rzeczywistych

(lub zespolonych) o rozmiarach MxN

• Macierz a skalar

– W pewnych kontekstach macierz przeciwstawia się

skalarowi, czyli pojedynczej liczbie (rzeczywistej lub

zespolonej)

– Nie przeczy to faktowi, że skalar można traktować jako

szczególny przypadek macierzy (o rozmiarach 1x1)

– Przekształcenie danych/wyników z postaci macierzowej

do skalarnej jest jednak często bardzo pożądane (z

względu na ułatwioną interpretację wyników skalarnych)

2

Macierz w zapisie zadań

• W algebrze macierze są zazwyczaj stosowane do

zapisywania układów równań/nierówności

• Np. układ równań:

2x

1

-3x

2

+4x

3

=4

3x

1

+2x

2

-1x

3

=2

może być wyrażony w postaci:

• Ax=b

gdzie A=

b=

x=

2

-3

4

3

2

-1

4

2

x

1

x

2

3

Macierz -- transpozycja

• Ze względu na wymienne traktowanie wierszy i

kolumn macierzy jedną z podstawowych

(nienumerycznych) operacji macierzowych jest tzw.

transpozycja macierzy

• Oznaczenie:

– X – macierz oryginalna
– X

T

– macierz transponowana

• Definicja macierzy transponowanej:

– teoretycznie: X

T

:=[x

ji

], i:=1..M, j:=1..N

– praktycznie: potraktowanie wierszy macierzy jako kolumn a

kolumn jako wierszy (zapisanie wierszy w kolumnach a

kolumn w wierszach)

• Oczywiście (X

T

)

T

=X

• Transponowanie nie powinno być mylone z obrotem!

4

Przykład transponowania

• Przykład macierzy o wymiarach 3x4:

X

X

T

(X

T

)

T

7

4

-2

4

4

5

5

1

-1

3

2

0

7

4

-1

4

5

3

-2

5

2

4

1

0

7

4

-2

4

4

5

5

1

-1

3

2

0

5

Wektory

• Szczególnymi przypadkami macierzy są tzw. wektory

– wektor kolumnowy (krótko: wektor), np.:

• x=

– wektor wierszowy (powstały wskutek transponowanie

wektora kolumnowego), np.:

• x

T

=

• Rozmiar wektora: liczba jego elementów
• Każda macierz może być traktowana jako zbiór tzw.

linii, czyli wektorów wierszowych lub wektorów

kolumnowych

21

-3

12

21

-3

12

6

Macierze i wektory szczególne

• Wektory 1, 0, e

j

,

• Macierze I, 0, diagonalna, jedynkowa: E=11

T

• wektory ortogonalne, ortonormalne
• macierz diagonalna
• macierz odwrotna
• zależności (AB)

T

=B

T

A

T

7

Macierz w zapisie zadań

• Zapisy macierzowe są szczególnie przydatne do

przedstawiania ogólnych przekształceń danych

• Np. w teorii programowania liniowego (PL) dla

pewnych zadań PL (zwanych prymalnymi)
definiuje się tzw. symetryczne zadania dualne

• Prymalny:

Dualny:

max c

T

x

min b

T

y

p.o. Axb

p.o. A

T

yc

x0

y0

8

Macierz -- element przekształcający #1

• Jeżeli pewien wektor o rozmiarze N reprezentuje

punkt/obserwację przestrzeni N-wymiarowej, to
wiele różnych operacji przekształcających ten punkt
w tej przestrzeni można przedstawić w postaci
mnożenia przez pewną macierz kwadratową, np.:

• Przykłady:

– Przemnożenie dowolnego wektora 2-elementowego przez

macierz A

NxN

realizuje symetrię punktową (względem

punktu 0)

– Przemnożenie dowolnego wektora 2-elementowego przez

macierz B

NxN

realizuje obrót o kąt  (względem punktu 0)

A=

B=

-1

0

0

-1

cos() sin()

-

sin()

cos(

)

9

Macierz -- element przekształcający #2

• Z tego punktu widzenia macierz jest elementem

przekształcającym

– W algebrze właściwości macierzy są badane, ponieważ

pozwalają na ujawnienie właściwości samego przekształcenia

– Np. dopóki wyznacznik macierzy kwadratowej A jest różny od

zera, to przekształcenie polegające na przemnożeniu wektora
x przez macierz A jest odwracalne

• Mnożenie wektorów N-wymiarowych przez macierze

niekwadratowe przekształca je do innych wymiarów

– Np.: wskutek przemnożenia wektora N-elementowego x

Nx1

przez macierz o rozmiarach A

MxN

powstaje wektor y

Mx1

:

y

Mx1

=A

MxN

*x

Nx1

10

Macierz -- nośnik danych

• Równie często jednak macierz jest nośnikiem

danych

– Najbardziej typowe zastosowania:

• Statystyczna analiza danych: obserwacje w wierszach
• Teoria sygnałów: obserwacje w kolumnach

Statystyka:

Teoria sygnałów:

0.7

0.4

0.2

0.4

0.4

0.5

0.5

0.1

0.1

0.3

0.2

0.0

7

4

-1

4

5

3

-2

5

2

4

1

0

11

Przekształcenia liniowe

• Idea przekształceń liniowych
• Czeste wystepowanie w algebrze liniowej
• Pojęcie kombinacji liniowej zmiennych

– Kombinacja afiniczna
– Kombinacja wypukła

• Pojęcie kombinacji liniowej wektorów
• Pojęcie niezależności wektorów

12

Podstawowe operacje macierzowe

• Dodawanie macierzy
• Mnozenie przez skalar

13

Przekształcenia macierzowe #1

• Mnożenie wektora przez wektor

– Mnożenie wektora przez wektor jest najprostszą

multiplikatywną operacją macierzową

– Istnieją dwie (różne od siebie) wersje takiego

przekształcenia

• Tzw. iloczyn skalarny wektorów
• Tzw. iloczyn macierzowy wektorów

– Na początek dokładniej omówiony zostanie iloczyn

skalarny

14

Przekształcenia macierzowe #2

• Iloczyn skalarny wektorów

– Dopuszczalne jest jedynie mnożenie wektorów o tej

samej liczbie elementów

– Bez względu na ich rozmiar wynik mnożenia wektora

przez wektor jest pojedynczą liczbą (skalarem)

– Formalnie, iloczyn skalarny s może powstać tylko z

przemnożenia wektora wierszowego przez kolumnowy:

x

1

x

2

x

3

x

a

1

a

2

a

3

=

a

1

x

1

+

a

2

x

2

+a

3

x

3

=
:

s

15

Przekształcenia macierzowe #3

• Mnożenie macierzy przez wektor

– Jednym z najczęściej rozważanych przekształceń

macierzowych w algebrze jest mnożenie macierzy przez
wektor

• macierz -- element przekształcający
• wektor -- element danych

– Aby operacja ta była dopuszczalna, macierz A traktuje

się jako zbiór wektorów wierszowych a

iT

, które mnoży się

przez dany wektor (kolumnowy) x

x

a

1

T

x

a

2

T

x

x

=

a

1

T

a

2

T

16

Przekształcenia macierzowe #4

• Gdy dane podlegające przekształcaniu zebrane są

w macierzy to mnożeniu podlegają całe macierze

– Operacja mnożenia macierzy przez macierz

odzwierciedla jednak sytuację, w której zarówno macierz
danych jak i macierz przekształcającą traktuje się jak
zbiór wektorów (kolumnowych względnie wierszowych)

– Wynikiem takiej operacji jest macierz odpowiednich

iloczynów skalarnych

x

1

x

2

x

3

a

1

T

x

1

a

1

T

x

2

a

1

T

x

3

a

2

T

x

1

a

2

T

x

2

a

2

T

x

3

x

=

a

1

T

a

2

T

17

Właściwości operacji macierzowych

• Łączność

– dodawania: A+(B+C)=(A+B)+C
– mnożenia: A(BC)=(AB)C

• Rozdzielność

– mnożenia względem dodawania: A*(B+C)=A*B+A*C

• Przemienność

– dodawania: A+B=B+A

• Ponieważ mnożenie macierzy nie jest przemienne,

mówiąc o mnożeniu macierzy A przez macierz B

należy precyzować, czy jest to mnożenie

– prawostronne: A*B,

czy

– lewostronne: B*A

18

Mnożenie lewostronne i prawostronne

• Różnice w mnożeniu

lewostronnym/prawostronnym mogą być
wykorzystane przy dokonywaniu mnożenia przez
macierze diagonalne

– lewostronne:

– prawostronne

1

2

3

4

3

0

0

2

3

*1+0*

3

3

*2+0*

4

0*1+

2

*

3

0*2+

2

*

4

3

*1

3

*2

2

*3

2

*4

x

=

=

3

0

0

2

1

2

3

4

1*

3

+2*

0

1*0+2*

2

3*

3

+4*

0

3*0+4*

2

1*

3

2*

2

3*

3

4*

2

x

=

=

19

Szczególne operacje macierzowe #1

• Normalizowanie danych

– dane są obserwacje x

ij

zapisane w macierzy X (rozmiar MxN)

– przez normalizację tych danych rozumie się wykonanie operacji

– gdzie:

• są średnimi zmiennych x

j

(czyli kolumn macierzy X)

• s

j

są odchyleniami standardowych tych zmiennych

– operacja ta może być przedstawiona w zapisie macierzowym

jako:

Z = (I–E/M)XD

– gdzie:

• D jest macierzą diagonalną odwrotności s

j

• M jest liczbą wierszy macierzy X

j

j

ij

ij

s

x

x

z





j

x

20

Szczególne operacje macierzowe #2

• Obliczanie macierzy kowariancji

– dane są obserwacje x

ij

zapisane w macierzy X (rozmiar MxN)

– przez macierz kowariancji rozumie się macierz S

x

=[s

ij

], gdzie

(bez uwzględnienia dzielenia przez liczbę obserwacji)

– dla znormalizowanych danych operacja ta może być

przedstawiona w zapisie macierzowym jako:

S

x

= X

T

X











M

1

k

j

kj

i

ki

ij

)

x

)(x

x

(x

s

21

Wyznacznik macierzy -- wprowadzenie

• Tzw. wyznacznik macierzy jest jednym z wielu

współczynników opisujących macierze (inne

współczynniki: ślad macierzy, rząd macierzy, itd.)

• Wyznacznik dotyczy tylko macierzy kwadratowych
• Oznaczenie: det(A) lub |A|
• Z pewnych względów wyznacznik ma znaczenie

kluczowe, szczególnie gdy dotyczy macierzy

przekształcających

– powód: można na jego podstawie wywnioskować, czy

przekształcenie jest odwracalne (tak, gdy det(A)0)

– teoretycznie odpowiedź na to pytanie jest prosta:

albo det(A)=0 albo det(A)0

– w praktyce jednak problem ten jest bardziej złożony

(ze względu na niedokładności numeryczne)

22

Wyznacznik a odwracalność operacji

• Gdy det(A)0 to operacja Ax jest odwracalna, co

oznacza, że na podstawie y można odtworzyć
takie x, że: y=Ax

• Przekształcenie odwrotne realizuje się jako

mnożenie przez macierz A

–1

, czyli macierz

odwrotną do A

• Definicja macierzy odwrotnej: AA

–1

=I= A

–1

A

23

Definicja wyznacznika

• Definicja permutacyjna wyznacznika
• Obliczanie wyznacznika przez rozwinięcie

wiersza/kolumny

24

Podstawowe właściwości wyznacznika

• Udowodniono szereg twierdzeń pozwalających na

natychmiastowe określenie wartości wyznacznika

– Jeżeli dowolna linia macierzy jest wektorem zerowym, to

wartością jej wyznacznika jest zero

• Wniosek: Wyznacznikiem macierzy zerowej jest zero

– Jeżeli dwie dowolne linie macierzy zostaną zamienione

miejscami, to wyznacznik macierzy zmieni znak na
przeciwny

• Wniosek: Jeżeli macierz zawiera jakiekolwiek dwie identyczne

linie, to jej wyznacznik wynosi zero

– Jeżeli dowolna linia macierzy jest kombinacją liniową innych

linii tej macierzy, to wyznacznik macierzy wynosi zero

• Wniosek: Wyznacznik macierzy jest różny od zera gdy jej

wszystkie linie są wektorami niezależnymi liniowo

25

Idea kontroli wartości wyznacznika

• Załóżmy, że wyznacznik pewnej macierzy jest

różny od zera, ale bliski zeru (i wynosi np. 0.01)

– Jakie cechy elementów tej macierzy decydują o tym, że

tak jest?

– Jak krótko scharakteryzować wartość wyznacznika

macierzy w kategoriach wartości jej elementów?

• Co łączy elementy macierzy oraz wartość jej wyznacznika

(oprócz definicji, która jednak jest na tyle skomplikowana,
że trudno o jej interpretację w tych kategoriach)?

• Jakie przekształcenie elementów macierzy doprowadzi jej

wyznacznik do wartości zero
(oprócz trywialnego przemnożenia przez zero)?

• Jak skutecznie kontrolować wyznacznik?

26

Kontrola wartości wyznacznika #1

• Doprowadzenie wyznacznika do zera:

– Metody „inwazyjne”

• Wyzerowanie dowolnej linii macierzy (przemnożenie przez 0)
• Wstawienie dowolnej linii macierzy w miejsce innej

(skopiowanie)

– Metody „nieinwazyjne”

• Znalezienie takiego przekształcenia, które przekształci i-tą

linię macierzy w j-tą linię tej macierzy

– W wyniku takiej operacji otrzymujemy przekształcenie, które

definiuje relację pomiędzy macierzami -- powstałe relacje można

by poddawać systematycznym badaniom

– Problem: które linie wybrać? (numery linii mogłyby być

parametrami, ale to generowałoby nadmierną liczbę parametrów)

• Podstawowe problemy powyższych metod:

– Jakie linie kontrolować? (wiersze/kolumny?)
– Które z nich poddawać przekształceniom?

27

Kontrola wartości wyznacznika #1

• Problem kontroli linii macierzy ma pewne

rozwiązanie szczególne (kompleksowe):

– Pytanie: Jakie linie kontrolować? (wiersze/kolumny?)

• Odpowiedź: Zarówno wiersze, jak i kolumny

– Pytanie: Które wiersze/kolumny poddawać

przekształceniom?

• Odpowiedź: Wszystkie

28

Kontrola wartości wyznacznika #1

• Dalsze pytania i odpowiedzi przedstawiają się

następująco:

– Pytanie: Jak kontrolować elementy macierzy? Mnożyć/dzielić

przez pewien parametr? Dodawać/odejmować parametr?

• Odpowiedź: Przez odjęcie parametru od wartości elementu

– Pytanie: Ile parametrów zastosować do kontrolowania

macierzy o rozmiarach NxN? (min: 1 parametr, max: N

2

parametrów)

• Odpowiedź: Zastosować minimalną liczbę parametrów (czyli

jeden), ale umożliwić mu kontrolowanie każdego wiersza i
każdej kolumny

– Pytanie: Od których elementów macierzy odjąć parametr?

• Odpowiedź: Od wszystkich elementów głównej przekątnej

macierzy. Pozwala to na kontrolowanie (jednego) elementu w
każdym wierszu i każdej kolumnie

29

Parametryzacja macierzy

• Ilustracja parametryzacji macierzy A=[a

ij

], i=1..4,

j=1..4

a

11

–

a

12

a

13

a

14

a

21

a

22

–

a

23

a

24

a

31

a

32

a

33

–

a

34

a

41

a

42

a

43

a

44

–

30

Macierz charakterystyczna

• Sparametryzowaną wersję macierzy A można zapisać

w postaci przekształcenia macierzowego: A-I

• Macierz A-I ta nosi nazwę macierzy

charakterystycznej macierzy A

• Macierz charakterystyczna jest także macierzą

kwadratową, możliwe jest więc zdefiniowanie

wyznacznika tej macierzy: det(A-I)

– Ponieważ macierz charakterystyczna jest zależna od

parametru , sprawdzenie, czy jej wyznacznik jest równy

zero jest możliwe dopiero po przypisaniu konkretnej wartości

parametrowi 

Możliwe jest także inne postępowanie:
– ustalenie takiej wartości parametru , dla której wyznacznik

macierzy jest równy zero

31

Równanie charakterystyczne

• Zależne od  równanie det(A-I)=0 nazywa się

równaniem charakterystycznym macierzy A

• Dla macierzy o rozmiarach NxN lewa strona tego

równania jest wielomianem stopnia N (co wynika z
metody obliczania wyznacznika macierzy)

• Rozwiązaniem tego równania jest N (niekoniecznie

różnych) wartości zespolonych

32

Wartości własne macierzy

• Rozwiązania równania charakterystycznego

macierzy nazywane są wartościami własnymi tej
macierzy

– niem. eigenwert
– ang. eigenvalue

• Zbiór wartości własnych macierzy nazywa się

widmem (lub spektrum) tej macierzy

• Wartości własne informują jednoznacznie o tym,

co należy zrobić z przekątną macierzy, aby
doprowadzić jej wyznacznik do zera

33

Wartości własne -- przykład -- obliczenia

• Obliczyć wartości własne następującej macierzy A=

• Macierz charakterystyczna A-I=

• Wielomian charakterystyczny (po zastosowaniu wzoru na

wyznacznik macierzy o rozmiarach 2x2):

det(A–I) = (3–)*(2–) – 2*1 = 6 – 3* – 2* + 

2

– 2*1 = 

2

– 5 +

4

• Równanie charakterystyczne (w tym przypadku kwadratowe):



2

– 5

1

+ 4

0

= 0

• Rozwiązanie powyższego równania kwadratowego:

Wyróżnik równania: (–5)*(–5) – 4*1*4 = 25 – 16 = 9













2

2

1

3





















2

2

1

3

1

2

2

2

3

5

1

2

9

)

5

(

1





















4

2

8

2

3

5

1

2

9

)

5

(

2





















34

Wartości własne -- przykład -- wyniki

• Zbiorem wartości własnych macierzy A jest {1, 4}
• Co się dzieje po zastosowaniu każdej z tych

wartości
(czyli odjęciu jej od elementów głównej
przekątnej)?



1

=1:



2

=4:

0

1

2

1

2

det

1

2

2

1

1

3

det

2

2

1

3

det

1

1

































































































0

2

2

1

1

det

4

2

2

1

4

3

det

2

2

1

3

det

2

2





































































































35

Wartości własne -- właściwości

• Wartości własne macierzy charakteryzują się

wielką liczbą nietrywialnych właściwości, m.in.:

– Suma wszystkich wartości własnych jest równa śladowi

macierzy

– Iloczyn wszystkich wartości własnych jest równy

wyznacznikowi macierzy

• Wiele innych właściwości/twierdzeń dotyczy

wartości własnych, równania
charakterystycznego, np.:

– Każda macierz spełnia własne równanie

charakterystyczne

– W powyższym przykładzie: A

2

– 5A

1

+ 4A

0

= 0



















































































































































0

0

0

0

4

0

0

4

4

0

0

4

4

0

0

4

10

10

5

15

6

10

5

11

1

0

0

1

4

2

2

1

3

5

2

2

1

3

2

2

1

3

36

Przekształcenie identycznościowe wektora

• Niech x będzie wektorem N-elementowym, natomiast A --

macierzą o wymiarach NxN

• Operacja Ax przekształca x w pewien inny wektor y

(czyli Ax=y)

• Problem przekształcenia identycznościowego:

– Pytanie: czy istnieją takie wektory x, że Ax=x?

• Odpowiedź: tak, dla każdej A zachodzi: A0=0

(rozwiązanie trywialne)

– Pytanie: czy istnieją rozwiązania nietrywialne powyższego problemu,

a więc takie wektory, że przemnożenie ich przez macierz
przekształca
je na nie same? Lub konkretniej:

• takie wektory x0, że Ax=x?
lub (w osłabionej postaci):
• takie wektory x0, że Ax jest proporcjonalne do x, czyli Ax=sx

(gdzie s jest różnym od zera skalarem)?

37

Przekształcenie identycznościowe --

przykłady

• Dla macierzy A z powyższego przykładu:

• Ale:









































6

5

2

1

2

2

1

3

















































6

7

1

2

2

2

1

3













































2

5

1

2

2

2

1

3









































4

4

1

1

2

2

1

3













































2

1

2

1

2

2

1

3









































4

2

4

2

2

2

1

3

38

Rozwiązanie przekształcenie

identycznościowego

• Zakładając, że k=[k

1

,k

2

, ..., k

N

]

T

, rozwiązania problemu

przekształcenia identycznościowego można poszukiwać

zapisując i rozwiązując następujące równanie:

Ak=k

lub równoważną mu postać:

(A–I)k=0

• Podobnie, rozwiązania problemu przekształcenia

proporcjonalnościowego można poszukiwać rozwiązując:

Ak=sk

lub równoważną mu postać:

(A–Is)k=0

• Jeżeli w powyższym równaniu za współczynnik

proporcjonalności s przyjmie się wartość własną  macierzy,

to niezerowe rozwiązanie tego równania nazywa się

wektorem własnym macierzy (odpowiadającym wartości

własnej )

39

Wektory własne macierzy

• Ponieważ każda macierz o rozmiarze NxN posiada

co najwyżej N (niekoniecznie różnych) wartości

własnych, to oznacza to, że macierz ta posiada

także co najwyżej N (niekoniecznie różnych)

wektorów własnych

• Wektor własny macierzy to taki niezerowy wektor,

który w wyniku przemnożenia przez tę macierz

ulega przekształceniu na wektor proporcjonalny do

samego siebie

– współczynnikami proporcjonalności są odpowiednie

wartości własne macierzy

– jeżeli jedna z wartości własnych macierzy jest równa 1, to

istnieje wektor własny tej macierzy, który w wyniku

przemnożenia przez tę macierz nie ulega zmianie

(przekształcenie identycznościowe)

40

Właściwości wektorów własnych

• Wektory własne są niezerowymi rozwiązaniami

następującego równania:

(A–I)k=0 (gdzie  jest wartością własną macierzy A)

co pociąga za sobą następujące konsekwencje:

– Jeżeli k jest wektorem własnym, to jest nim także każdy

wektor postaci sk, gdzie s jest niezerowym skalarem
(współczynnikiem proporcjonalności)

– Ponieważ wartości własne  macierzy są tak dobrane,

aby wyznacznik macierzy A–I wynosił 0, to rozwiązanie

k równania (A–I)k=0 jest określone niejednoznacznie

(istnieje wiele takich rozwiązań)

41

Obliczanie wektorów własnych -- przykład

#1

• Przykład

 

1

=1, lewe strony równań

– układ równań:

2k

1

+k

2

= 0

2k

1

+k

2

= 0

– rozwiązanie (parametryczne, parametr )

k

1

= 

k

2

= –2k

1

– odpowiadający wektor własny -- każdy wektor postaci:





























































































































































2

1

2

1

2

1

2

1

2

1

1

k

k

2

k

k

2

k

k

1

2

1

2

k

k

1

1

0

0

1

2

2

1

3

k

k

1

0

0

1

2

2

1

3















 α

2

α

42

Obliczanie wektorów własnych -- przykład

#2

• Przykład (c.d.)

 

1

=4, lewe strony równań

– układ równań:

–k

1

+k

2

= 0

2k

1

–2k

2

= 0

– rozwiązanie (parametryczne, parametr )

k

1

= 

k

2

= k

1

– odpowiadający wektor własny -- każdy wektor postaci:





































































































































































2

1

2

1

2

1

2

1

2

1

1

k

2

k

2

k

k

k

k

2

2

1

1

k

k

4

1

0

0

1

2

2

1

3

k

k

1

0

0

1

2

2

1

3















β

β

43

Obliczanie wektorów własnych -- przykład

#3

• Rozwiązanie (postać ogólna)

– wektor własny odpowiadający wartości 

1

=1:

– wektor własny odpowiadający wartości 

1

=4:

• Rozwiązanie (postać szczególna dla =1, =1)

– wektor własny odpowiadający wartości 

1

=1:

– wektor własny odpowiadający wartości 

1

=4:













β

β













 α

2

α













 2

1













1

1

44

Dobór wektorów własnych

• Ze względu na parametryczność rozwiązań układu

równań definiującego wektory własne, możliwe jest

tworzenie bardzo różnych instancji tych wektorów

• W wielu różnych zastosowaniach parametry dobiera

się w taki sposób, aby powstałe wektory własne były:

– unormowane, tzn.: k

i

k

i

=1

– wzajemnie ortogonalne, tzn.: k

i

k

j

=0 dla ij

• Rozwiązania tej postaci są także najczęściej

generowane przez funkcje/biblioteki komputerowe

• ???Rozwiązanie istnieje (przyjmując normalizację

nawet dla identycznych wartości własnych generuje

się rózne wektory własne) , macierz wektorów

własnych jest odwracalna

45

Macierz wektorów własnych

• Niech K=[k

1

, k

2

, ..., k

N

] będzie macierzą utworzoną z kolejnych

wektorów własnych pewnej macierzy A

• Jeżeli wektory własne k

i

macierzy A są unormowane oraz

ortogonalne, to zachodzi następująca zależność:

K

T

K= =

=I

• Ponieważ:

– jeżeli: K

T

K=I to (K

T

K)

T

=I

T

, czyli KK

T

=I

T

– oraz: I

T

=I

to wynika z tego, że także KK

T

=I

1

0

0

0

0

1

0

0

0

0

1

0

0

0

0

1

k

1

k

1

k

1

k

2

...

k

1

k

N

k

2

k

1

k

2

k

2

k

2

k

N

k

N

k

1

k

N

k

2

k

N

k

N

46

Podstawy rozkładu EVD

• Niech ={

1

, 

2

, ..., 

N

} będzie zbiorem wartości własnych

pewnej macierzy, a wektory k

1

, k

2

, ..., k

N

odpowiadającymi im

wektorami własnymi tej macierzy

• Z definicji wektorów własnych zachodzi:

Ak

1

= k

1



1

, Ak

2

= k

2



2

, ..., Ak

N

= k

N



N

• Ponieważ lewe i prawe strony powyższych równości są

wektorami, to równania te można zapisać w postaci

macierzowej:

[ Ak

1

, Ak

2

, ..., Ak

N

] = [ k

1



1

, k

2



2

, ..., k

N



N

]

• Jednocześnie:

– zakładając, że K=[ k

1

, k

2

, ..., k

N

]

[ Ak

1

, Ak

2

, ..., Ak

N

] można przedstawić jako AK

– zakładając, że L=diag([ 

1

, 

2

, ..., 

N

])

[ k

1



1

, k

2



2

, ..., k

N



N

] można przedstawić jako KL

• Ostatecznie początkowy układ równości można zapisać jako:

AK = KL

47

Rozkład EVD macierzy #1

•

Obie strony równania:

AK = KL

można przemnożyć prawostronnie przez K

–1

otrzymując:

AKK

–1

= KLK

–1

•

Ponieważ KK

–1

=I powstaje równanie

A = KLK

–1

•

Dla unormowanych i ortogonalnych wektorów własnych
składających się na macierz K zachodzi: K

–1

=K

T

, a więc:

A = KLK

T

•

Każdą kwadratową macierz A można przedstawić w
postaci iloczynu KLK

T

, gdzie K jest macierzą wektorów

własnych a L macierzą wartości własnych macierzy A

48

Rozkład EVD macierzy #2

• Warunki istnienia/jednoznaczności, itd., rozkładu:

– rozkład istnieje, gdy A jest macierzą kwadratową, jednak

wartości własne mogą być w ogólności wartościami
zespolonymi

– gdy macierz A jest kwadratowa i symetryczna to jej

wartości własne są wartościami rzeczywistymi

• odpadają problemy z analizą liczb zespolonych

– gdy macierz A jest kwadratowa i symetryczna to

wszystkie wektory własne są ortogonalne

• odpadają problemy z zapewnianiem ortogonalności

wektorów

49

Analiza nienadzorowana -- wariancja

• Jeżeli zmienne (atrybuty) danych są podzielone na

warunkowe i decyzyjne (analiza nadzorowana), to
ilość informacji „zawartej” w pewnym atrybucie
warunkowym można wyrażać poprzez miary
zależności pomiędzy tym atrybutem a atrybutem
decyzyjnym (entropia)

• W sytuacji gdy w zbiorze nie zdefiniowano

atrybutów decyzyjnych, każdy atrybut musi być
oceniony indywidualnie

– za miarę informacyjności przyjmuje się wariancję atrybutu,

co można wytłumaczyć tak, że atrybut nie wykazujący
żadnej zmienności (wariancja 0), nie niesie żadnej
informacji

50

Procedura PCA

• Dana jest macierz danych: X (obserwacje w

wierszach)

• Oblicz macierz kowariancji S

x

– S

x

pozwala ocenić wariancje zmiennych

(elementy głównych przekątnych)

– wynikowa macierz S

x

jest z definicji symetryczna

• Oblicz wartości/wektory własne
• Utwórz macierze L i K
• Przemnóż X przez K

51

Rozkład EVD macierzy a metoda PCA

• Dane są macierze:

– macierz danych oryginalnych X
– macierz kowariancji danych oryginalnych S

x

=X

T

X

– macierz danych przekształconych Y=XK, gdzie K jest macierzą

wektorów własnych macierzy kowariancji S

x

=X

T

X, czyli S

x

=KLK

T

• Wtedy:

– macierz kowariancji danych przekształconych S

y

można wyrazić jako:

– S

y

= Y

T

Y = (XK)

T

XK = K

T

X

T

XK = K

T

S

x

K = K

T

KLK

T

K = ILI = L

• Wniosek:

– Jeżeli przekształci się dane oryginalne X do postaci Y za pomocą

mnożenia przez macierz K to macierz kowariancji zmiennych

przekształconych Y wyraża się macierzą diagonalną utworzoną z

wartości własnych macierzy S

x

• wariancje zmiennych przekształconych są równe wartościom własnym

macierzy S

x

-- można je poznać tuż po wyliczeniu wartości własnych

• kowariancje zmiennych przekształconych są równe zero -- zmienne te są

niezależne (liniowo)

52

Mechanizm tworzenia nowych zmiennych #1

• Dane są macierze:

– macierz danych oryginalnych X
– macierz przekształcająca K

• Nowe dane (Y) powstają w rezultacie operacji

Y=XK

k

1

k

2

k

3

y

11

y

12

y

13

y

21

y

22

y

23

y

31

y

32

y

33

...

...

...

y

N1

y

N2

y

N3

x

=

x

1

T

x

2

T

x

3

T

...

x

N

T

53

Mechanizm tworzenia nowych zmiennych #2

• Element macierzy y

ij

= jest iloczynem skalarnym

wiersza x

iT

oraz kolumny k

j

: y

ij

= x

iT

k

j

• Liczba nowych obserwacji = liczba starych

obserwacji

• Liczba nowych zmiennych = liczba starych

zmiennych

k

1

k

2

k

3

x

1

T

k

1

x

1

T

k

2

x

1

T

k

3

x

2

T

k

1

x

2

T

k

2

x

2

T

k

3

x

3

T

k

1

x

3

T

k

2

x

3

T

k

3

...

...

...

x

N

T

k

1

x

N

T

k

2

x

N

T

k

3

x

=

x

1

T

x

2

T

x

3

T

...

x

N

T

54

Mechanizm tworzenia nowych zmiennych #3

• Liczba nowych zmiennych zależy od liczby

kolumn macierzy przekształcającej K

• Zmniejszenie liczby kolumn tej macierzy prowadzi

do zmniejszenia nowych zmiennych

k

1

k

2

k

k

3

3

y

11

y

12

y

y

13

13

y

21

y

22

y

y

23

23

y

31

y

32

y

y

33

33

...

...

...

...

y

N1

y

N2

y

y

N3

N3

x

=

x

1

T

x

2

T

x

3

T

...

x

N

T

55

Przekształcenie odwrotne

• W rezultacie przekształcenia PCA (czyli operacji

Y=XK) tworzone są nowe zmienne

• Pytania:

– jak na podstawie nowych zmiennych odtworzyć stałe?
– jak to zrobić, jeżeli zredukowano liczbę nowych zmiennych?

• Odpowiedzi:

– odtworzenia starych zmiennych na podstawie nowych

można dokonać dokonując przekształcenia odwrotnego

• ponieważ Y=XK, to YK

–1

=XKK

–1

, i wtedy YK

–1

=XI

• czyli X=YK

–1

, ponieważ K

–1

=K

T

, wystarczy wykonać YK

T

• odtworzenie wszystkich zmiennych oryginalnych jest tylko

możliwe przez przemnożenie niezredukowanej macierzy Y,

toteż jeżeli pewne zmienne przekształcone (czyli kolumny

macierzy Y) zostały zredukowane, to należy odtworzyć je przed

wykonaniem mnożenia, zastępując oryginalne zmienne ich

wartościami średnimi

56

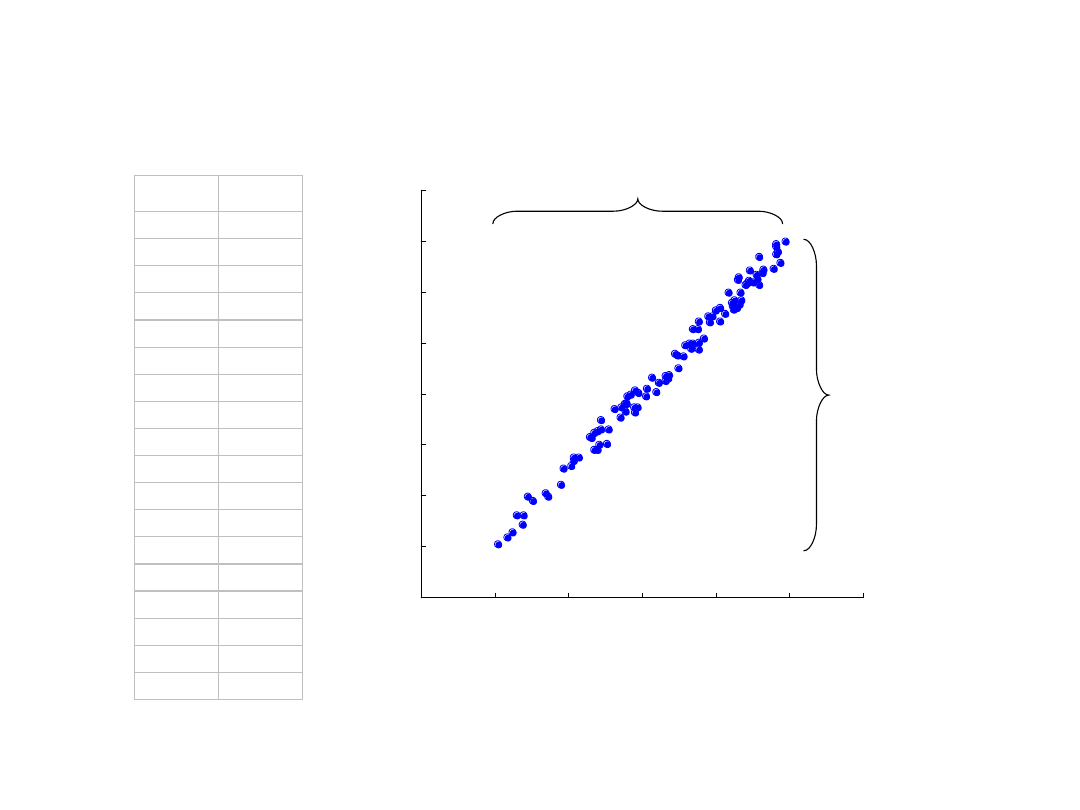
Zasada zachowania informacji (wariancji)

• W rezultacie przekształcenia PCA suma wariancji nowych

zmiennych jest równa sumie wariancji starych zmiennych
(co nie oznacza, ze poszczególne wariancje nie ulegają
zmianie!)

K

y

11

y

12

y

y

13

13

x

=

0

1

2

3

4

5

6

7

8

9

10

0

1

2

3

4

5

6

7

8

9

10

x

1

x

2

x

3

57

-5

0

5

10

15

20

25

-5

0

5

10

15

20

25

30

35

Przykład: PCA dla danych dwuwymiarowych

x

1

x

2

13.34

19.37

17.57

25.89

5.40

8.33

14.63

21.99

1.95

3.00

11.60

16.71

11.76

16.49

7.25

12.36

18.24

27.17

8.99

14.70

17.31

27.05

6.77

9.45

10.29

14.67

7.02

9.44

1.52

3.04

...

...

...

...

...

...

duża
wariancja

duża
wariancja

58

Utworzenie macierzy przekształcającej

S

x

27.4 40.6

40.6 60.9

L

88.1

0

0

0.2

K

0.55 0.83

0.83

-

0.55

K

T

0.55 0.83

0.83

-

0.55

S

x

27.4 40.6

40.6 60.9

x

x

=



1



2

0.2 88.1

k

1

k

2

0.83 0.55

-0.55 0.83

59

Wykorzystanie macierzy przekształcającej

x

1

x

2

13.34

19.37

17.57

25.89

5.40

8.33

14.63

21.99

1.95

3.00

11.60

16.71

11.76

16.49

7.25

12.36

18.24

27.17

8.99

14.70

17.31

27.05

6.77

9.45

10.29

14.67

7.02

9.44

1.52

3.04

...

...

...

...

...

...

K

0.55 0.83

0.83

-

0.55

x

=

y

1

y

2

23.13

-0.68

30.73

-2.30

9.71

1.51

25.89

-1.63

3.50

2.84

20.02

-0.03

19.98

0.23

13.86

-0.04

32.11

-2.73

16.75

-0.45

31.37

-3.30

11.47

1.68

17.65

0.48

11.64

1.86

3.22

2.50

...

...

...

...

...

...

60

-5

0

5

10

15

20

25

-5

0

5

10

15

20

25

30

35

Nowe zmienne (zmienne przekształcone)

y

1

y

2

23.13

-0.68

30.73

-2.30

9.71

1.51

25.89

-1.63

3.50

2.84

20.02

-0.03

19.98

0.23

13.86

-0.04

32.11

-2.73

16.75

-0.45

31.37

-3.30

11.47

1.68

17.65

0.48

11.64

1.86

3.22

2.50

...

...

...

...

...

...

duża
wariancja

b.
mała

61

Porównanie wariancji i redukcja zmiennych

• Wariancje zmiennych oryginalnych:

– Var(x

1

)=27.4, Var(x

2

)=60.9

– suma: 27.4 + 60.9 = 88.3

• Wariancje zmiennych przekształconych:

– Var(y

1

)=88.1, Var(y

2

)=0.2

– suma: 88.1 + 0.2 = 88.3

• Wniosek: ze względu na małą pojemność informacyjną

(wyrażającą się małą wariancją) zmienna y

2

może zostać

pominięta w dalszych analizach

• W praktyce redukowanie zmiennych sprowadza się do

utworzenia nowych zmiennych, takich, że ich wartości są

wartościami średnimi zmiennej redukowanej

• Wszystkie zmienne po redukcji będą oznaczane przez z

i

1

2

0

50

100

1

2

0

50

100

62

Nowe zmienne (zmienne zredukowane)

z

1

z

2

23.13

0.00

30.73

0.00

9.71

0.00

25.89

0.00

3.50

0.00

20.02

0.00

19.98

0.00

13.86

0.00

32.11

0.00

16.75

0.00

31.37

0.00

11.47

0.00

17.65

0.00

11.64

0.00

3.22

0.00

...

...

...

...

...

...

0

10

20

30

40

-5

0

5

10

15

20

25

30

35

63

Wykorzystanie macierzy odwrotnej

K

T

0.55 0.83

0.83

-

0.55

x

=

z

1

z

2

23.13

0.00

30.73

0.00

9.71

0.00

25.89

0.00

3.50

0.00

20.02

0.00

19.98

0.00

13.86

0.00

32.11

0.00

16.75

0.00

31.37

0.00

11.47

0.00

17.65

0.00

11.64

0.00

3.22

0.00

...

...

...

...

...

...

u

1

u

2

13.48

19.22

18.86

24.60

3.99

9.73

15.44

21.18

-0.39

5.35

11.29

17.03

11.26

17.00

6.93

12.67

19.83

25.57

8.97

14.72

19.31

25.05

5.24

10.98

9.61

15.35

5.36

11.10

-0.59

5.15

...

...

...

...

...

...

64

Zmienne odtworzone częściowo

(wygładzone)

-5

0

5

10

15

20

25

-5

0

5

10

15

20

25

30

35

u

1

u

2

13.48

19.22

18.86

24.60

3.99

9.73

15.44

21.18

-0.39

5.35

11.29

17.03

11.26

17.00

6.93

12.67

19.83

25.57

8.97

14.72

19.31

25.05

5.24

10.98

9.61

15.35

5.36

11.10

-0.59

5.15

...

...

...

...

...

...

65

Zmienne odtworzone w pełni

-5

0

5

10

15

20

25

-5

0

5

10

15

20

25

30

35

x

1

x

2

13.34

19.37

17.57

25.89

5.40

8.33

14.63

21.99

1.95

3.00

11.60

16.71

11.76

16.49

7.25

12.36

18.24

27.17

8.99

14.70

17.31

27.05

6.77

9.45

10.29

14.67

7.02

9.44

1.52

3.04

...

...

...

...

...

...

66

Metody doboru zmiennych redukowanych

• Niech ={

1

, 

2

, ..., 

N

} będzie zbiorem

posortowanych nierosnąco wartości własnych
macierzy kowariancji

– Znajdź średnią wartość wszystkich 

i

i utwórz tylko

zmienne odpowiadające wartościom

– Utwórz tylko zmienne 1..S, przy

minimalnym S, dla którego zachodzi:

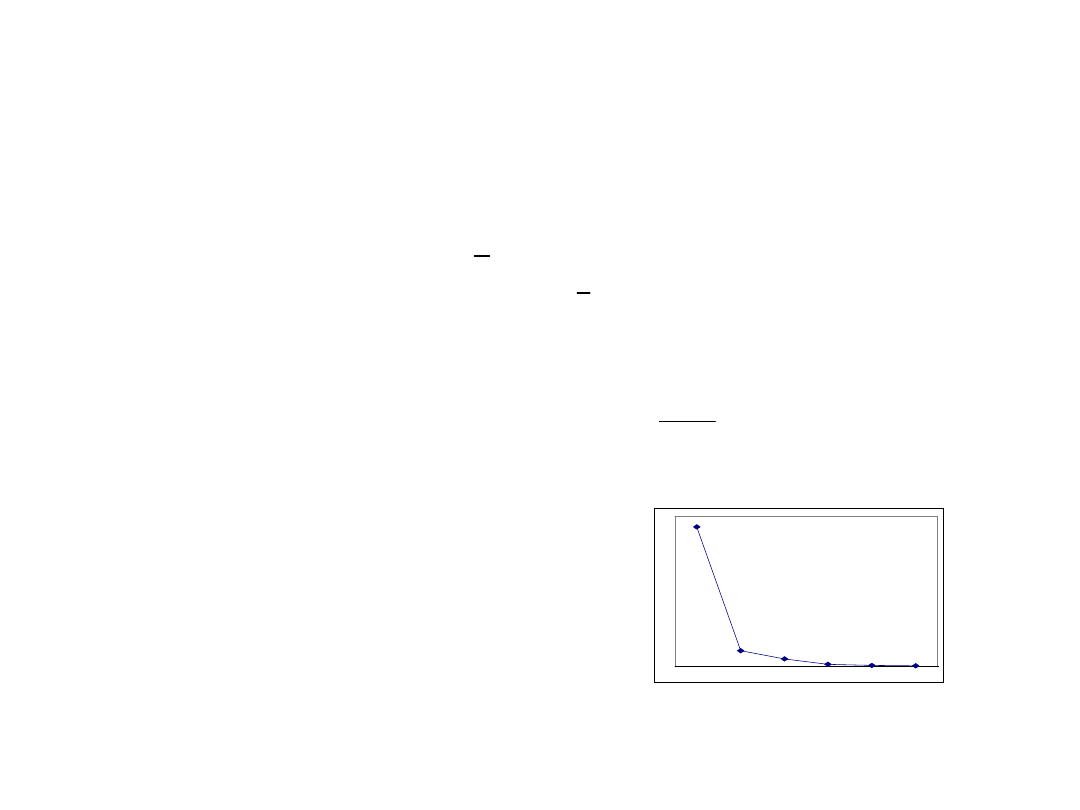
– Dobierz wizualnie zmienne na

podstawie tzw. wykresu osypiska:

0

13

1

2

3

4

5

6

λ

λ

λ

i



p











N

1

i

i

S

1

i

i

λ

λ

67

Zastosowania PCA: przykład biologiczny

• Jolicoeur i Mosiman (1960) dokonywali pomiarów

skorupy żółwi, otrzymując oryginalne zmienne:

– długość
– szerokość
– wysokość

• Ze względu na względnie stałe proporcje powyższych

wielkości (duża korelacja) zmienne oryginalne możne
przekształcić wykorzystując PCA i otrzymując:

– wielkość (98.64% informacji)
– kształt-A (0.94%) i kształt-B (0.41%)

• Podobne badania

– białe leghorny (Wright, 1954)

68

Zastosowania PCA: przykład psychologiczny

• Birren i Morrison (1961) badali wyniki testów

Wechslera (testy na inteligencję dla dorosłych).
Obserwowano:

– wyniki testu (11 zmiennych), oraz dodatkowo
– wiek i wykształcenie

• W rezultacie przekształcenia PCA otrzymano

zmienne, które (po zanalizowaniu korelacji z
oryginalnymi wynikami testów) zinterpretowano
następująco:

– ogólna wydajność intelektualna (51.47%)
– doświadczenie (10.90%)
– miernik wyobraźni przestrzennej (6.15%)
– miernik umiejętności rachunkowych (5.48%)