C:\Documents and Settings\M_Burzała\Moje dokumenty\Moje
dokumenty\Wyklady_2007\Ekonometria\DODATEK_MACIERZE.doc
1
MACIERZE, WYZNACZNIKI
Macierze - działania
Transpozycja - przestawienie wierszy i kolumn bez zmiany ich kolejności
A= [a
ij
]
mxn
A
T
=A’= [a
ji
]
nxm
Dodawanie dotyczy tylko macierzy tego samego wymiaru
[a
ij
]+[b
ij
]=[a
ij
+b
ij
]
Mnożenie a) przez liczbę
α[a
ij
]=[αa
ij
]
b) przez macierz - wtedy i tylko wtedy, gdy liczba kolumn pierwszej macierzy jest równa
liczbie wierszy drugiej macierzy
A = −
2
3
1 4
5
1
B =
3
1 2
0
2
3 1
4
−
−
−
A
[3x2]
x B
[2x3]
= AB
[3x3]
3 -1 2 0
-2 -3 1 4
2 3 0 -11 7 12
-1 4 -11 -11 2 16
5 1 13 -8 11 4
schemat Falka mnoż. AB
iloczyny i-tego wiersza i k-tej kolumny
[
]
=
10
8
4
15
12
6
5
4
2
5
4
2
2
3
1
[
]
2
4 5
1
3
2
= 24
7
2
3
5
1
2
11
13
⋅
=
Własności - nie jest przemienne AB ≠ BA
jest łączne = (AB)C = A(BC)
jest rozdzielne względem dodawania i odejmowania
(A+-B)C = AC+-BC, C(A+-B)=CA+-CB
Minor (podwyznacznik) macierzy - powstaje przez skreślenie pewnej liczby wierszy i kolumn
(M
ik
- skreślony i-ty wiersz i k-ta kolumna).
Dopełnienie algebraiczne D
ik
= (-1)
i+k
M
ik
Rząd macierzy największy stopień wyjętego z niej różnego od zera minora
Macierz odwrotna – istnieje, jeśli macierz kwadratowa A jest nieosobliwa tzn. | A | ≠ 0
C:\Documents and Settings\M_Burzała\Moje dokumenty\Moje
dokumenty\Wyklady_2007\Ekonometria\DODATEK_MACIERZE.doc
2
A
A
A
D
−
=
⋅
1
1
A
D
- transponowana macierz dopełnień algebraicznych macierzy A
A =
=
2
7
3
3
9
4
1
5
3
54+45+28-27-40-63= 127-130 = -3
2 7 3 Metoda Sarrusa
3 9 4
[M
ik
] =
9
4
5
3
3 4
1
3
3
9
1
5
7
3
5
3
2
3
1
3
2
7
1
5
7
3
9
4
2
3
3 4
2
7
3
9
=
7
5
6
6
3
3
1
1
3
−
−
Macierz dopełnień otrzymujemy mnożąc wszystkie minory przez (-1)
i+k
[D
ik
] =
7
5
6
6
3
3
1
1
3
−
−
−
−
A
D
= [D
ik
]’=
7
6
1
5
3
1
6
3
3
−
−
−
−
A
-1
=
1
3
−
7
6
1
5
3
1
6
3
3
−
−
−
−
Wyznacznik liczony wg definicji - suma iloczynów elementów dowolnego wiersza (kolumny)
przez ich dopełnienia algebraiczne.
wg 2 kolumny
W =
−
−
−
−
= ⋅ −
−
−
−
+ ⋅ −
−
−
−
+
+
5
3
1
2
2
0
4
3
3 6
2
0
4
0
5
2
3
1
2
4
3
3
2
0
4
5
2
6
1
5
1
2
2
4
3
4
5
2
1 2
3 2
(
)
(
)
Przykład na rząd macierzy M =
1
3
4
3
2
1
1
4
7
−
−
−
= 0 M
33
=
1
3
3 2
= -7 ≠ 0 rz(M) =2
Macierz nieosobliwa W(A) ≠ 0
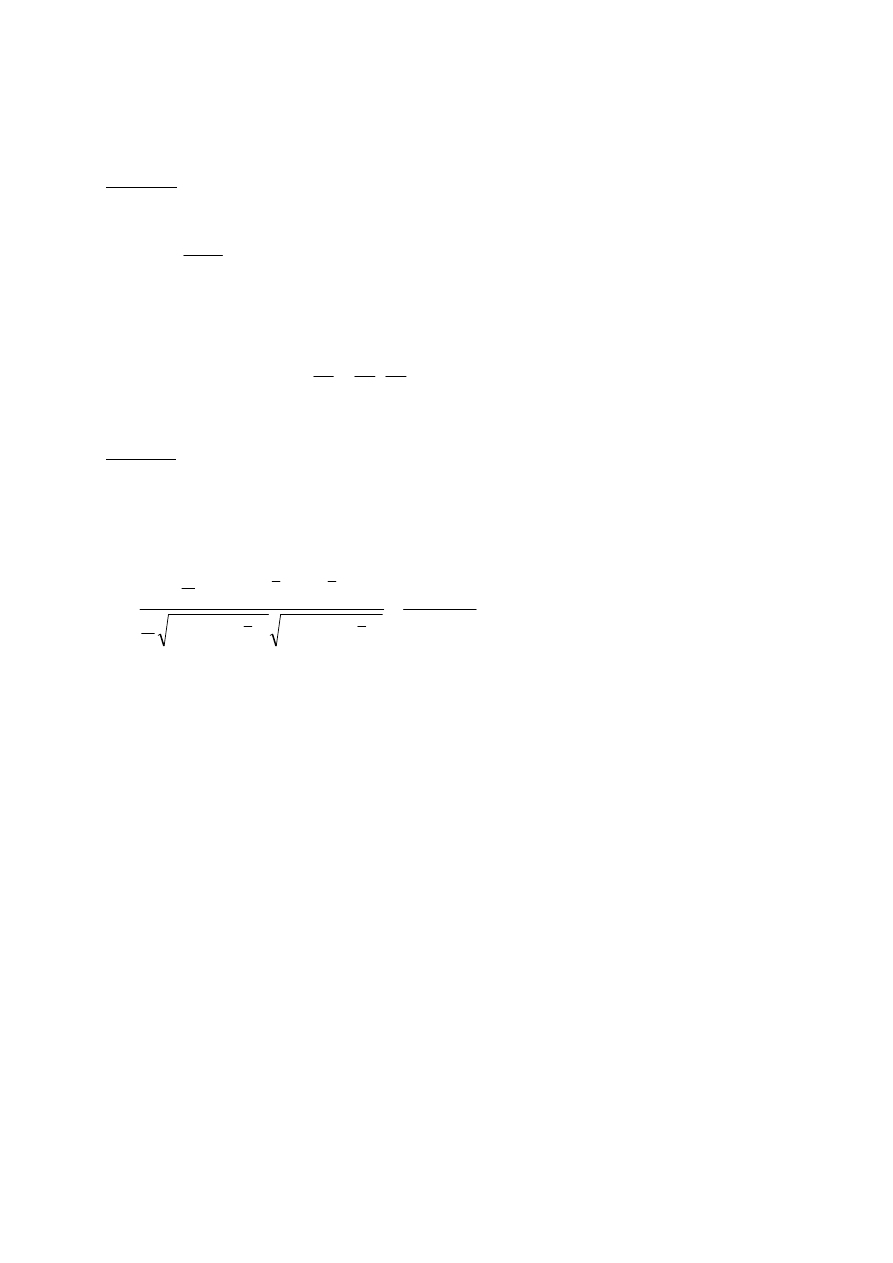
C:\Documents and Settings\M_Burzała\Moje dokumenty\Moje
dokumenty\Wyklady_2007\Ekonometria\DODATEK_MACIERZE.doc
3
Pochodne
(a
x
)’ = a
x
ln a
(log
a
x)’ =
1
x
a
ln
(x
n
)’ = nx
n-1
(k)’ - stała = 0
pochodna funkcji złożonej
dy
dx
dy
du
du
dx
=
⋅
y =(2x + 3)
6
y = u
6
y’ = 6(2x+3)
5
*2
Korelacja
Siłę liniowego związku między dwoma zmiennymi X i Y mierzy współczynnik korelacji liniowej
(Pearsona):
y
X
T
t
t
T
t
t
T
t
t
t
s
s
Y
X
y
y
x
x
T
y
y
x
x
T
)
,
cov(
)
(
)
(
1
)
)(
(
1
1
2
1
2
1
=
−
−
−
−
=
∑
∑
∑
=
=
=
ρ
T – liczba obserwacji,
cov(X,Y)
– kowariancja między zmiennymi X i Y,
s
x
, s
y
- odchylenie standardowe wartości zmiennych X i Y.