Raport z projektu

Przedmiot: Algorytmy i złożoność

PROJEKT: WIEŻE HANOI

Autor: Kamil Adamuszek

1.

Opis problemu wież Hanoi

“W wielkiej świątyni Benares w Hanoi, pod kopułą, która zaznacza środek świata, znajduje się płytka z

brązu, na której umocowane są trzy diamentowe igły, wysokie na łokieć i cienkie jak talia osy. Na jednej z
tych igieł, w momencie stworzenia świata, Bóg umieścił 64 krążki ze szczerego złota. Największy z nich leży
na płytce z brązu, a pozostałe jeden na drugim, idąc malejąco od największego do najmniejszego. Jest to
wieża Brahma. Bez przerwy we dnie i w nocy kapłani przekładają krążki z jednej diamentowej igły na drugą,
przestrzegając niewzruszonych praw Brahma. Prawa te chcą, aby kapłan na służbie brał tylko jeden krążek
na raz i aby umieszczał go na jednej z igieł w ten sposób, by nigdy nie znalazł się pod nim krążek mniejszy.
Wówczas, gdy 64 krążki zostaną przełożone z igły, na której umieścił je Bóg w momencie stworzenia świata,
na jedną z dwóch pozostałych igieł, wieża, świątynia, bramini rozsypią się w proch i w jednym oka mgnieniu
nastąpi koniec świata.”

2.

Rozwiązanie dla 3 krążków

Problem dla 3 krążków można rozwiązać za pomocą algorytmu rekurencyjnego lub iteracyjnego.

Przykład algorytmu rekurencyjnego:

void Hanoi(int k, int s)

{

if (k == 0) return;

Hanoi(k – 1, -s);

Przenies(k, s); // Przenoszenie k-tego krążka od s pozycji

Hanoi(k– 1, -s);

}

Problem ten można rozwiązać za pomocą algorytmu iteracyjnego. Aby tego dokonać należy zauważyć, że
krążki są przemieszczane za pomocą wzoru: przykładowo k-ty krążek jest przenoszony z 1 słupka co
2

k

-2

k-1

o y=(-1)

k+1

, gdzie gdy y= 1 to krążek jest przenoszony na wieżę po swojej prawej stronie, a gdy y= -1

to krążek jest przenoszony na wieżę po swojej lewej stronie.

int il_przenies = pow(il_do_przel) - 1;

for (int j = 1; j <= il_przenies; j++)

{ //Sprawdzanie który krazek ma byc przesuniety

int k = 0;

while (true)

{

int a = pow(k);

int b = a * 2;

//Korzystajac z numeru przeniesienia obliczane jest ktory krazek ma

//zostać przemieszczony. Wykonywane to jest przy wykorzystaniu

// j-2

k

% 2

k+1

==0, gdzie a=2

k

, b=2

k+1

if (((j - a) % b) == 0)

{ //Przesuwanie krazka

kreg[k] += ((k + 1) % 2) ? 2 : 1;

kreg[k] = kreg[k] % 3;

il_przel++;

ofstream plik;

plik.open("wynik.txt", ios::app | ios::ate);

plik << "Przeniesienie " << k + 1 << "-tego krazka na " << kreg[k] + 1 << " slupek" <<endl;

plik.close();

break;

}

k++;

}

3.

Testy dla k krążków i s słupków(wież)

Il. kr.

3 słup.

4 słup.

5 słup.

6 słup. 7 słup. 8 słup.

9 słup.

10 słup. 11 słup.

12 słup.

1

1

1

1

1

1

1

1

1

1

1

2

3

3

3

3

3

3

3

3

3

3

3

7

7

5

5

5

5

5

5

5

5

4

15

15

9

7

7

7

7

7

7

7

5

31

31

15

11

9

9

9

9

9

9

6

63

63

27

17

13

11

11

11

11

11

7

127

127

49

27

19

15

13

13

13

13

8

255

255

93

47

29

21

17

15

15

15

9

511

511

179

85

47

31

23

19

17

17

10

1023

1023

351

159

83

49

33

25

21

19

11

2047

2047

693

307

153

83

51

35

27

23

12

4095

4095

1377

601

291

151

85

53

37

29

13

8191

8191

2743

1187

565

285

151

87

55

39

14

16383

16383

5475

2359

1113

551

283

153

89

57

15

32767

32767

10937

4701

2207

1081

545

283

155

91

16

65535

65535

21861

9383

4393

2139

1067

543

285

157

17

131071 131071

43707

18747

8763

4255

2109

1061

543

287

18

262143 262143

87399

37473

17503

8485

4191

2095

1059

545

4.

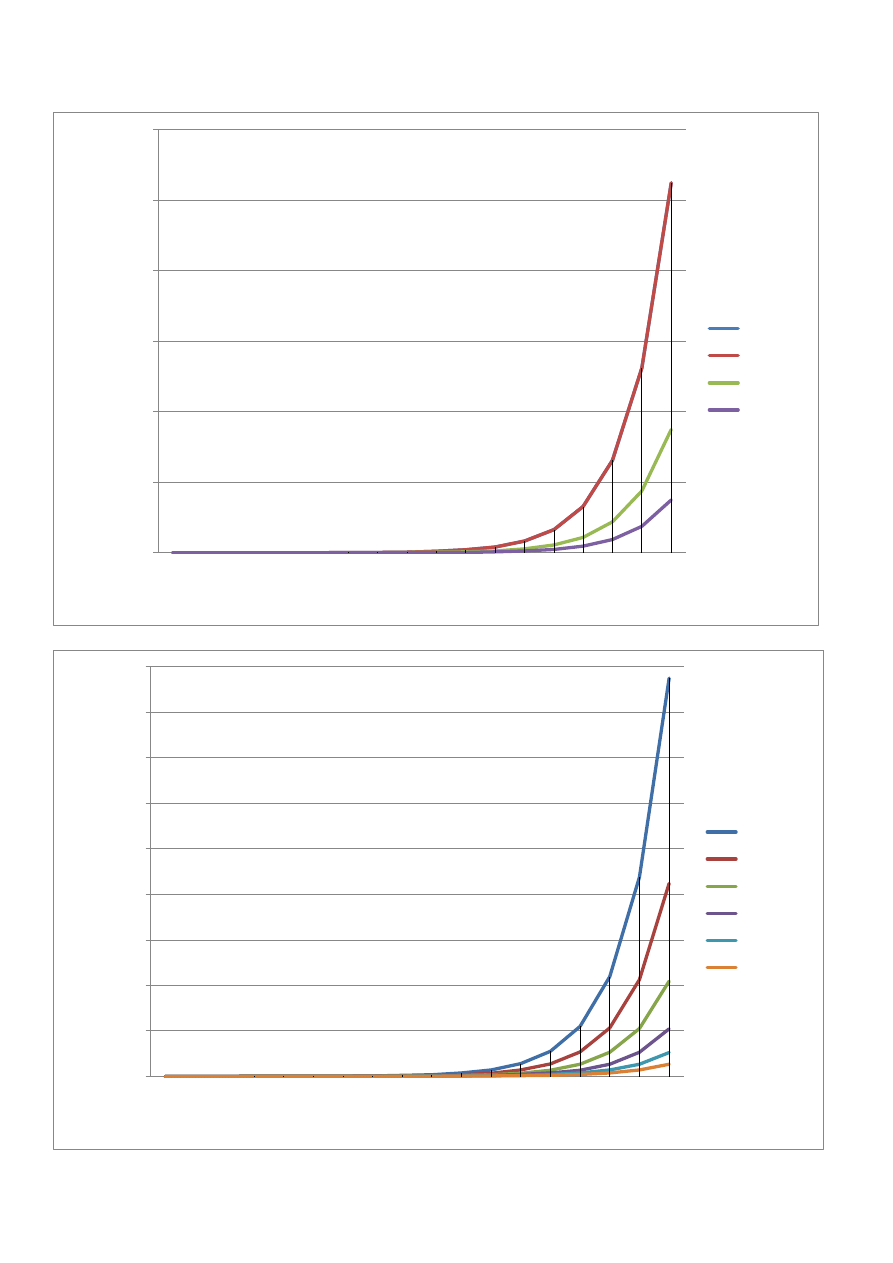
Wykresy

0

50000

100000

150000

200000

250000

300000

1

2

3

4

5

6

7

8

9

10 11 12 13 14 15 16 17 18

Il

o

ść

p

rz

e

n

ie

si

e

ń

Ilość krążków

3 słupki

4 słupki

5 słupków

6 słupków

0

2000

4000

6000

8000

10000

12000

14000

16000

18000

1

2

3

4

5

6

7

8

9

10 11 12 13 14 15 16 17 18

Il

o

ść

p

rz

e

n

ie

si

e

ń

Ilość krążków

7 słupków

8 słupków

9 słupków

10 słupków

11 słupków

12 słupków

5.

Algorytm dla 3 słupków

Wieżę Hanoi z k krążkami oznaczamy przez s

n

. Z wyników testów wynika, że

s

1

=2

1

-1; s

2

=2

2

-1; s

3

=2

3

-1;s

4

=2

4

-1;… Na tej podstawie należy przypuszczam, że s

n

=2

n

-1 dla pewnej liczby

krążków n. Powyższą zależność można sprawdzić indukcyjnie. Wiemy że s

1

=2

1

-1=1, załóżmy że s

n

=2

n

-1, a

więc s

n+1

=2*s

n

+1=2*(2

n

-1)+1=2

(n+1)

-1. Pokazałem zatem że złożoność algorytmu wynosi O(2

n

).

6.

Algorytm dla 4 słupków

Pomimo tego, że dla 4 słupków algorytm zachowuje się w inny sposób niż dla 3 słupków to

złożoność obliczeniowa jest taka sama jak dla 3 słupków. Jest to wynikiem tego, że np. dla n
krążków pierwszym krokiem jest przeniesienie k-1 krążków na inny słupek metodą dla 3 słupków, a
następnie k-tego krążka. Krok ten powtarza się do momentu przeniesienie wszystkich krążków.

7.

Algorytm dla 5 słupków

Analizując wyniki dla 5 słupków otrzymuję poniższy wzór rekurencyjny:

2*n-1

dla n=1,2,3

s

n

=

2*s

n-1

-n+2

dla n=2*k+3

2*s

n-1

-n+3

dla n=2*k+2

Nieudało mi się uprościć tej funkcji rekurencyjnej, ale można zauważyć złożoność algorytmu dla 5

słupków. Na przykład:

S

6

=2*(s

5

)-n+3=2*(2*(s

4

)-n+2)-n+3=2*(2*(2*(s

3

)-n+3)-n+2)-n+3=2*(2*(2*(2*3-1)-n+3)-n+2)-n+3=

=2*(2*(2

2

*3-2-n+3)-n+2)-n+3=2*(2*(2

2

*3-n+1)-n+2)-n+3=2*(2

3

*3-2*n+2-n+2)-n+3=

=2*(2

3

*3-3*n-4)-n+3=2

4

*3-6n+8-n+3=3*2

4

-7n+11

Uogólniając wzór i podpierając się notacją asymptotyczną złożoność algorytmu wynosi

O(3*2

n

)=3*O(2

n

)

8. Wnioski

Algorytm dla 3 słupków ma złożoność obliczeniową O(2

n

). Wraz z wzrostem ilości słupków

wydajność algorytmu wzrasta, a ilość potrzebnych przełożeń maleje. Nie znaleziono dotychczas algorytmu,
który dokonał by przełożenia wszystkich krążków w minimalnej liczbie ruchów. Akceptowane więc są
wszystkie rozwiązania, które dadzą wynik nie gorszy od naszego i będą miały nie gorszą złożoność.