Raport z projektu 

Przedmiot: Algorytmy i złożoność

 

PROJEKT:LICZBY PIERWSZE

 

Autor: Kamil Adamuszek

 

 

 

 

 

  

 

 

 

 

 

 

 

 

 

 

 

1.  Zadanie 

Porównaj złożoność i czasy dwóch algorytmów  wyznaczania liczb pierwszych.  

2.  Metoda naiwna(prosta) 

Metoda ta polega na sprawdzaniu podzielności przykładowej liczby a przez liczby od 2 

do a-1. Jeśli żadna z tych liczb nie jest podzielnikiem a  to liczba  a  jest liczbą pierwszą. 
Algorytm tej metody wygląda następująco: 

 

for (liczba=2;liczba<(granica+1);liczba++) 
  { 
  for (dzielnik=2;dzielnik<(liczba+1);dzielnik++) 
  { 
    if (liczba%dzielnik==0) 
      { 
if (liczba!=dzielnik) 
  

{ 

  

 

dzielnik=liczba+1; 

} 
  

else 

  

{ 

printf(fp,"%d",liczba); 
} 
} 
} 
} 

 

Algorytm ten jest prosty i efektywny w przypadku ,gdy chcemy zbadać pierwszość 

niewielkiego zakresu liczb. Jednak do badania dużego przedziału nie powinno się go jednak 
używać, ponieważ  ten algorytm znajdowania liczb pierwszych ma złożoność obliczeniową 
rzędu O(n

2

) lub O(√n) po optymalizacji polegającej na sprawdzaniu podzielności liczby a 

przez liczby od 2 do √a 

 
 

3.  Metoda zwana sitem Eratostenesa 

Algorytm ten jest nazywany sitem, ponieważ „odsiewa” wszystkie liczby złożone z 

podanego przedziału. Eratostenes zauważył, że liczby złożone są wielokrotnościami kolejnych 
liczb pierwszych (np. 4, 6, 8,... - są wielokrotnościami 2; natomiast 6, 9, 12,... są 
wielokrotnościami 3 itd.). Wystarczy więc z danego przedziału pozbyć się wszystkich 
wielokrotności 2, z liczb, które zostaną wykreślić kolejno wszystkie wielokrotności 3, potem 
wielokrotności 5 (bo 4 zostało już wykreślone) itd. "Odsiewając" w ten sposób liczby złożone, 
pozostawiamy same liczby pierwsze. 

 
 

Realizację sita Eratostenesa ilustruje poniższy fragment programu, który wypisuje 

liczby pierwsze używając tablicy boolowskiej. 

tab = new bool[zakres + 1]; 
  for(liczba = 2; liczba <= zakres; liczba++) 
  tab[liczba] = true; 
  do = (unsigned int)sqrt(zakres); 

 for(liczba = 2; liczba <= dok;  liczba++) 

    if(tab[liczba]) 
    { 
     d = liczba * liczba; 
      while(d <= zakres) 
      { 
        tab[d] = false; d += liczba; 
} 
    } 
  for(liczba = 2; liczba <= zakres; liczba++) if(tab[liczba]) 
{   
cout<<liczba<<"\n"; 
} 
cout << endl; 

           delete [] tab; 

 

Jest to metoda o wiele szybsza o metody naiwnej(prostej). Jej złożoność czasowa jest 

rzędu O(n log log n). 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

4.  Testy 

Próba została wykonana około 300 razy dla obydwóch metod obliczeniowych. Czas 

natomiast został zmierzony  w milisekundach. 

Ilość liczb 

Czas wykonania algorytmu w przypadku 

metody naiwnej 

Czas wykonania w 

przypadku metody zwanej 

sitem Eratostenesa 

0 

0 

0 

10000 

76 

16 

20000 

282 

28 

30000 

586 

38 

40000 

996 

48 

50000 

1504 

58 

60000 

2123 

67 

70000 

2830 

81 

80000 

3646 

90 

90000 

4551 

99 

100000 

5511 

108 

 

 
 
 
 
 
 
 
 
 
 
 
 
 
 

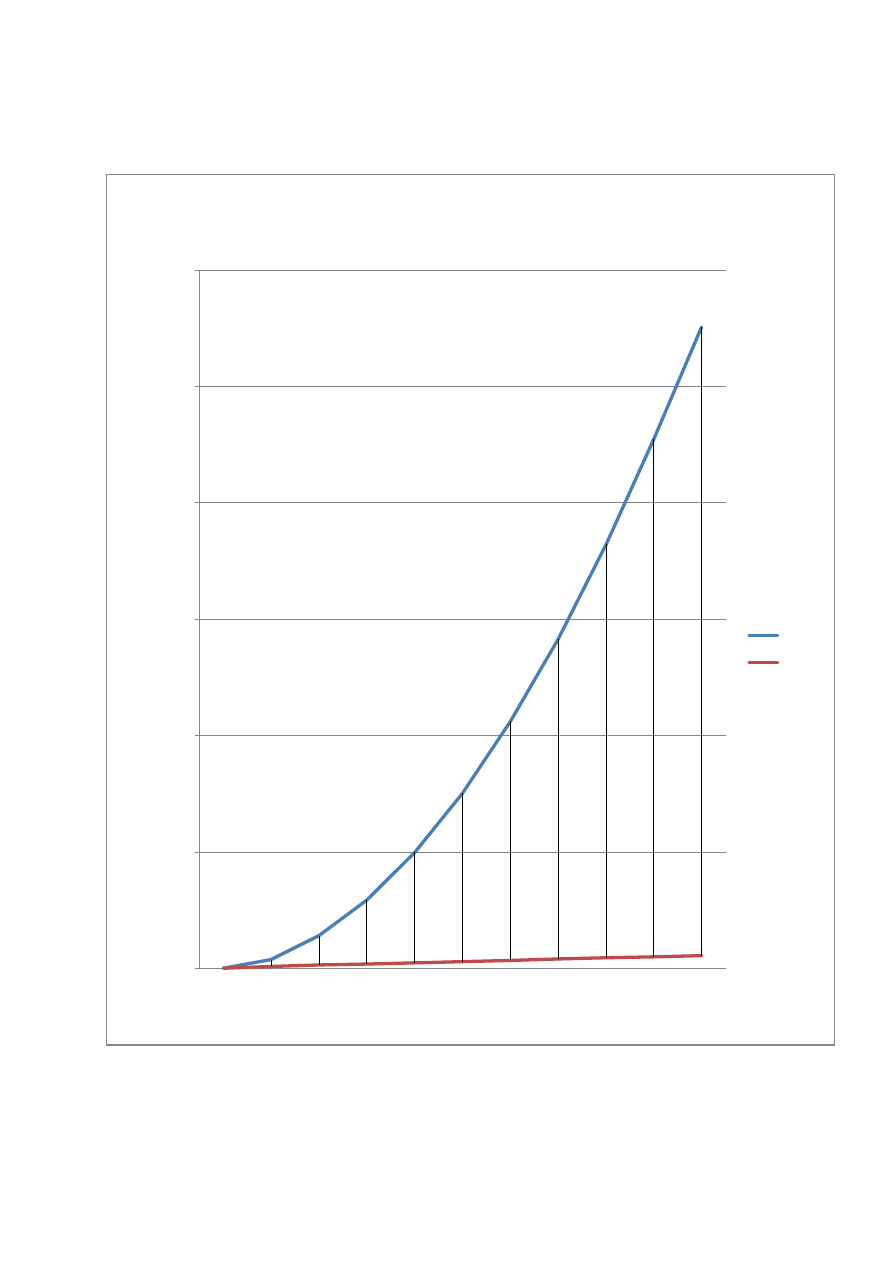
5.  Porównanie zależności między czasem działania algorytmu a zakresem 

 

 

 

 

0

1000

2000

3000

4000

5000

6000

0

10000 20000 30000 40000 50000 60000 70000 80000 90000 100000

Cz

as 

w ms

 

Zakres 

Porównanie metody naiwnej z metodą zwaną 

sitem Erastotenesa 

Czas

Czas 2

6.  Wnioski 

Metoda naiwna jest akceptowalna dla niewielkiego zakresu liczb jest to 

według mnie zakres 2-2000 dla większego zakresu metoda to jest mało wydajna gdyż 
jest czas wykonania gwałtownie wzrasta. Metoda zwana sitem Eratostenesa jest 
efektywna dla każdego zakresu, ponieważ czas jej wykonania nie wzrasta gwałtownie 
jak w przypadku metody naiwnej lecz logarytmicznie. Złożoność czasowa sita 
Eratostenesa wynosi O(n log log n).