WOJSKOWA AKADEMIA

TECHNICZNA

Sprawozdanie laboratoryjne z przedmiotu

WSTĘP DO AUTOMATYKI

Temat: Modelowanie układów dynamicznych w środowisku MATLAB - SIMULINK.
Wykonujący ćwiczenie: Paweł Madejski
Prowadzący: mgr inż. Małgorzata Rudnicka - Schmidt
Data wykonania: 08.01.2008r
Grupa szkoleniowa: I7X1S1

TREŚĆ ZADANIA:
Dla danych wartości: k, T i ksi:

1. Wyznaczyć:

•

współczynniki: b

0

, a

0

, a

1

,

•

macierze: A, B, C, D,

•

bieguny: p1, p2

2. Stosując pakiet SIMULINK zbudować modele badanego układu:

•

model analogowy - wykorzystując elementy podstawowe: integrator (blok
Integrator), sumator, wzmacniacz (blok Gain),

•

model odpowiadający opisowi w przestrzeni stanów (blok State - Space),

•

model transmitancyjny w dwóch postaciach:

4. transmitancji Laplace’a (wykorzystać blok Transfer Fcn)
5. transmitancji w postaci zero - biegunowej (blok Zero - Pole)

3. Podać na wejście układu sygnał skokowy (blok Step).

4. Zarejestrować sygnał wejściowy i odpowiedź skokową układu we wszystkich czterech

modelach układu (blok Scope).

5. Narysować na wspólnym wykresie sygnał wejściowy oraz odpowiedzi otrzymane w wyniku

symulacji (funkcja plot), wykorzystując dane zapisane w przestrzeni roboczej MATLABa
(blok To Workspace, lub Out)

6. Zbadać wpływ współczynnika tłumienia ξ na charakter odpowiedzi skokowej, zarejestrować

odpowiedź skokową dla czterech wartości współczynnika tłumienia:

ksi=0.1 ksi=0.3 ksi=0.6 ksi=1.2

7. Zbadać wpływ stałej czasowej T na charakter odpowiedzi skokowej, zarejestrować

odpowiedź skokową dla czterech wartości stałej czasowej T:

T=0.2 T=0.4 T=0.7 T=1.5

DANE DO ĆWICZENIA:

k = 10.0
T = 0.1
ksi = 0.20

OBLICZENIA PARAMETRÓW MODELU:

b

0

= k/ T ^2

b

0

= 1,5 / (o,4)^2 = 9,375

a

0

= 1 / T^2

a

0

= 1/ (0,4)^2 = 6,25

a

1

= 2* ksi / T

a

1

= 2* 0,2 / 0,4 = 1

PIERWIASTEK(∆) = PIERWIASTEK( (2* ksi * T)^2 – 4*T^2*1)
P1 = - (2*ksi * T) – PIERWIASTEK(∆) / 2*T^2

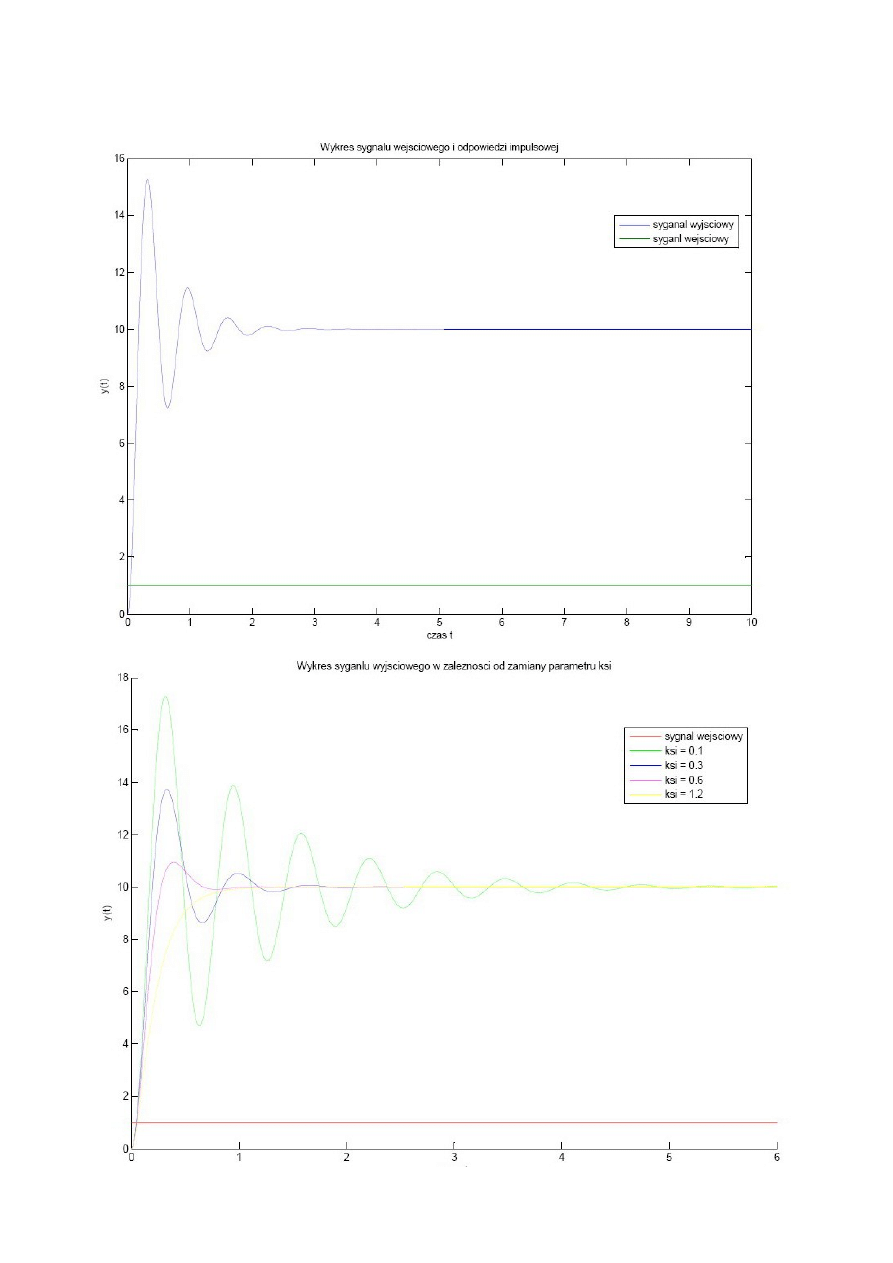
WYKRESY:

WNIOSKI:

Analizując wykres sygnału wyjściowego od parametru ksi można zauważyć, że wraz ze

wzrostem wartości ksi wykres odpowiedzi skokowej stabilizuje się szybciej (potrzeba mniej czasu
na stłumienie oscylacji). Nie trudno też zauważyć, że przy mniejszych wartościach ksi występuje
większa amplituda wychyleń odpowiedzi skokowej.

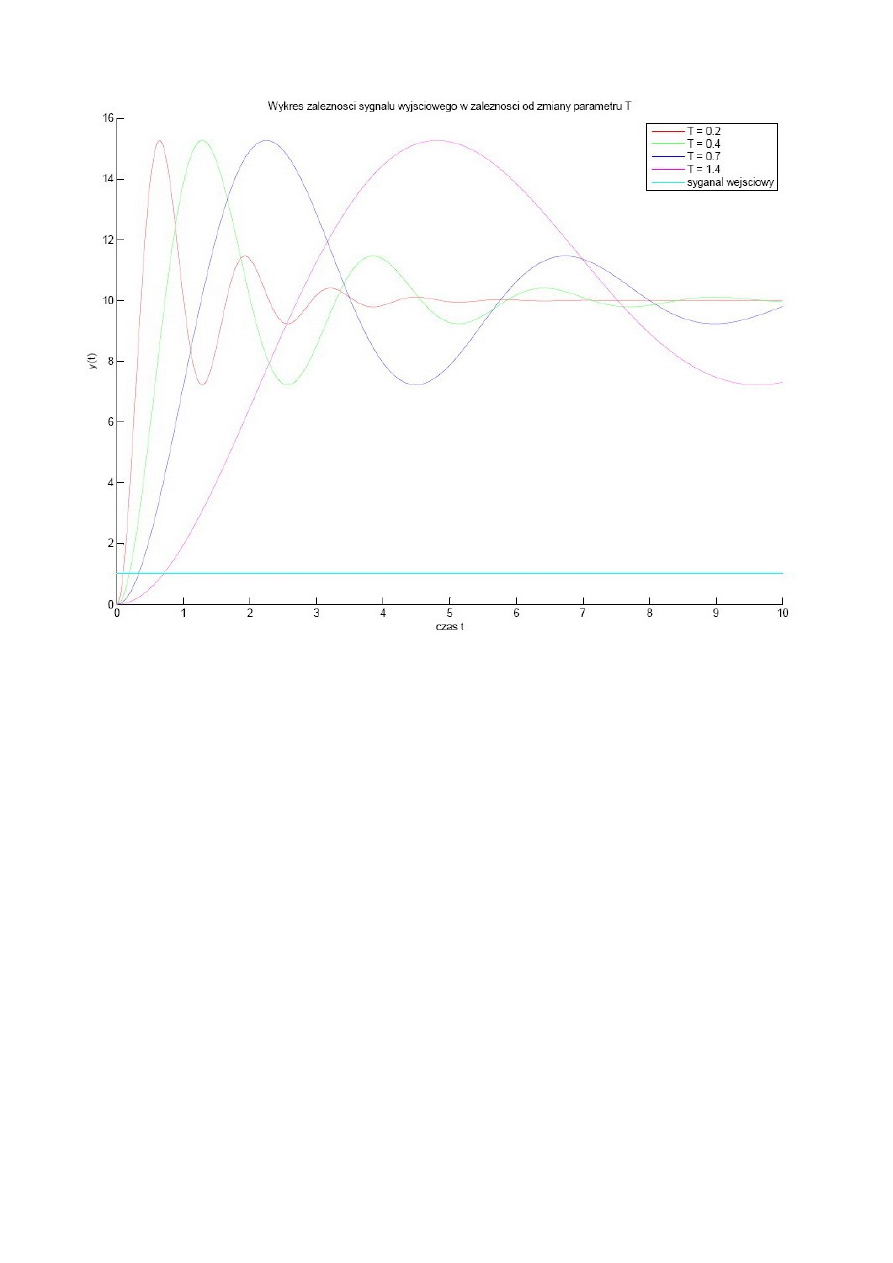
Analizując wykres odpowiedzi skokowej w zależności od różnych wartości stałej czasowej

T wyglądają można dojść do podobnych wniosków jak w przykładzie powyżej aczkolwiek jest to
zależność odwrotna do omówionej. Łatwo zauważyć, iż w tym przypadku wraz ze wzrostem
wartości T odpowiedź skokowa jest tłumiona wolniej, a amplituda jest stała i nie zmienia się bez
względu na zmiany T.