Projektowanie fitrów LC dolno­ i górnoprzepustowych

Dane wyjściowe: 
1) typ filtru: 

  dolno­/górnoprzepustowy,

2) charakterystyka: 

  Butterwortha (maks. płaska), Czebyszewa, Cauera (eliptyczna),

3) dopuszczalne zafalowania:

  0,028, 0,1 lub 0,28 dB (dla filtrów Czebyszewa i Cauera),

4) maksymalne tłumienie w paśmie przep.:

  A

p

  (dla filtrów Butterwortha),

5) częstotliwość graniczna pasma przenoszenia: f

p

,

6) częstotliwość graniczna pasma zaporowego:  f

s

,

7) tłumienie w paśmie zaporowym

  A

s

,

8) impedancja dopasowania

  Z

0

Procedura obliczeń
1) Obliczyć znormalizowaną częstotliwość pasma zaporowego:

dolnoprzeupstowy :



s

=

f

s

f

p

górnoprzepustowy :



s

=

f

p

f

s

częstotliwość znormalizowana  



s

 jest większa od 1 dla obu typów filtru (zachodzi tu transformacja 

charakterystyki górnoprzepustowej w charakterystykę prototypową dolnoprzepustową).

2) Dla filtru Butterwortha i Czebyszewa określić rząd filtru z zależności:

Butterwortha:

N =

log10

0,1 A

s

−

1−log10

0,1 A

p

−

1

2 log

s

Czebyszewa :

N =

cosh

−

1





10

0,1 A

s

−

1

10

0,1 A

p

−

1



cosh

−

1



s

uzyskany wynik należy zaokrąglić w górę do liczby nieparzystej (filtr rzędu nieparzystego jest łatwiejszy w 
realizacji ze względu na większą symetrię).

3) Dla filtru Cauera dobrać spełniający wymagania filtr z tabeli (uwzględnić A

p

, A

s

 oraz 



s

).

4) Dla filtru Butterwortha, jeśli A

p

 ≠ 3dB, obliczyć 3dB pulsację graniczną:



0

=

2 f

p



10

0,1 A

p

−

1



1

2N

dla filtru dolnorzepustowego, lub:



0

=

2  f

p



10

0,1 A

p

−

1



1

2N

dla filtru górnorzepustowego

w pozostałych przypadkach (filtry Czebyszewa i Cauera) należy podstawić 



0

 = 2

f

p

 a częstotliwość 

graniczna jest określana zawsze na poziomie tłumienia A

p

.

5)  Obliczyć pojemność i indukcyjność podstawową:

L

0

=

Z

0



0

C

0

=

1

Z

0



0

6) Obliczyć wartości elementów na podstawie współczynników K

n

 odczytanych dla wybranego filtru:

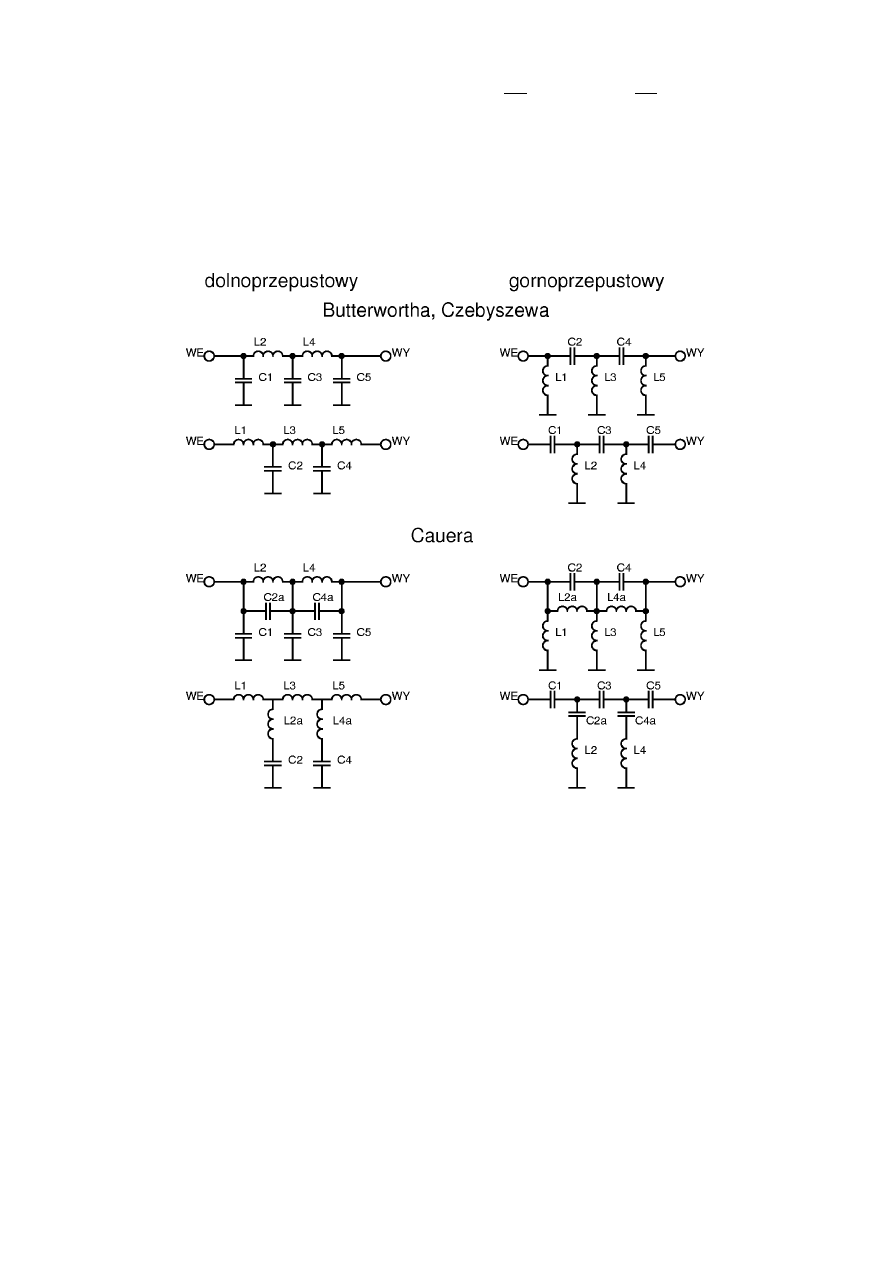
dolnoprzepustowy :

L

n

=

K

n

L

0

C

n

=

K

n

C

0

górnoprzepustowy :

L

n

=

L

0

K

n

C

n

=

C

0

K

n

Dla filtrów Cauera współczynniki dla elementów dodatkowych (oznaczonych na schemacie indeksem a) są 
podane w dolnej linii każdego wiersza tabeli. 



0sn

 oznaczają znormalizowane względem 



p  

pulsacje maksimów 

tłumienia w paśmie zaporowym.

Literatura:
Е. Red: Sprawocznoje posobie po wysokoczastotnoj schiemotiechnikie, Mir, Moskwa 1990.
J. Izydorczuk, J. Konopacki: Filtry analogowe i cyfrowe, Wydawnictwo Jacka Skalmierskiego, Katowice 2003

Rys. 1. Schematy filtrów LC dolno- i górnoprzepustowych

Tabela 1. Współczynniki elementów dla filtrów Butterwortha i Czebyszewa

Typ, A

p

N

K

n

1

2

3

4

5

6

7

8

9

Butterworth

3

1,000

2,000

1,000

5

0,618

1,618

2,000

1,618

0,618

7

0,445

1,247

1,802

2,000

1,802

1,247

0,445

9

0,347

1,000

1,532

1,879

2,000

1,879

1,532

1,000

0,347

Czebyszew

0,028dB

3

0,775

1,069

0,775

5

0,879

1,359

1,727

1,359

0,879

7

0,930

1,431

1,874

1,634

1,874

1,431

0,930

9

0,951

1,459

1,922

1,696

2,009

1,696

1,922

1,459

0,951

Czebyszew

0,100dB

3

1,028

1,147

1,028

5

1,144

1,371

1,972

1,371

1,144

7

1,178

1,423

2,094

1,574

2,094

1,423

1,178

9

1,193

1,443

2,132

1,617

2,202

1,617

2,132

1,443

1,193

Czebyszew

0,280dB

3

1,345

1,141

1,345

5

1,445

1,306

2,283

1,306

1,445

7

1,488

1,343

2,387

1,451

2,387

1,343

1,488

9

1,501

1,356

2,419

1,481

2,480

1,481

2,419

1,356

1,501