X L V I I I K O N F E R E N C J A N AU K O W A

KOMITETU INŻ YNIERII LĄ DOWEJ I WODNEJ PAN

I KOMITETU NAUKI PZITB

Opole – Krynica

2002

Marian KLASZTORNY

1

Kazimierz MYŚ LECKI

2

Czesław MACHELSKI

3

Monika PODWÓ RNA

4

ANALIZA DYNAMICZNA TYPOSZEREGU BELKOWYCH

MOSTÓ W STALOWYCH OBCIĄ ŻONYCH POCIĄ GIEM

PORUSZAJĄ CYM SIĘ Z DUŻYMI PRĘ DKOŚCIAMI

1. Wstę p

Jednotorowe, swobodnie podparte, belkowe mosty stalowe, z pełnościenną konstrukcją no-
śną i pomostem zamkniętym, były szeroko stosowane na liniach kolejowych w ubiegłym
stuleciu. W zwią zku z modernizacją wielu linii kolejowych na świecie, w celu dostosowania
ich do ruchu pocią gó w z prędkościami do 300 km/h, aktualny staje się problem modelowania
fizycznego i matematycznego układu most – tor – pocią g ruchomy (MTP).

Dotychczas, dynamiczne zachowanie układó w MTP było badane eksperymentalnie lub

symulowane na dość prostych modelach liniowych, m.in. [1-5]. W niniejszej pracy przepro-
wadzono analizę dynamiczną typoszeregu belkowych mostó w stalowych, o rozpiętościach
l = 15-30 m, obcią żonych pocią giem poruszają cym się z prędkościami 100-300 km/h. W
modelu układu MTP uwzględniono m.in. szybkozmienną konfigurację, tłumienie geome-
tryczne oraz nieliniowe fizycznie elementy, tj. podsypkę i łą czniki szyn z podkładami. Ana-
lizę ograniczono do drgań w pionowej płaszczyźnie quasi-symetrii układu, pokrywają cej się
z osią toru. Celem analizy jest określenie przydatności mostó w rozpatrywanego typu do
przenoszenia obcią żeń poruszają cych się z dużymi prędkościami.

2. Modelowanie fizyczne i matematyczne układu most – tor – pociąg ruchomy

Układ MTP można podzielić na cztery podukłady inercyjne, tj. stalową konstrukcję nośną
mostu (KN), szyny na moście i w strefach dojazdowych do mostu (S), podkłady na moście
i w strefach dojazdowych (P) oraz zbió r mas resorowanych pojazdó w szynowych (MR).

1

Dr hab. inż., prof. PW, Zakład Mechaniki Instytutu Mechaniki i Konstr. Pol. Warszawskiej

2

Dr inż., Zakład Wytrzymałości Materiałó w Instytutu Inżynierii Lą dowej Pol. Wrocławskiej

3

Dr inż., Zakład Mostó w Instytutu Inżynierii Lą dowej Politechniki Wrocławskiej

4

Mgr inż., Zakład Dynamiki Budowli Instytutu Inżynierii Lądowej Politechniki Wrocławskiej

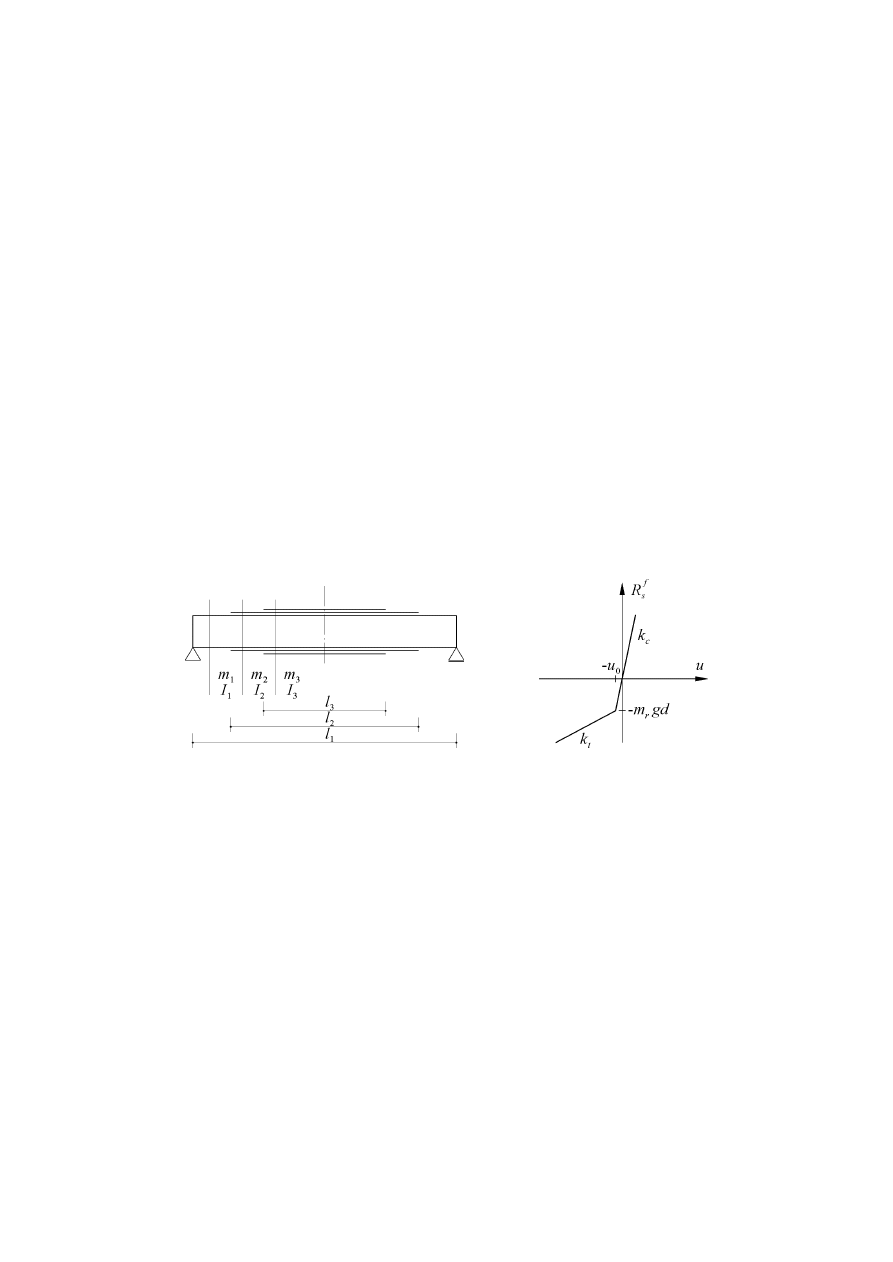
86

Modelem fizycznym stalowej konstrukcji nośnej mostu jest balastowana, odcinkowo

pryzmatyczna belka Eulera, wykonana z materiału liniowo lepkosprężystego. Schemat mo-
delu podukładu KN pokazano na rys. 1, gdzie: l

i

– długość i-tego zestawu nakładek; m

i

–

masa na jednostkę długości, odniesiona do i-tego zestawu nakładek; I

i

– centralny moment

bezwładności przekroju porzecznego przy zginaniu w płaszczyźnie pionowej, odniesiony do
i-tego zestawu nakładek. Drgania belki aproksymowano globalnie szeregiem sinusowym.

Szyny bezstykowe modelowane są przez liniowo lepkosprężystą belkę Eulera, odkształ-

calną giętnie, zaró wno na obiekcie mostowym, jak i w strefach dojazdowych do mostu. Do
dyskretyzacji podukładu S zastosowano klasyczne belkowe elementy skończone zginane, o
czterech stopniach swobody. Węzły dyskretyzacji pokrywały się z lokalizacją podkładó w.
Tłumienie geometryczne uwzględniono w sposó b przybliżony, wprowadzając zewnętrzne
sztuczne tłumienie wiskotyczne nadkrytyczne, o wspó łczynniku c

a

, w skrajnych elementach

skończonych. Poza strefami dojazdowymi do mostu założono, że tor jest niepodatny.

Wspó łczesne łą czniki szyn z podkładami, stosowane na liniach szybkiego ruchu, mają

najczęściej formę łapek sprężystych i podkładek polietylenowych. Modelem fizycznym
łą cznikó w są skupione więzi lepkosprężyste, z nieliniową charakterystyką sprężystą pokaza-
ną na rys. 2, gdzie: k

c

– sztywność na ściskanie, k

t

– sztywność na rozcią ganie układu łą czni-

kó w na jednym podkładzie, m

r

– masa pary szyn (z łą cznikami) na jednostkę długości.

Uwzględniono statyczne obcią żenie wstępne łą cznikó w. Więzi zlokalizowane są nad pod-
kładami, rys. 3. Podkłady strunobetonowe są odwzorowane przez masy skupione, drgają ce
pionowo.

Rys. 1. Schemat konstrukcji nośnej mostu

Rys.2. Charakterystyka sprężysta

łą cznikó w szyn z podkładami

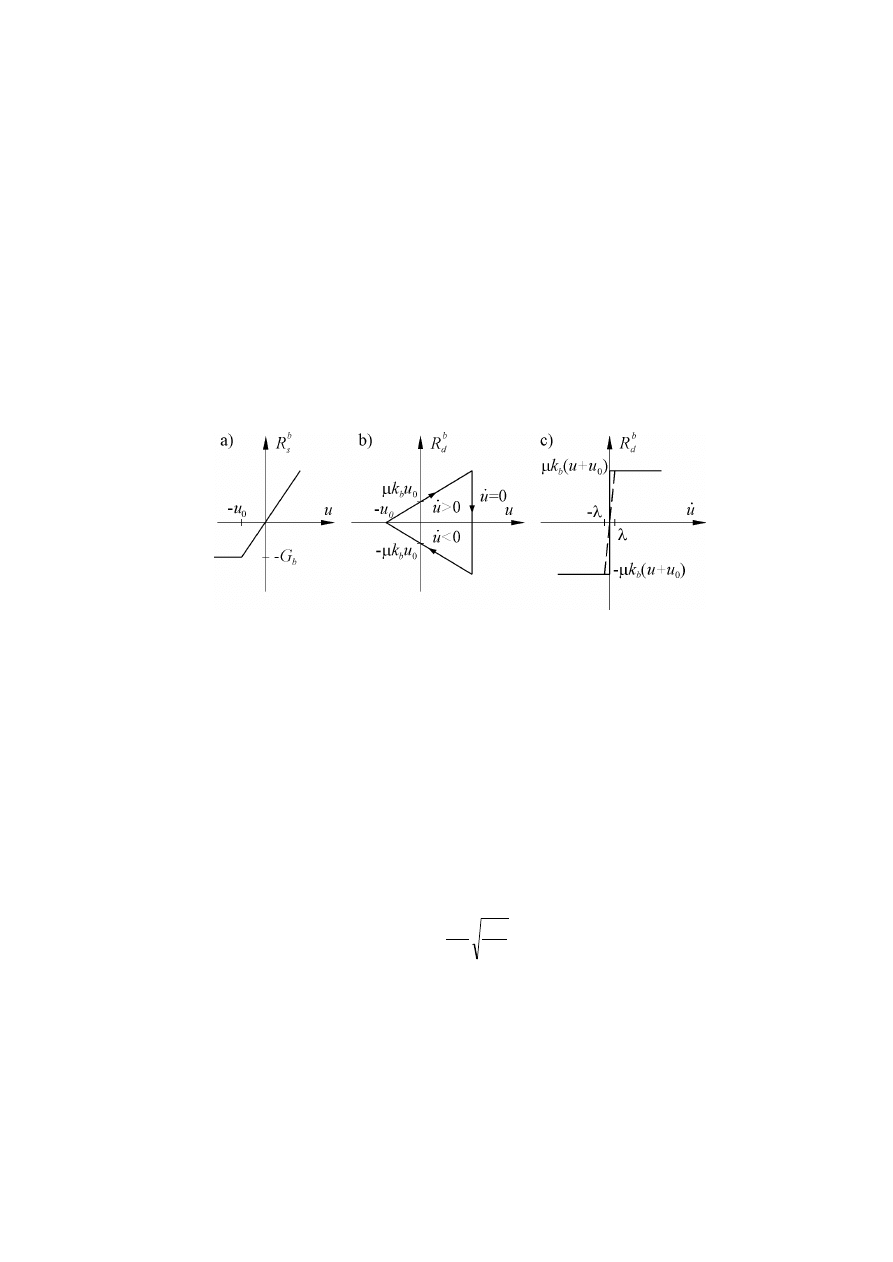
Warstwa podsypki tłuczniowej jest modelowana przez gęsty zbió r nieliniowych fizycz-

nie więzi sprężysto-tłumią cych, zlokalizowanych pod podkładami, rys. 3. Więzi reagują
tylko na ściskanie i wykazują własności tłumią ce zbliżone do tarcia suchego, proporcjonal-
nego do naciskó w dynamicznych podkładó w na podsypkę. Nieliniowe charakterystyki więzi
odwzorowują cej odcinek podsypki o długości ró wnej rozstawowi podkładó w d, z uwzględ-
nieniem statycznego obcią żenia wstępnego, przedstawiono na rys. 4, gdzie: k

b

– sztywność

podsypki na ściskanie, G

b

– statyczne obcią żenie wstępne,

m

– wspó łczynnik tarcia suchego.

W celu zapewnienia zbieżności procesu numerycznego całkowania ró wnań ruchu układu
MTP, charakterystykę tłumią cą ucią glono za pomocą sztucznego tłumienia wiskotycznego
nadkrytycznego w wą skim przedziale (-

l

,

l

).

Modele matematyczne, odpowiadają ce modelom fizycznym podukładó w KN, S,

szczegó łowo sformułowano w pracy [3]. Wzory definiują ce siły interakcji, przenoszone
przez łą czniki szyn z podkładami i podsypkę, podano w pracy [6].

87

Większość superszybkich pocią gó w pasażerskich składa się z pojazdó w szynowych na

niezależnych dwuosiowych wó zkach jezdnych [7]. Płaski model pojazdu szynowego można
wó wczas przyją ć w postaci układu o sześciu stopniach swobody, opisanego szczegó łowo w
pracach [3, 5, 6]. Zestawy kołowe odwzorowane są przez ruchome masy skupione, przy
czym pominięto siły bezwładności tych mas w ruchu pionowym. Ramy wó zkó w jezdnych
(łą cznie z silnikami trakcyjnymi) oraz nadwozie modelowane są jako sztywne tarcze,
„sztywno prowadzone” w kierunku osi toru. Zawieszenia pierwszego i drugiego stopnia są
liniowymi więziami lepkosprężystymi.

W niniejszej pracy przyjęto obciążenie ruchome mostu w postaci pociągu typu Shinkansen,

złożonego z powtarzalnych jednostek napędowych, powszechnie stosowanego na liniach japoń-
skich [2]. Założono, że prędkość pociągu v jest stała. Formuły określające dynamiczne interakcje
przenoszone przez zawieszenia pojazdó w podano w pracy [6]. Macierzowe ró wnania ró wnowagi
dynamicznej podukładó w układu MTP wyznaczono, stosując metodę sformułowaną w monogra-
fii [3] i rozwiniętą w pracach [5, 6]. W metodzie tej wykorzystuje się ró wnania Lagrange’a oraz
stosuje się zapis ró wnań ró wnowagi dynamicznej częściowo w niejawnej postaci, z siłami inte-
rakcji jako niewiadomymi pośrednimi. Są to interakcje przenoszone przez zawieszenia pojazdó w
szynowych, łączniki szyn z podkładami oraz podsypkę.

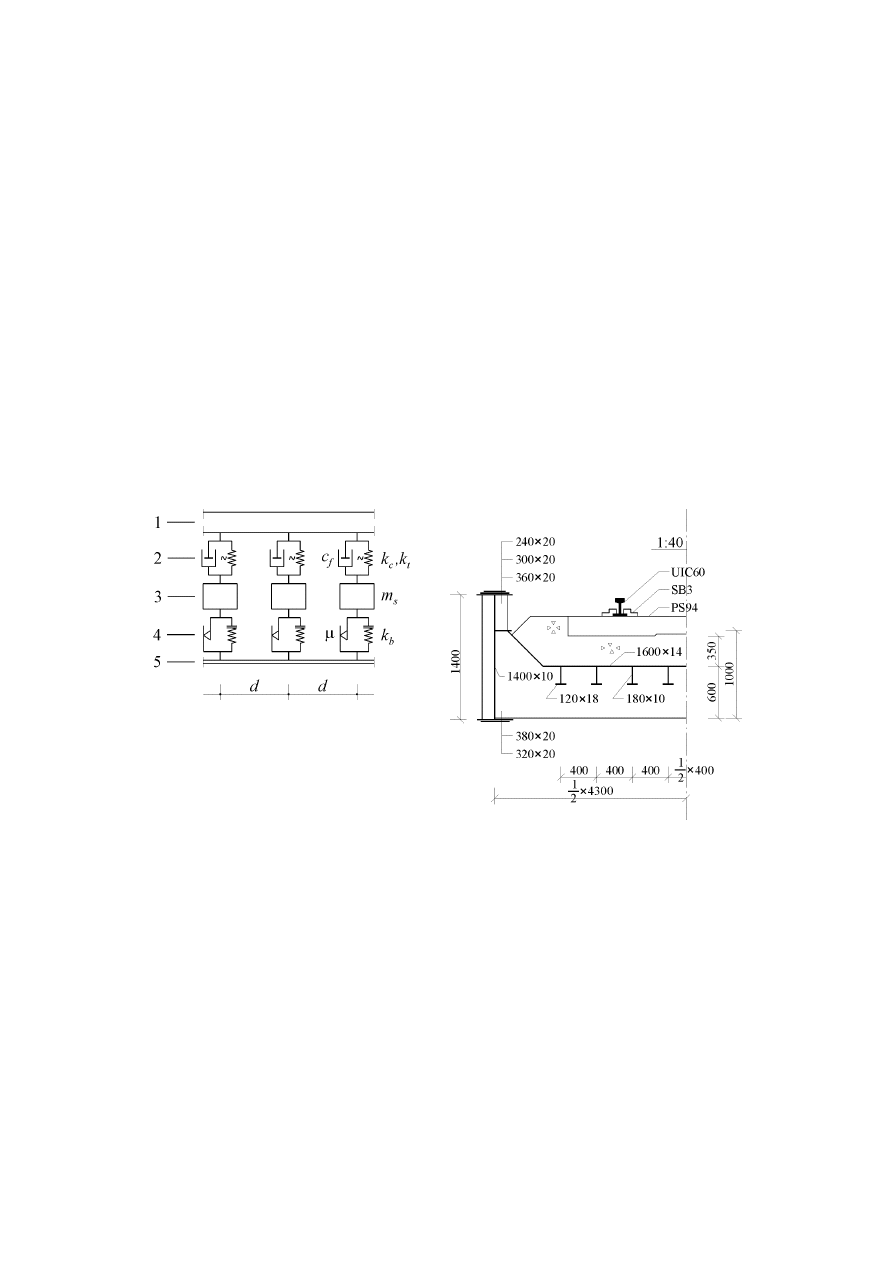
Rys. 3. Odcinek toru bezstykowego:

1 – belka modelują ca szyny,
2 – więzi modelują ce łą czniki
szyn z podkładami,
3 – podkłady,
4 – więzi modelują ce podsypkę
tłuczniową ,
5 – płyta pomostowa.

Rys. 5. Przekró j poprzeczny mostu SB15
w środku rozpiętości

Wynikowe ró wnania ruchu układu MTP mają postać

(

)

ï

ï
î

ï

ï
í

ì

=

+

+

=

=

+

+

+

=

b

b

b

b

b

b

b

s

s

s

r

r

r

r

a

r

r

r

o

o

o

F

q

K

q

K

q

B

F

q

B

F

q

K

q

C

K

q

B

F

q

B

&

&

&

&

&

&

&

&

&

&

k

k

(1)

gdzie:

b

s

r

o

q

q

q

q

,

,

,

- podwektory wspó łrzędnych uogó lnionych, opisują ce drgania podu-

kładó w MR, S, P, KN; B

o

– macierz bezwładności podukładu MR; B

r

, K

r

– macierz bez-

88

władności i sztywności podukładu S; C

a

– macierz tłumienia wynikają ca ze sztucznego tłu-

mienia nadkrytycznego, w obszarze skrajnych elementó w skończonych podukładu S;

k

–

czas retardacji dla stali; B

s

– macierz bezwładności podukładu P; B

b

, K

b

– macierze bez-

władności i sztywności podukładu KN;

b

s

r

o

F

F

F

F

,

,

,

– podwektory obcią żeń uogó lnionych

podukładó w MR, S, P, KN. Sprzężenie ró wnań (1) jest ukryte w wektorach prawych stron,
wyrażonych przez zbiory interakcji liniowych (zawieszenia pojazdó w) i nieliniowych (łą cz-
niki szyn z podkładami, podsypka). Szczegó łowa struktura macierzy i wektoró w występują-
cych w ró wnaniach (1) została podana w pracach [3, 6].

Sprzężone ze sobą ró wnania (1) opisują nieliniowe drgania nieustalone, quasi-ustalone

i swobodne układu MTP, w pionowej płaszczyźnie quasi-symetrii układu. Opracowano proce-
durę rekurencyjno-iteracyjną numerycznego całkowania tych ró wnań, z częściowym wykorzy-
staniem bezwarunkowej stabilności metody średniego przyspieszenia Newmarka [6].

Rys. 4. Charakterystyka sprężysta i tłumią ca odcinka podsypki o długości d

3. Analiza dynamiczna typoszeregu belkowych mostów stalowych

Opracowano typoszereg belkowych mostó w stalowych, o pełnościennej konstrukcji nośnej, z
pomostem zamkniętym, jednotorowych i jednoprzęsłowych [8], zgodnie z polskimi normami
[9, 10]. Typoszereg obejmuje sześć obiektó w, o analogicznej geometrii przekroju poprzecz-
nego, pokazanej na rys. 5. Wartości podstawowych parametró w mostó w tworzą cych typo-
szereg podano w tablicy 1, gdzie W

3

oznacza wskaźnik zginania dla włó kien dolnych w

środku rozpiętości belek głó wnych. Belki głó wne mają trzy zestawy nakładek, dla wszyst-
kich obiektó w określone przez wzory

3

2

3

1

3

2

1

84

.

0

,

56

.

0

,

45

.

0

,

70

.

0

,

I

I

I

I

l

l

l

l

l

l

=

=

=

=

=

.

(2)

Z przeprowadzonych symulacji drgań swobodnych podukładu most – tor (MT) wyni-

ka, że jest mu przyporzą dkowana podstawowa częstotliwość quasi-liniowych drgań swobod-
nych, któ rą można szacować ze wzoru

3

3

2

1

2

925

.

0

m

EI

l

f

p

»

,

(3)

gdzie E = 206 GPa jest modułem Younga dla stali.

W układzie MTP podukład MT jest poddany działaniu periodycznego wymuszenia parame-

trycznego i siłowego [3]. Prędkości krytyczne pociągu, któ rym odpowiadają rezonanse siłowe
podstawowego układu modalnego podukładu MT można prognozować ze wzoru [5]

89

[

]

km/h

6

.

3

1

,

i

f

b

v

o

i

cr

=

,

(4)

gdzie i jest numerem składowej harmonicznej wymuszenia siłowego. Prognozowane warto-
ści prędkości krytycznych pocią gu typu Shinkansen, odpowiadają ce obiektom mostowym
wymienionym w tablicy 1, zestawiono w tablicy 2.

Tablica 1. Typoszereg belkowych mostó w stalowych [8]

Kod mostu

l

m

m

3

kg/m

I

3

m

4

W

3

m

3

SB15
SB18
SB21
SB24
SB27
SB30

15
18
21
24
27
30

5380
5780
6170
6520
6650
6770

0.0428
0.0658
0.0967
0.1406
0.1936
0.2688

0.0558
0.0750
0.1005
0.1280
0.1580
0.1990

Tablica 2. Prognozowane prędkości krytyczne pocią gu Shinkansen dla typoszeregu mostó w

Symulacje procesó w dynamicznych i quasi-statycznych w układzie MTP zostały wy-

konane przy założeniu toru ustabilizowanego, w okresie letnim. W skład toru wchodzą szyny
UIC 60, łą czniki typu SB 3 oraz podkłady strunobetonowe PS 94. Wartości średnie parame-
tró w fizycznych toru, opisują ce nieliniowy model przyjęty w niniejszej pracy, oszacowano
na podstawie danych zawartych m.in. w pracach [3,11-14] i zestawiono poniżej:

,

0.36

,

MN/m

90

,

MN/m

165

,

kg

294

,

m

60

.

0

,

kNs/m

16

,

MN/m

5

.

32

,

MN/m

120

,

s

00025

.

0

,

cm

6110

,

kg/m

130

4

=

m

=

=

=

=

=

=

=

=

k

=

=

bz

b

s

f

t

c

r

r

k

k

m

d

c

k

k

I

m

gdzie: I

r

– moment bezwładności pary szyn, przy zginaniu w płaszczyźnie pionowej; c

f

–

wspó łczynnik tłumienia lepkiego łącznikó w przypadających na jeden podkład; m

s

– masa

podkładu, k

bz

– sztywność podsypki na ściskanie na odcinku d, w strefach dojazdowych do

mostu, z uwzględnieniem podatności podtorza. Parametry

l

,

,'

a

c

l

estymowano na podstawie

symulacji testowych. Przyjęto

.

m/s

05

.

0

λ

,

kNs/m/m

500

,

m

8

'

=

=

=

a

c

l

Dalsze zwiększa-

nie

a

c

l ,'

lub zmniejszanie

l

zmienia odpowiedź dynamiczną podukładu KN o mniej niż 1%.

Wartości parametró w fizycznych pojazdó w szynowych, wchodzących w skład pocią gu Shin-
kansen, są m.in. zestawione w pracach [2, 5]. Przyjęto liczbę pojazdó w N=12.

v

km/h

Kod mostu

f

1

Hz

i=1

i=2

i=3

SB15
SB18
SB21
SB24
SB27
SB30

8.27
6.87
5.92
5.32
4.88
4.62

744
617
533
479
439
415

372
309
266
239
220
208

248
206
178
160
146
139

90

Drgania układu MTP były symulowane z wykorzystaniem własnego programu użytkowego

DYRAB [15]. Program służy do symulacji układu MTP w warunkach dynamicznego i quasi-
statycznego przejazdu pociągu przez most. Postprocesor programu umożliwia graficzną wizuali-
zację dynamicznych i quasi-statycznych przebiegó w czasowych ugięć oraz naprężeń normalnych
w skrajnych włó knach belek głó wnych, w dowolnym przekroju poprzecznym. Jedna seria obli-
czeń na PC 1.3 GHz trwa 1 – 15 minut, w zależności od parametró w wejścia.

Przeprowadzono studyjną analizę dynamiczną obiektó w mostowych z tablicy 1, obciążo-

nych pociągiem Shinkansen, poruszającym się z prędkościami v=100 – 300 km/h. Analizowano
odpowiedź dynamiczną i quasi-statyczną podukładu KN, w zakresie przebiegó w czasowych
ugięć i naprężeń normalnych oraz wspó łczynnikó w dynamicznych ugięć i naprężeń.

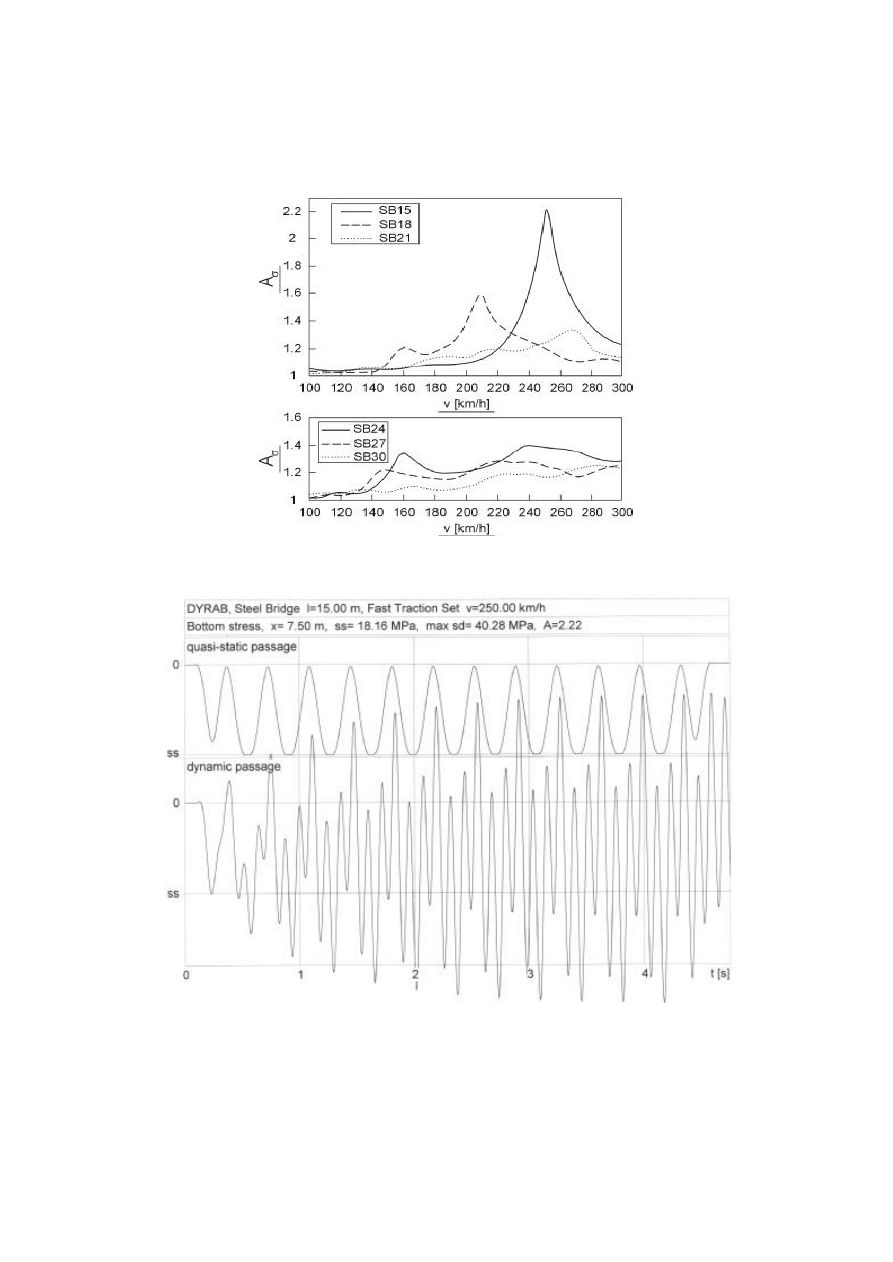
Na rys. 6 pokazano wykresy wspó łczynnika dynamicznego dla naprężeń normalnych w

dolnych włó knach w środku rozpiętości belek głó wnych, obliczanego z klasycznego wzoru

( )

( )

t

t

A

s

d

s

s

=

s

max

max

,

(5)

gdzie

s

d

(t),

s

s

(t) – dynamiczny i quasi-statyczny przebieg czasowy naprężeń.

Przebiegi czasowe naprężeń w najbardziej niekorzystnym przypadku, t.j. dla mostu

SB15 obcią żonego pocią giem poruszają cym się z prędkością v=250 km/h, przedstawiono na
rys. 7. Rysunek ten ilustruje jednocześnie grafikę generowaną przez program DYRAB.

Na podstawie przeprowadzonych symulacji dynamicznych i quasi-statycznych ukła-

dó w MTP, częściowo zilustrowanych na rys. 6, 7, sformułowano następują ce wnioski dla
belkowych mostó w stalowych rozpatrywanego typu:

·

Prędkości krytyczne pocią gu Shinkansen, odpowiadają ce rezonansowi siłowemu
podstawowego układu modalnego podukładu MT, wywołanemu przez podstawową
składową harmoniczną wymuszenia siłowego, są praktycznie nieosią galne.

·

Teoretyczna prognoza prędkości krytycznych pocią gu Shinkansen, odpowiadają -
cych rezonansowi siłowemu podstawowego układu modalnego, wywołanemu przez
trzecią składową harmoniczną wymuszenia siłowego, w większości przypadkó w
została potwierdzona przez symulacje drgań.

·

Liczba N=12 jest wystarczają ca do wyznaczenia drgań quasi-ustalonych mostu.

·

Mosty małych rozpiętości

(

)

m

15

12

-

=

l

nie są dostosowane do przenoszenia ob-

cią żeń poruszają cych się z prędkościami v= 240 – 300 km/h. Mogą wó wczas wy-
stą pić stany rezonansowe, któ rym odpowiadają wspó łczynniki dynamiczne

2

>

s

A

.

Prowadzi to do zmęczenia niskocyklowego nakładek belek głó wnych.

·

W przypadku dużych prędkości pocią gó w (v = 160 – 300 km/h) najbardziej ko-
rzystne są mosty średnich rozpiętości (l = 21 – 30 m). Jest to zwią zane przede
wszystkim ze zmniejszaniem się amplitud wymuszenia podukładu MT ze wzrostem
rozpiętości. Ponadto wzrasta moc tłumienia przez podsypkę w tych mostach.

·

Wspó łczynniki dynamiczne dla ugięć KN są o kilka procent mniejsze lub ró wne
wspó łczynnikom dynamicznym dla naprężeń normalnych w KN.

·

Największe wspó łczynniki dynamiczne dla naprężeń normalnych odpowiadają
przekrojowi w środku rozpiętości przęsła.

·

Pod względem jakościowym, przebiegi czasowe naprężeń dynamicznych w istotny
sposó b zależą od położenia analizowanego przekroju KN.

·

Opracowane nieliniowe modele fizyczne układu MTP są dość złożone i zbliżają
prognozowane teoretycznie drgania układu do drgań w układach rzeczywistych.

91

Rys. 6. Wykresy wspó łczynnika dynamicznego dla naprężeń normalnych w dolnych włó k-

nach belek głó wnych obiektó w mostowych zestawionych w tablicy 1

Rys. 7. Dynamiczny i quasi-statyczny przebieg czasowy naprężeń normalnych w dolnych

włó knach belek głó wnych mostu SB15, obcią żonego pocią giem Shinkansen z v=250 km/h

92

Literatura

[1] FRYBA L., Vibrations of solids and structures under moving load. Academia, Praha, 1972.
[2] MATSUURA A., Dynamic behaviour of bridge girder for high speed railway bridge.

RTRI Quarterly Reports. 1979, Vol. 20, No. 2.

[3] KLASZTORNY M., Drgania jednotorowych mostó w kolejowych wywołane ruchem

pociągó w poruszających się z dużymi prę dkoś ciami. WPWr, Wrocław, 1987.

[4] NIEMIERKO A., Some design and performance problems related to behaviour of

bridge structures on high speed railway lines. Arch. Civil Eng., 1996, Vol.42, No.4,
pp.401-423.

[5] KLASZTORNY M., Vertical vibrations of a multi-span beam steel bridge induced by a

superfast passenger train. Structural Eng. & Mechanics. 2001, Vol.12, No.3, pp. 267-281.

[6] KLASZTORNY M. & PODWÓ RNA M., New computational algorithms in dynamics

of bridge – track – moving train system. CD Proc. 2

nd

European Conf. on Computational

Mechanics, Cracow (Poland). 2001, Minisymposium 28. Paper No 110: 1-20.

[7] ROMANISZYN Z., WOLFRAM T., Nowoczesny tabor szynowy. IPS PK, Krakó w, 1997.

[8] MACHELSKI Cz., Typoszereg stalowych mostó w kolejowych. Raport serii SPR

Nr135/01. Instytut Inżynierii Lą dowej PWr, Wrocław, 2001.

[9] PN-82/S-10052. Obiekty mostowe. Konstrukcje stalowe. Projektowanie.

[10] PN-85/S-10030. Obiekty mostowe. Obciążenia.
[11] AHLBECK, D.R., MEACHAM H.C & PRAUSE R.H., The development of analytical

models for railroad track mechanics. Proc. Symp. on Railroad Track Mechanics. Perga-

mon Press, 1975, 239-263.

[12] DUKKIPATI R.V. & AMYOT J.R., Computer aided simulation in railway dynamics.

New York – Basel: Marcel Dekker, Inc, 1988.

[13] ESVELD C., Modern railway track. Germany, 1989.
[14] KRUŻYŃ SKI M., PIOTROWSKI A., PODWÓ RNA M., Badania doświadczalne wy-

cinka toru kolejowego. Raport serii SPR Nr1/02, IIL PWr, Wrocław, 2002.

[15] KLASZTORNY M., MYŚ LECKI K., Program komputerowy DYRAB do obliczeń dy-

namicznych mostó w kolejowych. Raport Nr IMiK/4/1999. IMiK PW, Warszawa, 1999.

DYNAMIC ANALYSIS OF A SERIES-OF-TYPES OF STEEL BEAM

BRIDGES LOADED BY A TRAIN MOVING AT HIGH SPEEDS

Summary

A planar, physical and mathematical, nonlinear model of the bridge – track – moving train
system has been presented. The theory is related to single-track, simply-supported bridges,
with a steel beam superstructure and a ballasted closed platform. A series-of-types of the
bridges undertaken has been designed in accordance with Polish codes. The dynamic and
quasi-static responses of the bridges to a Shinkansen train moving at velocity v = 100 – 300
km/h have been simulated, using own computer software. Practical usability of steel beam
bridges on high speed railway lines has been verified.

Praca została wykonana w ramach projektu badawczego Nr 8 T07E 024 20, finansowanego
w latach 2001 – 2003 przez Komitet Badań Naukowych.