ANALIZA DYNAMIKI ZJAWISK (badanie szeregu czasowego)

Szereg czasowy jest to szereg przedstawiający kształtowanie się zjawiska w czasie

(ciąg wyników obserwacji uporządkowanych w czasie).

• szereg czasowy okresów - gdy dane dotyczą rozmiarów zjawiska w pewnych okresach (np. rok, kwartał, miesiąc). Przykład: szereg przedstawiający produkcję energii elektrycznej w kolejnych miesiącach kilku lat.

• Szereg czasowy momentów - gdy dane dotyczą pewnego ściśle określonego momentu (stan w dniu lub godzinie). Przykład: szereg przedstawiający liczbę ludności pewnego miasta na dzień 31.XII w kolejnych kilku latach.

Przyjęte oznaczenia:

y₁, y₂ , y₃ , . . . . . . . . . y_n - wyrazy szeregu czasowego

tj. poziom zjawiska w poszczególnych okresach (lub momentach)

gdzie:

n - liczba badanych okresów (momentów),

y₁- poziom zjawiska w okresie pierwszym (początkowym),

y₂- poziom zjawiska w okresie drugim,

itd.

Uwaga: W niektórych publikacjach poziom zjawiska w okresie początkowym oznacza się jako y₀. Należy zwrócić uwagę, że w takiej sytuacji badanych okresów jest zawsze o jeden więcej niż wynosi wskaźnik n. Na przykład n=4 oznaczałoby, że badanych jest 5 okresów (mamy bowiem wówczas y₀, y₁ , y₂ , y₃ , y₄ ).

Przeciętny poziom zjawiska

obliczamy:

1. za pomocą średniej arytmetycznej - w przypadku szeregów czasowych okresów

Uwaga: W mianowniku mamy liczbę badanych okresów. Gdybyśmy wyrazy szeregu oznaczyli od y₀ poczynając, wówczas powyższy wzór wyglądałby nieco inaczej (w mianowniku dodana byłaby jedynka)

2. za pomocą średniej chronologicznej - w przypadku szeregów czasowych momentów

Uwaga: W mianowniku mamy liczbę badanych okresów minus 1. Gdybyśmy wyrazy szeregu oznaczyli od y₀ poczynając, wówczas powyższy wzór wyglądałby nieco inaczej (w mianowniku nie odejmowana byłaby jedynka).

Miary dynamiki zjawisk

łańcuchowe

• 
  Przyrosty (absolutne, względne)

jednopodstawowe

łańcuchowe

• 
  Indeksy (indywidualne, agregatowe)

jednopodstawowe

Miary dynamiki jednopodstawowe (tj. o podstawie stałej) - służą do określenia zmian, jakie nastąpiły w poziomie zjawiska w porównaniu z okresem (momentem) przyjętym jako podstawowy (bazowy). Najczęściej za podstawę porównań przyjmuje się okres (moment) pierwszy.

Miary dynamiki łańcuchowe (tj. o podstawie ruchomej) - służą do określenia zmian jakie nastąpiły w poziomie zjawiska z okresu na okres (z momentu na moment). Jako podstawę odniesienia przyjmuje się poziom zjawiska w okresie (momencie) poprzednim

Przyrosty absolutne jednopodstawowe:

za podstawę porównań przyjęto wielkość y₁

tj. poziom zjawiska w okresie (momencie) t = 1,

za podstawę porównań przyjęto wielkość y_k

tj. poziom zjawiska w okresie (momencie) t = k.

Przyrosty absolutne łańcuchowe:

Przyrosty absolutne informują, o ile wzrósł (lub zmalał) poziom zjawiska w okresie badanym w porównaniu z poziomem w okresie bazowym (a więc są to wielkości mianowane).

Przyrosty względne jednopodstawowe:

Przyrosty względne łańcuchowe:

Przyrost względny to stosunek przyrostu absolutnego do poziomu zjawiska w okresie bazowym - tzw. wskaźnik tempa przyrostu.

Przyrosty względne można wyrażać w procentach:

Przyrost względny x 100% = procentowy przyrost względny zwany tempem zmian

(tempem przyrostu lub spadku)

Przyrost względny (tempo zmian) informuje, o ile procent poziom zjawiska w danym okresie jest wyższy (lub niższy) od poziomu zjawiska w okresie bazowym.

Indeksy indywidualne jednopodstawowe:

Indeksy indywidualne łańcuchowe:

Indeks to stosunek wielkości danego zjawiska w okresie badanym do poziomu w okresie bazowym.

Indeksy są wielkością niemianowaną i można je wyrażać w procentach (czyli x 100%).

Uwaga

0 < i < 1 ⇔ 0% < i [%] < 100% oznacza spadek poziomu zjawiska,

i > 1 ⇔ i [%] > 100% oznacza wzrost poziomu zjawiska.

PRZYKŁAD 1

Dynamika liczby dzieci w szkole „S” w latach 2001-2006 (stan na dzień 1 września) przedstawia się następująco:

Tabela 1

Rok	Liczba dzieci	Przyrosty absolutne (w zł)		Przyrosty względne		Indeksy indywidualne
				jednopodstawowe	łańcuchowe	Jednopodstawowe	łańcuchowe	jednopodstawowe	łańcuchowe
t	yt	Δ t /1	Δ t / t - 1	d t /1	d t / t - 1	i t /1	i t / t - 1
2001 2002 2003 2004 2005 2006	323 320 329 346 422 386	0 -3 6 23 99 63	- -3 9 17 76 -36	0 -0,01 0,02 0,07 0,31 0,20	- -0,01 0,03 0,05 0,22 -0,09	1 0,99 1,02 1,07 1,31 1,20	- 0,99 1,03 1,05 1,22 0,91

Podając przyrosty względne i indeksy w procentach otrzymujemy:

Tabela 2

Nr okresu (rok)	Liczba dzieci	Przyrosty absolutne (w zł)		Przyrosty względne		Indeksy indywidualne
				jednopodstawowe	łańcuchowe	Jednopodstawowe	łańcuchowe	jednopodstawowe	łańcuchowe
t	yt	Δ t /1	Δ t / t - 1	d t /1 *100%	d t / t - 1 *100%	i t /1 *100%	i t / t - 1 *100%
1 2 3 4 5 6	323 320 329 346 422 386	0 -3 6 23 99 63	- -3 9 17 76 -36	0 -1 2 7 31 20	- -1 3 5 22 -9	100 99 102 107 131 120	- 99 103 105 122 91

Interpretacja poszczególnych miar (patrz tabela 1)

Na przykład:

63 oznacza, że …

-36 oznacza, że …

0,20 oznacza, że …

-0,09 oznacza, że …

1,20 oznacza, że …

0,91 oznacza, że …

Uwaga

Zależność między przyrostami względnymi a indeksami:

(jednopodstawowe),

(łańcuchowe).

(gdy posługujemy się procentami - zamiast 1 dodajemy 100).

Średnie tempo zmian zjawiska w czasie:

średnie tempo zmian w badanych okresach, tzw. stopa wzrostu

(można również wyrażać w procentach),

gdzie:

- średnia geometryczna z indeksów łańcuchowych, tj.:

Zauważmy, że:

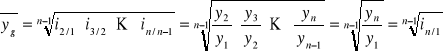
czyli wyrażenie pod pierwiastkiem jest w efekcie indeksem jednopodstawowym
.

Uwaga: Zauważmy, że stopień pierwiastka w powyższym wzorze jest taki jak liczba indeksów łańcuchowych pod pierwiastkiem (czyli o 1 mniejszy niż liczba badanych okresów).

Cd. Przykładu 1

Oznacza, że liczba dzieci w szkole wzrastała z roku na rok średnio o 3,6%.

Średnie tempo zmian zjawisk w czasie (stopa wzrostu) wykorzystywane jest dla celów prognozowania. Konieczne jest wówczas założenie, że średnie tempo zmian w okresie prognozowanym nie ulegnie zmianie.

Uwaga:

Poziom zjawiska w okresie n wyznaczyć można ze wzoru:

gdzie:

y_n - poziom zjawiska w okresie n,

y₁ - poziom zjawiska w okresie pierwszym,

- średnia geometryczna liczona według wzorów podanych powyżej.

(wzór ten zastosujemy gdy znamy y₁)

Powyższy wzór na y_n możemy również zapisać w postaci:

gdzie:

y_n+k - poziom zjawiska w okresie n+k,

y_n - poziom zjawiska w okresie n,

k - numer okresu prognozowanego (k = 1, 2, …)

(wzór ten zastosujemy gdy znamy y_n)

Cd. Przykładu 1

Np. liczbę dzieci w szkole w 7 okresie (w roku 2007) obliczymy

- według pierwszego wzoru

Lub:

- według drugiego wzoru (niewielkie różnice wyniku ze

względu na zaokrąglenie średniej geometrycznej)

Na podobnej zasadzie możemy szacować poziom zjawiska w przeszłości, przy założeniu że średnie tempo zmian w okresie poprzedzającym okres badany było takie samo. Na przykład:

Cd. Przykładu 1

Mając dane:

Możemy obliczyć:

(„0” - okres bezpośrednio poprzedzający okres numer „1”,

czyli u nas y₀ to liczba dzieci w szkole w dniu 1 września 2000 r.)

(„-1” - okres bezpośrednio poprzedzający okres numer „0”,

czyli u nas y-₁ to liczba dzieci w szkole w dniu 1 września 1999 r.)

Ogólny wzór na poziom zjawiska w okresie poprzedzającym zapiszemy:

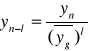
gdzie:

l - liczba okresów (momentów) wstecz od okresu n, (l = 1, 2, …).

(wyjaśnienie: jeśli n=1 oznacza rok pierwszy badany, którym jest np. rok 2001, to przyjmując np. l=2 wyznaczymy poziom zjawiska w roku 1999).

Zależności między indeksami jednopodstawowymi a łańcuchowymi

Uwaga !!!

Przekształcenia wykonujemy operując indeksami wyrażonymi w ułamkach

(nie w %)

kolejne dzielenie indeksów jednopodstawowych przez

indeks jednopodstawowy dla okresu k

• 
  indeksy jednopodstawowe indeksy jednopodst.

(gdy podstawą jest okres t = 1) (o dowolnej podstawie k)

Np.: gdy podstawą jest okres k = 3

itd.

Przykład:

(kolumna dana) (kolumna szukana)

t	yt	Indeks jednopodstawowy i t /1	Indeks jednopodstawowy i t /3
1 2 3 4 5 6	y1 y2 y3 y4 y5 y6	1 0,99 1,02 1,07 1,31 1,19	0,98 (bo 1:1,02=0,98) 0,97 (bo 0,99:1,02=0,97) 1 (bo 1,02:1,02=1) 1,05 (bo 1,07:1,02=1,05) 1,28 (bo 1,31:1,02=1,28) 1,17 (bo 1,19:1,02=1,17)

dzielenie dwóch kolejnych indeksów jednopodstawowych

(„późniejszy” przez „wcześniejszy”)

• 
  indeksy jednopodstawowe indeksy łańcuchowe

,

,

.

Np.:

0,99 : 1 = 0,99

itd.

Przykład:

(kolumna dana) (kolumna szukana)

t	yt	Indeks jednopodstawowy i t /1	Indeks łańcuchowy i t /t-1
1 2 3 4 5 6	y1 y2 y3 y4 y5 y6	1 0,99 1,02 1,07 1,31 1,19	- (nie da się obliczyć) 0,99 (bo 0,99:1=0,99) 1,03 (bo 1,02:0,99=1,03) 1,05 (bo 1,07:1,02=1,05) 1,22 (bo 1,31:1,07=1,22) 0,91 (bo 1,19:1,31=0,91)

mnożenie kolejnych (od pierwszego włącznie)

indeksów łańcuchowych

• 
  indeksy łańcuchowe indeksy jednopodstawowe

,

,

.

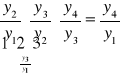
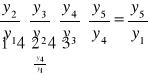
Np.:

itd.

Przykład:

(kolumna szukana) (kolumna dana)

t	yt	Indeks jednopodstawowy i t /1	Indeks łańcuchowy i t /t-1
1 2 3 4 5 6	y1 y2 y3 y4 y5 y6	1 (bo i 1/1=1) 0,99 (bo i 2/1=0,99) 1,02 (bo 0,99*1,03=1,02) 1,07 (bo 0,99*1,03*1,05=1,07) 1,31 (bo 1,07*1,22=1,31) 1,19 (bo 1,31*0,91=1,19)	- 0,99 1,03 1,05 1,22 0,91

9

---