Testowanie hipotez dla dwóch parametrów

Test dla dwóch średnich

H₀:
H₁:
(lub H₁:
lub H₁:
)

Model A.

Założenia stosowalności:

1. obie populacje generalne mają rozkłady normalne:

~
,
~

2. odchylenia standardowe
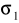
   i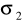
   obu populacji są nieznane, ale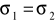
   

3. próby pobrane są niezależnie,

przy czym wystarczają próby małe (
i
)

Stosujemy test t-Studenta.

• Obliczamy:

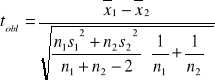
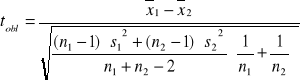
Statystyka t_obl ma (przy założeniu prawdziwości H₀) rozkład t-Studenta z liczbą stopni swobody
.

• Znajdujemy wartość krytyczną
  

(
)

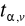
• Porównujemy:

Obliczoną z próby wartość statystyki t_obl porównujemy z wartością krytyczną
i podejmujemy odpowiednią decyzję co do odrzucenia bądź pozostawienia hipotezy H₀.

Model B.

Założenia stosowalności:

1. Rozkłady obu populacji generalnych są dowolne (mogą być nieznane):

2. odchylenia standardowe
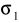
   i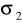
   obu populacji są nieznane, ale skończone

3. próby pobrane są niezależnie,

przy czym obie próby muszą być duże (
i
)

Stosujemy test u.

• Obliczamy:

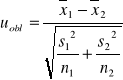
ewentualnie: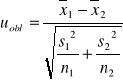
gdyż
więc
i

• Znajdujemy wartość krytyczną
  

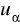
• Porównujemy:

Test dla dwóch wariancji (odchyleń standardowych)

(
)

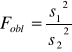
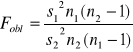
Przy czym
,

Test dla dwóch wskaźników struktury

H₀:

H₁:

(lub H₁:
lub H₁:
)

Model.

Założenia stosowalności:

1. obie populacje generalne mają rozkład zero-jedynkowy z parametrami odpowiednio

p₁ i p₂

(tzn. p₁ - odsetek elementów wyróżnionych w pierwszej populacji,

p₂ - odsetek elementów wyróżnionych w pierwszej populacji

(wymaga się, aby p₁ i p₂ były
),

2. próby losowane niezależnie,

3. obie próby muszą być bardzo duże (n₁ i n₂
   ).

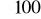
Stosujemy test U.

• Obliczamy:

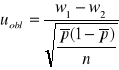
gdzie:
,

- średni wskaźnik struktury z obu prób

Statystyka u_obl ma (przy założeniu prawdziwości H₀) rozkład normalny standaryzowany.

• Znajdujemy wartość krytyczną
  

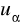
• Porównujemy:

Obliczoną z próby wartość statystyki u_obl porównujemy z wartością krytyczną
i podejmujemy odpowiednią decyzję co do odrzucenia bądź pozostawienia hipotezy H₀.

Wnioskowanie w analizie korelacji i regresji

Test istotności dla współczynnika korelacji liniowej r Pearsona

- współczynnik korelacji liniowej Pearsona w próbie,

- współczynnik korelacji liniowej Pearsona w populacji.

H₀:

H₁:

Model

Założenia:

- cechy X i Y mają rozkład normalny lub zbliżony do normalnego

- próba n elementowa niekoniecznie duża

,

.

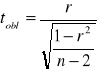
Przykład

Badano, czy zachodzi liniowa korelacja między czasem poświęconym na negocjacje dotyczące sprzedaży i wynikających z nich zyskiem. Pobrano losową próbę 27 transakcji rynkowych, notując czas potrzebny do zawarcia transakcji sprzedaży oraz wynikający z transakcji zysk.

Współczynnik korelacji z próby wyniósł r = 0,424

H₀:
(brak korelacji liniowej w populacji wszystkich transakcji),

H₁:
(istnieje dodatnia korelacja liniowa w populacji)

Przyjmiemy

a zatem:

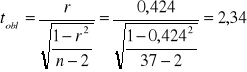
Wartość krytyczną
w rozkładzie t-Studenta odczytujemy dla liczby stopni swobody
i podwojonego poziomu istotności, czyli
z tego względu, że hipoteza alternatywna jest sformułowana jednostronnie, więc obszar krytyczny testu jest jednostronny (tu prawostronny).

A zatem:

=1,708

Porównujemy wartość empiryczną statystyki z wartością krytyczną:

, tzn.:

,

czyli wartość obliczona statyki testowej należy do obszaru krytycznego, a zatem hipotezę zerową odrzucamy i przyjmujemy hipotezę alternatywną o istnieniu dodatniej korelacji liniowej między badanymi cechami.

Test siły korelacji

Model

Założenia:

- cechy X i Y mają rozkład normalny lub zbliżony do normalnego

- próba n elementowa niekoniecznie duża

Test u następującej postaci:

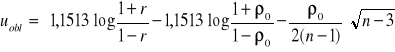
Testy istotności dla parametrów strukturalnych funkcji regresji

Model regresji liniowej prostej w populacji generalnej:

Estymacja parametrów modelu

yi	xi
y1 y2 … yn	x1 x2 … xn

- estymator parametru
(wyrazu wolnego)

- estymator parametru
(współczynnika regresji)

Liniowe równanie regresji prostej w próbie:

Test dla współczynnika regresji

(lub podjąć decyzję w oparciu o przedział ufności dla
)

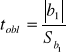
gdzie:

- ocena parametru

- ocena błędu standardowego szacunku parametru

- liczba zmiennych objaśniających

(tj. dla regresji prostej
)

Test dla wyrazu wolnego

(lub podjąć decyzję w oparciu o przedział ufności dla
)

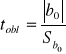
gdzie:

- ocena parametru

- ocena błędu standardowego szacunku parametru

Test istotności dla współczynnika korelacji rang r_s Spearmana

- współczynnik korelacji rang Spearmana w próbie,

- współczynnik korelacji rang Spearmana w populacji.

H₀:

H₁:

Model I.

Gdy liczebność próby jest bardzo mała:

,

.

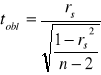
Model II.

Gdy liczebność próby nie jest bardzo mała:

.