W

Y K Ł A D Y Z

T

E O R I I

S

P R Ę Ż Y S T O Ś C I

P

ŁASKIE ZADANIA TEORII SPRĘŻYSTOŚCI

Politechnika Poznańska® Kopacz,

Krawczyk,

Łodygowski, Płotkowiak, Świtek, Tymper

1

Olga Kopacz, Krzysztof Krawczyk, Adam Łodygowski,

Michał Płotkowiak, Agnieszka Świtek, Krzysztof Tymper

Konsultacje naukowe: prof. dr hab. J

ERZY

R

AKOWSKI

Poznań 2002/2003

TEORIA SPRĘŻYSTOŚCI 6

PŁASKIE ZADANIA TEORII SPRĘŻYSTOŚCI

6.1. Płaski stan naprężenia

Płaski stan naprężenia zachodzi wówczas, gdy w każdym punkcie

ośrodka na wszystkich płaszczyznach o tym samym wektorze normalnym
składowe wektora naprężenia na jednej z płaszczyzn (i=3) są równe zeru.
Jeśli przyjmiemy, że płaszczyzny te są prostopadłe do osi x

3

, to

naprężenia

σ

3i

są tak małe, że można przyjąć je jako zerowe, a pozostałe

składowe tensora naprężenia nie zależą od x

3

. Również składniki sił

masowych wewnętrznych p

3

przyjmujemy jako zerowe. Przykładem

takiego stanu jest stan naprężenia w cienkiej tarczy obciążonej siłami
leżącymi w płaszczyźnie tarczy i równomiernie rozłożonymi na jej
grubości (np. ściana budynku). Tensor naprężenia ma zatem postać:





















=

0

0

0

0

0

22

21

12

11

σ

σ

σ

σ

σ

T

(6.1)

Towarzyszący mu tensor odkształceń wygląda następująco:





















=

33

22

21

12

11

0

0

0

0

ε

ε

ε

ε

ε

ε

T

(6.2)

Niezerowa wartość

ε

33

wynika ze wzoru na odkształcenia towarzyszące

naprężeniom:

(

)

22

11

33

σ

σ

ν

ε

+

−

=

E

(6.3)

W

Y K Ł A D Y Z

T

E O R I I

S

P R Ę Ż Y S T O Ś C I

P

ŁASKIE ZADANIA TEORII SPRĘŻYSTOŚCI

Politechnika Poznańska® Kopacz,

Krawczyk,

Łodygowski, Płotkowiak, Świtek, Tymper

2

Korzystając z wzorów na

σ

ij

(których w tym przypadku jest 3) i na

ε

ij

(których jest 4) otrzymamy układ 9 równań, z których po redukcji
niewiadomych można wyprowadzić wzory opisujące płaski stan
naprężenia w przemieszczeniach i w naprężeniach.

PSN w przemieszczeniach:

Dane są równania Lamego (dla 3D):

(

)

0

,

2

=

+

+

+

∇

i

i

i

p

u

ϑ

µ

λ

µ

(6.4)

oraz związki fizyczne:

kk

ij

ij

ij

ε

λδ

µε

σ

+

=

2

(6.5)

i geometryczne:

(

)

i

j

j

i

ij

u

u

,

,

2

1

+

=

ε

(6.6)

Przyjmujemy i = j = 3 (

σ

33

= 0)

(

)

0

2

3

,

3

2

,

2

1

,

1

3

,

3

=

+

+

+

⋅

u

u

u

u

λ

µ

(6.7)

Z tego:

(

)

2

,

2

1

,

1

3

,

3

2

u

u

u

+

+

−

=

µ

λ

λ

(6.8)

Dla: i = 1, j = 1

σ

13

= 0,

ε

13

= 0

i = 2, j = 3

σ

23

= 0,

ε

23

= 0

co oznacza, że
dla

i = 1,2

i

i

i

i

u

u

u

u

,

3

3

,

,

3

3

,

0

−

=

=

+

(6.9)

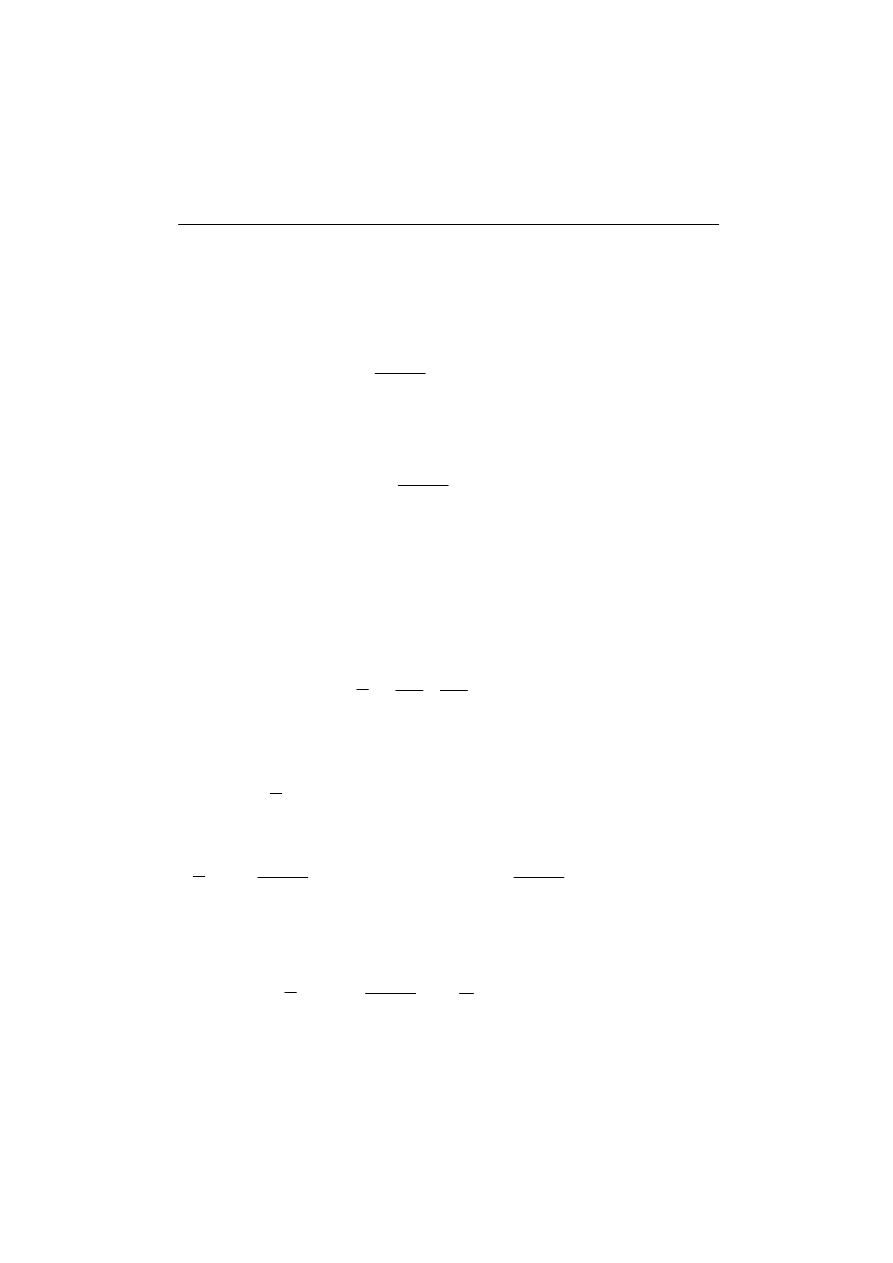
W

Y K Ł A D Y Z

T

E O R I I

S

P R Ę Ż Y S T O Ś C I

P

ŁASKIE ZADANIA TEORII SPRĘŻYSTOŚCI

Politechnika Poznańska® Kopacz,

Krawczyk,

Łodygowski, Płotkowiak, Świtek, Tymper

3

(6.9) różniczkujemy po x

3

i

i

i

u

u

u

3

,

3

3

,

3

33

,

−

=

−

=

(6.10)

(6.8) różniczkujemy po x

i

(

)

i

i

i

u

u

u

2

,

2

1

,

1

3

,

3

2

+

+

−

=

µ

λ

λ

(6.11)

Po podstawieniu (6.10) do (6.11) otrzymamy:

i

i

u

,

33

,

2

ϑ

µ

λ

λ

′

+

=

(6.12)

Gdzie:

2

,

2

1

,

1

22

11

u

u

+

=

+

=

′

ε

ε

ϑ

(6.13)

Wprowadzając operator Laplace’a w przestrzeni dwuwymiarowej

2

2

2

2

1

2

2

x

x

∂

∂

+

∂

∂

=

∇

(6.14)

Równanie Lamego można zapisać następująco:

(

)

(

)

(

)

0

3

,

3

,

33

,

2

=

+

+

′

+

+

+

∇

i

i

i

i

i

p

u

u

u

ϑ

µ

λ

µ

(6.15)

Po podstawieniu (6.10) i (6.11) do (6.15) uzyskamy:

(

)

(

)

0

2

2

,

,

2

=

+









+

−

+

+

′

+

+

′

+

+

+

∇

i

i

i

i

p

u

µ

λ

λ

µ

λ

ϑ

µ

λ

ϑ

µ

λ

λ

µ

µ

(6.16)

Czyli:

0

1

2

2

1

,

2

=

+









+

+

+

∇

i

i

i

p

u

µ

ϑ

µ

λ

λ

(6.17)

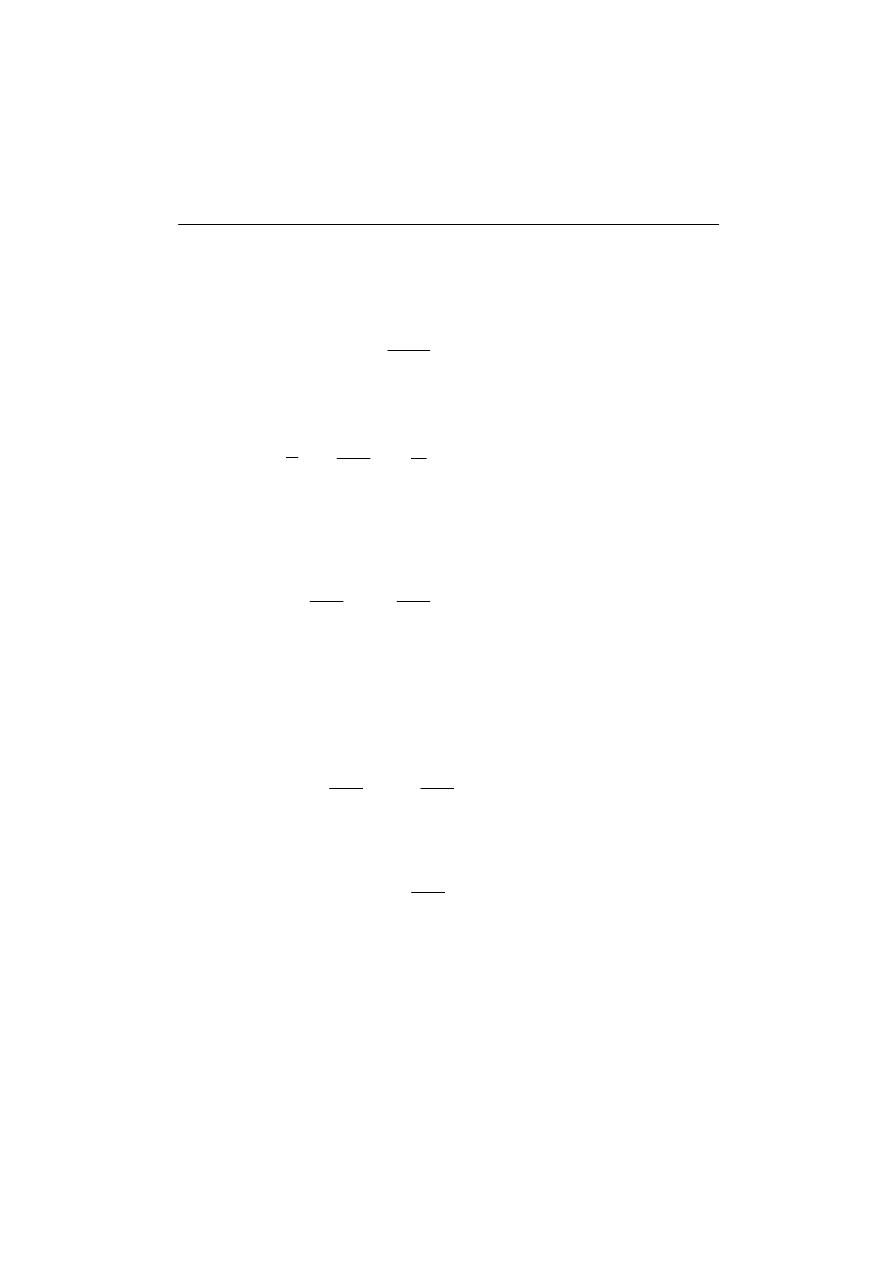
W

Y K Ł A D Y Z

T

E O R I I

S

P R Ę Ż Y S T O Ś C I

P

ŁASKIE ZADANIA TEORII SPRĘŻYSTOŚCI

Politechnika Poznańska® Kopacz,

Krawczyk,

Łodygowski, Płotkowiak, Świtek, Tymper

4

Wiemy, że

G

G

ν

ν

λ

µ

2

1

2

−

=

=

(6.18)

Więc równanie (6.17) uzyskuje postać:

2

,

1

,

0

1

1

1

,

2

=

=

+

′

−

+

+

∇

i

p

G

u

i

i

i

ϑ

ν

ν

(6.19)

PSN w naprężeniach:

Równania dla stanu trójosiowego:

(

)

i

j

j

i

k

k

ij

ij

ij

p

p

p

S

,

,

,

,

2

1

1

1

+

−

−

−

=

+

+

∇

δ

ν

ν

ν

σ

(6.20)

Gdzie:

33

22

11

σ

σ

σ

σ

+

+

=

=

ii

S

(6.21)

Dla i = j mamy:

k

k

k

k

kk

p

p

S

S

,

,

,

2

2

1

3

1

1

−

−

−

=

+

+

∇

δ

ν

ν

ν

(6.22)

Czyli

k

k

p

S

,

2

1

1

ν

ν

−

+

−

=

∇

(6.23)

Bo

S

S

kk

2

,

∇

=

(6.24)

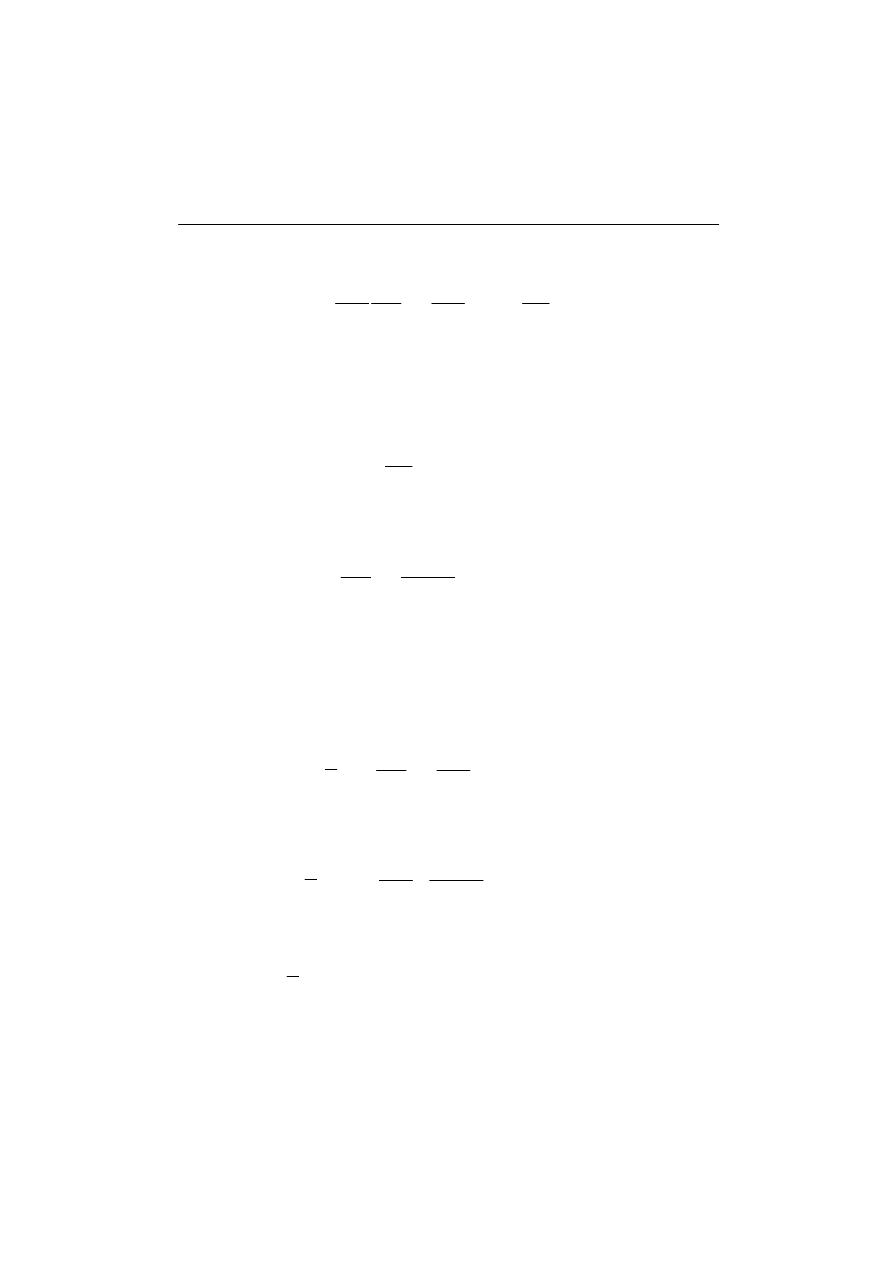
W

Y K Ł A D Y Z

T

E O R I I

S

P R Ę Ż Y S T O Ś C I

P

ŁASKIE ZADANIA TEORII SPRĘŻYSTOŚCI

Politechnika Poznańska® Kopacz,

Krawczyk,

Łodygowski, Płotkowiak, Świtek, Tymper

5

Dla i = j = 3

3

3

,

2

3

2

33

2

2

1

1

1

x

p

p

x

S

k

k

∂

∂

−

−

−

=

∂

∂

+

+

∇

ν

ν

ν

σ

(6.25)

Co wobec

0

0

0

3

3

3

33

=

∂

∂

=

=

x

p

p

σ

(6.26)

Można zapisać:

( )

k

k

p

x

S

,

2

3

2

1

1

ν

ν

ν

−

+

−

=

∂

∂

(6.27)

Wprowadźmy oznaczenie

12

11

σ

σ +

=

′

S

(6.28)

Do równania (6.23) i połączmy je z (6.27)

k

k

p

x

S

S

,

2

3

2

2

1

1

ν

ν

−

+

−

=

∂

∂

+

′

∇

(6.29)

Otrzymamy:

( )

k

k

p

S

,

2

1

1

1

1













−

+

+

−

+

−

=

′

∇

ν

ν

ν

ν

ν

(6.30)

Czyli ostatecznie:

( )

2

,

1

,

1

,

2

=

+

−

=

′

∇

j

i

dla

p

S

k

k

ν

(6.31)

W

Y K Ł A D Y Z

T

E O R I I

S

P R Ę Ż Y S T O Ś C I

P

ŁASKIE ZADANIA TEORII SPRĘŻYSTOŚCI

Politechnika Poznańska® Kopacz,

Krawczyk,

Łodygowski, Płotkowiak, Świtek, Tymper

6

Po rozpisaniu równanie (6.31) przyjmie postać:

(

)

(

) ( )









∂

∂

+

∂

∂

+

−

=

∂

+

∂

+

∂

+

∂

2

2

1

1

2

2

22

11

2

2

1

22

11

2

1

x

p

x

p

x

x

ν

σ

σ

σ

σ

(6.32)

Równanie (6.32) zawiera 2 niewiadome. Aby je wyznaczyć posługujemy się
dodatkowo równaniami równowagi Naviera

ji

ij

i

j

ji

p

σ

σ

σ

=

=

+

0

,

(6.33)

które po rozpisaniu przyjmują postać

0

0

2

2

22

1

12

1

2

21

1

11

=

+

∂

∂

+

∂

∂

=

+

∂

∂

+

∂

∂

p

x

x

p

x

x

σ

σ

σ

σ

(6.34)

Ostatecznie mamy układ 3 równań z 3 niewiadomymi

σ

11

,

σ

12

i

σ

22

.

6.2. Płaski stan odkształcenia

Płaski stan odkształcenia zachodzi wówczas, gdy w każdym punkcie ośrodka
ciągłego

ε

i3

= 0, a pozostałe współrzędne tensora odkształcenia zależą tylko od

zmiennych x

1

i x

2

. Tensor opisujący taki stan ma tylko 4 składowe:





















=

0

0

0

0

0

22

21

12

11

ε

ε

ε

ε

ε

T

(6.35)

Tensor naprężenia przybiera natomiast postać:





















=

33

22

21

12

11

0

0

0

0

σ

σ

σ

σ

σ

σ

T

(6.36)

W

Y K Ł A D Y Z

T

E O R I I

S

P R Ę Ż Y S T O Ś C I

P

ŁASKIE ZADANIA TEORII SPRĘŻYSTOŚCI

Politechnika Poznańska® Kopacz,

Krawczyk,

Łodygowski, Płotkowiak, Świtek, Tymper

7

σ

33

≠

0

wynika z przekształcenia wzoru na odkształcenia towarzyszące

naprężeniom:

(

)

[

]

(

)

22

11

33

33

22

11

33

33

0

1

σ

σ

ν

σ

ε

σ

σ

ν

σ

ε

+

=

=

+

−

=

E

(6.37)

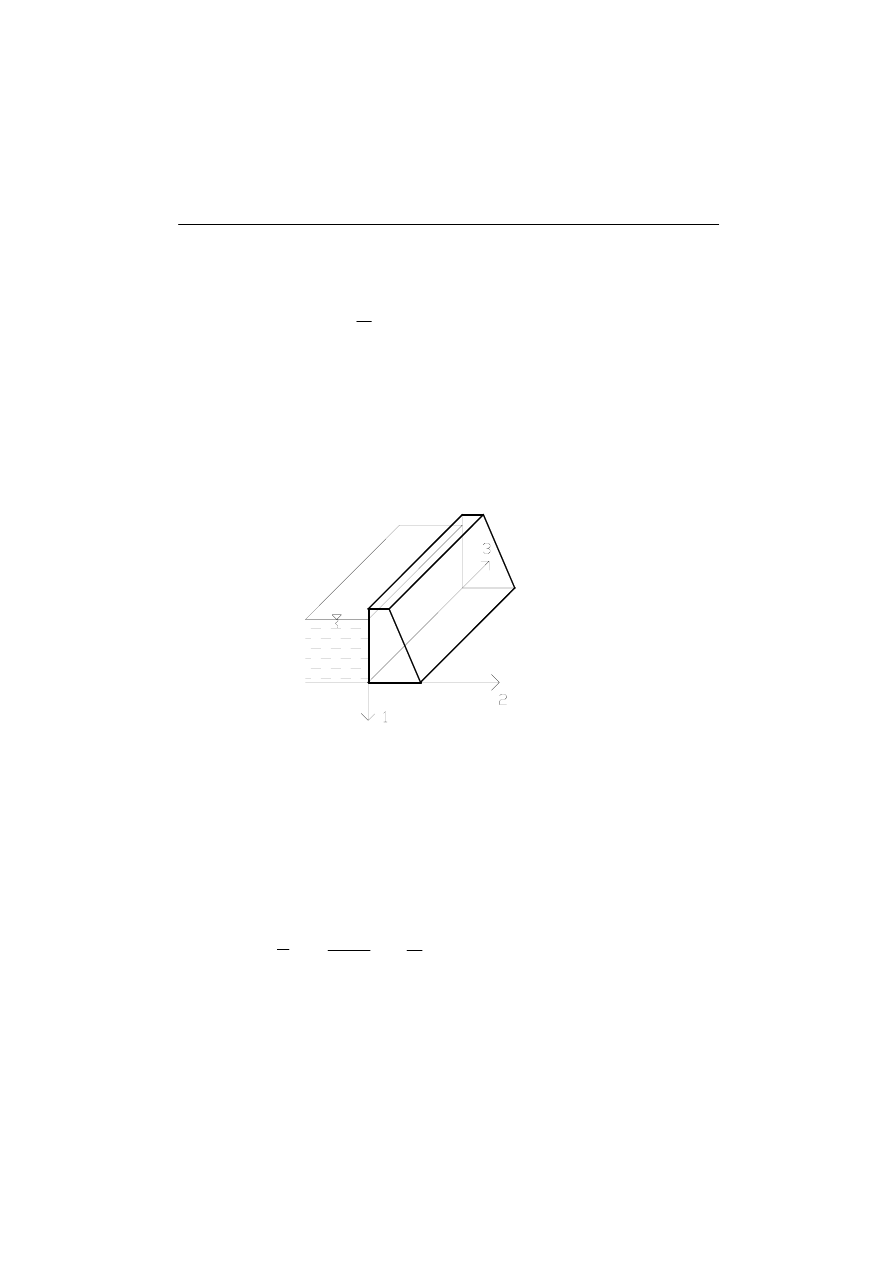
W takim stanie odkształcenia znajduje się np. zapora wodna, w której jeden
wymiar jest zdecydowanie większy od pozostałych i obciążenie skierowane jest
prostopadle do tego wymiaru

Rys. 1. Zapora wodna jako przykład płaskiego stanu odkształcenia

Równania równowagi dla PSO w przemieszczeniach:

Wykorzystamy wprost równania Lamego pomijając trzecie równanie (i = 3)
(wobec

ε

33

= 0 przyjmujemy, że u

3

= 0) oraz zakładamy, że u

1

i u

2

są funkcjami

zmiennych x

1

i x

2

i nie zależą od x

3

. Otrzymamy:

2

,

1

0

1

2

1

1

,

2

=

=

+

′

−

+

∇

i

p

G

u

i

i

i

ϑ

ν

(6.38)

Równania równowagi dla PSO w naprężeniach:

W

Y K Ł A D Y Z

T

E O R I I

S

P R Ę Ż Y S T O Ś C I

P

ŁASKIE ZADANIA TEORII SPRĘŻYSTOŚCI

Politechnika Poznańska® Kopacz,

Krawczyk,

Łodygowski, Płotkowiak, Świtek, Tymper

8

Równania Beltramiego – Mitchela dla i = j = 3 (p

3

= 0):

k

k

p

x

S

,

2

3

2

33

2

1

1

1

ν

ν

ν

σ

−

−

∂

∂

+

−

=

∇

(6.39)

(

)

(

)

22

11

2

3

2

2

2

33

2

2

33

2

22

11

2

2

σ

σ

σ

σ

σ

σ

+

∂

∂

+

′

∇

=

′

∇

∇

+

′

∇

=

∇

+

+

∇

=

∇

x

S

S

S

S

(6.40)

Z zależności

ε

33

= 0 otrzymujemy

(

)

S

′

=

+

=

ν

σ

σ

ν

σ

22

11

33

(6.41)

Równanie (6.23); po podstawieniu do niego (6.39) i (6.40) przyjmie postać:

(

)

(

)

[

]

k

k

p

x

x

S

,

22

11

22

11

2

3

2

22

11

2

3

2

2

1

1

1

1

1

ν

ν

ν

ν

σ

σ

ν

σ

σ

ν

σ

σ

−

+

−

=

−

−

−

+

+

+

∂

∂

+

−

+

∂

∂

+

′

∇

(6.42)

Po redukcji wyrazów podobnych otrzymamy:

2

2

1

1

,

,

2

1

1

x

p

x

p

p

p

S

k

k

k

k

∂

∂

+

∂

∂

=

−

−

=

′

∇

ν

(6.43)

Uogólniony płaski stan odkształcenia:

0

)

,

(

0

2

1

3

3

3

3

33

≠

=

=

∂

∂

=

x

x

u

u

x

u

ε

(6.44)

W

Y K Ł A D Y Z

T

E O R I I

S

P R Ę Ż Y S T O Ś C I

P

ŁASKIE ZADANIA TEORII SPRĘŻYSTOŚCI

Politechnika Poznańska® Kopacz,

Krawczyk,

Łodygowski, Płotkowiak, Świtek, Tymper

9

6.3. Algorytm rozwiązywania zadań w płaskim stanie w teorii
sprężystości

W naprężeniach:

1)

( )

k

k

p

S

,

2

1

ν

+

−

=

′

∇

(6.45)

Równania Naviera:
2)

0

1

2

21

1

11

=

+

∂

∂

+

∂

∂

p

x

x

σ

σ

(6.46)

3)

0

2

2

22

1

12

=

+

∂

∂

+

∂

∂

p

x

x

σ

σ

(6.47)

Związki fizyczne:
4)

(

)

(

)

(

)

j

i

G

E

E

E

ij

ij

≠

=

+

−

=

−

=

−

=

dla

2

1

1

22

11

33

11

22

22

22

11

11

σ

ε

σ

σ

ν

ε

νσ

σ

ε

νσ

σ

ε

(6.48)

Znając

ε

ij

wyznaczymy u

i

ze wzoru:

(

)

i

j

j

i

ij

u

u

,

,

2

1

+

=

ε

(6.49)

Następnie stwórzmy macierz fizyczną:

W

Y K Ł A D Y Z

T

E O R I I

S

P R Ę Ż Y S T O Ś C I

P

ŁASKIE ZADANIA TEORII SPRĘŻYSTOŚCI

Politechnika Poznańska® Kopacz,

Krawczyk,

Łodygowski, Płotkowiak, Świtek, Tymper

10





















−

⋅

−

=

ν

ν

ν

ν

1

0

0

0

1

0

1

1

2

E

D

(6.50)

Wyznaczmy macierz odwrotną do niej:





















−

−

−

⋅

=

−

ν

ν

ν

1

0

0

0

1

0

1

1

1

E

D

(6.51)

Naprężenia można wyrazić wzorem:

ε

D

σ

⋅

=

(6.52)

Natomiast odkształcenia:

σ

D

ε

⋅

=

−

1

(6.53)

W odkształceniach:

1)

k

k

p

S

,

2

1

1

ν

−

−

=

′

∇

(6.54)

2)

0

1

2

21

1

11

=

+

∂

∂

+

∂

∂

p

x

x

σ

σ

(6.55)

3)

0

2

2

22

1

12

=

+

∂

∂

+

∂

∂

p

x

x

σ

σ

(6.56)

(

)

22

11

33

σ

σ

ν

σ

+

=

(6.57)

W

Y K Ł A D Y Z

T

E O R I I

S

P R Ę Ż Y S T O Ś C I

P

ŁASKIE ZADANIA TEORII SPRĘŻYSTOŚCI

Politechnika Poznańska® Kopacz,

Krawczyk,

Łodygowski, Płotkowiak, Świtek, Tymper

11

4) Związki fizyczne

( )

[

]

( )

[

]

j

i

G

E

E

ij

ij

≠

=

=

−

−

+

=

−

−

+

=

dla

2

0

1

1

1

1

33

11

22

22

22

11

11

σ

ε

ε

νσ

σ

ν

ν

ε

νσ

σ

ν

ν

ε

(6.58)

Macierz fizyczna:

( )(

)





















−

−

−

⋅

−

+

=

ν

ν

ν

ν

ν

ν

ν

2

1

0

0

0

1

0

1

2

1

1

E

D

(6.59)

Macierz odwrotna:





















−

−

−

−

⋅

+

=

−

1

0

0

0

1

0

1

1

1

ν

ν

ν

ν

ν

E

D

(6.60)

Naprężenia można wyrazić wzorem:

ε

D

σ

⋅

=

(6.61)

Natomiast odkształcenia:

σ

D

ε

⋅

=

−

1

(6.62)

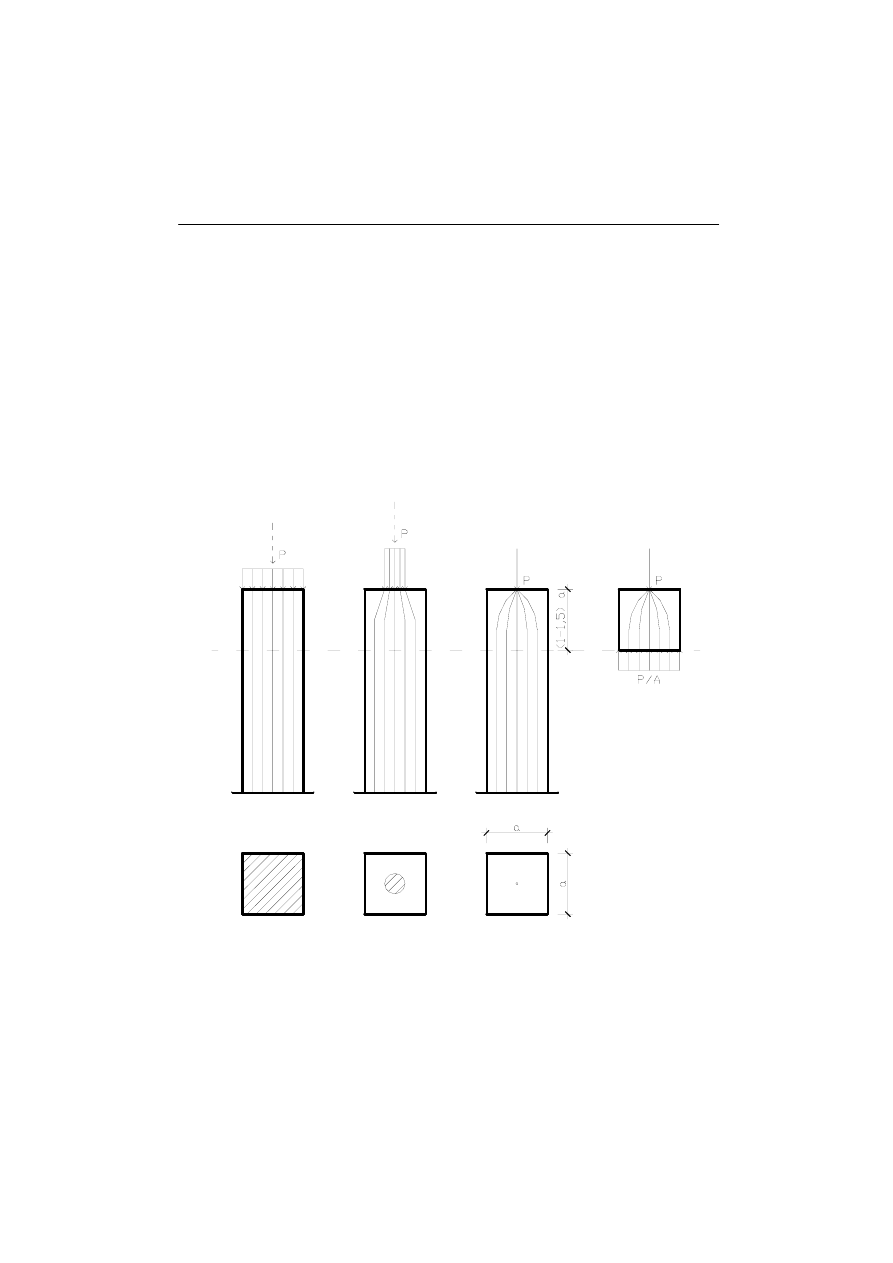
W

Y K Ł A D Y Z

T

E O R I I

S

P R Ę Ż Y S T O Ś C I

P

ŁASKIE ZADANIA TEORII SPRĘŻYSTOŚCI

Politechnika Poznańska® Kopacz,

Krawczyk,

Łodygowski, Płotkowiak, Świtek, Tymper

12

6.4. Zasada de Saint-Venanta:

Aby rozwiązać równania różniczkowe teorii sprężystości musimy mieć warunki
brzegowe wyrażone w

ε

,

σ

i u. W praktycznych zadaniach warunki brzegowe

często określa siła skupiona. Aby przejść od siły do naprężeń stosujemy zasadę
de Saint-Venanta, która brzmi następująco:

„Jeśli dany układ sił działających na niewielki obszar ciała sprężystego
(będącego w stanie równowagi) zastąpimy innym układem statycznie
równoważnym i działającym bezpośrednio na ten obszar, to w odległości od
obszaru przewyższającej znacznie jego rozmiary powstają jednakowe stany
naprężenia, odkształcenia i przemieszczenia.”

σ =

Rys.2. Ilustracja graficzna zasady de Saint-Venanta

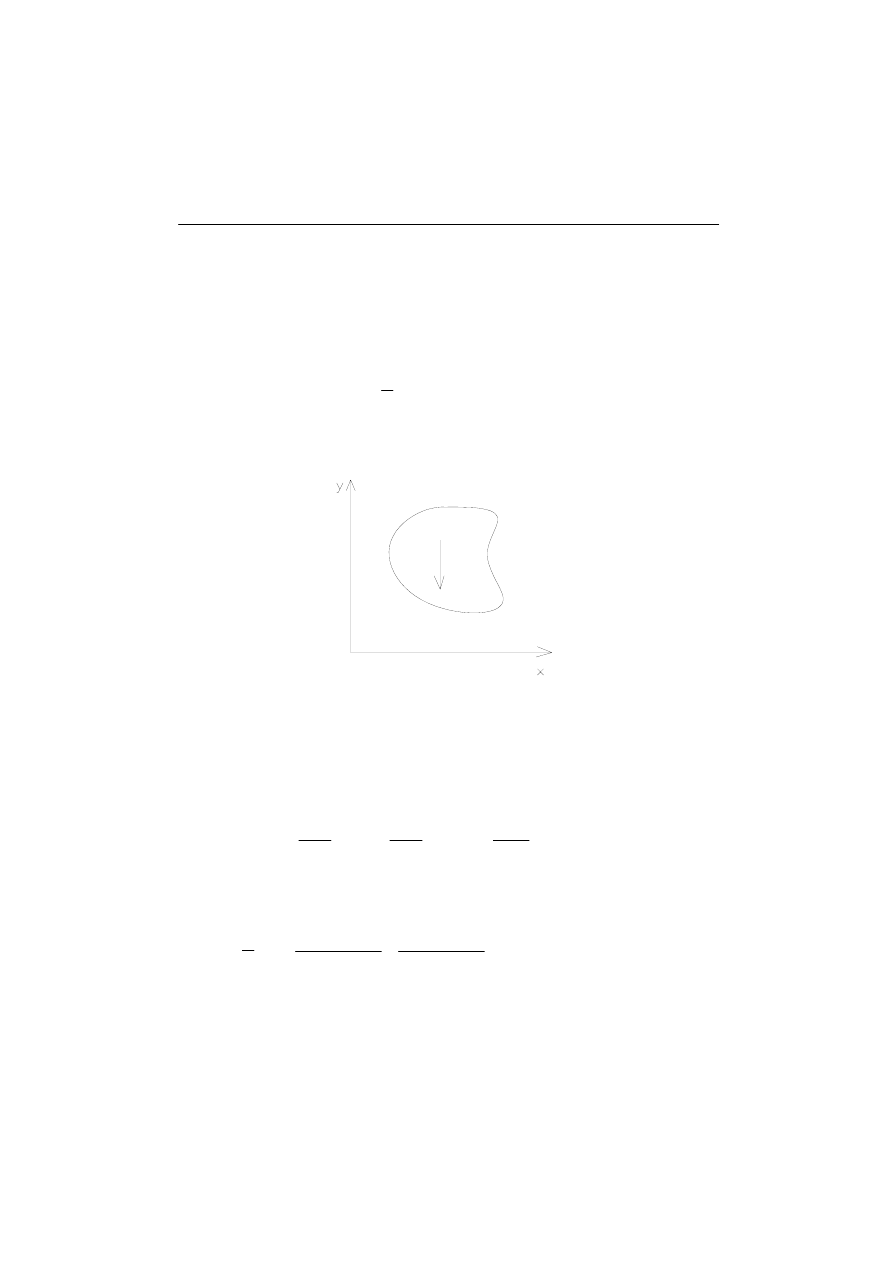
W

Y K Ł A D Y Z

T

E O R I I

S

P R Ę Ż Y S T O Ś C I

P

ŁASKIE ZADANIA TEORII SPRĘŻYSTOŚCI

Politechnika Poznańska® Kopacz,

Krawczyk,

Łodygowski, Płotkowiak, Świtek, Tymper

13

6.5. Rozwiązywanie zadań płaskich teorii sprężystości

Funkcja naprężeń Airy’ego

Rozwiążmy równanie jednorodne (postać ta jest identyczna dla PSN i PSO)

0

2

=

′

∇

S

(6.63)

Przyjmijmy oznaczenia:

σ

11

=

σ

x

,

σ

22

=

σ

y

,

σ

12

=

σ

21

=

τ

xy

=

τ

yx

Rys. 3. Obciążenia masowe działające na ciało

Rozważamy ciało obciążone tylko siłami masowymi (p

1

= 0, p

2

= -g, )

znak „-” wynika z przeciwnego zwrotu sił masowych w stosunku do osi y
Szukamy:

σ

x

,

σ

y

,

τ

xy

Załóżmy istnienie funkcji F(x,y), takiej, że:

gx

y

x

F

x

F

y

F

xy

y

x

+

∂

∂

∂

−

=

∂

∂

=

∂

∂

=

2

2

2

2

2

,

,

τ

σ

σ

(6.64)

Funkcja ta musi spełniać warunki równań podane w PSN

(

) (

)

( )

k

k

y

x

y

x

p

y

x

S

,

2

2

2

2

2

1

ν

σ

σ

σ

σ

+

−

=

∂

+

∂

+

∂

+

∂

=

′

∇

(6.65)

Oraz podane w PSO:

W

Y K Ł A D Y Z

T

E O R I I

S

P R Ę Ż Y S T O Ś C I

P

ŁASKIE ZADANIA TEORII SPRĘŻYSTOŚCI

Politechnika Poznańska® Kopacz,

Krawczyk,

Łodygowski, Płotkowiak, Świtek, Tymper

14

(

) (

)

k

k

y

x

y

x

p

y

x

S

,

2

2

2

2

2

1

1

ν

σ

σ

σ

σ

−

−

=

∂

+

∂

+

∂

+

∂

=

′

∇

(6.66)

Aby obydwa warunki były spełnione jednocześnie musi zachodzić:

0

2

1

2

2

1

1

,

=

∂

∂

+

∂

∂

=

∂

∂

+

∂

∂

=

y

p

x

p

x

p

x

p

p

k

k

(6.67)

0

4

2

2

2

2

2

2

2

2

=

∇

=









∂

∂

+

∂

∂









∂

∂

+

∂

∂

F

y

F

x

F

y

x

(6.68)

Równanie (6.68) oznacza, że funkcja F(x,y) jest funkcją biharmoniczną.
Warunki równowagi:

( )

0

0

0

=

−

+

∂

∂

+

∂

∂

=

+

∂

∂

+

∂

∂

g

y

x

y

x

y

xy

xy

x

σ

τ

τ

σ

(6.69)

Podstawiając (6.64) do (6.69) otrzymamy:

0

0

0

2

3

2

3

2

3

3

=

−

∂

∂

∂

+

+

∂

∂

∂

−

=









+

∂

∂

∂

−

+

∂

∂

∂

g

y

x

F

g

y

x

F

y

x

F

y

x

F

(6.70)

Z powyższego widać, że wszystkie warunki są spełnione.

W

Y K Ł A D Y Z

T

E O R I I

S

P R Ę Ż Y S T O Ś C I

P

ŁASKIE ZADANIA TEORII SPRĘŻYSTOŚCI

Politechnika Poznańska® Kopacz,

Krawczyk,

Łodygowski, Płotkowiak, Świtek, Tymper

15

Przykład zastosowania funkcji Air’ego

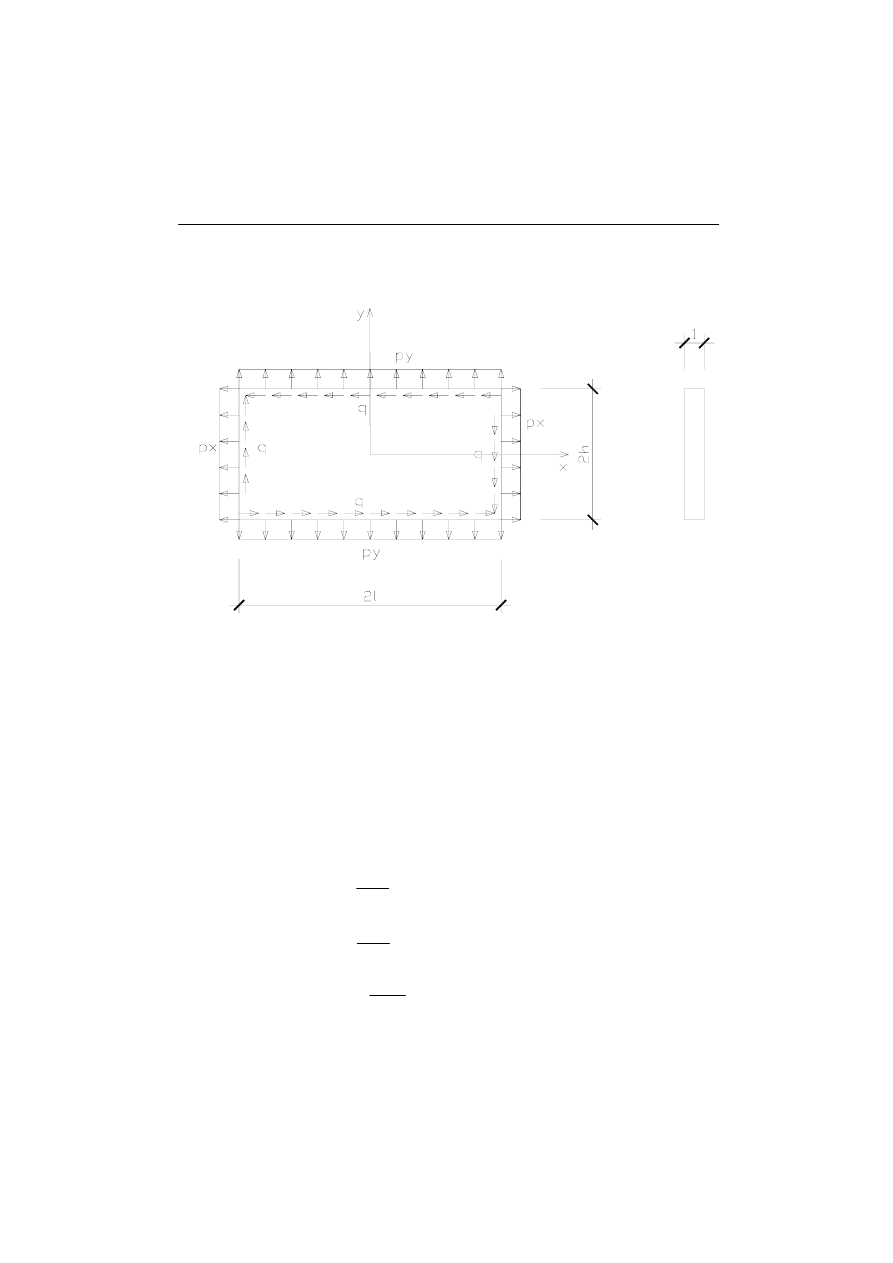
Rys. 4. Płaska tarcza z określonymi warunkami brzegowymi – ilustracja zadania

Naszym zadaniem jest określić stan naprężenia w dowolnym punkcie tarczy.

Rozwiązanie:
Przyjmiemy funkcje F(x,y) w postaci:

( )

2

2

,

Cy

Bxy

Ax

y

x

F

+

+

=

(6.71)

Funkcja jest biharmoniczna, więc spełnia warunki PSN i PSO.
Wyznaczmy naprężenia:

0

2

2

2

2

2

2

2

+

−

=

+

∂

∂

∂

−

=

=

∂

∂

=

=

∂

∂

=

B

gx

y

x

F

A

x

F

C

y

F

xy

y

x

τ

σ

σ

(6.72)

W

Y K Ł A D Y Z

T

E O R I I

S

P R Ę Ż Y S T O Ś C I

P

ŁASKIE ZADANIA TEORII SPRĘŻYSTOŚCI

Politechnika Poznańska® Kopacz,

Krawczyk,

Łodygowski, Płotkowiak, Świtek, Tymper

16

gx = 0, jako że nie podano ciężaru tarczy.
Warunki brzegowe:

q

B

p

A

A

p

h

y

p

C

C

p

l

x

y

y

y

x

x

x

−

=

=

=

=

⇒

±

=

=

=

=

⇒

±

=

2

2

2

2

σ

σ

(6.73)

Po podstawieniu do równań (6.72) otrzymamy ostateczny wynik – wzory na
naprężenia w dowolnym punkcie tarczy:

q

p

p

xy

y

y

x

x

=

=

=

τ

σ

σ

(6.74)