Algorytmy i Struktury Danych

Sortowanie

AGH Krak´

ow

(AGH Krak´

ow)

AISD

1 / 1

Wst ˛ep

Sortowanie

Sortowanie

To jeden z podstawowych problemów informatycznych.

Polega na uporz ˛

adkowaniu zbioru danych wzgl ˛edem pewnych

cech charakterystycznych ka˙zdego elementu tego zbioru, bior ˛

ac

pod wag ˛e warto´s´c

klucza

elementu.

Algorytmy sortowania s ˛

a stosowane w celu uporz ˛

adkowania

danych, umo˙zliwienia stosowania wydajniejszych algorytmów (np.
wyszukiwania) i prezentacji danych w sposób czytelniejszy dla
człowieka.

P.J.Matuszyk (AGH)

AiSD

AGH KISiM 2007

3 / 75

Wst ˛ep

Klasyfikacja metod sortowania

Według

rodzaju sortowanej struktury

:

sortowanie tablic liniowych,

sortowanie list,

Według

miejsca sortowania

(rodzaju pami ˛eci):

zewn ˛etrzne,

wewn ˛etrzne.

Według

zu˙zycia pami ˛eci

:

intensywne (in situ) – nie potrzebuj ˛

a (w zasadzie) dodatkowej

pami ˛eci,

ekstensywne – potrzebuj ˛

a pami ˛eci pomocniczej

Według

stabilno´sci

:

czy dokonuje zb ˛ednych przestawie ´n, czy utrzymuj ˛

a kolejno´s´c

wyst ˛epowania dla elementów o tym samym kluczu.

P.J.Matuszyk (AGH)

AiSD

AGH KISiM 2007

4 / 75

Wst ˛ep

Klasyfikacja metod sortowania

Według

ilo´sci etapów

algorytmu sortuj ˛

acego:

jednoetapowe (bezpo´srednie) – w zasadzie nie potrzebuj ˛

a

dodatkowej pami ˛eci;
dwuetapowe (po´srednie):

etap logiczny – nie przestawia rekordów, ale zdobywa informacje n/t

ustawienia rekordów i zapisuje je w pewien sposób,

etap fizyczny (nie zawsze potrzebny);

Według

efektywno´sci

:

proste (do krótkich plików) —- O(n

2

)

,

szybkie —- O(n log n).

http://www.cs.ubc.ca/ harrison/Java/sorting-demo.html

P.J.Matuszyk (AGH)

AiSD

AGH KISiM 2007

5 / 75

Wst ˛ep

Klasyfikacja metod sortowania

Czy u˙zywaj ˛

a

tylko operacji porównania

(<, >, 6, >)?

Comparison sort

u˙zywa jedynie

relacji porównania

(porz ˛

adek liniowy),

zło˙zono´s´c najlepszego
przypadku:

Ω(

n log n)

.

Non-comparison sort

u˙zywa tak˙ze innych cech
sortowanego ci ˛

agu,

zło˙zono´s´c najlepszego
przypadku:

Ω(

n)

.

Ci ˛

ag n ró˙znych elementów — tylko jedna z n! permutacji odpowiada

posortowanemu ci ˛

agowi.

Je˙zeli algorytm posortuje ci ˛

ag po f (n) krokach, to nie mo˙ze rozró˙zni´c wi ˛ecej ni˙z

2

f (n)

przypadków (porównanie daje w wyniku jedn ˛

a z dwóch odpowiedzi). A

zatem:

2

f (n)

> n!

⇒

f (n) > log(n!) = Ω(n log n)

Ostatnie oszacowanie na podstawie wzoru Stirlinga:

n! ≈

n
e

n

√

2πn

P.J.Matuszyk (AGH)

AiSD

AGH KISiM 2007

6 / 75

Proste sortowanie

Sortowanie b ˛

abelkowe

Sortowanie b ˛

abelkowe (bubble-sort)

Algorytm kontroli monotoniczno´sci: sprawdzanie monotoniczno´sci
kolejnych s ˛

asiednich n − 1 par.

Po jednym przebiegu wyprowadza rekord z najwy˙zszym
(najni˙zszym) kluczem.
W kolejnych przebiegach brana pod uwag ˛e tylko nieposortowana
cz ˛e´s´c pliku.

4|2|5|1|7 -> 2|4|5|1|7 -> 2|4|5|1|7 -> 2|4|1|5|7

^-^

^-^

^-^

^-^

2|4|1|5|7 -> 2|4|1|5|7 -> 2|1|4|5|7

^-^

^-^

^-^

2|1|4|5|7 -> 1|2|4|5|7

^-^

^-^

1|2|4|5|7

^-^

P.J.Matuszyk (AGH)

AiSD

AGH KISiM 2007

8 / 75

Proste sortowanie

Sortowanie b ˛

abelkowe

Sortowanie b ˛

abelkowe (bubble-sort)

Ci ˛

agła kontrola monotoniczno´sci → zmienna logiczna:

Przed ka˙zdym przebiegiem:

false

, po przestawieniu:

true

.

Je´sli

true

, to sortuj dalej, je´sli nie —- zako ´ncz.

Wariant wahadłowy (cocktail-sort) –– ze "zderzakami":
przebiegi na przemian: raz od lewej, raz od prawej.

W zderzakach informacja, gdzie nast ˛

apiło przestawienie —-

przegl ˛

ad w przeciwnym kierunku zaczynamy od tego miejsca i tak

a˙z do dotkni ˛ecia si ˛e zderzaków.

Procedura pomocnicza:

template

<

typename

T>

void

swap(T& x, T& y) {

T z(x);

x = y;

y = z;

}

P.J.Matuszyk (AGH)

AiSD

AGH KISiM 2007

9 / 75

Proste sortowanie

Sortowanie b ˛

abelkowe

Sortowanie b ˛

abelkowe (bubble-sort)

template

<

typename

T>

void

bubble_sort(T* arr,

long

n) {

long

i = -1, j;

bool

if_swap;

do

{

if_swap =

false

;

for

(++i, j = n - 1; j > i; --j) {

if

(arr[j] < arr[j - 1]) {

swap(arr[j], arr[j - 1]);

// zamiana

if_swap =

true

;

}

}

while

(if_swap);

}

P.J.Matuszyk (AGH)

AiSD

AGH KISiM 2007

10 / 75

Proste sortowanie

Sortowanie b ˛

abelkowe

Sortowanie b ˛

abelkowe (bubble-sort)

Własno´sci

Zło˙zono´s´c pami ˛eciowa: O(1),
Zło˙zono´s´c obliczeniowa:

najlepszego przypadku: O(n)
gdy tablica jest wst ˛epnie posortowana,
najgorszego przypadku: O(n

2

)

(n

2

/

2 porówna ´n, 3/2n

2

podstawie ´n)

gdy tablica jest wst ˛epnie odwrotnie posortowana.

P.J.Matuszyk (AGH)

AiSD

AGH KISiM 2007

11 / 75

Proste sortowanie

Sortowanie przez wstawianie

Sortowanie przez wstawianie (insert-sort) [Steinhaus,
1958]

Pierwszy krok

: podział na cz ˛e´s´c posortowan ˛

a i nieposortowan ˛

a:

pusta i cała tablica lub
pierwszy rekord i reszta lub
pewna naturalnie posortowana cz ˛e´s´c i reszta.

Kolejne kroki

→ p ˛etla:

pobranie rekordu (np. pierwszego lepszego) i wstawienie go do
posortowanej cz ˛e´sci tablicy.

Sposób przegl ˛

adania cz ˛e´sci posortowanej

:

sekwencyjne przegl ˛

adanie cz ˛e´sci posortowanej od prawej strony

(stabilno´s´c, natychmiastowe przestawienie rekordu),
przeszukiwanie binarne.

P.J.Matuszyk (AGH)

AiSD

AGH KISiM 2007

12 / 75

Proste sortowanie

Sortowanie przez wstawianie

Sortowanie przez wstawianie (insert-sort)

Zalety:

u˙zyteczny dla tablic do 10 elementów,
wydajny dla danych wst ˛epnie posortowanych: O(n + d ), gdzie d to
ilo´s´c inwersji,
stabilny.

5|2|7|1|4

2: 5|*|7|1|4 -> 2|5|7|1|4
^--^

7: 2|5|*|1|4 -> 2|5|7|1|4
^----^

1: 2|5|7|*|4 -> 2|5|*|7|4 -> 2|*|5|7|4 -> 1|2|5|7|4
^------^

-----^

---^

4: 1|2|5|7|4 -> 1|2|5|*|7 -> 1|2|*|5|7 -> 1|2|4|5|7
^--------^

-------^

-----^

P.J.Matuszyk (AGH)

AiSD

AGH KISiM 2007

13 / 75

Proste sortowanie

Sortowanie przez wstawianie

Sortowanie przez wstawianie (insert-sort)

template

<

typename

T>

void

insert_sort(T* arr,

long

n) {

T x;

for

(

long

j = 1, i; j < n; ++j){

x = arr[j];

//wstaw arr[j] w posortowany ci ˛

ag arr[0..j-1];

for

(i = j - 1; i >= 0 && x < arr[i]; --i)

arr[i + 1] = arr[i];

arr[i + 1] = x;

}

}

Zło˙zono´s´c pami ˛eciowa: O(1),
Zło˙zono´s´c obliczeniowa:

przypisania: ´srednia O(n + d ), najgorszego przypadku O(n

2

)

,

porównania: ´srednia O(n + d ), najgorszego przypadku O(n

2

)

.

P.J.Matuszyk (AGH)

AiSD

AGH KISiM 2007

14 / 75

Proste sortowanie

Sortowanie przez selekcj ˛e

Sortowanie przez selekcj ˛e (wybieranie) (select-sort)

Pierwszy krok

: podział na cz ˛e´s´c posortowan ˛

a i nieposortowan ˛

a.

Kolejne kroki

→ p ˛etla:

wyszukujemy (w cz ˛e´sci nieposortowanej) rekord do przestawienia
(najcz ˛e´sciej z kluczem najmniejszym),
rekord ten mo˙zna zamieni´c z lewym nieposortowanym rekordem
(ale narusza to stabilno´s´c).

U˙zyteczny do 20 elementów.

Niestabilny; aby uczyni´c go stabilnym nale˙zy zamieni´c w warunku
wyszukiwania nierówno´s´c ostr ˛

a na nieostr ˛

a.

P.J.Matuszyk (AGH)

AiSD

AGH KISiM 2007

15 / 75

Proste sortowanie

Sortowanie przez selekcj ˛e

Sortowanie przez selekcj ˛e (select-sort)

|9,1,6,8,4,3,2,0 -> 0|1,6,8,4,3,2,9

^

^-------------^

0|1,6,8,4,3,2,9 -> 0,1|6,8,4,3,2,9

^

0,1|6,8,4,3,2,9 -> 0,1,2|8,4,3,6,9

^

^-------^

0,1,2|8,4,3,6,9 -> 0,1,2,3|4,8,6,9

^

^---^

0,1,2,3|4,8,6,9 -> 0,1,2,3,4|8,6,9

^

0,1,2,3,4|8,6,9 -> 0,1,2,3,4,6|8,9

^

^-^

0,1,2,3,4,6|8,9 -> 0,1,2,3,4,6,8|9

^

P.J.Matuszyk (AGH)

AiSD

AGH KISiM 2007

16 / 75

Proste sortowanie

Sortowanie przez selekcj ˛e

Sortowanie przez selekcj ˛e (wybieranie) (select-sort)

template

<

typename

T>

void

select_sort(T* arr,

long

n) {

for

(

long

i = 0, min_i, j; i < n - 1; ++i) {

for

(min_i = i, j = i + 1; j < n; ++j)

if

(arr[j] < arr[min_i])

min_i = j;

if

(min_i != i)

swap(arr[min_i], arr[i]);

}

}

Ilo´s´c operacji podstawienia: zawsze 3(n − 1).

Ilo´s´c operacji porównania: zawsze Θ(n

2

)

.

P.J.Matuszyk (AGH)

AiSD

AGH KISiM 2007

17 / 75

Proste sortowanie

Sortowanie grzebieniowe

Sortowanie grzebieniowe (comb-sort)

Uogólnienie metody b ˛

abelkowej:

za rozpi ˛eto´s´c r przyjmij długo´s´c tablicy n, podziel rozpi ˛eto´s´c przez

1.24733095 . . .

(w praktyce 1.3), odrzu´c cz ˛e´s´c ułamkow ˛

a;

badaj kolejno wszystkie pary obiektów odległych o rozpi ˛eto´s´c r
(je´sli s ˛

a uło˙zone niemonotonicznie — zamie ´n miejscami);

wykonuj powy˙zsze w p ˛etli dziel ˛

ac rozpi ˛eto´s´c przez 1.3 do czasu,

gdy rozpi ˛eto´s´c osi ˛

agnie warto´s´c 1.

Gdy rozpi ˛eto´s´c spadnie do 1 metoda zachowuje si ˛e tak jak
sortowanie b ˛

abelkowe.

Tylko wtedy mo˙zemy okre´sli´c, czy dane s ˛

a ju˙z posortowane czy

nie.
W tym celu mo˙zemy u˙zy´c zmiennej typu

bool

, która jest

ustawiana po zamianie elementów tablicy miejscami.

P.J.Matuszyk (AGH)

AiSD

AGH KISiM 2007

18 / 75

Proste sortowanie

Sortowanie grzebieniowe

Sortowanie grzebieniowe (comb-sort)

Combsort11

:

najkorzystniejsza warto´s´c rozpi ˛eto´sci to 11,
je˙zeli obliczona rozpi ˛eto´s´c wynosi 9 lub 10 –– zamieniamy j ˛

a na 11,

zysk ok. 20%,
potrzebna specjalna uwaga dla tablic wst ˛epnie posortowanych,
w praktyce metoda nieznacznie wolniejsza od quick-sort!

Zło˙zono´s´c obliczeniowa: prawdopodobnie O(n log n).

Metoda niestabilna.

P.J.Matuszyk (AGH)

AiSD

AGH KISiM 2007

19 / 75

Proste sortowanie

Sortowanie grzebieniowe

Sortowanie grzebieniowe (comb-sort)

6,7,9,3,2,5

// n = 6 -> r=4

6,7,9,3,2,5 -> 2,7,9,3,6,5 -> 2,5,9,3,6,7

^-------^

^-------^

// r = 3

2,5,9,3,6,7 -> 2,5,9,3,6,7 -> 2,5,9,3,6,7 -> 2,5,7,3,6,9

^-----^

^-----^

^-----^

// r = 2

2,5,7,3,6,9 -> 2,5,7,3,6,9 -> 2,3,7,5,6,9 -> 2,3,6,5,7,9

^---^

^---^

^---^

^---^

// r = 1

2,3,6,5,7,9 -> 2,3,6,5,7,9 -> 2,3,6,5,7,9 -> 2,3,5,6,7,9

^-^

^-^

^-^

^-^

P.J.Matuszyk (AGH)

AiSD

AGH KISiM 2007

20 / 75

Proste sortowanie

Sortowanie grzebieniowe

Sortowanie grzebieniowe (comb-sort)

inline long

newGap(

long

gap) {

gap = (gap * 10) / 13;

if

(gap == 9 || gap == 10) gap = 11;

return

(gap > 1) ? gap : 1;

}

template

<

typename

T>

void

comb_sort(T* arr,

long

n) {

long

gap = n;

do

{

gap = newGap(gap);

for

(

long

i = 0, j; i < n - gap; ++i) {

j = i + gap;

if

(arr[i] > arr[j])

swap(arr[i], arr[j]);

}

}

while

(gap > 1);

bubble_sort(arr, n);

}

P.J.Matuszyk (AGH)

AiSD

AGH KISiM 2007

21 / 75

Proste sortowanie

Sortowanie Shella

Sortowanie Shella (Shell-sort) [Shell, 1959]

Uogólnienie sortowania przez wstawianie; dwie obserwacje:

sortowanie przez wstawianie jest efektywne dla tablic "prawie"
posortowanych,
sortowanie przez wstawianie jest nieefektywne poniewa˙z przesuwa
elementy o jedn ˛

a pozycj ˛e.

Idea:

sortowany zbiór dzielimy na podzbiory, których elementy s ˛

a odległe

od siebie w sortowanym zbiorze o pewien odst ˛ep h,
ka˙zdy z tych podzbiorów sortujemy alg. przez wstawianie,
nast ˛epnie odst ˛ep zmniejszamy — powoduje to powstanie nowych
podzbiorów (b ˛edzie ich ju˙z mniej),
sortowanie powtarzamy i znów zmniejszamy odst ˛ep, a˙z osi ˛

agnie on

warto´s´c 1 — wtedy: insert-sort.

P.J.Matuszyk (AGH)

AiSD

AGH KISiM 2007

22 / 75

Proste sortowanie

Sortowanie Shella

Sortowanie Shella (Shell-sort)

Generacja ci ˛

agu odst ˛epów h

i

wg

Knutha

→

O(n

1.15

)

(?):

h

1

=

1, obliczamy h

k

=

3h

k −1

+

1 do momentu a˙z h

k

> n, wtedy

h = h

k

/

9

ka˙zdy odst ˛ep w nowej iteracji i wynosi h

i

=

h

i−1

/

3

1, 4, 13, 40, 121, 364, . . .

wg

Hibbarda

→

O(n

1.5

) = O(

n

√

n):

h

i

=

2

i

− 1, czyli: 1, 3, 7, 15, 31, . . .

wg

Pratta

→

O(n log

2

n):

h

i

=

2

p

3

q

, czyli: 1 2 3 4 6 9 8 12 18 27 16 24 36 54 81 :. . .

wg

Segedwicka

→

O(n

4/3

)

:

h

i

=

9(4

i

− 2

i

) +

1 lub

h

i

=

4

i+1

+

3 · 2

i

+

1, czyli: 1, 8, 23, 77, 281, 1073, . . .

wg

Incerpi-Segedwicka

:

h

i

=

2

i+5

− 7 dla i = 2, 3 oraz h

i

=

2

i+5

− 45 dla i = 4 . . . 9

→

O(n

1+1/i

)

h

i

= α

p

(

1 + α)

q

→

O(n

1+ε/ log n

)

wg

Marcina Ciury

(najlepszy znany ci ˛

ag):

1, 4, 10, 23, 57, 132, 301, 701, kolejne: ×2.3.

P.J.Matuszyk (AGH)

AiSD

AGH KISiM 2007

23 / 75

Proste sortowanie

Sortowanie Shella

Sortowanie Shella (Shell-sort)

6,7,9,3,2,5

// n = 6 -> r=4

6,7,9,3,2,5 -> 2,7,9,3,6,5 -> 2,5,9,3,6,7

^-------^

^-------^

// r = 3

2,5,9,3,6,7 -> 2,5,9,3,6,7 -> 2,5,9,3,6,7 -> 2,5,7,3,6,9

^-----^

^-----^

^-----^

// r = 2

2,5,7,3,6,9 -> 2,5,7,3,6,9 -> 2,3,7,5,6,9 -> 2,3,6,5,7,9

^---^

^---^

^---^---^

^---^---^

// r = 1

2,3,6,5,7,9 -> 2,3,6,5,7,9 -> 2,3,6,5,7,9 -> 2,3,5,6,7,9

^-^

^-^

^-^

^-^

P.J.Matuszyk (AGH)

AiSD

AGH KISiM 2007

24 / 75

Proste sortowanie

Sortowanie Shella

Sortowanie Shella (Shell-sort)

// wg Knutha

template

<

typename

T>

void

shell_sort(T arr[],

long

n) {

long

h;

for

(h = 1; h < n; h = 3 * h + 1);

h /= 9;

if

(!h) h++;

T x;

for

(

long

i, j; h > 0; h /= 3) {

for

(j = h; j < n; ++j){

x = arr[j];

for

(i = j - h; i >= 0 && x < arr[i]; i -= h)

arr[i + h] = arr[i];

arr[i + h] = x;

}

}

}

P.J.Matuszyk (AGH)

AiSD

AGH KISiM 2007

25 / 75

Szybkie metody sortowania

Metody szybkie sortowania wykorzystuj ˛

ace

porównania

Metody szybkie

maj ˛

a asymptotycznie

optymaln ˛

a

zło˙zono´s´c obliczeniow ˛

a, która wynosi

O(n log n)

P.J.Matuszyk (AGH)

AiSD

AGH KISiM 2007

27 / 75

Szybkie metody sortowania

Sortowanie przez scalanie

Sortowanie przez scalanie (merge-sort)

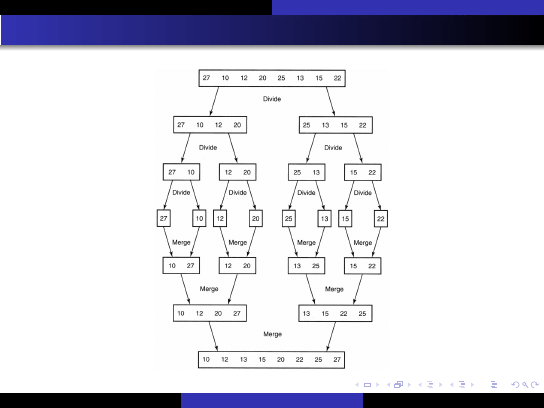
Algorytm oparty jest na metodzie "dziel i zwyci ˛e˙zaj".

Tablica jest dzielona na podtablice, licz ˛

ace po n/2 elementów;

Sortujemy ka˙zd ˛

a tablic ˛e rekurencyjnie.

Scalanie podtablic w jedn ˛

a posortowan ˛

a tablic ˛e.

template

<

typename

T>

void

merge_sort(T arr[],

int

n) {

const int

g = n/2, h = n - g;

vector<T> U(g), V(h);

copy(arr, 0, g, U);

copy(arr, g, n, V);

merge_sort(U, g);

merge_sort(V, h);

merge(arr, U, V, g, h);

}

P.J.Matuszyk (AGH)

AiSD

AGH KISiM 2007

28 / 75

Szybkie metody sortowania

Sortowanie przez scalanie

Sortowanie przez scalanie (merge-sort)

P.J.Matuszyk (AGH)

AiSD

AGH KISiM 2007

29 / 75

Szybkie metody sortowania

Sortowanie przez scalanie

Procedura scalania

template

<

typename

T>

void

merge(T arr[], T U[], T V[],

int

g,

int

h) {

int

i = 0, j = 0, k = 0;

for

(; i < g && j < h; ++k)

if

(U[i] < V[j])

arr[k] = U[i++];

else

arr[k] = V[j++];

if

(i > g)

copy(arr[k..h+g], V[j..h])

else

copy(arr[k..h+g], U[i..g])

}

P.J.Matuszyk (AGH)

AiSD

AGH KISiM 2007

30 / 75

Szybkie metody sortowania

Sortowanie przez scalanie

Sortowanie przez scalanie (merge-sort)

Zło˙zono´s´c pami ˛eciowa: potrzeba dodatkowo tablice o rozmiarze
2n,

Zło˙zono´s´c obliczeniowa: O(n log n).

P.J.Matuszyk (AGH)

AiSD

AGH KISiM 2007

31 / 75

Szybkie metody sortowania

Sortowanie kopcowe

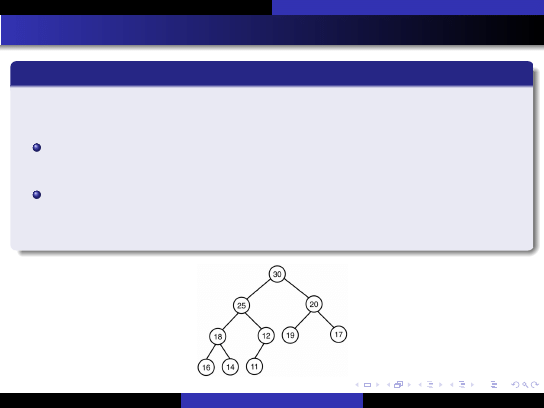
Kopiec (sterta)(heap)

Kopcem (stogiem)

nazywamy cz ˛e´sciowo pełne drzewo binarne spełniaj ˛

ace nast ˛epuj ˛

ace

warunki:

warto´sci przechowywane w w ˛ezłach nale˙z ˛

a do zbioru

uporz ˛

adkowanego,

(

własno´s´c kopca

) warto´s´c przechowywana w ka˙zdym w ˛e´zle jest

wi ˛eksza lub równa warto´sciom przechowywanym w jego w ˛ezłach
potomnych.

P.J.Matuszyk (AGH)

AiSD

AGH KISiM 2007

32 / 75

Szybkie metody sortowania

Sortowanie kopcowe

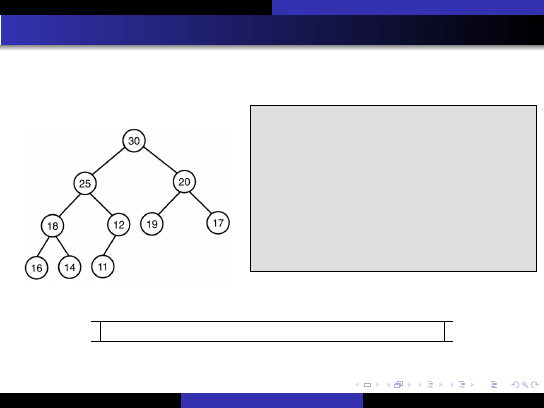
Reprezentacja tablicowa kopca

Zakładamy indeksacj ˛e tablicy od 1!

inline long

father(

long

son) {

return

son >> 1;

}

inline long

lson(

long

father) {

return

father << 1;

}

inline long

rson(

long

father) {

return

father << 1 + 1;

}

1

2

3

4

5

6

7

8

9

10

30

25

20

18

12

19

17

16

14

11

P.J.Matuszyk (AGH)

AiSD

AGH KISiM 2007

33 / 75

Szybkie metody sortowania

Sortowanie kopcowe

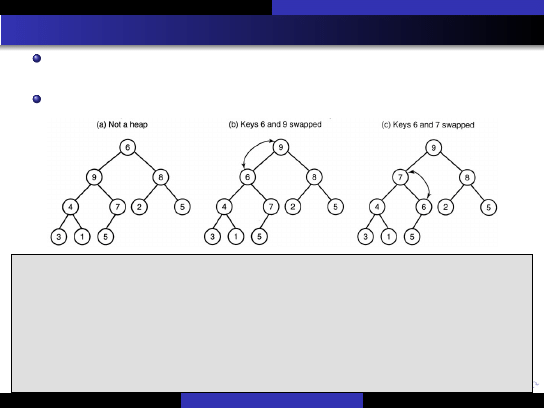
Przywracanie własno´sci kopca (bottom-up)

Zało˙zenie: poddrzewa o korzeniach

lson(i)

oraz

rson(i)

s ˛

a

kopcami, ale drzewo o korzeniu

i

nie jest kopcem.

Procedura

siftdown

(przesiewanie w dół) O(log n):

template

<

typename

T>

void

siftdown(T* arr,

long

i,

long

n) {

for

(

long

l = i << 1; l <= n; i = l, l = i << 1) {

if

(l + 1 <= n && arr[l + 1] > arr[l])

++l;

if

(arr[i] >= arr[l])

return

;

swap(arr[i], arr[l]);

}

}

P.J.Matuszyk (AGH)

AiSD

AGH KISiM 2007

34 / 75

Szybkie metody sortowania

Sortowanie kopcowe

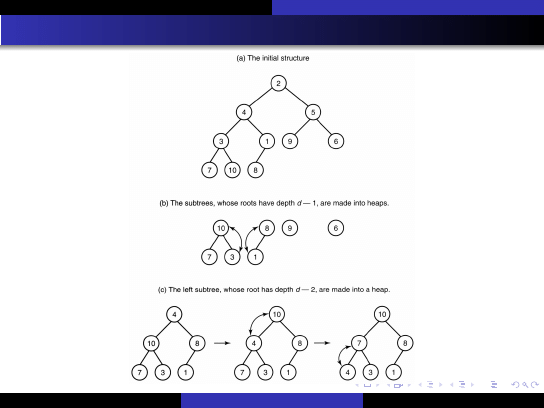
Budowanie kopca z tablicy (bottom-up)

P.J.Matuszyk (AGH)

AiSD

AGH KISiM 2007

35 / 75

Szybkie metody sortowania

Sortowanie kopcowe

Budowanie kopca z tablicy (bottom-up)

Li´scie s ˛

a ju˙z jednoelementowymi kopcami.

Zaczynamy przywraca´c własno´s´c kopca dla w ˛ezłów nie b ˛ed ˛

acych

li´s´cmi, zaczynaj ˛

ac od najni˙zszego poziomu.

template

<

typename

T>

void

buildheapBU(T* arr,

long

n) {

for

(

long

i = n >> 1; i; --i)

siftdown(arr, i, n);

}

czas działania

siftdown

zale˙zy od wysoko´sci h w ˛ezła i.

w n-elementowym kopcu jest co najwy˙zej dn/2

h

e w ˛ezłów o

wysoko´sci h (licz ˛

ac od dołu, dla li´sci h = 1),

czas działania

siftdown

dla w ˛ezła o wysoko´sci h jest O(h), a

zatem dla w ˛ezłów i ∈ [1, n/2]:

log n

X

h=0

O(h)

n

2

h

=

n

log n

X

h=0

O(h)

2

h

= O(

n)

bo

∞

X

i=0

i

2

i

=

2

P.J.Matuszyk (AGH)

AiSD

AGH KISiM 2007

36 / 75

Szybkie metody sortowania

Sortowanie kopcowe

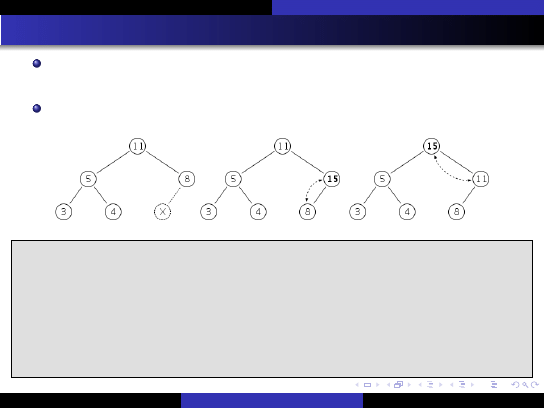
Przywracanie własno´sci kopca (top-down)

Zało˙zenie: drzewo o korzeniu

1

i

n

elementach jest kopcem; na

pozycj ˛e

n + 1

dodajemy nowy element.

Procedura

siftup

(przesiewanie w gór ˛e) O(log n):

template

<

typename

T>

void

siftup(T* arr,

long

i) {

for

(

long

f; i > 1; i = f) {

f = i >> 1;

// father

if

(arr[f] >= arr[i])

return

;

swap(arr[f], arr[i]);

}

}

P.J.Matuszyk (AGH)

AiSD

AGH KISiM 2007

37 / 75

Szybkie metody sortowania

Sortowanie kopcowe

Budowanie kopca z tablicy (top-down)

Na pocz ˛

atku kopiec zawiera tylko pierwszy element tablicy

(rozmiar kopca = 1).

Dokładamy do kopca o rozmiarze n kolejny n + 1-y element tablicy.

template

<

typename

T>

void

buildheapTD(T* arr,

long

n) {

for

(

long

i = 2; i <= n; ++i)

siftup(arr, i);

}

czas działania

buildheapTD

jest rz ˛edu O(n).

P.J.Matuszyk (AGH)

AiSD

AGH KISiM 2007

38 / 75

Szybkie metody sortowania

Sortowanie kopcowe

Sortowanie kopcowe (heap-sort) [Floyd, Williams,
1964]

template

<

typename

T>

void

heap_sort(T* arr,

long

n) {

--arr;

// teraz indeks 1 pokazuje na element 0 !

buildheapXX(arr, n);

while

(n > 1) {

// przenosimy max. elem. na koniec kopca

swap(arr[1], arr[n]);

// przywracamy własno´

s´

c kopca dla

// mniejszego kopca

siftdown(arr, 1, --n);

}

}

Zło˙zono´s´c obliczeniowa: O(n log n)
bo n − 1 wywoła ´n procedury

siftdown

+ O(n) na budowe kopca.

P.J.Matuszyk (AGH)

AiSD

AGH KISiM 2007

39 / 75

Szybkie metody sortowania

Sortowanie kopcowe

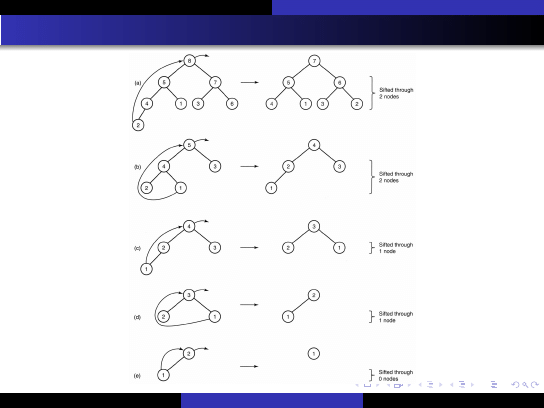
Sortowanie kopcowe (heap-sort)

P.J.Matuszyk (AGH)

AiSD

AGH KISiM 2007

40 / 75

Szybkie metody sortowania

Sortowanie kopcowe

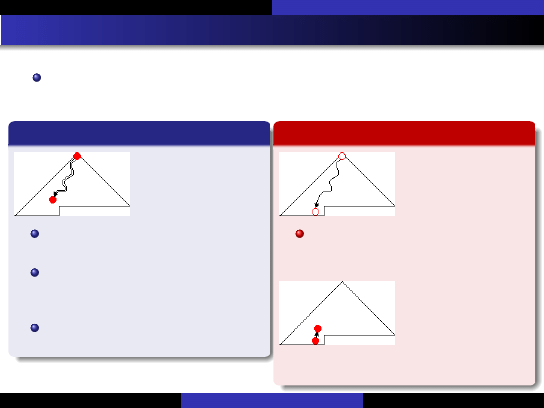
Bottom-up heap-sort [Wegner, 1993]

Mo˙zna zmniejszy´c liczb ˛e porówna ´n i podstawie ´n w algorytmie heapsort,
zyskuj ˛

ac ok. 25% wydajno´sci.

Wersja klasyczna

siftdown

W korzeniu jest na pocz ˛

atku mały

element.

Na ka˙zdym poziomie porównujemy,
który syn jest wi ˛ekszy i zamieniamy
go z ojcem: (4<, 3=).

Z du˙zym prawdopodobie ´nstwem
element ten "spłynie" na dół.

Wersja bottom-up

moveup

Po usuni ˛eciu korzenia, przesuwamy
do góry najwi ˛ekszych synów: (2<,
1=).

siftup

W wolne

miejsce wstawiamy usuni ˛ety element i
przesiewamy go w gór ˛e: (2<, 3=).

P.J.Matuszyk (AGH)

AiSD

AGH KISiM 2007

41 / 75

Szybkie metody sortowania

Sortowanie kopcowe

Bottom-up heap-sort

template

<

typename

T>

long

moveup(T* arr,

long

n) {

long

i = 1, l = 2;

for

(; l + 1 <= n; i = l, l = i << 1) {

if

(arr[l + 1] > arr[l])

++l;

arr[i] = arr[l];

}

if

(l <= n) {

arr[i] = arr[l];

return

l;

}

return

i;

}

P.J.Matuszyk (AGH)

AiSD

AGH KISiM 2007

42 / 75

Szybkie metody sortowania

Sortowanie kopcowe

Bottom-up heap-sort [Wegner, 1993]

template

<

typename

T>

void

heap_sort(T* arr,

long

n) {

buildheapXX(--arr, n);

T x;

for

(

long

hole; n > 1;) {

x = arr[n];

arr[n] = arr[1];

hole = moveup(arr, --n);

arr[hole] = x;

siftup(arr, hole);

}

}

P.J.Matuszyk (AGH)

AiSD

AGH KISiM 2007

43 / 75

Szybkie metody sortowania

Sortowanie szybkie

Sortowanie szybkie (quick-sort) [Hoare, 1962]

Algorytm oparty jest na metodzie "dziel i zwyci ˛e˙zaj".

Tablica T[l..r] jest dzielona na dwie niepuste tablice: T[l..q] i
T[q+1..r] takie, ˙ze ka˙zdy element T[l..q] jest nie wi ˛ekszy od
ka˙zdego elementu T[q+1..r].

Indeks q jest obliczany przez procedur ˛e dziel ˛

ac ˛

a

partition

.

Dwie tablice s ˛

a sortowane rekurencyjnie.

Scalanie (kombinowanie) rozwi ˛

aza ´n nie jest konieczne, bo tablice

s ˛

a sortowane w miejscu.

template

<

typename

T>

void

quick_sort(T* arr,

long

l,

long

r) {

if

(l < r) {

long

p = partition(arr, l, r);

quick_sort(arr, l, p - 1);

quick_sort(arr, p + 1, r);

}

}

P.J.Matuszyk (AGH)

AiSD

AGH KISiM 2007

44 / 75

Szybkie metody sortowania

Sortowanie szybkie

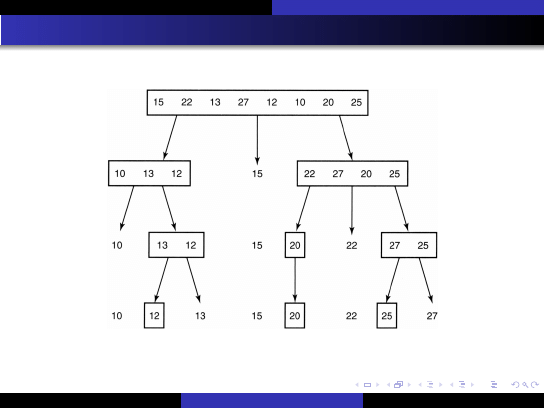
Sortowanie szybkie (quick-sort)

P.J.Matuszyk (AGH)

AiSD

AGH KISiM 2007

45 / 75

Szybkie metody sortowania

Sortowanie szybkie

Procedura

partition

Niezmiennik podziału tablicy

A

:

i

x

l

r

<= x

> x

?

n (= l)

Przegl ˛

adamy tablic ˛e od lewej do prawej, u˙zywaj ˛

ac zmiennych

i

oraz

n

dla zachowania powy˙zszego niezmiennika.

Po sprawdzeniu n-tego elementu mamy dwa przypadki:

A[n] > x

— w porz ˛

adku, idziemy dalej;

A[n] <= x

— przywracamy przwdziwo´s´c niezmiennika przez:

zwi ˛ekszenie warto´sci i i zamian ˛e miejscami elementów A[n] oraz
A[i]

na koniec, zamieniamy miejscami

A[r]

z

A[m + 1]

.

P.J.Matuszyk (AGH)

AiSD

AGH KISiM 2007

46 / 75

Szybkie metody sortowania

Sortowanie szybkie

Procedura

partition

template

<

typename

T>

long

partition(T* A,

long

l,

long

r){

T x = A[r];

long

i = l - 1;

for

(; l < r; ++l)

if

(A[l] <= x)

swap(A[++i], A[l]);

swap(A[i + 1], A[r]);

return

i + 1;

}

Zło˙zono´s´c obliczeniowa procedury

part

: O(n)

-1 0 1 2 3 4 5 6 7

2 8 7 1 3 5 6

4

2

8 7 1 3 5 6

4

2

8

7 1 3 5 6

4

2

8 7

1 3 5 6

4

2 1

7 8

3 5 6

4

2 1 3

8 7

5 6

4

2 1 3

8 7 5

6

4

2 1 3

8 7 5 6

4

2 1 3

4

7 5 6 8

Procedura ta zachowa si ˛e ´zle w przypadku identycznych
elementów lub tablicy wst ˛epnie posortowanej.

P.J.Matuszyk (AGH)

AiSD

AGH KISiM 2007

47 / 75

Szybkie metody sortowania

Sortowanie szybkie

Sortowanie szybkie (quick-sort)

Przypadek zrównowa˙zony:

T (n) = 2T (n/2) + Θ(n)

→

O(n log n)

Przypadek najgorszy:

T (n) = T (0) + T (n − 1) + Θ(n) = T (n − 1) + Θ(n)

→

O(n

2

)

Podziały zrównowa˙zone:

T (n) = T (αn) + T ((1 − α)n) + Θ(n)

→

O(n log n)

gdzie const = α ∈ (0, 1), poniewa˙z ka˙zdy podział w stałym
stosunku daje drzewo rekursji o wysoko´sci Θ(log n).

P.J.Matuszyk (AGH)

AiSD

AGH KISiM 2007

48 / 75

Szybkie metody sortowania

Sortowanie szybkie

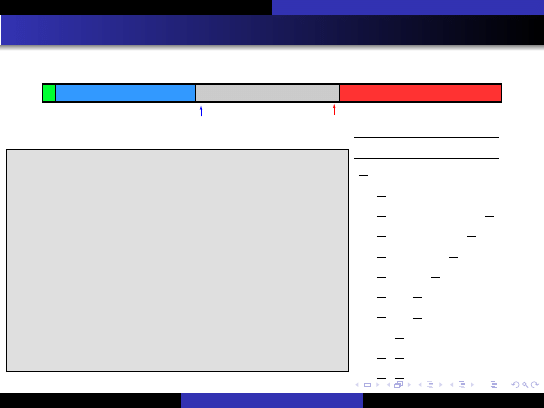
Procedura

partition

[wg Hoare’a]

Niezmiennik podziału tablicy

A

:

i

x

l

r

<= x

> x

?

j

template

<

typename

T>

long

partition(T* A,

long

l,

long

r) {

T

x = A[l];

long

i = l, j = r + 1;

for

(;;) {

do

++i;

while

(i <= r && A[i] < x);

do

--j;

while

(A[j] > x);

if

(i > j)

break

;

swap(A[i], A[j]);

}

A[l] = A[j];

A[j] = x;

return

j;

}

0 1 2 3 4 5 6 7

2

8 7 1 3 5 6 4

2

8 7 1 3 5 6 4

2

8 7 1 3 5 6 4

2

8 7 1 3 5 6

4

2

8 7 1 3 5

6 4

2

8 7 1 3

5 6 4

2

8 7 1

3 5 6 4

2

1

7

8 3 5 6 4

2

1

7

8 3 5 6 4

2

1

7 8 3 5 6 4

1

2

7 8 3 5 6 4

P.J.Matuszyk (AGH)

AiSD

AGH KISiM 2007

49 / 75

Szybkie metody sortowania

Sortowanie szybkie

Procedura

partition

[wg Hoare’a]

Ulepszenia

Eliminacja porównania — wprowadzenie wartownika:
wprowadzaj ˛

ac do tablicy wej´sciowej wartownika

A[r+1]=

∞

mo˙zemy wyeliminowa´c porównanie w pierwszej p ˛etli

do

...

while

:

template

<

typename

T>

long

partition(T* A,

long

l,

long

r) {

T

x = A[l];

// A[r + 1] = niesk.

long

i = l, j = r + 1;

for

(;;) {

do

++i;

while

(A[i] < x);

do

--j;

while

(A[j] > x);

if

(i > j)

break

;

swap(A[i], A[j]);

}

A[l] = A[j];

A[j] = x;

return

j;

}

P.J.Matuszyk (AGH)

AiSD

AGH KISiM 2007

50 / 75

Szybkie metody sortowania

Sortowanie szybkie

Sortowanie szybkie — modyfikacje

Do tej pory dzielili´smy tablice ze wzgl ˛edu na pierwszy albo ostatni
element — taki sposób mo˙ze jednak spowodowa´c nadmierne
zwi ˛ekszenie czasu i pami ˛eci dla pewnych cz ˛esto spotykanych
konfiguracji danych wej´sciowych.

Próbkowanie losowe

:

elementem rozdzielaj ˛

acym b ˛edzie losowo wybrany element:

template

<

typename

T>

long

rand_partition(T* arr,

long

l,

long

r) {

swap(arr[rand(l, r)], arr[l]);

return

partition(arr, l, r);

}

Mediana z trzech

:

bierzemy za element rozdzielaj ˛

acy median ˛e z trzech losowo

wybranych elementów podtablicy.

P.J.Matuszyk (AGH)

AiSD

AGH KISiM 2007

51 / 75

Szybkie metody sortowania

Sortowanie szybkie

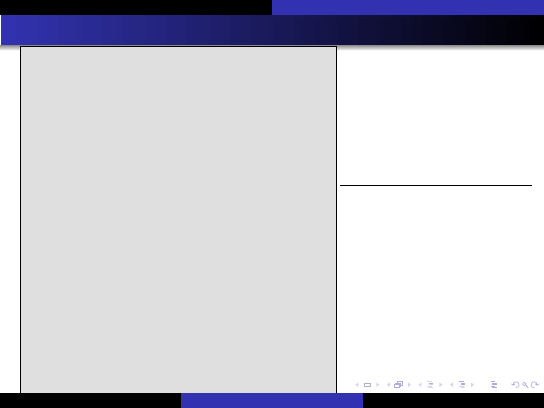
Procedura

partition

— mediana z trzech

template

<

typename

T>

long

partition(T* A,

long

l,

long

r) {

if

(r - l == 1) {

if

(A[r] < A[l])

swap(A[r], A[l]);

return

l;

}

// mediana z trzech

swap(A[l + 1], A[(l + r) >> 1]);

if

(A[l+1] > A[r]) swap(A[l + 1], A[r]);

if

(A[l]

> A[r]) swap(A[l],

A[r]);

if

(A[l+1] > A[l]) swap(A[l + 1], A[l]);

// wła´

sciwe dzielenie tablicy

T x = A[l];

long

i = l + 1, j = r;

for

(;;) {

do

++i;

while

(A[i] < x);

do

--j;

while

(A[j] > x);

if

(i > j)

break

;

swap(A[i], A[j]);

}

A[l] = A[j];

A[j] = x;

return

j;

}

A[(l+r)>>1]

l

A[l]

A[l+1]

A[r]

min

↔

max

min

←−−−−−

−−−−−→

max

max ↔

min

W rezultacie dostajemy:

A[l+1] <= A[l] <= A[r]

P.J.Matuszyk (AGH)

AiSD

AGH KISiM 2007

52 / 75

Szybkie metody sortowania

Sortowanie szybkie

Eliminacja rekursji ko ´ncowej

Drugie rekurencyjne wywołanie procedury

quicksort

nie jest

potrzebne:

template

<

typename

T>

void

quick_sort(T arr[],

int

l,

int

r) {

int

p;

while

(l < r) {

p = partition(arr, l, r);

quick_sort(arr, l, p - 1);

l = p + 1;

}

}

P.J.Matuszyk (AGH)

AiSD

AGH KISiM 2007

53 / 75