Modeling of tool wear during hard turning with self-propelled rotary tools

H.A. Kishawy

, Lei Pang

, M. Balazinski

Machining Research Laboratory, Faculty of Engineering and Applied Science, University of Ontario, Institute of Technology, Ontario, Canada

Department of Mechanical Engineering, Ecole Polytechnique de Montreal, Quebec, Canada

a r t i c l e

i n f o

Article history:
Received 15 December 2010
Received in revised form
4 August 2011
Accepted 9 August 2011

Available online 23 August 2011

Keywords:
Hard turning
Self-propelled rotary tools
Tool wear
Genetic algorithm

a b s t r a c t

In this paper, an attempt is made to evaluate the self-propelled rotary carbide tool performance during
machining hardened steel. Although several models were developed and used to evaluate the tool wear
in conventional tools, there were no attempts in open literature for modeling the progress of tool wear
when using the self-propelled rotary tools. Flank wear model for self-propelled rotary cutting tools is
developed based on the work-tool geometric interaction and the empirical function. A set of cutting
tests were carried out on the AISI 4340 steel with hardness of 54–56 HRC under different cutting speeds
and feeds. The progress of tool wear was recorded under different interval of time. A genetic algorithm
was developed to identify the constants in the proposed model. The comparison of measured and
predicted ﬂank wear showed that the developed model is capable of predicting the rate of rotary tool
ﬂank wear progression.

1. Introduction

Turning instead of grinding hardened steel is an economical

method to generate a high quality machined surface. During the
past few years, there has been a signiﬁcant industrial interest in
using dry machining rather than grinding of hardened steel and
other difﬁcult-to-machine materials. As an example, dry hard
turning of automotive differential side gears is a successful
industrial application of this technology. Dry hard turning reduces
both the machining time and the speciﬁc cutting energy, and
eliminates the health and environmental hazards associated with
coolant usage in conventional machining operations. However,
severe tool wear has been an obstacle to the application of hard
turning. Therefore, the control of tool wear and its effect on the
integrity of machined surface have been a major technical
challenge. Since the high speciﬁc forces and temperatures in the
small contact area between the tool and the workpiece have
much impact on tool wear, hard turning requires tool materials
with high wear and temperature resistance. In addition, indenta-
tion hardness of at least three times higher than the workpiece
hardness is essential, as demonstrated by Nakayama et al.

[12]

Since the tool wear and plastic deformation of the cutting edge
affect the quality and integrity of the machined surface, ceramics
and CBN tools are commonly recommended for hard turning.

Chip removal and wear mechanism of hard turning using CBN,

PCBN and ceramic cutting tools has been studied by many
researchers.

Matsumoto et al.

[11]

performed cutting tests on AISI 4340 steels

with various hardness values, ranging from 29 to 57 HRC, using
ceramic (Al

–TiC) inserts. Chip morphology study using scanning

electron microscopy (SEM) showed that the 50 HRC is the critical
hardness beyond which the segmented chips are produced. They also
found that the cutting force decreases with the increase in the
hardness from 29 to 49 HRC. However, when the hardness exceeded
50 HRC, the cutting forces suddenly increased.

Lin and Chen

[8]

carried out the experimental study on the

various cutting characteristics of a CBN tool during the turning of
AISI 52100 bearing steel (HRC 64). At low cutting speed (44.5
m/min), the ﬂank wear rate is low and not sensitive to the feed
rate. However, for the high cutting speed (144.5 m/min), the ﬂank
wear rate becomes quite large and sensitive to the feed rate. For
the commonly used small depth of cut (0.2 mm) during hard
turning, the thrust force was found greater than the cutting force.
While for a greater depth of cut (0.4 mm) the cutting force
becomes greater than the thrust force. This phenomenon was
attributed to the size effects since only the tool nose circle of the
cutting chin is engaged in cutting at shallow depth of cut.

Luo et al.

[9]

studied the wear behavior for CBN and ceramic tools

during hard turning of AISI 4340 steels with the hardness values in a
range of 35–60 HRC. They found that the main wear mechanism for
CBN tools is the abrasion of the binder material by hard carbide
particles of the workpiece, while adhesion and abrasion wear
mechanisms are dominant for ceramic tools. When the hardness of
the work material is less than 50 HRC, the wear rate of both tool
materials decrease with the increase in the work material hardness.
However, the trend becomes opposite when 50 HRC is reached.

The reason why the tool ﬂank wear rate decreases with the

material hardness for softer materials is out of the scope of the

Contents lists available at

SciVerse ScienceDirect

journal homepage:

www.elsevier.com/locate/ijmecsci

International Journal of Mechanical Sciences

0020-7403/$ - see front matter & 2011 Elsevier Ltd. All rights reserved.
doi:10.1016/j.ijmecsci.2011.08.009

Corresponding author.

E-mail address: hossam.kishawy@uoit.ca (H.A. Kishawy).

International Journal of Mechanical Sciences 53 (2011) 1015–1021

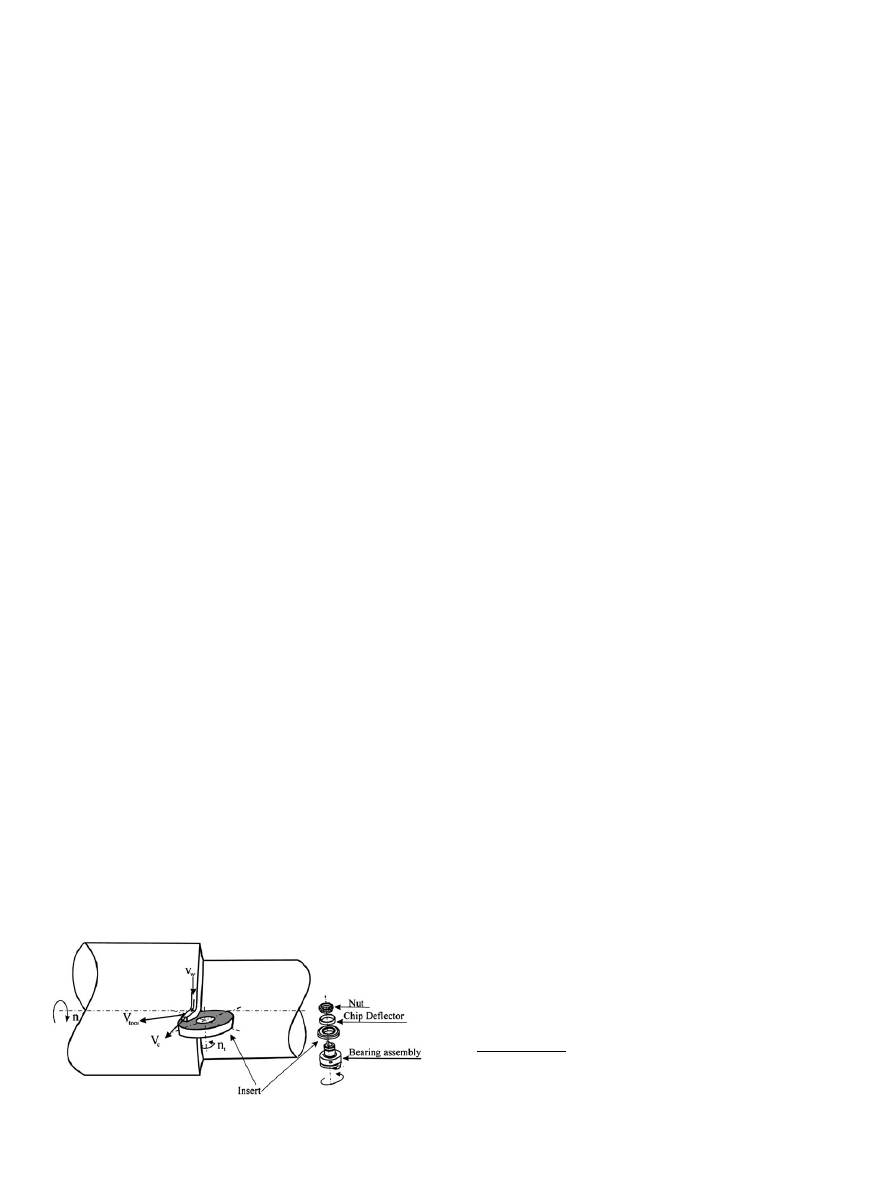
current study. However, from the experimental observations
introduced above, the main conclusion may be summarized as:

(1) Severe tool ﬂank wear occurs when the material hardness is

above 50 HRC.

(2) Not only the cutting speed, but also the feed may have

dominant effect on the tool wear rate during hard turning.

(3) Carbide single point cutting tools cannot be used for hard

turning.

Rotary cutting tool is a cutting tool in the form of a disk that

rotates about its axis, as shown in

Fig. 1

. Two types of rotary tools

are typically used in industry and research, namely driven and
self-propelled. For the driven tool, the rotational motion of the
insert is provided by an external source, while action of the chip
ﬂow over the tool rake face drives the insert to rotate for self-
propelled tools. During cutting, as a result of the tool spinning,
each section of the cutting edge is only engaged in cutting for a
short period of time, allowing each portion of the cutting edge to
cool down between engagements. Compared to conventional
non-rotating tools, this leads to inherently high cooling capability
and makes it possible to use economical carbide inserts during
hard turning without sacriﬁcing tool performance and machined
surface integrity. Superior wear resistance and prolonged tool life
were observed in earlier studies on rotary tools made of different
materials. Shaw et al.

[14]

used a rotary tool to machine mild steel

and concluded that machining with rotary tools reduced the
consumed power by 30%. Kishawy and Gerber

[6]

developed a

thermal model to study the characteristic of heat transfer during
machining with rotary tools. It was concluded that there is an
optimum tool spinning speed at which the tool temperature is
minimum. Based on the moving heat source theory, Dessoly et al.

[3]

developed a ﬁnite element model to predict the temperature

distribution along the rotary cutting edge and much lower cutting
temperatures were observed when compared to that obtained
with conventional non-rotating tools. Kishawy and Wilcox

[7]

evaluated the rotary tool performance during hard turning of AISI
4340 steels with hardness 54–56 HRC. The performance of
carbide and TiN coated carbide inserts were compared in the
ﬁxed and rotating conditions. There was no evidence of crater
wear was observed in the rotary tools and the good resistance to
tool ﬂank wear was observed compared with ﬁxed tools under the
same cutting conditions. Later on, Kishawy et al.

[5]

evaluated the

performance of self-propelled rotary tools and machined surface
quality during machining waspaloy and titanium alloys. The
coated carbide and micrograin carbide tool materials were used
for comparison. Again, the evenly distributed ﬂank wear was
observed to be the dominant mode of the tool failure in rotary
tools, while the crater wear to be the dominant mode in standard
non-rotary tools. The micrograin carbide inserts showed superior
wear resistance when compared to the coated carbide inserts.
This was attributed to the rotating action of the cutting edge.
Since the rotation is constantly replenishing the cutting edge,

thermally induced failure becomes less critical as opposed to the
structural integrity of the insert.

Several models attempting to simulate the tool ﬂank wear rate

during machining have been proposed. Choudhury and Srinivas

[1]

developed a tool wear model in which the variation of the

normal load with respect to ﬂank wear, wear coefﬁcient, hardness
of the cutting tool and the index of the diffusion coefﬁcient were
considered as inputs. The HSS inserts and the AISI 1045 steel were
used in the experiments to obtain the constants in the model. The
cutting velocity and the index of diffusion coefﬁcient were found
to have the most signiﬁcant effect on the tool ﬂank wear rate. Luo
et al.

[10]

developed an empirical tool ﬂank wear rate model for

carbide insert. In this model, the total ﬂank wear rate was
considered as the combination of abrasive/adhesive and diffusion
wear rates. The simulated thrust force and the tool-workpiece
temperature, together with the cutting conditions and the hard-
ness of the tool materials, are the main inputs to the model. The
measured tool ﬂank wear data was used for the model calibration.
Poulachon et al.

[13]

investigated the tool wear mechanism when

hard turning of AISI 52100 steels with hardness values 38–60
HRC, using polycrystalline cubic boron nitride (PCBN) tools. A
generalized Talor’s law was proposed to take account of the effect
of cutting conditions and the workpiece hardness. Based on the
constants calibrated by the experimental data, it was found that
the effect of the workpiece hardness is equivalent to that of
cutting speed on the tool ﬂank wear rate. Dawson and Kurfess

[2]

developed a ﬂank wear progression model for hard turning with
PCBN cutting tools based on the analysis of the geometric tool–
work interactions and the existing empirical relations between
tool ﬂank wear and cutting conditions.

Based on the several machinability studies, as mentioned above,

self-propelled rotary tools are proved to be an efﬁcient tool to
reduce the tool wear and thus improve tool life. The models
introduced above are all for single point cutting tools. Unfortu-
nately, there are no attempts in the open literature to model the
ﬂank wear progression in self-propelled rotary tools. The objectives
of this study are to evaluate the tool performance during cutting a
difﬁcult to cut material and develop a wear model to predict the
progress of tool wear when using self-propelled rotary carbide
tools in hard turning process. The presented work in this study is
based on the analysis of Dawson and Kurfess

[2]

and extended here

for self-propelled rotary tools during hard turning. A genetic
algorithm was developed to identify the wear constants in the
model, so that less cutting tests were required.

2. Tool wear model development

Flank wear develops on the ﬂank face of the tool and is a result

of the rubbing action between the cutting tool and the newly
generated workpiece surface. When the rotary tool is applied, the
ﬂank wear is a wear land along the perimeter of the insert. To
model the ﬂank wear for rotary tool, ﬁrst assume that the rotary
insert is ﬁxed just like single point tool.

Fig. 2

shows the cross

section view of tool tip engaged in the workpiece.

Fig. 2

, the large triangle is also the cross section area of the

ﬂank wear.

is the working rake angle and

is the working

clearance angle. From this two-dimensional cross section of ﬂank
wear, the worn area (larger triangle in

Fig. 2

) can be calculated by

Eq. (1)

A ¼

tan

2ð1þ tan

tan

1Þ

Fig. 3

shows two circles that represent the circumferences of

the rotary insert at two successive revolutions of the workpiece.
The volume of the removed material can then be calculated by

Fig. 1. A typical rotary tool during machining.

H.A. Kishawy et al. / International Journal of Mechanical Sciences 53 (2011) 1015–1021

1016

extruding the worn area along the contact length between tool
and workpiece L

. After one revolution of the workpiece, the

rotary tool center travels a linear distance equivalent to the feed.
Once the feed (f), depth of cut (d) and the radius of the rotary tool
(R) are known, the contact length L

, which is the curve formed by

the angle

, can be calculated by Eq. (2). The volume of removed

material (V) on the ﬂank land can be approximated by the product
of worn area A and contact length L

, as shown in Eq. (3)

R cos

tan

2Þ

V ¼ L

3Þ

Dawson and Kurfess

[2]

summarized the previous volume loss

models and proposed that the volume lost due to abrasion and
adhesion is linearly proportional to the cutting length L, as shown
in Eq. (4), where k is the empirical coefﬁcient addressing the
relation between the sliding interface pressure and the tool
hardness

V ¼ kL

4Þ

Since the cutting length L is the product of cutting velocity v

and the cutting time t, from Eqs. (1), (3) and (4), the expression of
the tool wear VB for the ﬁxed tool can be developed in terms of
the cutting condition, tool geometry and the coefﬁcient k

ﬃﬃﬃ

VB ¼ k

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

2ð1þ tan

tan

5Þ

For the rotary cutting tool, due to the fact that the tool ﬂank

wear is almost evenly distributed along the circumferences of the
cutting edge, the average tool wear VB

is expected to be

equivalent to the ratio between the instantaneous contact length
and the circumferences of the tool. Consequently, there is a factor
n (Eq. (6)) which should be included in the Eq. (5) to calculate the
ﬂank wear of rotary tool (Eq. (7))

n ¼

6Þ

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

2ð1 þ tan

tan

7Þ

Substituting Eqs. (2) and (6) into Eq. (7), the ﬁnal expression of

the rotary tool ﬂank wear progression can be obtained

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ
½

cos

Rd=RÞ þ tan

f =2RÞvt

tan

=ð

1 þ tan

tan

8Þ

As mentioned earlier, k

incorporates the effect of tool hard-

ness and the normal pressure at the sliding interface. Accurate
determination of normal pressure at the sliding interface depends
on the force model that can precisely represent the friction
characteristic at the chip–tool interface. However, the robust
model for the secondary deformation zone has not been estab-
lished yet, based on the authors’ literature survey. Furthermore, it
is impossible to measure the tool hardness at the elevated
temperature during cutting. Therefore, the coefﬁcient k

needs

to be calibrated.

As proposed by Dawson and Kurfess

[2]

, the coefﬁcient k

for a

speciﬁc work-tool combination can be expressed in terms of the
cutting speed and the feed, as shown in Eq. (9)

v,f Þ ¼ k

9Þ

Once the constants k

, k

and k

are calibrated with a number of

experimental tests, the ﬂank wear model can be established and
applied to predict rotary tool ﬂank wear at a certain cutting time.

3. Experimental procedure

Dry hard turning tests were performed to determine the

constants in Eq. (9) and to evaluate the accuracy of the model.
Cutting tests were performed using a 10 HP CNC lathe. Several bars
of AISI 4340 steel of 80 to 100 mm diameter and 200 mm length
were heat-treated to obtain the required hardness of 54–56 HRC.

Several self-propelled rotary tools with 27 mm diameter were

used in the experiment. The package of rotary tool includes an
insert cartridge and a tool holder. The insert is made of carbide
with 01 rake angle and 01 clearance angle. When the insert
cartridge and tool holder were set up together, the cutting edge
has a 51 normal rake angle and 51 clearance angle.

The cutting tests were stopped at constant time intervals and

using a tool maker’s microscope, the tool ﬂank wear (VB

) measure-

ments were conducted at four locations, which had approximately
equal distance along the perimeter of the insert. These readings
were then averaged to obtain the ﬁnal ﬂank wear value.

Table 1

shows the cutting conditions and the tool ﬂank wear at different
cutting time. For all the tests, the depth of cut was ﬁxed at 0.2 mm.

Fig. 4

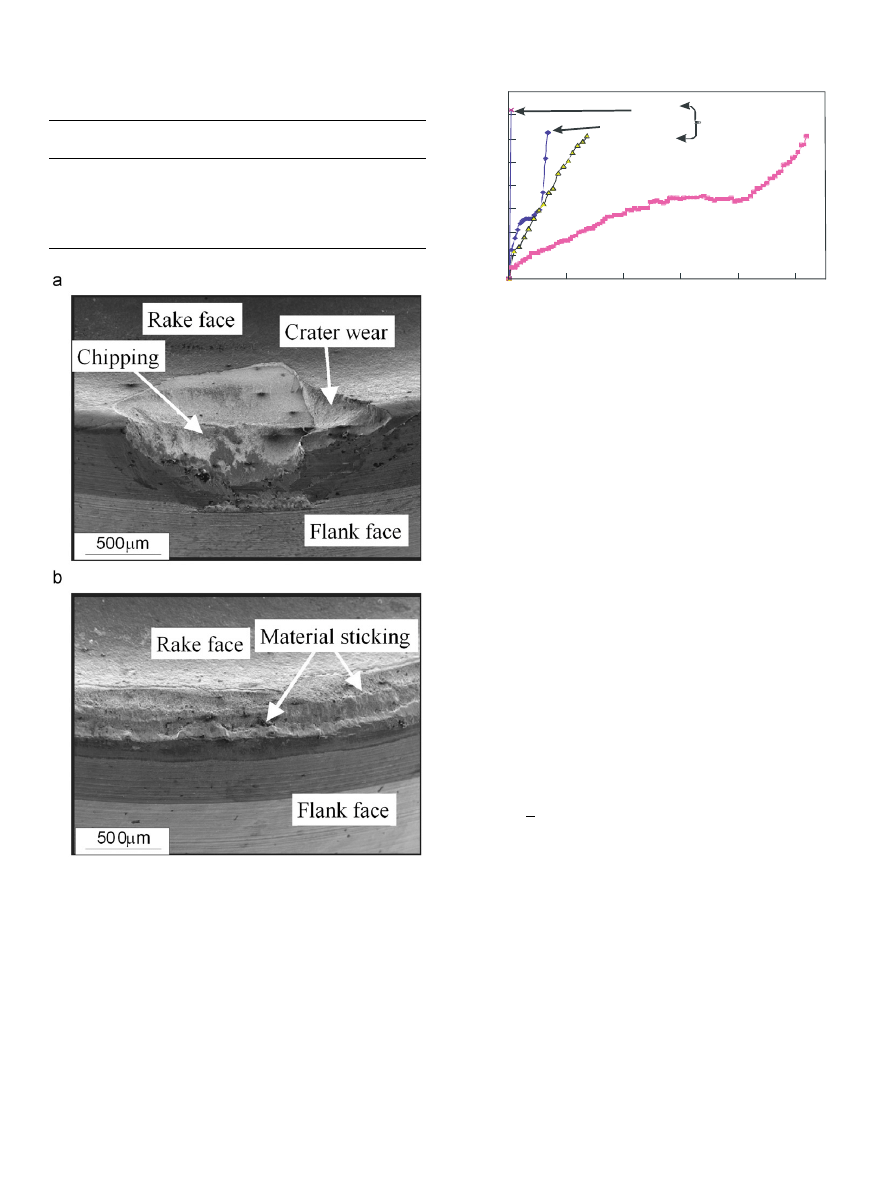
shows the SEM images of carbide tools after hard

turning. One insert is ﬁxed and the other one is allowed to rotate.
It was observed that for a speciﬁc cutting condition the tool life
has increased signiﬁcantly when inserts is allowed to rotate. For
tool life criteria of 0.3 mm and for speed of 130 m/min and feed of
0.1 mm/rev, the tool life increases from around 250 m cutting
distance for the ﬁxed tool to over 2600 m cutting distance for the
rotating inserts. Catastrophic failure was the mode of tool wear
for the ﬁxed tool while ﬂank wear was observed as the dominant
mode of tool failure for the self-propelled one. For the case of
rotating insert (

Fig. 4

b) there was no evidence of crater wear that

is normally severe in hard turning due to the high temperature,
especially with carbide tools. These images further proved the
cooling efﬁciency of the rotary tool and therefore a longer tool life
can be expected in comparison to a regular non-rotating insert.

The improvement of the tool life as a result of the insert

rotation is illustrated in

Fig. 5

. The progress of tool wear is

depicted for rotating and non-rotating circular inserts under the

Fig. 2. Cross section view of tool showing worn area due to ﬂank wear.

Fig. 3. Top view of cutting tool engaged with workpiece.

H.A. Kishawy et al. / International Journal of Mechanical Sciences 53 (2011) 1015–1021

1017

same cutting condition. The tested ﬁxed and rotating coated
carbide tools were also used under the same cutting condition
to verify the observed phenomenon. As can be seen, an improve-
ment in tool performance is achieved when rotary tools are used.
It should be mentioned here that examining the cutting tools
showed that uncoated carbide inserts were chipped when used as
a ﬁxed tools. Analyzing the progress of coated carbide tools
showed that the tool ﬂank wear starts with a rapid increase
when using ﬁxed tool. However, gradual increase in the tool ﬂank
wear was observed in the case of rotating insert. Similar relative
observation was found when using coated carbide tool. This can
be attributed to the reduction of the effective cutting speed due to
the insert rotation, and to the fact that the amount of wear is

distributed along the effective length of the cutting edge when
using rotating circular insert.

4. Model identiﬁcation using genetic algorithm

The accurate identiﬁcation of the constants in the developed

tool wear model is crucial to the robustness of the model. Least
squares regression is the most commonly used technique for the
model identiﬁcation. However, for nonlinear multivariable opti-
mization problems, the local sampling nature of the iterative least
squares makes it strongly dependent on the assumed starting
points. To reduce the tendency of being entrapped in the local
optima, a genetic algorithm (GA) based identiﬁcation system was
developed using Matlab. The program utilized the ‘‘parallel
computing’’ scheme so that much less time is needed to achieve
the optima. In this section, the developed GA model identiﬁcation
algorithm will be introduced.

4.1. Objective function

For any optimization method, an objective function (or cost

function) needs to be established and optimized. In this study, the
objective function is deﬁned as the norm of the difference
between the calculated and experimental results, as shown in
Eq. (10)

Min : FðXÞ ¼

i ¼ 1

cal

XÞP

exp

10Þ

where F(X) is the error function, X is the set of the parameters for
the tool wear model, N is the number of experimental observa-
tions; and P

cal

XÞ and P

exp
i

are the calculated and experimental

values at a given instant, respectively.

4.2. Genetic algorithm

Genetic algorithm (GA), ﬁrst developed by Holland

[4]

, resem-

bles the process of natural selection in search for better char-
acteristics within a changing population. The parameters to be
optimized are encoded and represented by a string of binary
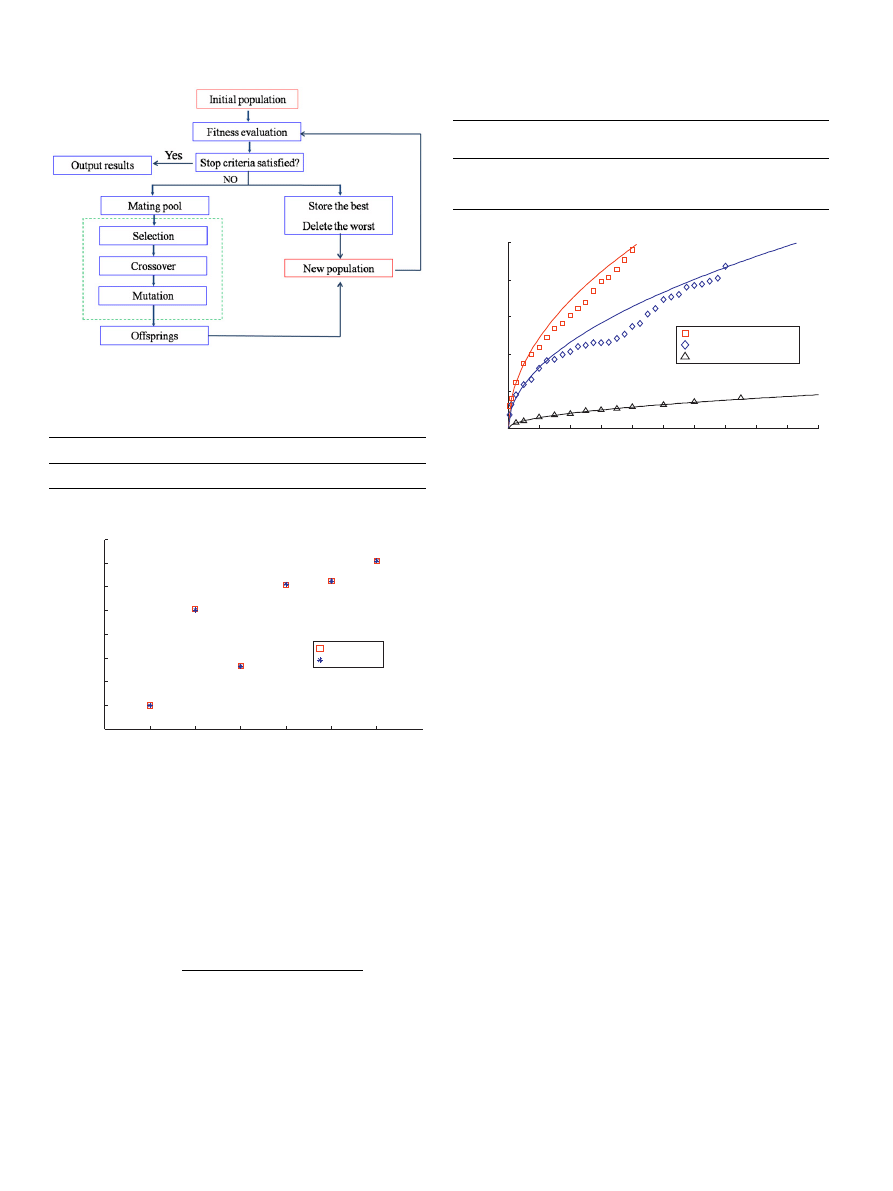
numbers (BINs). These BINs are called genes and the whole string
is called chromosome. A initial population of chromosomes is
randomly generated (as shown in

Fig. 6

) and evaluated by the

objective function. Based on the results of objective function,
these individuals in the current generation go through the
following procedure and generate new solutions. The procedure
is then repeated until the certain termination criteria are satisﬁed.

Table 1
Cutting tests for coefﬁcient identiﬁcation.

Test
number

Cutting speed (m/
min)

Feed (mm/
rev)

Cutting time
(min)

VB
(mm)

139

0.203

0.020

139

0.54

2.75

0.101

218

0.3

1.00

0.053

315

0.203

4.23

0.122

446

0.15

2.50

0.125

446

0.3

0.1

0.142

Fig. 4. Modes of tool wear during hard turning with rotary carbide tool. (a) Fixed
tool (after few seconds). (b) Rotating tool (end of the tool life).

0.05

0.1

0.15

0.2

0.25

0.3

0.35

0.4

4000

6000

8000

10000

Carbide

Coated carbide

Coated carbide
(Rotating)

Non rotating

Cutting distance (m)

Tool wear (mm)

2000

Carnbide (Rotating)

Fig. 5. Progress of tool wear for ﬁxed and rotating tool (V ¼ 120 m/min, f ¼0.2 mm/
rev, d ¼ 0.1 mm).

H.A. Kishawy et al. / International Journal of Mechanical Sciences 53 (2011) 1015–1021

1018

4.2.1. Selection scheme

Roulette selection combined with elitism was adopted as the

selection scheme so that the improvement for each generation
can be achieved without sacriﬁcing population diversity. In this
study, an elitist strategy is executed by allowing the ‘‘most ﬁt’’
individual to propagate directly to the new generation and
discarding the ‘‘least ﬁt’’ one. The left M individuals are put into
the selection pool. For each individual, the probability P(i) of
being chosen as a parent depends on the ﬁtness F

, which can be

calculated by the following equations:

Þ ¼

max

11Þ

PðiÞ ¼

12Þ

i ¼ 1

PðiÞ ¼ 1

13Þ

In which M is the population size, g

(X) is the objective value of

the ith individual and F

max

is the maximum objective value in the

current solution space. Based on the ﬁtness value, the individuals
are selected by spinning the Roulette wheel. The individual with
higher ﬁtness has higher possibility to be selected for further
crossover and mutation operation.

4.2.2. Crossover and mutation operators

Crossover is the mechanism of generating new solutions by

mating selected parent. The number of parent solutions selected
for the operation is commonly governed by a user deﬁned cross-
over rate P

. Single point-crossover (SPC), Multipoint-crossover

(MPC), and Uniform-crossover (UC) are widely applied strategies.
In SPC, each time only one parameter will be changed and the
diversity of the new population is limited. In UC, all the para-
meters may be changed and the good solutions may be lost.
Considering three parameters need to be identiﬁed in the devel-
oped wear model, two-point-crossover operation is used in this
study so that each time one or two parameters will be changed. In
this manner, the limitation of diversity can be reduced and the
good solution can be kept.

In order to achieve the computing efﬁciency, the ‘simultaneous

operation’ was performed instead of traditional ‘line-by-line
operation’ in such a manner as shown below.

For the given four parent solutions represented by binary

strings, for instance, create a matrix containing two crossover
positions for every two parents. The number of rows of position
matrix is the half of the rows of solution space. The four offspring
solutions can then be generated by exchanging the sub-stings
between the two crossover points simultaneously without any
loop, as demonstrated in

Fig. 7

In GA, mutation is the random process of selecting one

element of the chromosome and replacing it with a randomly
generated gene. Usually, mutation is performed as a background
parameter with very low probability. Mutation guarantees that
the probability of search at any given area is never zero. More-
over, it provides an opportunity of recovering good qualities lost
by other genetic operations. The probability of mutation, P

, is

usually ranged between 0.001 and 0.01. In the current study, the
multipoint mutation was used in a similar manner of the

crossover operation to guarantee the simultaneous calculation,
as shown in

Fig. 8

. That is, generate i j numbers between 0 and

1; compare each number with mutation rate P

; if it is less than

, binary integer (BIN) with the same index becomes (1-BIN).

4.2.3. Terminating criteria

Since GA is a stochastic search method, it is very difﬁcult to

assign convergence criteria. Terminate criteria are usually forced
into a GA program by (1) specifying maximum number of
generations; (2) terminating if no improvement occurs in last
certain number of generations and (3) terminating if a solution is
found whose objective function value or a user-designed error
function value is below a predeﬁned value. The third criterion
saves unnecessary computation time when the algorithm can
rapidly reach the global optima and therefore was adopted in this
study. The error between experimental data and the calculated
results is deﬁned in Eq. (14)

e ¼

i ¼ 1

cal

XÞP

exp

100

14Þ

The program is terminated when e

o5, meaning that the error

is smaller than 5%. The ﬂow chart of the genetic algorithm is
shown in

Fig. 9

Fig. 6. Chromosome strings arrangement.

Position Matrix

Before crossover

After crossover

Fig. 7. Simultaneous crossover operations.

Position Matrix

Before Mutation

After Mutation

Fig. 8. Simultaneous mutation operations.

H.A. Kishawy et al. / International Journal of Mechanical Sciences 53 (2011) 1015–1021

1019

4.3. Results and model veriﬁcation

Using the developed identiﬁcation algorithm and the mea-

sured data in

Table 1

, the rotary tool ﬂank wear model (Eq. (8))

was found, as shown in Eq. (15). The governing parameters used
in the genetic algorithm are listed in

Table 2

1:119

2:5099

2:5072

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ
½

cos

ðð

RdÞ=RÞ þ tan

f =2RÞvt

tan

=ð

1 þ tan

tan

15Þ

It is interesting to note from the above model that cutting

speed and feed have very similar inﬂuence on the tool ﬂank wear
rate. This high sensitivity of the ﬂank wear to the feed rate in the
high cutting speed regime observed by Lin and Chen

[8]

during

hard turning using single point CBN cutting tool was also found
based on the authors’ experimental tests on the self-propelled
rotary carbide tools, and this feature can be captured well by the
developed ﬂank wear rate model. However, the cutting speed

range (139–446 m/min) in the current study did not cover the
very low cutting speeds. Therefore, the phenomenon that only the
cutting speed dominates the tool ﬂank wear in the low cutting
speed regime cannot be described by the developed model.

To examine the accuracy of the obtained constants, the

predicted tool wear values were compared with the measure-
ments for the six tests, as shown in

Fig. 10

. With the maximum

error of 0.39%, the constants in Eq. (15) can be considered good
enough to express the model.

To validate the tool wear model, another three sets of test

were performed under the cutting conditions that different from
those used for constant identiﬁcation, as shown in

Table 3

. The

tool ﬂank wear were measured until the tool wear reached
0.25 mm or the cutting time reached 15 min. On the other hand,
the tool ﬂank wear were simulated based on the proposed model
under same operation conditions.

Fig. 11

shows the comparison of the measured (discrete

points) and simulated (solid lines) ﬂank wear. The good agree-
ment was observed between the model prediction and experi-
mental measurements. The proposed model is basically capable of
predicting the carbide rotary tool ﬂank wear when hard turning of
AISI 4340 steels.

5. Conclusions

A new ﬂank wear model for self-propelled rotary cutting tools

was developed based on the work-tool geometric interaction and
the empirical function. The three constants in the model were
determined by the developed genetic algorithm in conjugation of
several cutting tests. The developed identiﬁcation algorithm can be
readily used for any other nonlinear multivariable system identi-
ﬁcation problems. During the cutting tests and tool wear model
development, the feed rate was found to have similar impact as the
cutting speed on the rotary tool ﬂank wear progression in hard
turning for the cutting speed range 139–446 m/min. The good
agreement between simulated and measured ﬂank wear have
ensured the effectiveness of the proposed model.

Fig. 9. Flow chart of the genetic algorithm.

Table 2
GA parameters.

Population size

Bit length

Crossover rate

Mutation rate

Stop criterion

400

0.8

0.1

o5%

0.02

0.04

0.06

0.08

0.1

0.12

0.14

0.16

Number of Tests

Tool Flank Wear (mm)

mesured
calculated

Fig. 10. Comparisons of predicted and experimental data used for constant
identiﬁcation.

0.05

0.1

0.15

0.2

0.25

Cutting Time (minutes)

Tool Flank Wear (mm)

v = 355, f = 0.203
v = 235, f = 0.285
v = 174.8, f = 0.203

Fig. 11. Comparison of measured and predicted rotary tool ﬂank wear.

Table 3
Cutting conditions for model veriﬁcation.

Test
number

Cutting speed (m/
min)

Speed Feed (mm/
rev)

Depth of cut
(mm)

174

0.203

0.2

235

0.285

0.2

355

0.203

0.2

H.A. Kishawy et al. / International Journal of Mechanical Sciences 53 (2011) 1015–1021

1020

Acknowledgments

The authors would like to acknowledge the National Science

and Engineering Research Council of Canada (NSERC) for provid-
ing the fund for the research support.

References

[1] Choudhury SK, Srinivas P. Tool wear prediction in turning. Journal of

Materials Processing Technology 2004;153–154:276–80.

[2] Dawson TG, Kurfess TR. Modeling the progression of ﬂank wear on uncoated

and ceramic-coated polycrystalline cubic boron nitride tools in hard turning.
Journal of Manufacturing Science and Engineering 2006;128:104–9.

[3] Dessoly V, Melkote SN, Lescalier C. Modeling and veriﬁcation of cutting tool

temperatures in rotary tool turning of hardened steel. International Journal of
Machine Tools and Manufacture 2004;44:1463–70.

[4] Holland JH. Adaptation in natural and artiﬁcial systems. 2nd ed.MIT Press; 1992.
[5] Kishawy HA, Becze CE, McIntosh DG. Tool performance and attainable surface

quality during the machining of aerospace alloys using self-propelled rotary
tools. Journal of Materials Processing Technology 2004;152:266–71.

[6] Kishawy HA, Gerber AG. A model for the tool temperature during machining

with a rotary tool. In: Proceedings of the ASME International Mechanical
Engineering Congress and Exposition. New York; 2001. p. 1–8.

[7] Kishawy HA, Wilcox J. Tool wear and chip formation during hard turning

with self-propelled rotary tools. International Journal of Machine Tools and
Manufacture 2003;43:433–9.

[8] Lin Z-C, Chen D-Y. A study of cutting with a CBN tool. Journal of Materials

Processing Technology 1995;49:149–64.

[9] Luo SY, Liao YS, Tsai YY. Wear characteristics in turning high hardness alloy

steel by ceramic and CBN tools. Journal of Materials Processing Technology
1999;88:114–21.

[10] Luo X, Cheng K, Holt R, Liu X. Modeling ﬂank wear of carbide tool insert in

metal cutting. Wear 2005;259:1235–40.

[11] Matsumoto Y, Barash MM, Liu CR. Cutting mechanism during machining of

hardened steel. Materials Science and Technology 1987;3:299–305.

[12] Nakayama K, Arai M, Kanda T. Machining characteristics of hard materials.

CIRP Annals—Manufacturing Technology 1988;37:89–92.

[13] Poulachon G, Moisan A, Jawahir IS. Tool-wear mechanisms in hard turning

with polycrystalline cubic boron nitride tools. Wear 2001;250:576–86.

[14] Shaw MC, Smith PA, Cook NA. The rotary cutting tool. Transactions on ASME

1952;74:1065–76.

H.A. Kishawy et al. / International Journal of Mechanical Sciences 53 (2011) 1015–1021

1021

Document Outline

Modeling of tool wear during hard turning with self-propelled rotary tools

Wyszukiwarka

Podobne podstrony:
87 1237 1248 Machinability and Tool Wear During the High Speed Milling of Some Hardened
WEiP (4 Prognozowanie na podstawie modeli ekonometrycznych 2011)
Modeling and tool wear in drilling of CFRP
Kaliszewska Czeremska (2011) Modeling excessive internet use A revision of R Davis s cognitive beha
2011 2 KOSZE
higiena dla studentów 2011 dr I Kosinska
Plan pracy na 2011 pps
W 8 Hormony 2010 2011
wm 2011 zad 2
Zawal serca 20 11 2011
PRK 23 10 2011 org
PIW 4z 2011
pmp wykład podmioty 2011 2012

więcej podobnych podstron

2011 H A Kishawy Lei Pang, M Balazinski Modeling oftool wear during hard turning with self propelled rotary tools

Document Outline