
POLITECHNIKA ŚWIĘTOKRZYSKA
Katedra Urządzeń Elektrycznych i Techniki Świetlnej
Materiałoznawstwo Elektryczne
ĆWICZENIE 11
BADANIE OBWODU MAGNETYCZNEGO ZE SZCZELINĄ
I. WIADOMOŚCI TEORETYCZNE
1. Własności magnetyczne materiałów
Wszystkie substancje możemy podzielić pod względem własności magnetycznych na trzy grupy:
−
diamagnetyki,
−
paramagnetyki,
−
ferromagnetyki (lub krócej: magnetyki).
W przypadku diamagnetyków indukowany w czasie wzrostu natężenia pola zewnętrznego magnetycz-
ny moment wewnętrzny, skierowany przeciwnie do tego pola, utrzymuje się nadal po ustaleniu się warto-
ś
ci H pola zewnętrznego. Na skutek tego ciało wykazuje bardzo słaby moment magnetyczny o odwrot-
nym znaku do znaku pola zewnętrznego. Następuje odejmowanie się pól magnetycznych, co powoduje,
ż
e indukcja B w diamagnetyku jest przy tym samym natężeniu pola magnetycznego H mniejsza niż in-
dukcja B
0
w próżni. Oznacza to, że przenikalność magnetyczna diamagnetyków jest mniejsza od przeni-
kalności próżni.
Zjawisko paramagnetyzmu zachodzi w ciałach, których atomy mają nieparzystą liczbę elektronów. W
przypadku działania zewnętrznego pola magnetycznego na paramagnetyki, do pola tego dodają się w
niewielkiej ilości nieskompensowane momenty magnetyczne elektronów. Takie częściowe porządkowa-
nie kierunków jest procesem powolnym – w pierwszej chwili wszystkie ciała wykazują własności diama-
gnetyczne - dopiero później w paramagnetykach pojawia się uporządkowana indukcja zgodna z polem
zewnętrznym. Przenikalność magnetyczna paramagnetyków jest niewiele większa od przenikalności
próżni.
Materiały magnetyczne (magnetyki) można podzielić na dwie grupy:
a)
materiały magnetycznie miękkie,
b)
materiały magnetycznie twarde.
Do opisywania materiałów magnetycznie miękkich służą następujące wielkości i charakterystyki:
−
indukcja nasycenia B
nas
,
−
komutacyjna krzywa magnesowania B = f(H),
−
przenikalność magnetyczna normalna początkowa
µ
pocz
,
−
przenikalność magnetyczna normalna maksymalna
µ
max
,
−
stratność magnetyczna
∆
P
Fe
.
Materiały ferromagnetyczne mają tzw. strukturę domenową, tj. składającą się z obszarów zwanych do-
menami Weissa w których występuje równoległe ustawienie momentów magnetycznych atomów w wyniku
porządkującego działania sił wymiany. Sąsiadujące ze sobą domeny są oddzielone tzw. ściankami Blocha
o grubości 30
µ
m. Magnetyk nie poddany działaniu zewnętrznego pola magnetycznego jest na zewnątrz
obojętny na skutek chaotycznego ustawienia domen. W przypadku działania zewnętrznego pola magne-
tycznego o określonym kierunku wektora H, ścianki Blocha, w miarę wzrostu natężenia pola magnetycz-
nego, ulegają stopniowym przesunięciom aż do zupełnego ich zaniku, wskutek czego powstaje jedna domena
o kierunku najbardziej zbliżonym do kierunku wektora H. Dalszy wzrost natężenia pola powoduje stop-
niowe obracanie się wektorów wypadkowego momentu magnetycznego kryształu do pozycji zgodnej z
kierunkiem wektora H. Jest to tzw. stan nasycenia. Kolejny wzrost natężenia pola nie powoduje już wzro-
Ć
wiczenie 11
2
stu indukcji własnej B
w
, która uzyskuje wartość B
wnas
. Indukcja wypadkowa B (B = B
w
+ B
0
) wzrasta
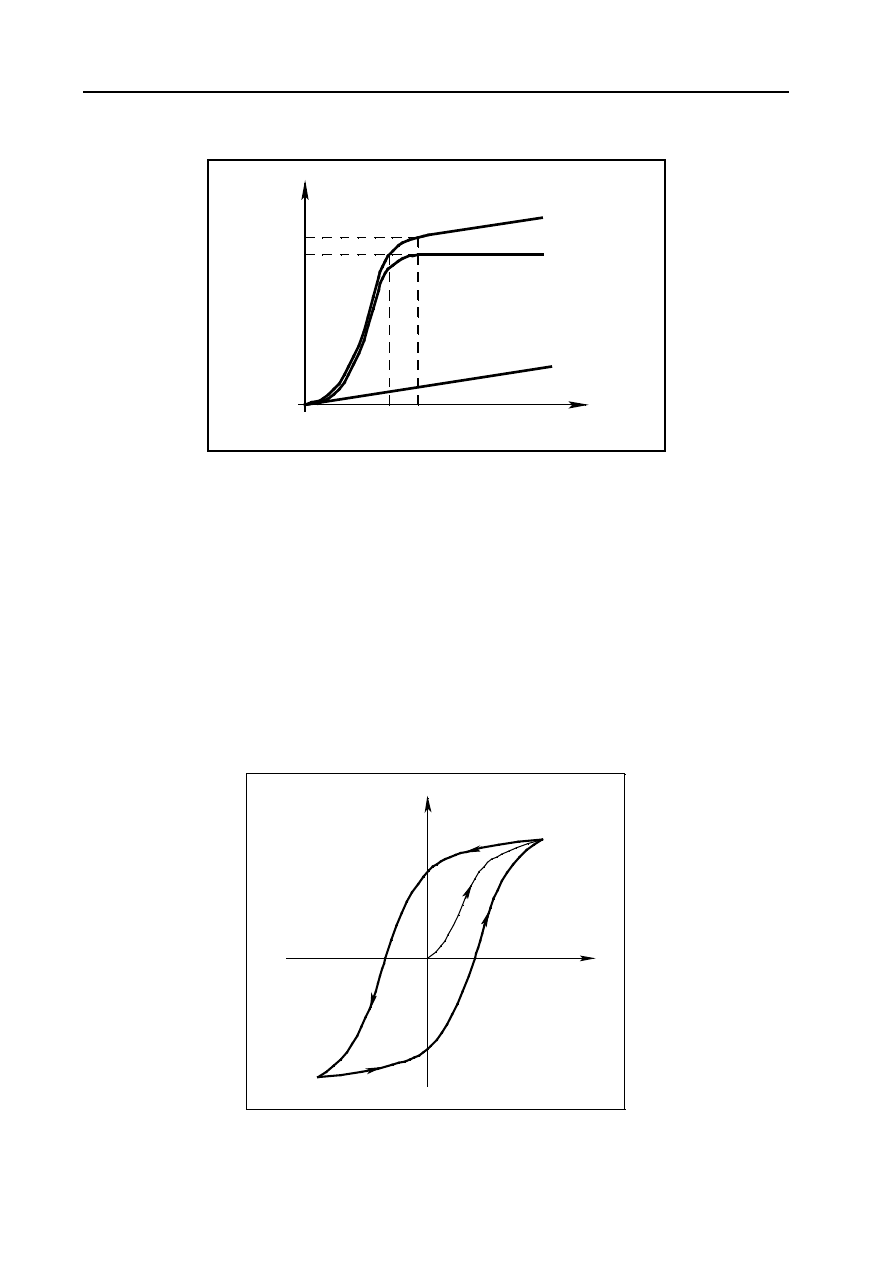
nieznacznie i liniowo z nachyleniem odpowiadającym magnesowaniu próżni (rys. 11.1).
B
B
H
P
ar
ap
ro
c
es
i
o
bs
za
r
n
a
sy
ce
n
ia
P
rz
es
u
w
an
ie
ś
ci
an
ek
B
lo
c
h
a
O
br
ac
a
n
ie
d
ip
o
li
wnas
B
nas
B
w
B
0
B
m
H
Rys. 11.1. Krzywa magnesowania ferromagnetyka: B - indukcja wypadkowa, B
w
- in-
dukcja własna (magnetyzacja), B
0
- indukcja w próżni
Indukcja nasycenia B
nas
zależy od rodzaju materiału i temperatury. Wzrost temperatury powoduje ni-
weczenie porządkujących sił wymiany przez drgania cieplne atomów. W temperaturze zwanej temperatu-
rą Curie następuje rozpad domen i ferromagnetyk zachowuje się jak paramagnetyk.
Jeżeli po namagnesowaniu ferromagnetyka będziemy zmniejszać natężenie pola magnetycznego H do
zera, to zależność B = f
(H) nie będzie pokrywać się z pierwotną krzywą magnesowania. Zjawisko to
wyjaśnia się zachowywaniem przez większość domen Weissa uzyskanego uprzednio stanu uporządko-
wania. Stan taki charakteryzowany jest przez tzw. pozostałość magnetyczną B
r
.
W celu zmniejszenia indukcji B
r
do zera należy zmienić kierunek magnesowania na przeciwny i wy-
tworzyć pole magnetyczne o natężeniu H
c
zwanym natężeniem powściągającym. Wówczas część domen
przybierze nową orientację, obróconą o 180
°
względem orientacji poprzedniej. Strumień magnetyczny
tych domen zrównoważy strumień domen utrzymujących nadal poprzednią orientację. Pełny cykl prze-
magnesowania ferromagnetyka (z głębokim wejściem w obszary nasycenia dodatniego i ujemnego) nosi
nazwę granicznej pętli histerezy. Pętlę taką przedstawia rysunek 11.2 w postaci krzywej abcdefa.
r
B
H
f
c
c
H
d
e
B
b
a
Rys. 11.2. Graniczna pętla histerezy magnetycznej: B
r
- pozostałość
magnetyczna, H
c
- natężenie powściągające

Badanie obwodu magnetycznego ze szczeliną
3
Jedną z podstawowych wielkości charakteryzujących materiał magnetyczny jest przenikalność ma-
gnetyczna normalna określona zależnością
µ =
B
H
.
(11.10
Jest to przenikalność magnetyczna bezwzględna. W praktyce częściej posługujemy się przenikalno-
ś
cią magnetyczną względną
µ
µ
µ
r
=
0
, gdzie
µ
0
= 4
π⋅
10
–7
H/m.
(11.2)
Przenikalność magnetyczna ferromagnetyków zależy od natężenia pola magnetycznego H i to w spo-
sób niejednoznaczny a także od temperatury.
Ciała diamagnetyczne charakteryzują się stałością przenikalności magnetycznej, przy czym
µ
r
jest
liczbą nieco mniejszą od jedności (woda –
µ
r
= 0,999991, rtęć –
µ
r
= 0,999997, miedź –
µ
r
= 0,999998).
Ciała paramagnetyczne mają również stałą przenikalność magnetyczną względną, przy czym
µ
r
jest
liczbą nieco większą od jedności, np. powietrze (
µ
r
= 1,000004), platyna (
µ
r
= 1,000015), aluminium (
µ
r
=
1,000001).
W przypadku magnetyków wprowadza się trzy rodzaje przenikalności magnetycznej:
−
normalną,
−
różniczkową,
−
odwracalną.
Przenikalność magnetyczna
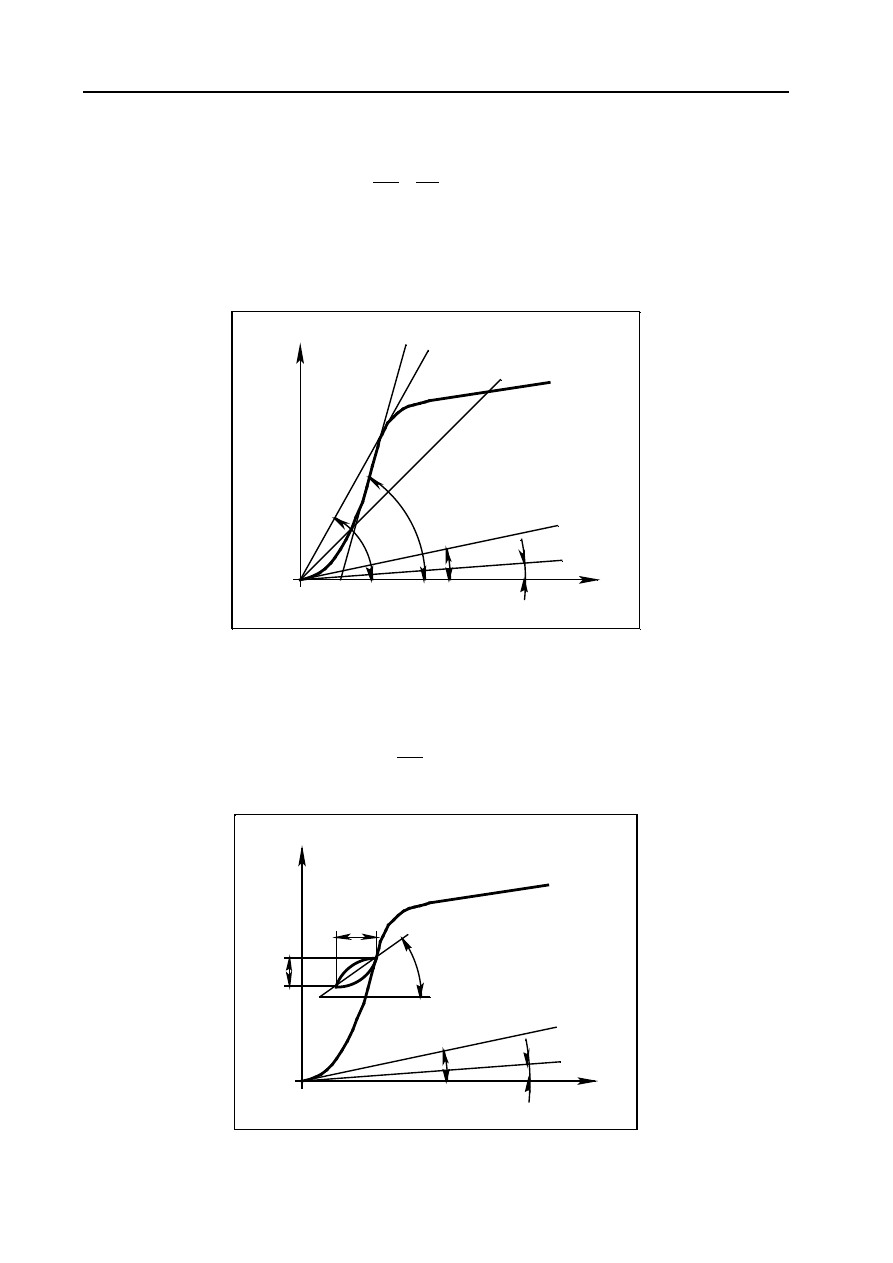
normalna związana jest z pierwotną krzywą magnesowania (rys. 11.3).
Określa ją zależność
µ
α
=
= ⋅
B
H
k tg .
(11.3)
α
α
max
B
st
y
cz
n
a
α
pocz
α
0
H
Rys. 11.3. Interpretacja przenikalności magnetycznej normalnej
Z rysunku 11.3 wynika, że przenikalność magnetyczna normalna wzrasta ze wzrostem H od wartości
początkowej
µ
pocz
= k
⋅
tg
α
pocz
(
α
pocz
jest kątem nachylenia stycznej do krzywej w punkcie H = 0) do
wartości
µ
max
odpowiadającej tangensowi największego kąta nachylenia prostej przechodzącej przez
punkt zero i stycznej do krzywej magnesowania, a następnie maleje do
µ
0
przy H
→
∞
. Współczynnik k
jest współczynnikiem skali – przy jednakowych podziałkach obu osi k = 1. Kąt
α
0
odpowiada nachyleniu
prostej magnesowania próżni,
µ
0
= k
⋅
tg
α
0
.
Ć
wiczenie 11
4
Przenikalność magnetyczna różniczkowa również jest związana z pierwotną krzywą magnesowania
(rys. 11.4). Definiowana jest jako
µ
β
d
H
B
H
dB
dH
k tg
=
=
= ⋅
→
lim
∆
∆
∆
0
.
(11.4)
Przenikalność magnetyczna
różniczkowa jest proporcjonalna do tangensa kąta
β
jaki tworzy styczna
do pierwotnej krzywej magnesowania. Dla H = 0
µ
d
=
µ
pocz
, ponieważ
α
pocz
=
β
pocz
. Największa wartość
przenikalności magnetycznej różniczkowej
µ
dmax
jest większa od maksymalnej przenikalności normalnej
gdyż
β
max
>
α
max
. Przy H
→
∞
przenikalność magnetyczna różniczkowa maleje asymptotycznie do
µ
0
.
α
0
st
y
cz
n
a
β
max
B
s
ty
c
z
n
a
α
max
β =
H
pocz
β
=
α
pocz
Rys. 11.4. Interpretacja przenikalności magnetycznej różniczkowej
Z przenikalnością magnetyczną odwracalną (rewersyjną) mamy do czynienia w przypadku nakładania się
na pole magnetyczne o znacznym natężeniu H pola magnetycznego okresowo zmiennego. Definiowana jest
następująco
µ
γ
rev
H
B
H
k tg
=
= ⋅
→
lim
∆
∆
∆
0
.
(11.5)
Przenikalność ta jest proporcjonalna do tg
γ
(rys. 11.5) i jest mniejsza od
µ
i
µ
d
.
H
α
0
pocz
γ
α
pocz
=
0
γ
B
∆
H
∆
B
Rys. 11.5. Interpretacja przenikalności magnetycznej odwracalnej
Badanie obwodu magnetycznego ze szczeliną
5
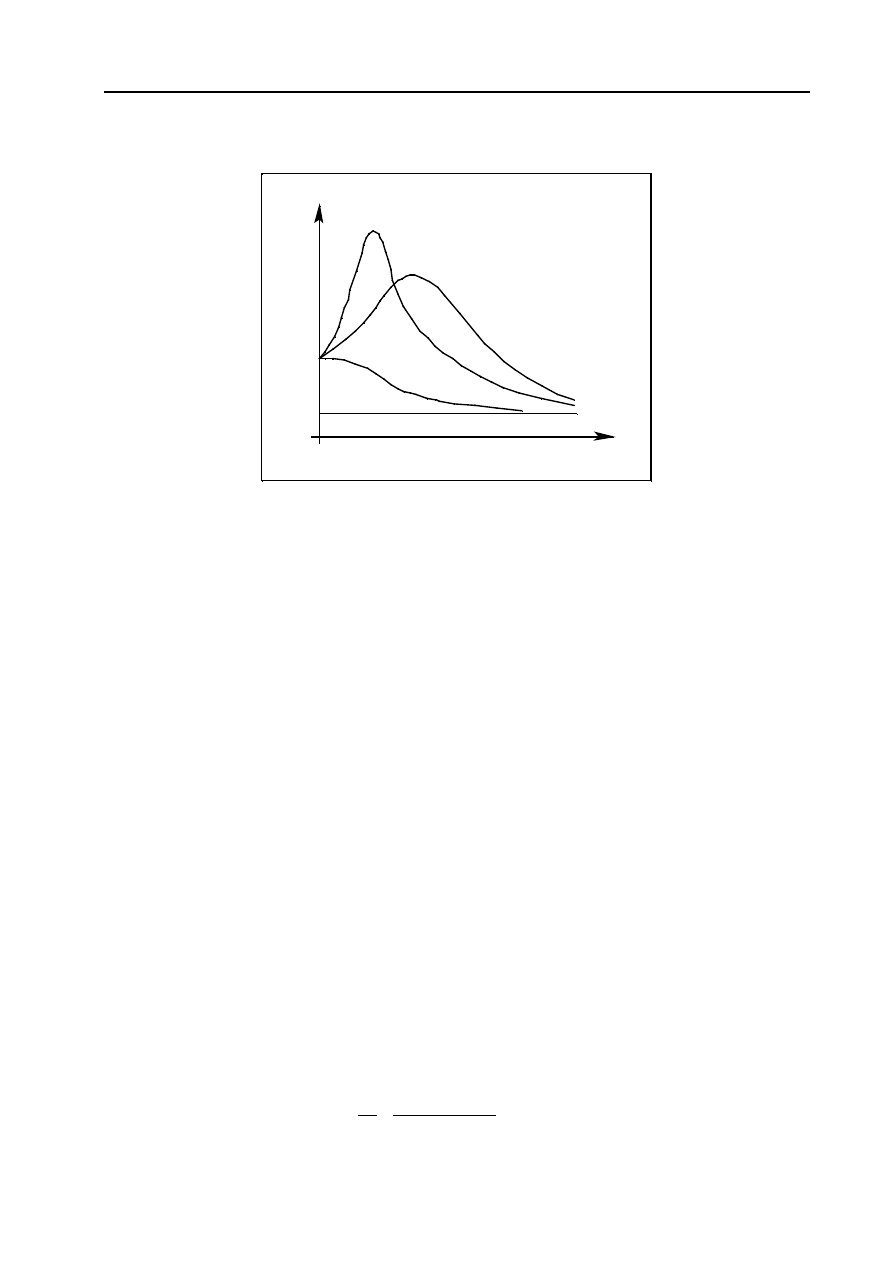
Rysunek 11.6 przedstawia zależność zdefiniowanych przenikalności magnetycznych od natężenia pola ma-
gnetycznego H.
H
µ
0
µ
rev
µ
pocz
µ
µ
d
µ
Rys. 11.6. Zależność przenikalności magnetycznych od natężenia pola ma-
gnetycznego
2. Obwody magnetyczne ze szczeliną
W obwodach magnetycznych występują często szczeliny powietrzne. Zmieniają one własności obwodu
magnetycznego (zmienia się opór magnetyczny), jednocześnie w magnetycznym rdzeniu cewki wytwarzany
jest jednak strumień o wiele większy niż w przypadku układu bezrdzeniowego.
Szczeliny magnetyczne występują w maszynach elektrycznych, dławikach, przekaźnikach itp.
Prawidłowe działanie obwodu magnetycznego ze szczeliną wymaga wytworzenia w szczelinie odpowied-
niego strumienia magnetycznego
Φ
. Wymagania najczęściej dotyczą indukcji magnetycznej B czyli gęstości
tego strumienia a zagadnienie sprowadza się ogólnie rzecz biorąc do obliczenia amperozwojów magnesujących
potrzebnych dla zapewnienia tej indukcji.
Prawo przepływu dla obwodu magnetycznego ze szczeliną ma postać
H l
H
1 1
2
+
=
δ θ
,
(11.6)
gdzie: H
1
- natężenie pola magnetycznego w rdzeniu, l
1
- średnia długość drogi strumienia w rdzeniu, H
2
- natę-
ż
enie pola magnetycznego w szczelinie,
δ
- grubość szczeliny powietrznej,
θ
= I
⋅
z - przepływ.
Gęstość strumienia w szczelinie jest taka sama jak w rdzeniu przy bardzo wąskich szczelinach. Zazwyczaj
jednak należy przyjąć przekrój szczeliny nieco większy niż rdzenia. Dla obwodu magnetycznego z rysunku
11.8 przekrój szczeliny obliczamy z wzoru
S
a
b
2
= + ⋅ +
(
) (
)
δ
δ
.
(11.7)
Dla wymaganej indukcji B
2
strumień magnetyczny w szczelinie będzie wynosił
Φ =
⋅
= + ⋅ + ⋅
S
B
a
b
B
2
2
2
(
) (
)
δ
δ
(11.8)
i będzie równy strumieniowi w rdzeniu. Ponieważ jednak przekrój rdzenia jest mniejszy to indukcja w
rdzeniu będzie wynosić
B
S
a
b
a b
B
1
1
2
=
=
+ ⋅ +
⋅
⋅
Φ
(
) (
)
δ
δ
.
(11.9)
Ć
wiczenie 11
6
Mając obliczoną indukcję B
1
odczytujemy natężenie pola H
1
z krzywej magnesowania danego materiału
(patrz rysunek 11.9). Wymagany przepływ (lub prąd magnesujący) obliczamy z prawa przepływu
θ
µ
δ
=
+
⋅
H l
B
1 1
2
0
,
(11.10)
gdzie
µ
0
= 4
π⋅
10
–7
- przenikalność magnetyczna próżni.
3. Pytania kontrolne
1.
Własności magnetyczne materiałów
2.
Omówić proces magnesowania ferromagnetyków
3.
Definicje przenikalności magnetycznych
4.
Zależność przenikalności magnetycznej od natężenia pola magnetycznego
5.
Sposób obliczania obwodów magnetycznych ze szczeliną
Literatura
1.
Kobus A., Tuszyński J., Warsza Z. L.:
Technika hallotronowa. WNT, Warszawa 1980
2.
Kolbiński K., Słowikowski J.:
Materiałoznawstwo elektrotechniczne. WNT, Warszawa 1988
3.
Paciorek Z., Stryszowski S.:
Laboratorium inżynierii materiałowej. Skrypt Politechniki Święto-
krzyskiej nr 209, Kielce 1991
4.
Starczakow W.:
Materiałoznawstwo elektryczne. Skrypt Politechniki Łódzkiej, Łódź 1969
II. BADANIA
1. Zdjęcie charakterystyki B = f(
θθθθ
) dla materiału magnetycznego ze szczeliną
Wykonujemy pomiary napięcia Halla U
H
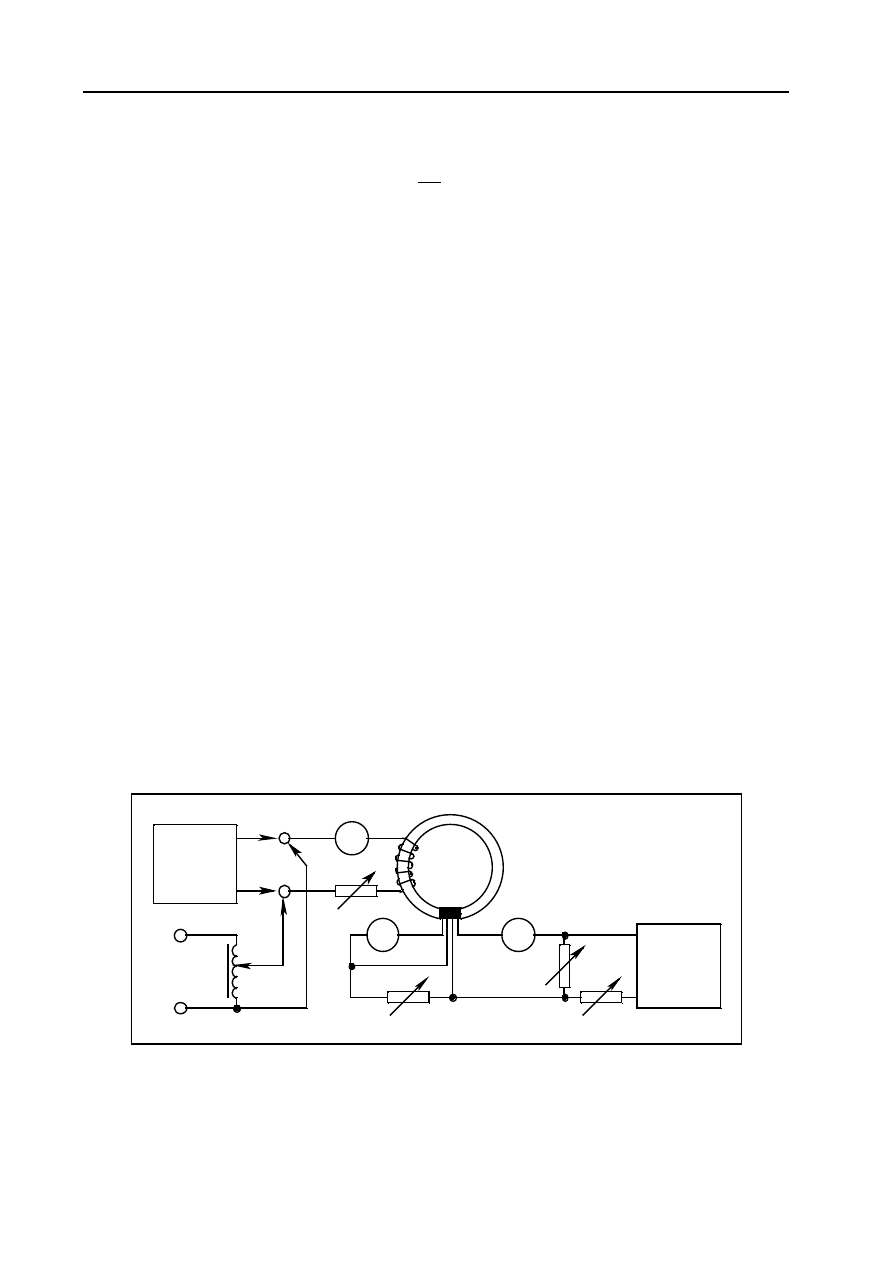
w funkcji prądu płynącego przez uzwojenie próbki. Schemat
układu pomiarowego przedstawia rysunek 11.7.
mA
mV
ZS
ZM
220 V
Próbka
Tr
−
+
H
U
H
1
R
A
2
R
4
R
3
R
Rys. 11.7. Schemat układu pomiarowego: ZM - zasilacz prądu magnesującego, Tr - transformator regulacyjny, H
- hallotron, U
H
- napięcie Halla mierzone przez miliwoltomierz, ZS - zasilacz prądu sterującego, R
1
,
R
2
, R
3
, R
4
- rezystory regulacyjne
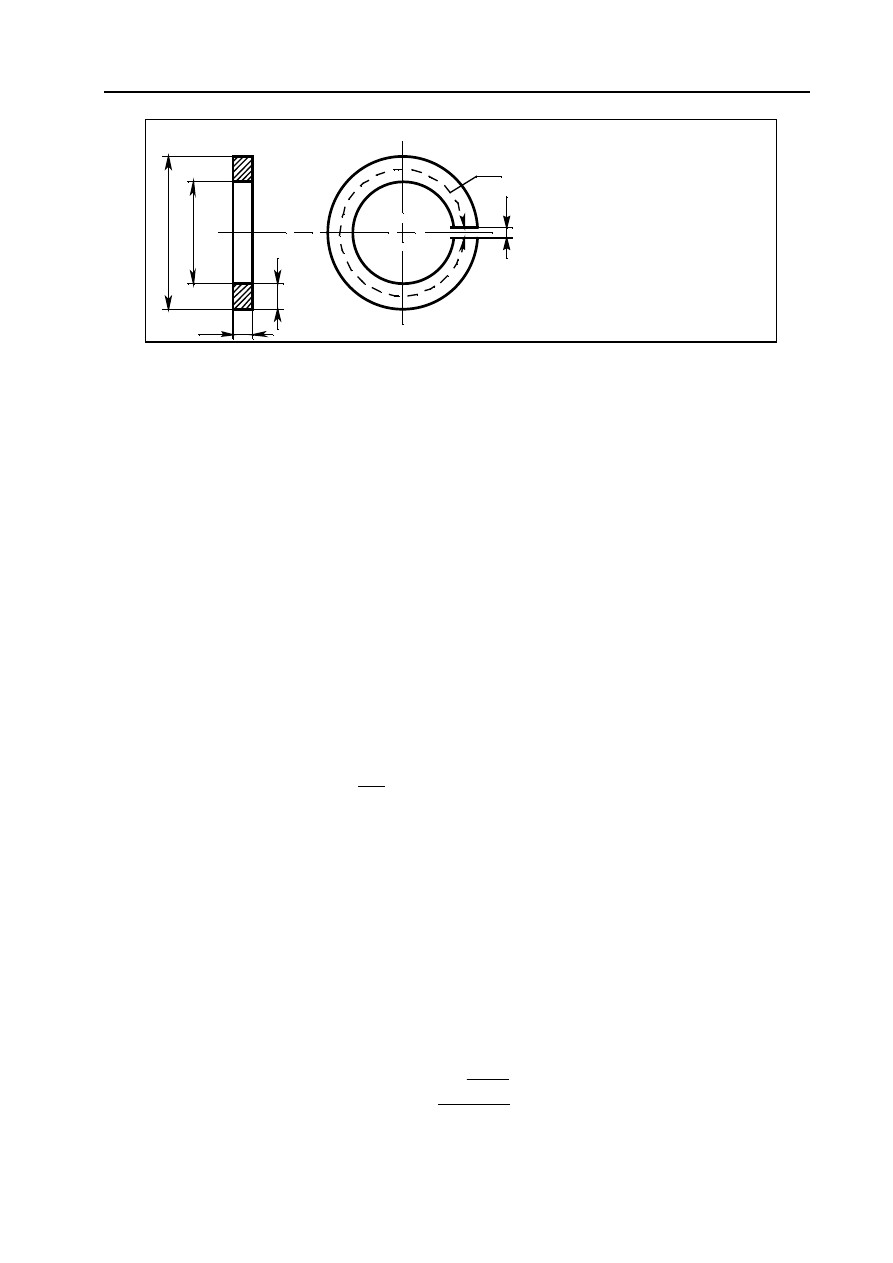
Badanie obwodu magnetycznego ze szczeliną
7
Rys. 11.8. Badany obwód magnetyczny
Kolejność czynności:
−
załączyć zasilacz prądu sterującego,
−
ustawić prąd sterujący hallotronu na 10 mA,
−
rozmagnesować rdzeń za pomocą prądu przemiennego (ustawić prąd ok. 15 A a następnie powoli
zmniejszyć do zera),
−
za pomocą rezystorów (R
2
) skompensować ewentualne napięcie asymetrii
,
−
załączyć źródło prądu magnesującego,
−
zmieniając prąd magnesujący odczytywać napięcie Halla w celu zdjęcia charakterystyki magne-
sowania i pętli histerezy magnetycznej.
Etapy pomiaru:
magnesowanie (+)
- prąd magn. 0
÷
12 A (krzywa magnesowa-
nia),
odmagnesowywanie
- prąd magn. 12 A
÷
0 (pętla histerezy),
odmagnesowywanie i magnesowanie (-)
- prąd magn. 0
÷
-12 A (pętla histerezy),
magnesowanie (-)
- prąd magn. -12 A
÷
0 (pętla histerezy),
odmagnesowywanie i magnesowanie (+)
- prąd magn. 0
÷
12 A (pętla histerezy),
−
dla poszczególnych punktów pomiarowych obliczyć indukcję w szczelinie rdzenia oraz ampe-
rozwoje magnesujące
B
U
H
=
γ
,
θ = ⋅
I z
,
(11.11)
gdzie: B - indukcja w szczelinie w „T”, U
H
- napięcie Halla w „mV”,
γ
- czułość hallotronu w
„mV/T” (czułość ta wynosi 0,5
⋅
10
4
mV/T),
θ
- amperozwoje magnesujące, I - prąd magne-
sujący w „A”, z - liczba zwo-jów uzwojenia magnesującego.
Aby wyznaczyć indukcję B i natężenie pola H w materiale magnetycznym trzeba posłużyć się prawem
przepływu:
θ
δ
=
⋅
+
⋅
ś
r
0
l
H
H
gdzie: H
0
– natężenie pola magnetycznego w szczelinie,
δ
- grubość szczeliny, H – natężenie pola
w rdzeniu, długość drogi magnetycznej w rdzeniu.
Biorąc pod uwagę powyższy wzór oraz zależność H
0
= B
0
/
µ
0
możemy wyznaczyć natężenie pola
w rdzeniu
ś
r
0
0
l
B
H
µ
δ
θ
⋅
−
=
Dane obwodu magnetycznego:
a = 45 mm,
b = 32 mm,
d = 120 mm,
D = 210 mm,
δ
= 6 mm,
z = 180,
l
ś
r
= 514 mm.
b
a
δ
l
sr
d
D
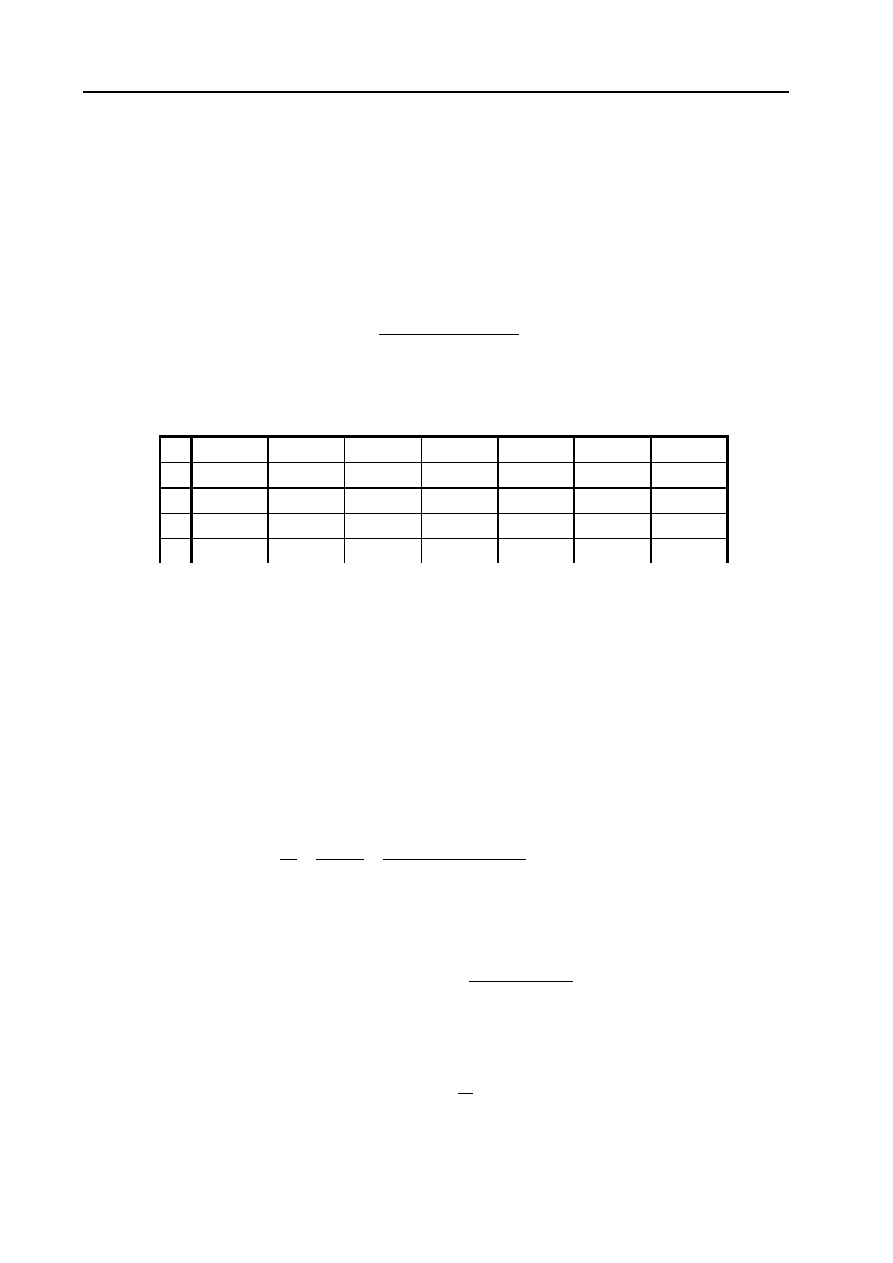
Ć
wiczenie 11
8
Przy wąskiej szczelinie można przyjąć, że indukcja w rdzeniu jest równa indukcji w szczelinie. Po-
nieważ w naszym przypadku szczelina jest dosyć duża (wymiary obwodu magnetycznego przedstawia
rysunek 11.8) należy przyjąć przekrój szczeliny większy niż przekrój rdzenia. wynika to z faktu, że stru-
mień magnetyczny w szczelinie „rozmietla się”. Indukcję w rdzeniu można wyznaczyć z równości stru-
mieni
φ
0
=
φ
.
B
0
⋅
S
0
= B
⋅
S,
B
0
⋅
(a +
δ
)
⋅
(b +
δ
) = B
⋅
a
⋅
b.
gdzie: S
0
– przekrój szczeliny, S – przekrój rdzenia
Indukcja w rdzeniu wynosi:
b
a
)
b
)(
a
(
B
B
0
⋅
+
+
⋅
=
δ
δ
.
−
wyniki pomiarów i obliczeń przedstawić w tabeli 11.1.
Tab. 11.1. Wyniki pomiarów i obliczeń
Lp.
I
U
H
θ
B
0
H
0
= B
0
/
µ
0
B
H
–
A
mV
Az
T
A/m
T
A/m
1
2
3
2. Opracowanie wyników pomiarów
−
wykreślić charakterystykę B
0
= f
(
θ
) dla obwodu magnetycznego ze szczeliną,
−
wykreślić charakterystykę B = f(H) dla rdzenia pracującego ze szczeliną,
−
obliczyć prąd magnesujący potrzebny dla otrzymania indukcji w szczelinie B
0
= 0,8 T w przy-
padku zastosowania na obwód magnetyczny staliwa oraz żelaza elektrolitycznego. Wymiary
obwodu pozostają bez zmian.
Przykład obliczenia:
strumień magnetyczny w szczelinie
Φ
= S
0
⋅
B
0
[Wb],
przekrój szczeliny
S
0
= (a +
δ
)
⋅
(b +
δ
) [m
2
],
przekrój rdzenia
S = a
⋅
b [m
2
],
obliczamy indukcję w rdzeniu
b
a
B
)
b
(
)
a
(
S
B
S
S
B
0
0
0
⋅
⋅
δ
+
⋅
δ
+
=
⋅
=
Φ
=
[T],
(11.12)
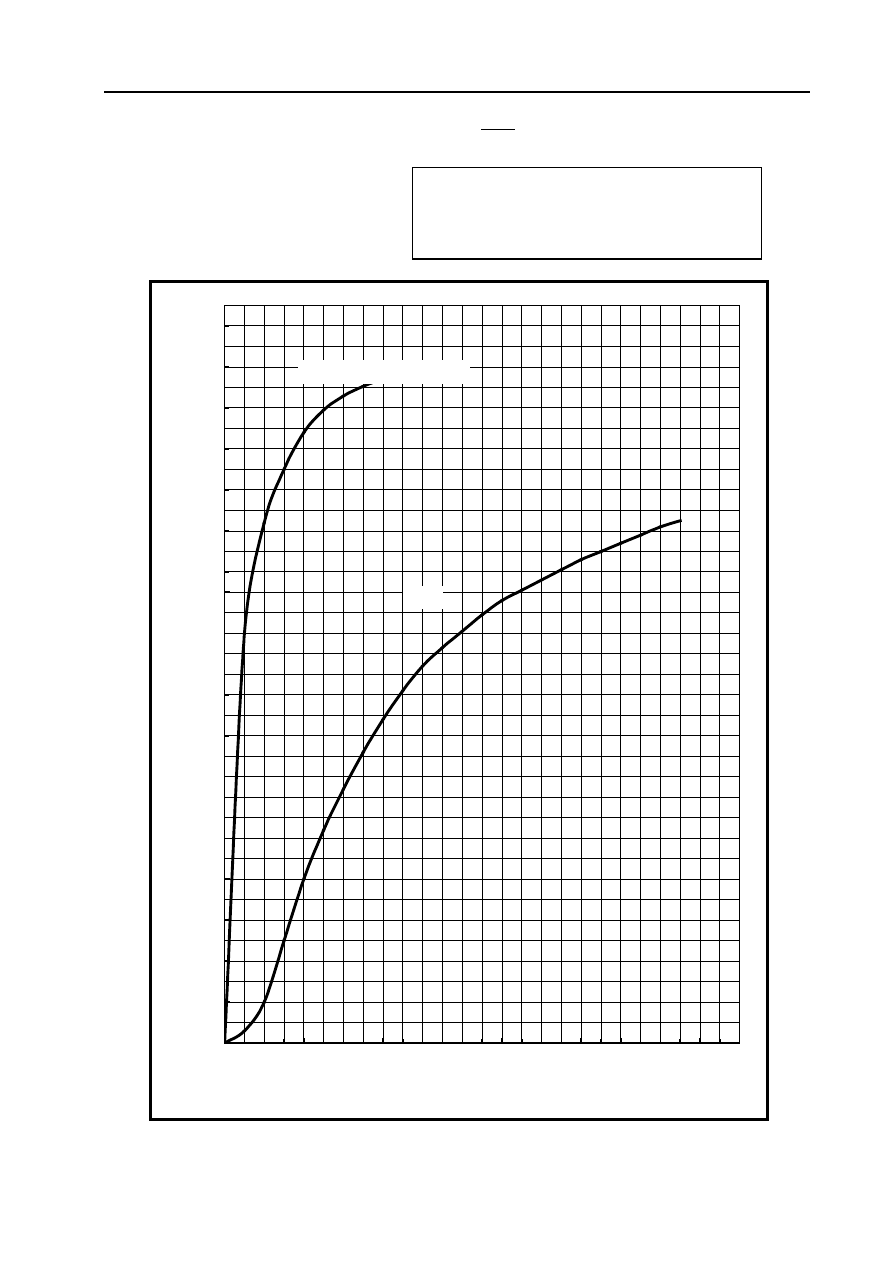
dla obliczonej wartości indukcji w rdzeniu odczytujemy wartość natężenia pola magnetycznego
w rdzeniu (H) z załączonej krzywej magnesowania B = f
(H) (rys. 11.9).
Prąd magnesujący obliczamy korzystając z prawa przepływu
δ
⋅
+
⋅
=
⋅
=
θ
0
ś
r
H
l
H
z
I
,
z
H
l
H
I
0
ś
r
δ
⋅
+
⋅
=
,
(11.13)
gdzie H
0
= B
0
/
µ
0
- natężenie pola magnetycznego w szczelinie,
−
obliczyć maksymalną przenikalność magnetyczną (normalną) materiałów (z załączonych wykre-
sów).
µ
α
max
max
= ⋅
=
k tg
B
H
,
(11.14)
Badanie obwodu magnetycznego ze szczeliną
9
przenikalność magnetyczna względna
µ
µ
µ
'
max
max
=
0
.
Jednostki: 1T (tesla) = 1Wb/m
2
= 10
4
Gs (gauss),
1Wb (weber) = 1V
⋅
s,
1H
(henr) = 1Wb/A = 1V
⋅
s/A
0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1
1,1
1,2
1,3
1,4
1,5
1,6
1,7
1,8
0
100
200
300
400
500
600
700
800
900 1000 1100 1200 1300
Natężenie pola magnetycznego H, (A/m.)
In
d
u
k
cj
a
m
ag
n
et
y
cz
n
a
B
,
(
T
)
Rys. 11.9. Krzywe magnesowania B = f
(H)
stal
Żelazo elektrolityczne

Ć
wiczenie 11
10
3. Wnioski
−
omówić wpływ szczeliny na własności magnetyczne obwodu magnetycznego (krzywą magne-
sowania i statyczną pętlę histerezy),
−
omówić wpływ krzywej magnesowania materiału ferromagnetycznego na własności obwodu
magnetycznego ze szczeliną. Czy własności magnetyczne materiału mają znaczący wpływ na
wartość prądu magnesującego potrzebnego do uzyskania wymaganej indukcji w szczelinie?
Wyszukiwarka
Podobne podstrony:
II seria, Ćwiczenie 11 Badanie obwodu ze szczeliną
ćwiczenie 11 Badanie filtrów aktywnych
ĆWICZENIE NR 11 - Badania polowe i pobieranie próbek gruntów, Mechanika Gruntów
Fizjologia Cwiczenia 11 id 1743 Nieznany
Biologia Cwiczenia 11 id 87709 Nieznany (2)
cwiczenie 11
sprawko z ćwiczenia 11, Farmacja, II rok farmacji, I semstr, fizyczna, Fizyczna, Sprawozdania z fizy
W4 Badanie chorego ze zmianami układu chorego., Medycyna Ratunkowa - Ratownictwo Medyczne
Patomorfologia cwiczenia ,11,11
11 Klasyfikacja robotów ze względu na obszar zastosowania
MIKROEKONOMIA ĆWICZENIA 5 (11 12 2011)
2 15 4 kanaly ze szczelinami (v Nieznany
cwiczenie ii badanie napedu z silnikiem reluktancyjnym przel
cwiczenie 11 id 125145 Nieznany
Badanie obwodu szeregowego RLC Nieznany (2)
Cwiczenie 1, Skrypty, UR - materiały ze studiów, studia, studia, 3 STASZEK, Woiągi
Cwiczenie 11 Rozklad naprezen pod fundamentem ( )
cwiczenia 11
więcej podobnych podstron