Metody sztucznej inteligencji

wykªad 4

(dla studentów Wydziaªu MT Politechniki ‘laskiej

- na prawach rekopisu)

06 kwietnia 2006

Obliczanie prawdopodobie«stw zdarze«

Prawdopodobie«stwo, »e oboje John i Mary zadzwonia, je±li sªy-
cha¢ alarm pomimo »e nie bedzie ani wªamania, ani trzesienia
ziemi:

P(J ∧ M ∧ A ∧ ¬B ∧ ¬E)

= P(J |A)P(M |A)P(A|¬B ∧ ¬E)P(¬B)P(¬E)

= 0.90 × 0.70 × 0.001 × 0.999 × 0.998 = 0.00062

1

Budowanie sieci przekona«

•

Sie¢ przekona« jest zbudowana poprawnie, je±li ka»dy wezeª
jest warunkowo niezale»ny od swoich poprzedników w upo-
rzadkowaniu wezªów

•

Rodzicami wezªa X

i

powinny by¢ wszystkie takie wezªy, które

bezpo±rednio wpªywaja na ten wezeª:

P(X

i

|X

i−1

, . . . , X

1

) = P(X

i

|P arents(X

i

))

(1)

przy zaªo»eniu, »e P arents(X

i

)

⊆ {X

i−1

, . . . , X

1

}

2

Ogólna procedura

•

Wybierz zbiór relewantnych zmiennych {X

i

}

opisujacych dziedzine

•

Wybierz uporzadkowanie zmiennych {X

i

}

•

Dopóki pozostaja jeszcze zmienne w {X

i

}

:

wybierz zmienna X

i

i dodaj dla niej wezeª do sieci

ustal minimalny zbiór zmiennych P arents(X

i

)

warunkowo

niezale»nych

okre±l tablice prawdopodobie«stw warunkowych dla tego

wezªa

3

Wnioskowanie w sieciach przekona«

Zadaniem systemu wnioskowania probabilistycznego jest oblicze-
nie rozkªadu prawdopodobie«stwa a posteriori dla zbioru zmien-
nych zapytania (query variables), gdy dane sa dokªadne warto±ci
zmiennych-dowodów (evidence variables)

4

Rodzaje wnioskowania w sieciach przekona«

(1)

•

Wnioskowanie diagnostyczne (od efektów do przyczyn)

Wiemy »e JohnCalls

wnioskujemy P(Burglary|JohnCalls) = 0.016

•

Wnioskowanie przyczynowe (od przyczyn do efektów)

Wiemy, »e Burglary

wnioskujemy P(JohnCalls|Burglary) = 0.86,

P(M aryCalls|Burglary) = 0.67

5

Rodzaje wnioskowania w sieciach przekona«

(2)

•

Wnioskowanie miedzyprzyczynowe (pomiedzy przyczynami
wspólnego skutku)

je±li wiemy, »e Alarm, to P(Burglary|Alarm) = 0.376

gdy wiemy dodatkowo, »e Earthquake, to

P(Burglary|Alarm ∧ Earthquake) = 0.003

6

Rodzaje wnioskowania w sieciach przekona«

(3)

•

Wnioskowanie mieszane (ªaczy dwa lub wiecej powy»szych
rodzajów wnioskowa«):

JohnCalls = T rue (efekt) oraz Eartquake = F alse (przy-

czyna) daje:
P(Alarm|J ohnCalls ∧ ¬Eartquake) = 0.03

[jednoczesne zastosowanie wnioskowania diagnostycznego
i przyczynowego]

P(Burglary|J ohnCalls ∧ ¬Eartquake) = 0.0017

[jednoczesne zastosowanie wnioskowania diagnostycznego
i miedzyprzyczynowego]

7

Zastosowanie sieci przekona«

Podstawowe: Obliczanie warto±ci miary przekonania (ang. be-

lief ) dotyczacego zmiennych zapytania, gdy sa okre±lone warto±ci
dowodów

Inne: • Podejmowanie decyzji opartych na prawdopodobie«st-

wach reprezentowanych w sieci i warto±ciach u»yteczno±ci
dla agenta

•

Decydowanie jakie dodatkowe dowody zgromadzi¢, by pozyska¢
u»yteczna informacje

•

Analiza wra»liwo±ci w celu okre±lenia które atrybuty maja
najwiekszy wpªyw na prawdopodobie«stwo wyniku

8

Wnioskowanie w wielokrotnie poªaczonych

sieciach przekona«

•

Metody grupowania

transformacje sieci w probabilistycznie równowa»ne polidrzewo

•

Metody warunkowania

transformacja poprzez konkretyzacje zmiennych poprzez pod-
stawienia, a nastepnie poprzez analize polidrzew dla ka»dego
mo»liwego podstawienia

•

Symulacja stochastyczna

9

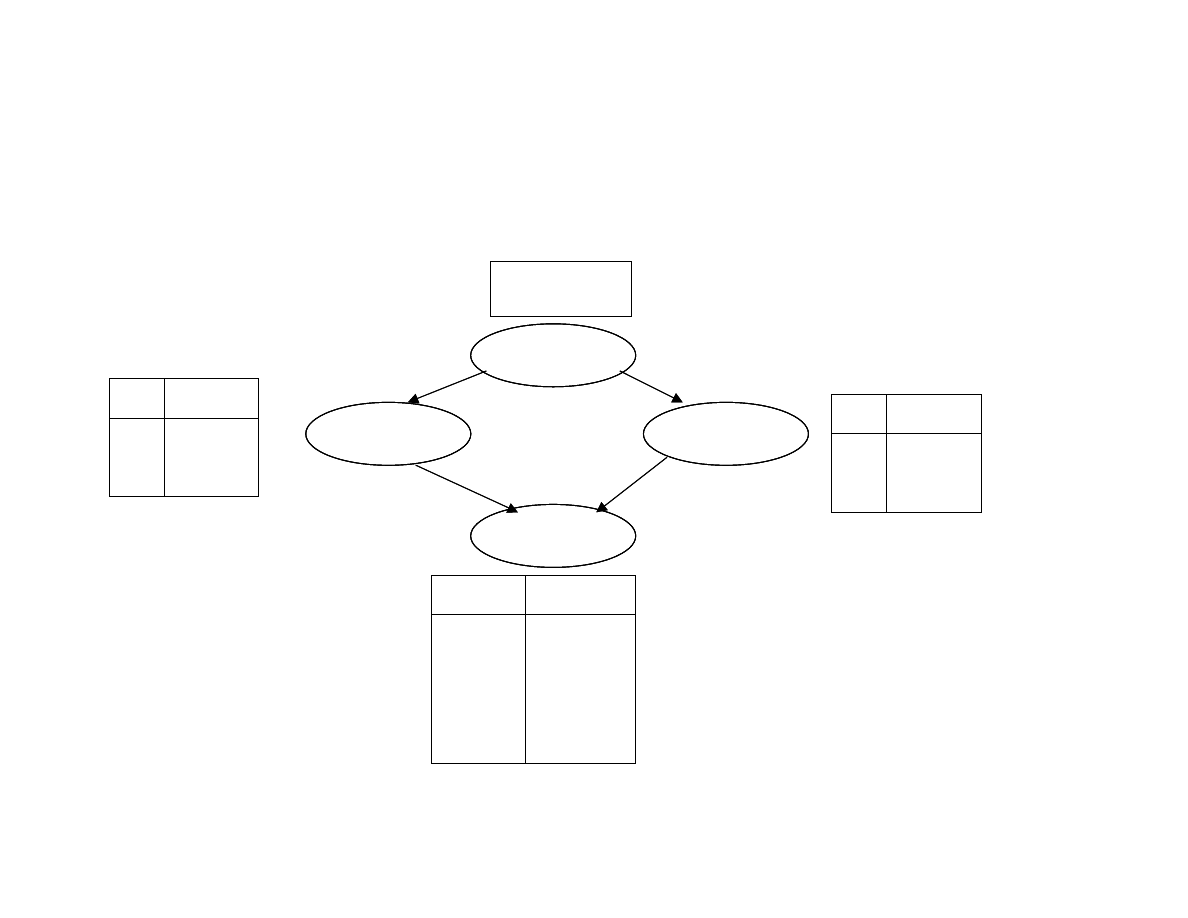
Przykªad sie¢ wielokrotnie poªaczona (1)

Cloudy

Sprinkler

Rain

Wet grass

Cloudy

Cloudy

Sprinkler

Sprinkler

Rain

Rain

Wet grass

Wet grass

P(C)=0.5

P(C)=0.5

C
T
F

P(S)
0.10
0.50

C
T
F

P(S)
0.10
0.50

C
T
F

P(S)
0.10
0.50

C
T
F

P(R)
0.80
0.20

C
T
F

P(R)
0.80
0.20

C
T
F

P(R)
0.80
0.20

S
T
T
F
F

R
T
F
T
F

P(W)
0.99
0.90
0.90
0.00

S
T
T
F
F

R
T
F
T
F

P(W)
0.99
0.90
0.90
0.00

S
T
T
F
F

R
T
F
T
F

S
T
T
F
F

R
T
F
T
F

P(W)
0.99
0.90
0.90
0.00

10

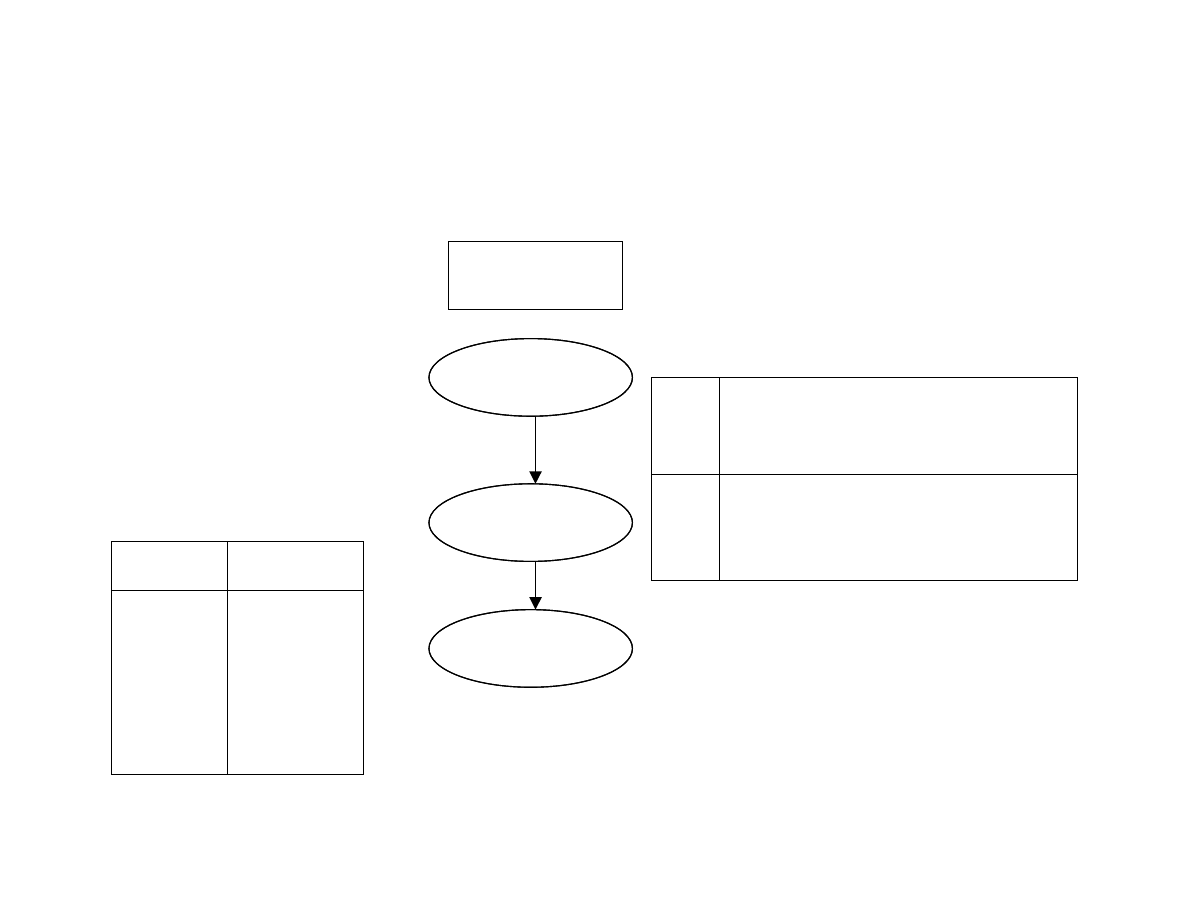
Przykªad sie¢ wielokrotnie poªaczona (2)

Cloudy

Cloudy

Spr+Rain

Spr+Rain

Wet grass

Wet grass

P(C)=0.5

P(C)=0.5

S +
T
T
F
F

R
T
F
T
F

P(W)
0.99
0.90
0.90
0.00

S +
T
T
F
F

R
T
F
T
F

P(W)
0.99
0.90
0.90
0.00

S +
T
T
F
F

R
T
F
T
F

S +
T
T
F
F

R
T
F
T
F

P(W)
0.99
0.90
0.90
0.00

C
T
F

P(S+R=x)

TT
.08
.40

TF
.02
.10

FT
.72
.40

FF
.18
.10

C
T
F

P(S+R=x)

TT
.08
.40

TF
.02
.10

FT
.72
.40

FF
.18
.10

C
T
F

P(S+R=x)

TT
.08
.40

TF
.02
.10

FT
.72
.40

FF
.18
.10

11

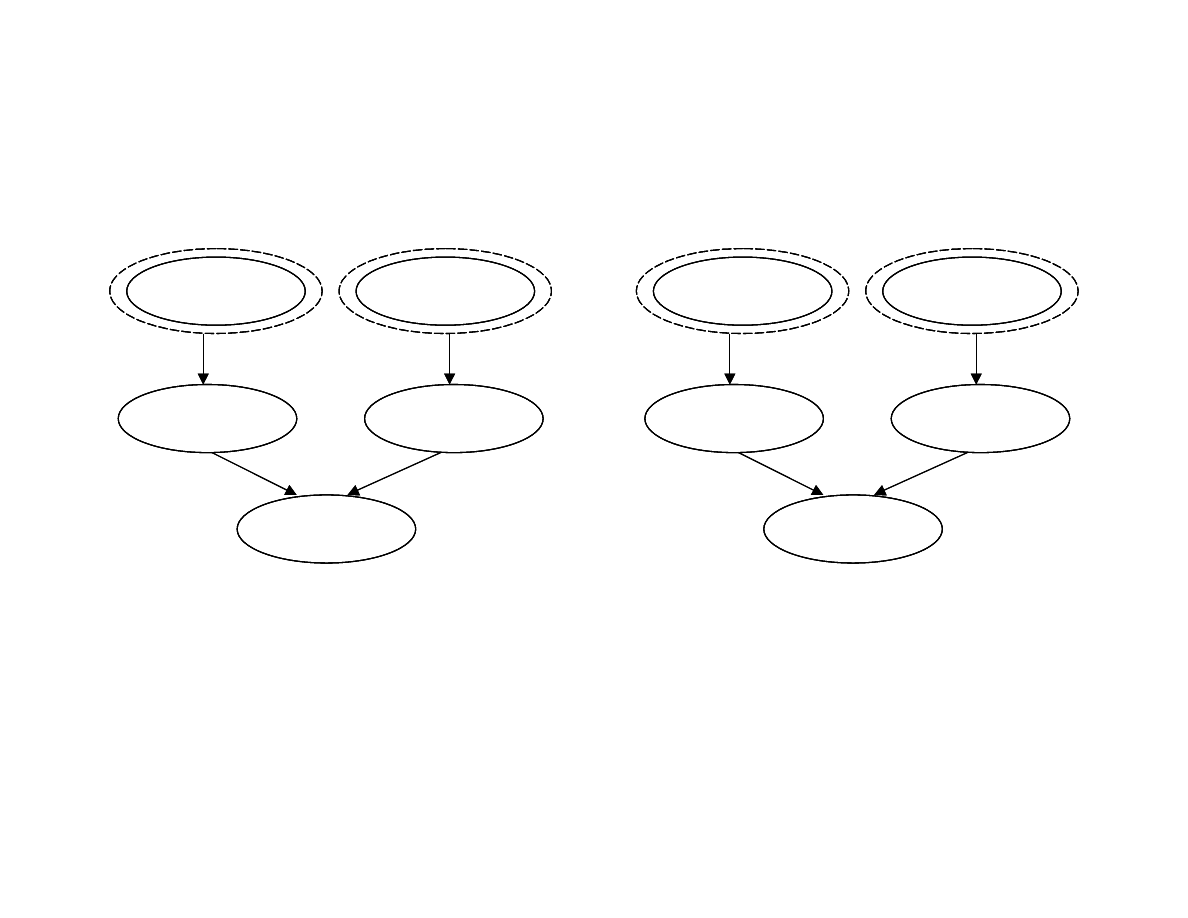
Przykªad sie¢ wielokrotnie poªaczona (2)

Sprinkler

Rain

Wet grass

+Cloudy

+Cloudy

Sprinkler

Sprinkler

Rain

Rain

Wet grass

Wet grass

+Cloudy

+Cloudy

+Cloudy

+Cloudy

Sprinkler

Rain

Wet grass

-Cloudy

-Cloudy

Sprinkler

Sprinkler

Rain

Rain

Wet grass

Wet grass

-Cloudy

-Cloudy

-Cloudy

-Cloudy

Transformacja polidrzewa na kilka prostszych polidrzew.

P(X|E)

jest obliczane jako ±rednia wa»ona warto±ci obliczonych

dla ka»dego polidrzewa

12

Metoda symulacji stochastycznej

•

Ka»da runde symulacji rozpoczyna losowy wybór warto±ci
dla ka»dego wezªa poczatkowego sieci (z uwzglednieniem
prawdopodobie«stw a priori)

•

Warto±ci w wezªach po±rednich przyjmuje sie losowo z uwzgled-
nieniem prawdopodobie«stw warunkowych

•

Po wystarczajacej liczbie iteracji estymuje sie

P(X|E) ≈ N(X ∧ E)/N(E)

gdzie N liczby uzyskanych wyników

13

Inne podej±cia do rozumowania niepewnego

•

Rozumowanie domy±lne (default reasoning)

•

Podej±cie bazujace na reguªach

•

Teoria Dempstera-Schafera

•

Zbiory rozmyte i logika rozmyta

14

Rozumowanie domy±lne (przykªad)

•

Widze samochód parkujacy na ulicy. Chocia» widze jedynie
jego trzy koªa, przyjmuje do wiadomo±ci, »e ma cztery koªa.

•

Ten wniosek przyjmuje domy±lnie, ze wzgledu na brak in-
nych dowodów wskazujacych na to, »e ten samochód ma
inna liczbe kóª ni» cztery.

•

Takie rozumowanie nie jest monotoniczne.

15

Metody bazujace na reguªach

•

Systemy bazujace na reguªach sa monotoniczne.

•

Przykªad: system MYCIN, w którym zastosowano stopie«
pewno±ci (certainty factor).

16

Reprezentowanie ignorancji

•

Stopie« przekonania to prawdopodobie«stwo zdarzenia, »e
dowody wspieraja stwierdzenie

•

Miara jest funkcja przekonania (belief ) Bel(X)

•

Dla poszczególnych zdarze« deniowane sa przedziaªy mini-
malnego i maksymalnego przekonania o sªuszno±ci danego
stwierdzenia

•

Szeroko±¢ przedziaªu odpowiada naszej niewiedzy; gdy jest
zbyt szeroki, nale»y zebra¢ dalsze dowody

17

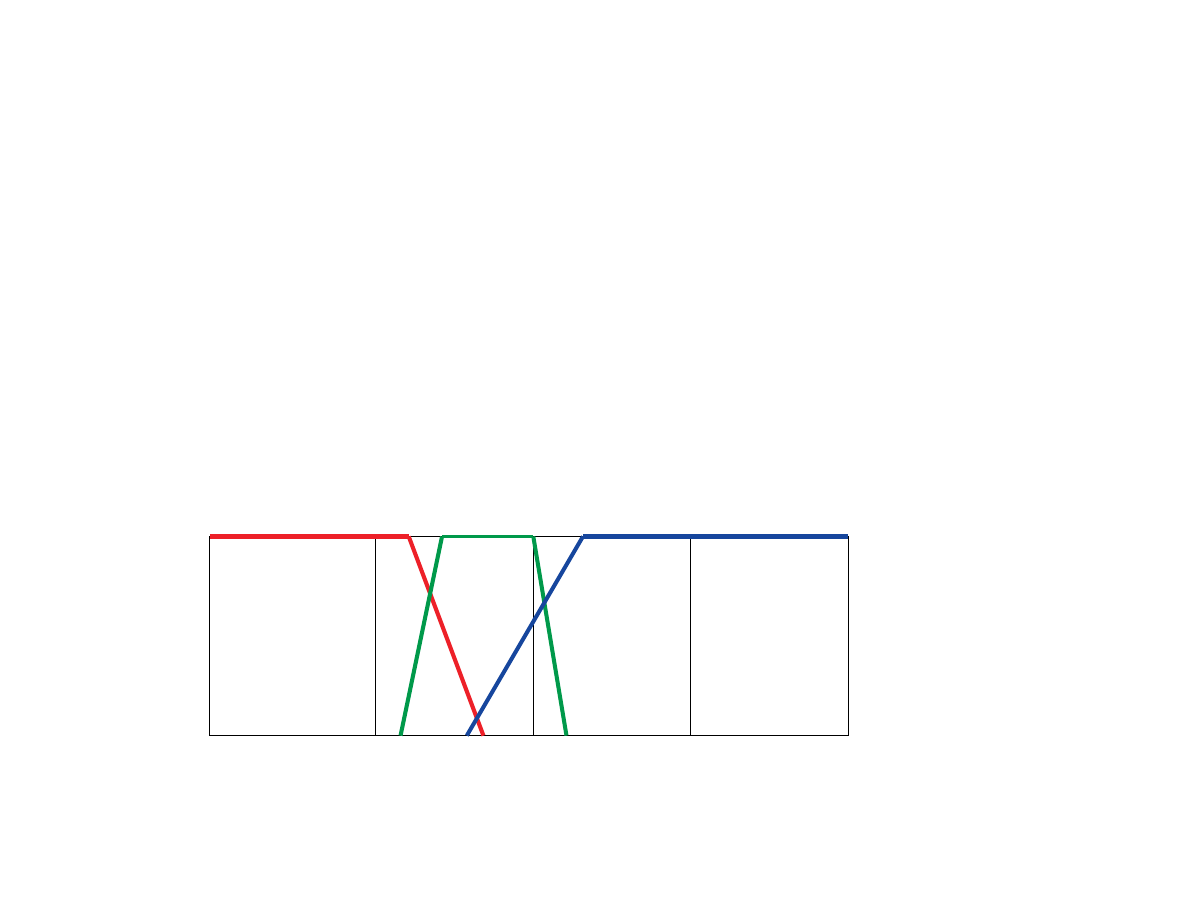
Zbiory rozmyte i logika rozmyta (1)

•

Rodzaj rozumowania niepewnego

•

Dla elementu deniuje sie dodatkowo funkcje przynale»no±ci

do danego zbioru

•

Mo»liwa jest przynale»no±¢ cze±ciowa

0

1

m(A)

100

140

180

220

260

18

Zbiory rozmyte i logika rozmyta (2)

•

W logice rozmytej rozwa»a sie rozmyty stopie« prawdzi-
wo±ci
T(A) =

stopie« prawdziwo±ci zdarzenia A

•

Reguªy obliczania T ( ) dla zda« zªo»onych:

T(A ∧ B) = min{T(A), T(B)}

T(A ∨ B) = max{T(A), T(B)}

T(

¬A) = 1 − T(A)

•

Uwaga!! T(A ∨ ¬A) 6= T(T rue)!!

19

Probabilistyczne systemy rozumowania

podsumowanie (1)

•

Warunkowa niezale»no±¢ umo»liwia strukturalizacje informa-
cji o niepewnej dziedzinie

•

Sieci przekona« sa naturalnym ±rodkiem reprezentacji infor-
macji o warunkowej niezale»no±ci

•

Sie¢ przekona« reprezentuje ªaczny rozkªad prawdopodobie«-
stwa dla danej dziedziny

20

Probabilistyczne systemy rozumowania

podsumowanie (2)

•

Rozumowanie w sieci przekona« polega na obliczeniu rozkªadu
prawdopodobie«stwa dla zbioru zmiennych zapytania, gdy
dany jest zbiór dowodów

•

Sieci przekona« sa najbardziej uniwersalne ze wzgl. na mo»li-
wo±¢ stosowania ró»nych typów wnioskowania (diagnosty-
czne, przyczynowe, miedzyprzyczynowe, mieszane)

21

Probabilistyczne systemy rozumowania

podsumowanie (3)

•

Stopie« zªo»ono±ci rozumowania w sieci przekona« zale»y od

struktury sieci (najªatwiej dla polidrzew)

•

Dla bardziej zªo»onych sieci istnieje wiele ró»nych metod

rozumowania

•

Do wnioskowania mo»na stosowa¢ stochastyczna symulacje

(wymaga mniej oblicze«)

•

Znanych jest wiele innych metod wnioskowania z uwzglednie-

niem niepewno±ci

22

Uczenie (si¦) na podstawie ob-

serwacji

23

Gªówna idea

•

Percepcje s¡ wykorzystywane nie tylko do wyboru odpowied-
niej akcji, lecz tak»e do powi¦kszania zdolno±ci systemu
wnioskowania (agenta) do dziaªania w przyszªo±ci (ucze-
nia si¦)

•

Uczenie si¦ zachodzi jako wynik interakcji pomi¦dzy sys-
temem wnioskowania (agentem) i otoczeniem

•

Jest wiele form uczenia, od zapami¦tywania do tworzenia
zªo»onych teorii

24

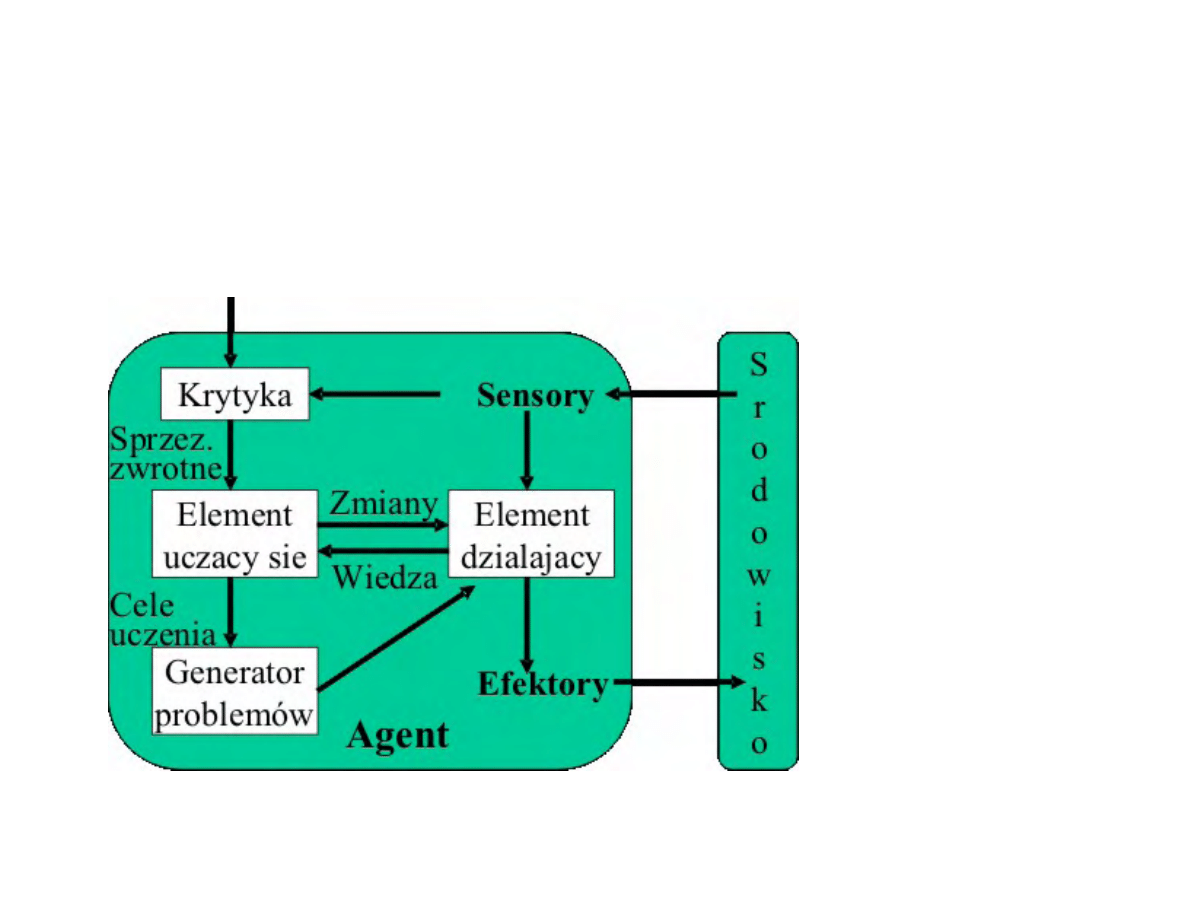
Ogólny model systemu wnioskowania

(agenta) ucz¡cego si¦ (1)

25

Ogólny model systemu wnioskowania

(agenta) ucz¡cego si¦ (2)

•

Element ucz¡cy si¦ - odpowiada za dokonywanie ulepsze«

•

Element dziaªaj¡cy - odpowiada za wybór zewn¦trznych
dziaªa«

•

Krytyka - dostarcza elementowi ucz¡cemu si¦ informacji o
tym, jak dobrze dziaªa agent

•

Generator problemów - sugeruje akcje, które b¦d¡ prowadzi¢
do nowych i informatywnych do±wiadcze«

26

Ogólny model systemu wnioskowania

(agenta) ucz¡cego si¦ (3)

•

Dost¦pne sprz¦»enia zwrotne:

uczenie nadzorowane (agent zna zarówno percepcje, jak

i wynik ich klasykacji)

uczenie ze wzmocnieniem (agent jest nagradzany lub

karany, w zale»no±ci od wyniku akcji; klasykacja nie jest

agentowi znana)

uczenie nienadzorowane (klasykacja nieznana)

•

Rola wiedzy podstawowej - uczenie zwi¦ksza nieznacznie

wiedz¦ posiadan¡ przez agenta

27

Indukcja drzew decyzyjnych

•

Jeden z najprostszych algorytmów uczenia maszynowego

•

Šatwa do wdro»enia

28

Cechy drzew decyzyjnych

•

Obiekty s¡ opisane przez zbiory ich cech

•

Drzewo zwraca klasykacj¦ (decyzj¦) TAK/NIE (mog¡ by¢
przypadki wieloklasowe - bardziej ogólne)

•

Drzewo reprezentuje funkcj¦ Boolowsk¡

29

Budowa drzewa decyzyjnego

•

Ka»dy wewn¦trzny w¦zeª odpowiada testowi dotycz¡cemu
warto±ci jakiego± atrybutu

•

Ka»dej kraw¦dzi wychodz¡cej z danego w¦zªa przyporz¡d-
kowana jest jedna warto±¢ atrybutu w¦zªowego

•

Li±ciom przyporz¡dkowane s¡ warto±ci Boolowskie, zwracane
je±li osi¡gni¦to dany li±¢

30

Przykªad: czy czeka¢ na stolik?

•

Alternate: w pobli»u jest
inna restauracja?

•

Bar: czy w restauracji jest
bar gdzie mo»na poczeka¢?

•

Fri/Sat: Pi¡tek/Sobota

•

Hungry: jeste± gªodny?

•

Patrons: ile jest ludzi w
restauracji?

•

Price: zakres cen

•

Raining: czy pada?

•

Reservation: czy zarezer-
wowali±my wcze±niej?

•

Type: rodzaj restauracji -
chi«ska, wªoska, Burger.

•

WaitEstimate: szacowany
czas oczekiwania w min.

31

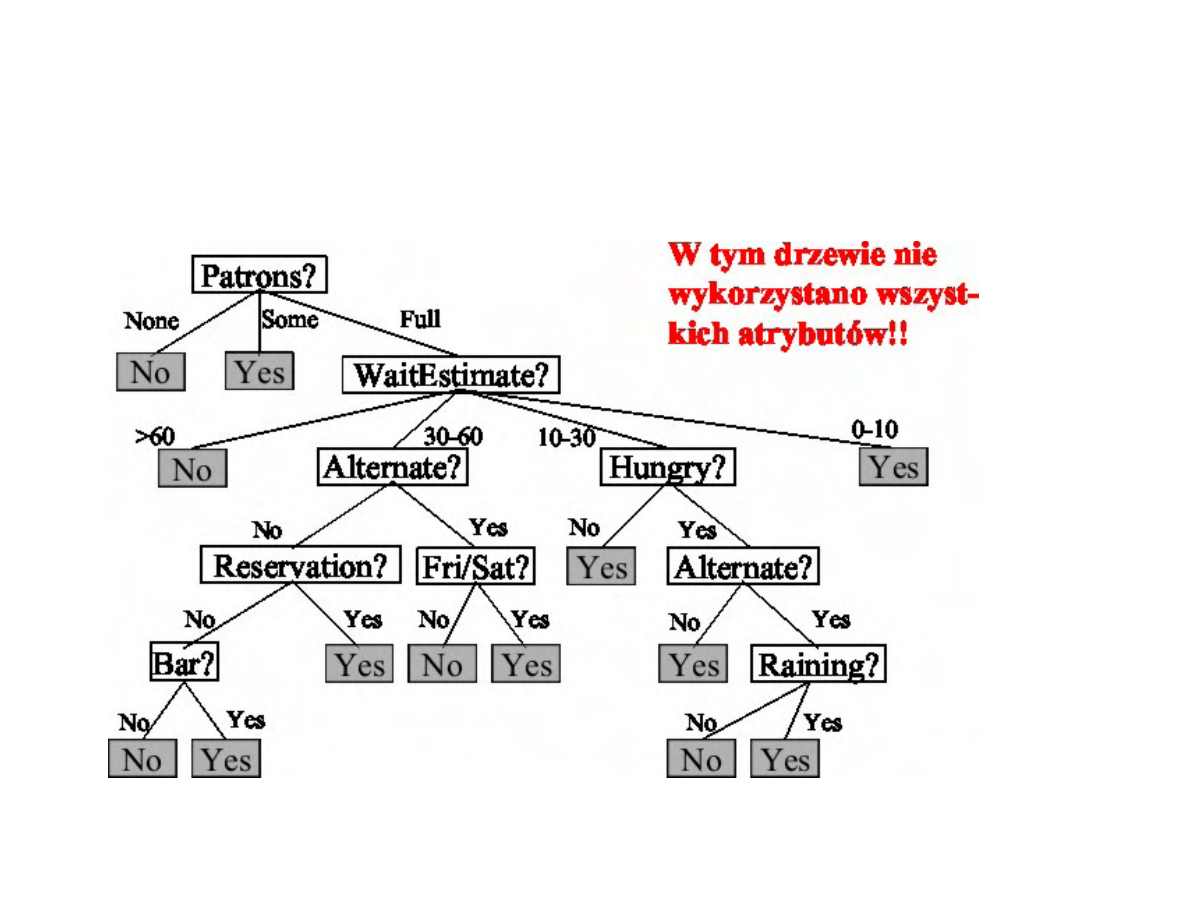
Czy czeka¢ na stolik?

32

Indukcja drzew decyzyjnych ze zbioru przykªadów

•

Przykªad opisywany jest przez warto±ci atrybutów (warunku)
oraz przez warto±¢ atrybutu decyzyjnego

•

Przykªady tworz¡ zbiór trenuj¡cy

•

Brzytwa Ockhama:
Najbardziej prawdopodobna jest najprostsza spo±ród hipotez
zgodnych ze wszystkimi obserwacjami

33

Algorytm indukcji drzew decyzyjnych

34

Algorytm indukcji drzew decyzyjnych

35

Uwagi dotycz¡ce indukcji drzew

•

Podstawowy problem - wybór

•

Indukcja niezupeªna (nie mamy wszystkich mo»liwych przy-
kªadów)

•

Programy realizuj¡ce uczenie maszynowe dziaªaj¡ bardzo szy-
bko i efektywnie

•

Drzewa decyzyjne mog¡ by¢ bardzo rozbudowane - cz¦sto si¦
je przycina kosztem nieco gorszej sprawno±ci klasykacji

36

Ocena sprawno±ci algorytmu uczenia (1)

•

Zgromad¹ dostatecznie liczny zbiór przykªadów

•

Podziel go na rozª¡czne zbiory: trenuj¡cy i testowy

•

Stosuj¡c zbiór trenuj¡cy jako przykªady, uzyskaj indukcyjnie

hipotez¦ H

•

Stosuj¡c przykªady testowe, okre±l jaka ich cz¦±¢ jest po-

prawnie klasykowana przez H

•

Powtarzaj te kroki dla zbiorów trenuj¡cych ró»nych wiel-

ko±ci, losowo wybieranych

37

Ocena sprawno±ci algorytmu uczenia (2)

•

Ilo±¢ informacji [bity] zawartej w poprawnej odpowiedzi, gdy zbiór trenu-

j¡cy zawiera p przykªadów pozytywnych i n negatywnych:

I(

p

p + n

,

n

p + n

) =

−

p

p + n

log

2

p

p + n

−

n

p + n

log

2

n

p + n

(2)

•

Ilo±¢ informacji dost¦pna po testowaniu atrybutu A:

P ozostalo(A) =

ν

X

i=1

p

i

+ n

i

p + n

I(

p

i

p

i

+ n

i

,

n

i

p

i

+ n

i

)

(3)

Atrybut A dzieli zbiór E na podzbiory E

1

, . . . , E

ν

; p

i

, n

i

to liczby przykªadów

pozytywnych i negatywnych w tym podzbiorze

•

Przyrost ilo±ci informacji:

Gain(A) = I(

p

p + n

,

n

p + n

)

− P ozostalo(A)

(4)

38

Zwi¦kszenie mo»liwo±ci zastosowania drzew

decyzyjnych

•

Brakuj¡ce dane (nie zapisane; zbyt kosztowne ich uzyskanie)

•

Atrybuty wielowarto±ciowe

•

Atrybuty o warto±ciach ci¡gªych (rzeczywistych) - wyma-
gana dyskretyzacja

39

Niektóre problemy

•

Bª¦dne dane (np. sprzeczne przykªady - takie same warto±¢
atrybutów warunku, ró»ne warto±ci atrybutu decyzyjnego)
drzewo klasykuje bª¦dnie

•

Nadmierne dopasowanie zbyt szczegóªowy klasykator, du»o
bª¦dów dla nowych przykªadów

•

Rada - PRZYCINANIE DRZEWA

40

Podstawowe pytanie

Sk¡d wiadomo, »e algorytm uczenia pozwoliª utworzy¢ teori¦,
która b¦dzie poprawna?

41

Odpowied¹ intuicyjna

•

Ka»da hipoteza, która jest powa»nie bª¦dna, zostanie na
pewno znaleziona z wysokim prawdopodobie«stwem jedynie
dla maªej liczby przykªadów, poniewa» to prowadziªoby do
bª¦dnych przewidywa«

•

Wniosek:
Jest nieprawdopodobne, »eby hipoteza zgodna z wystar-
czaj¡co licznym zbiorem trenuj¡cym, byªa powa»nie bª¦d-
na

•

Uczenie PAC (Probably Approximately Correct)

42

Ile potrzeba przykªadów (1)?

• X

zbiór wszystkich mo»liwych przykªadów

• D

rozkªad prawdopodobie«stwa, z którego losuje si¦ przykªady

• H

zbiór mo»liwych hipotez

• f ∈ H

prawdziwa funkcja, któr¡ staramy si¦ przybli»y¢ za

pomoc¡ hipotezy h ∈ H

• m

- liczba przykªadów w zbiorze trenuj¡cym

43

Ile potrzeba przykªadów (2)?

•

Bª¡d (h ∈ H ró»ne od aproksymowanej funkcji f):

error(h) = P{h(x) 6= f (x) | x wylosowane z D}

(5)

•

Hipoteza jest w przybli»eniu poprawna, je±li dla maªej liczby
ε

:

error(h) ≤ ε

(6)

•

Gdy δ dopuszczalne prawdopodobie«stwo bª¦dnej hipotezy:

m ≥

1

ε

ln

1

δ

+ ln

|H|

(7)

44

Podsumowanie (1)

•

Zdolno±¢ uczenia si¦ systemu wnioskowania (agenta) jest is-
totna ze wzgl¦du na dziaªanie w nieznanym ±rodowisku

•

W systemie wnioskowania (agencie) ucz¡cym si¦ mo»na wyró»ni¢:

element dziaªaj¡cy, odpowiedzialny za wybór akcji

element ucz¡cy (si¦), odpowiedzialny za modykowanie

elementu dziaªaj¡cego

•

Mo»liwe s¡ ró»ne formy uczenia, ze wzgl¦du na: element
dziaªaj¡cy, sprz¦»enia zwrotne oraz dost¦pn¡ wiedz¦

45

Podsumowanie (2)

•

Uczenie si¦ jakiegokolwiek skªadnika elementu dziaªaj¡cego
mo»e by¢ interpretowane jako uczenie si¦ aproksymacji
funkcji

•

Uczenie si¦ aproksymacji funkcji na podstawie przykªadów
nazywa si¦ uczeniem indukcyjnym

•

Drzewa decyzyjne s¡ skutecznym ±rodkiem uczenia si¦ zde-
terminowanych funkcji Boole'a

46

Podsumowanie (3)

•

Brzytwa Ockhama sugeruje wybór najprostszej hipotezy pa-
suj¡cej do obserwowanych przykªadów

•

Okre±lenie najwi¦kszego przyrostu informacji umo»liwia
znalezienie prostych drzew decyzyjnych

•

Osi¡gi algorytmu uczenia indukcyjnego okre±la si¦ za pomoc¡
ª¡cznego bª¦du klasykacji

47