
M. Zając, Hybrid Achromatic Spectacle Lens
1
HYBRID ACHROMATIC SPECTACLE LENS
Marek Zając
Institute of Physics
Wrocław University of Technology
Wybrzeże Wyspiańskiego 27
PL 50-370 Wrocław, Poland
e-mail: zajac@if.pwr.wroc.pl
Key words:
hybrid lens, spectacle lens, aberrations.
ABSTRACT
Spectacle lens is a very particular optical imaging element of great practical importance. Although its
construction is very simple some demands are specific (in particular remarkable shift of output pupil). A
number of classic spectacle lens designs is known for long time, however some new possibilities of
aberration correction appear if we use a hybrid (diffractive-refractive).
Hybrid lens is an optical system composed of a classic refractive ("glass") lens and a diffractive
microstructure deposited on one of its surfaces. Imaging properties of such lens can be expressed in
terms of dimensionless parameters:
2
1
ρ
ρ
−
=
ζ
(describing the shape of refractive part),
β
α
=
β
z
z
(describing the geometry of diffraction fringes) and
R
D
Φ
Φ
=
/
η
(describing the distribution of focusing
power between diffractive and refractive part). By proper choice of parameter η we can compensate
chromatic aberration. Thanks to other free parameters astigmatism can be corrected also what is
reasonable choice for spectacle lens.
In this contribution the possibilities of particular Seidel aberration correction of hybrid lens are be
presented. As an illustration some examples of spectacle hybrid lenses are shown and its imaging
characteristics compared with imaging characteristics of commercially available refractive lenses.

M. Zając, Hybrid Achromatic Spectacle Lens
2
I. INTRODUCTION
Single lens of spherical surfaces has limited possibilities of aberration correction. In particular it is
impossible to correct chromatic aberration. This effect is very inconvenient for spectacle wearers [1-3].
In conventional optics it is possible to correct chromatic aberration but at least two lenses are necessary
if limiting to thin lenses only. Unfortunately doublets are not useful for spectacles. Correction of
chromatic aberration can be easily obtained if using hybrid lens [4 - 7].
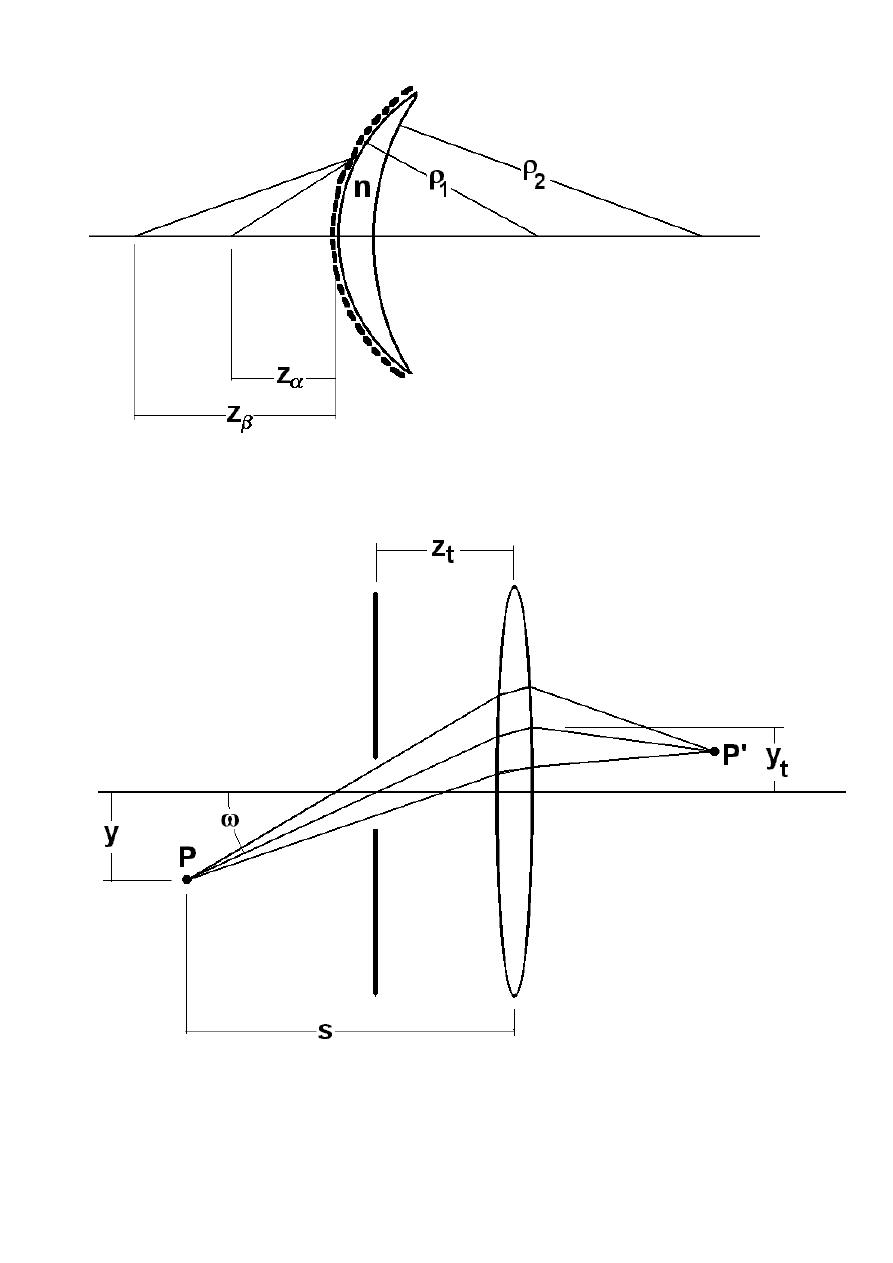
As a hybrid lens, in this paper, a refractive lens made of glass of refractive index
n and having
spherical surfaces of radii of curvature equal ρ
1
and ρ
2
is considered. On one of its surfaces (let us
assume: the first) there is deposited diffractive microstructure of fringe geometry equivalent to
interference field generated by two spherical waves of wavelength λ originated from the points,
P
α
and
P
β
, located on the lens axis in the distances
z
α
and
z
β
from the lens. - see Figure 1. This structure can be
manufactured interferometrically or, better, synthetically with a kinoform profile which assures high
diffraction efficiency. Object point to be imaged is located in the point P of coordinates (
y, s) and its
image is formed in the point P' of coordinates (
y', s')
II. MONOCHROMATIC ABERRATIONS OF HYBRID LENS
In the following text we use dimensionless parameters describing construction parameters of the lens
as well as imaging geometry. The shape of refractive part is defined by the ratio ζ of curvature radii of
both surfaces:
2
1
ρ
ρ
−
=
ζ
. We remind that
1
<
ζ
describes positive meniscus lens,
0
1
<
ζ
<
describes
negative meniscus lens. The diffractive structure is defined by the parameter
β
α
=
β
z
z
, and the ratio of
diffraction refraction focusing powers is given by parameter
R
D
Φ
Φ
=
η
. The location of object point
is defined by the parameters expressing the field-of-view angle
s
y /
=
ω
and normalized object distance
s
⋅
Φ
= /
1
ν
.
It can be shown [5, 6, 9, 10] that III-order Seidel aberration coefficients (S for spherical aberration, C
for coma, F for field curvature and A for astigmatism) of hybrid lens with diffractive microstructure
deposited on the first surface, and input pupil in contact with this surface are expressed as follows
ζ
+
−
−
β
−
µ
βη
β
−
ζ
+
−
−
β
−
µ
η
β
−
η
+
η
+
+
η
+
ζ
+
−
−
+
ζ
+
η
+
η
+
η
+
η
+
η
+
ζ
+
+
+
+
η
+
ζ
+
−
−
η
+
η
+
η
+
η
+
η
+
ζ
+
+
−
+
η
+
ζ
+
−
ζ
+
+
+
−
η
+
ζ
+
−
−
Φ
=
2
2
3
2
2
2
2
2
2
3
)
1
)(
1
(
1
)
1
(
)
1
)(
1
(
1
)
1
(
)
1
(
)
1
(
)
1
)(
1
)(
1
(
1
1
1
)
1
)(
1
(
1
1
)
1
)(
1
)(
1
(
1
1
1
)
1
)(
1
(
1
1
)
1
)(
1
)(
1
(
1
)
1
(
)
1
)(
1
)(
1
(
1
n
n
n
n
n
v
v
n
n
v
v
n
n
v
v
n
v
v
S
, (1)
+
+
+
+
+
+
−
+
+
+
+
−
+
+
+
−
+
+
−
−
Φ
=
η
η
η
ζ
η
η
ζ
ζ
η
ζ
ω
1
)
1
)(
1
(
1
)
1
)(
1
(
1
)
1
)(
1
)(
1
(
1
(
)
1
(
)
1
)(
1
)(
1
(
1
2
v
n
n
n
v
v
n
v
v
C
, (2)
+
+
Φ
−
=
)
1
(
1
1
2
η
ω
n
F
, (3)
2
ω
Φ
−
=
A
. (4)

M. Zając, Hybrid Achromatic Spectacle Lens
3
Coefficient describing distortion equals zero by identity.
The above expressions were derived under assumption that the object pupil coincides with the lens
surface. Otherwise the input pupil shift on the distance
t
z in front of the lens results in the perpendicular
shift of center of the lens acting area on the amount
t
y - see Figure 2
t
t
t
z
z
y
⋅
ν
−
⋅
ω
=
1
. (5)
This causes change in aberration coefficients. Resulting aberration coefficients for the lens with
shifted pupil can be expressed by the respective coefficients of the lens with pupil in contact and value
t
y
S
S
t
=
, (6)
S
y
C
C
t
t
⋅
−
=
, (7)
S
y
C
y
A
A
t
t
t
⋅
+
⋅
−
=
2
2
, (8)
S
y
C
y
F
F
t
t
t
⋅
+
⋅
−
=
2
2
, (9)
S
y
C
y
F
y
A
y
D
D
t
t
t
t
t
⋅
−
⋅
+
⋅
−
⋅
−
=
3
2
3
2
. (10)
Coefficients A ,
C
, A , F , D are formally identical to the coefficients S, C, A, F, D but all
coordinates y are replaced by
t
y
y
− therein.
In the case of spherical aberration the respective expression does not depend on coordinate y so
S
S
≡
. Similarly is for the rest of coefficients if the object is located in infinity. Only for finite object
distance the value y appears explicitly in the above equations since
s
y
=
ω
.
In consequence the III-order aberration coefficients of hybrid lens can be expressed by a number of
parameters depending on construction of the lens (η, ζ, β) as well as imaging geometry (ν, z
t
). Proper
choice of these parameters allows to correct chosen aberrations.
III. CORRECTION OF CHROMATIC ABERRATION
The main advantage of hybrid lens is in possibility of chromatic aberration correction. The condition
for achromatisation for two wavelengths
λ
1
and
λ
2
is [6]
R
D
R
D
ν
ν
η
λ
−
=
Φ
Φ
=
0
0
, (11)
where
D
ν
is Abbe number of the lens material and
D
ν
its equivalent for diffractive structure defined
as
2
1
0
λ
−
λ
λ
=
ν
D
, (12)
where λ
0
is the base wavelength.
The Abbe number for diffractive structure has opposite sign than the Abbe number for optical glass.
In consequence both parts of achromatic hybrid doublet have the same sign of focusing power.
Moreover, since the value of Abbe number of diffractive part is smaller than this for refractive part
M. Zając, Hybrid Achromatic Spectacle Lens
4
approximately on an order of magnitude the diffractive structure bears only small part of the overall
focusing power, which is advantageous for technological reasons.
Unfortunately hybrid lens has considerable secondary spectrum.
Φ
=
Φ
−
−
=
∆
γ
ν
ν
D
R
D
R
P
P
s
s
2
'
'
, (13)
where s' is an image distance and P
R
and P
D
are partial dispersions of glass and its refractive structure
equivalent
2
1
0
1
λ
−
λ
λ
−
λ
=
D
P
. (14)
IV. CORRECTION OF MONOCHROMATIC ABERRATION
The imaging properties of achromatic hybrid lens are described by three parameters
η
0
, ζ and β; while
the last two are still unspecified. Therefore we can compensate two monochromatic aberrations. In the
case of spectacle lens it is reasonable to correct astigmatism. From the equation (7) it is seen that it is
easy to find condition for astigmatism correction if additionally S = 0.
Inserting (1), (2) and (5) into (7) and assuming that S = 0 we receive the equation from which the
value of parameter ζ
0
assuring correction of astigmatism can be found
+
+
+
+
+
+
−
+
+
+
+
−
+
+
+
−
+
+
−
−
−
Φ
=
0
0
0
0
0
0
1
)
1
)(
1
(
1
)
1
)(
1
(
1
)
1
)(
1
)(
1
(
1
(
)
1
(
)
1
)(
1
)(
1
(
1
1
1
η
η
η
ζ
η
η
ζ
ζ
η
ζ
v
n
n
n
v
v
n
v
v
vz
z
t
t
. (15)
For the object in infinity (ν = 0) we have the following solution
(
)
[
]
(
)(
) (
)(
)
[
]
Φ
+
+
−
+
+
−
+
+
Φ
=
t
t
z
n
n
n
n
z
2
1
1
1
1
1
1
1
2
0
2
0
0
0
η
η
η
ζ
. (16)
For near vision, i.e. if ν ≠ 0, the respective formula becomes rather complicated and hardly readable
so we do not give it here, however there are no problems in its exploiting if using any computer program
for symbolic calculations.
Finally we have to find the value of parameter β defining the diffractive microstructure inserting
values η
0
and ζ
0
found from (11) and (16) into formula (1) and solving the equation
0
)
,
,
,
,
(
0
0
=
β
η
ζ
ν
n
S
. (17)
Solving this equation by means of any symbolic calculation computer program we get two solutions
for β
0
. In consequence we have hybrid spectacle lens of corrected sphero-chromatic aberration and
astigmatism. Its construction parameters are expressed by parameters η
0
, ζ
0
, β
0
and Φ as follows
1
0
0
0
1
1
1
1
1
1
−
+
ζ
+
η
−
Φ
=
ρ
n
, (18)
1
0
0
0
2
1
1
1
1
−
+
ζ
ζ
+
η
−
Φ
=
ρ
n
, (19)

M. Zając, Hybrid Achromatic Spectacle Lens
5
1
0
0
0
1
1
1
−
α
β
−
+
η
η
Φ
=
z
, (20)
1
0
0
0
0
1
1
−
β
β
−
β
+
η
η
Φ
=
z
, (21)
V. EXAMPLES
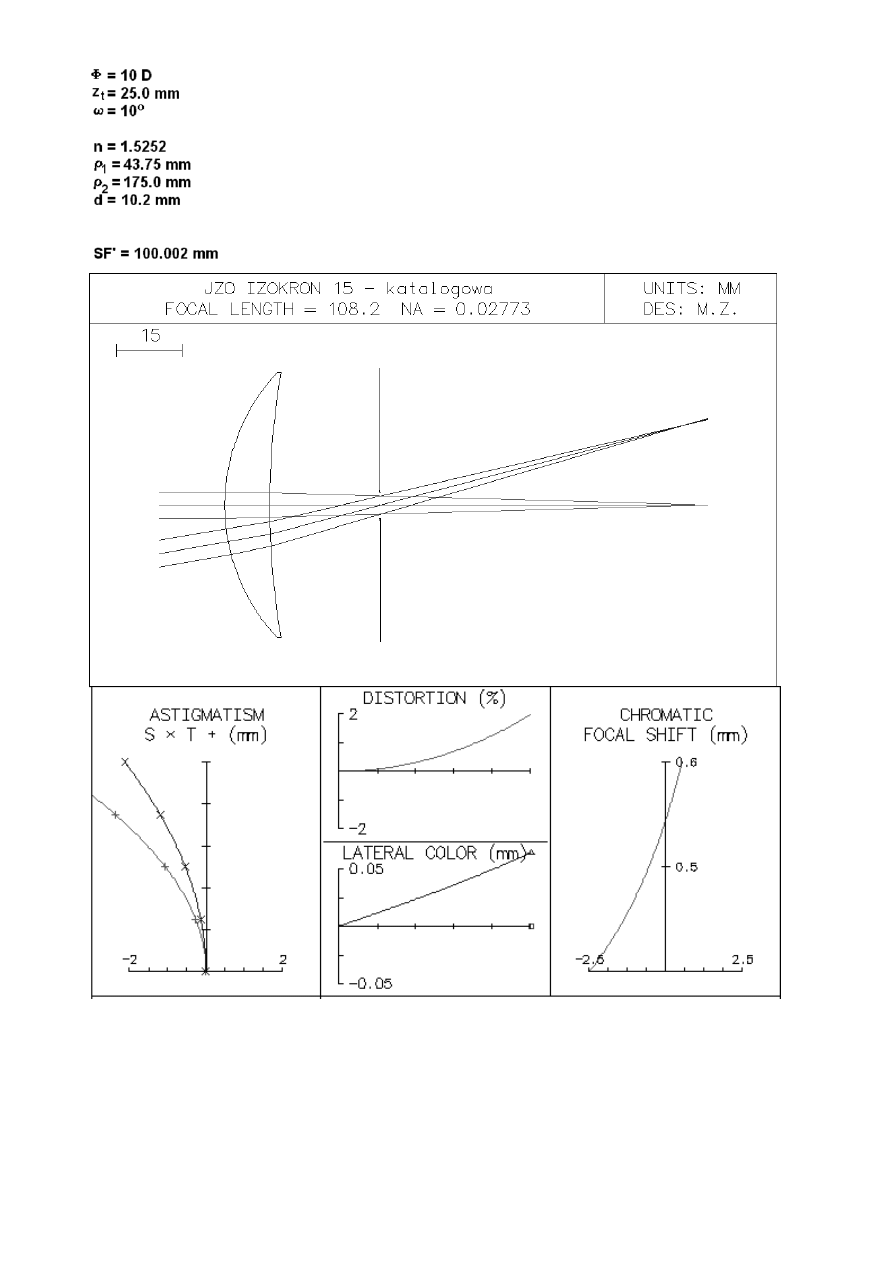
In order to illustrate the above calculations we analyzed examples of positive lens of high focusing
power (Φ = +10 D) made of two kinds of optical glass: standard crown type glass and high index glass.
In spite of remarkable chromatic aberration optical glasses of n > 1.7 are now widely used since they
allow to design thinner lenses of more flat surfaces.
The construction parameters of thin achromatic hybrid lens of corrected spherical aberration and
astigmatism are calculated according to the procedure presented in previous paragraph. As a base
wavelength λ
e
= 0.5460 nm was taken, and the achromatisation interval is limited by λ
F
= 04861 nm and
λ
d
= 0.5876 nm. Such choice is justified by the spectral sensitivity of human eye. For photopic (day)
vision the eye has maximum sensitivity around the wavelength λ
e
. On the blue end of the spectrum
sensitivity falls to about 19% for λ
F
and at the red end to about 27% for λ
HeNe
= 0.6328 nm [1]. It was
assumed that object is placed in infinity (spectacles for distant vision) and astigmatism is corrected for
field angle ω=10
o
. Aberration characteristics of the designed lenses were calculated with help of typical
computer program [14]. Since real lens cannot be infinitely thin the construction parameters have to be
changed slightly in order to assure thickness according to technology demands. New parameters were
found in such way that front focal plane of the lens was unchanged and aberrations remain the same or
even smaller. The necessary correction of construction parameters can be easily performed with help of
any lens design program (e.g. [14]).
For comparison typical commercially available glass lenses were considered [15]. Due to technology
limitations the catalogue lenses not always have optimally corrected aberrations. Therefore we modified
slightly its radii of curvature to minimize aberrations.
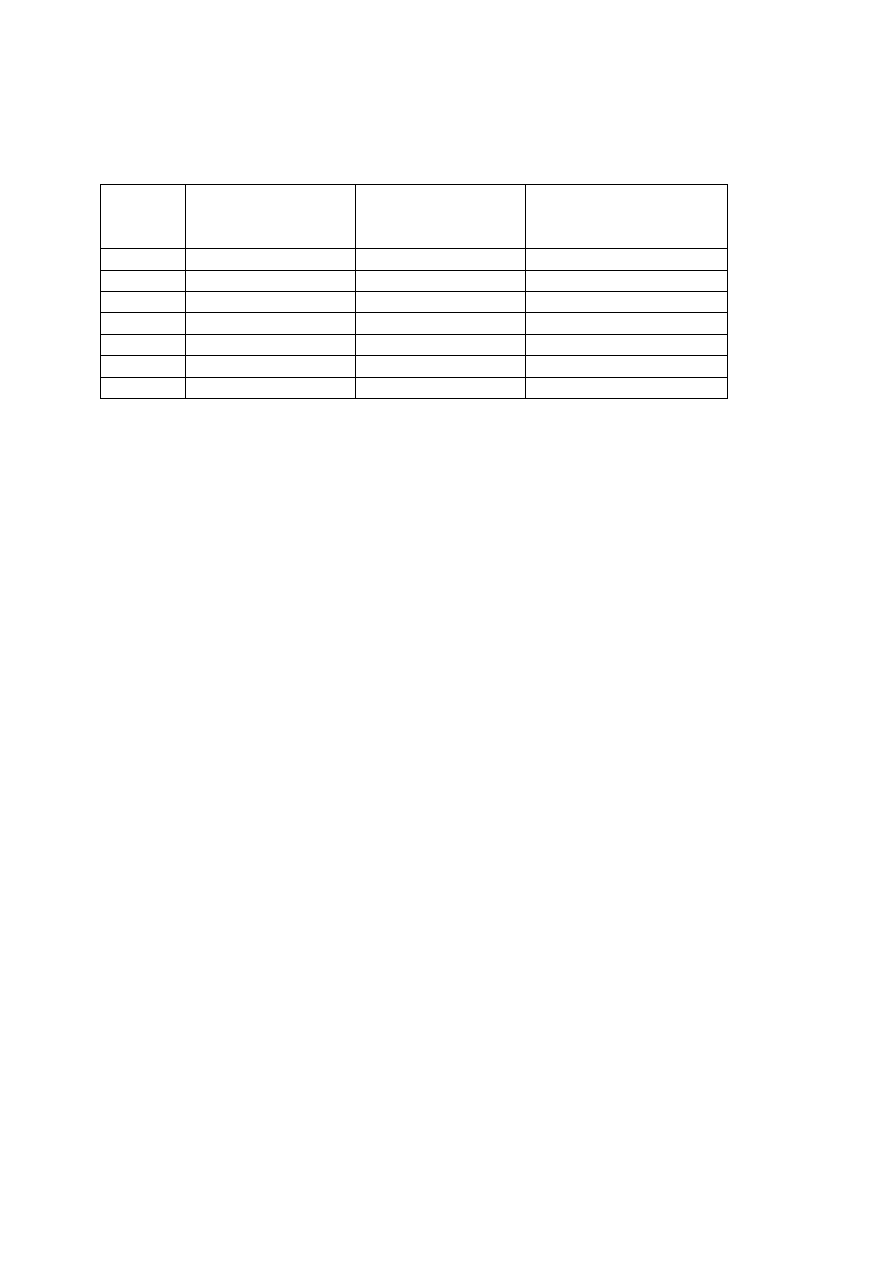
The construction parameters of exemplary lenses are collected in Table 1 and the aberration
characteristics of these lenses are presented in Figures 3 - 5.
VI. CONCLUSIONS
Presented examples prove that it is possible to design hybrid spectacle lens of relatively high focusing
power with astigmatism and chromatic aberration compensated substantially better than in the case of
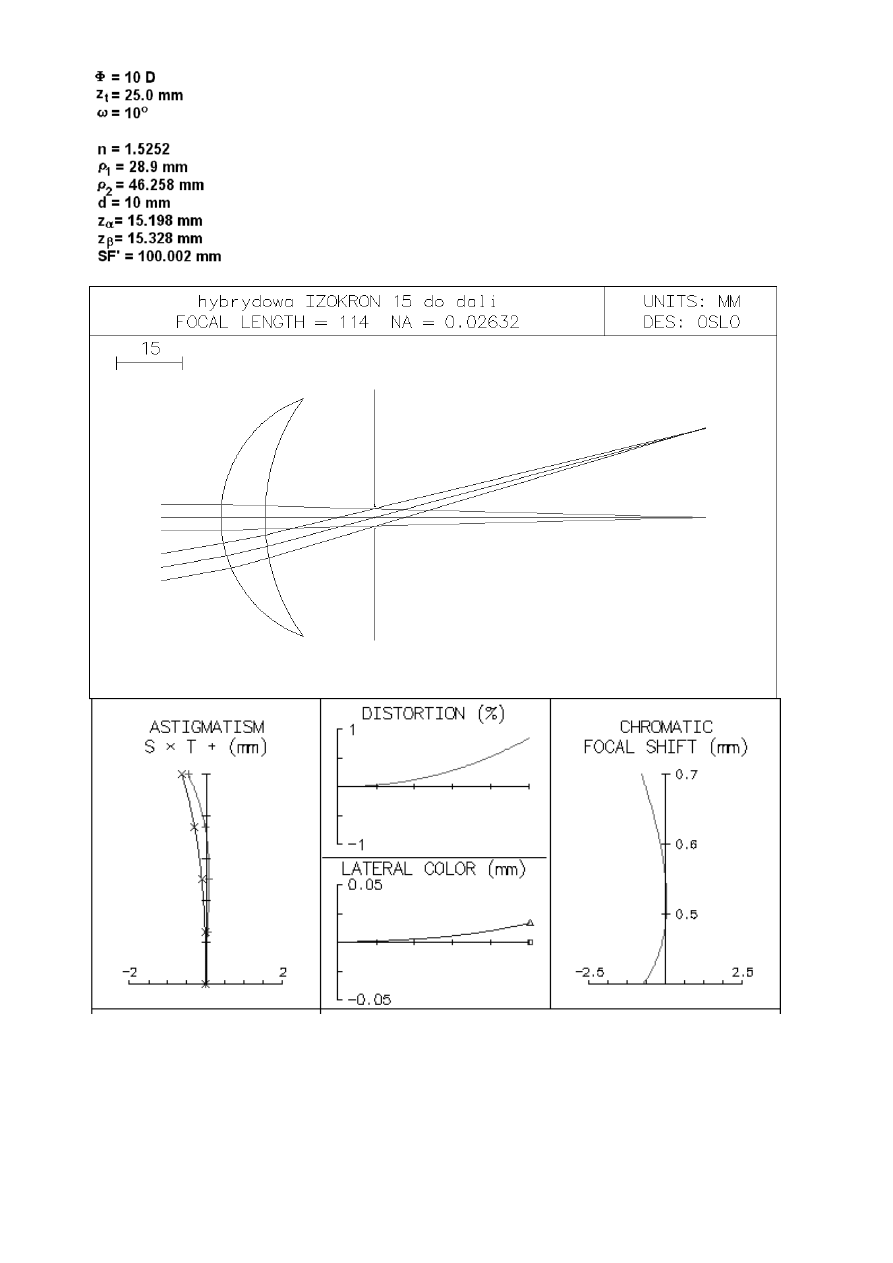
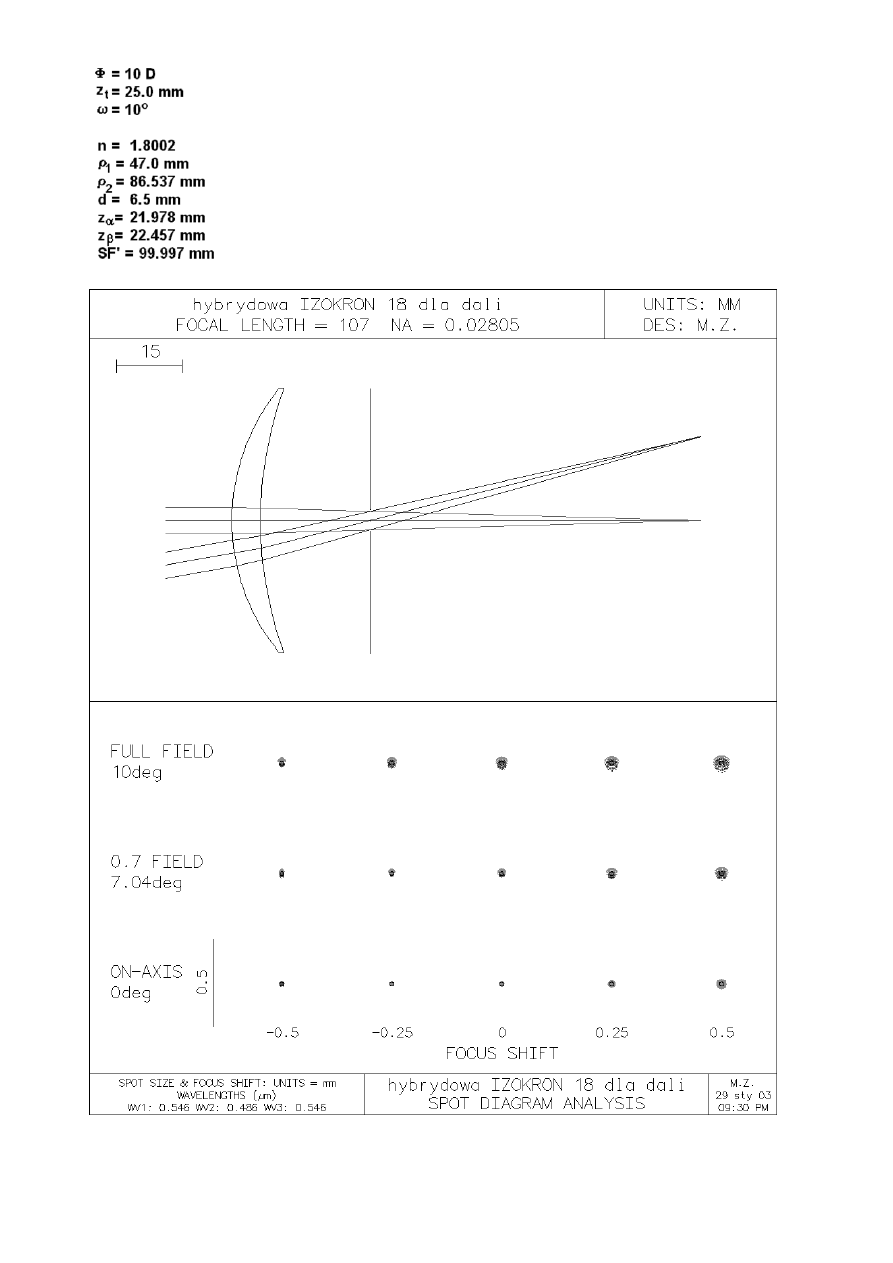
spherical glass lens. As it can be seen on figures 5 and 6 field curvature does not exceed 1 mm for the
whole field. For the lens of focusing power equal to 10 D it corresponds to 0.1 D and is fully acceptable.
Astigmatic difference is even smaller. Lateral color aberration is smaller than 0.025 mm what, for focal
length 100 mm, corresponds to approximately 0.9 angular minutes and is very small. Additionally
spherochromatic aberration is corrected.
ACKNOWLEDGMENT
This paper was presented at XIV Polish-Czech-Slovak Optical Conference "Wave and Quantum Aspects
of Contemporary Optics" Krzyżowa, 14-17 September 2002.

M. Zając, Hybrid Achromatic Spectacle Lens
6
REFERENCES
1. Kaiser P. M., Boynton R. M. Human color vision, OSA, Washington 1996.
2. Rynders M. C., Navarro R., Losada M.A. “Objective measurement of the off-axis longitudinal
chromatic aberration in the human eye”, Vis. Res., vol. 38, no. 4 (1998) 513-522.
3. Faubert J., Simonet P., Gresset J. “Effects of induced transverse chromatic aberration from an afocal
prismatic lens on spatio-temporal sensitivity”, Ophthalmic & Physiolo. Optics, vol. 19, no. 4 (1999)
336-346.
4. O'Shea D. C. “Specifying dispersion in the design of diffractive optics”, Applied Optics, vol.33,
no.34 (1994) 8124-8130.
5. Zając M., Nowak J., Dubik B. “On the possibility of sphero-chromatic aberration correction of single
holo-lens used as a spectral device”, Optica Applicata, vol.21, no.1 (1991) 33-47.
6. Koth S., Nowak J., Zając M. “Achromatic hybrid lens with corrected astigmatism and field
curvature”, Optik, vol. 106 (1997) 63-68.
7. Sweatt W., C. “Describing holographic optical elements as lenses”, J. Opt. Soc. Am., vol.67, no.6
(1977) 803-808.
8. Jagoszewski E., “Holographic optical elements”, Ofic. Wyd. Pol. Wrocł., Wrocław 1995 [in Polish].
9. Nowak J., Pietraszkiewicz K., Zając M., “Diffractive optical elements”, Ofic. Wyd. Pol.. Wrocł.
1997 [in Polish].
10. Nowak J, Zając M. “Design methodology of hybrid lens”, SPIE Proc, vol. 3829 (1998) 479-498.
11. Zhao, Liping; Lam, Yee Loy ; Zhou, Yan ; Yun, Zhisheng “Design of planar-binary optical visor”,
Proc SPIE; vol. 3778 (1999) 11-18
12. Zając M., Sawicz P., Nowak J. "Astigmatism and field curvature of hybrid imaging surface" Opt.
Appl., vol. 31 no 4 (2001) 799-806.
13. Zając M. "Possibilities of aberration correction in a single spectacle lens" Opt. Appl., vol. 31 no 4
(2001) 815-833;
14. OSLO LIGHT Programme, Sinclair Optics Ltd.
15. Courtesy JZO Sp.z o.o., Jelenia Gora, Poland.
M. Zając, Hybrid Achromatic Spectacle Lens
7
Table 1
Construction parameters of exemplary lenses
parameter
Hybrid lens,
crown glass
Hybrid lens,
high index glass
Modified commercial
glass lens
IZOKRON 15
n
d
1.5252
1.8002
1.5252
ρ
1
28.9
47.0
43.75
ρ
2
46.258
86.537
175.0
d
10
6.5.0
10.2
z
α
15.198
21.9780
-
z
β
15.328
22.457
-
SF'
100.02
99.997
99.94
M. Zając, Hybrid Achromatic Spectacle Lens
8
Fig. 1. Hybrid lens.
Fig. 2. Imaging by a lens with shifted input pupil.
M. Zając, Hybrid Achromatic Spectacle Lens
9
Fig. 3. Refractive lens (IZOKRON 15
) and its imaging characteristics.
M. Zając, Hybrid Achromatic Spectacle Lens
10
Fig. 4. Hybrid lens (crown glass) and its imaging characteristics.
M. Zając, Hybrid Achromatic Spectacle Lens
11
Fig. 5. Hybrid lens (high index glass) and its imaging characteristics.
Wyszukiwarka
Podobne podstrony:
Correction of Aperture Aberrations of Hybrid Lens
A New Hybrid Transmission designed for FWD Sports Utility Vehicles
HybridEp40 Transit Bus
Existence of the detonation cellular structure in two phase hybrid mixtures
Sedum hybridum
EasyConn Hybrid PL
In+maleficiis+voluntas+spectatur, Prawo, [ Prawo rzymskie ]
Audi Q5 hybrid quatro, od 2011
Hybridization14Demo
6D.Koniczyna szwedzka, Koniczyna szwedzka (białoróżowa) (Trifolium hybridum L
Hybrid Stepper Motors OK ok!!!
Lens
New hybrid drying technologies for heat sensitive foodstuff (S K Chou and K J Chua)
NMB HYBRID SERIES STEP MOTORS katalog
Caliber and?atures?tails for Seiko Quartz Hybrid Watches
Audi A8 hybrid, od 2012
P90X Turbofire Hybrid Worksheets
Hybrid Inorganic Organic Materials by Sol Gel Processing of Organofunctional Metal Alkoxides (2)
Nonlinear Control of a Conrinuously Variable Transmission (CVT) for Hybrid Vehicle Powertrains
więcej podobnych podstron