KINEMATYKA PUNKTU
Poło
ż
enie punktu w przestrzeni okre
ś
lamy przez podanie jego współrz
ę
dnych. Ruch
punktu, to zmiana poło
ż
enia punktu odniesiona (podzielona) do czasu.
Pr
ę
dko
ść
punktu mówi jak szybko zmienia si
ę
poło
ż
enie punktu.
Przyspieszenie punktu mówi jak szybko zmienia si
ę
pr
ę
dko
ść
punktu.
Pr
ę
dko
ś
ci
ą
ś
redni
ą
nazywamy wektor:
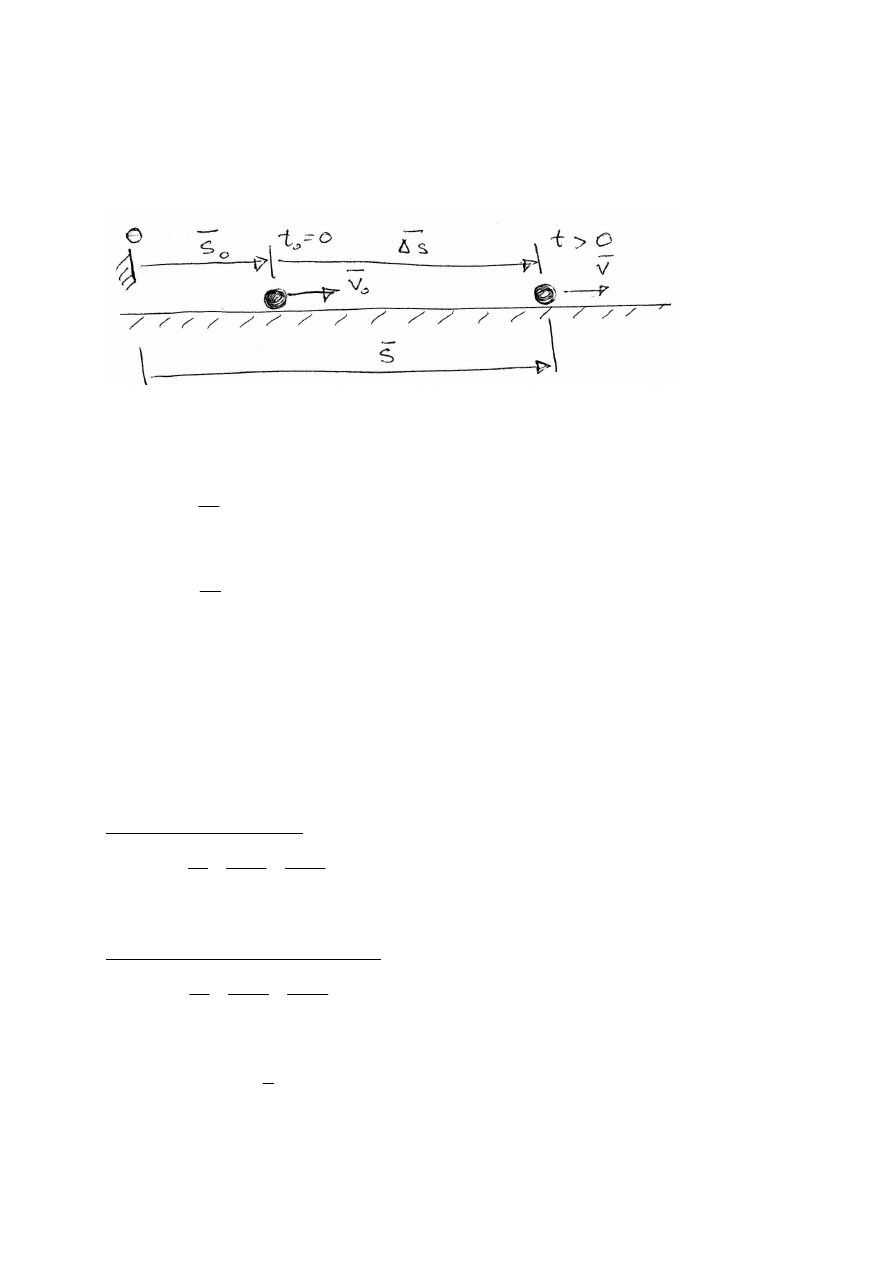
sr
s
v
t
=
△
△
0
s
s
s
= −
△
0
t
t
t
= −
△
Przyspieszeniem
ś
rednim nazywamy wektor:
sr
v
a
t
=
△
△
0
v
v
v
= −
△
0
t
t
t
= −
△
0
t
– chwila pocz
ą
tkowa
0
0
t
=
t
– ko
ń
cowa chwila czasu
t
△
– przyrost czasu – przedział czasu
0
s
– współrz
ę
dna punktu w chwili
0
0
t
=
, poło
ż
enie pocz
ą
tkowe
s
– współrz
ę
dna punktu w chwili
t
s
△
– przyrost współrz
ę
dnej drogowej – przyrost drogi
v
– pr
ę
dko
ść
punktu
a
– przyspieszenie punktu
Ruch jednostajny punktu – je
ż
eli pr
ę
dko
ść
punktu jest stała
0
0
0
s
s
s
s
s
v
const
t
t
t
t
−
−
=
=
=
=
−
△
△
0
s
s
vt
= +
–
równanie ruchu jednostajnego
Ruch jednostajnie zmienny punktu – je
ż
eli przyspieszenie punktu jest stałe
0
0
0
v v
v v
v
a
const
t
t
t
t
−
−
=
=
=
=
−
△
△
– równanie pr
ę
dko
ś
ci w ruchu jednostajnie zmiennym
– równanie ruchu jednostajnie zmiennego
0
s
,
0
v
,
a
– to wielko
ś
ci, które mog
ą
by
ć
dodatnie b
ą
d
ź
ujemne
0
2
0
0
1
2
v
v
at
s
s
v t
at
= +
= +
+
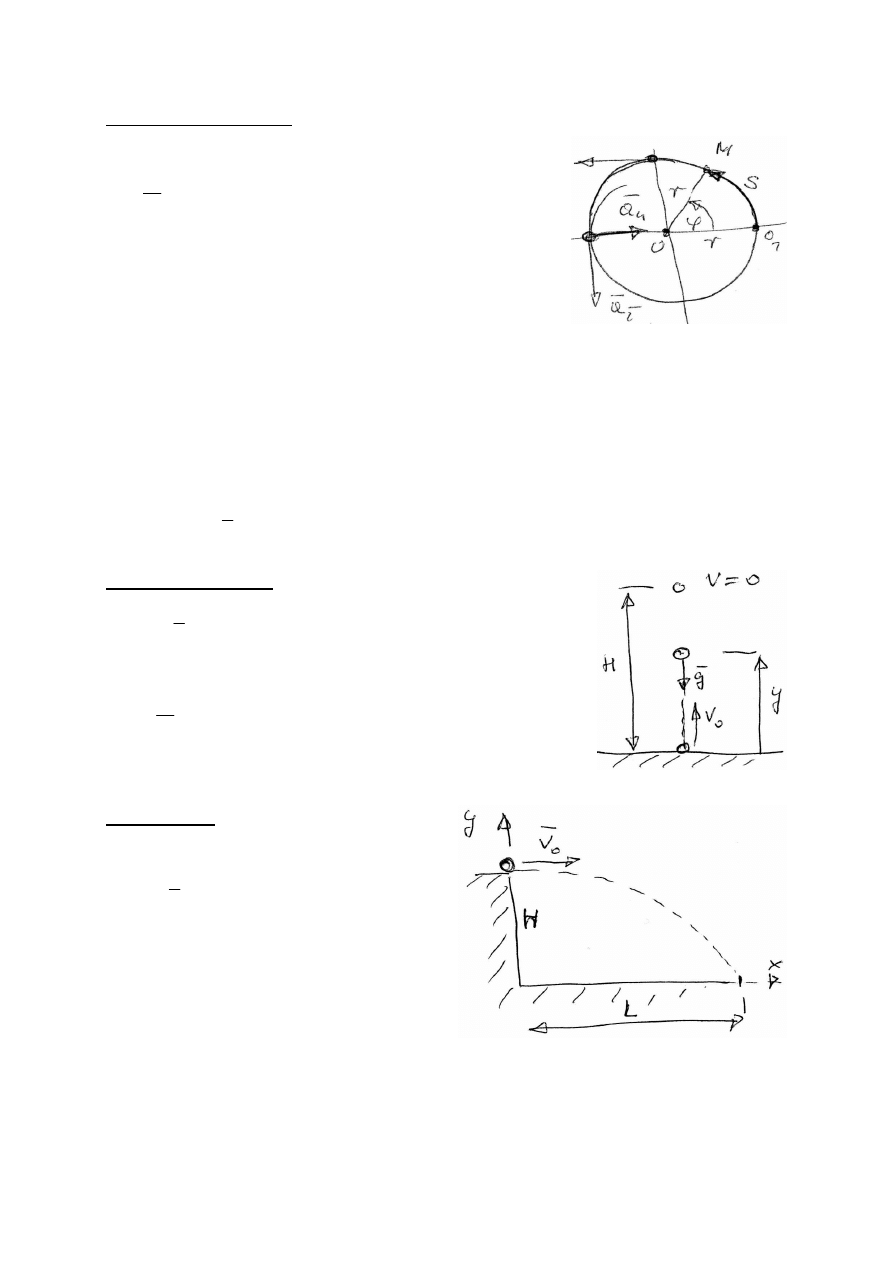
Ruch punktu po okr
ę
gu – mo
ż
e by
ć
jednostajny lub jednostajnie zmienny
v
– pr
ę
dko
ść
punktu jest zawsze styczna do toru
2
n
v
a
r
=
– przyspieszenie normalne, zawsze skierowane
do
ś
rodka krzywizny toru
a
τ
– przyspieszenie styczne – zawsze styczne do toru
n
a
a
τ
⊥
– zawsze
s
r
ϕ
=
,
v
r
ω
=
,
a
r
τ
ε
=
,
2
n
a
r
ω
=
ω
– pr
ę
dko
ść
k
ą
towa promienia
r
ε
– przyspieszenie k
ą
towe promienia
r
ϕ
– k
ą
t obrotu promienia
r
0
t
ϕ ϕ ω
=
+
– ruch jednostajny promienia
r
– pr
ę
dko
ść
k
ą
towa promienia
r
w ruchu jednostajnie zmiennym
– równanie ruchu jednostajnie zmiennego promienia
r
Rzut pionowy punktu
2
0
1
2
y
v t
g t
=
−
– równanie ruchu
0
v
v
g t
= −
– równanie pr
ę
dko
ś
ci
2
10
m
g
s
≈
– przyspieszenie ziemskie
Rzut poziomy
0
2
1
2
x
v t
y
H
g t
=
= −
równania ruchu
0
x
y
v
v
v
g t
=
= −
równania pr
ę
dko
ś
ci
L
– zasi
ę
g rzutu
0
2
0
0
1
2
t
t
t
ω ω ε
ϕ ϕ ω
ε
=
+
=
+
+
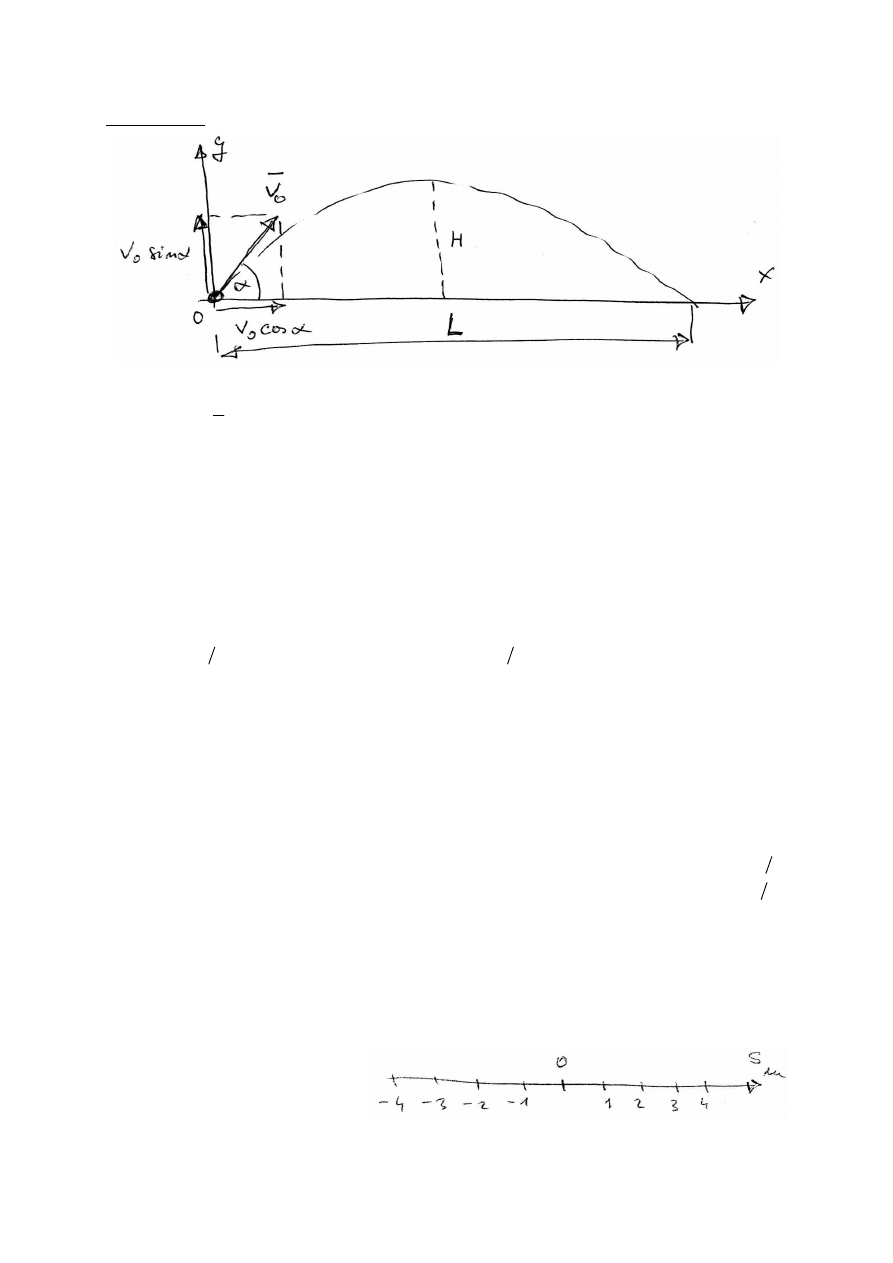
Rzut uko
ś
ny
0
2
0
cos
1
sin
2
x
v
t
y
v
t
g t
α
α
=
=
−
równania ruchu
0
0
cos
sin
x
y
v
v
v
v
g t
α
α
=
=
−
równania pr
ę
dko
ś
ci
H
– maksymalna wysoko
ść
rzutu
L
– zasi
ę
g rzutu
Zadania
1. Dwa pojazdy poruszaj
ą
si
ę
wzdłu
ż
tej samej drogi. Pojazd A z pr
ę
dko
ś
ci
ą
1
50
v
km h
=
, pojazd B z pr
ę
dko
ś
ci
ą
2
30
v
km h
=
. Przy drodze znajduj
ą
si
ę
dwie
miejscowo
ś
ci M
1
i M
2
odległe od siebie o 100 km. Wyznacz odległo
ść
mi
ę
dzy
pojazdami:
a) je
ś
li wyruszyły z miejscowo
ś
ci M
1
w tej samej chwili i poruszaj
ą
si
ę
w tym
samym kierunku;
b) je
ś
li wyruszyły z miejscowo
ś
ci M
1
w tej samej chwili i poruszaj
ą
si
ę
w przeciwnych kierunkach.
Pojazd A wyruszył z M
1
w kierunku M
2
, pojazd B z M
2
w tej samej chwili
i poruszaj
ą
si
ę
w tym samym kierunku. Wyznacz gdzie i kiedy si
ę
spotkaj
ą
.
2. Pojazd A wyruszył z miejscowo
ś
ci M
1
w kierunku M
2
z pr
ę
dko
ś
ci
ą
1
70
v
km h
=
a pojazd B z miejscowo
ś
ci M
2
w kierunku M
1
z pr
ę
dko
ś
ci
ą
2
50
v
km h
=
.
Odległo
ść
mi
ę
dzy miejscowo
ś
ciami wynosi 240 km. Gdzie i kiedy spotkaj
ą
si
ę
pojazdy?
3. Zaznacz na rysunku poło
ż
enie i wektor pr
ę
dko
ś
ci punktu w chwilach
0
0
t
=
,
1
1
t
s
=
,
2
2
t
s
=
je
ż
eli:
a)
2
3 [ ]
s
t m
= +
b)
2
3 [ ]
s
t m
= − +
c)
2
3 [ ]
s
t m
= −
d)
2
3 [ ]
s
t m
= − −
4. Poci
ą
g o długo
ś
ci
120
l
m
=
porusza si
ę
z pr
ę
dko
ś
ci
ą
1
50
v
km h
=
. Jak długo
b
ę
dzie mijał człowieka:
a) stoj
ą
cego przy torze;
b) poruszaj
ą
cego si
ę
z pr
ę
dko
ś
ci
ą
2
10
v
km h
=
w stron
ę
przeciwn
ą
do pr
ę
dko
ś
ci
poci
ą
gu.
5. Pojazd przejechał pewien odcinek
drogi w ci
ą
gu
50 min
z pr
ę
dko
ś
ci
ą
jak
na wykresie. Ustal jego pr
ę
dko
ść
ś
redni
ą
.
6. Ci
ęż
ki pojazd wyruszył z miejsca postoju z pr
ę
dko
ś
ci
ą
27 km h
, a
3 min .
pó
ź
niej
wyjechał za nim goniec na motocyklu by dostarczy
ć
informacj
ę
. Obliczy
ć
po jakim
czasie i w jakiej odległo
ś
ci od miejsca postoju goniec dogoni pojazd, je
ż
eli
pr
ę
dko
ść
motocyklisty wynosiła
72 km h
.
7. Łód
ź
płyn
ą
c w gór
ę
rzeki (pod pr
ą
d) z jednej miejscowo
ś
ci do drugiej odległych
o
30km
pokonuje t
ą
odległo
ść
w czasie
45 min
, a płyn
ą
c w dół rzeki (z pr
ą
dem) –
w czasie
30 min
. Obliczy
ć
pr
ę
dko
ść
łodzi wzgl
ę
dem wody oraz pr
ę
dko
ść
nurtu
rzeki.
8. Prom przepływa w poprzek rzeki z przystani A do B le
żą
cych na jednej linii
prostopadłej do nurtu rzeki. Pr
ę
dko
ść
nurtu rzeki
2
r
v
km h
=
, pr
ę
dko
ść
promu
wzgl
ę
dem wody
4
p
v
km h
=
. Pod jakim k
ą
tem do linii brzegu ma płyn
ąć
prom by
trafił do przeciwległej przystani, je
ż
eli szeroko
ść
rzeki
100 3
d
m
=
.
9. Pojazd ruszył z miejsca i ruchem jednostajnie przyspieszonym przebył drog
ę
200
s
m
=
, osi
ą
gaj
ą
c pr
ę
dko
ść
ko
ń
cow
ą
10
v
m s
=
. Oblicz przyspieszenie
pojazdu oraz czas w jakim to si
ę
zdarzyło.
10. Pojazd jad
ą
cy z pr
ę
dko
ś
ci
ą
0
30
v
m s
=
zahamował w czasie
15
t
s
=
. Oblicz
drog
ę
hamowania.
11. Punkt porusza si
ę
ze stanu spoczynku z przyspieszeniem
2
4
a
m s
=
. Oblicz jak
ą
b
ę
dzie miał
ś
redni
ą
pr
ę
dko
ść
w ci
ą
gu pierwszych 5 sekund od
0
t
do
1
t
i w ci
ą
gu
kolejnych 5 sekund od
1
t
do
2
t
.
0
0
t
=
,
1
5
t
s
=
,
2
10
t
s
=
12. Z balonu na wysoko
ś
ci
500
H
m
=
odczepiono worek z piaskiem, który spada
swobodnie.
a) jak długo b
ę
dzie spadał worek.
b) z jak
ą
pr
ę
dko
ś
ci
ą
zetknie si
ę
z ziemi
ą
.
c) jak
ą
pr
ę
dko
ść
b
ę
dzie miał w połowie wysoko
ś
ci.
d) okre
ś
l jego poło
ż
enie i pr
ę
dko
ść
w chwili
1
5
t
s
=
.
13. Kamie
ń
został wyrzucony w gór
ę
z pr
ę
dko
ś
ci
ą
0
20
v
m s
=
. Oblicz wysoko
ść
na
jak
ą
si
ę
wzniesie oraz czas wznoszenia. Jak długo kamie
ń
b
ę
dzie spadał z tej
wysoko
ś
ci i jak
ą
b
ę
dzie miał pr
ę
dko
ść
w chwili upadku?
14. Rozwi
ąż
zadanie Galileusza: z punktu A le
żą
cego na
obwodzie koła o
ś
rednicy
d
w płaszczy
ź
nie pionowej
poprowadzono ci
ę
ciwy. Traktuj
ą
c ka
ż
d
ą
z nich jako
równi
ę
oblicz ile czasu b
ę
dzie si
ę
zsuwa
ć
z punktu A bez
tarcia ciało zanim osi
ą
gnie obwód koła.
15. W
chwili,
gdy
autobus
jad
ą
cy
ruchem
jednostajnym
z
pr
ę
dko
ś
ci
ą
1
20
v
m s
=
przeje
ż
d
ż
ał obok stoj
ą
cego samochodu, ten ruszył z przyspieszeniem
2
2
a
m s
=
w pogoni za autobusem. Kiedy, gdzie i z jak
ą
pr
ę
dko
ś
ci
ą
samochód
dogoni autobus?
16. Jakie przyspieszenie normalne ma samochód poruszaj
ą
cy si
ę
na zakr
ę
cie
o promieniu krzywizny
200
r
m
=
z pr
ę
dko
ś
ci
ą
0
10
v
m s
=
?
17. Karuzela wykonuje w ci
ą
gu minuty
30
n
=
obrotów. Oblicz jak
ą
pr
ę
dko
ść
liniow
ą
i przyspieszenie normalne ma człowiek, który siedzi na karuzeli. Promie
ń
toru, po
którym porusza si
ę
człowiek wynosi
4
r
m
=
.
18. Wagon został wepchni
ę
ty na pochylni
ę
o nachyleniu 3% z pr
ę
dko
ś
ci
ą
0
18
v
km h
=
. Obliczy
ć
drog
ę
, jak
ą
przeb
ę
dzie wagon do chwili zatrzymania.
19. Pocisk wystrzelono poziomo z pr
ę
dko
ś
ci
ą
0
2 10
v
m s
=
z wysoko
ś
ci
100
H
m
=
.
Wyznaczy
ć
czas, po jakim pocisk spadnie na ziemi
ę
oraz k
ą
t nachylenia wektora
pr
ę
dko
ś
ci do pionu w chwili zetkni
ę
cia pocisku z ziemi
ą
.
20. Pod jakim k
ą
tem do poziomu trzeba rzuci
ć
ciało aby zasi
ę
g rzutu równał si
ę
najwi
ę
kszej wysoko
ś
ci na jak
ą
si
ę
wzniesie?
21. Pocisk wystrzelono pod k
ą
tem
60
α
=
do poziomu z pr
ę
dko
ś
ci
ą
400 m s
.
Wyznacz maksymaln
ą
wysoko
ść
na jak
ą
wzniesie si
ę
pocisk, czas do chwili
upadku, zasi
ę
g rzutu, pr
ę
dko
ść
z jak
ą
pocisk uderzy w ziemi
ę
.