ZAD 63

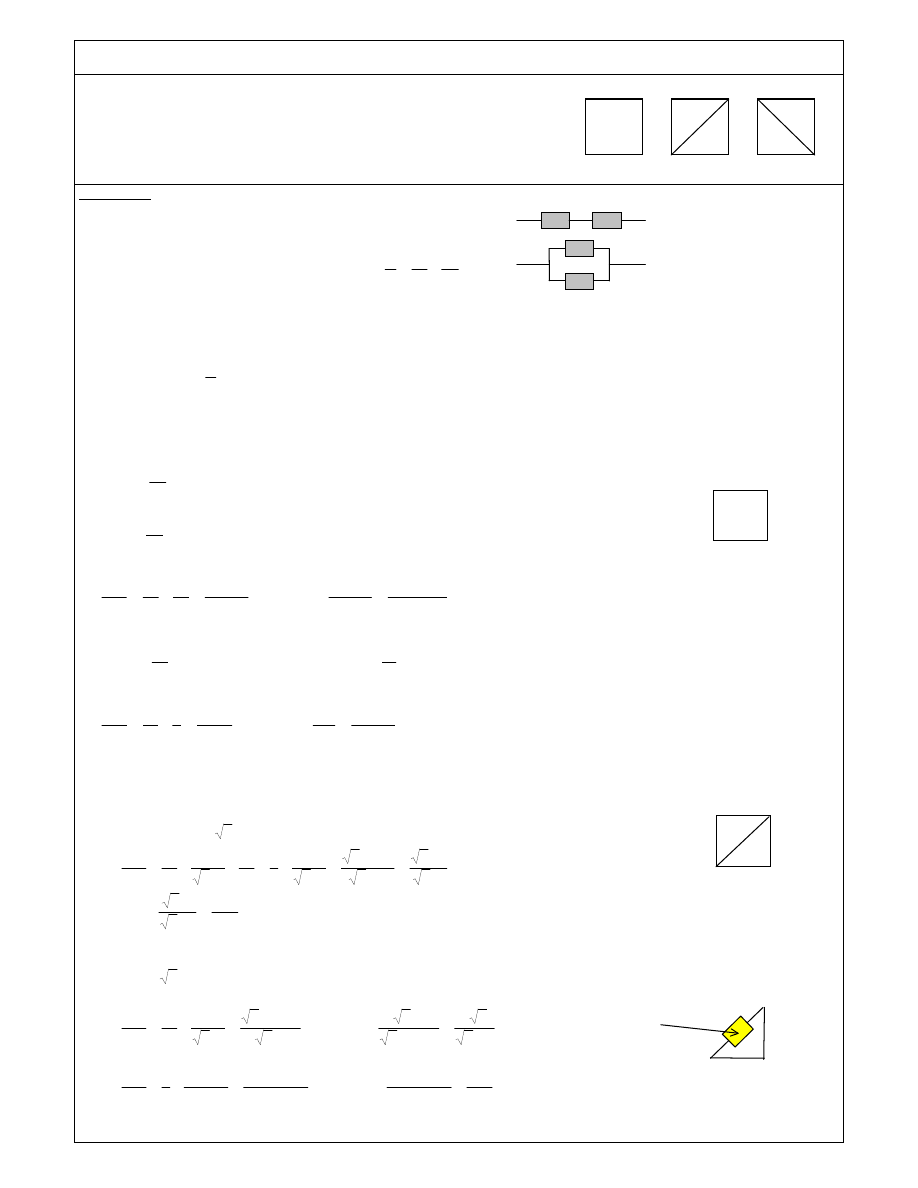
Oblicz opór zast pczy mi dzy punktami AB oraz AC dla układów wykonanych z

jednorodnych drutów oporowych o stałym przekroju przedstawionych na rysunku
obok. Opór odcinka AC wynosi 1

Ω.

Rozwi zanie

Dla poł czenia szeregowego oporów R

1

, R

2

zachodzi R = R

1

+ R

2

Dla poł czenia równoległego oporów R

1

, R

2

zachodzi

2

1

1

1

1

R

R

R

+

=

Oznaczmy długo boku kwadratu symbolem a, a opór tego odcinka symbolem r (r = 1 Ω).

Zgodnie z drugim prawem Ohma opór jest proporcjonalny do długo ci l przewodnika i

pola powierzchni przekroju S, co zapiszemy:

S

l

R

ρ

=

gdzie

ρ jest oporem wła ciwym (charakteryzuje materiał z którego zbudowany jest przewodnik)

Drut jest jednorodny (

ρ = const) oraz ma stały przekrój (S = const), wi c opór kawałka drutu o długo ci l ma warto (l/a) r⋅

a) Opór kawałka drutu wzdłu drogi ACB jest oporem poł czenia szeregowego odcinków AC oraz CB – wynosi:

Ω

=

Ω

⋅

=

=

⋅

=

2

1

2

2

2

r

r

a

a

R

ACB

Analogicznie

Ω

=

Ω

⋅

=

=

⋅

=

2

1

2

2

2

r

r

a

a

R

ADB

Opory R

ABC

oraz R

ADB

s poł czone równolegle, zatem opór zast pczy

Z

AB

R wyliczamy z zale no ci:

Ω

=

Ω

+

Ω

Ω

⋅

Ω

=

+

⋅

=

⋅

+

=

+

=

1

2

2

2

2

2

2

2

2

2

2

2

2

2

1

2

1

1

r

r

r

r

R

r

r

r

r

r

r

R

Z

AB

Z

AB

Podobnie mo na obliczy opór zast pczy

Z

AC

R . Wtedy

Ω

=

Ω

⋅

=

=

⋅

=

3

1

3

3

3

r

r

a

a

R

ADBC

oraz,

Ω

=

Ω

⋅

=

=

⋅

=

1

1

1

1

1

r

r

a

a

R

AC

Opory R

ADBC

oraz R

AC

s poł czone równolegle, zatem opór zast pczy

Z

AC

R wyliczamy z zale no ci:

Ω

=

Ω

Ω

⋅

=

=

+

=

+

=

75

,

0

4

1

3

4

3

3

3

1

3

1

1

2

2

2

r

r

R

r

r

r

r

r

R

Z

Z

AC

AC

b) Opór zast pczy mi dzy punktami AB

Opór zast pczy

Z

AB

R jest poł czeniem równoległym trzech oporów:

r

R

r

R

r

R

2

2

;

2

=

⋅

=

=

ADB

AB

ACB

oraz

.

Ω

=

Ω

⋅

=

+

⋅

=

⋅

+

=

⋅

+

⋅

=

⋅

+

=

+

⋅

+

=

59

,

0

1

42

,

2

42

,

1

1

2

2

2

1

2

2

2

2

1

1

2

1

2

1

2

1

1

2

r

R

r

r

r

r

r

r

r

r

r

R

Z

Z

AB

AB

eby znale opór zast pczy mi dzy punktami A i C nale y zauwa y , e dla trójk ta ABD mi dzy punktami AB mamy

poł czenie równoległe dwóch oporów:

r

R

r

R

2

2

=

⋅

=

ADB

AB

oraz

Zatem dla trójk ta ABD opór zast pczy mi dzy punktami A i B wyniesie

Ω

=

⋅

+

=

+

⋅

⋅

=

⋅

+

⋅

=

⋅

+

=

83

,

0

2

2

2

2

2

2

2

2

2

2

2

2

2

1

2

1

1

2

/

2

/

r

r

r

r

R

r

r

r

r

r

R

AB

AB

/

AB

R

Opór zast pczy mi dzy punktami A i C obliczymy z wzoru

(

)

(

)

Ω

=

Ω

=

+

⋅

+

=

⋅

+

+

+

=

+

+

=

65

,

0

83

,

2

83

,

1

2

1

1

1

/

/

/

/

/

r

R

r

r

R

R

r

r

R

r

r

R

r

R

r

R

Z

AC

Z

AB

AB

AB

AB

AB

AC

A

A

A

B

B

B

C

C

C

R

1

(poł czenie szeregowe)

(poł czenie równoległe)

R

1

R

2

R

2

A

C

B

r

r

r

D

r

A

C

B

r

r

A

C

B

r

r

r

D

r

√2

⋅r

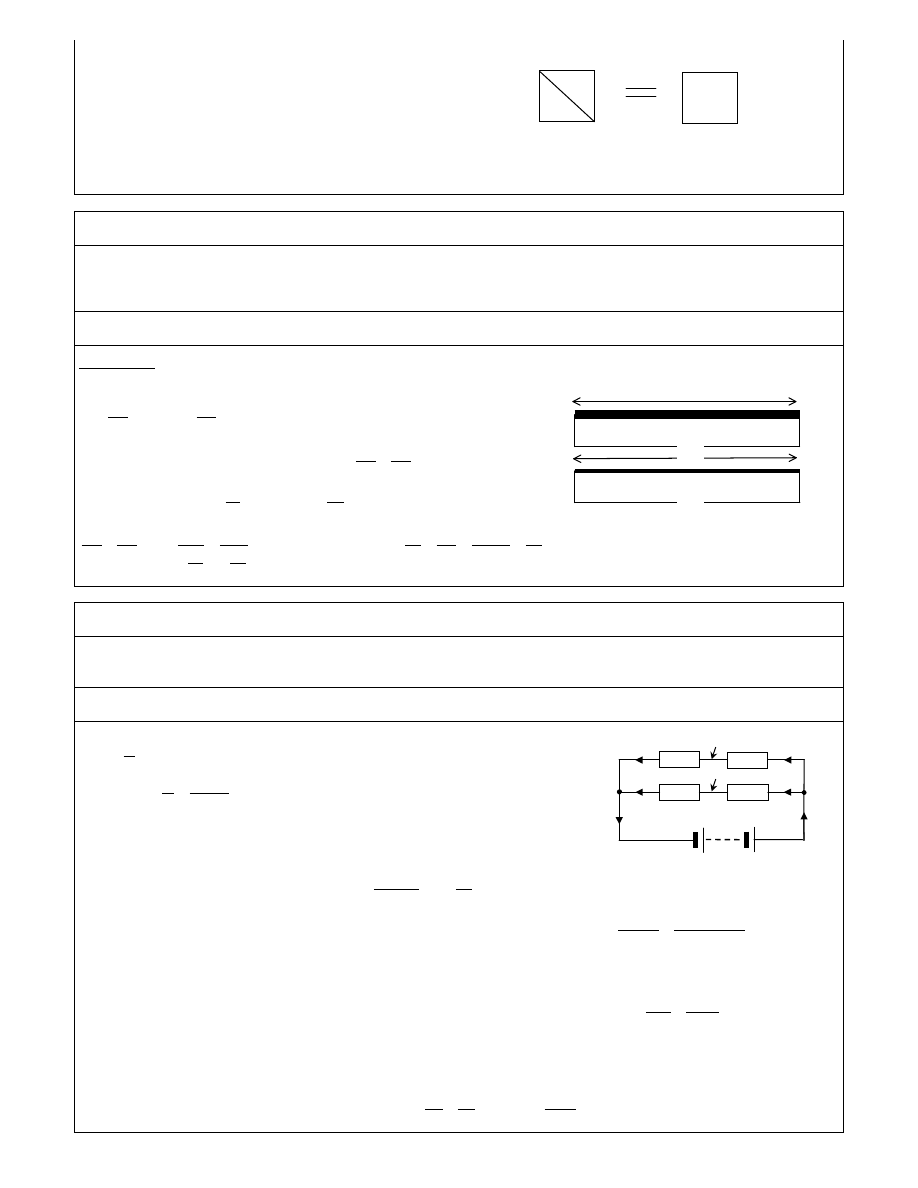
c) Opór zast pczy mi dzy punktami AB

Opór zast pczy mi dzy punktami AB nie daje si wyznaczy

dotychczasowym sposobem. Nie jest to bowiem ani poł czenie

równoległe ani szeregowe. Z symetrii układu wida jednak, e

Potencjały w punkcie C oraz D s takie same, wi c przez gał CD

nie mo e płyn pr d. Tym samym gał CD mo na wyeliminowa ,

przerysowa układ do postaci bez tej gał zi i rozwi za tak jak

w przypadku

a).

Opór zast pczy mi dzy punktami A i C rozwi zuje si podobnie jak dla przypadku

b)

ZAD 64

Na ko cach drutu oporowego panuje napi cie U

1

= 3 V. Ile razy nale y zmniejszy pole przekroju poprzecznego drutu, aby po

zmianie napi cia na U

2

= 5U

1

ilo ciepła wydzielaj cego si w drucie w jednostce czasu nie uległa zmianie (przy niezmienionej

długo ci drutu)?

Odp.: 25 razy

Rozwi zanie:
Ilo ciepła wydzielaj cego si w jednostce czasu to moc pr du. Mamy zatem:

1

2

1

1

R

U

P

=

oraz,

2

2

2

2

R

U

P

=

Z warunków zadania wynika, e P

1

= P

2

, wi c

2

2

2

1

2

1

R

U

R

U = (1)

Uwzgl dniaj c, e

1

1

S

l

R

ρ

=

, oraz

2

2

S

l

R

ρ

=

zapiszemy (1) w postaci:

( )

25

1

5

2

1

2

1

2

2

2

1

1

2

2

2

2

1

2

1

2

2

2

1

2

1

2

2

2

1

2

1

=

=

=

=

ρ

=

ρ

=

U

U

U

U

S

S

S

U

S

U

S

l

U

S

l

U

R

U

R

U

ZAD 65
Ile wynosi napi cie mi dzy punktami

A i B obwodu przedstawionego na rysunku obok. Jaki pr d popłynie przewodem o oporze

R

p

= 2

Ω, ł cz cym te punkty? Jak nale y zmieni warto oporu R

1

, by pr d nie popłyn ł? R

1

= 1

Ω, R

2

= 3

Ω, R

3

= 5

Ω, R

4

= 20

Ω,

a E = 12 V. Opór wewn trzny ogniwa równy zero.
Odp.:

Z prawa Ohma dla obwodu zamkni tego mamy

,

R

E

I

=

gdzie R jest oporem zast pczym układu oporów R

1

, R

2

, R

3

, i R

4

.

Zatem

A

3

3,45

V

12

48

,

=

=

=

R

E

I

W w le O

1

pr d I rozgał zia na dwa pr dy: I

A

oraz I

B,

Z I prawa Kirchoffa mamy

B

A

I

I

I

+

=

Napi cie pomi dzy punktami O

1

oraz O

2

jest

(

)

(

)

B

B

B

B

A

B

A

I

I

I

R

R

R

R

I

I

R

R

I

R

R

I

U

⋅

=

⋅

=

⋅

+

+

=

+

=

+

⋅

=

25

,

6

4

25

2

1

4

3

4

3

2

1

12

Wstawiaj c powy ej zale no c

A

B

I

I

I

−

=

otrzymujemy:

A

I

I

I

I

I

3

25

,

7

48

,

3

25

,

6

25

,

7

25

,

6

25

,

6

25

,

6

=

⋅

=

⋅

=

⋅

−

⋅

=

A

A

A

A

.

0,48A

A

3

,48

A

B

=

−

=

−

=

3

I

I

I

Napi cie pomi dzy punktami A i B wyniesie, zatem:

V

0,6

V

9

9,6

3

A

3

20

A

0,48

=

−

=

⋅

−

⋅

=

−

=

2

4

R

I

R

I

U

A

B

AB

Poł czenie punktów A i B przewodem o oporze R

P

spowoduje przepływ pr du o nat eniu:

V

0,3

2

V

0,6

=

=

=

p

AB

p

R

U

I

Aby przez opór R

P

nie popłyn ł pr d, potencjały w punkcie A i B musz by takie same, gdy wtedy U

AB

= V

B

−V

A

= 0. Czyli musi

zachodzi V

A

−V

O2

= V

B

−V

O2

,

co oznacza, e I

A

R

1

= I

B

R

3

. Podobnie musi zachodzi V

A

−V

O1

= V

B

−V

O1

, czyli I

A

R

2

= I

B

R

4

. Daje to

układ równa jak poni ej:

=

=

4

2

3

1

)

2

(

)

1

(

R

I

R

I

R

I

R

I

B

A

B

A

dalej, dziel c (1) przez (2) mamy

Ω

=

=

=

75

,

0

1

3

2

1

4

3

2

1

R

R

R

R

R

R

R

R

U

1

U

2

l

l

S

1

S

2

A

C

B

r

r

r

D

r

√2

⋅r

A

C

B

r

r

r

D

r

O

2

R

3

R

1

R

2

R

4

I

I

B

I

A

O

1

A

B

E

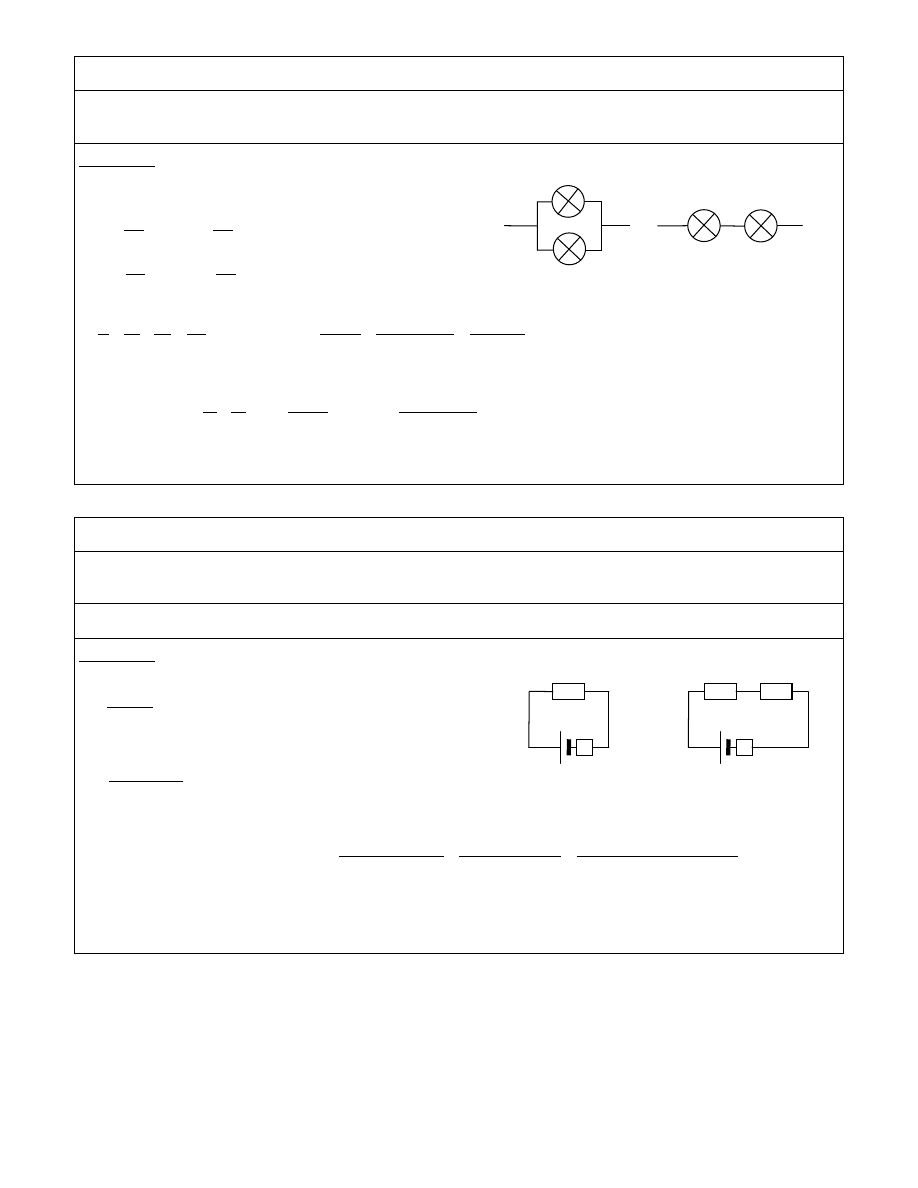
ZAD 66

Dwie arówki o mocach P

1

= 20 W i P

2

= 40 W na napi cie U = 220 V poł czono: a) równolegle, b) szeregowo. Obliczy opór

zast pczy tego układu

Rozwi zanie:

a) równolegle

2

2

2

2

2

2

1

2

1

1

2

1

P

U

R

R

U

P

P

U

R

R

U

P

=

=

=

=

(

)

( )

806,7

VA

60

V

4840

W

40

W

20

V

220

2

2

2

=

=

+

=

+

=

+

=

+

=

2

1

2

2

1

2

2

1

1

1

1

1

P

P

U

R

P

P

U

R

R

R

b) szeregowo

( )

Ω

=

+

=

+

=

+

=

+

=

3630

1

1

2

1

2

1

2

2

1

2

2

1

2

2

2

W

800

W

40

W

20

V

220

P

P

P

P

U

P

P

U

R

R

R

ZAD 67

W obwodzie zło onym z ogniwa i opornika R

1

=9

Ω płynie pr d o nat eniu I

1

=0,9A, a po doł czeniu szeregowym dodatkowego

opornika R

2

=6Ω nat enie pr du zmniejszyło si do I

2

=0,6A. Ile wynosi siła elektromotoryczna E i opór wewn trzny R

w

ogniwa?

Odp.: R

w

= 3 Ω

Ω

Ω

Ω, E = 10,8 V

Rozwi zanie:
Z prawa Ohma dla obwodu zamkni tego mamy:

E

R

I

R

I

R

R

E

I

w

w

=

+

+

=

1

1

1

1

1

(1),

gdzie E jest sił elektromotoryczn ródła (mierzon w woltach – V),
R

w

– oporem wewn trznym ródła (w omach

Ω).

E

R

I

R

I

R

I

R

R

R

E

I

w

w

=

+

+

+

+

=

2

2

2

1

2

2

1

2

(2)

Zatem jest to układ dwóch równa z niewiadomymi E oraz R

w

Z (1) liczymy E i wstawiamy do (2)

(

)

(

)

(

)

Ω

=

−

⋅

−

+

⋅

=

−

−

+

=

−

−

+

=

+

=

+

+

3

A

0,6

0,9

9

A

0,9

6

9

A

0,6

2

1

1

1

2

1

2

2

1

1

1

2

2

1

2

1

1

1

2

2

2

1

2

I

I

R

I

R

R

I

I

I

R

I

R

I

R

I

R

R

I

R

I

R

I

R

I

R

I

w

w

w

Obliczone R

w

wstawiamy np. do (1)

V

10,8

3

A

0,9

9

A

0,9

=

⋅

+

⋅

=

+

=

w

R

I

R

I

E

2

1

1

Mo na te sprawdzi poprawno wyniku wstawiaj c obliczone R

w

do (2), wtedy:

(

)

(

)

8

,

10

18

6

,

0

3

6

9

6

,

0

2

1

2

2

2

2

1

2

=

Ω

⋅

=

Ω

+

+

⋅

=

+

+

⋅

=

+

+

=

A

A

R

R

R

I

R

I

R

I

R

I

E

w

w

R

1

R

1

R

2

I

1

I

2

R

w

R

w

E

E

a) równolegle

b) szeregowo

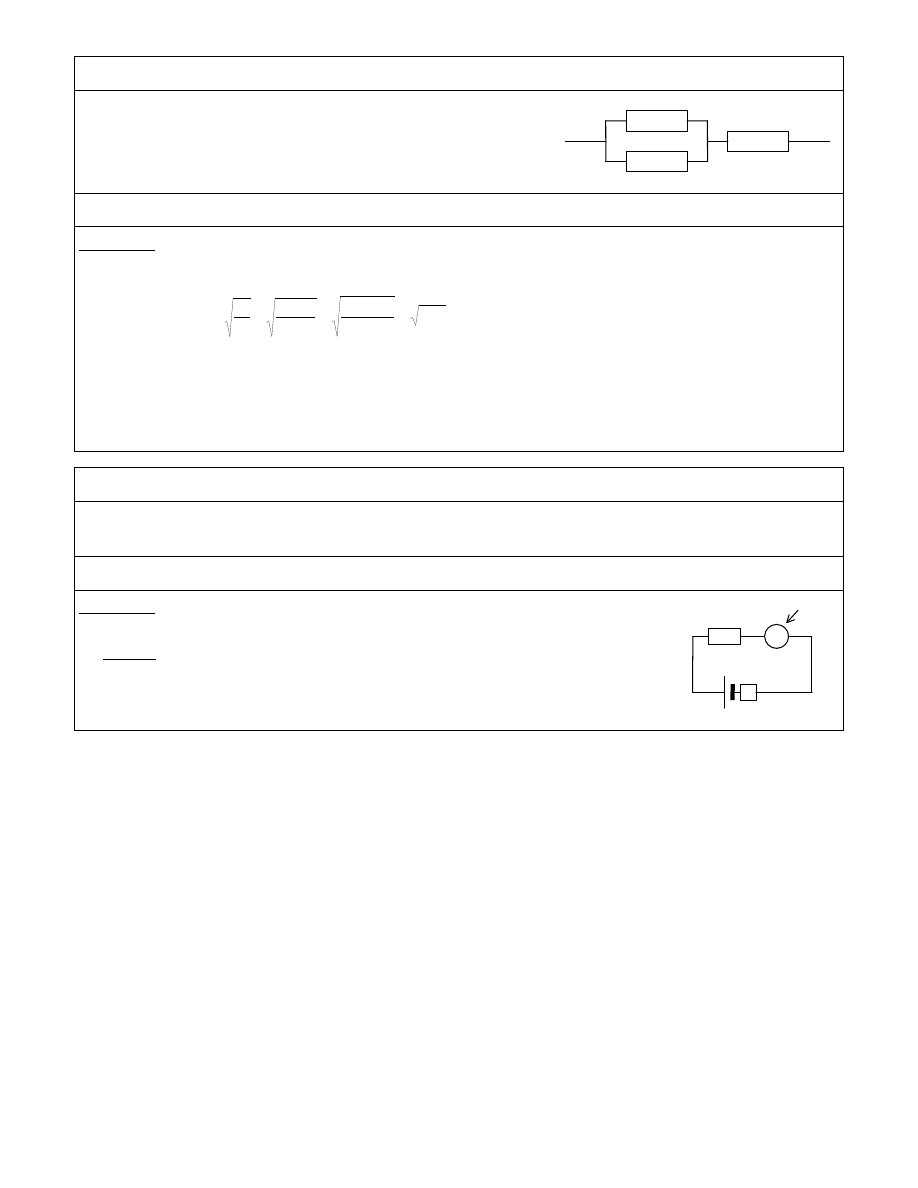
ZAD 68

Je eli w oporniku R

1

(rys. obok) wydziela si moc P

1

= 100 W, to jaka moc

wydziela si w oporniku R

3

?

Odp.: P

3

= 200 W

Rozwi zanie:

Informacja o mocy jaka wydziela si w oporniku R

3

, którego opór jest znany, jest jednocze nie informacj o nat eniu pr du jaki

przeze płynie. Mamy, bowiem

A

1

A

1

100

A

100

100

W

100

2

2

=

=

=

=

=

=

1

1

1

1

2

1

1

R

P

I

R

I

P

Z symetrii obwodu wynika, e przez gał zawieraj c opór R

1

płynie taki sam pr d jak przez gał zawieraj c opór R

2

(jako, e

R

1

= R

2

). Wobec tego przez opornik R

3

płynie pr d I

3

=I

1

+I

2

co wynika z pierwszego prawa Kirchhoffa, e suma nat e pr dów

pływaj cych do w zła równa jest sumie nat e pr dów wypływaj cych z w zła. Zatem

A

2

2

1

2

1

3

=

⋅

=

+

=

I

I

I

I

Moc wydzielaj c si na oporniku R

3

obliczymy z w wzoru

( )

W

200

50

A

2

2

2

=

⋅

=

=

3

2

3

3

R

I

P

ZAD 69

Amperomierz o oporze wewn trznym r = 0,1 Ω poł czono szeregowo z oporem R = 9 Ω i nast pnie doł czono do biegunów ogniwa o
oporze wewn trznym r

1

= 0,9 Ω. Jaka była siła elektromotoryczna E ogniwa, je eli amperomierz wskazał pr d o nat eniu I = 0,2 A?

Odp.: E = 2 V

Rozwi zanie:
Z prawa Ohma dla obwodu zamkni tego mamy:

(

)

(

)

(

)

V

2

A

=

⋅

Ω

+

+

=

⋅

+

+

=

⋅

+

+

=

+

+

=

2

,

0

9

,

0

9

1

,

0

1

1

1

I

R

r

r

I

R

r

r

E

R

r

r

E

I

(1),

R

1

= 100

Ω

R

2

= 100

Ω

R

3

= 50

Ω

R

1

A

I

r

1

E

r