
Inżynieria Środowiska
2011/12
Materiały
do wykładu 4
27 10 2011

siła zachowawcza
W
AA
=
0
W
AB(l
1
)
=
W
AB(l
2
)
W
AA
=
W
AB(s)
+
W
BA(l
1
)
B
W
AA
=
W
AB(s)
+
W
BA(l
2
)
A
s
l
1
l
2
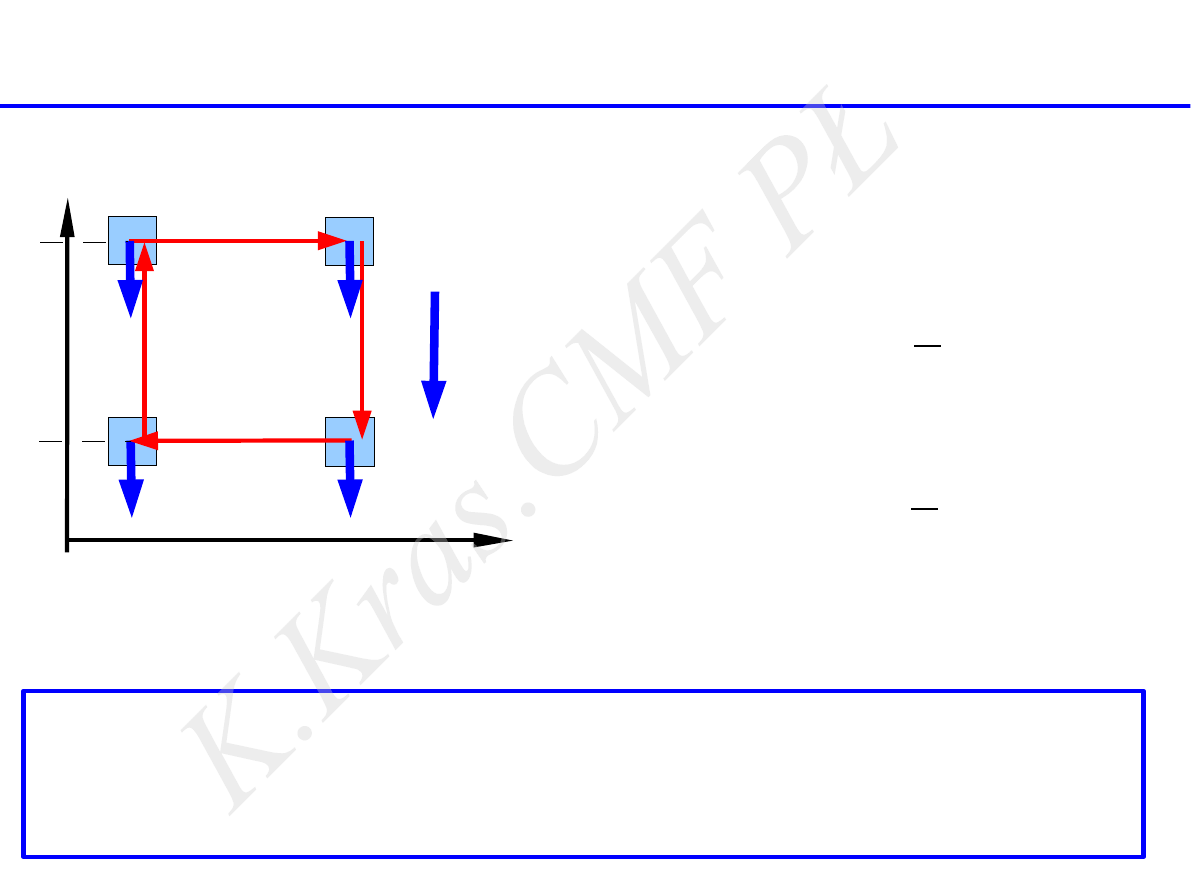
mg
mg
h
A
B
mg
C
mg
D
s
x
g
W
AB
=
mg⋅h = mg h cos = mg h−1
W
BC
=
mg⋅s = mg s cos
2
=
mg s⋅0 =0
W
CD
=
mg⋅h = mg h cos0 = mg h1
W
DA
=
mg⋅s = mg s cos
2
=
mg s⋅0 =0
W
AA
=
W
AB
W
BC
W
CD
W
DA
−
mgh0mgh0=0
praca siły mg na zamkniętej drodze
s
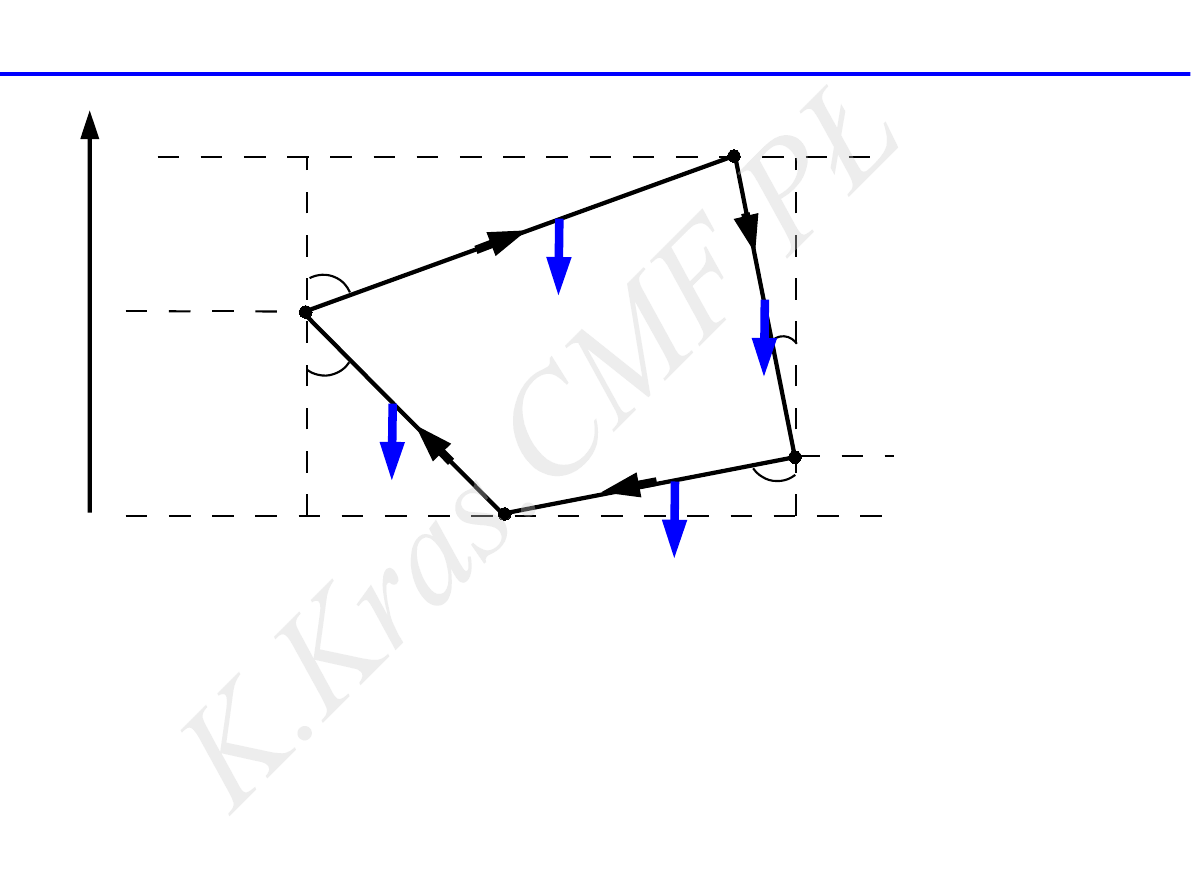
A
B
C
D
praca siły mg na zamkniętej drodze
a
b
c
d
α
β
γ
δ
⃗
mg
⃗
mg
⃗
mg
⃗
mg
W
AA
=
W
a
+
W
b
+
W
c
+
W
d
y
a
y
b
y
c
y
d
y
W
AA
= −
mg a cos α−mg b cosβ+mg c cos γ+mg d cos δ
W
AA
= −
mg (a
y
+
b
y
)+
mg (c
y
+
d
y
) =
0
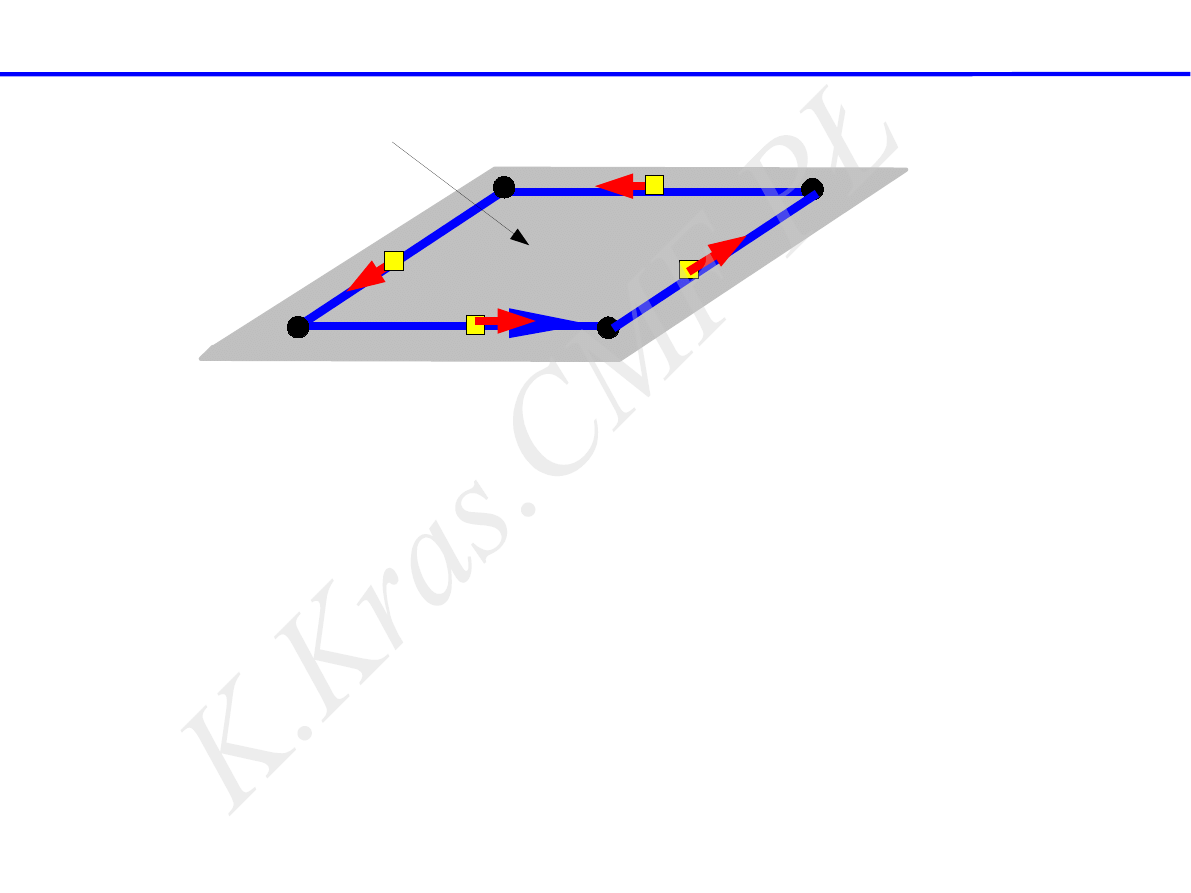
praca siły tarcia na drodze zamkniętej
A
B
⃗
T
⃗
T
⃗
T
f = const.
⃗
T
s
W
(
AB)
=⃗
T⋅⃗s = T s cosπ = =−T s
W
(
AA)
=−
Ts−Ts−Ts−Ts = −4T s ≠ 0
C
D
s
s
s
W
(
BC )
=⃗
T⋅⃗s = T s cos π = =−T s
W
(
CD)
=⃗
T⋅⃗s = T s cos π = =−T s
W
(
DA)
=⃗
T⋅⃗s = T s cos π = =−T s
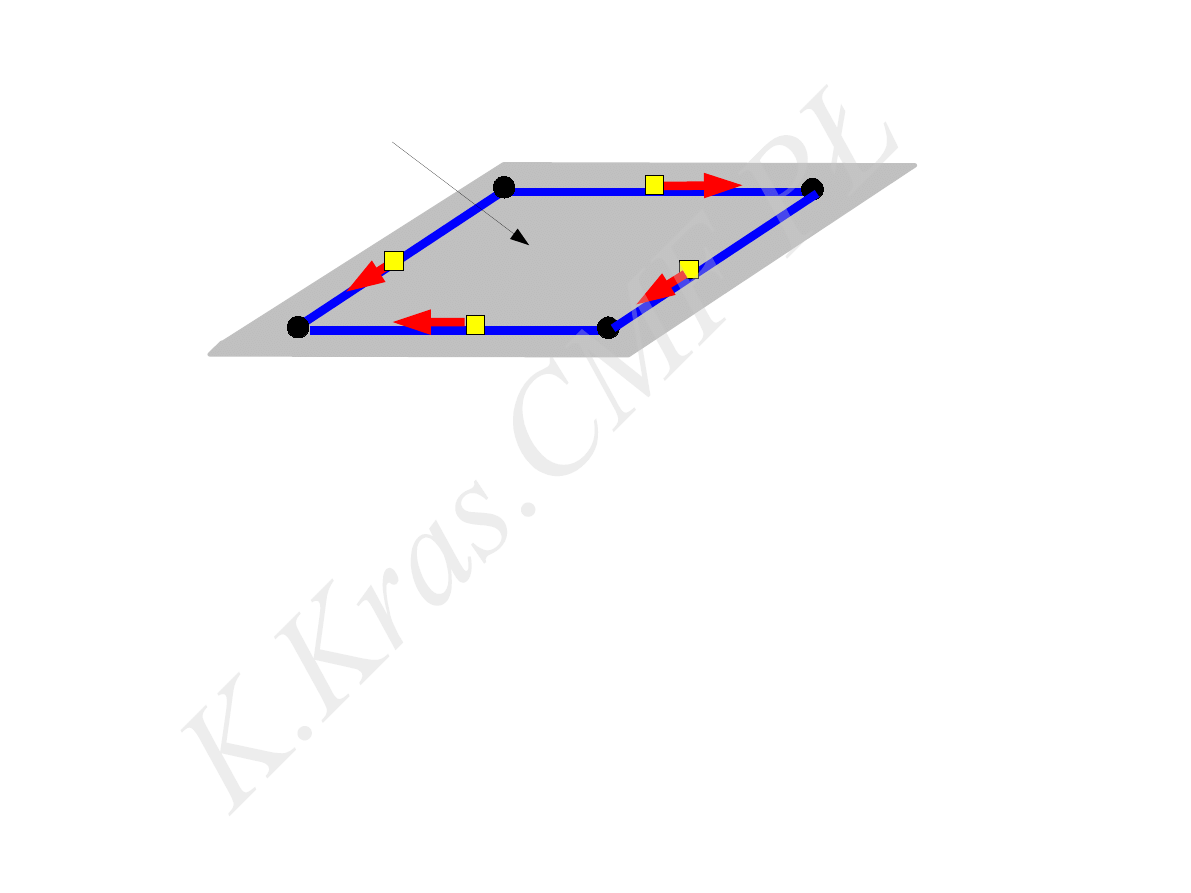
praca siły tarcia na drodze A-B
A
B
⃗
T
⃗
T
⃗
T
f = cons.
⃗
T
s
W
1( AB)
=−
T s
C
D
s
s
s
W
2( AB)
=
W
AD
+
W
DC
+
W
CB
=−
T s−T s−T s =−3T s
E
pB
=
E
pA
−
W
1( AB)
=
E
pA
+
Ts
E
pB
=
E
pA
−
W
2( AB)
=
E
pA
+
3Ts
?
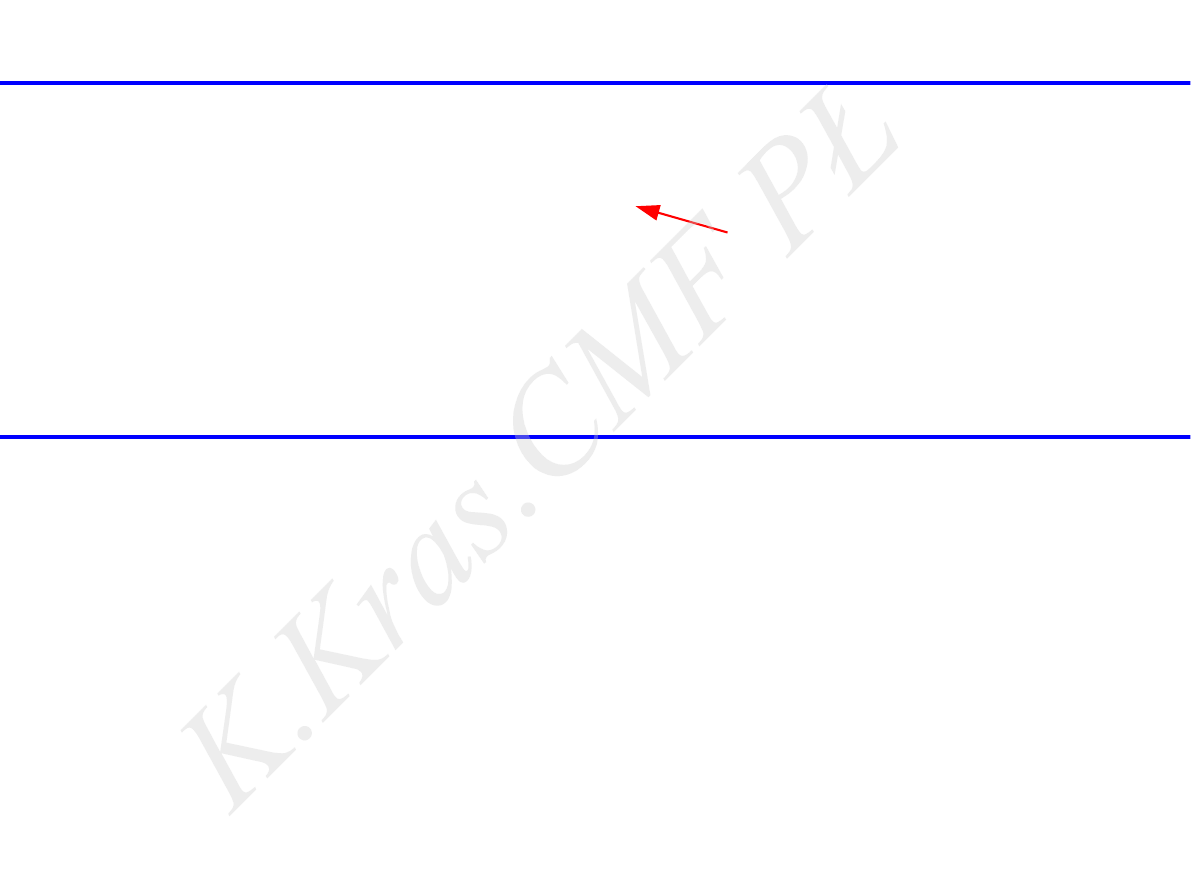
F =
F r
W = F⋅s = − E
p
r
siła zachowawcza
praca siły zachowawczej
zmiana energii potencjalnej
wyłącznie!
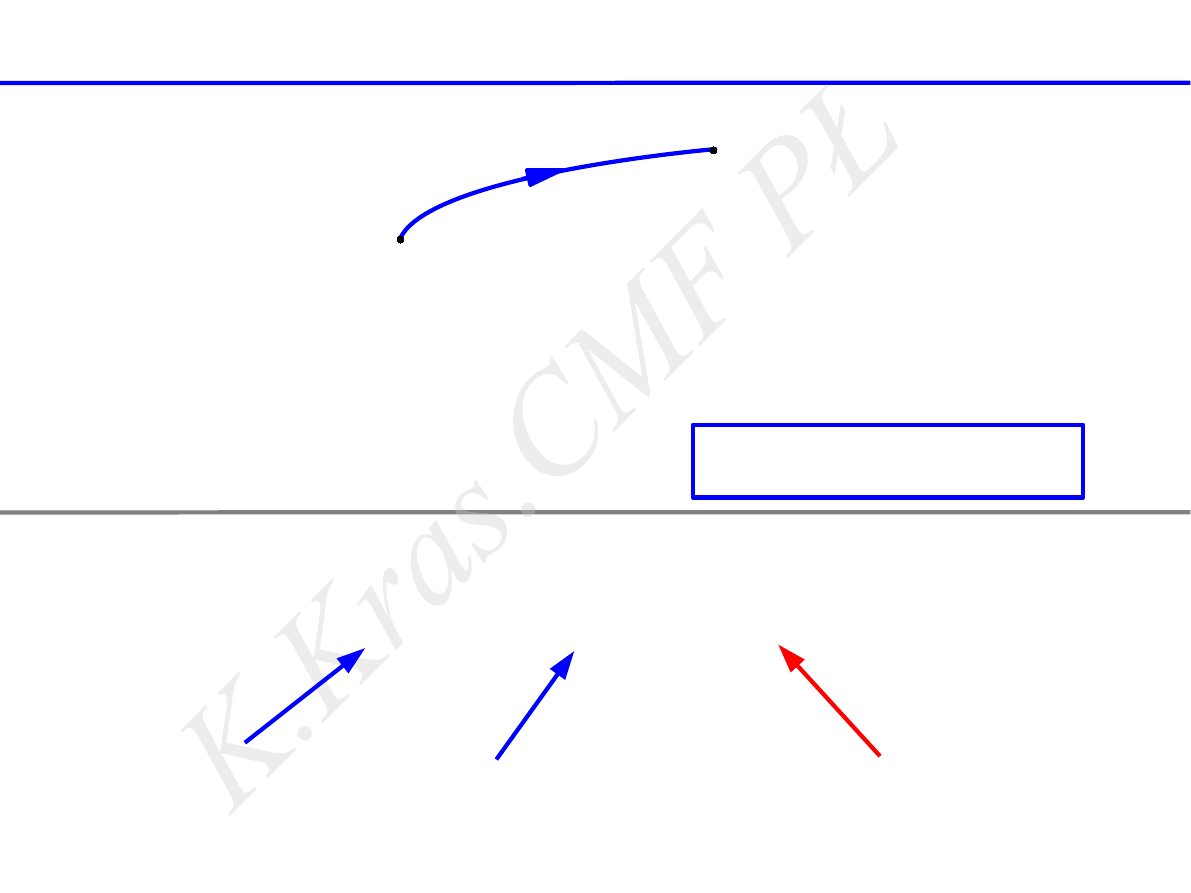
A
B
W
AB
E
pA
E
pB
E
pA
E
p
=
E
pB
E
pA
−
E
pB
=−
E
p
=
W
AB
praca siły zachowawczej
dowolna wartość E
pA
lub E
pB
E
pB
=
E
pA
−
W
AB
praca
siły zachowawczej
na drodze AB
energia
potencjalna
w punkcie B
energia
potencjalna
w punkcie A
energia mechaniczna
E = E
k
+
E
p
E
k
=
mV
2
2
E
p
energia kinetyczna
energia(e) potencjalna(e)
E
pA
+
E
kA
=
E
pB
+
E
kB
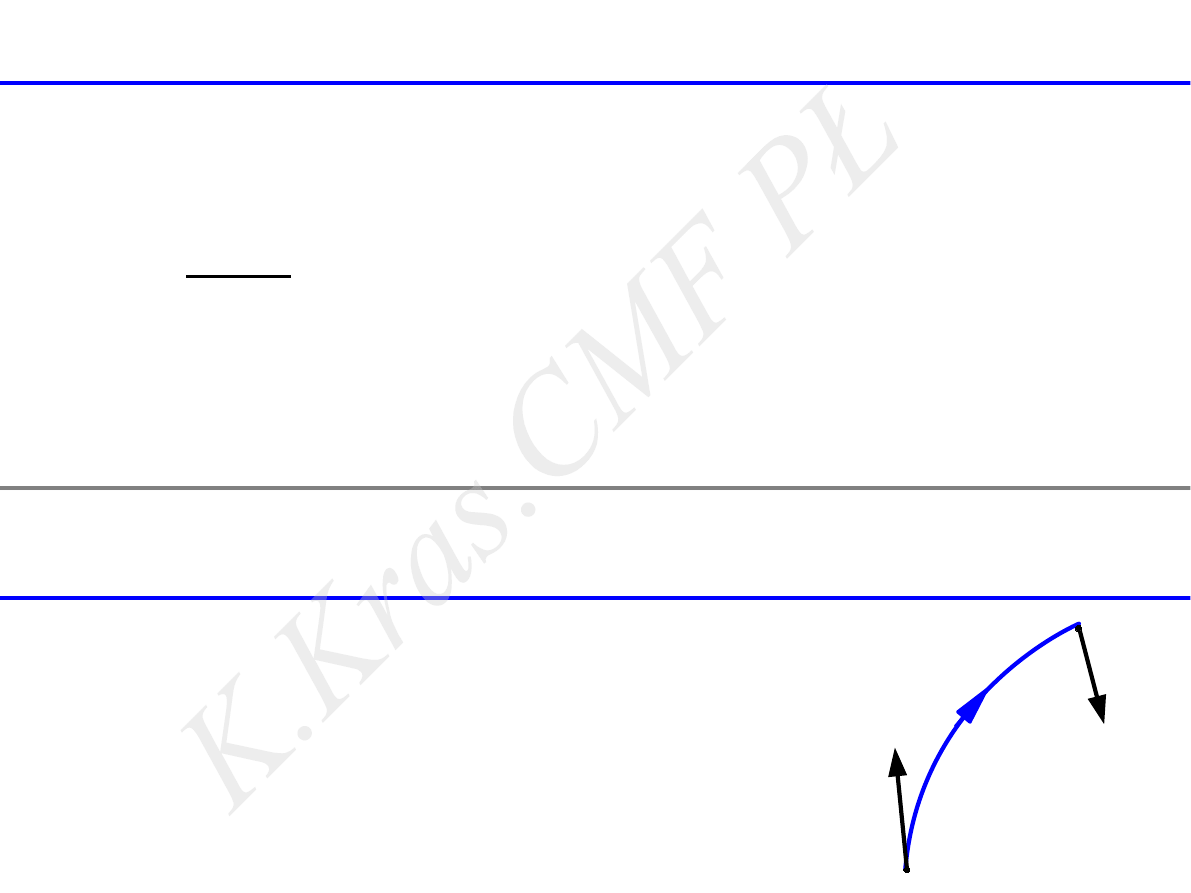
zasada zachowania energii mechanicznej
A
B
W
AB
E
pA
E
pB
⃗
V
A
⃗
V
B
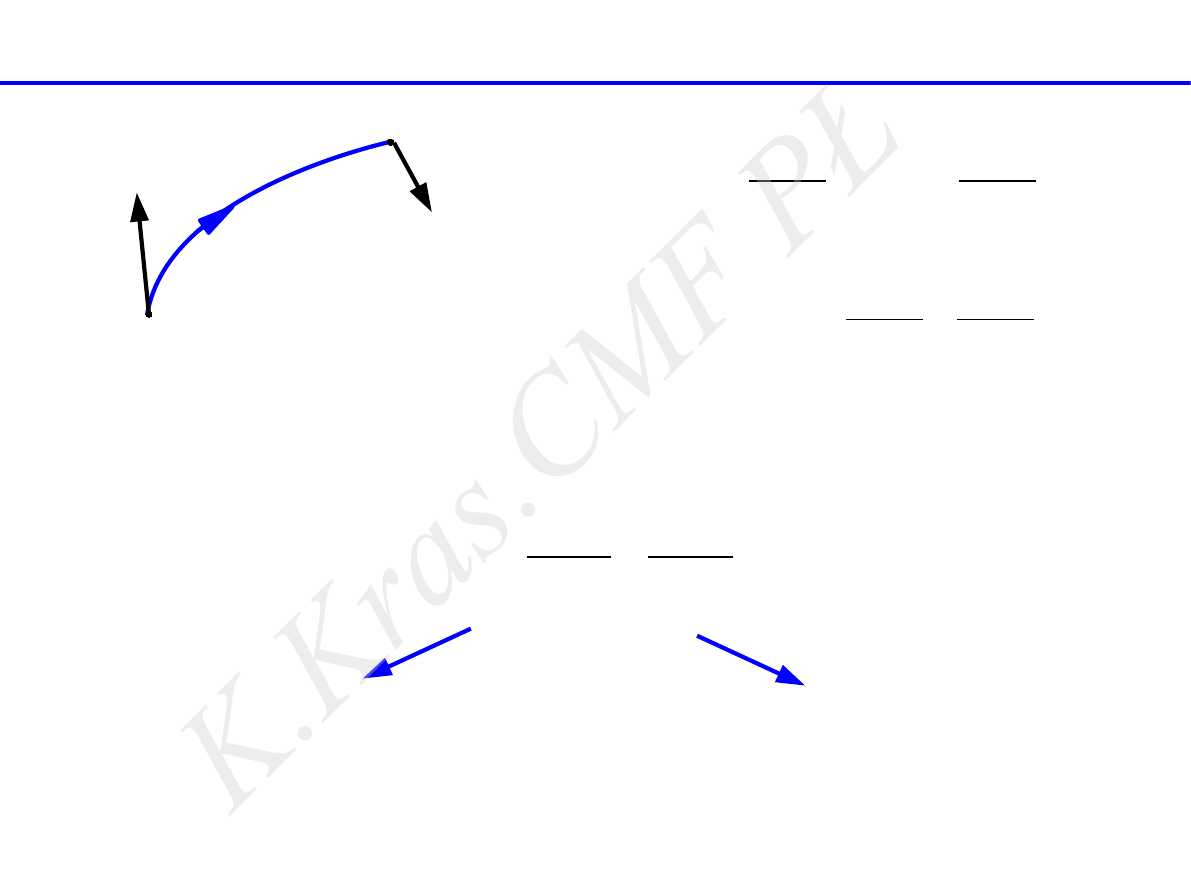
A
B
W
AB
E
pA
E
pB
⃗
V
A
⃗
V
B
zasada zachowania energii mechanicznej
E
pA
+
m V
A
2
2
=
E
pB
+
m V
B
2
2
E
pA
−
E
pB
=
m V
B
2
2
−
mV
A
2
2
E
pA
−
E
pB
=
W
AB
W
AB
=
m V
B
2
2
−
mV
A
2
2
W
AB
>
0⇒ V
B
>
V
A
W
AB
<
0⇒ V
B
<
V
A
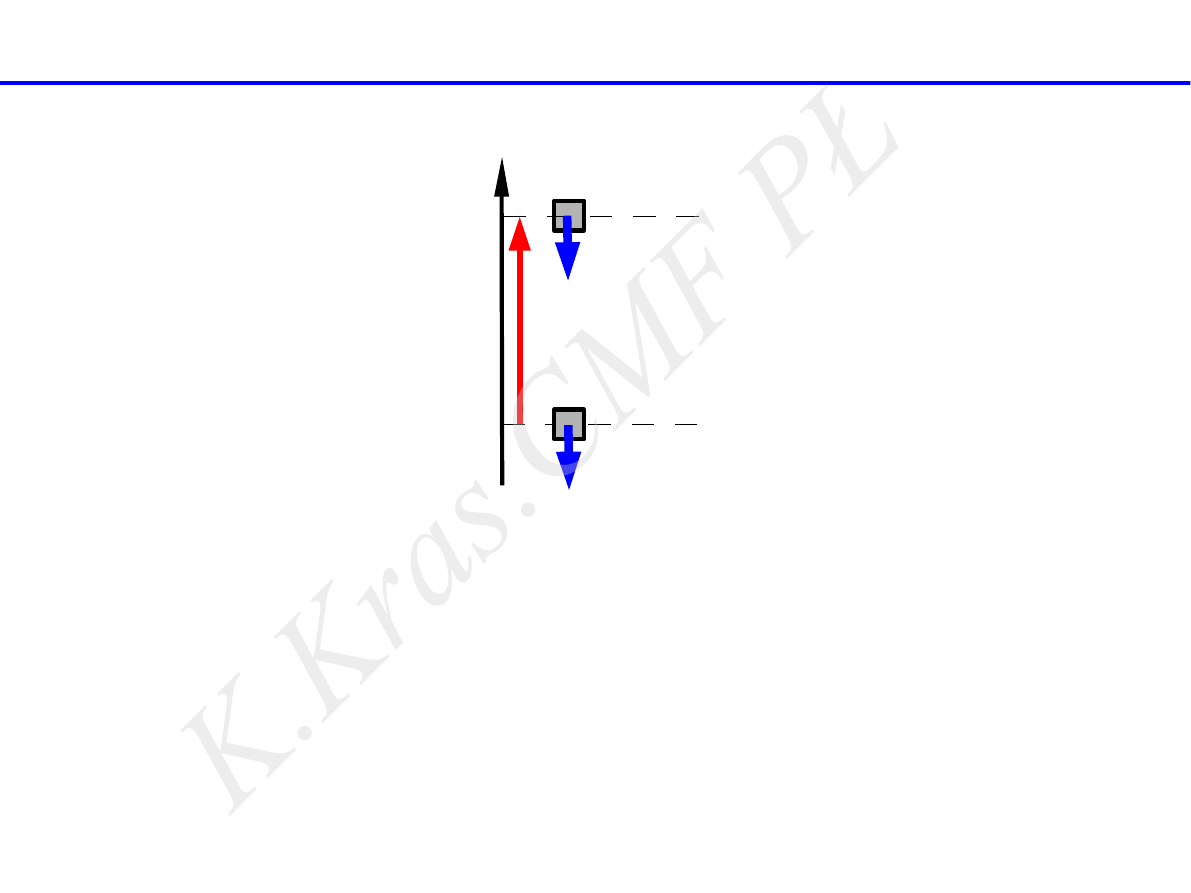
mg
mg
h
A
B
E
pA
E
pB
E
pB
=
E
pA
+Δ
E
p
=
E
pA
−
W
AB
=
E
pA
−[
mg h(−1)]
E
pB
=
E
pA
+
mg h>E
pA
y
energia
potencjalna
siły mg
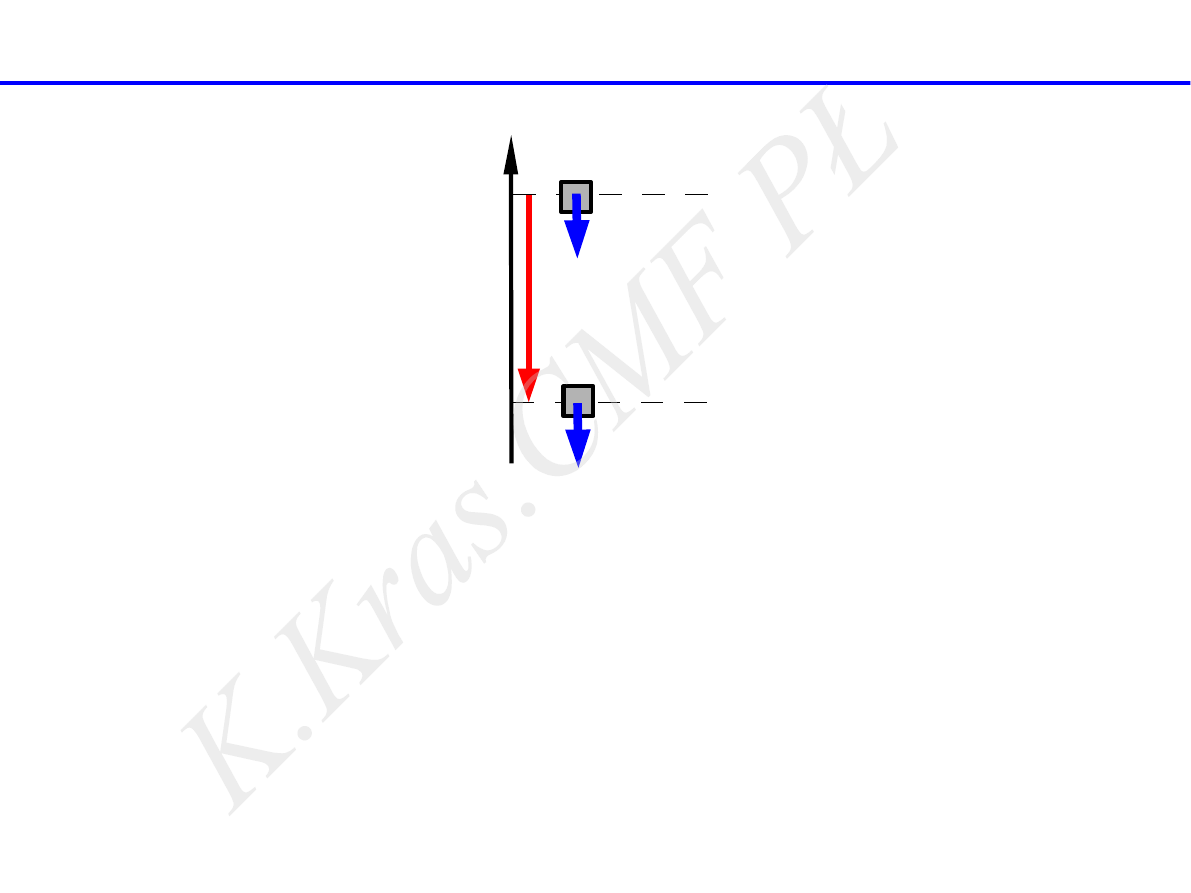
E
pA
=
E
pB
+Δ
E
p
=
E
pB
−
W
BA
=
E
pB
−[
mg h(1)]
E
pA
=
E
pB
−
mg h<E
pB
mg
mg
h
A
B
E
pA
E
pB
y
energia
potencjalna
siły mg
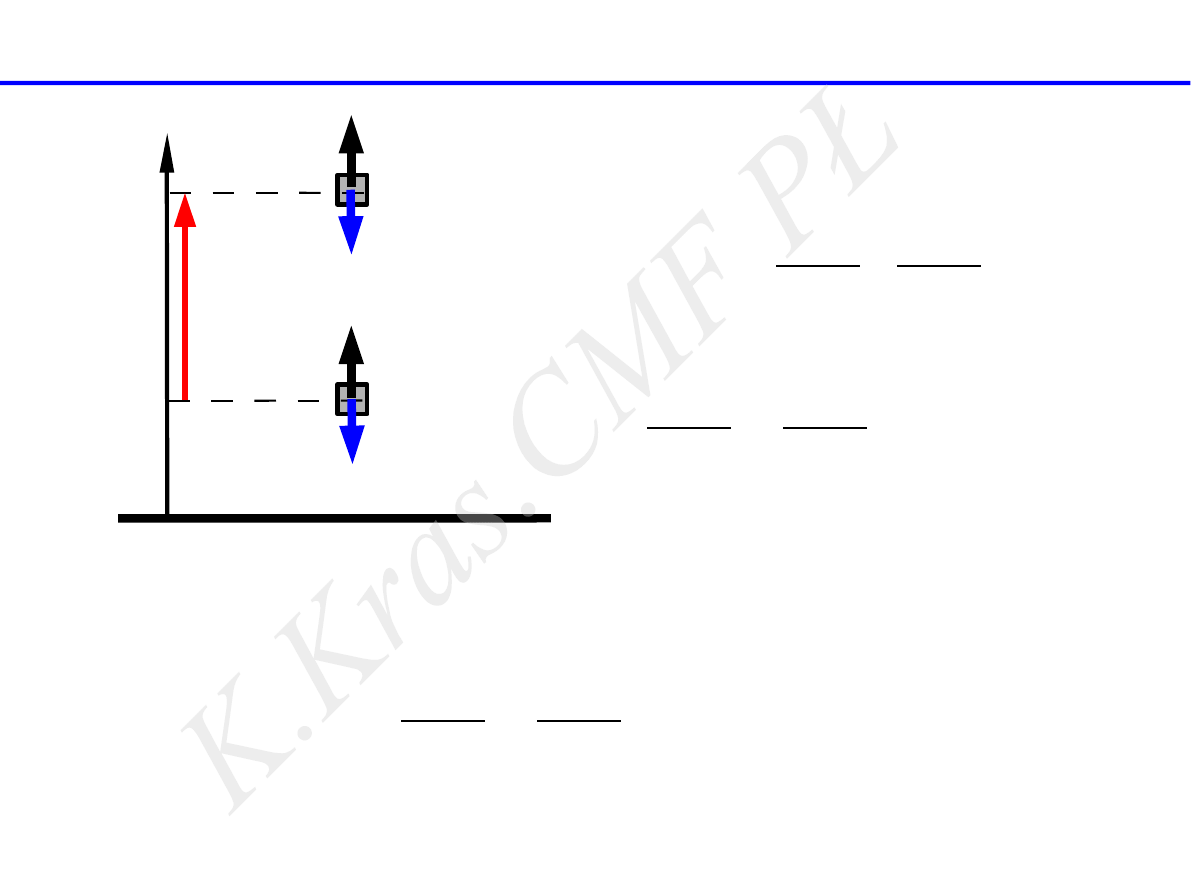
zasada zachowania energii mechanicznej w polu siły mg
mg
mg
h
A
B
E
pA
E
pB
y
V
B
V
A
W
AB
=
m V
B
2
2
−
mV
A
2
2
mV
B
2
2
=
m V
A
2
2
+
W
AB
W
AB
= ⃗
mg⋅⃗h = mg h cos π = mg h(−1)
mV
B
2
2
=
m V
A
2
2
−
mgh
V
B
<
V
A
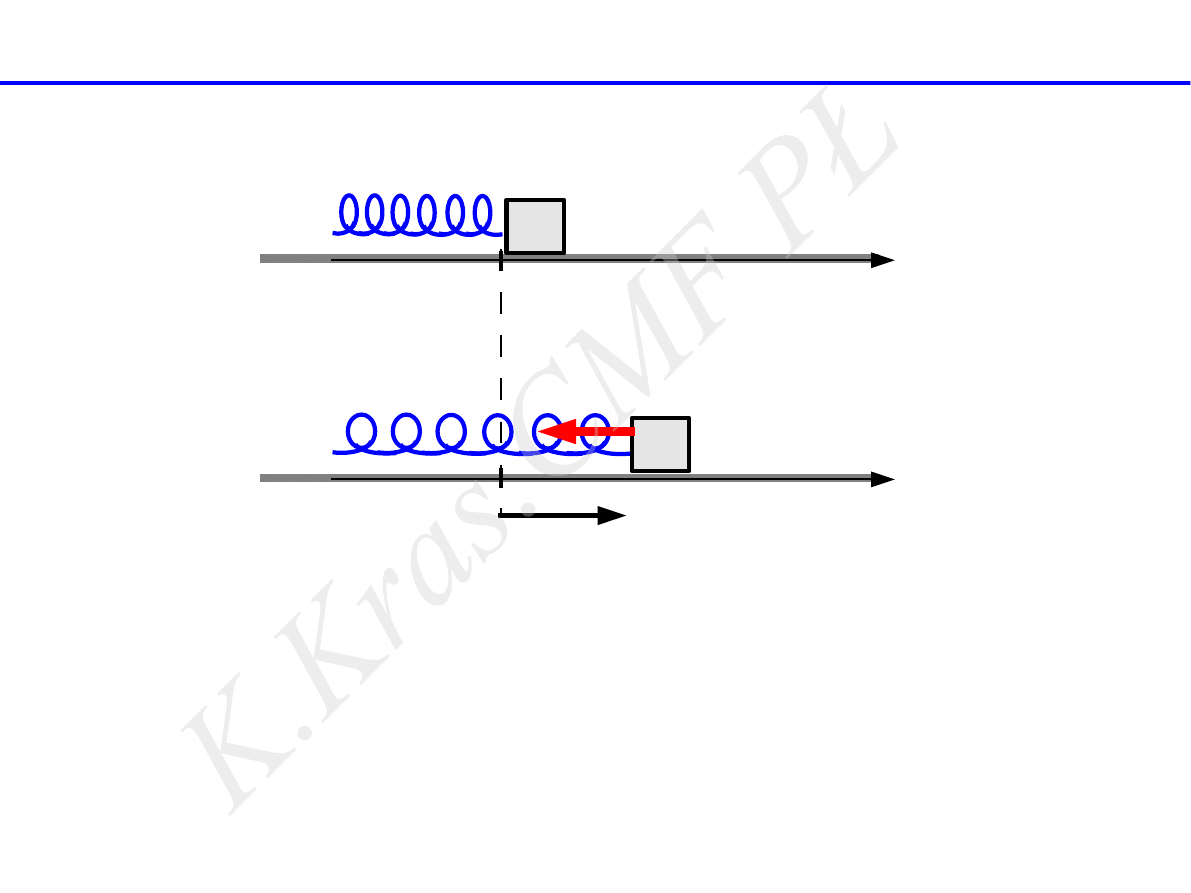
⃗
F
⃗
F = −k ⃗x
siła sprężystości
x=0
x
x
k
m
x=0
x
k
m
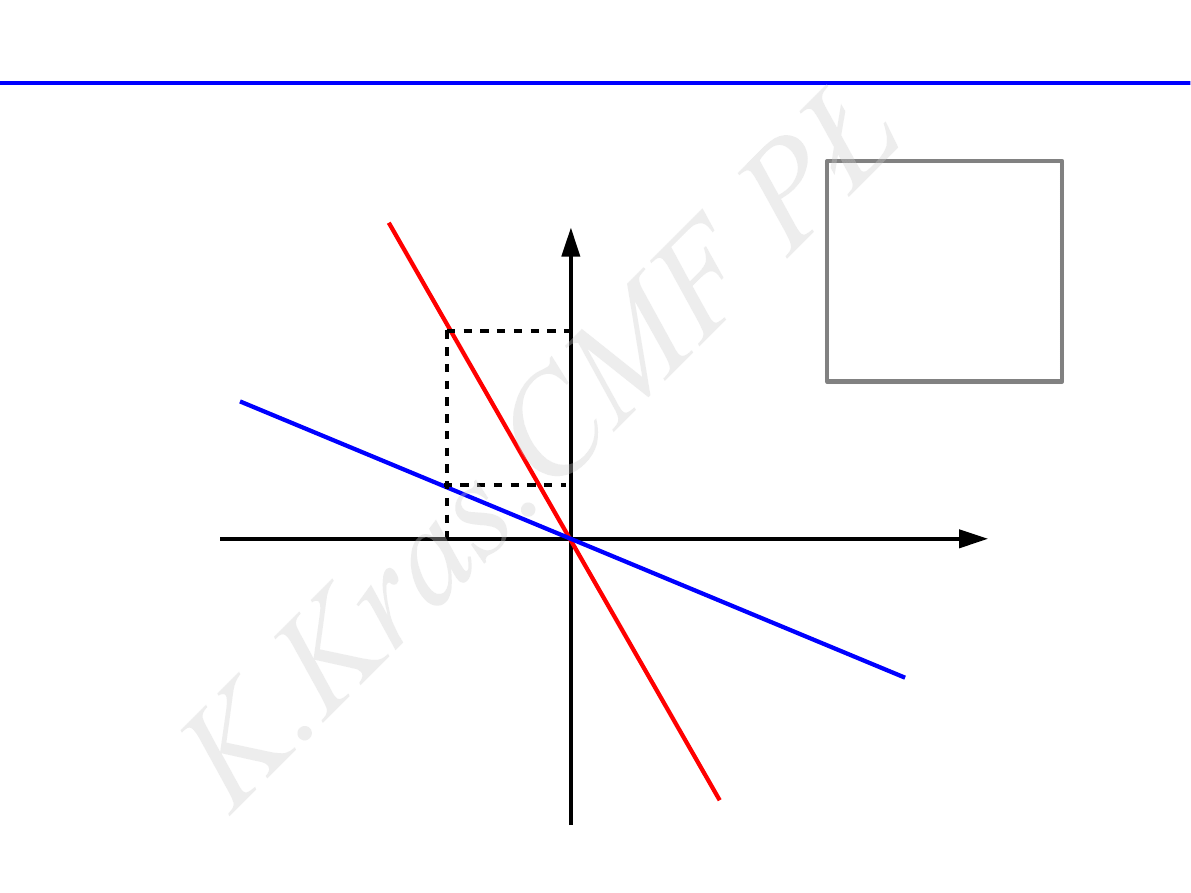
x
F
k
1
k
2
k
2
>
k
1
siła sprężystości
x
F
1
F
2
F
2
>
F
1
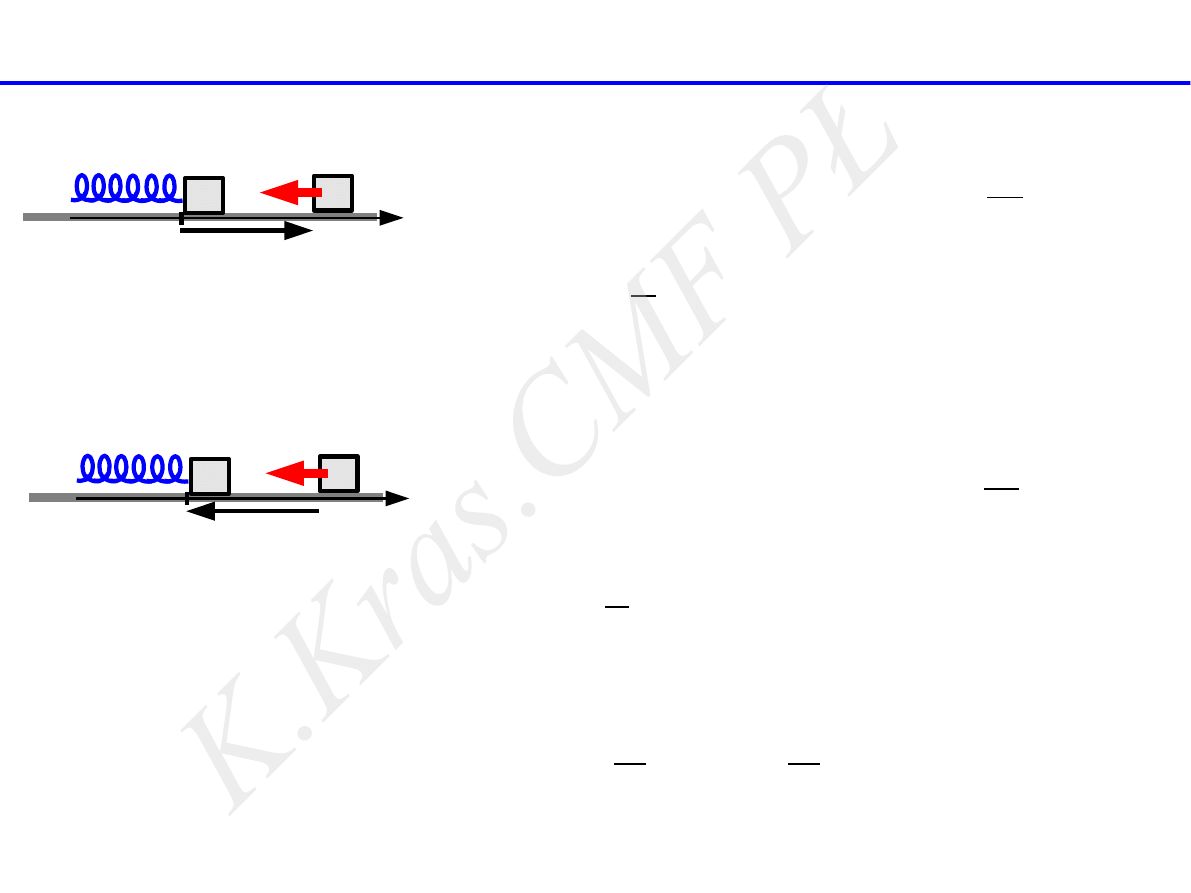
W
0, x
=
∫
0
x
⃗
F⋅⃗
dx =
∫
0
x
−
kx dx=−k
[
x
2
2
]
0
x
W
0, x
= −
1
2
k x
2
praca siły sprężystości
W
x ,0
=
∫
x
o
⃗
F⋅⃗
dx =
∫
x
0
−
kx dx=−k
[
x
2
2
]
x
0
W
x ,0
=
1
2
k x
2
x=0
x
k
m
m
x
⃗
F
x=0
x
k
m
m
x
⃗
F
W
0,0
=
W
0, x
+
W
x ,0
=−
1
2
k x
2
+
1
2
k x
2
=
0
siła zachowawcza
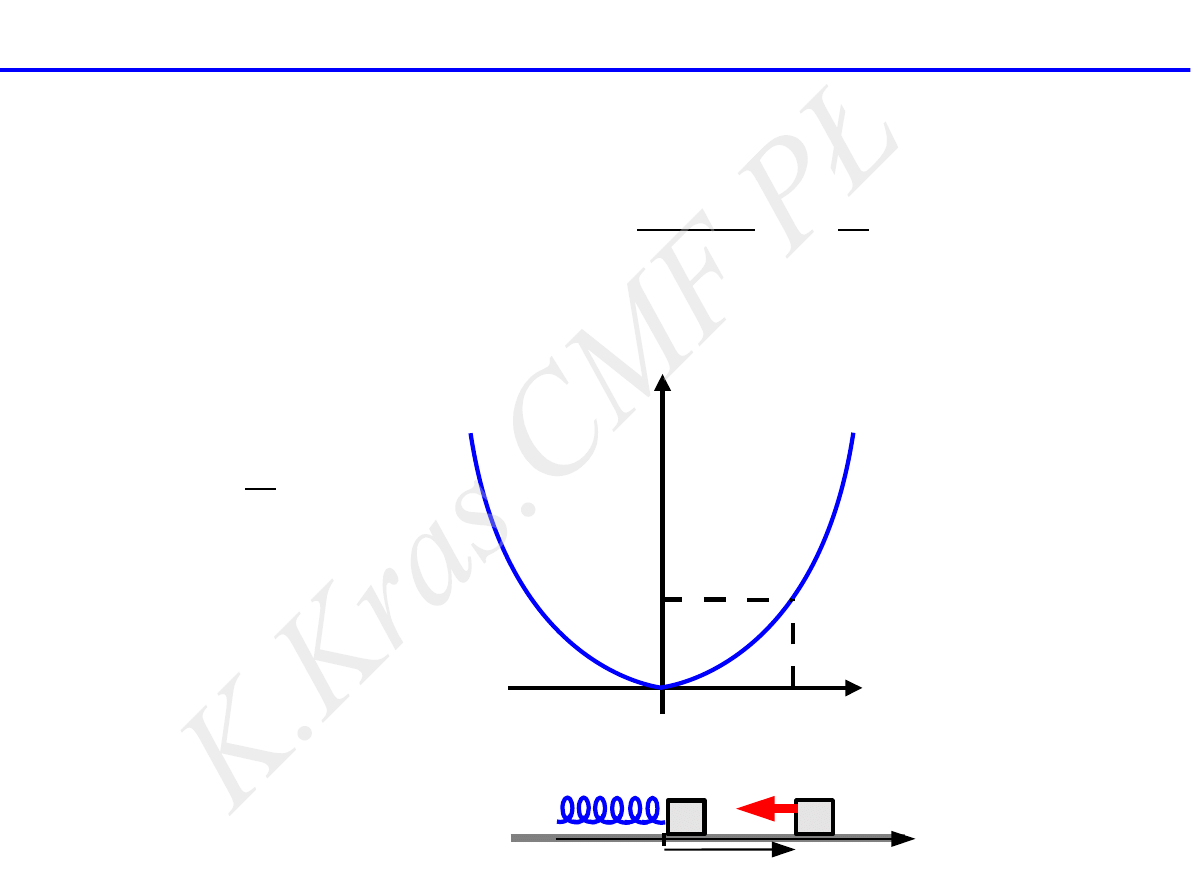
E
p
(
x) =
1
2
k x
2
energia potencjalna siły sprężystości
x = 0 ⇒ E
p
=
0
E
p
(
x) = E
p
(
0)−W
0, x
=
0−(
−
k x
2
2
) =
1
2
k x
2
(wybór)
x=0
x
k
m
⃗
F
x
m
x
E
p
0
E
p
(
x)
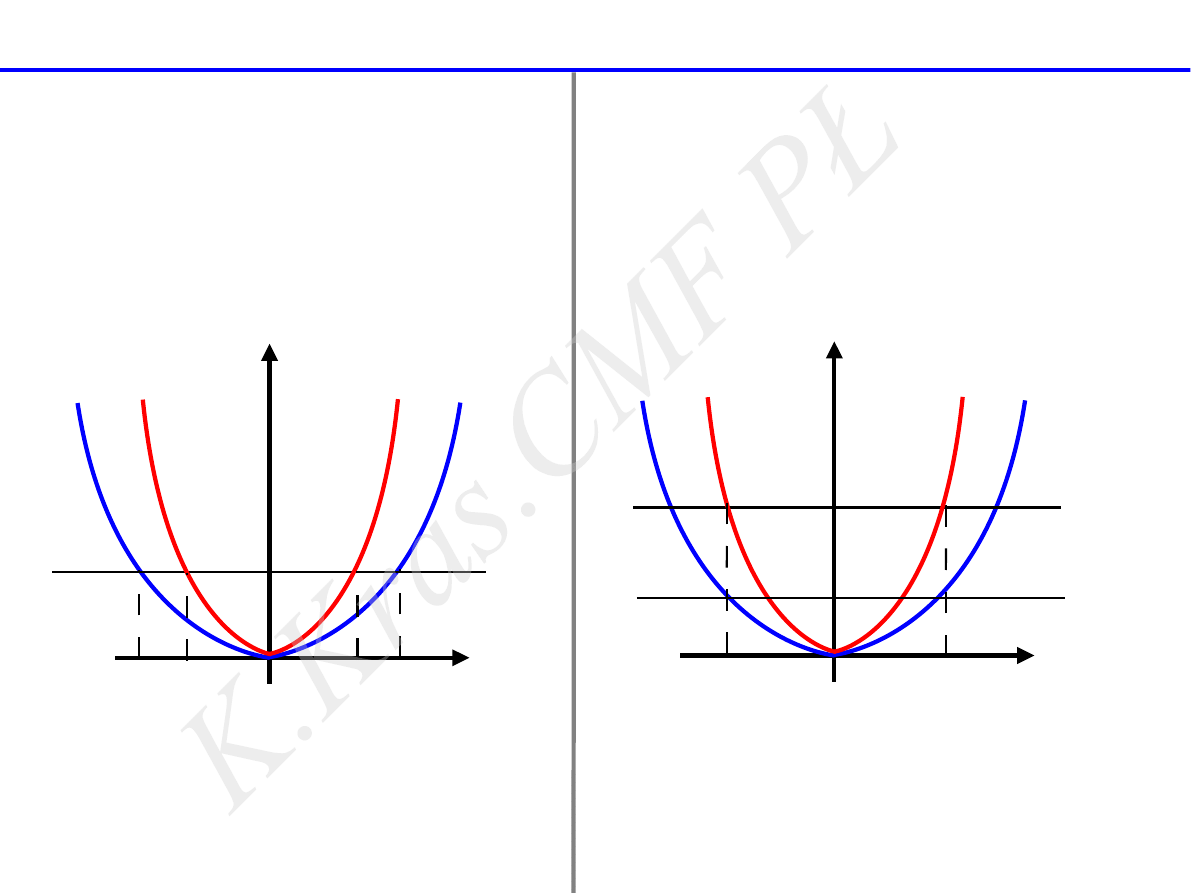
energia potencjalna siły sprężystości
k
2
>
k
1
x
E
p
0
E
p
(
x)
k
1
k
2
x
1
x
2
−
x
1
−
x
2
x
E
p2
0
E
p
(
x)
k
1
k
2
x
1
−
x
1
E
p1
k
2
>
k
1
Document Outline
- Slajd 1
- Slajd 2
- Slajd 3
- Slajd 4
- Slajd 5
- Slajd 6
- Slajd 7
- Slajd 8
- Slajd 9
- Slajd 10
- Slajd 11
- Slajd 12
- Slajd 13
- Slajd 14
- Slajd 15
- Slajd 16
- Slajd 17
- Slajd 18
Wyszukiwarka
Podobne podstrony:
Materiały do wykładu 4 (28 10 2011)
Materiały do wykładu 3 (20 10 2011)
Materiały do wykładu 3 (21 10 2011)
Materiały do wykładu 2 (13 10 2011)
Materiały do wykładu 4 (28 10 2011)
Materiały do wykładu 7 (18 11 2011)
Materiały do wykładu 7 (17 11 2011)
VAT w działalności gospodarczej Materialy do wykladu - VAT w dzialalnosci - 2011 rok, dostawy krajow
Materialy do wykladu 1 (06 10 2 Nieznany
Materiały do wykładu 6 (04 11 2011)
Materiały do wykładu 5 (03 11 2011)
więcej podobnych podstron