1
WYDZIAŁ ELEKTRYCZNY
Semestr III
Studia Niestacjonarne
Elektotechnika
Lista Nr 21
CAŁKI KRZYWOLINIOWE
Zad.1. Obliczyć
∫
K
dl
y
x
f
)
,
(
jeśli:
a)
y
x
y
x
f
=
)
,
(
K
– łuk paraboli
2
2
y
x =
leżący między punktami
(
)
2
,
1
,
(
)
2
,
2
b)
xy
y
x
f
=
)
,
(
K
:
1
,
0
sinh
)
(
,
cosh
)
(
∈
=
=
t
t
t
y
t
t
x
c)
y
x
y
x
f
−
=
1
)
,
(
{
}
4
0
4
2
:
)
,
(
≤
≤
=
−
=
x
y
x
y
x
K
d)
2
2
)
,
(
y
x
y
x
f
+
=
π
≤
≤
−
=
+
=
2
0
cos
sin
)
(
,
sin
cos
)
(
:
t
t
t
t
t
y
t
t
t
t
x
K
e)
xy
y
x
f
=
)
,
(
K
– łuk elipsy
1
2
2
2
2
=
+
b
y
a
x
leżący w I – szej ćwiartce układu współrzędnych
f)
y
y
x
f
=
)
,
(
K
– łuk paraboli
px
y
2
2
=
leżący między punktami
(
)
0
,
0
,
(
)
0
0
, y
x
g)
2
2
)
,
(
y
x
y
x
f
+
=
K
– prostoliniowy odcinek łączący punkty
(
) (
)
b
a
b
b
a
a
<
,
,
,
h)
x
e
y
y
x
f
−
⋅
=
)
,
(
K
– łuk krzywej
(
)
3
arctg
2
,
1
ln
2
+
−
=
+
=
t
t
y
t
x
pomiędzy punktami
0
=
t
i
1
=
t
i)
2
)
,
(
y
y
x
f
=
(
)
(
)
0
,
2
0
cos
1
)
(
,
sin
)
(
:
>
π
≤
≤
−
=
−
=
a
t
t
a
t
y
t
t
a
t
x
K
j)
4
1
)
,
(
2
2
+
+
=
y
x
y
x
f
{
}
1
0
2
:
)
,
(
≤
≤
=
=
x
x
y
y
x
K
k)
xy
y
x
f
=
)
,
(
K
jest brzegiem prostokąta o wierzchołkach:
)
2
,
0
(
,
)
2
,
4
(
,
)
0
,
4
(
,
)
0
,
0
(
l)
xy
y
x
f
=
)
,
(
K
jest brzegiem kwadratu:
0
>
=
+
a
a
y
x
ł)
2
2
)
,
(
y
x
y
x
f
+
=
K
jest okręgiem o równaniu:
ϕ
= sin
a
r
m)
y
x
y
x
f
3
4
)
,
(
3
−
=
K
jest łukiem asteroidy:
π
≤
≤
π
=
=
t
t
y
t
x
2
sin
,
cos
3
3
n)
(
)
2
2
2
2
1
)
,
(
y
x
y
x
y
x
f
+
+
=
K jest łukiem spirali hiperbolicznej:
ϕ
=
1
r
,
2
2
,
3
∈
ϕ
Zad.2.* Wyprowadzić wzór na obliczenie
∫
K
dl
y
x
f
)
,
(
w przypadku, gdy krzywa K dana jest we
współrzędnych biegunowych :
2
1
),
(
ϕ
≤
ϕ
≤
ϕ
ϕ
= r
r
.
Zad.3. Obliczyć następujące całki krzywoliniowe nieskierowane w przestrzeni:
a)
∫
K
dl
xyz
K
łuk krzywej
1
,
0
2
1
,
8
3
1
,
2
3
∈
=
=
=
t
t
z
t
y
t
x
b)
(
)
ds
y
x
z
L
∫
+
−
2
2
2
{
}
π
≤
≤
=
=
=
=
2
0
,
sin
,
cos
:
)
,
,
(
t
t
z
t
t
y
t
t
x
z
y
x
L
c)
(
)
dl
z
y
x
K
∫
+
+
2
2
2
K
– krzywa zamknięta
4
3
2
1
P
P
P
P
przy czym:
2
1
P
P
– łuk okręgu
0
,
2
2
2
=
=
+
z
a
y
x
3
2
P
P
– odcinek prostej
0
,
=
=
+
x
a
z
y
4
3
P
P
– łuk okręgu
0
,
2
2
2
=
=
+
y
a
z
x
2
d)
(
)
dl
cz
by
ax
K
∫
+
+
2
2
2
K
– odcinek łączący punkty
)
,
,
(
,
)
0
,
0
,
0
(
c
b
a
A
O
e)
ds
a
y
∫
Γ
2
≤
≤
=
=
=
=
Γ
1
0
3
,
2
,
:
)
,
,
(
3
2
t
t
a
z
t
a
y
at
x
z
y
x
f)
(
)
dl
x
y
K
∫
−
K – krzywa zamknięta
4
3
2
1
P
P
P
P
przy czym:
2
1
P
P
– odcinek łączący punkty
(
)
)
0
,
0
,
2
(
,
0
,
0
,
0
3
2
P
P
– łuk okręgu
0
,
2
2
2
=
=
+
z
y
x
4
3
P
P
– łuk paraboli
(
)
1
,
1
2
=
−
=
y
x
z
1
4
P
P
– odcinek łączący punkty
(
)
)
0
,
0
,
0
(
,
0
,
1
,
1
Zad.4. Obliczyć długość łuku krzywej K jeśli:
a)
K :
1
0
2
,
3
,
3
3
2
≤
≤
=
=
=
t
t
z
t
y
t
x
b)
K :
0
2
0
),
cos
1
(
),
sin
(
>
π
≤
≤
−
=
−
=
a
t
t
a
y
t
t
a
x
c)
K :
∞
<
≤
=
=
=
−
−
−
t
e
z
t
e
y
t
e
x
t
t
t
0
,
sin
,
cos
Zad.5. Wyznaczyć pole powierzchni :
a)
bocznej walca
2
2
2
R
y
x
=
+
ograniczonej płaszczyzną OXY oraz powierzchnią
R
y
R
z
2
+
=
b)
bocznej walca
1
2
2
=
+ y
x
ograniczonej płaszczyznami:
y
z
x
z
+
=
−
=
5
,
c)
walcowej o równaniach:
4
0
sin
,
cos
π
≤
≤
=
=
t
t
e
y
t
e
x
t
t
zawartej między płaszczyzną OXY oraz
powierzchnią
1
2
2
+
+
=
y
x
z
Zad.6. Obliczyć następujące całki krzywoliniowe skierowane:
a)
(
)
∫
+
−
K
xdy
dx
xy
y
2
, gdzie K jest łukiem określonym równaniem:
1
0
,
≤
≤
=
x
x
y
b)
(
)
(
)
∫
−
+
−
K
dy
xy
y
dx
xy
x
2
2
2
2
wzdłuż krzywej K, którą jest łuk paraboli
2
x
y =
od punktu
)
9
,
3
(−
A
do
punktu
)
4
,
2
(
B
c)
∫
−
K
dy
x
xydx
2
2
, gdzie K łamana od punktu
)
0
,
0
(
O
przez punkt
)
0
,
2
(
A
do punktu
)
1
,
2
(
B
d)
(
)
∫
+
−
K
xdy
dx
y
4
, gdzie
(
)
(
)
{
}
π
≤
≤
−
=
−
=
=
2
0
,
cos
1
2
,
sin
2
:
)
,
(
t
t
y
t
t
x
y
x
K
jest łukiem cykloidy
e)
∫
−
+
K
dy
y
dx
y
x
1
1
, gdzie
π
≤
≤
π
−
=
−
=
=
3
6
,
cos
1
,
sin
:
)
,
(
t
t
y
t
t
x
y
x
K
f)
∫
+
K
xdy
dx
xy
3
, gdzie K jest łukiem paraboli
2
3x
y =
od punktu
)
0
,
0
(
A
do punktu
)
3
,
1
(
B
g)
∫
−
K
dy
x
xydx
2
2
, gdzie K – łuk paraboli
2
2 y
x =
od punktu
)
0
,
0
(
O
do punktu
)
1
,
2
(
A
h)
(
)
(
)
∫
+
+
−
K
dy
y
x
dx
y
x
, gdzie
{
}
π
≤
≤
=
=
=
t
t
y
t
x
y
x
K
0
,
sin
2
,
cos
4
:
)
,
(
jest łukiem elipsy
i)
∫
+
K
xdy
ydx
, gdzie
π
≤
≤
=
=
=
4
0
,
sin
,
cos
:
)
,
(
t
t
r
y
t
r
x
y
x
K
3
j)
∫
+
+
K
ydz
xdy
zdx
3
2
, gdzie K łamana o początku w punkcie
)
0
,
0
,
0
(
O
końcu w punkcie
)
1
,
1
,
1
(
B
i wierzchołku
)
0
,
1
,
1
(
A
k)
(
)
(
)
∫
+
−
+
+
K
zdz
dy
y
x
dx
y
x
2
2
, gdzie K łamana o początku w punkcie
)
0
,
0
,
0
(
O
końcu w punkcie
)
2
,
2
,
2
(
C
i wierzchołkach
)
0
,
0
,
2
(
A
,
)
0
,
2
,
2
(
B
l)
(
)
∫
−
+
−
K
dz
x
yzdy
dx
z
y
2
2
2
2
, gdzie
1
,
0
,
,
,
:
3
2
∈
=
=
=
t
t
z
t
y
t
x
K
m)
∫
+
+
K
xdz
zdy
ydx
, gdzie
{
}
π
≤
≤
=
=
=
=
2
0
,
,
sin
,
cos
:
)
,
,
(
t
bt
z
t
a
y
t
a
x
z
y
x
K
n)
∫
+
−
+
K
xydz
dy
y
R
z
yzdx
2
2
, gdzie
π
≤
≤
π
=
=
=
2
0
,
2
,
sin
,
cos
:
t
at
z
t
R
y
t
R
x
K
o)
∫
−
K
dy
x
ydx
2
, gdzie krzywa zamknięta
1
3
2
1
P
P
P
P
K =
, przy czym:
2
1
P
P
jest łukiem asteroidy
t
a
x
3
cos
=
,
t
a
y
3
sin
=
;
3
2
P
P
odcinkiem prostej
a
x
y
=
−
;
1
3
P
P
półokręgiem o środku w początku
układu współrzędnych i promieniu a
Zad.7. Obliczyć całkę krzywoliniową skierowaną
∫
−
K
dy
x
dx
y
2
2
po łuku zamkniętym K, który jest okręgiem
(
)
(
)
1
1
1
2
2
=
−
+
−
y
x
skierowanym dodatnio.
Zad.8. Obliczyć
(
)
(
)
∫
+
−
−
K
dy
y
x
dx
x
y
2
2
, gdzie K jest brzegiem obszaru D:
2
2
2
R
y
x
≤
+
,
0
≥
x
0
≥
y
,
0
>
R
skierowanym dodatnio.
Zad.9. Obliczyć
∫
+
K
xdy
xydx
po elipsie K o równaniu
2
2
2
2
2
2
b
a
y
a
x
b
=
+
skierowanej ujemnie względem
swego wnętrza.
Zad.10. Stosując tw. Greena obliczyć całki krzywoliniowe:
a)
(
)
(
)
∫
+
−
+
K
dy
y
x
dx
y
x
2
2
2
2
, K – brzeg trójkąta o wierzchołkach
)
3
,
1
(
),
2
,
2
(
),
1
,
1
(
C
B
A
skierowany dodatnio
b)
∫
−
K
ydy
x
dx
xy
2
2
, K – okrąg o równaniu
2
2
2
R
y
x
=
+
skierowany przeciwnie do ruchu wskazówek
zegara
c)
(
)
(
)
[
]
∫
−
−
−
K
x
dy
y
dx
y
e
sin
1
cos
1
, gdzie K jest brzegiem obszaru D określonego nierównościami:
x
y
x
sin
0
,
0
≤
≤
π
≤
≤
skierowanym dodatnio
d)
(
)
∫
+
+
K
dy
y
x
ydx
, K – krzywa zamknięta złożona z łuku paraboli
2
x
y =
i odcinka prostej
4
=
y
skierowana dodatnio
e)
∫
+
K
dy
x
dx
y
2
2
, K – okrąg o równaniu
x
y
x
2
2
2
=
+
skierowany zgodnie z ruchem wskazówek zegara
f)
(
)
[
]
∫
+
+
+
+
+
K
dy
y
x
x
xy
y
dx
y
x
2
2
2
2
ln
, gdzie K jest brzegiem obszaru D określonego następująco:
e
x
x
y
,
1
,
ln
∈
≤
skierowanym dodatnio
4
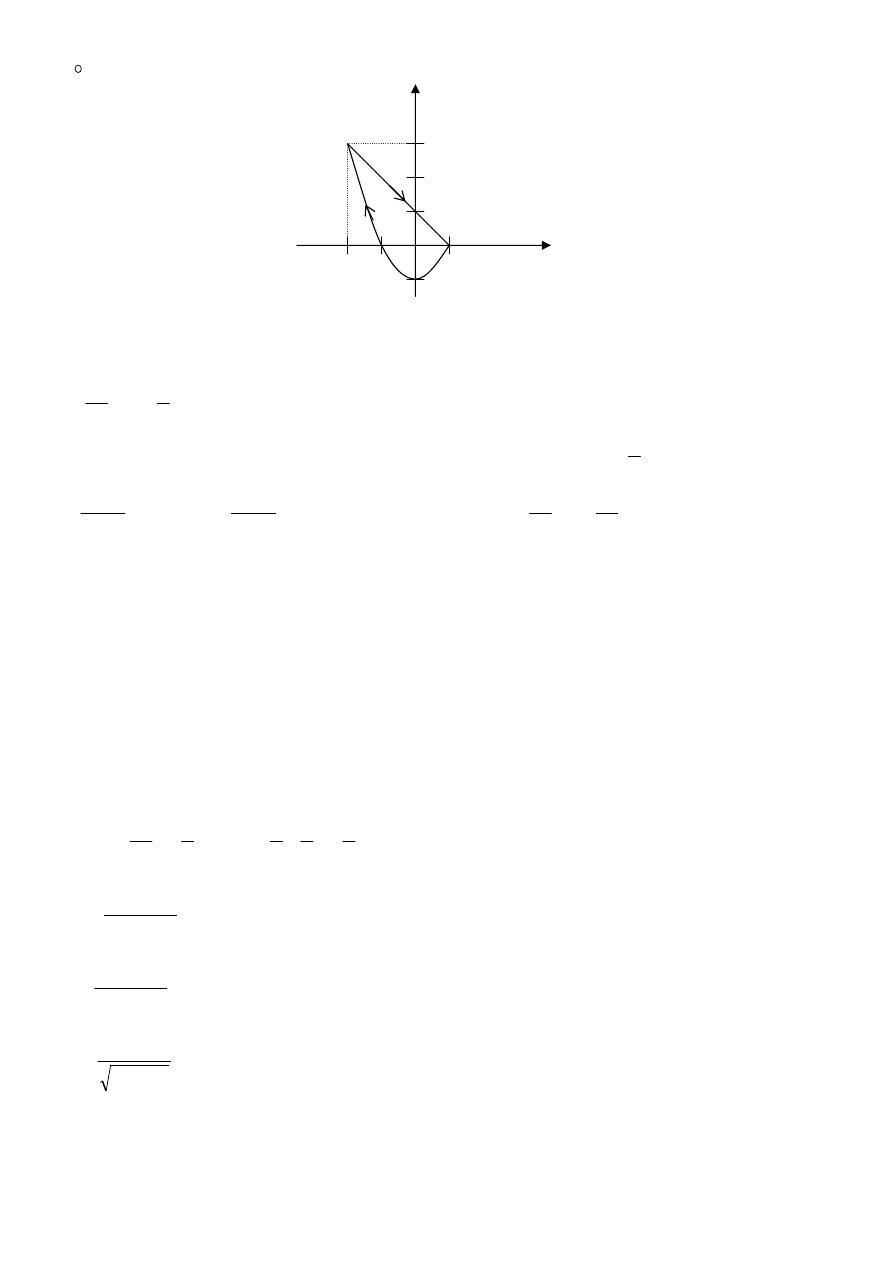
g)
(
)
(
)
∫
−
−
+
K
dy
y
x
dx
y
x
, K – krzywa zamknięta podana na poniższym rysunku
Zad.11. Sprawdzić, czy podane niżej wyrażenia są różniczkami zupełnymi funkcji
)
,
(
y
x
F
, jeśli tak, znaleźć
funkcję pierwotną
)
,
(
y
x
F
a)
dy
y
x
dx
x
y
2
2
2
+
−
b)
(
)
dy
xe
dx
e
y
y
−
−
−
+ 1
c)
(
)
dy
y
x
y
ydx
x
2
sin
2
cos
2
2
2
−
+
d)
(
)
dy
y
y
x
dx
y
x
−
+
+
−
2
ln
2
e)
dy
y
x
y
dx
x
y
x
−
+
+
2
2
sin
2
sin
f)
dy
x
y
dx
x
y
2
4
2
2
+
−
Zad.12. Obliczyć wartości podanych niżej całek:
a)
(
)(
)
(
)
( )
∫
−
−
−
1
,
1
1
,
1
dy
dx
y
x
b)
(
)
(
)
(
)
∫
−
b
a
x
ydy
ydx
e
,
0
,
0
sin
cos
c)
(
)
[
]
(
)
( )
∫
−
−
1
,
1
0
,
0
2
2
3
4
ydy
x
dx
x
y
x
d)
(
)
(
)
dy
x
y
x
y
x
y
dx
x
y
x
y
∫
π
π
+
+
−
,
2
,
1
2
2
cos
sin
cos
1
wzdłuż drogi nie przecinającej osi OY
e)
(
)
(
)
(
)
∫
−
−
−
0
,
1
1
,
0
2
y
x
ydx
xdy
wzdłuż drogi nie przecinającej prostej
x
y =
f)
(
)
(
)
∫
−
2
,
1
1
,
2
2
x
xdy
ydx
wzdłuż drogi nie przecinającej osi OY
g)
(
)
(
)
∫
+
+
8
,
6
0
,
1
2
2
y
x
ydy
xdx
wzdłuż drogi nie przecinającej przez początek układu współrzędnych
(
)
(
)
(
)
(
)
dy
y
y
x
dx
xy
x
∫
−
−
−
+
+
0
,
3
1
,
2
4
2
2
3
4
5
6
4
)
0
,
1
(
A
)
3
,
2
(−
B
-1
1
x
y