127
WYKŁAD Nr 9
CAŁKI NIEOZNACZONE
PODSTAWOWE POJĘCIA I TWIERDZENIA
Def.9.1. (funkcja pierwotna)
Niech F będzie funkcją różniczkowalną. Funkcja F jest funkcją pierwotną funkcji f na przedziale X,
jeżeli
)
(
)
(
x
f
x
F
=
′
dla
X
x ∈
.
Przykłady funkcji pierwotnych :
a)
Dla funkcji
2
)
(
x
x
f
=
na zbiorze R funkcjami pierwotnymi są m.in. funkcje:
2
3
3
3
1
bo
3
1
)
(
x
x
x
x
F
=
′
=
;
2
3
3
7
3
1
bo
7
3
1
)
(
x
x
x
x
F
=
′
+
+
=
b)
Dla funkcji
2
1
1
)
(
x
x
f
−
=
na przedziale
(
)
1
,
1
−
funkcjami pierwotnymi są m.in. funkcje:
(
)
2
1
1
arcsin
1
bo
arcsin
1
)
(
x
x
x
x
F
−
=
′
+
+
=
;
(
)
2
1
1
arccos
5
bo
arccos
5
)
(
x
x
x
x
F
−
=
′
−
−
=
Tw.9.1. (podstawowe twierdzenie o funkcjach pierwotnych)
Niech F będzie funkcją pierwotną funkcji f na przedziale X. Wtedy:
a)
funkcja
R
∈
+
=
C
C
x
F
x
G
gdzie
,
)
(
)
(
, jest funkcją pierwotną funkcji f na X
b)
każdą funkcję pierwotną funkcji f na przedziale X można przedstawić w postaci
R
∈
+
C
C
x
F
,
)
(
Def.9.2. (funkcja całkowalna)
Funkcję f, która posiada na pewnym przedziale funkcję pierwotną nazywamy funkcją
całkowalną
(w sensie Newtona) na tym przedziale.
Tw.9.2.
Każda funkcja ciągła na przedziale X ma na tym przedziale funkcję pierwotną.
Def.9.3. (całka nieoznaczona)
Całką nieoznaczoną
funkcji f na przedziale X nazywamy zbiór wszystkich funkcji pierwotnych, a
oznaczamy przez
∫
dx
x
f
)
(
.
∫
∈
+
=
R
C
C
x
F
dx
x
f
,
)
(
)
(
F
(x) – funkcja pierwotna funkcji f
f
(x) – funkcja podcałkowa
x
– zmienna całkowania
C
– stała całkowania
128
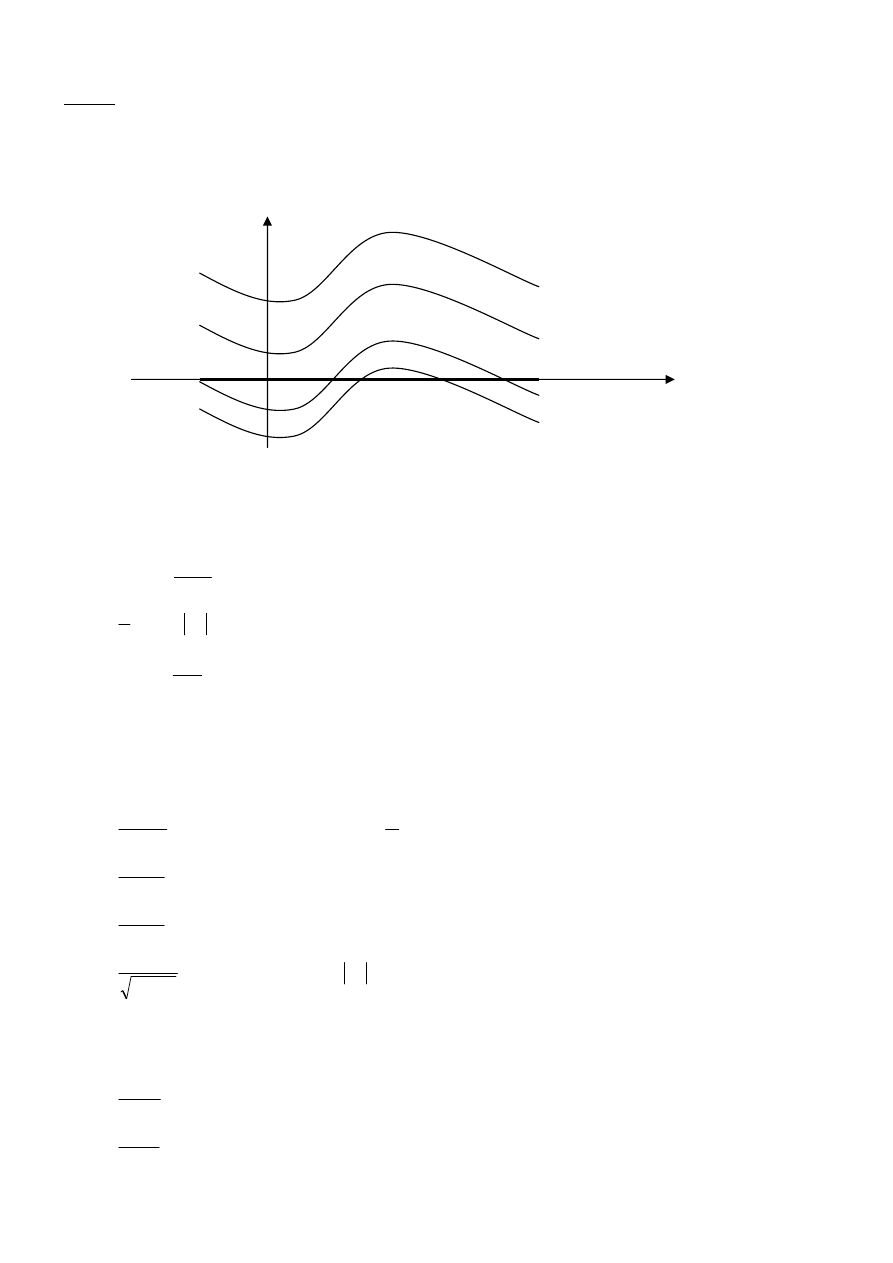
Uwaga: Wykres dowolnej funkcji pierwotnej
)
(x
F
funkcji
)
(x
f
nazywa się krzywą całkową. Danej
funkcji
)
(x
f
odpowiada nieskończenie wiele krzywych całkowych. Wszystkie krzywe całkowe danej
funkcji możemy otrzymać z jednej z nich za pomocą przesunięcia równoległego o wektor równoległy do
osi OY.
Poniższy rysunek przedstawia niektóre krzywe całkowe pewnej funkcji f.
CAŁKI NIEOZNACZONE FUNKCJI ELEMENTARNYCH
1)
∫
∈
=
R
x
C
dx
,
0
2)
{ }
∫
>
−
∈
+
+
=
+
0
,
1
\
,
1
1
x
C
x
dx
x
R
α
α
α
α
3)
∫
≠
+
=
0
,
ln
1
x
C
x
dx
x
4)
∫
∈
≠
>
+
=
R
x
a
a
C
a
a
dx
a
x
x
,
1
,
0
,
ln
5)
∫
∈
+
=
R
x
C
e
dx
e
x
x
,
6)
∫
∈
+
−
=
R
x
C
x
xdx
,
cos
sin
7)
∫
∈
+
=
R
x
C
x
xdx
,
sin
cos
8)
∫
∈
+
≠
+
=
,
,
2
,
tg
cos
1
2
Z
Z
k
k
x
C
x
dx
x
π
π
- zbiór liczb całkowitych
9)
∫
∈
≠
+
−
=
,
,
ctg
sin
1
2
Z
k
k
x
C
x
dx
x
π
10)
∫
∈
+
=
+
,
arctg
1
1
2
R
x
C
x
dx
x
11)
∫
<
+
=
−
1
,
sin
arc
1
1
2
x
C
x
dx
x
12)
∫
∈
+
=
R
x
C
x
xdx
,
ch
sh
13)
∫
∈
+
=
R
x
C
x
xdx
,
sh
ch
14)
∫
∈
+
=
,
th
ch
1
2
R
x
C
x
dx
x
15)
∫
≠
+
−
=
0
,
cth
sh
1
2
x
C
x
dx
x
y= F
(x)+A
y= F
(x)
y= F
(x)+B
y= F(x)+C
X
x
y
129
Przykłady całek nieoznaczonych:
a)
∫
+
=
+
+
=
+
C
x
C
x
dx
x
6
1
5
6
1
5
5
b)
∫
+
=
C
dx
x
x
5
ln
5
5
c)
∫
∫
+
−
=
+
−
=
+
+
−
=
=
−
+
−
−
C
x
C
x
C
x
dx
x
dx
x
4
4
1
5
5
5
4
1
4
1
5
1
d)
∫
∫
+
=
+
=
+
+
=
=
+
C
x
x
C
x
C
x
dx
x
dx
x
5
5
6
1
5
1
5
1
5
6
5
5
6
1
5
1
e)
C
x
C
x
C
x
dx
x
dx
x
+
=
+
=
+
+
−
=
=
∫
∫
+
−
−
5
4
5
4
1
5
1
5
1
5
4
5
5
4
1
5
1
1
Bezpośrednio z Def.9.3. wynikają dwa proste twierdzenia:
Tw.9.3. (o pochodnej całki)
Pochodna całki nieoznaczonej jest równa funkcji podcałkowej tzn.
(
)
)
(
)
(
x
f
dx
x
f
=
′
∫
Tw.9.4. (o całce pochodnej)
Całka nieoznaczona pochodnej funkcji jest sumą tej funkcji i dowolnej stałej tzn.
∫
+
=
′
C
x
f
dx
x
f
)
(
)
(
Tw.9.5. (o działaniach na całkach nieoznaczonych)
Jeżeli funkcje f i g są całkowalne w pewnym przedziale X (tzn. mają funkcje pierwotne na X), to funkcje
,
,
,
f
A
g
f
g
f
⋅
−
+
gdzie A dowolna stała, są całkowalne w X, przy czym dla każdego
X
x ∈
:
1)
[
]
∫
∫
∫
+
=
+
dx
x
g
dx
x
f
dx
x
g
x
f
)
(
)
(
)
(
)
(
2)
[
]
∫
∫
∫
−
=
−
dx
x
g
dx
x
f
dx
x
g
x
f
)
(
)
(
)
(
)
(
3)
∫
∫
=
⋅
dx
x
f
A
dx
x
f
A
)
(
)
(
Tw.9.6. (o całkowaniu przez części)
Jeżeli funkcje f i g mają ciągłe pochodne w pewnym przedziale X, to
(∗)
∫
∫
⋅
′
−
⋅
=
′
⋅
dx
x
g
x
f
x
g
x
f
dx
x
g
x
f
)
(
)
(
)
(
)
(
)
(
)
(
Wzór (∗) nazywamy wzorem na całkowanie przez części.
Wzór ten wymaga wydzielenia z funkcji pod całką lewej strony czynnika, dla którego funkcja pierwotna
(całka) jest znana.

130
Uzasadnienie wzoru (∗) z Tw.9.6.
[
]
)
(
)
(
)
(
)
(
)
(
)
(
x
g
x
f
x
g
x
f
x
g
x
f
′
⋅
+
⋅
′
=
′
⋅
{wzór na pochodną iloczynu}
[
]
∫
∫
∫
∫
′
⋅
+
⋅
′
=
′
⋅
+
⋅
′
=
′
⋅
dx
x
g
x
f
dx
x
g
x
f
dx
x
g
x
f
x
g
x
f
dx
x
g
x
f
)
(
)
(
)
(
)
(
)]
(
)
(
)
(
)
(
[
)
(
)
(
czyli
[
]
∫
∫
∫
′
⋅
+
⋅
′
=
′
⋅
dx
x
g
x
f
dx
x
g
x
f
dx
x
g
x
f
)
(
)
(
)
(
)
(
)
(
)
(
ale z drugiej strony
[
]
∫
⋅
=
′
⋅
)
(
)
(
)
(
)
(
x
g
x
f
dx
x
g
x
f
{na podstawie Tw.9.4.}
zatem mamy:
)
(
)
(
)
(
)
(
)
(
)
(
x
g
x
f
dx
x
g
x
f
dx
x
g
x
f
⋅
=
′
⋅
+
⋅
′
∫
∫
stąd po przeniesieniu
dx
x
g
x
f
∫
⋅
′
)
(
)
(
na drugą stronę otrzymujemy:
dx
x
g
x
f
x
g
x
f
dx
x
g
x
f
∫
∫
⋅
′
−
⋅
=
′
⋅
)
(
)
(
)
(
)
(
)
(
)
(
Przykłady całkowania przez części:
a)
(
)
(
)
∫
∫
∫
=
+
−
=
−
⋅
−
−
⋅
=
−
=
=
′
=
′
=
=
⋅
xdx
x
x
dx
x
x
x
x
x
g
x
f
x
x
g
x
x
f
xdx
x
cos
cos
cos
1
cos
cos
)
(
1
)
(
sin
)
(
)
(
sin
C
x
x
x
+
+
−
=
sin
cos
b)
=
+
−
=
−
=
⋅
−
⋅
=
=
=
′
=
′
=
=
⋅
=
∫
∫
∫
∫
C
x
x
x
dx
x
x
xdx
x
x
x
x
x
g
x
x
f
x
g
x
x
f
xdx
xdx
ln
ln
1
ln
)
(
1
)
(
1
)
(
ln
)
(
ln
1
ln
C
x
x
+
−
=
)
1
(ln
c)
(
)
(
)
∫
∫
∫
=
+
−
=
−
⋅
−
−
⋅
=
−
=
=
′
=
′
=
=
xdx
e
x
e
dx
x
e
x
e
x
x
g
e
x
f
x
x
g
e
x
f
xdx
e
x
x
x
x
x
x
x
cos
cos
cos
cos
cos
)
(
)
(
sin
)
(
)
(
sin
∫
−
+
−
=
=
=
′
=
′
=
=
xdx
e
x
e
x
e
x
x
g
e
x
f
x
x
g
e
x
f
x
x
x
x
x
sin
sin
cos
sin
)
(
)
(
cos
)
(
)
(
całkując dwukrotnie przez części otrzymaliśmy po prawej stronie nieznaną całkę, w celu jej wyznaczenia
zapisujemy następującą równość:
∫
∫
−
+
−
=
xdx
e
x
e
x
e
xdx
e
x
x
x
x
sin
sin
cos
sin
przenosimy nieznaną
∫
dx
x
e
x
sin
na jedną stronę, wówczas:
x
e
x
e
xdx
e
x
x
x
sin
cos
sin
2
+
−
=
∫
dzieląc przez 2 mamy:
C
x
x
e
xdx
e
x
x
+
+
−
=
∫
)
sin
cos
(
2
1
sin
131
Tw.9.7. (o całkowaniu przez podstawienie)
Jeśli funkcja
)
(x
g
t =
jest różniczkowalna w przedziale
(
)
d
c
,
oraz
(
)
(
)
b
a
d
c
g
,
,
:
→
, funkcja
)
(t
f
jest
całkowalna w przedziale (a, b),to zachodzi następująca równość
(∗∗)
[
]
∫
∫
=
′
⋅
dt
t
f
dx
x
g
x
g
f
)
(
)
(
)
(
dla
)
(x
g
t =
Wzór (∗∗) nazywamy wzorem na całkowanie przez podstawienie (zamianę zmiennych).
Uwaga: Z Tw.9.7. wynika, że w praktyce możemy korzystać z dwóch wzorów:
(1)
[
]
∫
∫
=
=
′
=
=
′
⋅
dt
t
f
dt
dx
x
g
t
x
g
dx
x
g
x
g
f
)
(
)
(
)
(
)
(
)
(
lub
(2)
[
]
∫
∫
′
⋅
=
′
=
=
=
dt
t
h
t
h
f
dt
t
h
dx
t
h
x
dx
x
f
)
(
)
(
)
(
)
(
)
(
Który z podanych wzorów zastosujemy, zależeć będzie od funkcji podcałkowej. Należy tutaj kierować się
zasadą, że podstawienie ma całkę upraszczać.
Przykłady całkowania przez podstawienie:
a)
(
)
(
)
C
x
C
t
dt
t
dt
t
dt
dx
dt
dx
t
x
dx
x
+
+
=
+
⋅
=
=
⋅
=
=
=
=
+
=
+
∫
∫
∫
8
8
7
7
7
5
2
16
1
8
2
1
2
1
2
1
2
1
2
5
2
5
2
b)
C
e
C
e
dt
e
dt
dx
x
t
x
dx
x
e
dx
x
e
x
t
t
x
x
+
=
+
=
=
=
+
=
=
+
⋅
=
+
∫
∫
∫
arctg
2
2
arctg
2
arctg
1
1
arctg
1
1
1
c)
∫
∫
∫
∫
+
−
=
+
−
=
−
=
−
=
−
=
=
−
=
=
=
C
x
C
t
dt
t
dt
t
dt
xdx
dt
xdx
t
x
dx
x
x
xdx
cos
ln
ln
1
)
(
1
sin
sin
cos
cos
sin
tg
d)
∫
∫
∫
=
=
⋅
=
=
=
=
=
dt
te
dt
t
e
tdt
dx
t
x
t
x
dx
e
t
t
x
2
2
2
2
{całkujemy przez części pamiętając, że zmienną jest teraz t}
=
[
]
(
)
C
e
e
x
C
e
te
dt
e
te
e
t
g
t
f
e
t
g
t
t
f
x
x
t
t
t
t
t
t
+
−
⋅
=
+
−
=
−
=
=
=
′
=
′
=
∫
2
)
(
2
2
)
(
1
)
(
)
(
)
(
132
CAŁKI WAŻNIEJSZYCH TYPÓW FUNKCJI
Korzystając z metody całkowania przez podstawienie można wyprowadzić następujące wzory:
1.
0
)
(
,
)
(
ln
)
(
)
(
≠
+
=
′
∫
x
f
C
x
f
dx
x
f
x
f
2.
0
)
(
,
)
(
1
)
(
)
(
2
≠
+
−
=
′
∫
x
f
C
x
f
dx
x
f
x
f
3.
{ }
∫
∪
∈
+
+
=
′
⋅
+
0
,
1
)
(
)
(
)
(
1
N
m
C
m
x
f
dx
x
f
x
f
m
m
4.
∫
>
+
=
′
0
)
(
,
)
(
2
)
(
)
(
x
f
C
x
f
dx
x
f
x
f
5.
∫
∈
+
=
′
f
x
f
x
f
D
x
C
e
dx
x
f
e
,
)
(
)
(
)
(
Aby uzasadnić te wzory, wystarczy zastosować podstawienie
dt
dx
x
f
t
x
f
=
′
=
)
(
,
)
(
.
Otrzymamy wtedy odpowiednio:
Ad.1.
∫
∫
+
=
+
=
=
′
C
x
f
C
t
dt
t
dx
x
f
x
f
)
(
ln
ln
1
)
(
)
(
Ad.2.
∫
∫
+
−
=
+
−
=
=
′
C
x
f
C
t
dt
t
dx
x
f
x
f
)
(
1
1
1
)
(
)
(
2
2
Ad.3.
∫
∫
+
+
=
+
+
=
=
′
⋅
+
+
C
m
x
f
C
m
t
dt
t
dx
x
f
x
f
m
m
m
m
1
)
(
1
)
(
)
(
1
1
Ad.4.
∫
∫
∫
+
=
+
=
+
=
=
=
′
−
C
x
f
C
t
C
t
dt
t
dt
t
dx
x
f
x
f
)
(
2
2
2
1
1
)
(
)
(
2
1
2
1
Ad.5.
∫
∫
+
=
+
=
=
′
C
e
C
e
dt
e
dx
x
f
e
x
f
t
t
x
f
)
(
)
(
)
(
Przykłady zastosowania tych wzorów:
a)
(
)
C
e
dx
e
e
dx
e
e
x
x
x
x
x
+
+
=
+
′
+
=
+
∫
∫
1
ln
1
1
1
b)
(
)
∫
∫
∫
+
−
=
′
=
=
C
x
dx
x
x
dx
x
x
x
x
dx
ln
1
ln
ln
ln
1
ln
2
2
2
133
c)
(
) (
)
∫
∫
+
=
′
⋅
=
C
x
dx
x
x
xdx
x
6
sin
sin
sin
cos
sin
6
5
5
d)
(
)
C
x
x
dx
x
x
x
x
dx
x
x
x
+
+
+
=
+
+
′
+
+
=
+
+
+
∫
∫
7
5
2
2
7
5
2
7
5
2
7
5
2
5
4
2
2
2
2
e)
(
)
∫
∫
∫
+
=
′
⋅
=
⋅
=
C
e
dx
x
e
dx
x
e
dx
x
e
x
x
x
x
tg
tg
2
tg
2
tg
tg
cos
1
cos
CAŁKOWANIE FUNKCJI WYMIERNYCH
Def.9.4. (funkcja wymierna, funkcja wymierna właściwa i niewłaściwa)
Funkcją wymierną
nazywamy iloraz dwóch wielomianów:
)
(
)
(
)
(
x
M
x
L
x
W
k
n
=
,
gdzie
)
(x
L
n
– wielomian stopnia n,
)
(x
M
k
– wielomian stopnia k.
Gdy
k
n <
(stopień wielomianu w liczniku jest mniejszy niż stopień wielomianu w mianowniku) wtedy
funkcję wymierną nazywamy właściwą, gdy
k
n ≥
– niewłaściwą.
Przykład funkcji wymiernej właściwej i niewłaściwej:
a)
8
3
2
3
5
)
(
2
4
+
+
+
=
x
x
x
x
W
– funkcja wymierna właściwa
b)
6
4
3
)
(
3
7
+
+
+
=
x
x
x
x
x
Q
– funkcja wymierna niewłaściwa.
Uwaga: Każdą funkcję wymierną można przedstawić w postaci sumy wielomianu i funkcji wymiernej
właściwej.
Przykład: Funkcję
1
2
)
(
3
+
+
=
x
x
x
P
zapisać w postaci sumy wielomianu i funkcji wymiernej właściwej.
Rozwiązanie:
(
)
(
)
(
)
(
)
(
)
3
2
1
43
42
1
wlasciwa
wymierna
funkcja
2
st.
wielomian
2
2
2
3
3
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
2
+
+
+
−
=
+
+
+
+
−
⋅
+
=
+
+
+
−
⋅
+
=
+
+
+
=
+
+
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
Uwaga: Można również wydzielić wielomian z licznika przez wielomian z mianownika, a następnie
podaną funkcję przedstawić w wymaganej postaci.

134
Def.9.5. (ułamki proste pierwszego i drugiego rodzaju)
Ułamkiem prostym pierwszego rodzaju
nazywamy funkcję wymierną właściwą postaci:
(
)
k
b
ax
A
+
,
gdzie
R
N
∈
∈
b
a
A
k
,
,
oraz
Ułamkiem prostym drugiego rodzaju
nazywamy funkcję wymierną właściwą postaci:
(
)
p
c
bx
ax
B
Ax
+
+
+
2
,
gdzie
R
N
∈
∈
c
b
a
B
A
p
,
,
,
,
oraz
, ∆ < 0,
)
4
(
2
ac
b −
=
∆
.
Uwaga: Każda funkcja wymierna właściwa jest sumą ułamków prostych pierwszego i drugiego rodzaju.
Przykład rozkładu na ułamki proste (bez obliczania współczynników rozkładu):
(
) (
)
(
)
(
)
(
) (
)
(
)
2
2
1
1
2
2
1
3
2
2
2
0
2
2
+
+
+
+
+
+
−
+
−
≡
+
+
+
−
+
<
∆
x
x
E
Dx
x
C
x
B
x
A
x
x
x
x
x
43
42
1
,
gdzie A,B,C,D,E – nieznane współczynniki rozkładu.
Aby wyliczyć te współczynniki rozkładu postępujemy następująco:
sprowadzamy prawą stronę do wspólnego mianownika,
porządkujemy licznik według potęg zmiennej x ,
porównujemy odpowiednie współczynniki przy kolejnych potęgach x z współczynnikami przy
tych samych potęgach x występujących w liczniku lewej strony,
z otrzymanego układu równań wyliczamy wszystkie nieznane współczynniki rozkładu.
ALGORYTM CAŁKOWANIA FUNKCJI WYMIERNYCH (tj. obliczania całek postaci
∫
dx
x
M
x
L
k
n
)
(
)
(
):
1. Sprawdzamy, czy
k
n ≥
? (stopień wielomianu licznika większy, bądź równy stopniowi mianownika)
Jeśli TAK dzielimy licznik przez mianownik {w wyniku dzielenia otrzymamy wielomian stopnia
(
)
k
n −
oraz resztę, w której stopień wielomianu z licznika jest niższy od stopnia wielomianu
z mianownika}
czyli
k
s
x
M
x
R
x
Q
x
M
x
L
k
s
k
n
k
n
<
+
=
−
gdzie
,
)
(
)
(
)
(
)
(
)
(
zatem
43
42
1
ej
wlasciw
wymiernej
funkcji
calka
)
(
)
(
)
(
)
(
)
(
∫
∫
∫
+
=
−
dx
x
M
x
R
dx
x
Q
dx
x
M
x
L
k
s
k
n
k
n
Aby obliczyć
∫
dx
x
M
x
L
k
n
)
(
)
(
musimy obliczyć całkę wielomianu oraz całkę funkcji wymiernej właściwej
(patrz punkt 2.).
Jeśli NIE zacznij algorytm od punktu 2.
135
2. Przypadek, gdy
k
s <
(stopień wielomianu w liczniku niższy niż w mianowniku).
Mianownik funkcji wymiernej właściwej
)
(
)
(
x
M
x
R
k
s
rozkładamy na czynniki liniowe oraz kwadratowe
nierozkładalne (tj. o
0
<
∆
).
3. Funkcję wymierną właściwą rozkładamy na ułamki proste (patrz przykład str. 134).
4. Wyznaczamy nieznane współczynniki tego rozkładu.
5. Obliczamy
∫
dx
x
M
x
R
k
s
)
(
)
(
jako sumę całek z otrzymanych ułamków prostych (patrz – CAŁKOWANIE
UŁAMKÓW PROSTYCH).
Uwaga: Całka funkcji wymiernej jest pewną kombinacją liniową następujących funkcji:
funkcji wymiernej
logarytmu naturalnego funkcji liniowej
logarytmu naturalnego funkcji kwadratowej o ∆ < 0
arkusatangensa funkcji liniowej
CAŁKOWANIE UŁAMKÓW PROSTYCH
a)
(
)
∫
∫
∫
∫
+
+
=
+
′
+
=
+
=
+
=
+
C
b
ax
a
A
b
ax
dx
b
ax
a
A
b
ax
adx
a
A
b
ax
dx
A
dx
b
ax
A
ln
(patrz str. 132)
b)
(
)
(
)
∫
∫
∫
∫
=
+
⋅
+
−
⋅
=
=
=
=
=
+
=
+
=
+
+
−
−
C
t
n
a
A
dt
t
a
A
t
dt
a
A
dt
adx
t
b
ax
b
ax
adx
a
A
dx
b
ax
A
n
n
n
n
n
1
1
1
(
)
C
b
ax
n
a
A
n
+
+
⋅
−
−
⋅
=
+
−
1
1
1
, n > 1
c)
∫
∫
∫
∫
=
+
+
+
=
+
+
+
=
+
+
+
=
<
∆
−
=
∆
=
+
+
+
dx
c
bx
ax
A
aB
ax
a
A
dx
c
bx
ax
A
B
x
a
a
A
dx
c
bx
ax
A
B
x
A
ac
b
dx
c
bx
ax
B
Ax
2
2
2
2
2
2
2
2
2
2
0
4
+
+
+
=
+
+
−
+
+
+
+
=
+
+
+
−
+
=
∫
∫
∫
c
bx
ax
a
A
dx
c
bx
ax
b
A
aB
a
A
dx
c
bx
ax
b
ax
a
A
dx
c
bx
ax
A
aB
b
b
ax
a
A
2
2
2
2
ln
2
2
2
2
2
2
2
2
∫
+
+
+
c
bx
ax
dx
K
2
, gdzie
−
⋅
=
b
A
aB
a
A
K
2
2
d)
=
∆
−
+
=
∆
−
+
=
∆
−
+
=
+
+
−
=
∆
<
∆
=
+
+
∫
∫
∫
2
2
2
2
2
2
2
4
2
1
4
2
4
2
4
,
0
a
a
b
x
dx
a
a
a
b
x
a
dx
a
a
b
x
a
c
bx
ax
ac
b
c
bx
ax
dx
=
+
∆
−
+
∆
−
=
+
∆
−
⋅
+
∆
−
=
+
∆
−
⋅
+
∆
−
⋅
=
∫
∫
∫
1
2
4
1
2
2
4
1
4
2
4
1
2
2
2
2
2
2
b
ax
dx
a
a
a
b
x
dx
a
a
a
b
x
dx
a
a
136
C
b
ax
C
t
t
dt
a
a
dt
dx
a
t
b
ax
+
∆
−
+
∆
−
=
+
∆
−
∆
−
=
+
∆
−
⋅
∆
−
=
=
∆
−
=
∆
−
+
=
∫
2
arctg
2
arctg
2
1
2
4
2
2
2
.
Przykłady obliczania całek funkcji wymiernych
1)
∫
∫
∫
+
+
=
+
=
+
=
+
C
x
x
dx
x
dx
dx
x
3
2
ln
2
5
3
2
2
2
5
3
2
5
3
2
5
przy założeniu
0
3
2
≠
+
x
Możemy również skorzystać z twierdzenia o całkowaniu przez podstawienie, wówczas:
∫
∫
∫
+
+
=
+
=
=
=
=
=
=
+
=
+
C
x
C
t
t
dt
t
dt
dt
dx
dt
dx
t
x
dx
x
3
2
ln
2
5
ln
2
5
2
5
2
1
5
2
1
2
3
2
3
2
5
2)
∫
+
+
dx
x
x
1
2
2
3
założenie:
0
1
2
≠
+
x
{
k
n =
– stopień licznika = stopień mianownika, zatem dzielimy licznik przez mianownik}
Po wydzieleniu wielomianów otrzymamy:
1
2
1
2
1
2
3
1
2
2
3
+
⋅
+
=
+
+
x
x
x
Stąd:
∫
∫
∫
∫
∫
∫
=
+
+
=
+
⋅
+
=
+
⋅
+
=
+
+
dx
x
dx
dx
x
dx
dx
x
dx
x
x
1
2
1
2
1
2
3
1
2
1
2
1
2
3
1
2
1
2
1
2
3
1
2
2
3
∫
+
+
+
=
+
+
=
C
x
x
dx
x
x
1
2
ln
4
1
2
3
1
2
2
4
1
2
3
3) Całki typu
∫
+
+
c
bx
ax
dx
2
obliczamy różnie w zależności od wyróżnika (tj.
ac
b
4
2
−
=
∆
)
a)
0
>
∆
(
)(
)
(
)(
)
(
)(
)
=
−
+
−
=
−
+
−
=
−
+
−
=
+
−
−
=
−
=
=
∆
=
+
−
−
∫
∫
∫
3
5
3
5
3
5
15
2
3
,
5
64
15
2
2
2
1
2
x
x
dx
x
x
dx
x
x
x
x
x
x
x
x
dx
(
)(
)
3
5
3
5
1
−
+
+
=
−
+
x
B
x
A
x
x
(*)
{funkcję podcałkową rozkładamy na ułamki proste}
(
)(
)
(
)
(
)
(
)(
)
3
5
5
3
3
5
1
−
+
+
+
−
=
−
+
x
x
x
B
x
A
x
x
{sprowadzamy prawą stronę do wspólnego mianownika przy
założeniu:
3
i
5
≠
−
≠
x
x
}
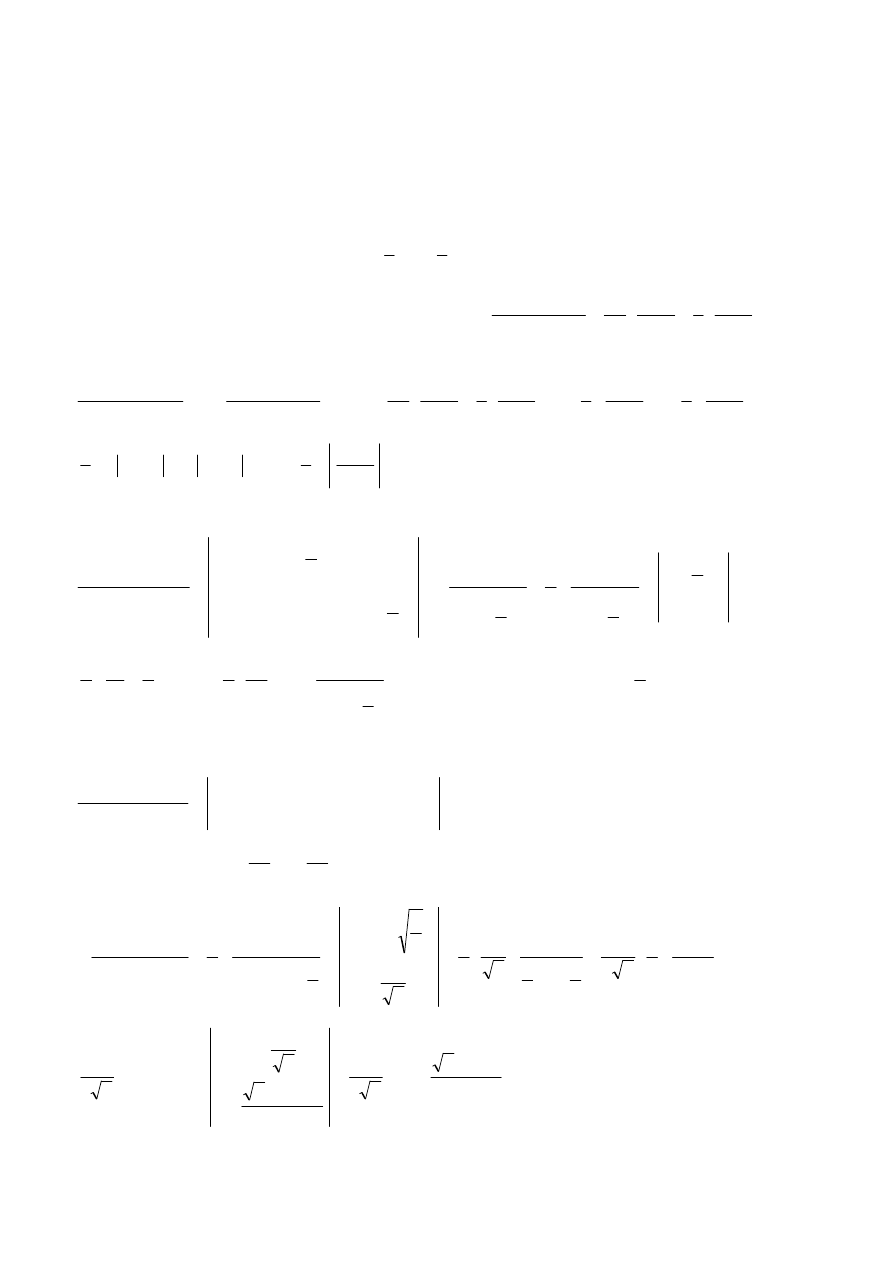
137
(
)
(
)
5
3
1
+
+
−
≡
x
B
x
A
{równość tożsamościowa liczników}
(
)
(
)
B
A
x
B
A
x
5
3
1
0
+
−
+
+
≡
+
⋅
{przyrównujemy współczynniki przy odpowiednich potęgach x}
=
+
−
=
+
1
5
3
0
B
A
B
A
Po rozwiązaniu układu otrzymujemy:
8
1
,
8
1
=
−
=
B
A
.
Po wstawieniu współczynników rozkładu do (*) mamy:
(
)(
)
3
1
8
1
5
1
8
1
3
5
1
−
⋅
+
+
⋅
−
=
−
+
x
x
x
x
Zatem
(
)(
)
∫
∫
∫
∫
∫
=
−
−
+
=
−
⋅
+
+
⋅
−
−
=
−
+
−
=
+
−
−
dx
x
dx
x
dx
x
x
dx
x
x
x
x
dx
3
1
8
1
5
1
8
1
3
1
8
1
5
1
8
1
3
5
1
15
2
2
(
)
C
x
x
C
x
x
+
−
+
=
+
−
−
+
=
3
5
ln
8
1
3
ln
5
ln
8
1
.
b)
0
=
∆
∫
∫
∫
=
=
=
−
=
−
=
−
=
−
=
+
−
=
=
∆
=
+
−
dt
dx
t
x
x
dx
x
dx
x
x
x
x
x
x
dx
2
5
2
5
4
1
2
5
4
2
5
4
25
20
4
2
5
,
0
25
20
4
2
2
2
2
0
2
∫
∫
+
−
−
=
+
−
⋅
=
=
=
−
C
x
C
t
dt
t
t
dt
2
5
4
1
1
4
1
4
1
4
1
2
2
przy założeniu:
2
5
≠
x
c)
0
<
∆
(
)
=
+
−
=
+
−
−
=
∆
=
+
−
∫
9
3
2
27
12
2
72
27
12
2
2
2
2
x
x
x
x
x
dx
{mianownik sprowadzono do postaci kanonicznej
tzn.
a
a
b
x
a
c
bx
ax
4
2
2
2
∆
−
+
=
+
+
, gdzie
ac
b
4
2
−
=
∆
}
(
)
(
)
∫
∫
∫
∫
=
+
⋅
=
+
⋅
=
=
=
−
=
+
−
=
+
−
=
1
9
2
2
2
3
2
9
2
9
2
3
2
1
2
3
2
9
3
2
9
3
2
1
9
3
2
2
2
2
2
t
dt
t
dt
dt
dx
t
x
x
dx
x
dx
(
)
(
)
C
x
x
t
t
x
C
t
+
−
=
−
⋅
=
=
−
=
+
=
3
3
2
arctg
2
3
1
3
3
2
2
3
3
arctg
2
3
1
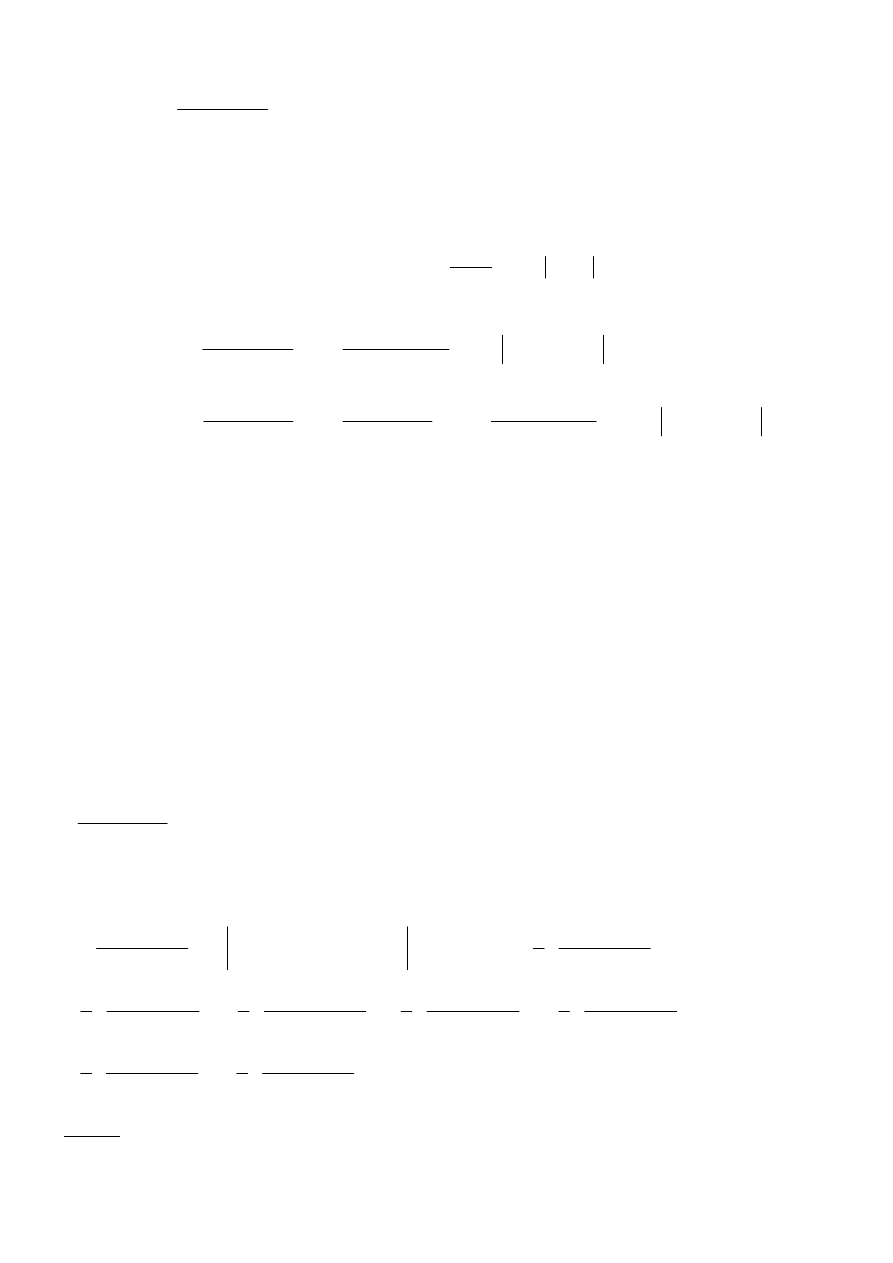
138
4) Całki typu
∫
≠
+
+
+
0
,
2
a
dx
c
bx
ax
n
mx
{w liczniku funkcji podcałkowej występuje funkcja liniowa, a w mianowniku funkcja kwadratowa}
Sprawdzamy, czy licznik jest pochodną funkcji z mianownika lub jest proporcjonalny do niej:
Jeśli TAK, korzystamy ze wzoru:
∫
+
=
′
C
x
f
dx
x
f
x
f
)
(
ln
)
(
)
(
Przykład:
a)
(
)
∫
∫
+
+
+
=
+
+
′
+
+
=
+
+
+
C
x
x
dx
x
x
x
x
dx
x
x
x
13
5
ln
13
5
13
5
13
5
5
2
2
2
2
2
b)
(
)
∫
∫
∫
+
+
−
=
+
−
′
+
−
=
+
−
−
=
+
−
−
C
x
x
dx
x
x
x
x
dx
x
x
x
dx
x
x
x
1
3
2
ln
2
1
3
2
1
3
2
2
1
3
2
)
3
4
(
2
1
3
2
6
8
2
2
2
2
2
Jeśli licznik NIE jest pochodną mianownika, ani nie jest proporcjonalny do niej to:
1. Licznik sprowadzamy do postaci: ⋅
A
(pochodna mianownika) + B, gdzie A, B – odpowiednio dobrane
stałe.
W tym celu postępujemy jak na str. 135 (patrz CAŁKOWANIE UŁAMKÓW PROSTCH podpunkt c) –
Sposób I
lub
Sposób II:
Obliczamy pochodną mianownika,
Dzielimy licznik przez pochodną mianownika,
Licznik przedstawiamy w wymaganej postaci
2. Daną całkę zapisujemy jako sumę dwóch całek, przy czym w pierwszej z nich licznik będzie pochodną
mianownika, natomiast drugą z całek obliczamy w zależności od znaku ∆ (patrz str. 135 – 136 całki typu
∫
+
+
c
bx
ax
dx
2
).
Przykład:
a)
(
)
=
−
=
′
+
−
=
+
−
−
∫
7
2
12
7
12
7
2
2
2
x
x
x
dx
x
x
x
{ Sposób I } =
(
)
∫
=
+
−
−
dx
x
x
x
12
7
2
2
2
1
2
=
+
−
+
+
−
−
=
+
−
−
+
−
=
+
−
−
=
∫
∫
∫
∫
dx
x
x
dx
x
x
x
dx
x
x
x
dx
x
x
x
12
7
3
2
1
12
7
7
2
2
1
12
7
4
7
7
2
2
1
12
7
4
2
2
1
2
2
2
2
∫
∫
+
−
+
+
−
−
=
dx
x
x
dx
x
x
x
12
7
1
2
3
12
7
7
2
2
1
2
2
Uwaga: Korzystając ze Sposobu II postępujemy, jak następuje:
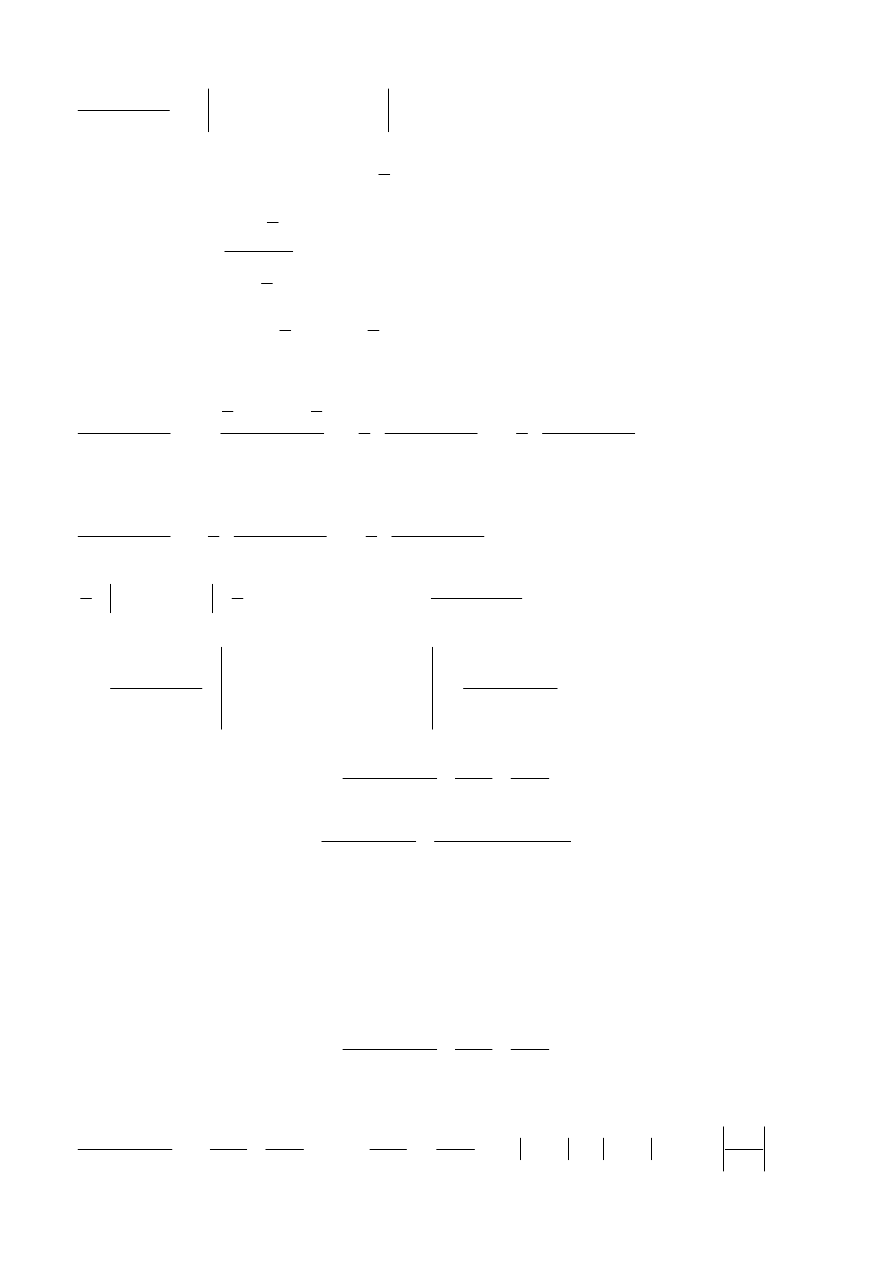
139
(
)
=
−
=
′
+
−
=
+
−
−
∫
7
2
12
7
12
7
2
2
2
x
x
x
dx
x
x
x
{dzielimy licznik przez pochodną mianownika}
Wówczas:
2
7
2
1
)
7
2
(
)
2
(
+
−
=
−
÷
−
x
x
x
2
3
stąd
(
)
2
3
7
2
2
1
2
+
−
=
−
x
x
zatem
(
)
∫
∫
∫
∫
+
−
+
+
−
−
=
+
−
+
−
=
+
−
−
dx
x
x
dx
x
x
x
dx
x
x
x
dx
x
x
x
12
7
1
2
3
12
7
7
2
2
1
12
7
2
3
7
2
2
1
12
7
2
2
2
2
2
Niezależnie z którego sposobu korzystamy dochodzimy do tej samej postaci całki, a mianowicie:
=
+
−
+
+
−
−
=
+
−
−
∫
∫
∫
dx
x
x
dx
x
x
x
dx
x
x
x
12
7
1
2
3
12
7
7
2
2
1
12
7
2
2
2
2
,
2
3
12
7
ln
2
1
1
2
I
x
x
+
+
−
=
gdzie
∫
+
−
=
12
7
2
1
x
x
dx
I
(
)(
)
(
)(
)
∫
∫
=
−
−
=
−
−
=
+
−
=
=
=
∆
=
+
−
=
4
3
4
3
12
7
4
,
3
1
12
7
2
2
1
2
1
x
x
dx
x
x
x
x
x
x
x
x
dx
I
(*)
(
)(
)
4
3
4
3
1
−
+
−
=
−
−
x
B
x
A
x
x
(
)(
)
(
)
(
)
(
)(
)
4
3
3
4
4
3
1
−
−
−
+
−
=
−
−
x
x
x
B
x
A
x
x
(
)
(
)
B
A
x
B
A
3
4
1
−
−
+
+
≡
=
−
−
=
+
1
3
4
0
B
A
B
A
Stąd
1
,
1
=
−
=
B
A
(
)(
)
4
1
3
1
4
3
1
−
+
−
−
=
−
−
x
x
x
x
wracając do (*) mamy:
(
)(
)
∫
∫
∫
∫
+
−
−
=
+
−
+
−
−
=
−
+
−
−
=
−
+
−
−
=
−
−
1
1
3
4
ln
4
ln
3
ln
4
3
4
1
3
1
4
3
C
x
x
C
x
x
x
dx
x
dx
dx
x
x
x
x
dx
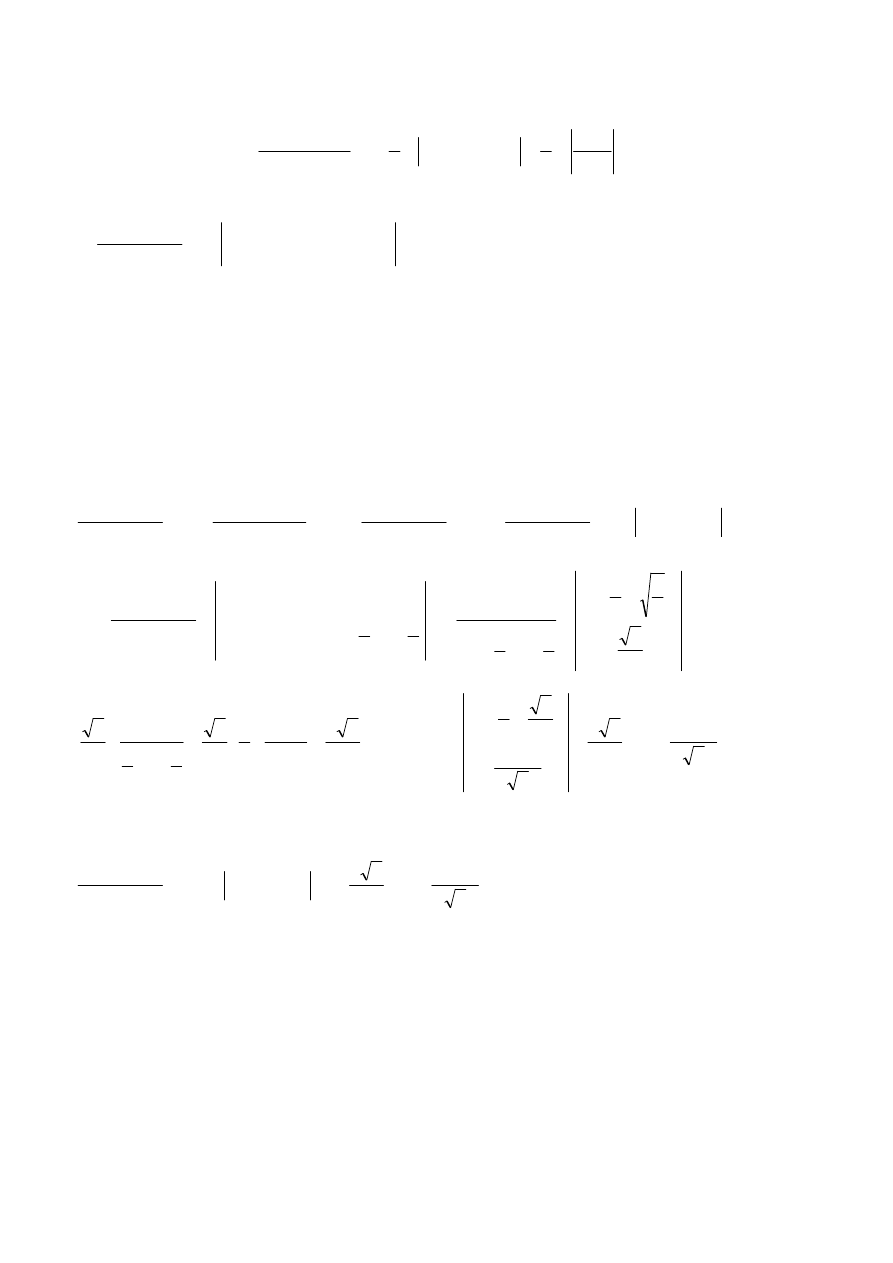
140
Ostatecznie
C
x
x
x
x
dx
x
x
x
+
−
−
+
+
−
=
+
−
−
∫
3
4
ln
2
3
12
7
ln
2
1
12
7
2
2
2
b)
(
)
∫
+
=
′
+
+
=
+
+
−
3
2
4
3
4
3
3
4
2
2
x
x
x
dx
x
x
x
{Sposób II} dzielimy licznik przez pochodną mianownika:
(
) (
)
6
4
2
3
2
3
4
−
−
=
+
÷
−
x
x
x
_____________
9
−
Zatem
(
)
9
3
2
2
3
4
−
+
=
−
x
x
Stąd
(
)
∫
∫
∫
∫
−
+
+
=
+
+
−
+
+
+
=
+
+
−
+
=
+
+
−
1
2
2
2
2
2
9
4
3
ln
2
4
3
9
4
3
3
2
2
4
3
9
3
2
2
4
3
3
4
I
x
x
x
x
dx
dx
x
x
x
dx
x
x
x
dx
x
x
x
∫
∫
=
=
=
+
=
+
+
=
+
+
=
+
+
−
=
∆
=
+
+
=
dt
dx
t
x
x
dx
x
x
x
x
x
dx
I
2
7
4
7
2
3
4
7
2
3
4
7
2
3
4
3
7
4
3
2
2
2
2
1
1
1
2
2
7
3
2
arctg
7
7
2
7
3
2
2
7
2
3
arctg
7
7
2
1
7
4
2
7
4
7
4
7
2
7
C
x
x
t
t
x
C
t
t
dt
t
dt
+
+
=
+
=
=
+
=
+
=
+
⋅
=
+
=
∫
∫
Ostatecznie
C
x
x
x
dx
x
x
x
+
+
⋅
−
+
+
=
+
+
−
∫
7
3
2
arctg
7
7
2
9
4
3
ln
2
4
3
3
4
2
2
Wyszukiwarka
Podobne podstrony:
Microsoft Word WE L9 Calki przez czesci i podstawienie, wymierne
Microsoft Word WE W11 Calka oznaczona
Microsoft Word WE L11 Calka oznaczona i zastosowanie
Microsoft Word WE W10 Calki tryg i niewym
Microsoft Word WE L10 Calki tryg, niewym
Microsoft Word WE L14 Szeregi Fouriera
Microsoft Word WE harmonogram egz
Microsoft Word WE L13 szeregi potęgowe
Microsoft Word WE wyniki E2 2009
Microsoft Word WE W14 Szeregi Fouriera
Microsoft Word WE W13 Szeregi funkcyjne i potegowe
Microsoft Word WE L12 szeregi liczbowe
projekt geomorfologia, Nowy Dokument programu Microsoft Word (3), Przekrój geologiczny przez dolinę
Microsoft Word W21 Calka krzywoliniowa
Microsoft Word W19 Calka podwojna
Microsoft Word W20 Calka potrojna
Microsoft Word L20 calka potrojna
więcej podobnych podstron