141
WYKŁAD Nr 10
CAŁKI NIEOZNACZONE
– c.d.
Def.10.1. (funkcja wymierna dwóch zmiennych)
Funkcja
)
,
( v
u
R
jest funkcją wymierną dwóch zmiennych u i v, jeżeli jest ilorazem dwóch wielomianów
względem tych zmiennych.
Przykład:
1
6
3
7
2
4
3
)
,
(
2
2
3
+
−
+
−
+
−
=
v
v
u
u
uv
v
u
v
u
R
jest funkcją wymierną zmiennych u i v.
CAŁKOWANIE FUNKCJI TRYGONOMETRYCZNYCH
A) Całka postaci
(
)
∫
dx
x
x
R
cos
,
sin
Całki funkcji zbudowanych „wymiernie” (tzn. za pomocą działań arytmetycznych) z
x
sin oraz
x
cos
można sprowadzić do całek funkcji wymiernych za pomocą podstawienia:
t
x
=
2
tg
Wówczas dla
(
)
π
π
−
∈
,
x
mamy:
dt
t
dx
t
x
t
x
2
1
2
arctg
2
arctg
2
+
=
=
=
Funkcje
x
sin ,
x
cos
musimy wyrazić przy pomocy
2
tg
x
=
+
=
+
=
=
=
⋅
=
2
cos
2
sin
1
2
cos
2
cos
2
sin
2
2
cos
2
sin
2
cos
2
cos
2
sin
2
1
2
cos
2
sin
2
2
cos
2
sin
2
2
2
sin
sin
2
2
2
2
2
2
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
2
2
1
2
2
tg
1
2
tg
2
t
t
x
x
+
=
+
=
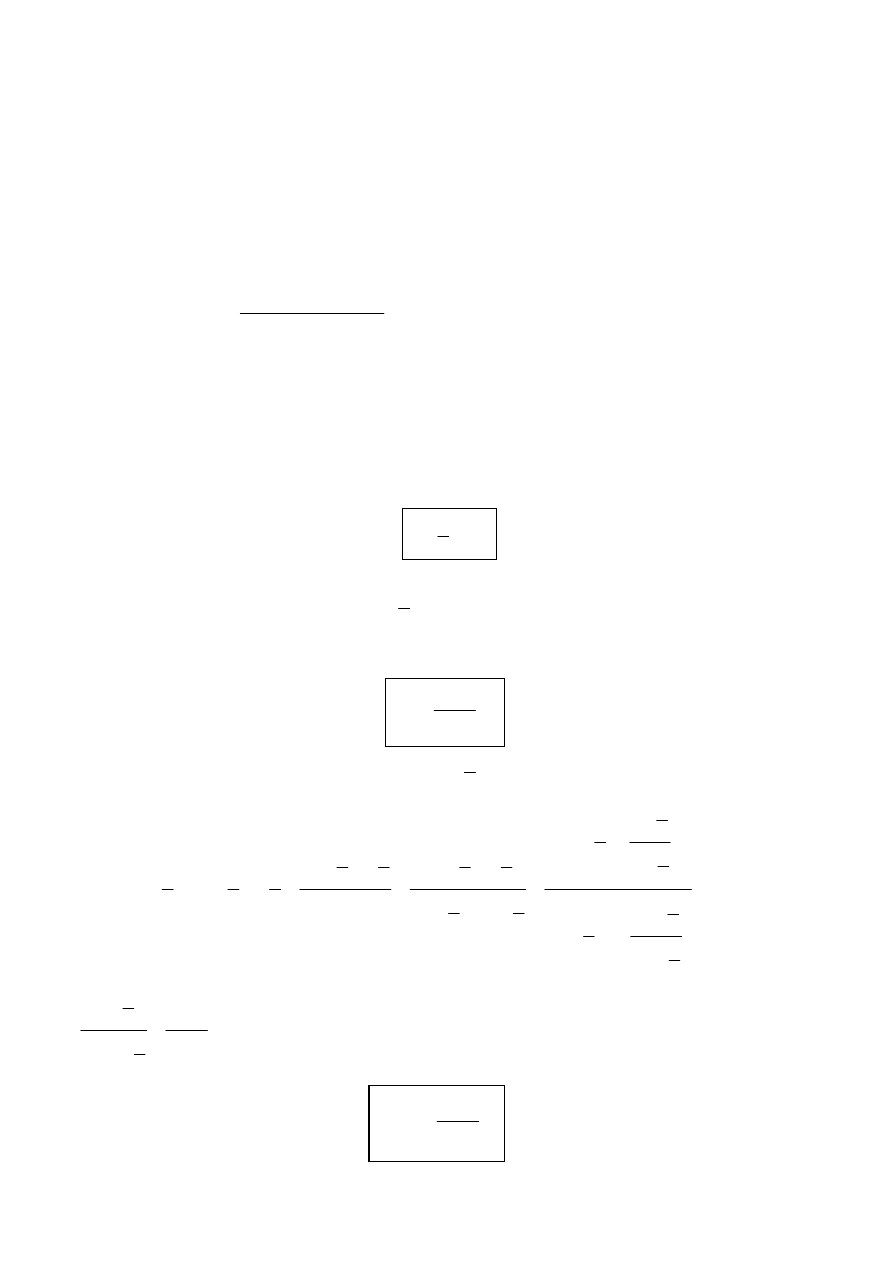
Ostatecznie
2
1
2
sin
t
t
x
+
=
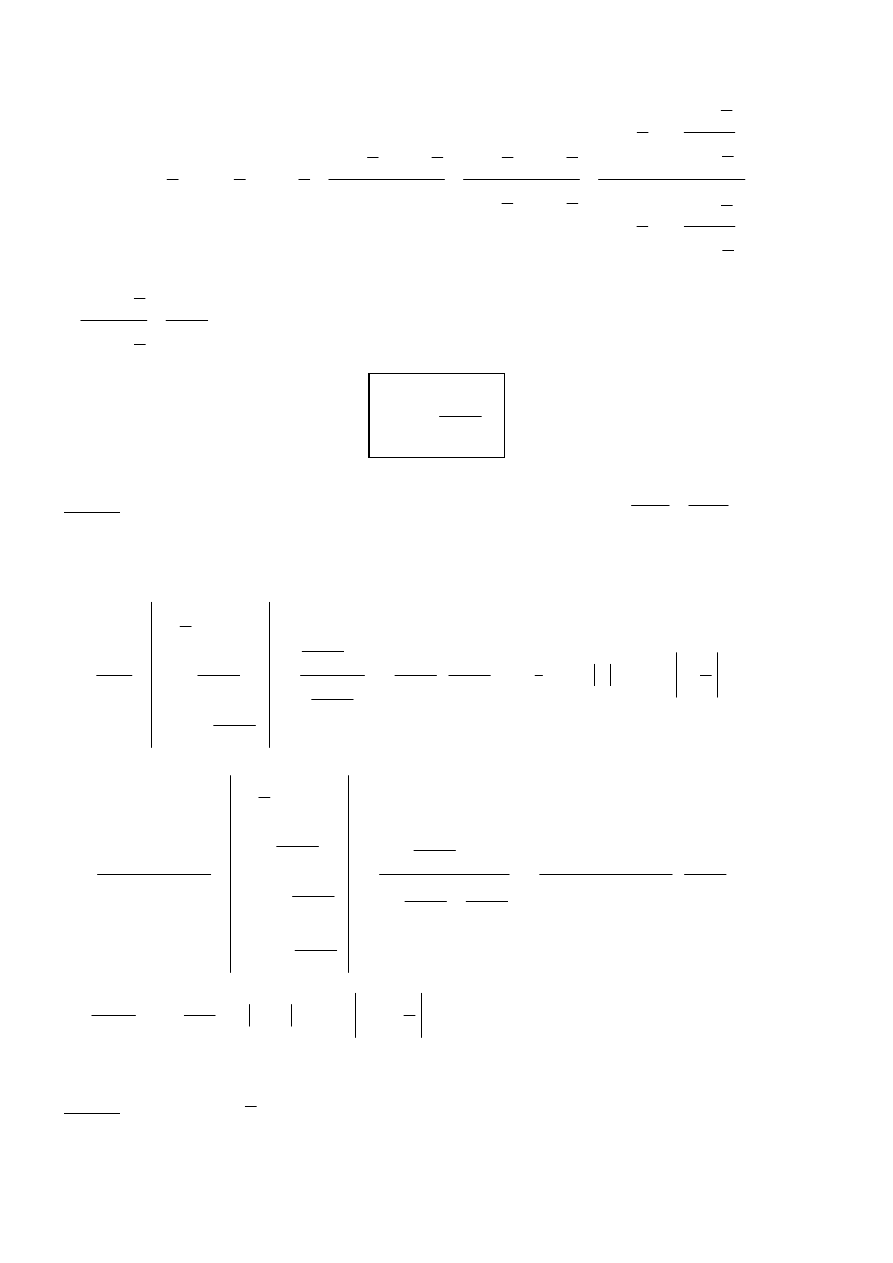
142
=
+
−
=
+
−
=
−
=
−
=
⋅
=
2
cos
2
sin
1
2
cos
2
cos
2
sin
1
2
cos
2
sin
2
cos
2
sin
2
cos
1
2
sin
2
cos
2
sin
2
cos
2
2
cos
cos
2
2
2
2
2
2
2
2
2
2
2
2
2
2
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
2
2
2
2
1
1
2
tg
1
2
tg
1
t
t
x
x
+
−
=
+
−
=
Ostatecznie
2
2
1
1
cos
t
t
x
+
−
=
Uwaga: Dość często w funkcji podcałkowej pojawia się
x
tg , wówczas
2
1
2
cos
sin
tg
t
t
x
x
x
−
=
=
.
Przykłady:
a)
C
x
C
t
dt
t
dt
t
t
t
t
t
dt
t
t
t
x
dt
t
dx
t
x
x
dx
+
=
+
=
=
+
⋅
+
=
+
+
=
+
=
+
=
=
=
∫
∫
∫
∫
2
tg
ln
ln
1
1
2
2
1
1
2
1
2
1
2
sin
1
2
2
tg
sin
2
2
2
2
2
2
b)
∫
∫
∫
=
+
⋅
−
+
+
+
+
=
+
−
+
+
+
+
=
+
−
=
+
=
+
=
=
=
+
+
dt
t
t
t
t
t
t
t
t
t
dt
t
t
t
x
t
t
x
dt
t
dx
t
x
x
x
dx
2
2
2
2
2
2
2
2
2
2
2
2
1
2
1
2
1
1
1
1
1
2
1
1
2
1
1
cos
1
2
sin
1
2
2
tg
cos
sin
1
∫
∫
+
+
=
+
+
=
+
=
+
=
C
x
C
t
t
dt
dt
t
2
tg
1
ln
1
ln
1
2
2
2
Uwaga: Podstawienie
t
x
=
2
tg
nazywamy
UNIWERSALNYM PODSTAWIENIEM
TRYGONOMETRYCZNYM

143
B) Całki postaci
(
)
∫
dx
x
x
x
x
R
cos
sin
,
cos
,
sin
2
2
,
gdzie funkcja podcałkowa jest funkcją wymierną względem
x
x
2
2
cos
,
sin
oraz
x
x
cos
sin
.
Wówczas dla
π
π
−
∈
2
,
2
x
stosujemy podstawienie:
t
x
=
tg
Zatem
dt
t
dx
t
x
2
1
1
arctg
+
=
=
Funkcje
x
x
2
2
cos
,
sin
i
x
x
cos
sin
przedstawiamy korzystając z funkcji
x
tg
x
x
x
2
2
2
cos
sin
tg
=
(
)
(
)
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
tg
1
tg
sin
tg
tg
1
sin
sin
tg
tg
sin
sin
1
tg
sin
cos
tg
sin
+
=
=
+
⋅
−
=
−
⋅
=
⋅
=
Stąd po dokonaniu podstawienia otrzymamy:
2
2
2
1
sin
t
t
x
+
=
x
x
x
x
x
x
x
2
2
2
2
2
2
2
tg
1
1
tg
1
tg
1
tg
tg
1
sin
cos
+
=
⋅
+
=
⋅
=
czyli
2
2
1
1
cos
t
x
+
=
x
x
x
x
x
x
x
x
x
2
2
2
2
tg
1
tg
tg
1
tg
1
tg
tg
1
sin
cos
sin
+
=
⋅
+
=
⋅
=
⋅
czyli
2
1
cos
sin
t
t
x
x
+
=
⋅
Przykład:
∫
∫
=
+
−
+
+
=
+
=
+
=
+
=
=
=
−
2
2
2
2
2
2
2
2
2
2
1
5
1
1
1
1
cos
sin
,
1
sin
1
1
tg
cos
sin
5
sin
t
t
t
t
dt
t
t
t
x
x
t
t
x
dt
t
dx
t
x
x
x
x
dx
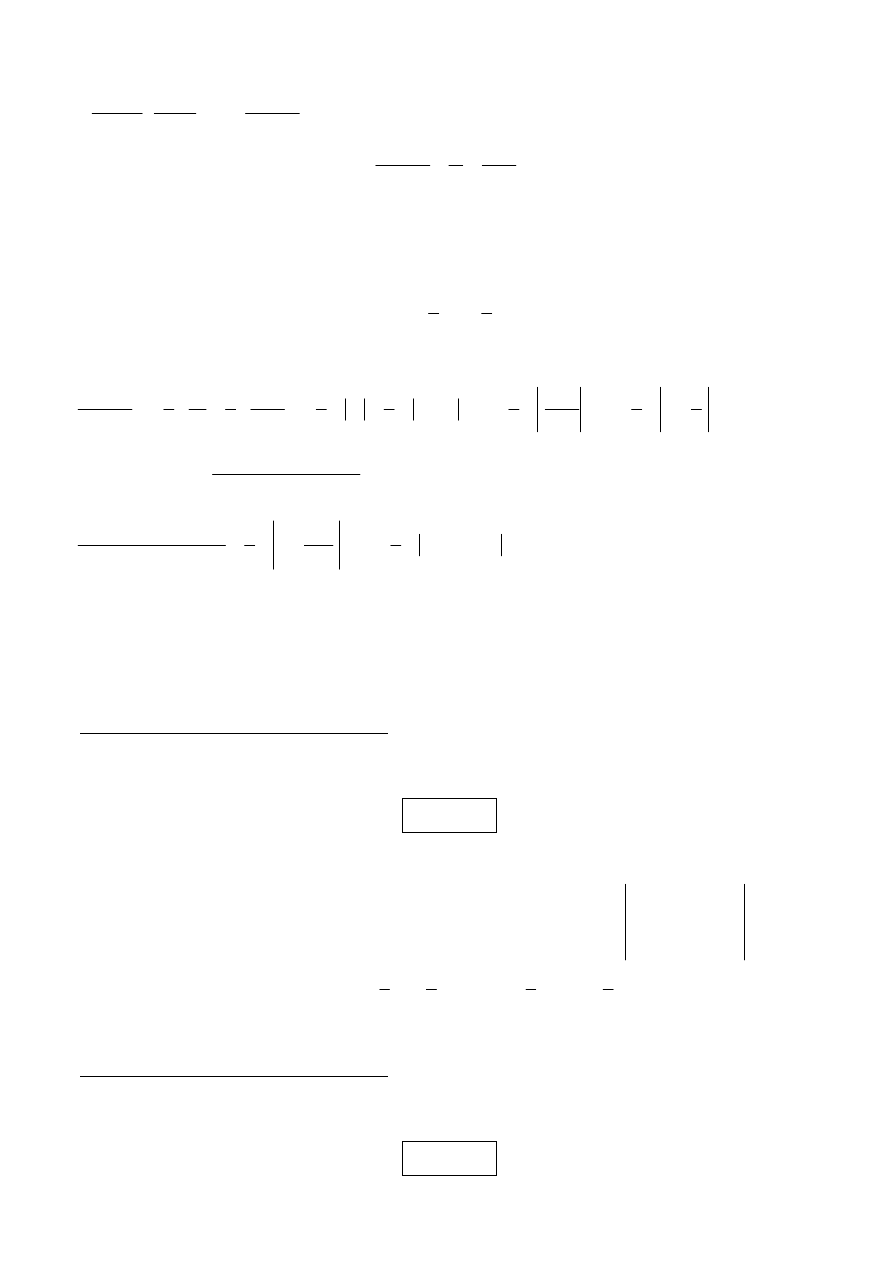
144
(
)
∫
∫
−
=
+
⋅
−
+
=
5
1
1
5
1
2
2
2
t
t
dt
dt
t
t
t
t
= {rozkładamy na ułamki proste – patrz Wykład Nr 9}
(
)
=
−
=
+
+
−
≡
−
+
=
−
1
5
0
5
1
5
5
1
A
B
A
Bt
A
At
t
B
t
A
t
t
Stąd
5
1
,
5
1
=
−
=
B
A
Zatem
(
)
∫
∫
∫
+
−
=
+
−
=
+
−
+
−
=
−
+
−
=
−
C
t
C
t
t
C
t
t
t
dt
t
dt
t
t
dt
5
1
ln
5
1
5
ln
5
1
5
ln
5
1
ln
5
1
5
5
1
5
1
5
Wracając do całki
∫
−
x
x
x
dx
cos
sin
5
sin
2
i podstawienia
t
x
=
tg
otrzymujemy:
C
x
C
x
x
x
x
dx
+
−
=
+
−
=
−
∫
ctg
5
1
ln
5
1
tg
5
1
ln
5
1
cos
sin
5
sin
2
.
C) Całki postaci
∫
dx
x
x
n
m
cos
sin
, gdzie
N
∈
n
m
,
, obliczamy różnymi sposobami w zależności
od tego czy m i n są liczbami parzystymi czy nieparzystymi.
Rozpatrujemy cztery przypadki:
1° m – liczba nieparzysta, n – liczba parzysta
(w funkcji podcałkowej sin x występuje w potędze nieparzystej, natomiast cos x w parzystej)
Wówczas stosujemy podstawienie:
t
x
=
cos
Przykład:
(
)
∫
∫
∫
=
−
=
=
−
=
=
⋅
⋅
−
=
=
dt
xdx
dt
xdx
t
x
dx
x
x
x
dx
x
x
x
dx
x
x
sin
sin
cos
sin
cos
cos
1
sin
cos
sin
cos
sin
2
2
2
2
2
3
(
)
(
)
(
)
∫
∫
+
+
−
=
+
−
−
=
−
−
=
−
⋅
⋅
−
=
C
x
x
C
t
t
dt
t
t
dt
t
t
5
3
5
3
4
2
2
2
cos
5
1
cos
3
1
5
1
3
1
1
2° m – liczba parzysta, n – liczba nieparzysta
(w funkcji podcałkowej cos x występuje w potędze nieparzystej, natomiast sin x w parzystej)
Wówczas stosujemy podstawienie:
t
x
=
sin
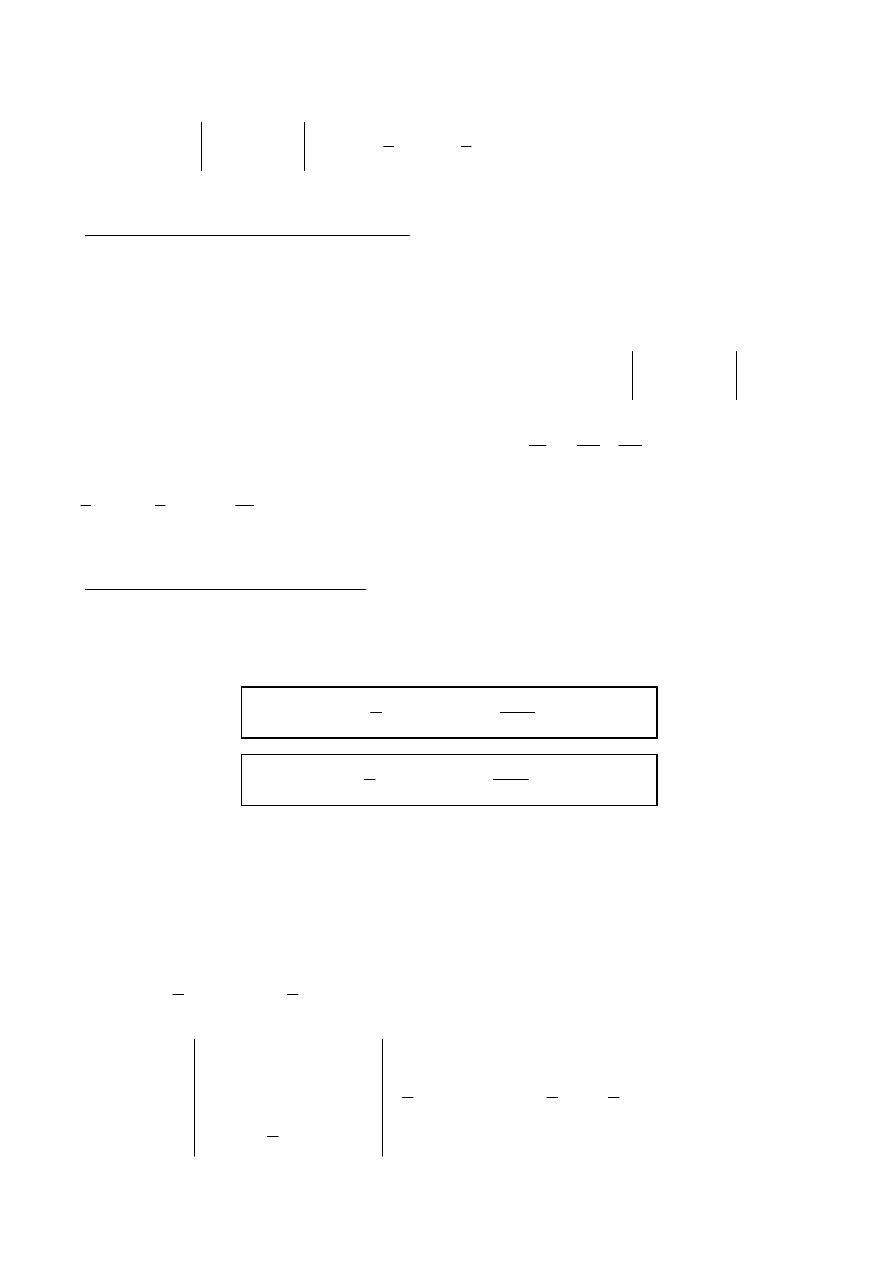
145
Przykład:
∫
∫
+
=
+
=
=
=
=
=
C
x
C
t
dt
t
dt
dx
x
t
x
dx
x
x
3
3
2
2
sin
3
1
3
1
cos
sin
cos
sin
3° m – liczba nieparzysta, n – liczba nieparzysta
Wówczas jedną z funkcji (najlepiej tę, która występuje w niższej potędze) zapisujemy jako iloczyn potęgi
parzystej i pierwszej, a następnie postępujemy zgodnie z 1° lub 2°.
Przykład:
(
)
∫
∫
∫
=
=
=
=
−
⋅
=
=
dt
dx
x
t
x
dx
x
x
x
dx
x
x
x
dx
x
x
cos
sin
cos
sin
1
sin
cos
cos
sin
cos
sin
2
2
7
4
7
5
7
(
)
(
)
(
)
∫
∫
∫
=
+
+
−
=
+
−
=
+
−
=
−
=
C
t
t
t
dt
t
t
t
dt
t
t
t
dt
t
t
12
10
2
8
2
2
1
1
12
10
8
11
9
7
4
2
7
2
2
7
C
x
x
x
+
+
−
=
12
10
8
sin
12
1
sin
5
1
sin
8
1
4° m – liczba parzysta, n – liczba parzysta
Wówczas korzystając z jedynki trygonometrycznej doprowadzamy funkcję podcałkową do funkcji
zależnej tylko od jednej z funkcji: sin x lub cos x, a następnie obliczamy całki korzystając ze WZORÓW
REKURENCYJNYCH (n > 2):
(*)
∫
∫
−
−
−
+
−
=
dx
x
n
n
x
x
n
dx
x
n
n
n
2
1
sin
1
cos
sin
1
sin
(**)
∫
∫
−
−
−
+
=
dx
x
n
n
x
x
n
dx
x
n
n
n
2
1
cos
1
sin
cos
1
cos
Przykład:
(
)
∫
∫
∫
∫
−
=
−
⋅
=
dx
x
dx
x
dx
x
x
dx
x
x
4
2
2
2
2
2
sin
sin
sin
1
sin
cos
sin
Zaczynamy od wyznaczenia całki
∫
dx
x
4
sin
korzystając ze wzoru (*), a mianowicie dla
4
=
n
mamy:
∫
∫
+
−
=
43
42
1
1
2
3
4
sin
4
3
cos
sin
4
1
sin
I
dx
x
x
x
dx
x
(
)
(
)
∫
∫
∫
∫
=
−
=
−
=
−
=
−
=
−
=
=
=
dx
x
dx
dx
x
x
x
x
x
x
x
x
dx
x
I
2
cos
2
1
2
1
2
cos
1
2
1
2
cos
1
2
1
sin
sin
2
1
2
cos
sin
cos
2
cos
sin
2
2
2
2
2
1

146
1
2
sin
4
1
2
1
C
x
x
+
−
=
.
Więc po wstawieniu otrzymujemy:
C
x
x
x
x
x
x
dx
x
dx
x
dx
x
x
+
−
+
+
−
=
−
=
∫
∫
∫
2
sin
4
1
2
1
4
3
cos
sin
4
1
2
sin
4
1
2
1
sin
sin
cos
sin
3
4
2
2
2
Ostatecznie
∫
+
−
+
=
C
x
x
x
x
dx
x
x
2
sin
16
7
8
7
cos
sin
4
1
cos
sin
3
2
2
Uwaga: Oczywiście do każdego z wymienionych typów całek (z punktów B), C)) można stosować
uniwersalne podstawienie trygonometryczne, ale rachunki znacznie się upraszczają przy zastosowaniu
podstawień wymienionych w tych punktach.
Uwaga: W przypadku funkcji podcałkowych
x
x
n
n
ctg
,
tg
, gdzie
2
>
n
można również wyprowadzić
wzory rekurencyjne. Wówczas:
2
ctg
ctg
1
1
ctg
tg
tg
1
1
tg
2
1
2
1
>
−
−
−
=
−
−
=
∫
∫
∫
∫
−
−
−
−
n
dx
x
x
n
dx
x
dx
x
x
n
dx
x
n
n
n
n
n
n
D) Całki postaci:
∫
∫
∫
dx
x
x
dx
x
x
dx
x
x
β
α
β
α
β
α
cos
cos
,
sin
sin
,
cos
sin
Obliczamy je przekształcając iloczyny wyrażeń podcałkowych na odpowiednie sumy korzystając
ze wzorów:
2
cos
2
sin
2
sin
sin
B
A
B
A
B
A
−
+
=
+
→
(
)
B
A
B
A
B
A
sin
sin
2
1
2
cos
2
sin
+
=
−
+
2
cos
2
cos
2
cos
cos
B
A
B
A
B
A
−
+
=
+
→
(
)
B
A
B
A
B
A
cos
cos
2
1
2
cos
2
cos
+
=
−
+
2
sin
2
sin
2
cos
cos
B
A
B
A
B
A
−
+
−
=
−
→
(
)
B
A
B
A
B
A
cos
cos
2
1
2
sin
2
sin
−
−
=
−
+
Przykłady:
a)
(
)
∫
−
−
=
−
+
B
A
B
A
B
A
dx
x
x
cos
cos
2
1
2
sin
2
sin
3
sin
5
sin
Stąd
=
−
=
+
x
B
A
x
B
A
3
2
5
2
czyli
=
−
=
+
x
B
A
x
B
A
6
10
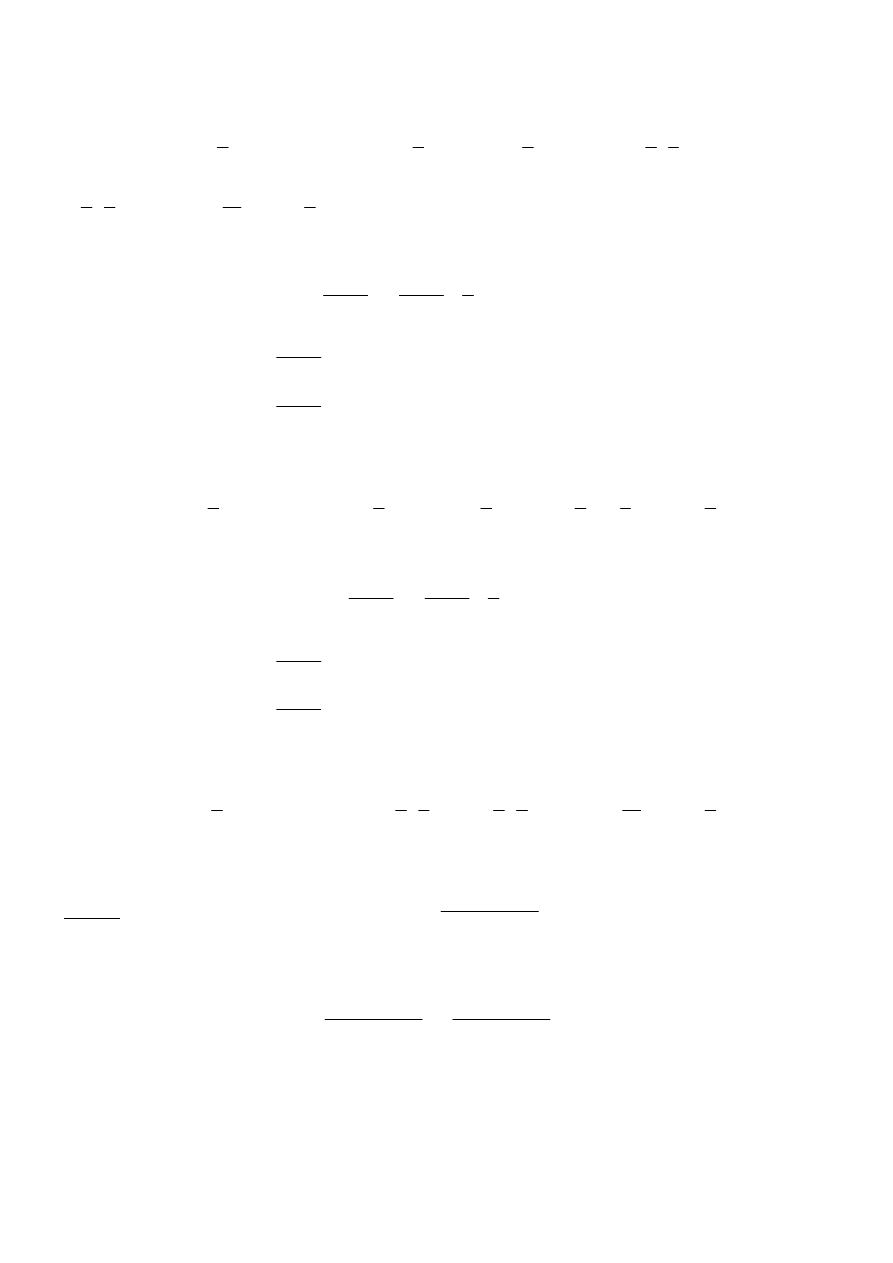
147
Zatem
x
B
x
A
2
,
8
=
=
(
)
∫
∫
∫
∫
+
⋅
−
=
+
−
=
−
−
=
x
dx
x
dx
x
dx
x
x
dx
x
x
8
sin
8
1
2
1
2
cos
2
1
8
cos
2
1
2
cos
8
cos
2
1
3
sin
5
sin
C
x
x
C
x
+
+
−
=
+
⋅
+
2
sin
4
1
8
sin
16
1
2
sin
2
1
2
1
b)
(
)
∫
+
=
−
+
B
A
B
A
B
A
dx
x
x
sin
sin
2
1
2
cos
2
sin
2
cos
3
sin
=
−
=
+
x
B
A
x
B
A
2
2
3
2
czyli
=
−
=
+
x
B
A
x
B
A
4
6
.
Stąd
x
B
x
A
=
=
,
5
(
)
∫
∫
∫
∫
+
−
−
⋅
=
+
=
+
=
C
x
x
xdx
dx
x
dx
x
x
dx
x
x
cos
2
1
5
cos
5
1
2
1
sin
2
1
5
sin
2
1
sin
5
sin
2
1
2
cos
3
sin
c)
(
)
∫
+
=
−
+
B
A
B
A
B
A
dx
x
x
cos
cos
2
1
2
cos
2
cos
2
cos
4
cos
=
−
=
+
x
B
A
x
B
A
2
2
4
2
czyli
=
−
=
+
x
B
A
x
B
A
4
8
.
Stąd
x
B
x
A
2
,
6
=
=
(
)
∫
∫
+
+
=
+
⋅
+
⋅
=
+
=
C
x
x
C
x
x
dx
x
x
dx
x
x
2
sin
4
1
6
sin
12
1
2
sin
2
1
2
1
6
sin
6
1
2
1
2
cos
6
cos
2
1
2
cos
4
cos
Uwaga: Często też spotykamy się z całkami typu:
∫
x
x
dx
m
n
cos
sin
,
N
∈
≠
≠
m
n
x
x
,
,
0
cos
,
0
sin
.
Aby rozwiązać całki tego typu postępujemy następująco:
dx
x
x
x
x
dx
m
n
m
n
∫
∫
=
cos
sin
1
cos
sin
,
a następnie w miejsce jedynki występującej w liczniku stosujemy jedynkę trygonometryczną
x
x
2
2
cos
sin
1
+
=
.
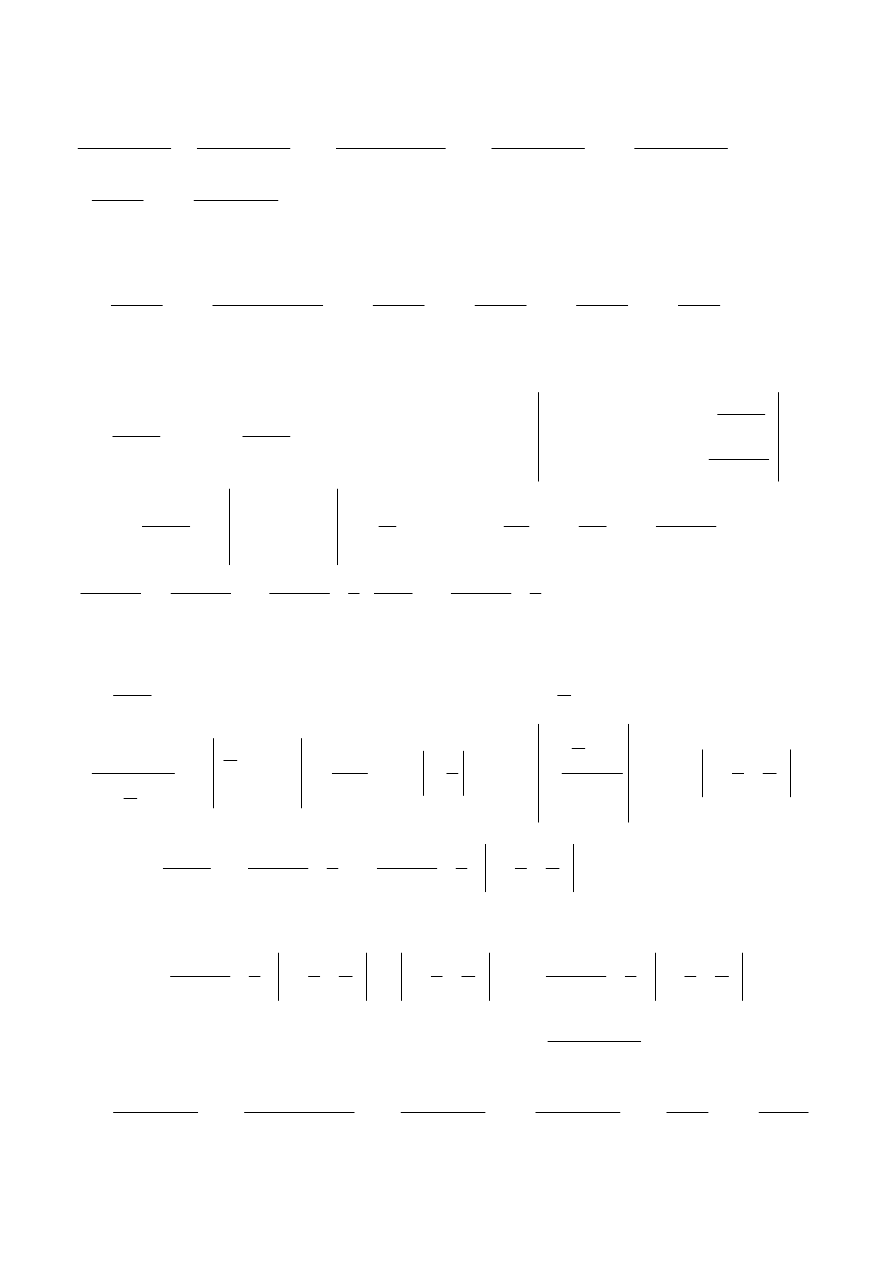
148
Przykład:
∫
∫
∫
∫
∫
=
+
=
+
=
=
dx
x
x
x
dx
x
x
x
dx
x
x
x
x
dx
x
x
x
x
dx
3
2
2
3
2
2
3
2
2
2
3
2
3
2
cos
sin
cos
cos
sin
sin
cos
sin
cos
sin
cos
sin
1
cos
sin
∫
∫
+
=
+
=
2
1
2
3
cos
sin
1
cos
1
I
I
dx
x
x
dx
x
.
Obliczamy pierwszą z całek:
4
3
3
2
3
2
3
2
3
2
2
3
1
cos
1
cos
sin
cos
cos
cos
sin
cos
cos
sin
cos
1
I
I
dx
x
dx
x
x
dx
x
x
dx
x
x
dx
x
x
x
dx
x
I
+
=
+
=
+
=
+
=
=
∫
∫
∫
∫
∫
∫
Wyznaczamy
3
I
:
∫
∫
=
=
=
dx
x
x
x
dx
x
x
I
3
3
2
3
cos
sin
sin
cos
sin
{całkujemy przez części}
=
=
=
′
=
′
=
=
x
x
g
x
x
f
x
x
x
g
x
x
f
2
3
cos
2
1
)
(
cos
)
(
cos
sin
)
(
sin
)
(
{
C
x
C
t
C
t
dt
t
t
dt
dt
xdx
dt
xdx
t
x
dx
x
x
x
g
+
=
+
=
+
−
−
=
−
=
−
=
−
=
=
−
=
=
=
∫
∫
∫
−
−
2
2
2
3
3
3
cos
2
1
2
1
2
sin
sin
cos
cos
sin
)
(
}
∫
∫
−
=
−
=
−
=
4
2
2
2
2
2
1
cos
2
sin
cos
1
2
1
cos
2
sin
cos
2
cos
cos
2
sin
I
x
x
dx
x
x
x
dx
x
x
x
x
.
Obliczamy
4
I
:
=
=
∫
dx
x
I
cos
1
4
{skorzystamy ze wzoru redukcyjnego
+
=
x
x
2
sin
cos
π
oraz przykładu a) ze str. 142}
∫
∫
+
+
=
+
+
=
+
=
=
=
=
+
=
+
=
4
4
4
4
2
tg
ln
2
2
tg
ln
2
tg
ln
sin
1
2
2
sin
1
C
x
C
x
C
u
du
u
du
dx
u
x
dx
x
π
π
π
π
Zatem
3
2
4
2
3
2
3
4
2
tg
ln
2
1
cos
2
sin
2
1
cos
2
sin
cos
sin
C
x
x
x
I
x
x
dx
x
x
I
+
+
−
=
−
=
=
∫
π
Wstawiając wyznaczone całki
4
3
, I
I
do całki
1
I
otrzymujemy:
1
2
1
2
4
3
1
4
2
tg
ln
2
1
cos
2
sin
4
2
tg
ln
4
2
tg
ln
2
1
cos
2
sin
C
x
x
x
C
x
x
x
x
I
I
I
+
+
+
=
+
+
+
+
−
=
+
=
π
π
π
.
Obliczamy drugą z całek występujących przy wyznaczaniu całki
∫
x
x
dx
3
2
cos
sin
, tj. całki
2
I
:
∫
∫
∫
∫
∫
∫
=
+
=
+
=
+
=
=
dx
x
x
dx
x
dx
x
x
x
dx
x
x
x
dx
x
x
x
x
dx
x
x
I
2
2
2
2
2
2
2
2
2
2
sin
cos
cos
1
cos
sin
cos
cos
sin
sin
cos
sin
cos
sin
cos
sin
1
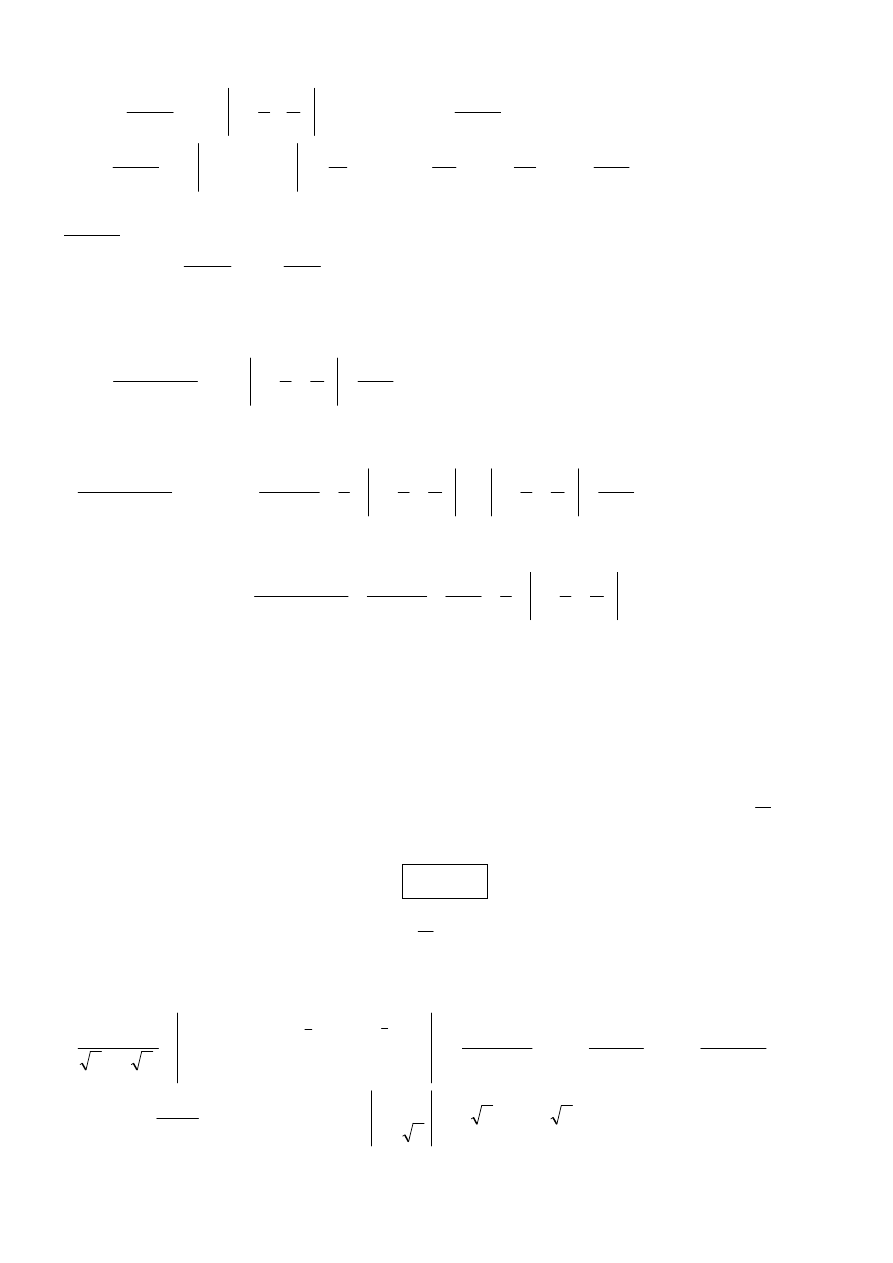
149
∫
+
+
=
+
=
5
2
4
4
2
tg
ln
sin
cos
I
x
dx
x
x
I
π
, gdzie
∫
=
dx
x
x
I
2
5
sin
cos
{całkujemy przez podstawienie} =
5
5
5
1
2
2
2
5
sin
1
1
1
cos
sin
sin
cos
C
x
C
t
C
t
dt
t
t
dt
dt
dx
x
t
x
dx
x
x
I
+
−
=
+
−
=
+
−
=
=
=
=
=
=
=
∫
∫
∫
−
−
.
Uwaga: Przy obliczaniu
5
I
można również skorzystać ze wzoru 2. ze strony 132 Wykładu Nr 9,
a mianowicie:
0
)
(
,
)
(
1
)
(
)
(
2
≠
+
−
=
′
∫
x
f
C
x
f
dx
x
f
x
f
.
Wracając do
2
I
mamy:
2
2
2
sin
1
4
2
tg
ln
cos
sin
1
C
x
x
dx
x
x
I
+
−
+
+
=
=
∫
π
Wracając do całki wyjściowej otrzymujemy:
C
x
x
x
x
x
I
I
x
x
dx
+
−
+
+
+
+
+
=
+
=
∫
sin
1
4
2
tg
ln
4
2
tg
ln
2
1
cos
2
sin
cos
sin
2
2
1
3
2
π
π
Zatem ostatecznie:
C
x
x
x
x
x
x
dx
+
+
+
−
=
∫
4
2
tg
ln
2
3
sin
1
cos
2
sin
cos
sin
2
3
2
π
CAŁKOWANIE FUNKCJI NIEWYMIERNYCH
A) Całkowanie funkcji zawierających pierwiastki z wyrażenia liniowego:
1)
Jeżeli funkcja podcałkowa jest funkcją wymierną potęg zmiennej x o wykładnikach postaci
n
m
)
,
(
N
∈
n
m
, m, n – liczby względem siebie pierwsze, to wykonujemy podstawienie:
N
t
x
=
gdzie N – wspólny mianownik ułamków postaci
n
m .
Przykład:
(
)
(
)
(
)
∫
∫
∫
∫
=
+
−
+
=
+
=
+
=
=
=
=
→
=
=
+
dt
t
t
dt
t
t
dt
t
t
t
dt
t
dx
t
x
t
x
t
x
x
x
dx
2
2
2
2
2
3
5
5
2
3
1
3
2
1
6
3
1
1
1
6
1
6
1
6
6
,
1
[
]
[
]
0
,
arctg
6
arctg
6
1
6
6
6
6
6
2
>
+
−
=
=
=
=
+
−
=
+
−
=
∫
∫
x
C
x
x
x
t
t
x
C
t
t
t
dt
dt
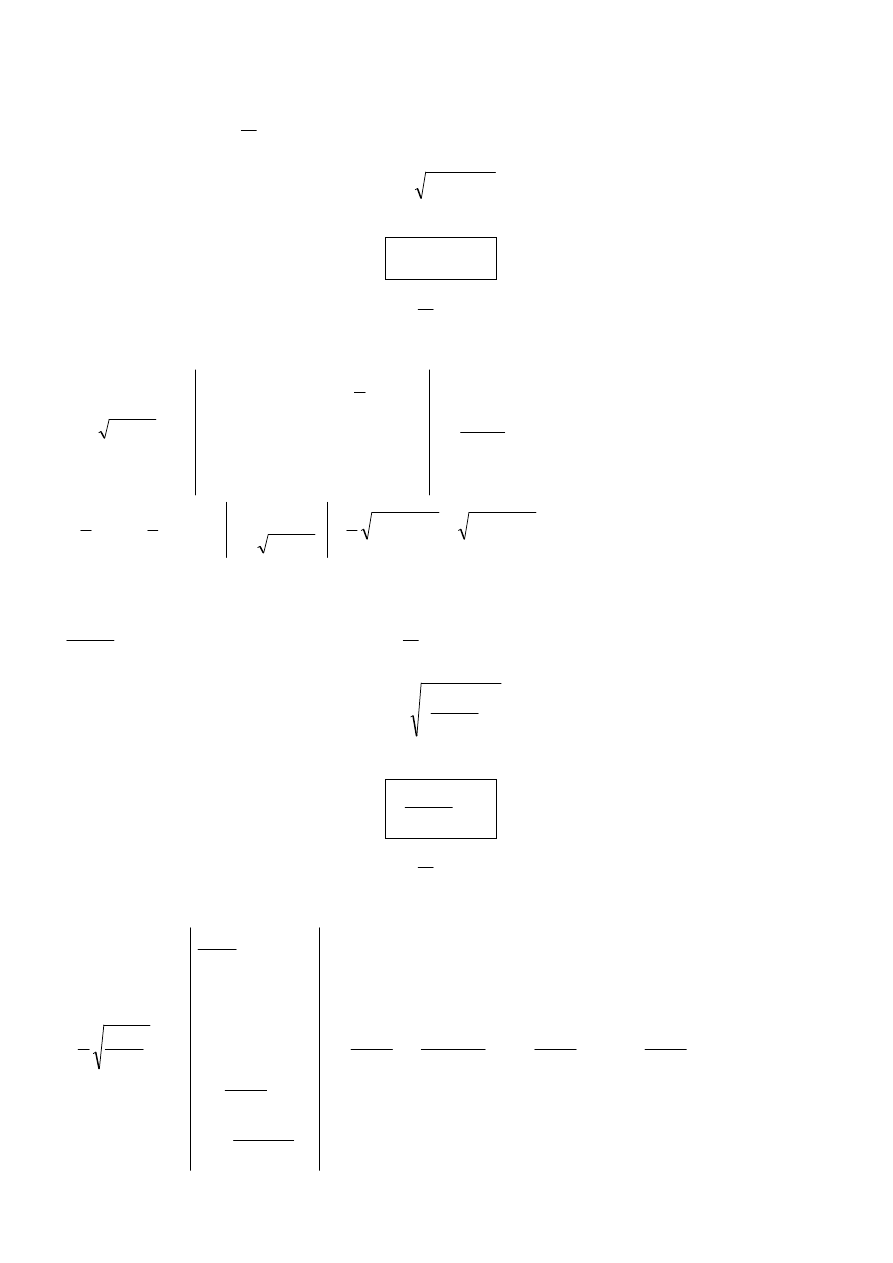
150
2) Jeżeli funkcja podcałkowa jest funkcją wymierną potęg zmiennej x oraz potęg dwumianu
b
ax
+
o wykładnikach postaci
n
m , czyli mamy do czynienia z całką
(
)
∫
+
dx
b
ax
x
R
n
m
,
,
to wykonujemy podstawienie:
N
t
b
ax
=
+
,
gdzie N – wspólny mianownik ułamków postaci
n
m .
Przykład:
(
)
(
)
∫
∫
∫
=
−
=
⋅
⋅
−
=
=
=
−
=
→
=
+
=
+
⋅
dt
t
t
dt
t
t
t
dt
t
dx
dt
t
dx
t
x
t
x
dx
x
x
4
8
3
4
3
3
4
4
4
5
2
2
5
2
4
2
5
2
1
5
2
5
2
(
)
(
)
0
5
2
,
5
2
5
2
9
1
5
2
5
2
5
1
5
9
1
4
5
4
9
4
4
5
9
>
+
+
+
−
+
=
+
=
=
+
=
+
⋅
−
=
x
C
x
x
x
t
t
x
C
t
t
3) Jeżeli funkcja podcałkowa jest funkcją wymierną potęg zmiennej x oraz potęg funkcji homograficznej
(
)
0
,
≠
−
+
+
bc
ad
d
cx
b
ax
o wykładnikach postaci
n
m ,czyli mamy do czynienia z całką
∫
+
+
dx
d
cx
b
ax
x
R
n
m
,
,
to wykonujemy podstawienie:
N
t
d
cx
b
ax
=
+
+
gdzie N – wspólny mianownik ułamków postaci
n
m .
Przykład:
(
)
(
)
(
)
∫
∫
∫
∫
=
−
−
−
=
−
=
−
⋅
⋅
−
=
−
=
−
=
=
−
⋅
=
−
=
−
=
−
=
−
dt
t
t
dt
t
t
dt
t
t
t
t
dt
t
t
dx
t
x
t
x
xt
x
xt
x
t
x
x
dx
x
x
x
2
2
2
2
2
2
2
2
2
2
2
2
2
2
1
2
1
2
1
4
2
1
1
4
1
2
2
1
2
2
2
2
1
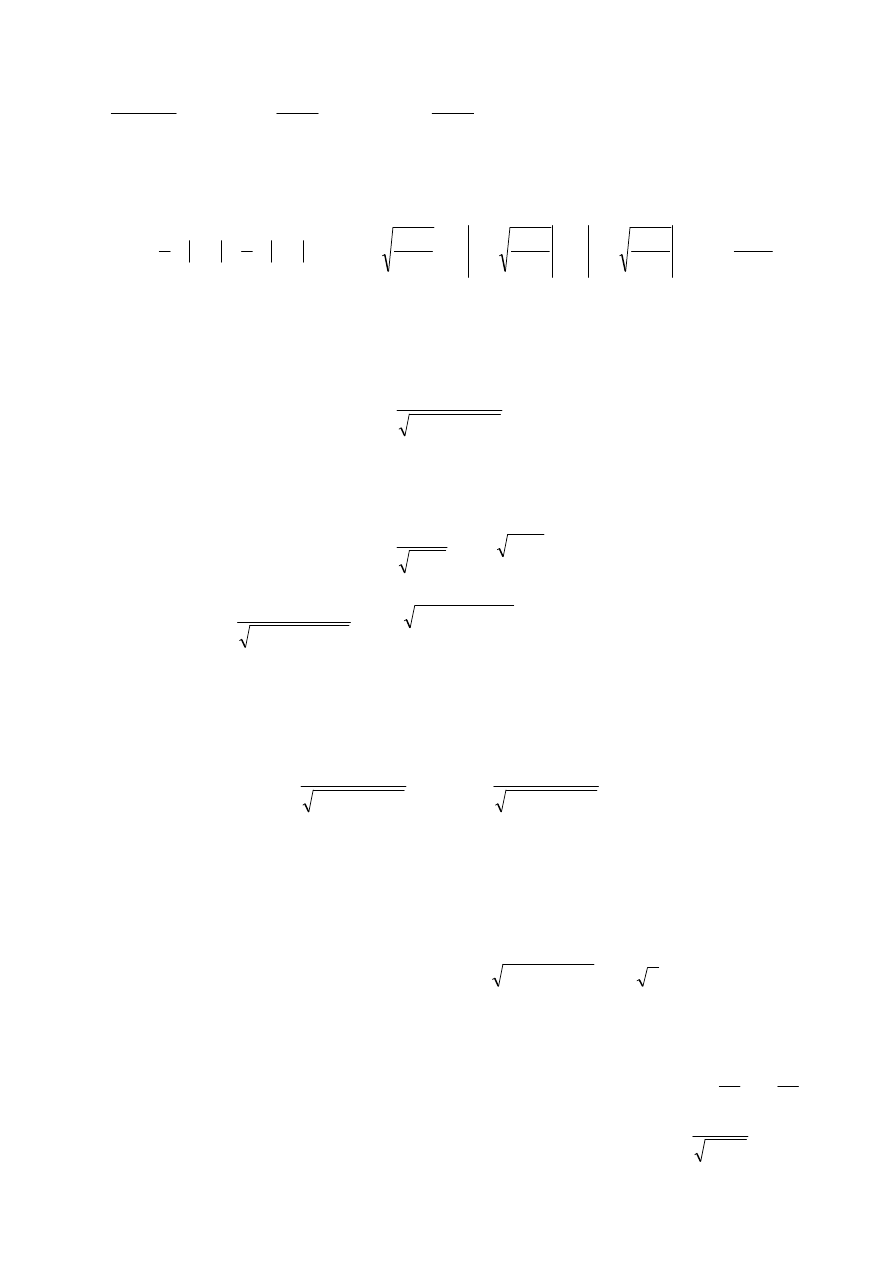
151
∫
∫
∫
=
−
+
−
=
−
−
−
=
−
−
−
−
=
4
3
42
1
1
2
2
2
2
1
1
2
2
1
1
1
2
1
1
1
2
I
dt
t
t
dt
t
dt
t
t
{całkę
1
I
obliczamy korzystając z rozkładu na ułamki proste – patrz Wykład 9, ostatecznie po jej
obliczeniu otrzymamy}
0
2
,
2
1
ln
2
1
ln
2
2
1
ln
2
1
1
ln
2
1
2
2
>
−
+
−
+
+
−
−
−
−
−
=
+
+
+
−
−
+
−
=
x
x
C
x
x
x
x
x
x
C
t
t
t
B) Całkowanie funkcji zawierających w liczniku funkcję liniową, a w mianowniku pierwiastek
kwadratowy z trójmianu kwadratowego
Całki typu:
(
)
∫
≠
+
+
+
0
2
a
c
bx
ax
dx
B
Ax
ALGORYTM OBLICZANIA TEJ CAŁKI
1. Sprawdzamy, czy licznik jest pochodną funkcji podpierwiastkowej?
Jeśli TAK to stosujemy wzór (***)
∫
+
=
′
C
x
f
dx
x
f
x
f
)
(
2
)
(
)
(
Przykład:
C
x
x
dx
x
x
x
+
+
+
=
+
+
+
∫
11
3
2
2
11
3
2
3
4
2
2
Jeśli NIE zacznij algorytm od punktu 2.
2. Jeśli licznik nie jest pochodną funkcji podpierwiastkowej, to całkę sprowadzamy do sumy dwóch całek
postaci:
∫
∫
+
+
+
+
+
i
2
2
2
c
bx
ax
dx
dx
c
bx
ax
b
ax
Wynik pierwszej z nich jest natychmiastowy na podstawie wzoru (***).
Drugą z tych całek obliczamy różnie w zależności od znaku współczynnika a przy
2
x
.
Rozpatrujemy dwa przypadki :
1°
0
>
a
Stosujemy PODSTAWIENIE EULERA:
x
a
t
c
bx
ax
−
=
+
+
2
Całkę sprowadzamy do całki funkcji wymiernej.
2°
0
<
a
Trójmian kwadratowy sprowadzamy do postaci kanonicznej
a
a
b
x
a
c
bx
ax
4
2
2
2
∆
−
+
=
+
+
, a
następnie poprzez odpowiednie podstawienie sprowadzamy daną całkę do całki typu
∫
−
2
1 t
dt
.
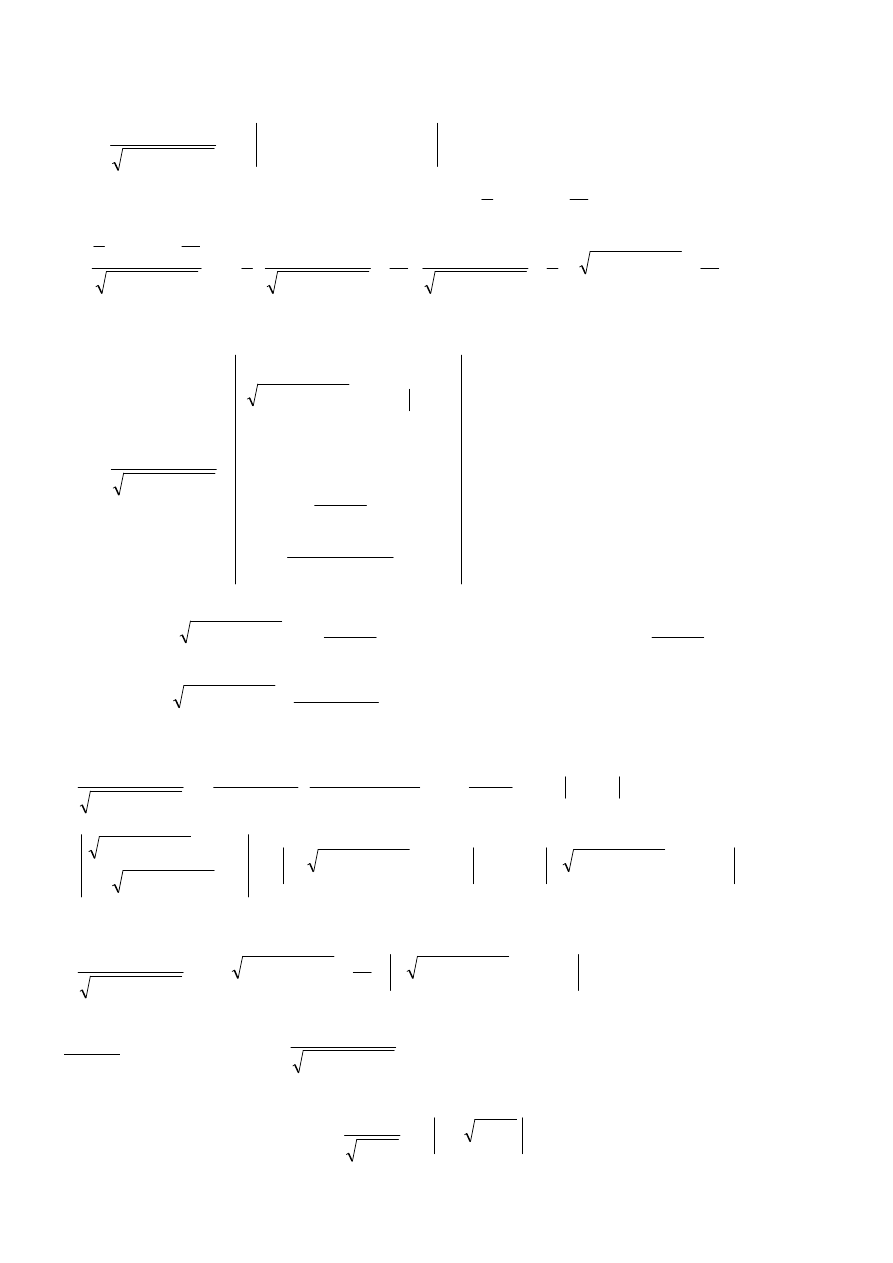
152
Przykłady:
a)
(
)
∫
=
−
=
′
+
−
=
+
−
+
5
2
19
5
19
5
2
3
2
2
x
x
x
dx
x
x
x
{dzielimy licznik przez pochodną funkcji
podpierwiastkowej, po wydzieleniu otrzymamy:
(
)
2
19
5
2
2
3
2
3
+
−
=
+
x
x
}
(
)
(
)
1
2
2
2
2
2
19
19
5
2
2
3
19
5
2
19
19
5
5
2
2
3
19
5
2
19
5
2
2
3
I
x
x
x
x
dx
x
x
dx
x
dx
x
x
x
+
+
−
⋅
=
+
−
+
+
−
−
=
+
−
+
−
=
∫
∫
∫
Obliczamy całkę
1
I
korzystając z podstawienia Eulera:
(
)
(
)
(
)
∫
−
+
−
=
−
−
=
−
=
−
+
−
=
+
−
−
=
+
−
>
=
=
+
−
=
dt
t
t
t
dx
t
t
x
t
x
t
x
tx
t
x
x
x
t
x
x
a
a
x
x
dx
I
2
2
2
2
2
2
2
2
2
2
1
5
2
19
5
2
5
2
19
19
5
2
2
19
5
19
5
0
,
1
19
5
=
Stąd
5
2
19
19
5
2
2
−
−
−
=
+
−
t
t
t
x
x
{wstawiamy za x wyrażenie
5
2
19
2
−
−
t
t
}
5
2
19
5
19
5
2
2
−
+
−
=
+
−
t
t
t
x
x
Zatem
(
)
(
)
∫
∫
∫
=
+
−
=
−
=
−
+
−
⋅
+
−
−
=
+
−
1
2
2
2
2
5
2
ln
5
2
2
5
2
19
5
2
19
5
5
2
19
5
C
t
dt
t
dt
t
t
t
t
t
t
x
x
dx
(
)
1
2
1
2
2
2
5
2
19
5
2
ln
5
19
5
2
ln
19
5
19
5
C
x
x
x
C
x
x
x
x
x
x
t
x
t
x
x
+
−
+
+
−
=
+
−
+
+
−
=
+
+
−
=
−
=
+
−
=
Ostatecznie:
∫
>
+
−
+
−
+
+
−
+
+
−
=
+
−
+
0
19
5
,
5
2
19
5
2
ln
2
19
19
5
3
19
5
2
3
2
2
2
2
x
x
C
x
x
x
x
x
dx
x
x
x
Uwaga: W przypadku całki
∫
+
+
c
bx
ax
dx
2
, gdzie
0
>
a
możemy funkcję podpierwiastkową zapisać
w postaci kanonicznej i poprzez odpowiednie podstawienie sprowadzić do całki typu:
C
t
t
t
dt
+
±
+
=
±
∫
1
ln
1
2
2
.
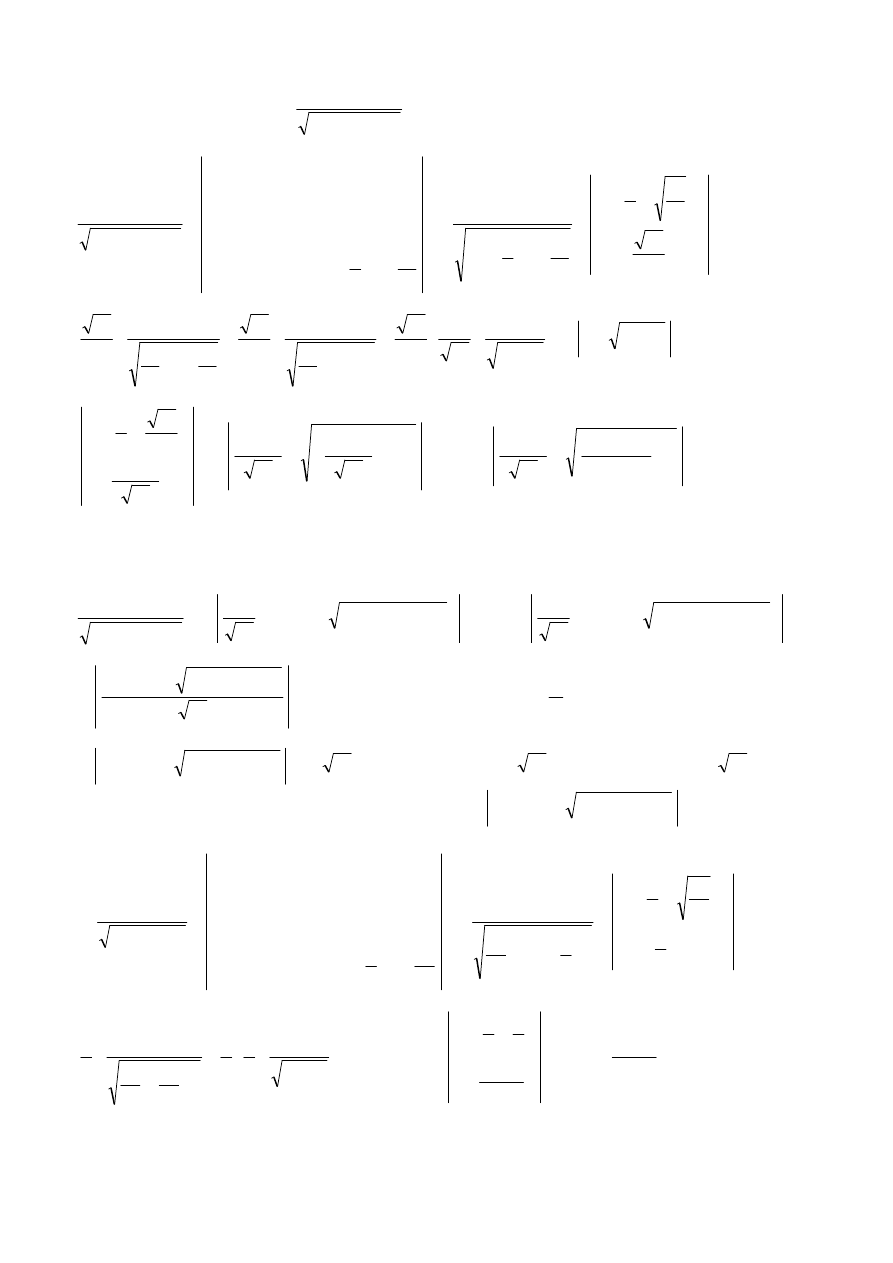
153
Wyznaczymy teraz całkę
∫
+
−
=
19
5
2
1
x
x
dx
I
korzystając z uwagi ze strony 152:
=
=
⋅
=
−
=
+
−
=
+
−
=
+
−
−
=
∆
>
=
=
+
−
∫
∫
dt
dx
t
x
x
dx
x
x
x
a
a
x
x
dx
2
51
4
51
2
5
4
51
2
5
4
51
2
5
19
5
51
0
,
1
19
5
2
2
2
2
(
)
=
+
+
+
=
+
⋅
=
+
=
+
=
∫
∫
∫
1
2
2
2
2
1
ln
1
51
2
2
51
1
4
51
2
51
4
51
4
51
2
51
C
t
t
t
dt
t
dt
t
dt
1
2
1
2
1
51
)
5
2
(
51
5
2
ln
1
51
5
2
51
5
2
ln
51
5
2
2
51
2
5
C
x
x
C
x
x
x
t
t
x
+
+
−
+
−
=
+
+
−
+
−
=
−
=
=
−
=
Otrzymamy wynik można doprowadzić do takiej postaci funkcji pierwotnej, jaką uzyskaliśmy
wykorzystując podstawienie Eulera, a mianowicie:
[
]
[
]
=
+
+
−
+
−
=
+
+
−
+
−
=
+
−
∫
1
2
1
2
2
76
20
4
5
2
51
1
ln
51
)
5
2
(
5
2
51
1
ln
19
5
C
x
x
x
C
x
x
x
x
dx
=
+
+
−
+
−
=
1
2
51
19
5
2
5
2
ln
C
x
x
x
{z własności logarytmu:
B
A
B
A
ln
ln
ln
−
=
} =
=
+
−
+
−
+
−
=
1
2
51
ln
19
5
2
5
2
ln
C
x
x
x
{ponieważ
51
ln
jest liczbą, więc
1
51
ln
C
+
−
pełni
rolę nowej stałej całkowania, oznaczmy ją przez
*
1
C
}
*
1
2
19
5
2
5
2
ln
C
x
x
x
+
+
−
+
−
=
.
b)
=
=
⋅
=
−
=
−
−
=
+
−
−
=
+
+
−
=
∆
<
−
=
=
−
+
∫
∫
dt
dx
t
x
x
dx
x
x
x
a
a
x
x
dx
2
5
4
25
2
1
2
1
4
25
4
25
2
1
6
25
0
,
1
6
2
2
2
2
∫
∫
+
−
=
−
=
=
−
=
+
=
−
⋅
=
−
=
C
x
x
t
t
x
C
t
t
dt
t
dt
5
1
2
arcsin
5
1
2
2
5
2
1
arcsin
1
5
2
2
5
4
25
4
25
2
5
2
2
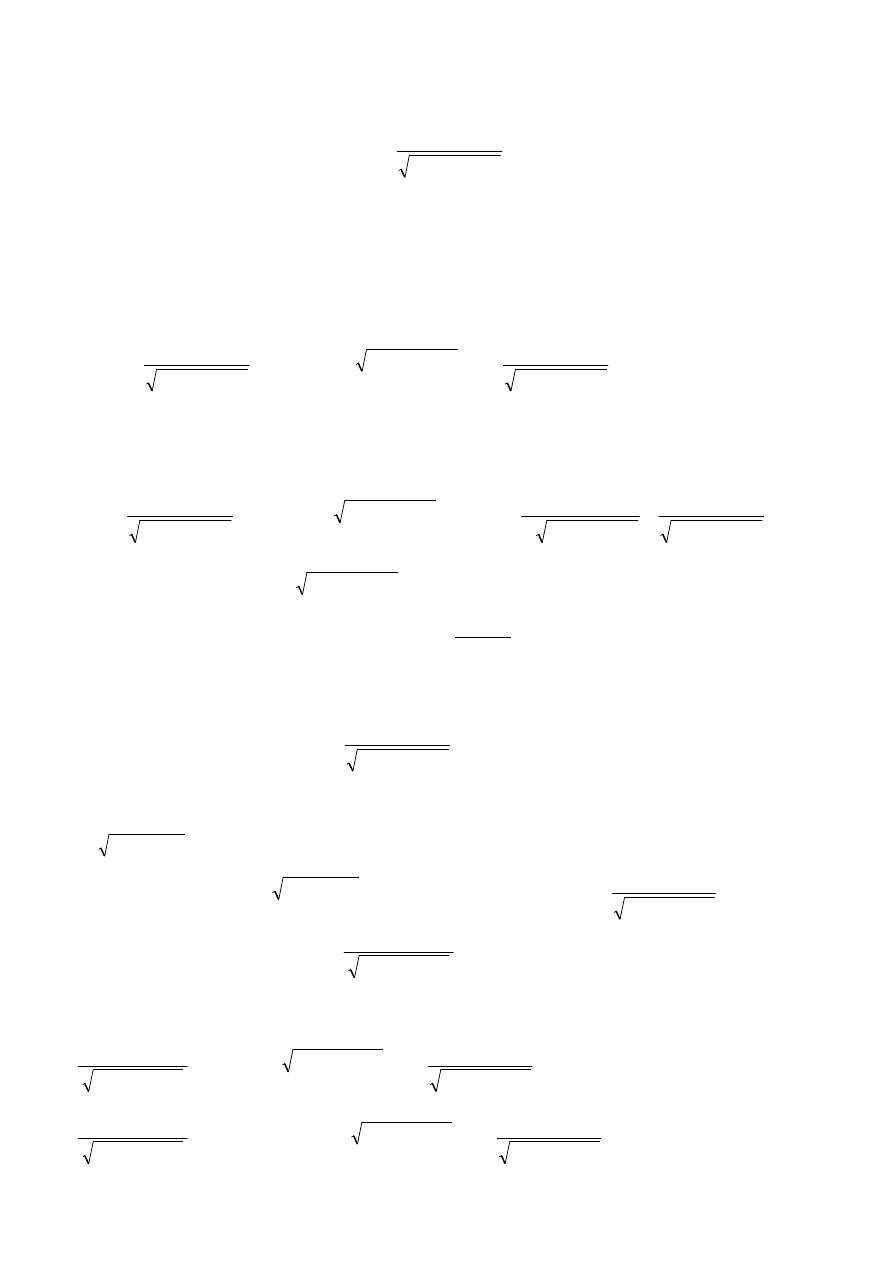
154
C) Metoda współczynników nieoznaczonych
dotyczy całek postaci:
∫
+
+
dx
c
bx
ax
x
W
n
2
)
(
gdzie
)
(x
W
n
- wielomian stopnia n,
0
≠
a
.
ALGORYTM OBLICZANIA CAŁKI
1. Całkę przedstawiamy w postaci:
∫
∫
+
+
+
+
+
⋅
=
+
+
−
c
bx
ax
dx
K
c
bx
ax
x
Q
dx
c
bx
ax
x
W
n
n
2
2
1
2
)
(
)
(
(****)
gdzie
)
(
1
x
Q
n
−
- wielomian stopnia n – 1 w POSTACI OGÓLNEJ, K – stała
2. Wyrażenie (****) różniczkujemy stronami:
[
]
c
bx
ax
K
c
bx
ax
b
ax
x
Q
c
bx
ax
x
Q
c
bx
ax
x
W
n
n
n
+
+
+
+
+
+
⋅
+
+
+
⋅
′
=
+
+
−
−
2
2
1
2
1
2
2
2
)
(
)
(
)
(
3. Mnożymy obustronnie przez
c
bx
ax
+
+
2
:
[
]
(
)
K
b
ax
x
Q
c
bx
ax
x
Q
x
W
n
n
n
+
+
⋅
+
+
+
⋅
′
≡
−
−
2
2
)
(
)
(
)
(
1
2
1
(*****)
4. Prawą stronę równości (*****) porządkujemy względem potęg x, przyrównujemy współczynniki przy
odpowiednich potęgach x występujące po lewej i prawej stronie równości, wyznaczamy nieznane
współczynniki oraz obliczamy całkę
∫
+
+
c
bx
ax
dx
2
.
Przykład
∫
=
−
+
⋅
dx
x
x
x
2
6
{mnożymy i dzielimy przez
2
6
x
x
−
+
, by sprowadzić do całki postaci
∫
+
+
−
dx
x
x
x
W
6
)
(
2
3
}
czyli mamy do czynienia z całką:
∫
+
+
−
+
+
−
dx
x
x
x
x
x
6
6
2
2
3
Zatem
∫
∫
+
+
−
+
+
+
−
⋅
=
+
+
−
+
+
−
6
6
)
(
6
6
2
2
2
2
2
3
x
x
dx
K
x
x
x
Q
dx
x
x
x
x
x
(
)
∫
∫
+
+
−
+
+
+
−
⋅
+
+
=
+
+
−
+
+
−
6
6
6
6
2
2
2
2
2
3
x
x
dx
K
x
x
C
Bx
Ax
dx
x
x
x
x
x
(1)
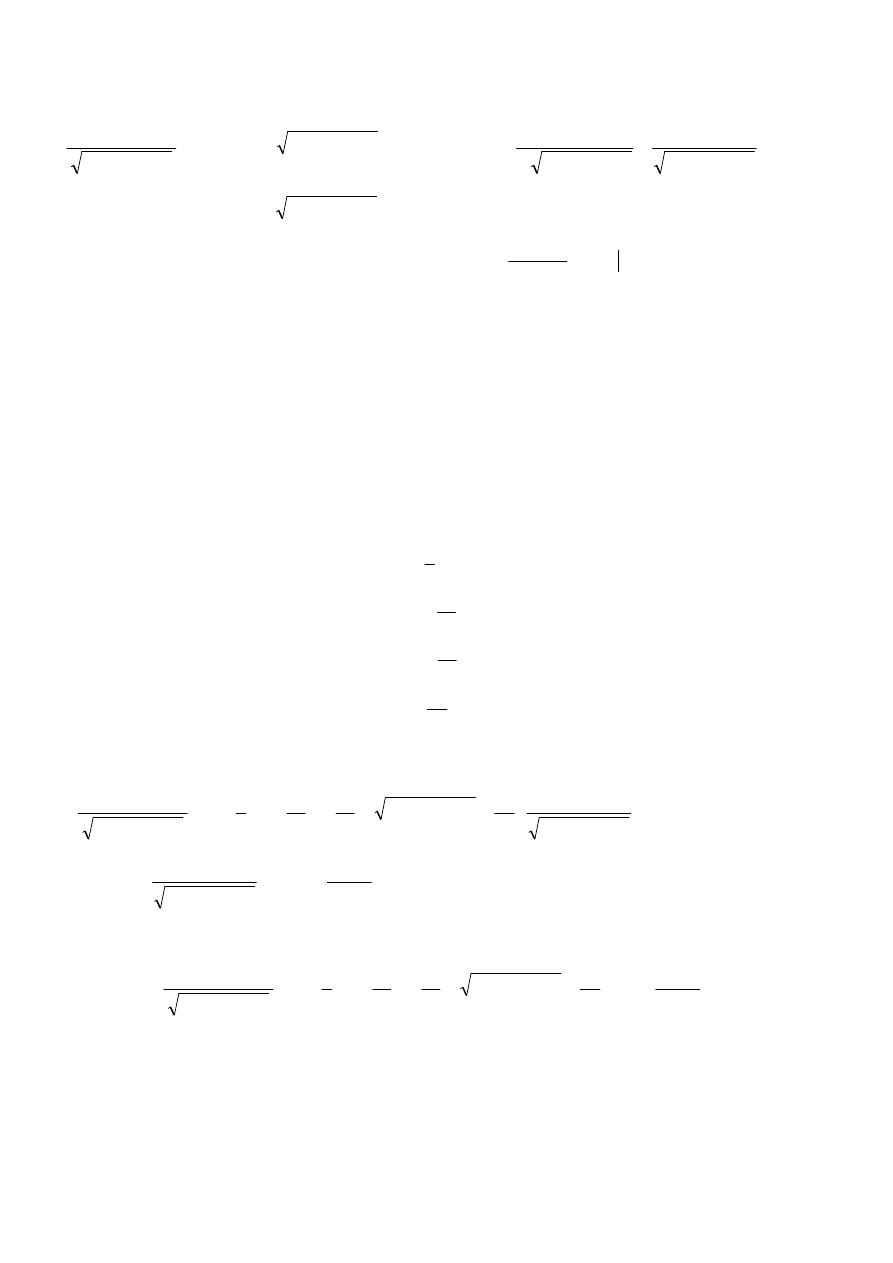
155
(1) różniczkujemy stronami:
(
)
(
)
6
6
2
1
2
6
2
6
6
2
2
2
2
2
2
3
+
+
−
+
+
+
−
+
−
⋅
+
+
+
+
+
−
⋅
+
=
+
+
−
+
+
−
x
x
K
x
x
x
C
Bx
Ax
x
x
B
Ax
x
x
x
x
x
mnożymy obustronnie przez
6
2
+
+
−
x
x
(
)
(
) (
)
2
2
1
2
6
2
6
2
2
2
3
⋅
+
+
−
⋅
+
+
+
+
+
−
⋅
+
≡
+
+
−
K
x
C
Bx
Ax
x
x
B
Ax
x
x
x
(
)
(
) (
)
(
)
K
x
C
Bx
Ax
x
x
B
Ax
x
x
x
2
1
2
6
2
4
12
2
2
2
2
2
3
+
+
−
⋅
+
+
+
+
+
−
⋅
+
≡
+
+
−
po wymnożeniu i pogrupowaniu względem potęg x prawej strony mamy:
(
)
(
)
(
)
K
C
B
x
C
B
A
x
B
A
Ax
x
x
x
2
12
2
3
24
4
5
6
12
2
2
2
3
2
3
+
+
+
−
+
+
−
+
−
≡
+
+
−
stąd otrzymujemy układ równań:
=
+
+
=
−
+
=
−
−
=
−
0
2
12
12
2
3
24
2
4
5
2
6
K
C
B
C
B
A
B
A
A
po rozwiązaniu układu otrzymujemy:
=
−
=
−
=
=
16
25
8
17
12
1
3
1
K
C
B
A
wyliczone wartości A, B, C, K wstawiamy do (1):
∫
∫
+
+
−
+
+
+
−
⋅
−
−
=
+
+
−
+
+
−
6
16
25
6
8
17
12
1
3
1
6
6
2
2
2
2
2
3
x
x
dx
x
x
x
x
dx
x
x
x
x
x
Ponieważ
∫
+
−
=
+
+
−
1
2
5
1
2
arcsin
6
C
x
x
x
dx
{patrz przykład b) ze strony 153}
Stąd:
C
x
x
x
x
x
dx
x
x
x
x
x
+
−
+
+
+
−
⋅
−
−
=
+
+
−
+
+
−
∫
5
1
2
arcsin
16
25
6
8
17
12
1
3
1
6
6
2
2
2
2
3
Wyszukiwarka
Podobne podstrony:
Microsoft Word WE L10 Calki tryg, niewym
Microsoft Word WE L9 Calki przez czesci i podstawienie, wymierne
Microsoft Word WE L14 Szeregi Fouriera
Microsoft Word WE harmonogram egz
Microsoft Word WE L13 szeregi potęgowe
Microsoft Word WE W9 Calka przez czesci, podst i wymierna
Microsoft Word WE wyniki E2 2009
Microsoft Word WE W14 Szeregi Fouriera
Microsoft Word WE W11 Calka oznaczona
Microsoft Word WE L11 Calka oznaczona i zastosowanie
Microsoft Word WE W13 Szeregi funkcyjne i potegowe
Microsoft Word WE L12 szeregi liczbowe
Microsoft Word W14 Szeregi Fouriera
New Microsoft Word Document (2)
Nowy Dokument programu Microsoft Word (5)
Nowy Dokument programu Microsoft Word
Nowy Dokument programu Microsoft Word
Microsoft Word zrodla infor I czesc pprawiona 2 do wydr
więcej podobnych podstron