156
WYKŁAD Nr 11
CAŁKA OZNACZONA (RIEMANNA)
Niech będzie dana funkcja
)
(x
f
określona, ograniczona na przedziale domkniętym
b
a
,
.
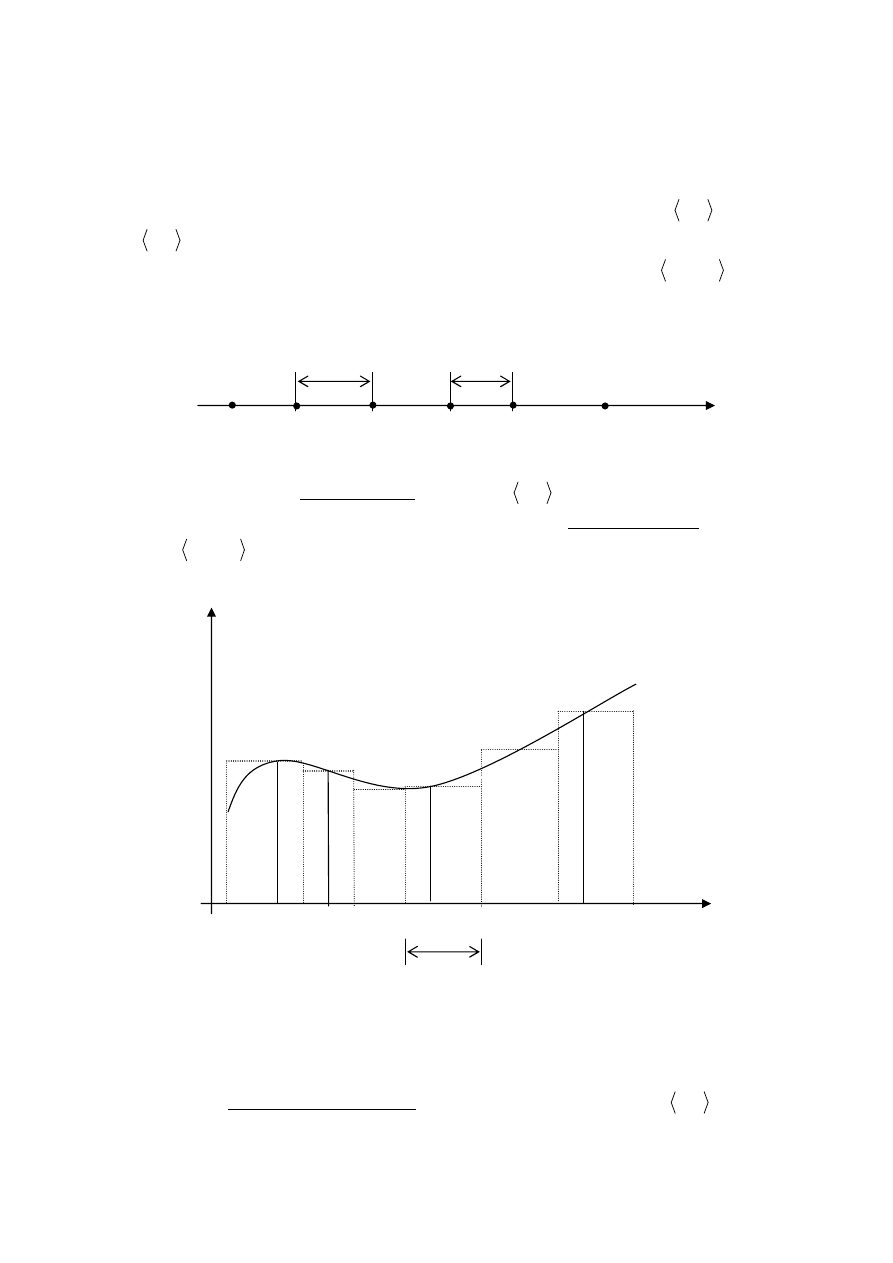
Przedział
b
a
,
dzielimy na n podprzedziałów (niekoniecznie równych) punktami:
n
x
x
x
x
...
,
,
,
2
1
0
,
gdzie
b
x
x
x
x
x
a
n
n
=
<
<
<
<
<
=
−1
2
1
0
...
. Otrzymujemy przedziały częściowe
n
i
x
x
i
i
...,
,
2
,
1
,
,
1
=
−
o długościach odpowiednio
1
−
−
=
∆
i
i
i
x
x
x
.
Punkty
n
x
x
x
...
,
,
2
1
określają pewien podział przedziału
b
a
,
na n podprzedziałów. Podział ten
oznaczamy
n
∆ . Liczbę
{
}
n
i
x
i
n
...,
,
2
,
1
,
max
=
∆
=
δ
nazywamy średnicą podziału
n
∆ . W każdym
z przedziałów
i
i
x
x
,
1
−
obieramy dowolnie punkt
n
i
i
...,
,
2
,
1
,
=
ξ
tzn.
i
i
i
x
x
≤
ξ
≤
−1
, a następnie
obliczamy
)
(
i
f
ξ .
Tworzymy sumę
(*)
∑
=
∆
⋅
ξ
=
∆
⋅
ξ
+
+
∆
⋅
ξ
+
∆
⋅
ξ
=
n
i
i
i
n
n
n
x
f
x
f
x
f
x
f
S
1
2
2
1
1
)
(
)
(
...
)
(
)
(
Sumę (*) nazywamy sumą całkową Riemanna funkcji
)
(x
f
y
=
na przedziale
b
a
,
odpowiadającą
podziałowi
n
∆ .
i
x
∆
2
x
∆
0
x
a
=
1
x
2
x
...
1
−
i
x
i
x
b
x
n
=
x
...
)
(
n
f
ξ
)
(
i
f
ξ
)
(
2
ξ
f
)
(
1
ξ
f
)
(x
f
y
=
x
x
x
x
x
x
x
x
n
n
n
i
i
i
ξ
ξ
ξ
ξ
−
−
1
1
3
2
1
1
0
...
...
i
x
∆
y

157
Komentarz:
Każdemu podziałowi przedziału
b
a
,
odpowiada nieskończenie wiele sum całkowych (*),
gdyż punkt
i
ξ w przedziale
i
i
x
x
,
1
−
można wybrać na nieskończenie wiele sposobów. Ponadto każdej
liczbie n odpowiada nieskończenie wiele różnych podziałów przedziału
b
a
,
na n podprzedziałów.
Zatem suma
n
S
zależy nie tylko od funkcji
)
(x
f
, liczby n, ale również od podziału przedziału i wyboru
punktów pośrednich
i
ξ .
Bierzemy, zatem pod uwagę ciąg podziałów
( )
n
∆
przedziału
b
a
,
.
Ciąg
( )
n
∆
nazywamy normalnym ciągiem podziałów przedziału
b
a
,
, jeśli odpowiadający mu ciąg
ś
rednic
( )
n
δ
dąży do zera, tzn.
0
lim
=
δ
∞
→
n
n
.
Każdemu ciągowi podziałów
( )
n
∆
odpowiada, zatem ciąg sum całkowych
( )
n
S
.
Def.11.1. (całka oznaczona)
Jeśli dla każdego normalnego ciągu podziałów
( )
n
∆
przedziału
b
a
,
odpowiadający mu ciąg sum
całkowych
( )
n
S
jest zbieżny do granicy właściwej, niezależnej od wyboru punktów pośrednich
i
ξ , to tą
granicę nazywamy całką oznaczoną funkcji
)
(x
f
na przedziale
b
a
,
, a oznaczamy
∫
b
a
dx
x
f
)
(
.
Powyższą definicję można zapisać symbolicznie:
∫
∑
=
→
δ
∆
⋅
ξ
=
b
a
n
i
i
i
x
f
dx
x
f
n
1
0
)
(
lim
)
(
Liczba a to dolna granica całkowania, liczba b – górna granica całkowania, przedział
b
a
,
– przedział
całkowania.
Fakt
: Jeśli funkcja
)
(x
f
jest ciągła na
b
a
,
to jest całkowalna na
b
a
,
.
INTERPRETACJA GEOMETRYCZNA CAŁKI OZNACZONEJ
Niech
)
(x
f
y
=
będzie funkcją ciągłą na
b
a
,
i
b
a
x
x
f
,
0
)
(
∈
≥
to
∫
b
a
dx
x
f
)
(
przedstawia pole
obszaru płaskiego D.
Uwaga: Jeśli
0
)
(
≤
x
f
to
∫
−
=
b
a
dx
x
f
D
)
(
.
y
∫
=
b
a
dx
x
f
D
)
(
x
)
(x
f
y
=
a
b
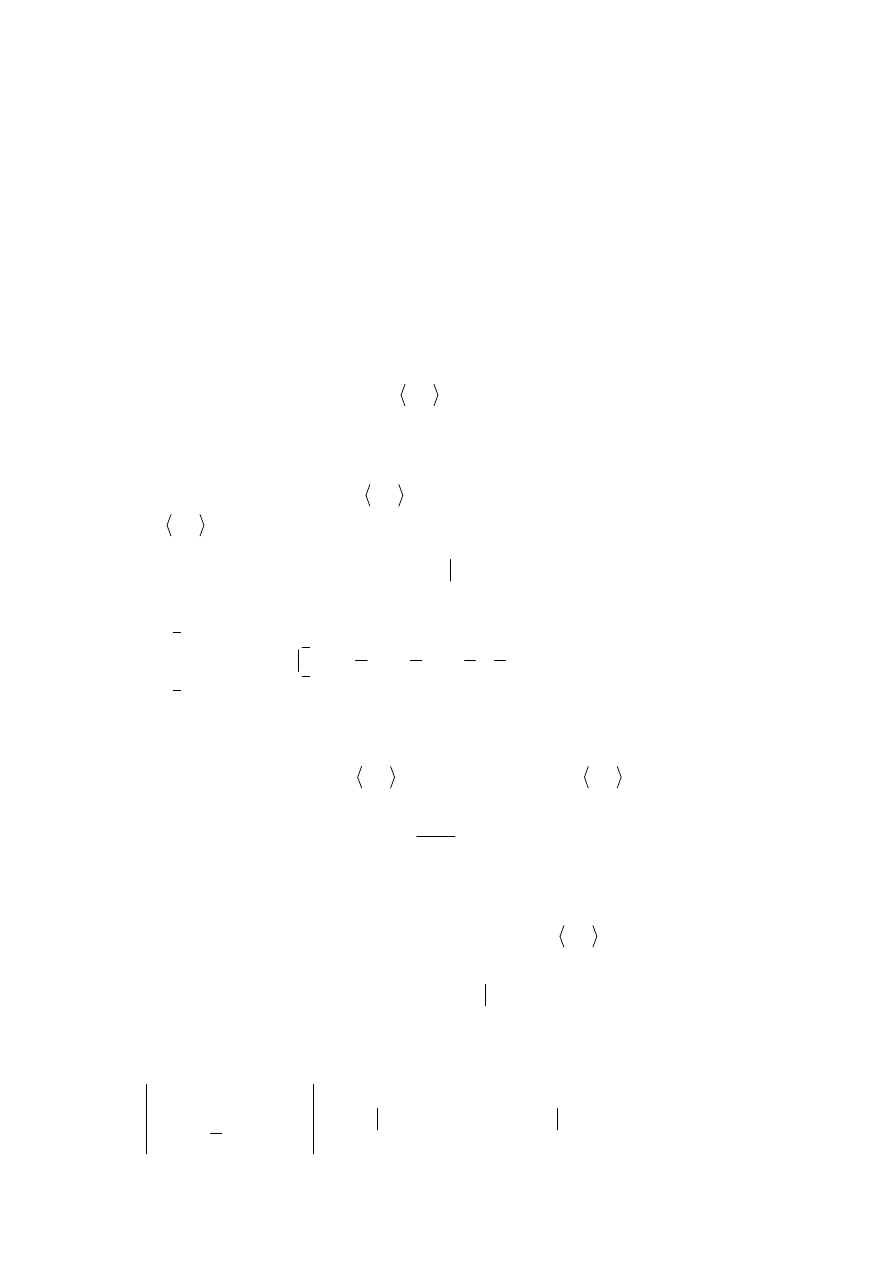
158
PODSTAWOWE WŁASNOŚCI CAŁKI OZNACZONEJ
Niech funkcje
)
(
i
)
(
x
g
x
f
całkowalne w rozważanych przedziałach.
Wówczas:
1.
∫
∫
−
=
a
b
b
a
dx
x
f
dx
x
f
)
(
)
(
2.
∫
∫
=
⋅
b
a
b
a
dx
x
f
A
dx
x
f
A
)
(
)
(
, gdzie A – dowolna stała
3.
[
]
∫
∫
∫
±
=
±
b
a
b
a
b
a
dx
x
g
dx
x
f
dx
x
g
x
f
)
(
)
(
)
(
)
(
4.
∫
∫
∫
∈
+
=
c
a
b
c
b
a
b
a
c
dx
x
f
dx
x
f
dx
x
f
,
,
)
(
)
(
)
(
Tw.11.1. (twierdzenie Newtona – Leibniza)
Jeżeli funkcja f jest ciągła na przedziale
b
a
,
oraz
)
(x
F
jest dowolną funkcją pierwotną funkcji
)
(x
f
na przedziale
b
a
,
to
)
(
)
(
)
(
)
(
a
F
b
F
x
F
dx
x
f
b
a
b
a
−
=
=
∫
Przykład:
2
1
2
1
1
6
sin
2
sin
sin
cos
2
6
2
6
=
−
=
π
−
π
=
=
π
π
π
π
∫
x
dx
x
Tw.11.2. (tw. całkowe o wartości średniej)
Jeżeli funkcja f jest ciągła na przedziale
b
a
,
to istnieje taki punkt
b
a
c
,
∈
, że
∫
−
=
b
a
dx
x
f
a
b
c
f
)
(
1
)
(
Tw.11.3. (tw. o całkowaniu przez części dla całek oznaczonych)
Jeśli
)
(
i
)
(
x
g
x
f
mają ciągłe pochodne
)
(
),
(
x
g
x
f
′
′
na przedziale
b
a
,
to
∫
∫
⋅
′
−
⋅
=
′
⋅
b
a
b
a
b
a
dx
x
g
x
f
x
g
x
f
dx
x
g
x
f
)
(
)
(
)
(
)
(
)
(
)
(
Przykład:
(
)
(
)
2
2
2
2
2
2
ln
)
(
1
)
(
1
)
(
ln
)
(
ln
2
2
2
2
e
e
e
e
e
x
e
e
dx
x
x
x
x
g
x
x
f
x
g
x
x
f
dx
x
e
e
e
e
e
e
e
e
=
−
−
−
=
−
−
=
−
=
=
=
′
=
′
=
=
∫
∫
159
Tw.11.4. (tw. o całkowaniu przez podstawienie dla całek oznaczonych)
Jeśli funkcja
)
(x
g
t
=
ma ciągłą pochodną
)
(x
g ′
na przedziale
b
a
,
i przekształca go na zbiór T, na
którym określona jest funkcja ciągła
)
(t
f
, a ponadto
β
=
α
=
)
(
,
)
(
b
g
a
g
, to
[
]
∫
∫
β
α
=
′
⋅
dt
t
f
dx
x
g
x
g
f
b
a
)
(
)
(
)
(
Przykład:
(
)
∫
∫
∫
=
−
−
=
⋅
−
=
−
=
−
⋅
=
−
=
=
−
=
−
=
−
0
1
0
1
0
1
2
1
2
1
0
2
3
1
1
0
3
1
3
2
2
1
2
1
2
1
0
1
1
0
2
1
2
1
1
t
t
dt
t
dt
t
t
x
dt
xdx
dt
xdx
t
x
dx
x
x
ZASTOSOWANIE CAŁEK OZNACZONYCH
A) POLE OBSZARU PŁASKIEGO
1. Pole
D
obszaru płaskiego D ograniczonego łukiem krzywej o równaniu
)
(x
f
y
=
,
b
a
x
,
∈
oraz
osią OX wyraża się wzorem:
∫
=
b
a
dx
x
f
D
)
(
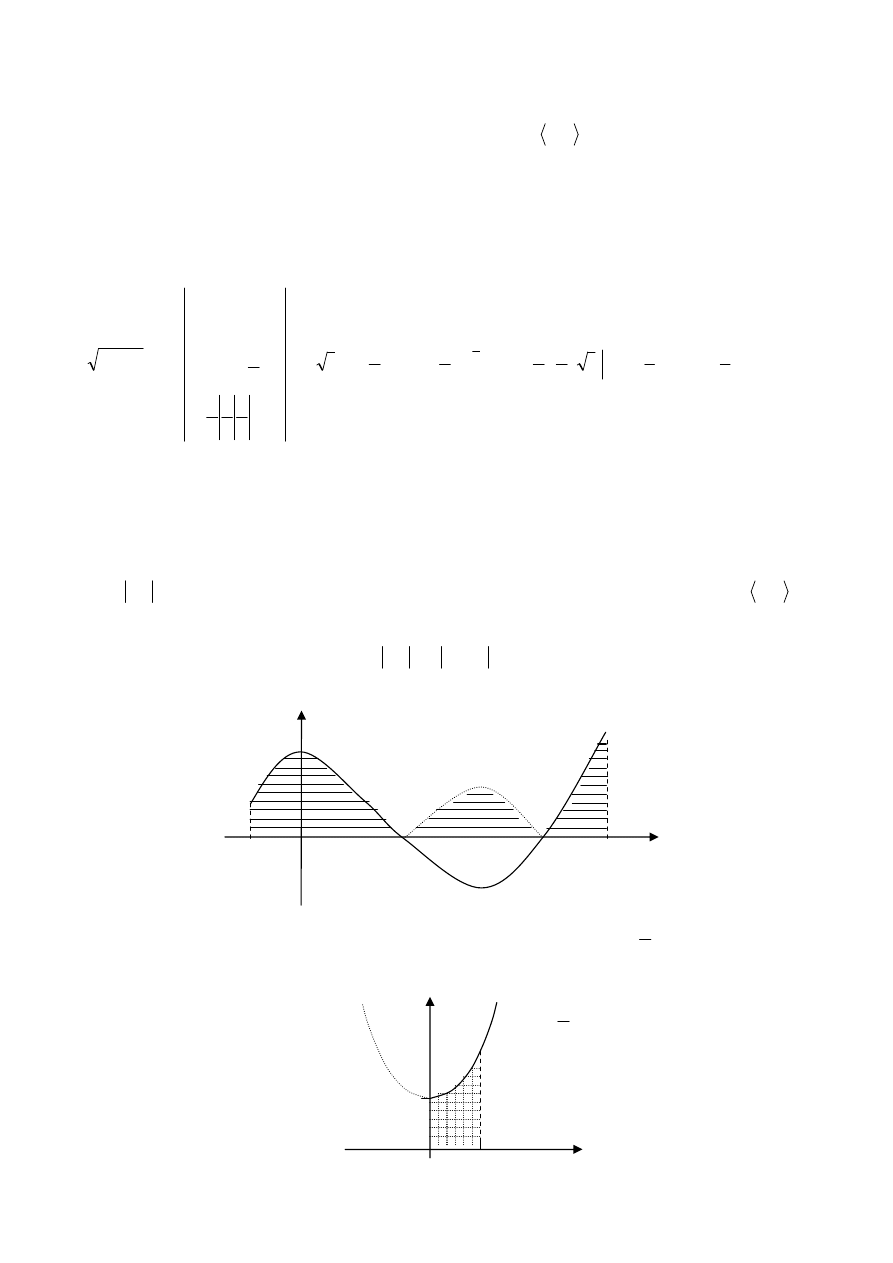
Przykład: Obliczyć pole obszaru ograniczonego linią łańcuchową
)
0
(
,
ch
>
=
a
a
x
a
y
, osią OX oraz
prostymi:
a
x
x
=
= ,
0
.
)
(x
f
y
=
x
y
a
b
x
a
x
a
y
ch
=
a
y
0
160
Rozwiązanie:
=
=
∫
dx
a
x
a
D
a
0
ch
{możemy opuścić moduł, gdyż
a
x
,
0
∈
∀
funkcja
a
x
a
x
f
ch
)
(
=
przyjmuje tylko
wartości dodatnie}
∫
∫
∫
=
=
→
=
=
=
=
=
1
0
0
0
ch
1
0
0
1
ch
ch
adt
t
a
a
t
x
adt
dx
dt
dx
a
t
a
x
dx
a
x
a
dx
a
x
a
a
a
=
(
)
e
e
a
e
e
a
a
a
t
a
dt
t
a
2
1
2
1
sh
0
sh
1
sh
sh
ch
2
2
1
2
2
2
1
0
2
1
0
2
−
=
−
=
=
−
=
=
=
−
∫
.
Ostatecznie:
0
,
2
1
2
2
>
−
=
a
e
e
a
D
.
2. Jeśli funkcja
)
(x
f
y
=
ciągła na przedziale
b
a
,
dana jest parametrycznie:
)
(
),
(
t
y
y
t
x
x
=
=
, gdzie
β
α
∈
,
t
, przy czym
b
x
a
x
=
β
=
α
)
(
,
)
(
, funkcje
)
(
),
(
t
y
t
x
oraz dodatnia pochodna
)
(t
x′
są ciągłe na
przedziale
β
α,
to pole figury płaskiej ograniczonej tą krzywą i osią odciętych wyraża się wzorem:
∫
β
α
′
⋅
=
dt
t
x
t
y
D
)
(
)
(
Jeśli
)
(t
x′
jest ujemna (tzn.
)
(t
x
jest funkcją malejącą) to
∫
β
α
′
⋅
−
=
dt
t
x
t
y
D
)
(
)
(
3. Jeśli krzywa dana jest we współrzędnych biegunowych:
2
1
,
),
(
ϕ
ϕ
∈
ϕ
ϕ
= r
r
, przy czym
)
(
ϕ
r
jest
ciągła w
2
1
,
ϕ
ϕ
i nieujemna oraz
π
≤
ϕ
−
ϕ
2
1
2
to pole wycinka AOB ograniczonego łukiem krzywej
AB
i dwoma promieniami wodzącymi OA i OB odpowiednio o równaniach
1
ϕ
=
ϕ
,
2
ϕ
=
ϕ
wyraża się
wzorem:
[
]
∫
=
2
1
2
)
(
2
1
ϕ
ϕ
ϕ
ϕ
d
r
D
ϕ
B
A
O
1
ϕ
2
ϕ
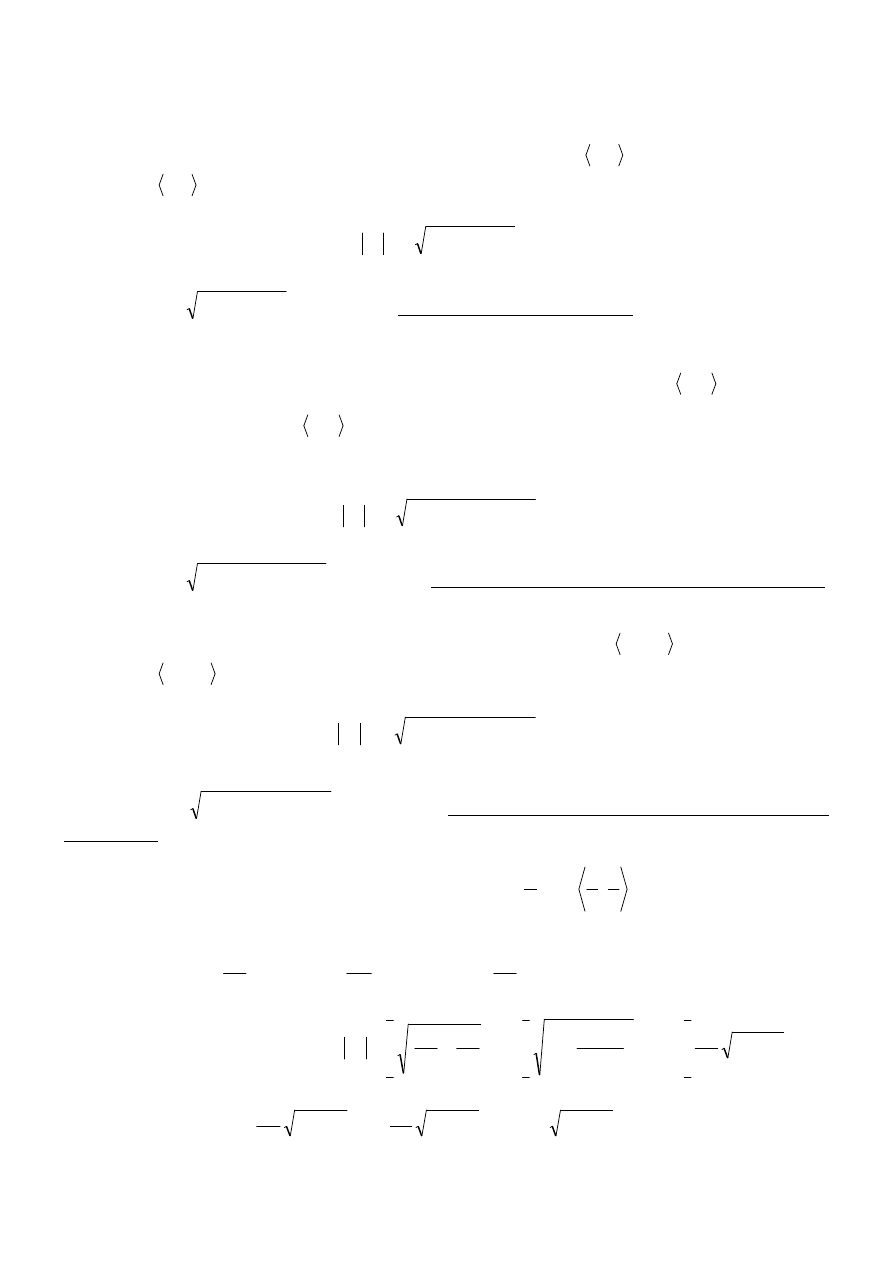
161
B) DŁUGOŚĆ ŁUKU KRZYWEJ
1. Długość łuku L krzywej danej równaniem
)
(x
f
y
=
, gdzie
b
a
x
,
∈
, funkcja
)
(x
f
ma ciągłą
pochodną w
b
a
,
określona jest wzorem:
[
]
dx
x
f
L
b
a
∫
′
+
=
2
)
(
1
Wyrażenie
[
]
dx
x
f
dL
2
)
(
1
′
+
=
nazywamy różniczką długości łuku krzywej
)
(x
f
y
=
.
2. Długość łuku krzywej danej równaniami parametrycznymi:
β
α
∈
=
=
,
)
(
)
(
t
t
y
y
t
x
x
, gdy funkcje
)
(
),
(
t
y
t
x
mają ciągłe pochodne
β
α,
, które nie znikają jednocześnie w żadnym punkcie tego przedziału
tzn.
[
]
[
]
0
)
(
)
(
2
2
>
′
+
′
t
y
t
x
, wyraża się wzorem:
[
]
[
]
dt
t
y
t
x
L
∫
β
α
′
+
′
=
2
2
)
(
)
(
Wyrażenie
[
]
[
]
dt
t
y
t
x
dL
2
2
)
(
)
(
′
+
′
=
nazywamy różniczką długości łuku krzywej danej parametrycznie.
3. Długość łuku krzywej określonej równaniem biegunowym:
2
1
,
),
(
ϕ
ϕ
∈
ϕ
ϕ
= r
r
, gdy
)
(
ϕ
r
ma ciągłą
pochodną w
2
1
,
ϕ
ϕ
wyraża się wzorem:
[
]
[
]
ϕ
ϕ
′
+
ϕ
=
∫
ϕ
ϕ
d
r
r
L
2
1
2
2
)
(
)
(
Wyrażenie
[
]
[
]
ϕ
ϕ
′
+
ϕ
=
d
r
r
dL
2
2
)
(
)
(
nazywamy różniczką długości łuku krzywej danej równaniem
biegunowym.
Przykład: Obliczyć długość łuku krzywej danej równaniem
3
4
,
4
3
,
6
∈
ϕ
ϕ
=
r
.
Rozwiązanie:
Obliczamy:
[
]
2
2
36
)
(
ϕ
=
ϕ
r
oraz
2
6
)
(
ϕ
−
=
ϕ
′
r
, stąd
[
]
4
2
36
)
(
ϕ
=
ϕ
′
r
.
Wstawiamy do wzoru i otrzymujemy:
ϕ
+
ϕ
ϕ
=
ϕ
ϕ
+
ϕ
=
ϕ
ϕ
+
ϕ
=
∫
∫
∫
d
d
d
L
3
4
4
3
2
2
3
4
4
3
4
2
3
4
4
3
4
2
1
1
6
1
36
36
36
=
{wykorzystujemy wzór:
(
)
C
d
+
+
+
+
+
−
=
+
∫
1
ln
1
1
1
1
2
2
2
2
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
} =
162
(
)
2
3
ln
2
5
2
ln
3
5
3
ln
4
5
6
4
5
4
3
ln
4
5
3
4
3
5
3
4
ln
3
5
4
3
6
1
4
3
4
3
ln
1
4
3
3
4
1
3
4
3
4
ln
1
3
4
4
3
6
1
ln
1
1
6
2
2
2
2
3
4
4
3
2
2
+
=
−
+
+
−
=
+
−
⋅
+
+
+
⋅
−
=
=
+
+
−
+
+
+
+
+
+
−
=
=
+
+
+
+
−
=
ϕ
ϕ
ϕ
ϕ
Ostatecznie otrzymujemy:
2
3
ln
2
5
+
=
L
.
C) OBJĘTOŚĆ BRYŁ OBROTOWYCH
1. Jeśli funkcja
)
(x
f
y
=
ciągła i nieujemna na przedziale
b
a
,
to objętość bryły powstałej przez obrót
dookoła osi OX obszaru ograniczonego tą krzywą, prostymi
b
x
a
x
=
= ,
oraz osią OX określona jest
wzorem:
∫
π
=
b
a
dx
x
f
V
)
(
2
2. Jeśli funkcja dana jest parametrycznie:
β
α
∈
=
=
,
),
(
),
(
t
t
y
y
t
x
x
, to objętość bryły obrotowej
wyraża się wzorem:
[
]
0
)
(
,
)
(
)
(
2
≥
′
′
⋅
π
=
∫
β
α
t
x
dt
t
x
t
y
V
[
]
0
)
(
,
)
(
)
(
2
≤
′
′
⋅
π
−
=
∫
β
α
t
x
dt
t
x
t
y
V
Przykład: Obliczyć objętość bryły powstałej w wyniku obrotu wokół osi OX cykloidy danej równaniem:
(
)
(
)
π
2
,
0
,
cos
1
2
,
sin
2
∈
−
=
−
=
t
t
y
t
t
x
.
)
(x
f
y
=
x
y
a
b
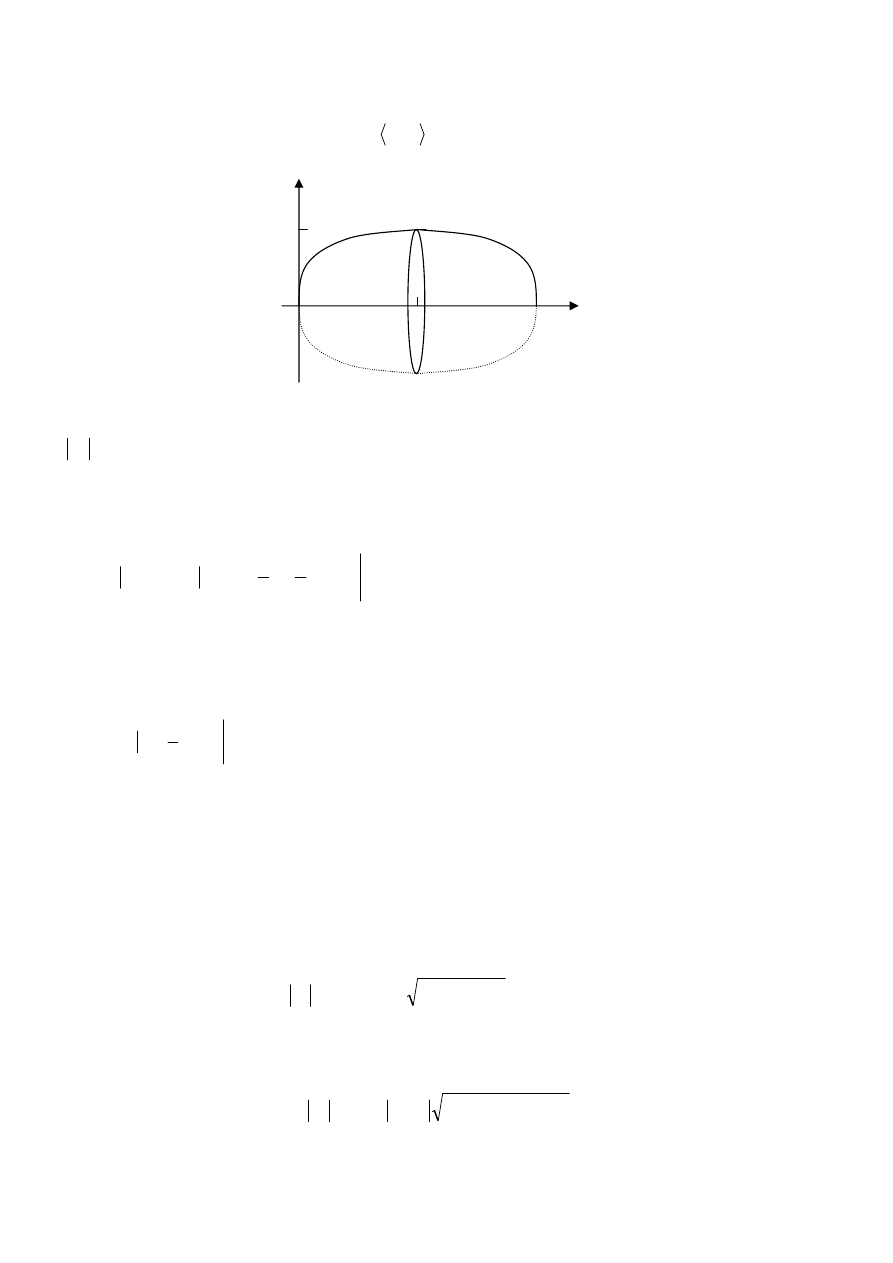
163
Rozwiązanie:
Obliczamy
)
cos
1
(
2
)
(
t
t
x
−
=
′
. Zatem
0
)
(
2
,
0
≥
′
π
∈
∀
t
x
t
.
(
)
[
]
=
−
+
−
=
=
−
+
−
=
−
=
=
−
⋅
−
=
∫
∫
∫
∫
∫
∫
∫
π
π
π
π
π
π
π
π
π
π
π
2
0
2
0
2
0
3
2
2
0
2
0
3
2
2
0
3
2
0
2
cos
cos
3
cos
3
8
)
cos
cos
3
cos
3
1
(
8
)
cos
1
(
8
)
cos
1
(
2
cos
1
2
dt
t
dt
t
dt
t
dt
dt
t
t
t
dt
t
dt
t
t
V
=
⋅
−
+
+
−
=
∫
π
π
π
π
π
2
0
2
2
0
2
0
2
0
cos
cos
2
sin
4
1
2
1
3
sin
3
8
dt
t
t
t
t
t
t
(**)
Obliczamy całkę:
(
)
(
)
0
sin
3
1
sin
2
cos
sin
cos
2
cos
sin
1
2
cos
sin
1
cos
cos
0
3
0
0
2
0
0
2
2
0
2
2
0
2
=
−
=
=
−
=
−
=
−
=
⋅
∫
∫
∫
∫
∫
π
π
π
π
π
π
π
t
t
dt
t
t
dt
t
dt
t
t
dt
t
t
dt
t
t
Zatem wracając do całki wyjściowej mamy: (**)
(
)
2
40
0
3
0
2
8
π
=
−
π
+
−
π
π
=
Ostatecznie objętość bryły powstałej w wyniku obrotu wokół osi OX cykloidy wynosi
2
40
π
.
D) POLE POWIERZCHNI OBROTOWEJ
1. Pole powierzchni obrotowej (będącej powierzchnią boczną bryły powstałej przez obrót wokół osi OX
obszaru ograniczonego krzywą
)
(x
f
y
=
, prostymi
b
x
a
x
=
= ,
oraz osią OX określona jest wzorem:
[
]
0
)
(
,
)
(
1
)
(
2
2
≥
′
+
=
∫
x
f
dx
x
f
x
f
S
b
a
π
2. Pole powierzchni obrotowej, jeśli krzywa dana jest parametrycznie wyraża się wzorem:
[
]
[
]
dt
t
y
t
x
t
y
S
∫
′
+
′
=
β
α
π
2
2
)
(
)
(
)
(
2
x
4
π
2
π
4
y
164
CAŁKI NIEWŁAŚCIWE
Def.11.2. (całka niewłaściwa I – go rodzaju – w obszarze nieograniczonym)
Jeżeli funkcja
)
(x
f
jest ciągła w
∞
+
,
a
oraz istnieje skończona granica:
∫
β
+∞
→
β
a
dx
x
f
)
(
lim
to granicę tę
nazywamy całką niewłaściwą na
∞
+
,
a
i oznaczamy
∫
∫
β
+∞
→
β
+∞
=
a
a
dx
x
f
dx
x
f
)
(
lim
)
(
Jeśli
∫
β
+∞
→
β
a
dx
x
f
)
(
lim
jest niewłaściwa lub nie istnieje to mówimy że
∫
+∞
a
dx
x
f
)
(
jest rozbieżna.
Analogicznie definiujemy:
•
całkę niewłaściwą I – go rodzaju na
b
,
∞
−
:
∫
∫
α
−∞
→
α
∞
−
=
b
b
dx
x
f
dx
x
f
)
(
lim
)
(
•
całkę niewłaściwą I – go rodzaju na
∞
+
∞
− ,
:
∫
∫
∫
+∞
∞
−
+∞
∞
−
+
=
c
c
dx
x
f
dx
x
f
dx
x
f
)
(
)
(
)
(
(
)
∞
+
∞
−
∈
,
c
Przykład:
=
+
+
+
=
+
+
+
=
+
∫
∫
∫
∫
∫
β
+∞
→
β
α
−∞
→
α
+∞
∞
−
+∞
∞
−
0
2
0
2
0
2
0
2
2
1
1
lim
1
1
lim
1
1
1
1
1
1
dx
x
dx
x
dx
x
dx
x
dx
x
(
)
(
)
π
=
π
+
π
−
−
=
−
β
+
α
−
=
+
=
+∞
→
β
−∞
→
α
β
+∞
→
β
α
−∞
→
α
2
2
0
arctg
lim
arctg
0
lim
arctg
lim
arctg
lim
0
0
x
x
Wniosek:
∫
+∞
∞
−
+
dx
x
2
1
1
jest zbieżna.
Def.11.3. (całka niewłaściwa II – go rodzaju – z funkcji nieograniczonej)
Jeżeli funkcja
)
(x
f
jest ciągła w
)
b
a
,
,
±∞
=
−
→
)
(
lim
x
f
b
x
oraz istnieje skończona granica:
∫
ε
−
→
ε
+
b
a
dx
x
f
)
(
lim
0
to granicę tę nazywamy całką niewłaściwą II – go rodzaju i oznaczamy
∫
∫
ε
−
→
ε
+
=
b
a
b
a
dx
x
f
dx
x
f
)
(
lim
)
(
0
Punkt b jest punktem osobliwym funkcji.
y
a
b
x
)
(x
f
y
=
165
Analogicznie definiujemy całkę z funkcji ciągłej w przedziale
(
b
a
,
∫
∫
ε
+
→
ε
+
=
b
a
b
a
dx
x
f
dx
x
f
)
(
lim
)
(
0
Gdy punkt osobliwy
c
leży wewnątrz przedziału
b
a
,
to całkę niewłaściwą definiujemy następująco:
∫
∫
∫
+
=
b
c
c
a
b
a
dx
x
f
dx
x
f
dx
x
f
)
(
)
(
)
(
Przykład: Zbadać zbieżność całek: a)
∫
−
1
0
2
1
dx
x
x
b)
(
)
∫
−
2
0
2
1
x
dx
.
Rozwiązanie:
a)
∫
−
1
0
2
1
dx
x
x
Wyznaczamy dziedzinę funkcji podcałkowej:
0
1
2
>
− x
Zatem
0
)
1
)(
1
(
>
+
−
x
x
Dziedzina funkcji podcałkowej:
(
)
1
,
1
−
∈
x
Funkcja podcałkowa
2
1
)
(
x
x
x
f
−
=
jest ciągła w
)
1
,
0
oraz
+∞
=
=
−
+
→
−
0
1
1
lim
2
1
x
x
x
(
)
(
)
1
1
0
1
1
1
lim
1
2
2
1
lim
1
2
2
1
lim
1
lim
1
2
0
1
0
2
0
1
0
2
0
1
0
2
0
1
0
2
=
−
−
=
−
−
−
−
=
=
−
⋅
−
=
−
−
−
=
−
=
−
+
+
+
+
→
−
→
−
→
−
→
∫
∫
∫
ε
ε
ε
ε
ε
ε
ε
ε
x
dx
x
x
dx
x
x
dx
x
x
Wniosek: Całka
∫
−
1
0
2
1
dx
x
x
jest zbieżna.
b)
(
)
∫
−
2
0
2
1
x
dx
Dziedzina funkcji podcałkowej:
0
1
≠
−
x
czyli
1
≠
x
.
Zatem punkt
1
=
x
jest punktem osobliwym funkcji podcałkowej, punkt ten leży wewnątrz przedziału
2
,
0
oraz
(
)
∞
=
=
−
→
0
1
1
1
lim
2
1
x
x
.
(
)
(
)
(
)
(
)
(
)
+∞
=
∞
+
+∞
=
+
−
+
−
+
−
−
=
−
−
+
+
−
−
=
−
+
−
=
−
+
−
=
−
+
+
+
+
+
+
→
→
+
→
−
→
+
→
−
→
∫
∫
∫
∫
∫
2
0
1
0
2
1
0
1
0
0
2
1
2
0
1
0
2
0
2
1
2
1
0
2
2
0
2
1
1
1
lim
1
1
1
lim
1
1
lim
1
1
lim
1
lim
1
lim
1
1
1
2
1
2
2
1
1
2
2
1
1
ε
ε
ε
ε
ε
ε
ε
ε
ε
ε
ε
ε
x
x
x
dx
x
dx
x
dx
x
dx
x
dx
Wniosek:
(
)
∫
−
2
0
2
1
x
dx
jest rozbieżna.
x
1
−
1
+
Wyszukiwarka
Podobne podstrony:
Microsoft Word WE L11 Calka oznaczona i zastosowanie
Microsoft Word WE W9 Calka przez czesci, podst i wymierna
Microsoft Word WE W10 Calki tryg i niewym
Microsoft Word WE L10 Calki tryg, niewym
Microsoft Word WE L9 Calki przez czesci i podstawienie, wymierne
Microsoft Word WE L14 Szeregi Fouriera
Microsoft Word WE harmonogram egz
Microsoft Word WE L13 szeregi potęgowe
Microsoft Word WE wyniki E2 2009
Microsoft Word WE W14 Szeregi Fouriera
Microsoft Word WE W13 Szeregi funkcyjne i potegowe
Microsoft Word WE L12 szeregi liczbowe
Microsoft Word W21 Calka krzywoliniowa
Microsoft Word W19 Calka podwojna
Microsoft Word W20 Calka potrojna
Microsoft Word L20 calka potrojna
więcej podobnych podstron