
187
WYKŁAD Nr 14
SZEREGI FOURIERA
Def.14.1. (szereg trygonometryczny)
Szeregiem trygonometrycznym nazywamy szereg funkcyjny postaci:
∑
+∞
=
π
+
π
+
1
0
sin
cos
2
n
n
n
l
x
n
b
l
x
n
a
a
gdzie:
0
>
l
, zaś
n
n
b
a
a
,
,
0
- pewne stałe (n = 1,2, ... ).
Uwaga
1: Wyrazami szeregu trygonometrycznego są sinusy i cosinusy kątów, będących wielokrotno-
ś
ciami kąta
l
x
π
, a suma tych wyrazów
)
(x
S
, jeśli istnieje, jest funkcją okresową zmiennej x o okresie 2l:
)
2
(
)
(
l
x
S
x
S
+
=
.
Def.14.2. (szereg Fouriera)
Szeregiem Fouriera odpowiadającym danej funkcji
)
(x
f
, całkowalnej w przedziale
l
l
,
−
nazywamy
szereg trygonometryczny o postaci:
∑
+∞
=
π
+
π
+
1
0
sin
cos
2
n
n
n
l
x
n
b
l
x
n
a
a
,
w którym współczynniki
n
n
b
a
i
są obliczane według wzorów Fouriera:
∫
−
π
=
l
l
n
dx
l
x
n
x
f
l
a
cos
)
(
1
dla
...
,
2
,
1
,
0
=
n
∫
−
π
=
l
l
n
dx
l
x
n
x
f
l
b
sin
)
(
1
dla
...
,
2
,
1
=
n
Fakt ten zapisujemy w następujący sposób:
∑
+∞
=
π
+
π
+
1
0
sin
cos
2
~
)
(
n
n
n
l
x
n
b
l
x
n
a
a
x
f
Uwaga
2: Szereg Fouriera odpowiadający funkcji
)
(x
f
może być zbieżny lub rozbieżny. Ale nawet wte-
dy, gdy jest zbieżny, suma jego nie musi być równa funkcji
)
(x
f
, dla której został zbudowany. Znak „~”
można zastąpić znakiem „=” tylko wtedy, gdy wykażemy, że szereg Fouriera stojący po prawej stronie
jest zbieżny i jego suma jest równa funkcji
)
(x
f
. Istnieją warunki wystarczające, które pozwalają stwier-
dzić, do czego, zbieżny jest szereg Fouriera odpowiadający danej funkcji.
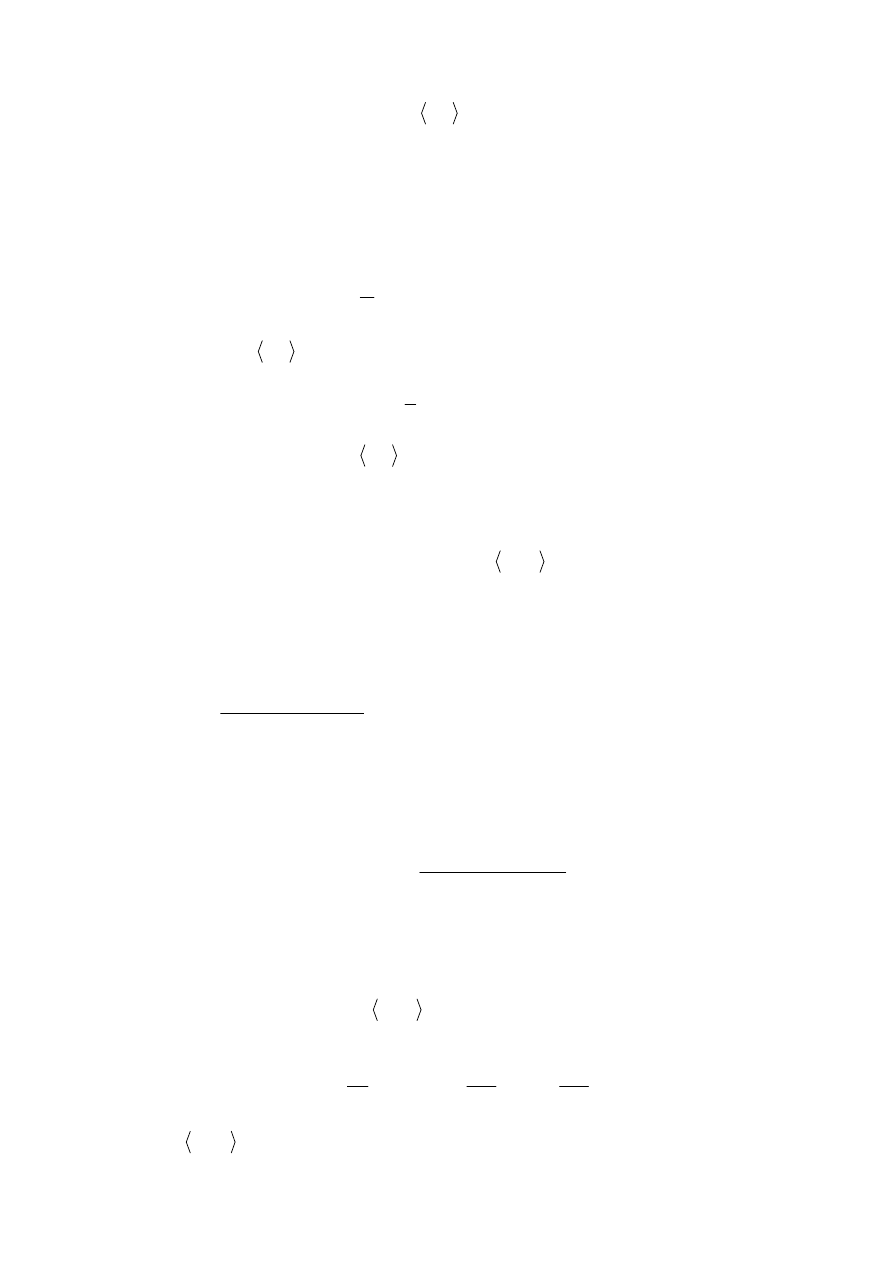
188
Def.14.3. (warunki Dirichleta)
Mówimy, że funkcja
)
(x
f
spełnia na przedziale
b
a
,
warunki Dirichleta, jeżeli:
1°
)
(x
f
przedziałami monotoniczna na przedziale
(
)
b
a
,
tj. przedział ten można podzielić na skończoną
liczbę podprzedziałów, wewnątrz których funkcja
)
(x
f
jest monotoniczna;
2°
)
(x
f
jest ciągła na przedziale
(
)
b
a
,
, z wyjątkiem, co najwyżej skończonej liczby punktów nieciągło-
ś
ci pierwszego rodzaju, przy czym w każdym punkcie nieciągłości
0
x
spełniony jest warunek:
+
=
+
→
−
→
)
(
lim
)
(
lim
2
1
)
(
0
0
0
x
f
x
f
x
f
x
x
x
x
3° na krańcach przedziału
b
a
,
spełnione są równości:
+
=
=
−
→
+
→
)
(
lim
)
(
lim
2
1
)
(
)
(
x
f
x
f
b
f
a
f
b
x
a
x
Funkcja
)
(x
f
spełniająca na przedziale
b
a
,
warunki Dirichleta, jest całkowalna w sensie Riemanna na
tym przedziale.
Tw.14.1. (kryterium zbieżności szeregu Fouriera)
Szereg Fouriera funkcji
)
(x
f
spełniającej na przedziale
l
l
,
−
warunki Dirichleta jest zbieżny przy
wszystkich wartościach x, przy czym jego suma s jest określona następująco:
w przedziale
(
)
l
l
,
−
:
1°
)
(
)
(
x
f
x
s
=
, gdy x jest punktem ciągłości;
2°
2
)
0
(
)
0
(
)
(
−
+
+
=
x
f
x
f
x
s
, gdy x jest punktem nieciągłości pierwszego rodzaju,
gdzie
)
0
(
),
0
(
−
+
x
f
x
f
– oznaczają odpowiednio granice prawo – i lewostronne funkcji
)
(x
f
w punkcie x;
na końcach przedziału
(
)
l
l
,
−
:
2
)
0
(
)
0
(
)
(
)
(
−
+
+
−
=
−
=
l
f
l
f
l
s
l
s
.
Jeśli funkcja
)
(x
f
jest wszędzie ciągła, to szereg jest bezwzględnie i jednostajnie zbieżny.
Tw.14.2. (tw. Dirichleta)
Jeżeli funkcja
)
(x
f
spełnia na przedziale
l
l
,
−
warunki Dirichleta to jest rozwijalna na tym przedziale
w szereg trygonometryczny Fouriera:
∑
+∞
=
π
+
π
+
=
1
0
sin
cos
2
)
(
n
n
n
l
x
n
b
l
x
n
a
a
x
f
dla każdego
l
l
x
,
−
∈
; jeżeli ponadto funkcja
)
(x
f
jest okresowa i ma okres 2l, to powyższa równość
zachodzi dla każdego x z dziedziny tej funkcji.
189
Uwaga
3: Jeżeli funkcja
)
(x
f
jest całkowalna na przedziale
l
l
,
−
, gdzie
0
>
l
, to:
ą
nieparzyst
funkcją
jest
)
(
gdy
0
)
(
x
f
dx
x
f
l
l
∫
−
=
parzystą
funkcją
jest
)
(
gdy
)
(
2
)
(
0
x
f
dx
x
f
dx
x
f
l
l
l
∫
∫
−
=
Uwaga
4: Iloczyn dwóch funkcji parzystych lub dwóch funkcji nieparzystych jest funkcją parzystą.
Uwaga
5: Iloczyn funkcji parzystej i funkcji nieparzystej jest funkcją nieparzystą.
SZEREG FOURIERA FUNKCJI NIEPARZYSTEJ
Jeśli funkcja
)
(x
f
jest nieparzysta (tzn.
)
(
)
(
x
f
x
f
−
−
=
)
to wszystkie współczynniki
0
=
n
a
,
natomiast
...
,
3
,
2
,
1
,
sin
)
(
2
0
=
π
=
∫
n
dx
l
x
n
x
f
l
b
l
n
(patrz Uwaga 3, 4, 5)
Szereg Fouriera funkcji nieparzystej zawiera wyłącznie sinusy i jest nazywany szeregiem sinusów.
SZEREG FOURIERA FUNKCJI PARZYSTEJ
Jeśli funkcja
)
(x
f
jest parzysta (tzn.
)
(
)
(
x
f
x
f
−
=
)
to wszystkie współczynniki
0
=
n
b
,
natomiast
∫
=
π
=
l
n
n
dx
l
x
n
x
f
l
a
0
...
,
2
,
1
,
0
,
cos
)
(
2
(patrz Uwaga 3, 4, 5)
Szereg Fouriera funkcji parzystej składa się ze stałej i cosinusów i jest nazywany szeregiem cosinusów.
Przykład: Rozwinąć na przedziale
π
π
−
,
w szereg Fouriera funkcję
x
x
f
=
)
(
.
Rozwiązanie:
W tym przypadku
π
=
l
.
Funkcja
x
x
f
=
)
(
jest funkcją parzystą (patrz Szereg Fouriera funkcji parzystej); jej wykres wraz
z okresowym przedłużeniem przedstawia Rys.1.
Rys.1.
Przedłużona funkcja jest ciągła, spełnia warunki Dirichleta.
y
-2π
2π
π
-π
x

190
Stąd na podstawie Tw.14.2. szereg Fouriera jest zbieżny do funkcji
x
x
f
=
)
(
wszędzie w przedziale
π
π
−
,
i do jej okresowego przedłużenia na zewnątrz tego przedziału.
Ponieważ przy
x
x
x
=
>
jest
0
, więc:
(
)
( )
[
]
1
1
2
1
cos
2
cos
2
sin
2
sin
1
sin
2
cos
2
2
2
0
2
0
0
0
0
−
−
=
=
−
=
=
−
=
−
=
=
∫
∫
∫
n
n
n
n
n
nx
n
nxdx
n
nxdx
n
nx
n
x
nxdx
x
a
π
π
π
π
π
π
π
π
π
π
π
π
Stąd
( )
[
]
1
1
2
2
−
−
=
n
n
n
a
π
dla
0
≠
n
, czyli współczynnik
0
a
(
0
=
n
) musimy obliczyć osobno:
π
π
π
π
π
π
π
π
π
π
π
=
⋅
=
=
=
⋅
=
∫
∫
∫
0
2
0
0
0
0
2
2
2
0
cos
2
0
cos
2
x
dx
x
dx
x
dx
x
x
a
Wynika stąd, że:
dla n parzystych mamy:
0
=
n
a
,
dla n nieparzystych mamy:
2
4
n
a
n
π
−
=
,
π
=
0
a
.
Współczynniki
...
,
2
,
1
,
0
=
=
n
b
n
, (ponieważ dana funkcja jest parzysta).
Ostatecznie:
π
≤
≤
π
−
+
+
+
π
−
π
=
x
x
x
x
x
...
5
5
cos
3
3
cos
cos
4
2
2
2
Uwaga
6: Funkcję
)
(x
f
, daną w przedziale
l
,
0
można w dowolny sposób przedłużyć na sąsiedni
przedział
)
0
,
l
−
, a tym samym można ją przedstawić za pomocą różnych szeregów Fouriera. Zwykle
funkcję taką przedstawiamy niepełnym szeregiem Fouriera, zawierającym sinusy lub cosinusy.
Szereg zawierający tylko cosinusy otrzymujemy przy parzystym przedłużaniu danej funkcji na sąsiadują-
cy z lewej strony przedział
)
0
,
l
−
.
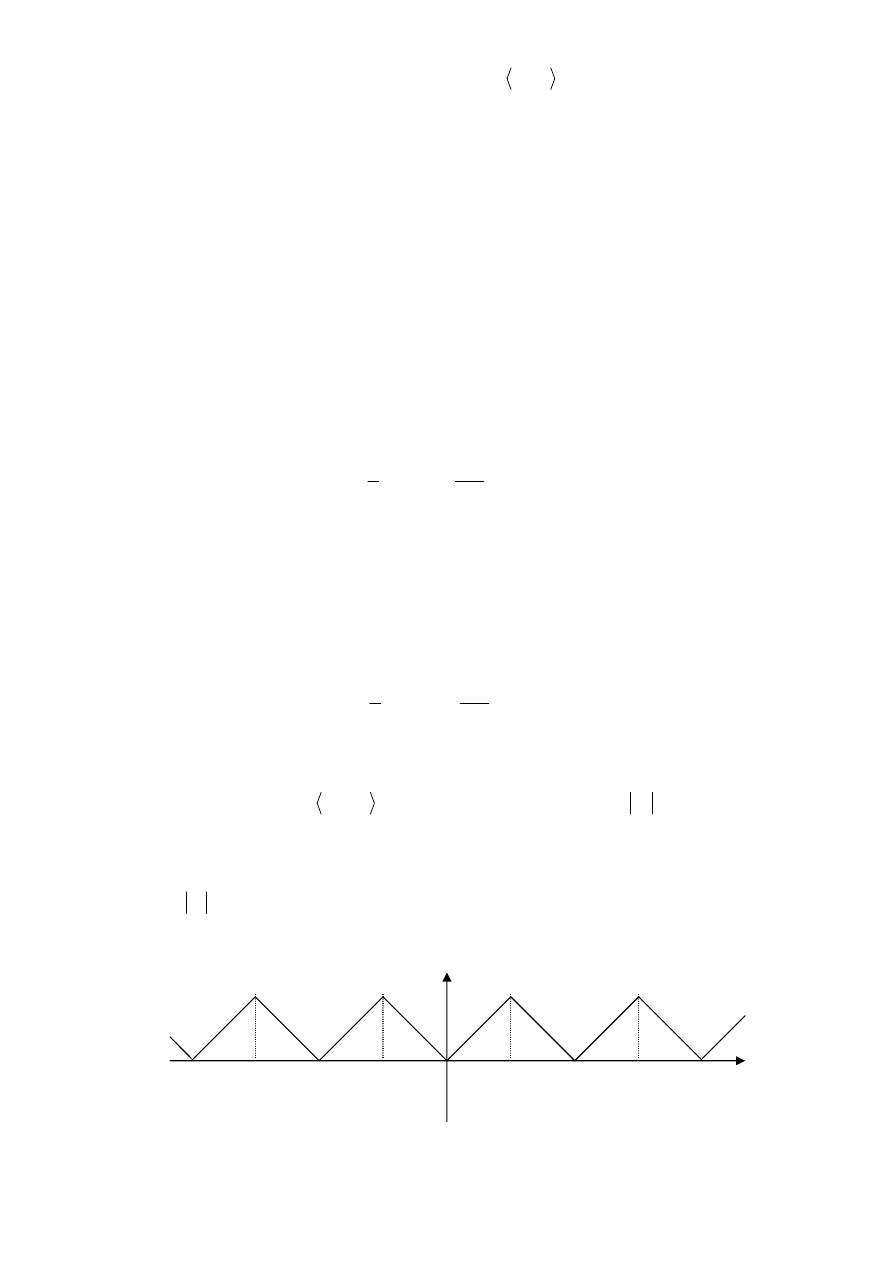
W tym przypadku wykres danej funkcji przedłużamy poprzez symetrię względem osi OY. (patrz Rys.2).
Rys.2. Przedłużenie parzyste
y
- l
l
x
191
Szereg zawierający tylko sinusy otrzymujemy przy nieparzystym przedłużaniu danej funkcji na sąsiadu-
jący z lewej strony przedział
)
0
,
l
−
.
W tym przypadku wykres danej funkcji przedłużamy poprzez symetrię względem początku układu
współrzędnych (patrz Rys.3)
Rys.3. Przedłużenie nieparzyste
Uwaga
7: Jeżeli funkcję
)
(x
f
w różnych częściach przedziału
l
l
,
−
określają różne wzory, to przy
rozwijaniu jej w szereg Fouriera w celu obliczenia współczynników, czyli odpowiednich całek, przedział
całkowania należy podzielić na części za pomocą punktów, w których wyrażenie analityczne funkcji ule-
ga zmianie, a następnie te całki obliczyć jako sumę całek po poszczególnych przedziałach.
Przy rozwijaniu w szereg Fouriera funkcji
)
(x
f
w przedziale
l
2
,
0
granicami całek będą 0 i 2l,
a w przypadku dowolnego przedziału
b
a
,
o długości 2l granicami będą liczby a i a+2l.
Przykład: Rozwinąć w szereg Fouriera względem sinusów funkcję:
≤
<
−
≤
≤
=
2
1
gdy
2
1
0
gdy
)
(
x
x
x
x
x
f
.
Rozwiązanie:
Wykres funkcji
)
(x
f
wraz z nieparzystym przedłużeniem na przedział
)
0
,
2
−
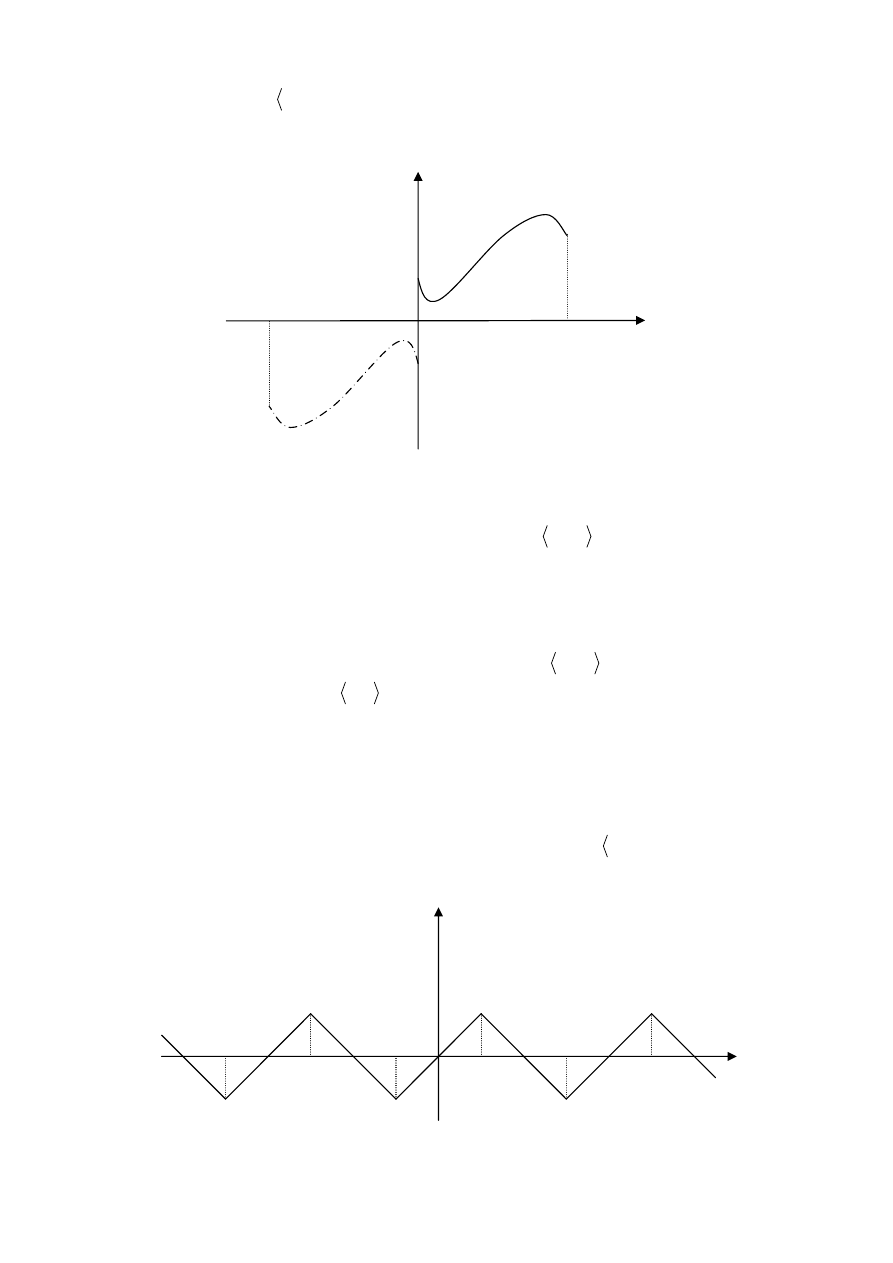
i dalszym okresowym
przedłużeniem na całą oś OX przedstawia Rys.4.
Rys.4.
y
x
l
- l
1
2
3
4
5
-1
-2
-3
-4
-5
y
x

192
Kryterium zbieżności można zastosować dla wszystkich x.
Korzystając ze wzorów na współczynniki dla szeregów Fouriera funkcji nieparzystej mamy:
0
=
n
a
,
...
,
2
,
1
,
0
=
n
(
)
...
,
2
,
1
,
2
sin
2
2
sin
2
sin
)
(
2
2
2
1
2
0
1
0
=
π
−
+
π
=
π
=
∫
∫
∫
n
dx
x
n
x
dx
x
n
x
dx
x
n
x
f
b
n
Podstawiając
t
x
=
π
2
i zmieniając granice całkowania otrzymamy:
(
)
+
π
+
−
π
=
−
π
π
+
π
=
∫
∫
∫
π
π
π
π
π
2
0
2
2
0
2
2
2
2
0
2
cos
4
cos
4
sin
4
sin
4
dt
nt
n
n
nt
t
dt
nt
t
dt
nt
t
b
n
(
)
2
sin
8
cos
4
cos
4
2
2
2
2
2
2
π
π
=
π
−
−
π
−
π
+
∫
π
π
π
π
n
n
dt
nt
n
n
nt
t
Stąd
−
π
+
π
−
π
π
=
...
2
5
sin
5
1
2
3
sin
3
1
2
sin
8
)
(
2
2
2
x
x
x
x
f
Szereg ten jest zbieżny do funkcji przedstawionej na rysunku dla wszystkich
R
∈
x
.
POSTAĆ ZESPOLONA SZEREGU TRYGONOMETRYCZNEGO FOURIERA
Na podstawie wzoru Eulera:
α
+
α
=
α
sin
cos
j
e
j
mamy:
l
x
n
j
l
x
n
e
l
x
n
j
π
+
π
=
π
sin
cos
oraz
l
x
n
j
l
x
n
e
l
x
n
j
π
−
π
=
π
−
sin
cos
Dodając i odejmując od siebie powyższe równości otrzymamy:
−
=
π
+
=
π
π
−
π
π
−
π
l
x
n
j
l
x
n
j
l
x
n
j
l
x
n
j
e
e
j
l
x
n
e
e
l
x
n
2
1
sin
oraz
2
1
cos
Zatem po wstawieniu powyższych wzorów do wyrażenia występującego w szeregu Fouriera
i pogrupowaniu mamy:
l
x
n
j
n
n
l
x
n
j
n
n
n
n
e
jb
a
e
jb
a
l
x
n
b
l
x
n
a
π
−
π
+
+
−
=
π
+
π
2
2
sin
cos

193
Po wprowadzeniu następujących oznaczeń:
2
,
2
,
2
0
0
n
n
n
n
n
n
jb
a
c
jb
a
c
a
c
+
=
−
=
=
−
,
...
,
2
,
1
=
n
szereg trygonometryczny Fouriera:
∑
+∞
=
π
+
π
+
1
0
sin
cos
2
n
n
n
l
x
n
b
l
x
n
a
a
możemy zapisać w postaci:
∑
∞
+
=
π
−
−
π
+
+
1
0
n
l
x
n
j
n
l
x
n
j
n
e
c
e
c
c
lub krótko
∑
+∞
∞
−
l
x
n
j
n
e
c
π
.
Tw.14.3. (o rozwijaniu funkcji rzeczywistej zmiennej rzeczywistej w zespolony szereg Fouriera)
Jeśli funkcja rzeczywista
)
(x
f
spełnia w przedziale
l
l
,
−
warunki Dirichleta, to jest rozwijalna na tym
przedziale w szereg zespolony Fouriera:
∑
+∞
−∞
=
=
n
l
x
n
j
n
e
c
x
f
π
)
(
przy czym:
...
,
2
,
1
,
0
,
)
(
2
1
±
±
=
=
∫
−
−
n
dx
e
x
f
l
c
l
l
l
x
n
j
n
π
Jeśli 2l jest okresem funkcji
)
(x
f
to ostatni wzór można przekształcić do postaci następującej:
...
,
2
,
1
,
0
,
)
(
2
1
2
0
±
±
=
=
∫
−
n
dx
e
x
f
l
c
l
l
x
n
j
n
π
Przykład: Rozwinąć funkcję
x
e
x
f
−
=
)
(
w zespolony szereg Fouriera w przedziale
(
)
π
π
−
,
.
Rozwiązanie:
W tym przypadku
π
=
l
.
Funkcja
)
(x
f
spełnia w przedziale
(
)
π
π
−
,
warunki Dirichleta.

194
Zatem
(
)
(
)
(
)
(
)
(
)
(
)
(
)
jn
e
e
e
e
jn
e
e
jn
e
dx
e
dx
e
e
c
jn
jn
jn
jn
x
jn
x
jn
jnx
x
n
+
π
−
=
+
π
−
=
+
π
=
π
=
π
=
π
−
π
−
π
π
π
+
−
π
+
π
−
π
+
−
π
π
−
+
−
π
π
−
−
−
∫
∫
1
2
1
2
1
2
2
1
2
1
1
1
1
1
Zgodnie ze wzorami Eulera:
π
±
π
=
π
±
n
j
n
e
jn
sin
cos
czyli
( )
n
jn
e
1
−
=
π
±
.
Wobec tego:
( )
(
)
(
)
jn
e
e
c
n
n
+
π
−
−
=
π
−
π
1
2
1
( )
∑
+∞
−∞
=
π
−
π
−
+
−
π
−
=
n
jnx
n
x
jn
e
e
e
e
1
1
2
.
W przedziale
(
)
π
π
−
,
szereg ten przedstawia funkcję
x
e
−
, natomiast w punktach
π
±
=
x
(krańce prze-
działu) szereg jest zbieżny do sumy równej
(
)
π
−
π
+ e
e
2
1
.
Wyszukiwarka
Podobne podstrony:
Microsoft Word WE L14 Szeregi Fouriera
Microsoft Word WE L13 szeregi potęgowe
Microsoft Word WE W13 Szeregi funkcyjne i potegowe
Microsoft Word WE L12 szeregi liczbowe
Microsoft Word W14 Szeregi Fouriera
Microsoft Word W14 Szeregi Fouriera
Microsoft Word WE W10 Calki tryg i niewym
Microsoft Word WE L10 Calki tryg, niewym
Microsoft Word WE L9 Calki przez czesci i podstawienie, wymierne
Microsoft Word WE harmonogram egz
Microsoft Word WE W9 Calka przez czesci, podst i wymierna
Microsoft Word WE wyniki E2 2009
Microsoft Word WE W11 Calka oznaczona
Microsoft Word WE L11 Calka oznaczona i zastosowanie
Microsoft Word W12 szeregi liczbowe
Szeregi Fouriera
New Microsoft Word Document (2)
Nowy Dokument programu Microsoft Wo
więcej podobnych podstron