Bez stresu przed lekcją
Kółko matematyczne
Projekty
Egzaminy
Sprawdź, czy zdasz
Ściąga
Szukaj
Twoja wyszukiwarka
W tej chwili stronę przegląda
26 użytkowników online.
Logowanie dla redaktorów
Nazwa użytkownika:
*
Hasło:
*
Zaloguj
STATYSTYKA MIESIĄCA
SIERPIEŃ
Nowych artykułów - 31
Liczba wizyt - 181 667
Wyświetlone strony - 712 154
LIPIEC
Nowych artykułów - 39
Liczba wizyt - 202 155
Wyświetlone strony - 755 648
CZERWIEC
Nowych artykułów - 26
Liczba wizyt - 201 327
Wyświetlone strony - 798 930
MAJ
Nowych artykułów - 18
Liczba wizyt - 233 468
Wyświetlone strony - 975 603
KWIECIEŃ
Nowych artykułów - 43
Liczba wizyt - 164 307
Wyświetlone strony
- 1 316 057
MARZEC
Nowych artykułów - 23
Liczba wizyt - 235 227
Wyświetlone strony
- 1 042 789
LUTY
Nowych artykułów - 53
Liczba wizyt - 203 442
Wyświetlone strony
- 1 217 610
STYCZEŃ
Nowych artykułów - 67
Liczba wizyt - 233 385
Wyświetlone strony - 982 829
›
›
Wartość bezwzględna
Data ostatniej modyfikacji:
2018-09-14
Oznaczenie
Wartość bezwzględną liczby a oznaczamy symbolem |a|.
W kalkulatorach i komputerach stosuje się oznaczenie abs (a), co jest skrótem od angielskiej
nazwy absolute value, oznaczającym właśnie wartość bezwzględną.
O tym, dlaczego w kalkulatorach i komputerach nie można stosować zapisu z kreskami,
przeczytasz w tekście
Kłopoty z wartością bezwzględną
Co to jest?
O wartości bezwzględnej można myśleć jako o pewnymdziałaniu na liczbach. Jest ono
jednak nietypowe, bo wykonywane na jednej liczbie, a nie na dwóch jak np. dodawanie. Działanie
to polega na "zapominaniu" znaku liczby.
przykłady
|5| = 5 |-5| = 5
|2,5| = 2,5 |-2,5|=2,5
Ogólnie mówiąc:
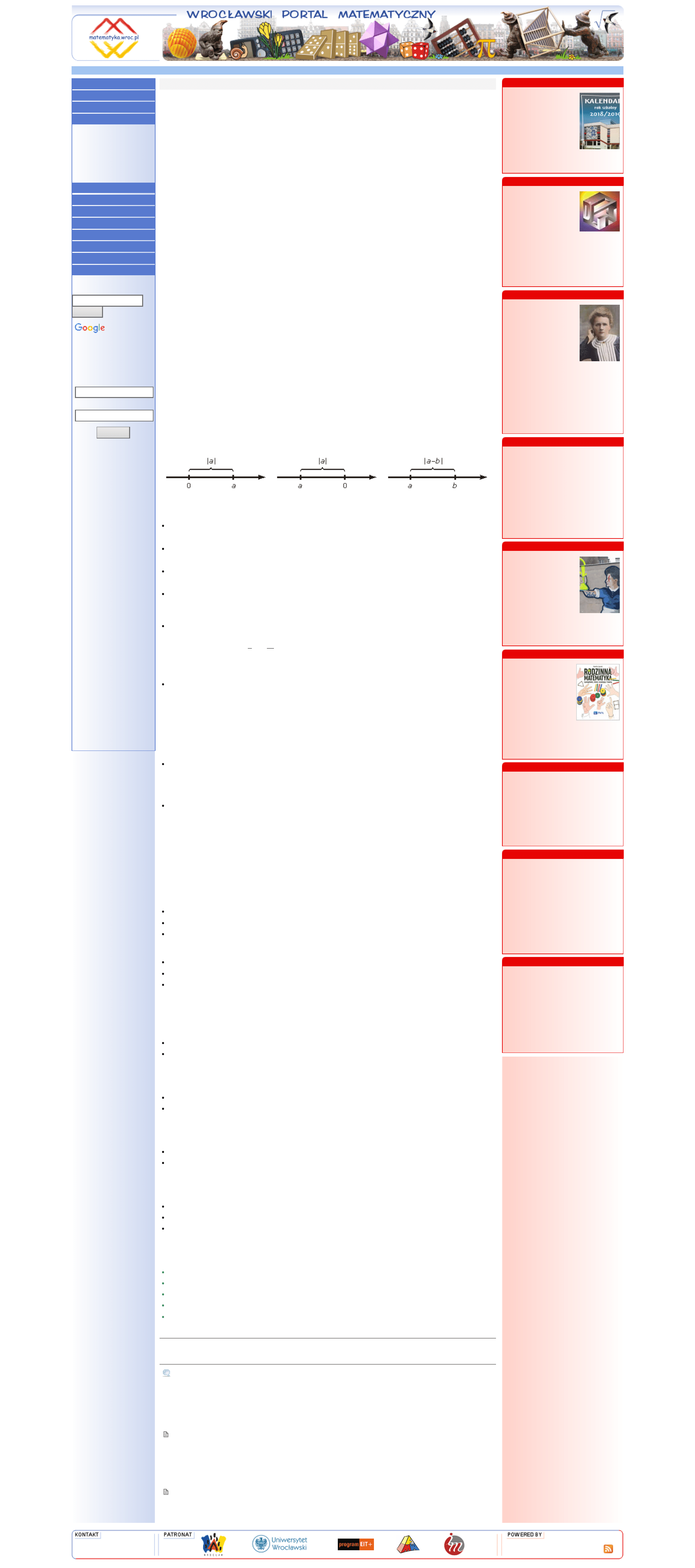
Interpretacja geometryczna
Wartość bezwzględna liczby to jej odległość od zera na osi liczbowej.
Wartość bezwzględna różnicy dwóch liczb, to ich odległość na osi liczbowej.
Własności
wartość bezwzględna każdej liczby jest nieujemna (czyli dodania lub równa zero), tzn.
|a|≥ 0
wartość bezwzględna jest zerem tylko dla zera, tzn.
|a|=0 ≡ a=0
wartości bezwzględne liczb przeciwnych są równe, np. |7|=|-7|=7, a ogólnie
|a|=|-a| oraz |a - b| = |b - a|
każda liczba jest nie większa od swojej wartości bezwzględnej i nie mniejsza od liczby przeciwnej
do swojej wartości bezwzględnej, tzn.
-|a| ≤ a ≤ |a|
wartość bezwzględna iloczynu / ilorazu dwóch liczb jest równa iloczynowi / ilorazowi ich wartości
bezwzględnych, tzn.
|a · b|=|a| · |b| oraz
(dla b≠0)
czyli wartość bezwzględną możemy rozdzielić na oba czynniki w mnożeniu oraz na licznik i
mianownik w ułamku
wartość bezwzględna sumy / różnicy dwóch liczb nie jest równa sumie / różnicy ich wartości
bezwzględnych, tzn.
|a + b| ≠ |a| + |b| oraz |a - b| ≠ |a| - |b|
czyli wartości bezwzględnej nie możemy rozdzielić na składniki w dodawaniu ani na odjemną i
odjemnik w odejmowaniu
przykłady
3
=
|5 + (-2)|
≠
|5| + |-2|
=
7
7
=
|5 - (-2)|
≠
|5| - |-2|
=
3
równość |a + b| = |a| + |b| zachodzi tylko wtedy, gdy liczby a i b są tego samego znaku
przykłady
|5 + 3| = |5| + |3|
|(-5) + (-3)| = |(-5)| + |(-3)|
zawsze zachodzą nierówności |a + b| ≥ |a| + |b| oraz |a - b| ≤ |a| + |b|.
przykłady
8 = |8| = |5 + 3| ≥ |5| + |3| = 5 + 3 = 8, czyli 8 ≥ 8
8 = |-8| = |(-5) + (-3)| ≥ |(-5)| + |(-3)| = 5 + 3 = 8, czyli -8 ≥ 8
8 = |8| = |11 - 3| ≤ |11| + |3| = 11 + 3 = 14, czyli 8 ≤ 14
8 = |-8| = |(-5) - 3| ≤ |(-5)| + |3| = 5 + 3 = 8, czyli 8 ≤ 8
Proste równania z wartością bezwzględną
1. |x| = a
dla a>0 rozwiązaniem równania jest a lub -a
dla a=0 rozwiązaniem równania jest liczba 0
dla a<0 rozwiązaniem równania jest zbiór pusty
przykłady
|x| = 17 rozwiązaniem jest x = 17 lub x = -17
|x| = -17 rozwiązaniem jest zbiór pusty
|x| = 0 rozwiązaniem jest liczba 0
Proste nierówności z wartością bezwzględną
1. |x| > a
dla a ≥ 0 rozwiązaniem jest zbiór (-∞, -a) (a, ∞)
dla a < 0 rozwiązaniem jest zbiór R
2. |x| ≥ a
dla a > 0 rozwiązaniem jest zbiór (-∞, -a] [a, ∞)
dla a ≤ 0 rozwiązaniem jest zbiór R
3. |x| < a
dla a > 0 rozwiązaniem jest przedział (-a, a)
dla a ≤ 0 rozwiązaniem jest zbiór pusty
4. |x| ≤ a
dla a > 0 rozwiązaniem jest przedział [-a, a]
dla a = 0 rozwiązaniem jest liczba 0
dla a < 0 rozwiązaniem jest zbiór pusty
przykłady
|x| ≤ 17 rozwiązaniem jest przedział [-17, 17]
|x| ≥ 17 rozwiązaniem jest zbiór (-∞, -17] [17, ∞)
|x| ≤ -17 rozwiązaniem jest zbiór pusty
|x| ≥ - 17 rozwiązaniem jest zbiór R
|x| ≤ 0 rozwiązaniem jest liczba 0
Anonimowy (niezweryfikowany), poniedziałek, 03/02/2014 - 17:01
Mamy: 8 = |-8| = |(-5) + (-3)| ≥ |(-5)| + |(-3)| = 5 + 3 = 8, czyli -8 ≥ 8. Od kiedy -8 jest
większe lub równe 8?
Qba (niezweryfikowany), wtorek, 04/02/2014 - 15:39
Nie ściemniaj! Pokazałeś przecież, że 8≥8, a to jest prawdą od zawsze.
Arcydzieło miesiąca
Nakładem IM UWr
ukazał się kalendarz na
bieżący rok szkolny.
Prezentuje on sylwetki
najbardziej do dziś
rozpoznawalnych na
świecie uczonych
związanych z Uniwersytetem
Wrocławskim w latach 1945-2018.
Impreza miesiąca
W dniach 20-26 IX we
Wrocławiu po raz 21.
odbywa się Festiwal
Nauki. Jego hasło
przewodnie to "1918-
2018". Ponad 20 ośrodków
badawczych i edukacyjnych
przygotowało ponad 1500 imprez
popularyzujących naukę.
Bohater miesiąca
W tegorocznym
rankingu BBC History
Magazine Maria
Skłodowska-Curie
uznana została za
najbardziej wpływową
kobietą wszech
czasów! Była niespełnioną miłością
krakowskiego matematyka Kazimierza
Żorawskiego (rektora UJ w latach
1917-1918). Pisała list polecający
Einsteinowi, gdy ten ubiegał się o
posadę uniwersytecką.
Odkrycie miesiąca
Maria Skłodowska-Curie znana jest
głównie jako fizyk i chemik, jednak z
podstawowego wykształcenia była też
matematykiem. Już po roku studiów
na paryskiej Sorbonie zdobyła
licencjat z fizyki z pierwszą lokatą, a
rok później - licencjat z matematyki z
drugą lokatą.
Cytat miesiąca
"Urodziłam się w
Warszawie" - od tych
słów zaczynała swoje
publiczne wystąpienia
jedyna w historii kobieta
- podwójna noblistka.
Taki tytuł nosi
poświęcony jej warszawski mural
umieszczony na Bibliotece dla Dzieci i
Młodzieży przy ul. Lipowej 3.
Lektura miesiąca
Nie tylko najmłodszym
czytelnikom na kolejny
rok szkolny polecamy
zadania i problemy z
mądrej i ciekawej
książki Kamili Łyczek
"Rodzinna
matematyka" wznowionej właśnie
nakładem PWN.
Trudne słowo
Liczba doskonała to taka liczba
naturalna, która jest równa sumie
wszystkich swoich dzielników
właściwych (tzn. mniejszych od niej).
Najmniejszą liczbą doskonałą jest 6 =
1 + 2 + 3, następną 28 = 1+2+4+7+14,
a kolejne to 496 i 8128.
Pytanie miesiąca
Jak znaleźć liczbę doskonałą?
Euklides w III w. p.n.e. podał taki
sposób: obliczaj sumy kolejnych potęg
dwójki (1+2+4+8+...); jeżeli któraś z
nich będzie liczbą pierwszą, pomnóż
ją przez ostatni składnik; otrzymasz
liczbę doskonałą. W XVIII w Euler
pokazał, że w ten sposób można
otrzymać wszystkie parzyste liczby
doskonałe.
Problem miesiąca
Dotychczas znaleziono 50 liczb
doskonałych - wszystkie parzyste. Nie
ma jednak dowodu, że liczby
doskonałe nieparzyste nie istnieją.
Jeśli tak, to muszą być większe od
10^1500, bo mniejsze liczby zostały
sprawdzone. Nie wiadomo też, czy
liczb doskonałych jest skończenie, czy
nieskończenie wiele.
WYKRESownik
Edytor wzorów TeXa
|a| = {
a,
−a,
gdy
gdy
a ≥ 0
a < 0
=
∣∣
a
b
∣∣
|a|
|b|
∪
∪
∪
Wyszukiwarka
Podobne podstrony:
Matematyka jest ciekawa, MATEMATYKA NA WESOŁO, matematyka
wartość bezwzględna2, Matematyka, Liceum
Wardach I - Matematyka podstawowa 01, wartosc bezwzgledna
wartość bezwzględna 3, Matematyka, Liceum
Równania i nierówności z parametrem i z wartością bezwzględną.Wyznaczanie pierwiastków równania., Ma
ź Zadanie domowe wartosc bezwzg logarytmy, matematyka
ź wartosc bezwzgledna, matematyka
wartość bezwzględna3, Matematyka, Liceum
Inne spojrzenie na wartosc bezwzgledna, Matematyka
wartość bezwzględna, Matematyka, Liceum
Wartość bezwzględna, Matematyka- zadania
matematyka, Wartość bezwzględna2, Wartość bezwzględna
IS Matematyka C S 03 f liniowa wartosc bezwzgledna
wartość bezwzględna 2, Matematyka, Liceum
IS Matematyka C S 03 f liniowa wartosc bezwzgledna
Matematyka jest nudna , bzdura
więcej podobnych podstron