Analiza mechanizmu dźwigniowego – Tomasz Olchawski, gr. 13, AiR
1
ANALIZA MECHANIZMU DŹWIGNIOWEGO
1. Synteza strukturalna i geometryczna mechanizmu
1.1. Budowa łańcucha kinematycznego – schemat ideowy
Symboliczny zapis struktury i parametrów projektowanego
mechanizmu przedstawia tabela 1
1.Struktura mechanizmu
)
(
0
)
(
3
)
(
2
)
(
1
0
−
−
−
−
−
O
O
O
P
p
z
p
2.Parametry kinematyczne
członu napędzającego 1
(0.25m,0.25
m
/
s
,0)
3.Masy i momenty
bezwładności członów (m
i
,J
si
)
(0,0);(6kg,0.5kgm
2
);(0,0)
4.Obciążenie uogólnionymi
siłami zewnętrznymi (P
i
,M
i
)
(0,0);(2N,0);(0,0.1Nm)
5.Uogólniona siła równoważąca
do wyznaczenia
P
R1
Tabela 1
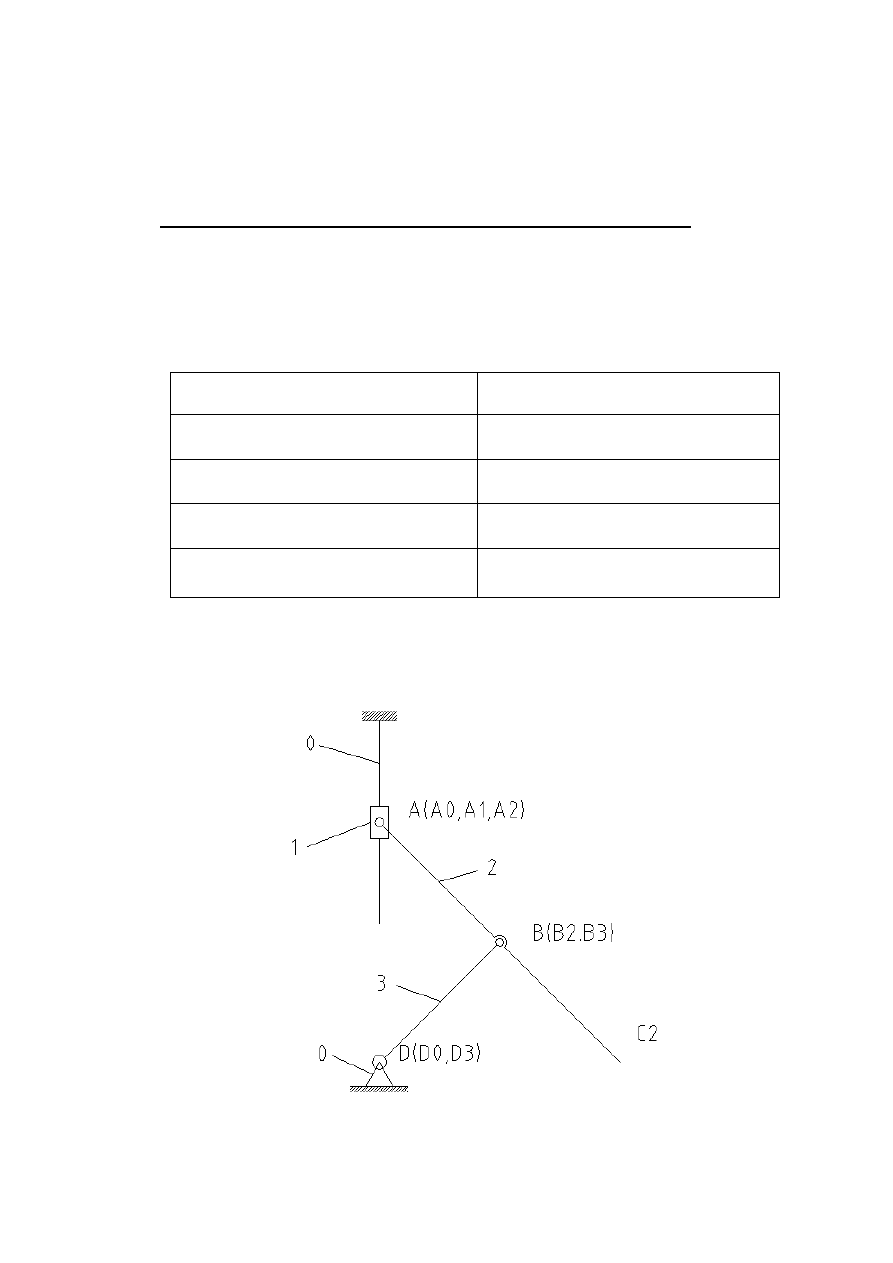
Schemat ideowy mechanizmu zbudowany na postawie
symbolicznego zapisu jego struktury:
Rysunek 1 – schemat ideowy łańcucha kinematycznego mechanizmu

Analiza mechanizmu dźwigniowego – Tomasz Olchawski, gr. 13, AiR
2
1.2. Ruchliwość i klasa mechanizmu
Ruchliwość mechanizmu:
4
5
2
3
p
p
n
w
−
⋅
−
⋅
=
3
=
n
,
- liczba członów ruchomych
0
4
=
p
,
- liczba par kinematycznych klasy 4
( )( )( )( )
[
]
0
,
3
3
,
2
2
,
1
1
,
0
4
5
=
p
– liczba par kinematycznych klasy 5
1
0
4
2
3
3
=
−
⋅
−
⋅
=
w
Ruchliwość mechanizmu wynosi 1.
Klasa mechanizmu:
Po odłączeniu członu napędzającego 1 pozostałe człony tworzą
grupę strukturalną. Po połączeniu członów ruchomych grupy
strukturalnej z podstawą jej ruchliwość wynosi 0.
0
3
2
2
3
=
⋅
−
⋅
=
gr
w
Jest to grupa strukturalna klasy 2.
Mechanizm składa się z członu napędzającego oraz grupy
strukturalnej klasy 2 więc jest to mechanizm klasy 2.
Nazwa strukturalna mechanizmu:
Mechanizm suwakowo-korbowy.
1.3. Ograniczenia geometryczne i wymiary mechanizmu
Przyjęte wymiary mechanizmu:
m
L
5
.
0
0
=
- długość prowadnicy 0
m
L
1
2
=
- długość członu 2
m
L
5
.
0
3
=
- długość członu 3
m
L
9
.
0
00
=
- odległość podstawy prowadnicy od
nieruchomego przegubu
Analiza mechanizmu dźwigniowego – Tomasz Olchawski, gr. 13, AiR
3
Na rysunku 1 człon 1 znajduje się w odległości 0.25 od początku
prowadnicy. Podczas ruchu tego mechanizmu (od najwyższego
położenia suwaka w dół) człon 2 porusza się ruchem obrotowym
względem suwaka 1 w kierunku przeciwnym do wskazówek zegara,
natomiast człon 3 obraca się względem punktu D0 w kierunku
zgodnym ze wskazówkami zegara.
Maksymalne wychylenie punktu C2 w prawo występuje gdy suwak 1
osiągnie swoje najniższe położenie. Ustawienie członu 2 w pozycji
pionowej jest niemożliwe gdyż odległość L
00
ma wartość mniejszą
niż wartość długości członu 2 (L
2
)
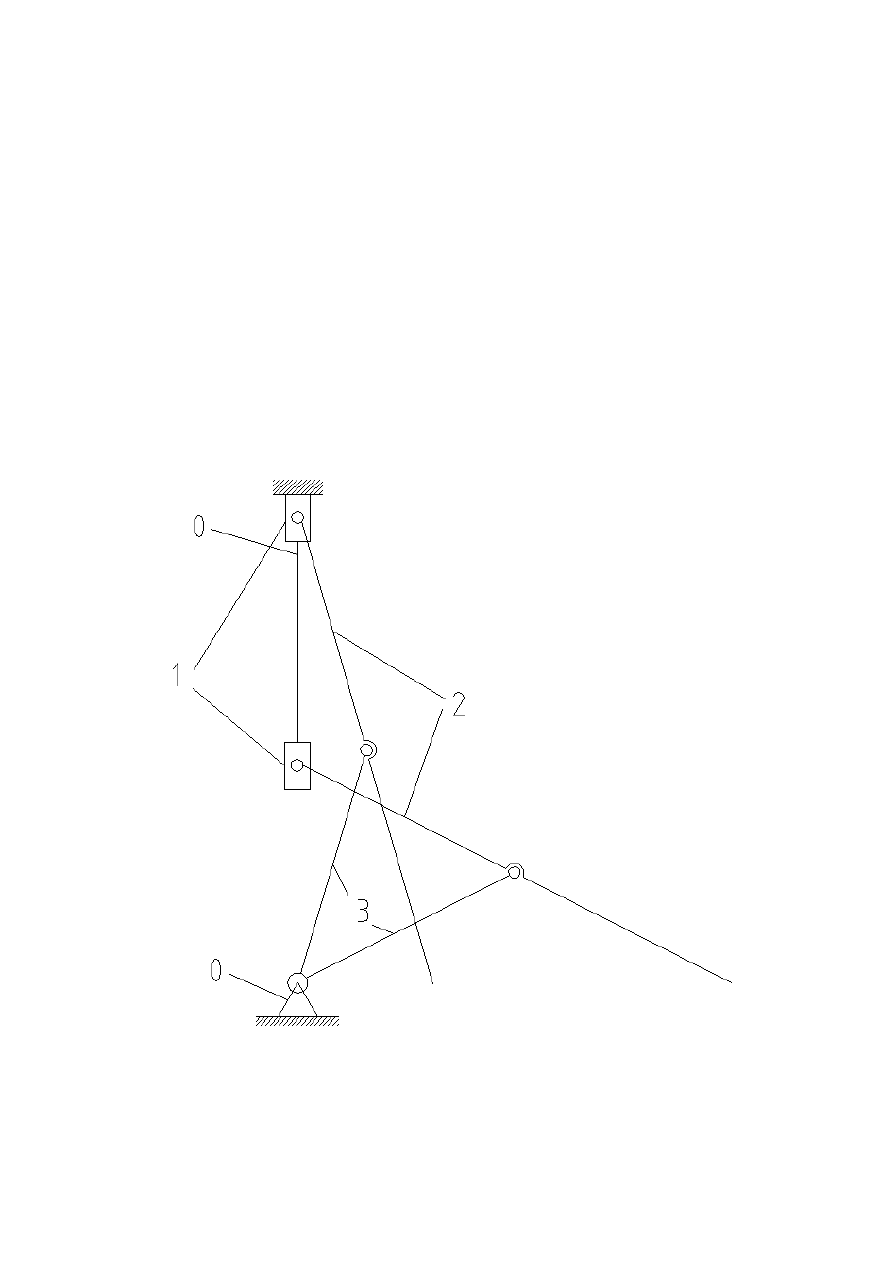
Rysunek 2 przedstawia skrajne położenia mechanizmu:
Rysunek 2
Analiza mechanizmu dźwigniowego – Tomasz Olchawski, gr. 13, AiR
4
1.4. Model mechanizmu w programie SAM
Rysunek 3 – model mechanizmu
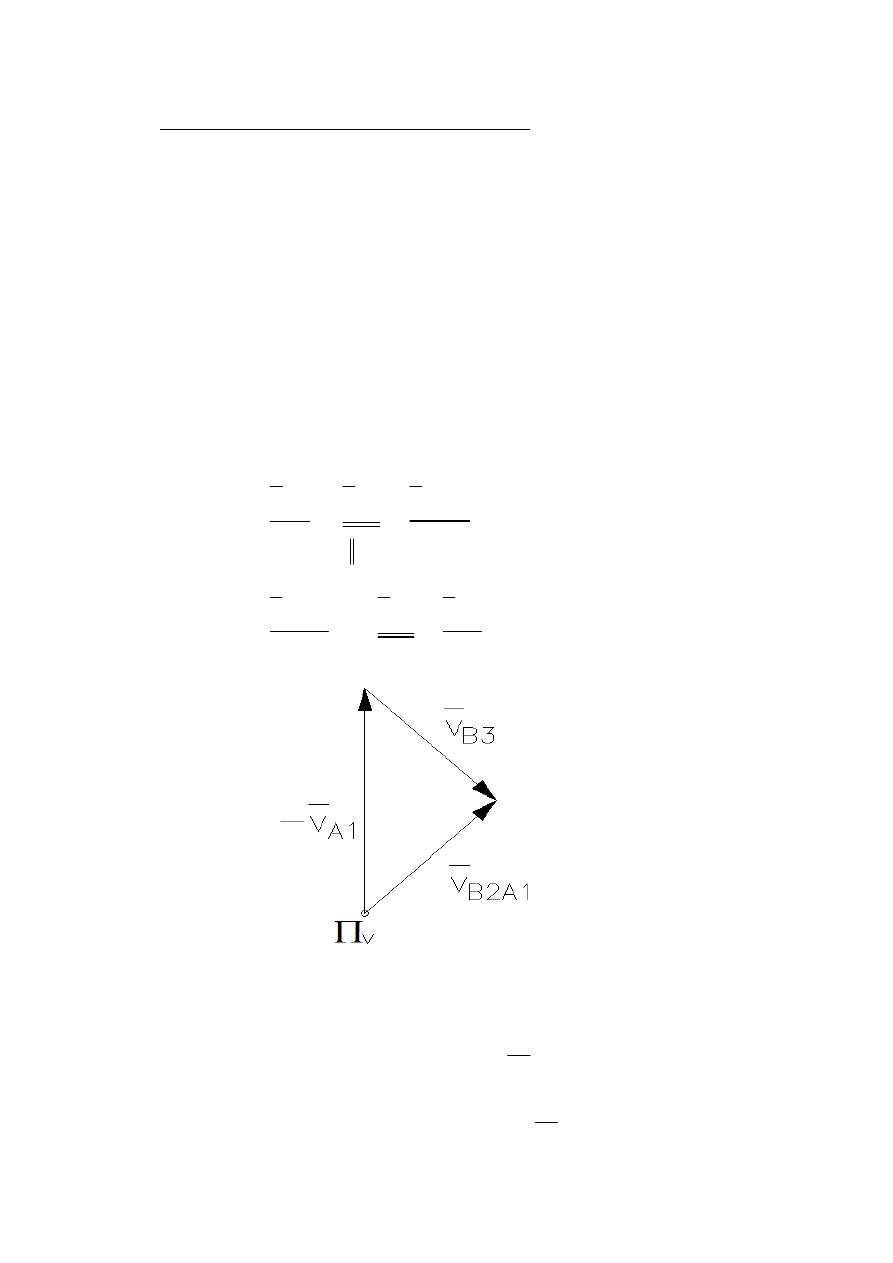
Analiza mechanizmu dźwigniowego – Tomasz Olchawski, gr. 13, AiR
5
2. Analiza kinematyczna mechanizmu
2.1. Analiza kinematyczna mechanizmu metodą
grafoanalityczną
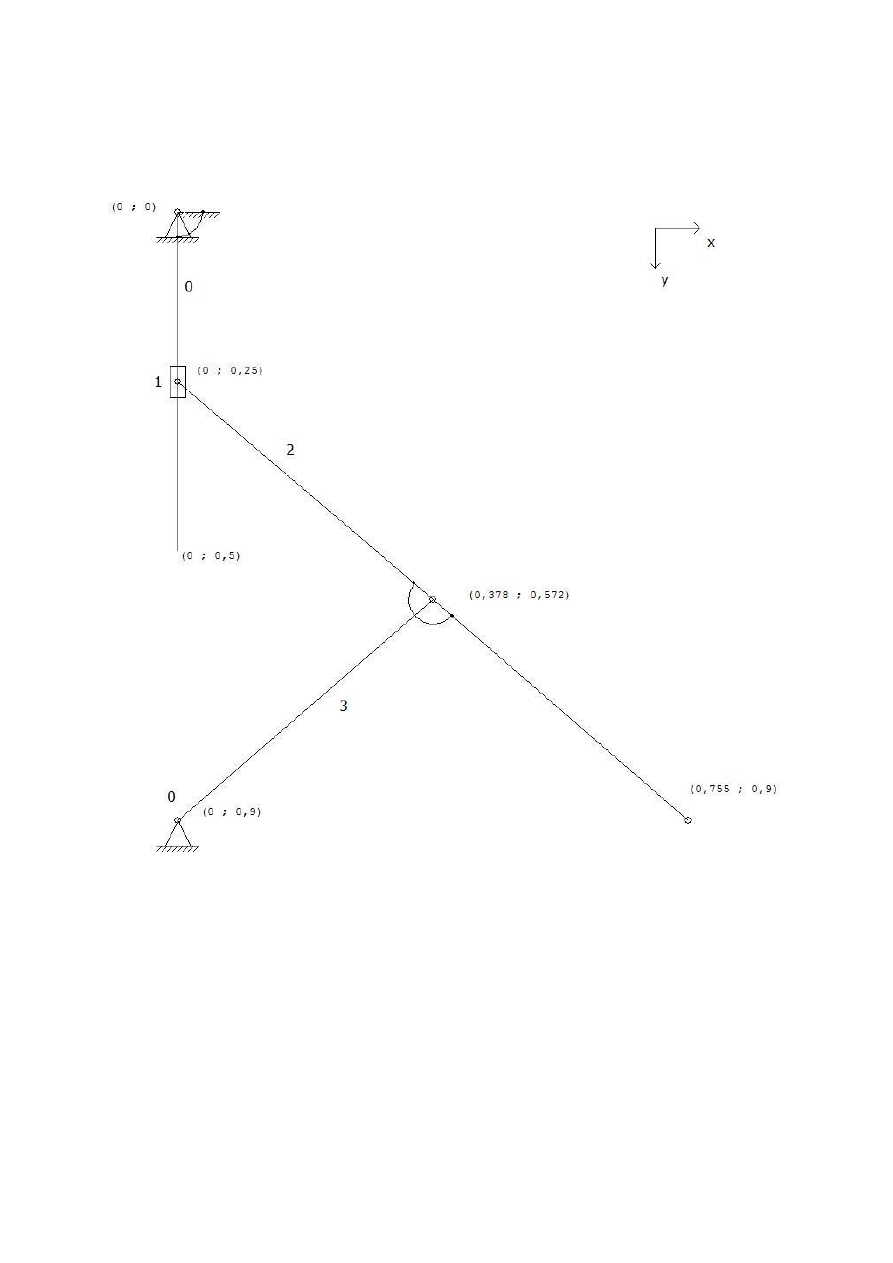
Zgodnie z przyjętymi parametrami analiza zostanie przeprowadzona
w momencie gdy suwak (1) przebył drogę równą połowie długości
prowadnicy (0) to jest 0,25m. Suwak porusza się ze stałą prędkością
zwróconą w dół, której wartość wynosi 0,25
m
/
s
a kierunek jest
zgodny z kierunkiem prowadnicy
Rysunki zostały wykonane w programie AutoCAD dlatego wartości
liczbowe zostały odczytane z podziałki w tym programie.
ANALIZA PRĘDKOŚCI
(podziałka prędkości w programie AutoCAD k
v
=0,0125
ms-1
/
mm
)
1
2
1
3
A
B
A
B
v
v
v
+
=
BD
⊥
OA
AB
⊥
3
1
1
2
B
A
A
B
v
v
v
+
−
=
Rysunek 4 – plan prędkości punktu B
s
m
v
k
v
B
v
B
163
.
0
)
(
3
3
=
⋅
=
s
m
v
k
v
A
B
v
A
B
163
.
0
)
(
1
2
1
2
=
⋅
=
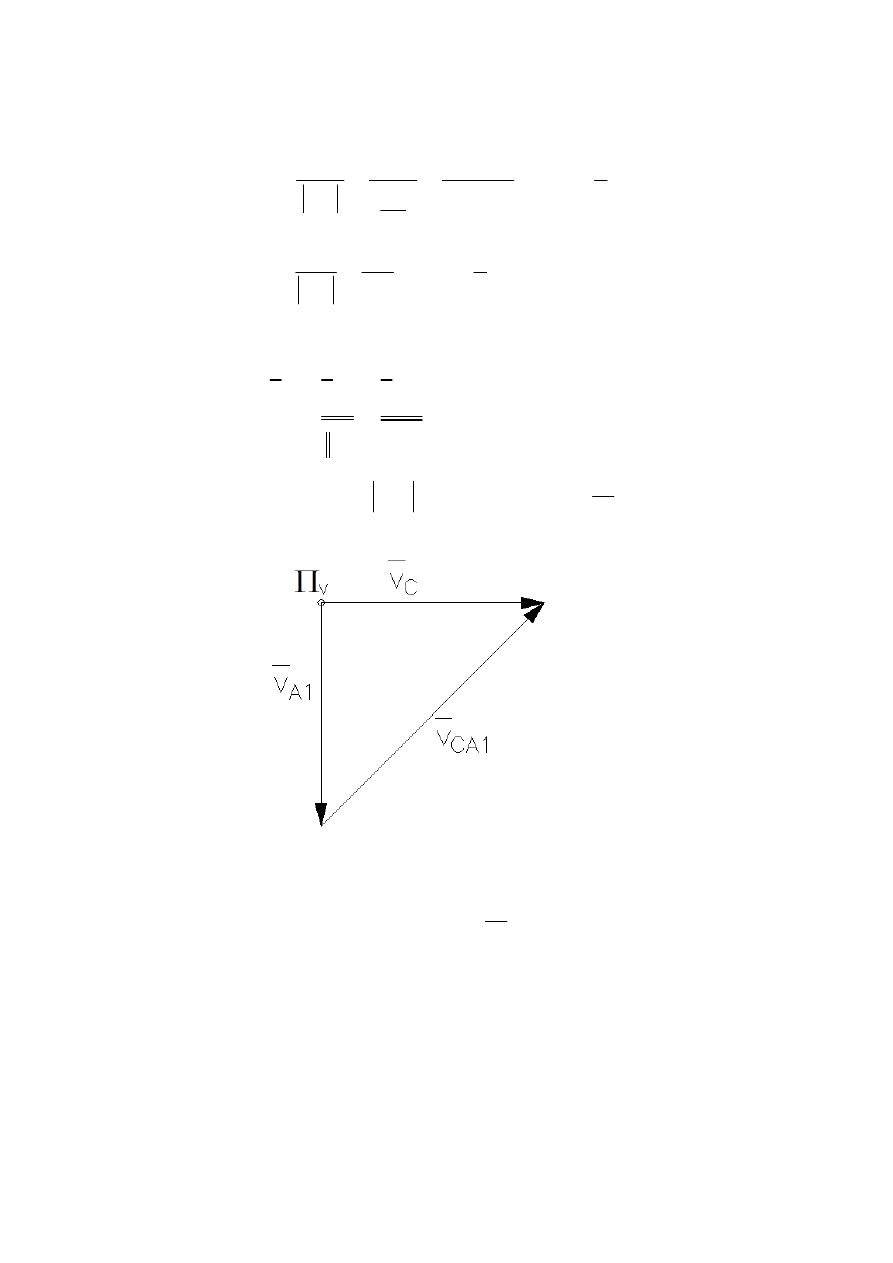
Analiza mechanizmu dźwigniowego – Tomasz Olchawski, gr. 13, AiR
6
i dalej:
s
L
v
BD
v
s
L
v
L
v
AB
v
B
B
A
B
A
B
A
B
1
326
.
0
1
326
.
0
2
2
3
3
3
3
2
1
2
2
1
2
1
2
2
=
=
=
=
⋅
=
=
=
ω
ω
następnie wyznaczamy prędkość punktu C:
1
1
CA
A
c
v
v
v
+
=
OA
AC
⊥
s
m
L
AC
v
CA
326
.
0
2
2
2
1
=
⋅
=
⋅
=
ω
ω
Rysunek 5 – plan prędkości punktu C
s
m
v
k
v
C
v
C
209
.
0
)
(
=
⋅
=
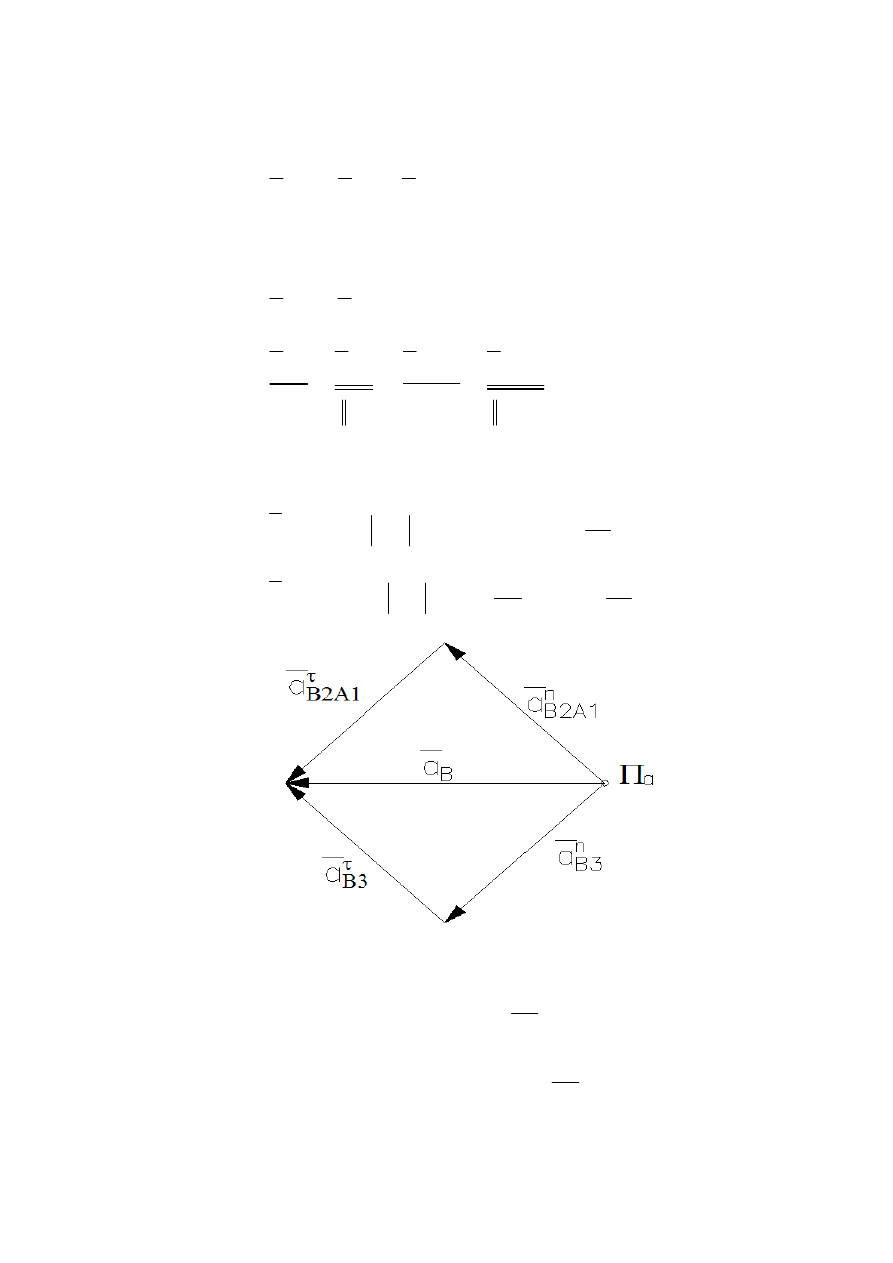
Analiza mechanizmu dźwigniowego – Tomasz Olchawski, gr. 13, AiR
7
ANALIZA PRZYSPIESZEŃ
(podziałka przyspieszeń w programie AutoCAD k
a
=0,0125
ms-2
/
mm
)
1
2
1
3
A
B
A
B
a
a
a
+
=
i
0
1
=
A
a
n
A
B
A
B
n
B
B
A
B
B
a
a
a
a
a
a
1
2
1
2
3
3
1
2
3
+
=
+
=
τ
τ
BD
⊥
BD
AB
⊥
AB
gdzie:
2
2
2
2
2
2
1
2
2
3
2
3
2
3
3
053
.
0
2
053
.
0
s
m
L
AB
a
s
m
L
BD
a
n
A
B
n
B
=
⋅
=
⋅
=
=
⋅
=
⋅
=
ω
ω
ω
ω
Rysunek 6 – plan przyspieszeń punktu B
2
3
3
045
.
0
)
(
s
m
a
k
a
B
a
B
=
⋅
=
τ
τ
2
1
2
1
2
045
.
0
)
(
s
m
a
k
a
A
B
a
A
B
=
⋅
=
τ
τ
Analiza mechanizmu dźwigniowego – Tomasz Olchawski, gr. 13, AiR
8
( ) ( )
2
2
3
2
3
069
.
0
s
m
a
a
a
B
n
B
B
=
+
=
τ
i dalej:
2
3
3
3
3
2
2
1
2
2
1
2
1
2
2
1
09
.
0
1
09
.
0
2
2
s
L
a
BD
a
s
L
a
L
a
AB
a
B
B
A
B
A
B
A
B
=
=
=
=
⋅
=
=
=
τ
τ
τ
τ
τ
ε
ε
następnie wyznaczamy przyspieszenie punktu C:
2
2
2
2
2
2
106
.
0
s
m
L
AC
a
n
C
=
⋅
=
⋅
=
ω
ω
2
2
2
2
09
.
0
s
m
L
AC
a
C
=
⋅
=
⋅
=
ε
ε
τ
( ) ( )
2
2
2
1319
.
0
s
m
a
a
a
C
n
C
C
=
+
=
τ
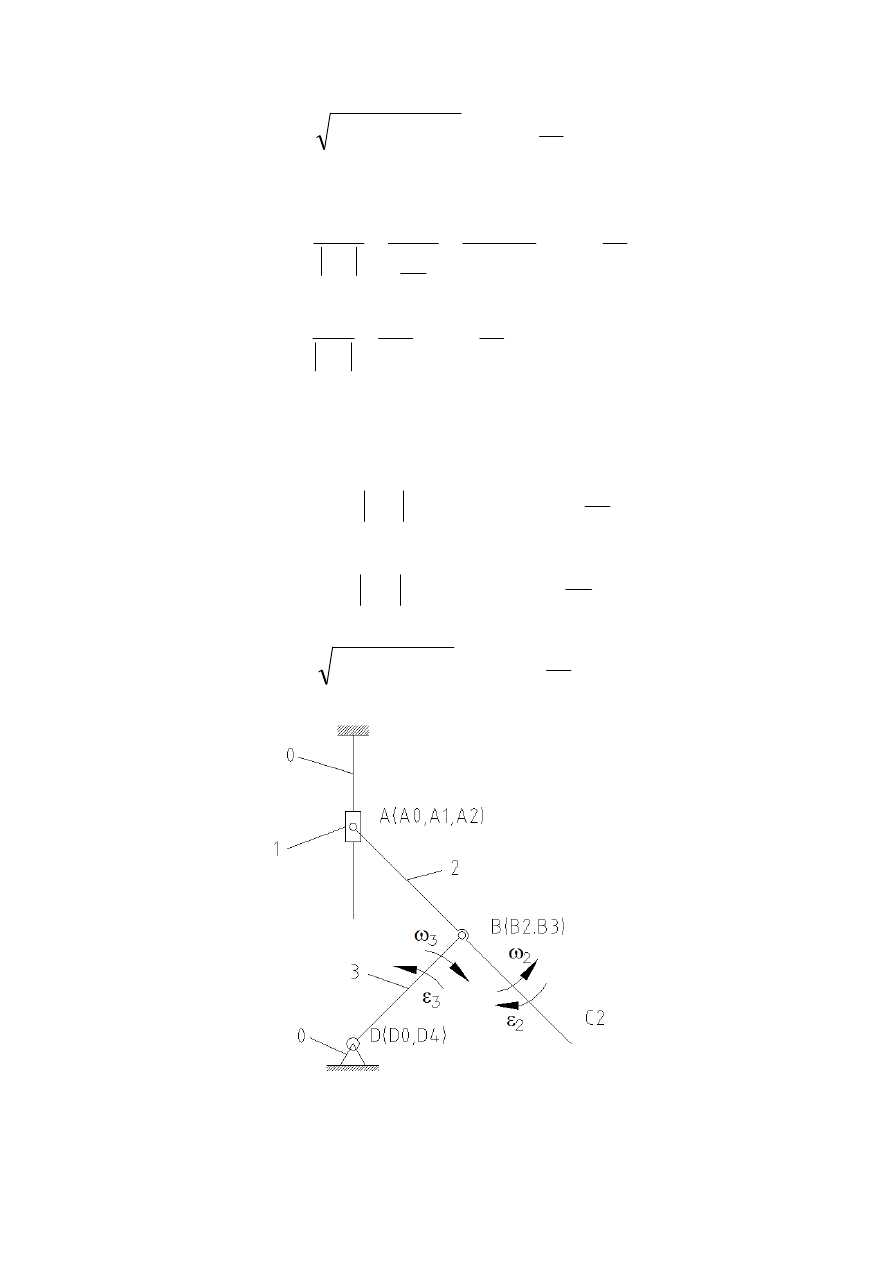
Rysunek 7 – schemat mechanizmu wraz z
prędkościami i przyspieszeniami kątowymi
Analiza mechanizmu dźwigniowego – Tomasz Olchawski, gr. 13, AiR
9
2.2. Analiza kinematyczna mechanizmu metodą
analityczną
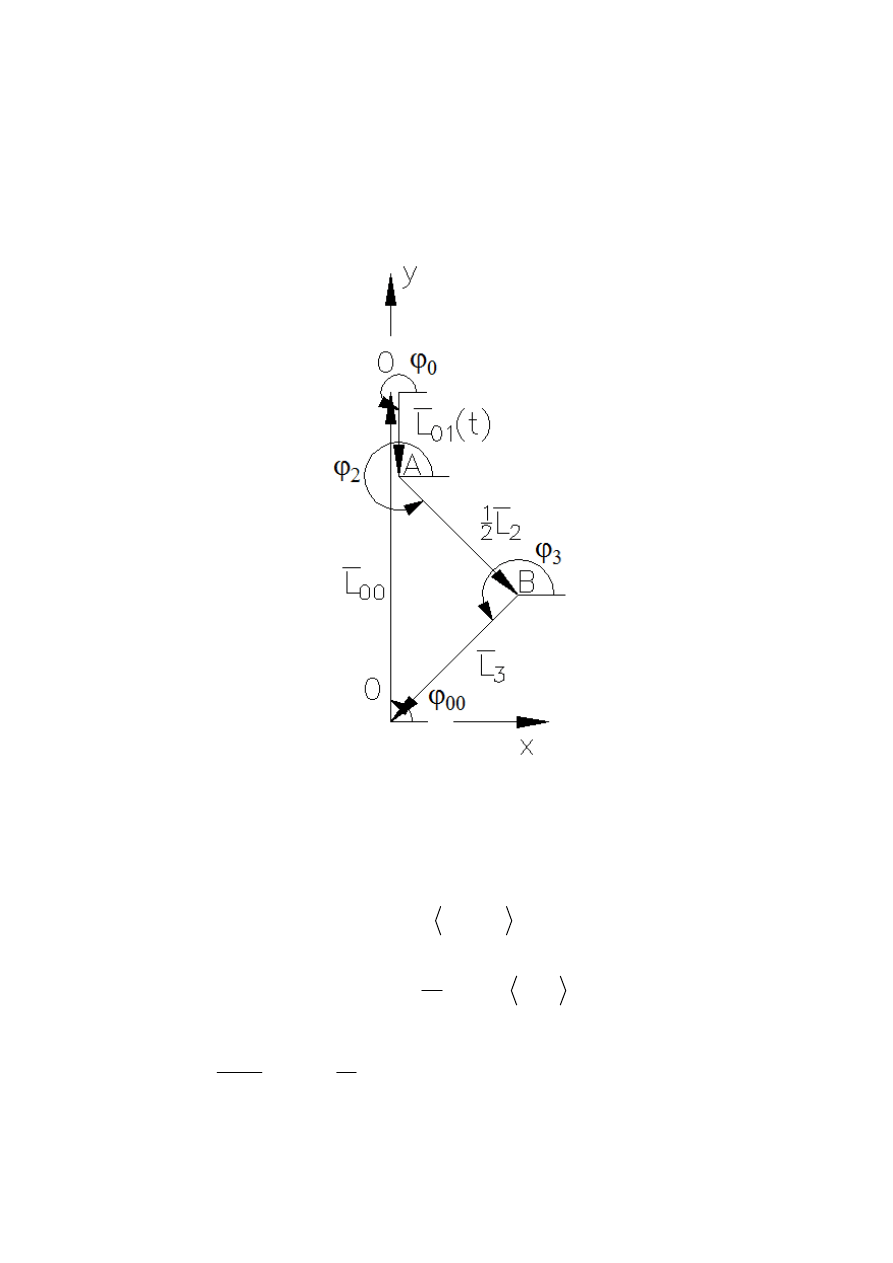
W celu analizy prędkości i przyspieszeń punktu B konstruujemy
zamknięty wektorowy wielobok sił:
Rysunek 8 – mechanizm w postaci
zamkniętego wieloboku sił
Dane:
t
v
t
L
A
⋅
=
1
01
)
(
i
m
t
L
5
.
0
;
0
)
(
01
∈
s
t
s
m
v
A
2
;
0
25
.
0
1
∈
⇒
=
00
3
2
00
0
;
;
;
2
;
2
3
L
L
L
π
ϕ
π
ϕ
=
⋅
=
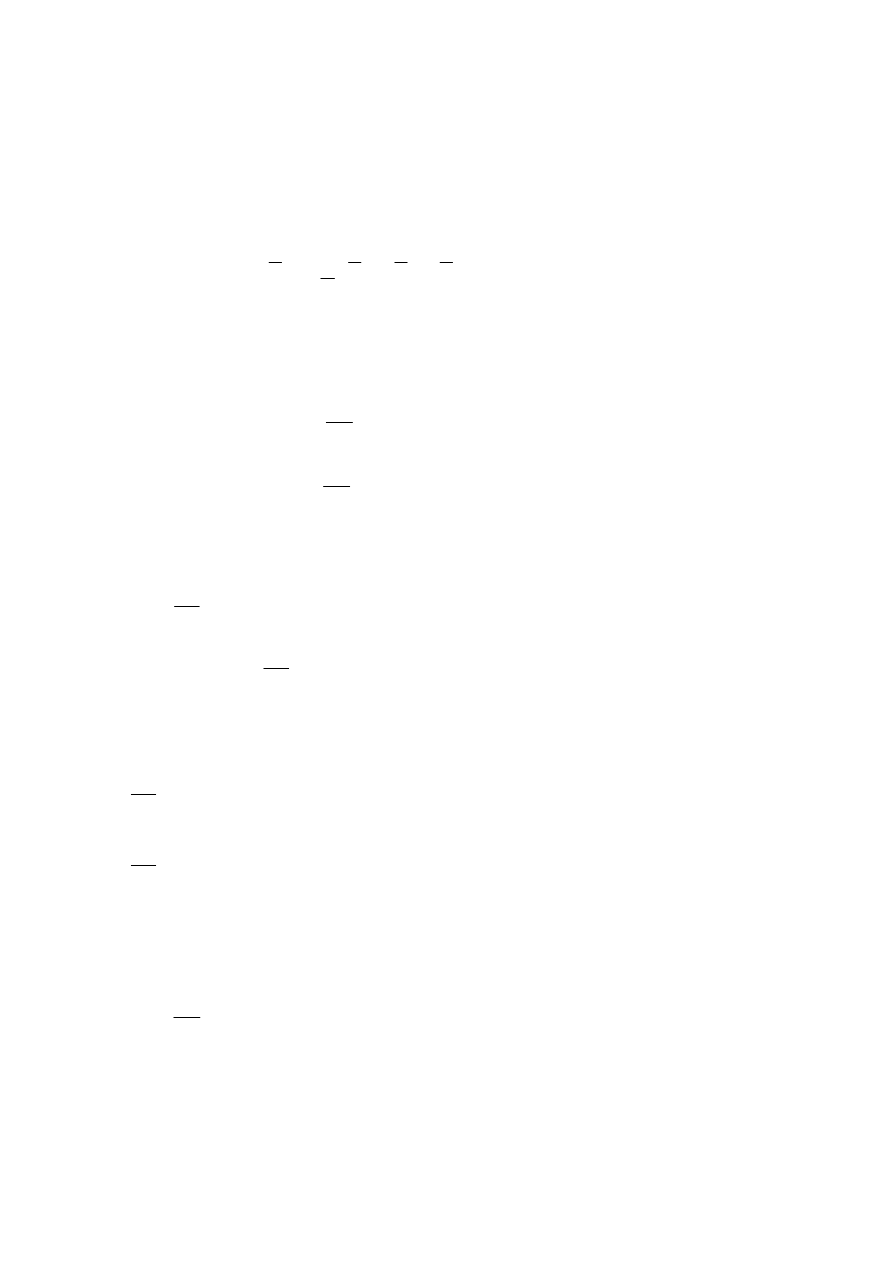
Analiza mechanizmu dźwigniowego – Tomasz Olchawski, gr. 13, AiR
10
Szukane:
C
C
B
B
a
v
a
v
;
;
;
;
;
;
;
;
;
3
2
3
2
3
2
ε
ε
ω
ω
ϕ
ϕ
Zamknięty wielobok wektorowy:
0
2
1
00
3
2
01
=
+
+
⋅
+
L
L
L
L
Po zrzutowaniu na przyjęte na rysunku 8 osie otrzymujemy:
0
)
sin(
)
sin(
)
sin(
2
)
sin(
:
0
)
cos(
)
cos(
)
cos(
2
)
cos(
:
00
00
3
3
2
2
0
01
00
00
3
3
2
2
0
01
=
⋅
+
⋅
+
⋅
+
⋅
=
⋅
+
⋅
+
⋅
+
⋅
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
L
L
L
L
y
L
L
L
L
x
Po uwzględnieniu danych otrzymujemy:
=
+
⋅
+
⋅
+
−
=
⋅
+
⋅
0
)
sin(
)
sin(
2
)
(
0
)
cos(
)
cos(
2
00
3
3
2
2
01
3
3
2
2
L
L
L
t
L
L
L
ϕ
ϕ
ϕ
ϕ
Przekształcamy układ równań:
(
)
(
)
⋅
+
⋅
⋅
−
⋅
−
−
=
⋅
⋅
=
⋅
)
(
sin
)
sin(
)
(
2
)
(
)
(
sin
2
)
(
cos
)
(
cos
2
3
2
2
3
3
3
00
01
2
00
01
2
2
2
2
3
2
2
3
2
2
2
2
ϕ
ϕ
ϕ
ϕ
ϕ
L
L
L
t
L
L
t
L
L
L
L
Dodajemy stronami:
(
)
(
)
2
3
3
3
00
01
2
00
01
2
2
)
sin(
)
(
2
)
(
2
L
L
L
t
L
L
t
L
L
+
⋅
⋅
−
⋅
−
−
=
ϕ

Analiza mechanizmu dźwigniowego – Tomasz Olchawski, gr. 13, AiR
11
I wyliczamy:
(
)
(
)
00
01
3
2
00
01
2
2
2
3
3
)
(
2
)
(
2
)
sin(
L
t
L
L
L
t
L
L
L
−
⋅
⋅
−
+
−
=
ϕ
oraz:
2
2
3
L
L =
ostatecznie:
(
)
⋅
−
=
3
00
01
3
2
)
(
arcsin
L
L
t
L
ϕ
Oraz z równania rzutów na oś y:
−
−
=
2
)
sin(
)
(
arcsin
2
3
3
00
01
2
L
L
L
t
L
ϕ
ϕ
W położeniu mechanizmu dla którego przeprowadzona była analiza
grafoanalityczna (tj. t=1s,L
01
(t)=0.25m)
rad
rad
849
.
3
542
.
220
576
.
5
458
.
319
3
2
≈
°
≈
≈
°
≈
ϕ
ϕ
W celu wyznaczenia prędkości kątowych różniczkujemy po czasie
równanie rzutów na oś y:
1
3
3
3
2
2
2
)
cos(
)
cos(
2
A
v
L
L
=
⋅
⋅
+
⋅
⋅
ϕ
ω
ϕ
ω
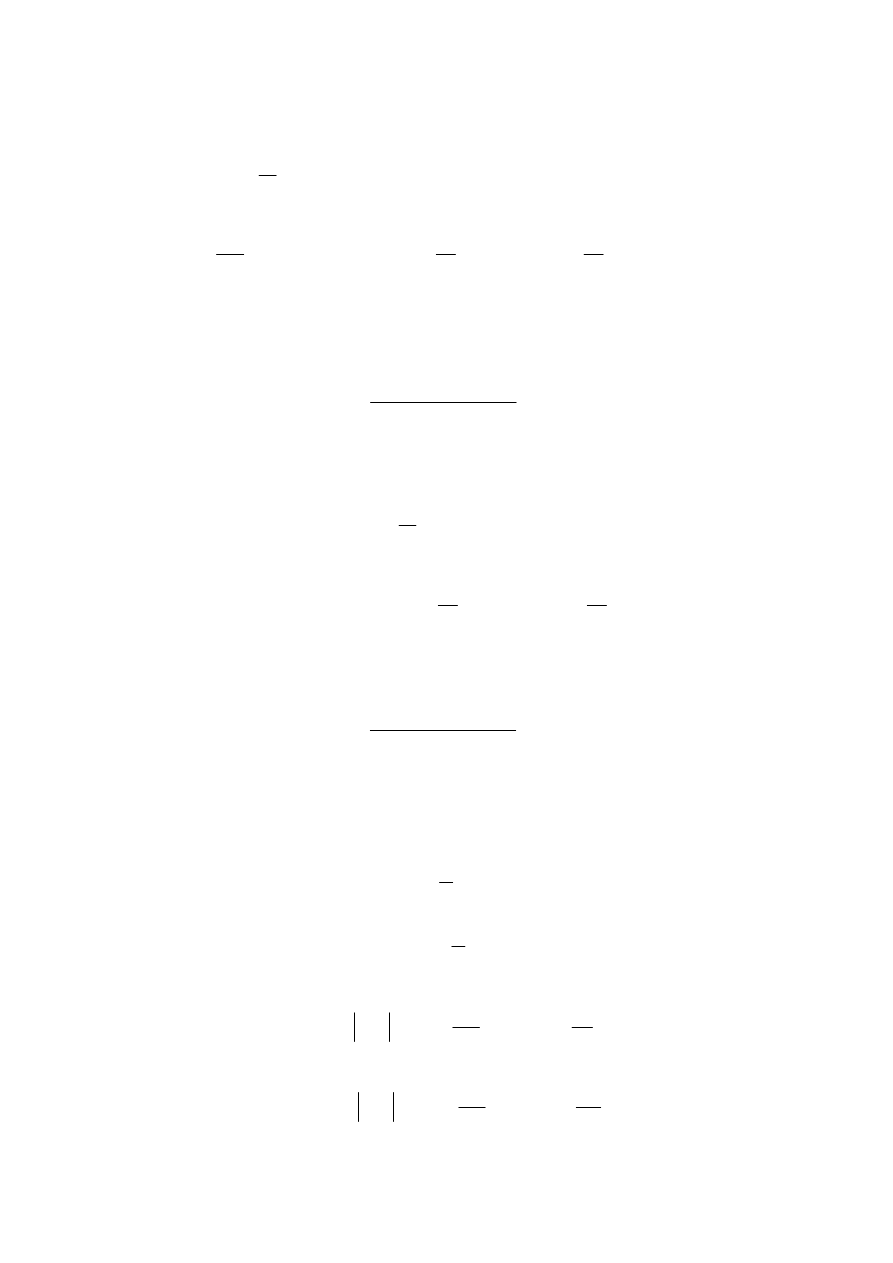
Analiza mechanizmu dźwigniowego – Tomasz Olchawski, gr. 13, AiR
12
Aby wyznaczyć prędkość kątową
2
ϕ
obracamy układ współrzędnych
o kąt
2
3
π
ϕ
−
−
⋅
=
+
−
⋅
⋅
3
1
3
2
2
2
2
cos
2
cos
2
ϕ
π
π
ϕ
ϕ
ω
A
v
L
Korzystając z okresowości i parzystości funkcji cosinus oraz
przesunięcia cosinusa i nieparzystości funkcji sinus otrzymujemy:
( )
(
)
2
3
2
3
1
2
sin
sin
2
ϕ
ϕ
ϕ
ω
−
⋅
⋅
⋅
=
L
v
A
Analogicznie aby wyznaczyć prędkość kątową
3
ϕ
obracamy układ
współrzędnych o kąt
2
2
π
ϕ
−
−
⋅
=
+
−
⋅
⋅
2
1
2
3
3
3
2
cos
2
cos
ϕ
π
π
ϕ
ϕ
ω
A
v
L
I otrzymujemy:
( )
(
)
3
2
3
2
1
3
sin
sin
ϕ
ϕ
ϕ
ω
−
⋅
⋅
=
L
v
A
W położeniu mechanizmu, dla którego przeprowadzona była analiza
grafoanalityczna (tj. t=1s,L
01
(t)=0.25m)
s
s
1
3288
.
0
1
3288
.
0
3
2
−
≈
≈
ω
ω
s
m
L
AB
v
B
1644
.
0
2
2
2
2
≈
⋅
=
⋅
=
ω
ω
2
2
2
2
2
2
0541
.
0
2
s
m
L
AB
a
n
B
≈
⋅
=
⋅
=
ω
ω
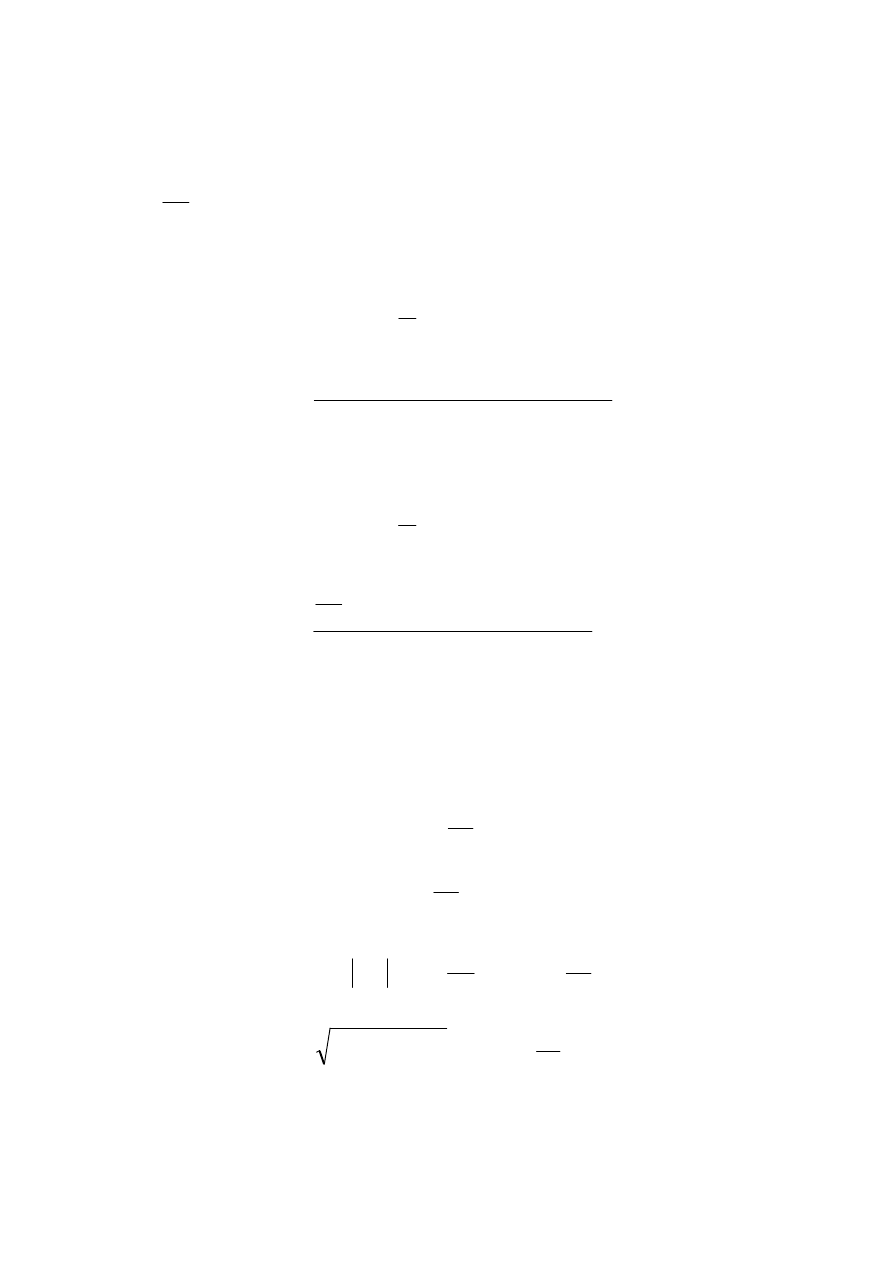
Analiza mechanizmu dźwigniowego – Tomasz Olchawski, gr. 13, AiR
13
W celu wyznaczenia przyspieszeń kątowych dwukrotnie
różniczkujemy po czasie równanie rzutów na oś y:
(
)
(
)
0
)
sin(
)
cos(
)
sin(
)
cos(
2
3
2
3
3
3
3
2
2
2
2
2
2
=
⋅
−
⋅
⋅
+
⋅
−
⋅
⋅
ϕ
ω
ϕ
ε
ϕ
ω
ϕ
ε
L
L
Aby wyznaczyć przyspieszenie kątowe
2
ε
obracamy układ
współrzędnych o kąt
2
3
π
ϕ
−
)
sin(
)
cos(
2
2
3
2
3
2
2
2
2
2
3
3
2
ϕ
ϕ
ϕ
ϕ
ω
ω
ε
−
⋅
−
⋅
⋅
+
⋅
⋅
=
L
L
L
Aby wyznaczyć przyspieszenie kątowe
3
ε
obracamy układ
współrzędnych o kąt
2
2
π
ϕ
−
)
sin(
)
cos(
2
3
2
3
2
3
2
3
3
2
2
2
3
ϕ
ϕ
ϕ
ϕ
ω
ω
ε
−
⋅
−
⋅
⋅
+
⋅
=
L
L
L
W położeniu mechanizmu, dla którego przeprowadzona była analiza
grafoanalityczna
2
3
2
2
1
0911
.
0
1
0911
.
0
s
s
≈
−
≈
ε
ε
2
2
2
2
0443
.
0
2
s
m
L
AB
a
B
≈
⋅
=
⋅
=
ε
ε
τ
( ) ( )
2
2
2
0699
.
0
s
m
a
a
a
B
n
B
B
≈
+
=
τ

Analiza mechanizmu dźwigniowego – Tomasz Olchawski, gr. 13, AiR
14
Aby wyznaczyć parametry kinematyczne punktu C znajdujemy jego
promień wodzący:
2
01
)
(
L
t
L
L
C
+
=
Rzutując na osie układu:
( )
⋅
+
−
=
=
2
2
01
2
2
sin
)
(
)
cos(
ϕ
ϕ
L
t
L
L
L
L
CY
CX
Różniczkując otrzymujemy:
( )
⋅
⋅
+
−
=
⋅
⋅
−
=
2
2
2
1
2
2
2
cos
)
sin(
ϕ
ω
ϕ
ω
L
v
v
L
v
A
CY
CX
W położeniu mechanizmu, dla którego przeprowadzona była analiza
grafoanalityczna
0
=
CY
v
( ) ( )
s
m
v
v
v
v
CX
CY
CX
C
2135
.
0
2
2
≈
=
+
=
Różniczkując dwukrotnie otrzymujemy:
(
)
( )
(
)
⋅
+
⋅
−
⋅
=
⋅
+
⋅
⋅
−
=
)
cos(
sin
)
sin(
)
cos(
2
2
2
2
2
2
2
2
2
2
2
2
ϕ
ε
ϕ
ω
ϕ
ε
ϕ
ω
L
a
L
a
CY
CX
W położeniu mechanizmu, dla którego przeprowadzona była analiza
grafoanalityczna
0
=
CY
a
(
) ( )
s
m
a
a
a
a
CX
CY
CX
C
1393
.
0
2
2
≈
=
+
=
Analiza mechanizmu dźwigniowego – Tomasz Olchawski, gr. 13, AiR
15
2.3. Wykresy kinematyczne - SAM
Sporządzono następujące wykresy:
)
(
);
(
);
(
);
(
);
(
);
(
);
(
);
(
);
(
);
(
3
2
3
2
3
2
t
a
t
v
t
a
t
v
t
t
t
t
t
t
C
C
B
B
ε
ε
ω
ω
ϕ
ϕ
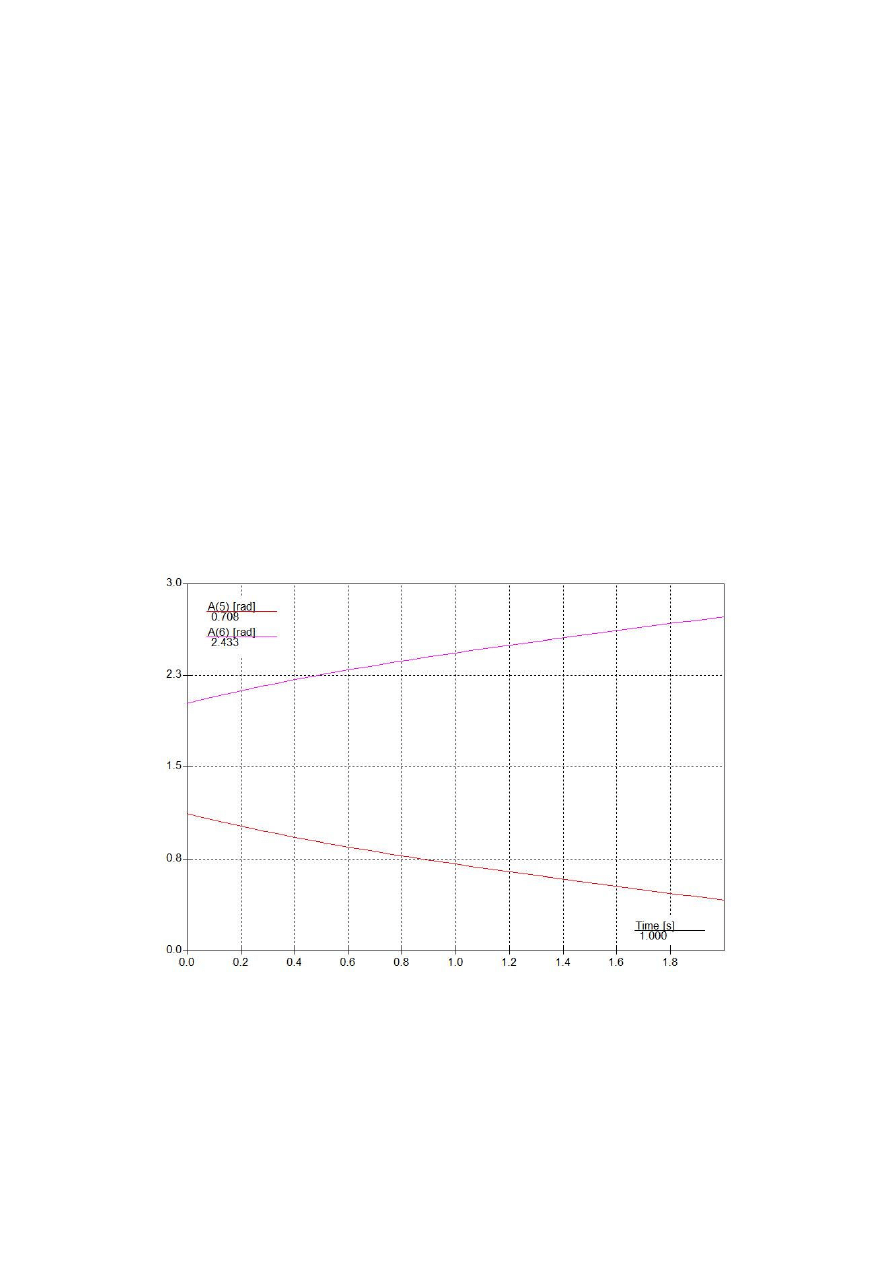
Odczytano wartości dla czasu t=1s tj. L
01
(t)=0.25m
)
849
.
3
(
708
.
0
)
1
(
)
576
.
5
(
433
.
2
)
1
(
3
2
rad
pi
rad
rad
pi
rad
=
+
=
=
+
=
ϕ
ϕ
Różnica wartości spowodowana jest innym zorientowaniem
kątów w programie SAM
Wykres 1 – zależności kątów od czasu
Analiza mechanizmu dźwigniowego – Tomasz Olchawski, gr. 13, AiR
16
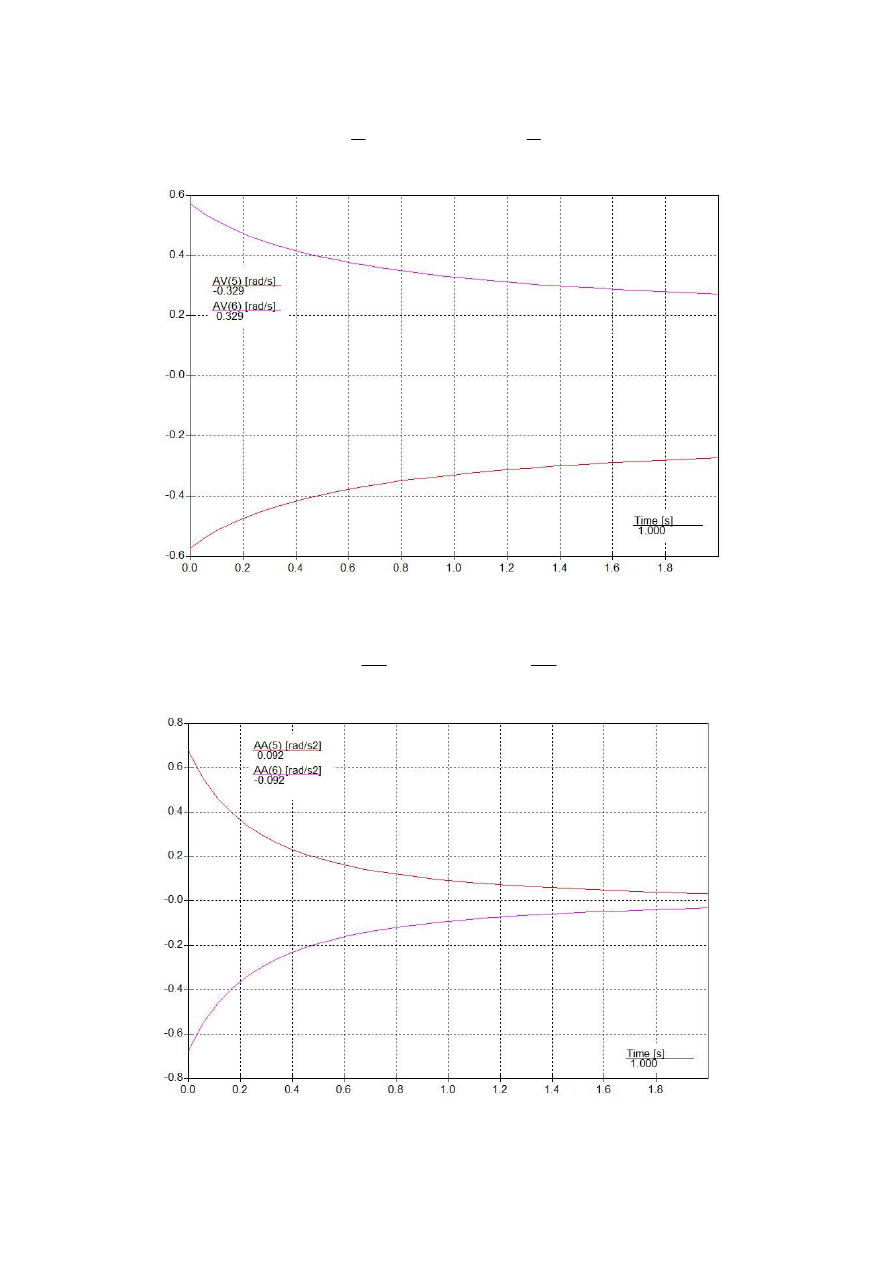
s
s
1
329
.
0
)
1
(
,
1
329
.
0
)
1
(
3
2
−
=
=
ω
ω
Wykres 2 – zależności prędkości kątowych od czasu
2
3
2
2
1
092
.
0
)
1
(
,
1
092
.
0
)
1
(
s
s
=
−
=
ε
ε
Wykres 3 – zależności przyspieszeń kątowych od czasu
Analiza mechanizmu dźwigniowego – Tomasz Olchawski, gr. 13, AiR
17
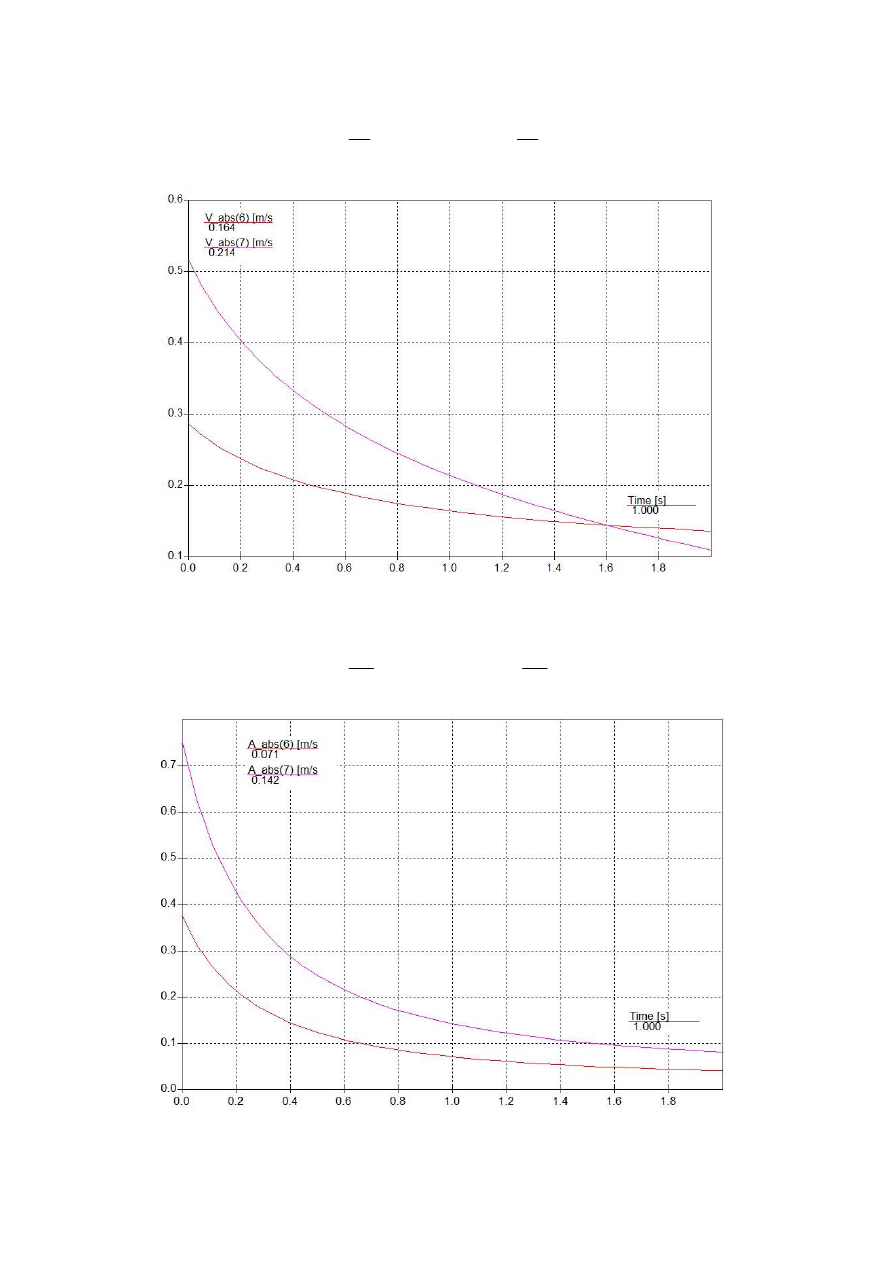
s
m
v
s
m
v
C
B
214
.
0
)
1
(
,
164
.
0
)
1
(
=
=
Wykres 4 – zależności prędkości liniowych od czasu
2
2
142
.
0
)
1
(
,
071
.
0
)
1
(
s
m
a
s
m
a
C
B
=
=
Wykres 5 – zależności przyspieszeń liniowych od czasu
Analiza mechanizmu dźwigniowego – Tomasz Olchawski, gr. 13, AiR
18
2.4. Wykresy kinematyczne – MATLAB
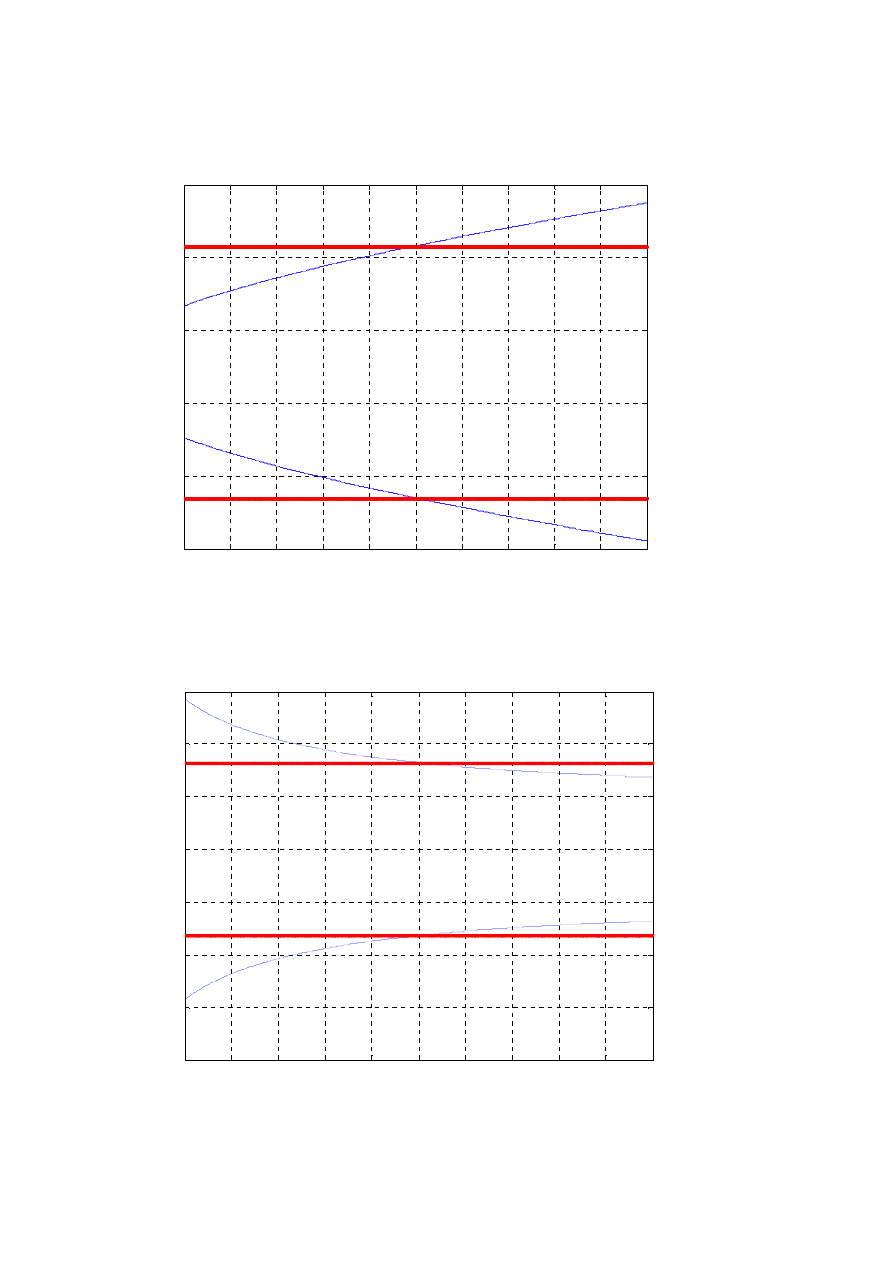
Wykres 6 – zależności kątów od czasu
Wykres 7 – zależności prędkości kątowych od czasu
0
0.2
0.4
0.6
0.8
1
1.2
1.4
1.6
1.8
2
3.5
4
4.5
5
5.5
6
t[s]
k
a
t[
ra
d
]
kat2=5.5756 kat3=3.8492
0
0.2
0.4
0.6
0.8
1
1.2
1.4
1.6
1.8
2
-0.8
-0.6
-0.4
-0.2
0
0.2
0.4
0.6
t[s]
w
[r
a
d
/s
]
w2=0.32898 w3=-0.32898
Analiza mechanizmu dźwigniowego – Tomasz Olchawski, gr. 13, AiR
19
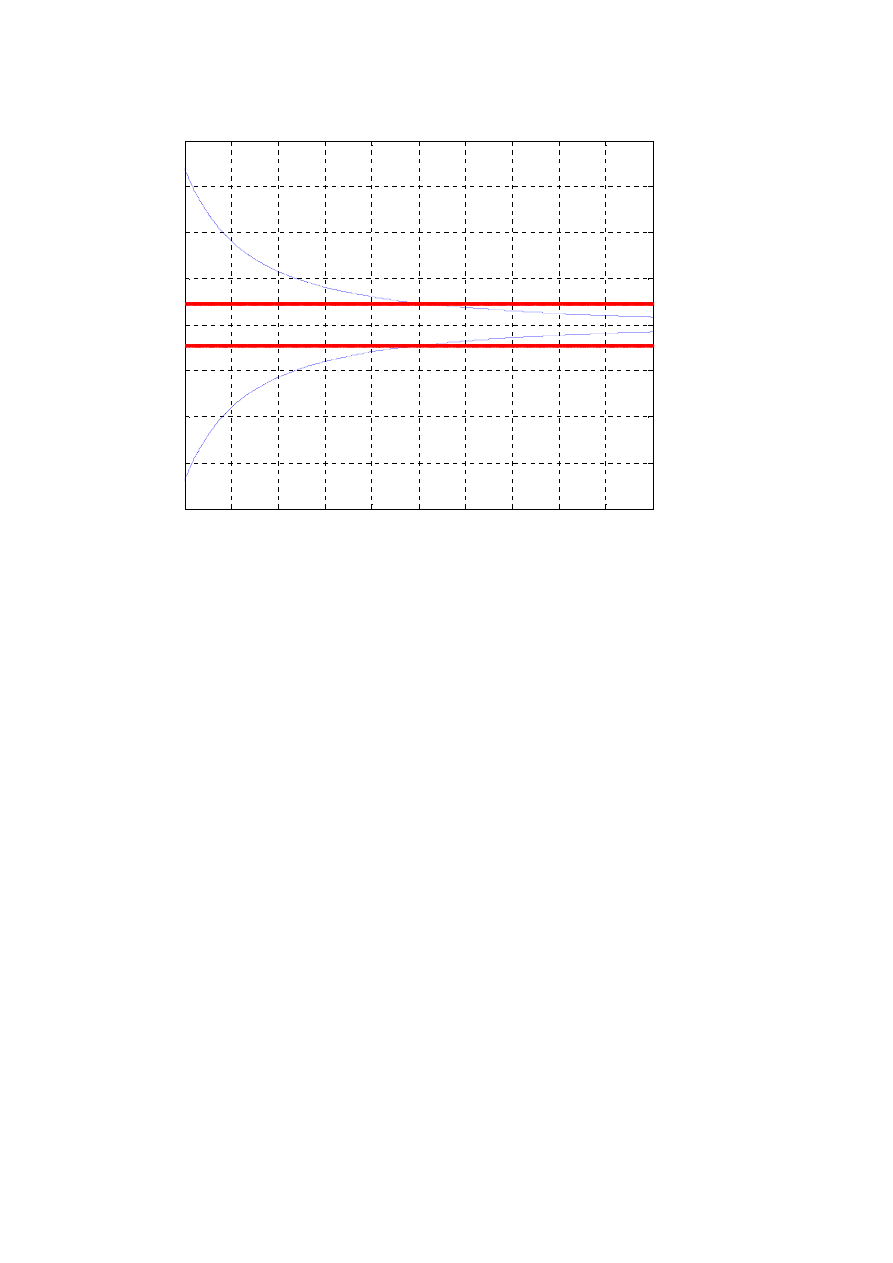
Wykres 8 - zależności przyspieszeń kątowych od czasu
0
0.2
0.4
0.6
0.8
1
1.2
1.4
1.6
1.8
2
-0.8
-0.6
-0.4
-0.2
0
0.2
0.4
0.6
0.8
t[s]
E
[r
a
d
/s
2
]
E2=-0.092569 E3=0.092569

Analiza mechanizmu dźwigniowego – Tomasz Olchawski, gr. 13, AiR
20
2.5. Porównanie wyników analizy kinematycznej dla
danego położeni mechanizmu
Tabela 2 zawiera porównanie wyników uzyskanych różnymi
metodami:
Parametr
Metoda
grafoanalityczna
Metoda
analityczna
SAM
MATLAB
[ ]
rad
2
ϕ
-
5.576
5.576
5.5756
[ ]
rad
3
ϕ
-
3.849
3.849
3.8492
s
1
2
ω
0.326
0.3288
0.329
0.32898
s
1
3
ω
0.326
-0.3288
-0.329
-0.32898
2
2
1
s
ε
0.09
-0.0911
-0.092
-0.092569
2
3
1
s
ε
0.09
0.0911
0.092
0.092569
s
m
v
B
0.163
0.1644
0.164
-
s
m
v
C
0.209
0.2135
0.214
-
2
s
m
a
B
0.069
0.0699
0.071
-
2
s
m
a
C
0.1319
0.1393
0.142
-
Tabela 2 – porównanie wyników analizy
Zgodność danych potwierdza, że nie zostały popełnione błędy
obliczeniowe. Metoda grafoanalityczna nie daje możliwości
oznaczenia kierunku danego parametru wektorowego dlatego też
występuje niezgodność znaków.
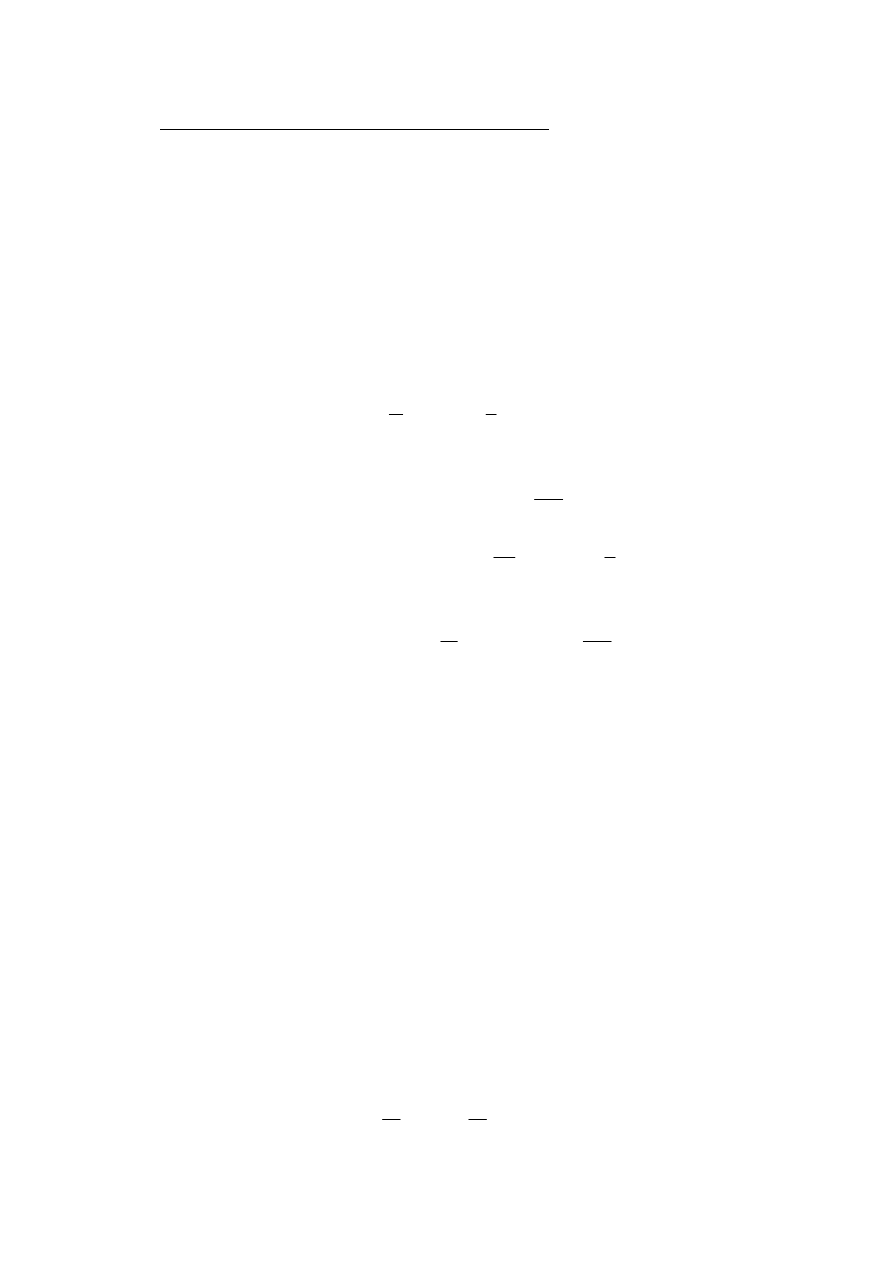
Analiza mechanizmu dźwigniowego – Tomasz Olchawski, gr. 13, AiR
21
3. Analiza kinetostatyczna mechanizmu
3.1. Obliczenie sił ciężkości, sił bezwładności i momentów
od sił bezwładności oraz przyjęcie zewnętrznych sił i
momentów oporu
Zgodnie z założeniami dla potrzeb analizy kinetostatycznej
pomijamy masy wszystkich członów za wyjątkiem członu 2, którego
masa wynosi m
2
=6kg, natomiast masowy moment bezwładności
J
2
=0.5kgm
2
. Jako, że mechanizm porusza się w płaszczyźnie
poziomej przy analizie pominiemy również siłę ciężkości, a zatem:
Siła bezwładności:
B
a
m
B
⋅
−
=
2
2
s
m
kg
a
m
B
B
42
.
0
07
.
0
6
2
2
2
=
⋅
=
⋅
=
Moment od siły bezwładności:
2
2
2
ε
⋅
−
= J
M
B
m
s
kgm
J
M
B
045
.
0
1
09
.
0
2
1
2
2
2
2
2
=
⋅
=
⋅
=
ε
Siła zewnętrzna oporu:
P
2
2
=
Moment zewnętrzny oporu:
m
M
1
.
0
3
=
3.2. Wyznaczenie reakcji w parach kinematycznych oraz
siły równoważącej metodą grafoanalityczną
W celu wyznaczenia reakcji w parach kinematycznych mechanizmu
uwalniamy od więzów grupę strukturalną złożoną z członów 2 i 3.
Rysunek 9 przedstawia układ sił i momentów przyłożonych do grupy
strukturalnej w zadanym analizowanym położeniu. Na rysunku
pominięto wzajemne reakcje członów 2 i 3, co więcej zachodzi
równość
:
32
23
R
R
−
=
Analiza mechanizmu dźwigniowego – Tomasz Olchawski, gr. 13, AiR
22
Rysunek 9 – układ sił i momentów przyłożonych
do grupy strukturalnej
Równania dynamiczne dla członów 2 i 3
0
0
23
03
03
3
32
2
2
12
12
2
=
+
+
=
Σ
=
+
+
+
+
=
Σ
R
R
R
P
R
P
B
R
R
P
n
i
n
i
τ
τ
Po dodaniu stronami otrzymujemy:
0
0
03
03
2
2
12
12
03
03
23
32
2
2
12
12
=
+
+
+
+
+
=
+
+
+
+
+
+
+
n
n
n
n
R
R
P
B
R
R
R
R
R
R
P
B
R
R
τ
τ
τ
τ
Aby graficznie rozwiązać to równanie należy analitycznie znaleźć
dwie niewiadome. Z równań momentów członów 2 i 3 względem
punktu B wyznaczmy składowe styczne reakcji R
12
i R
03
.
Przyjmujemy, że momenty obracające człon w kierunku zgodnym z
kierunkiem obrotu wskazówek zegara są ujemne.
Analiza mechanizmu dźwigniowego – Tomasz Olchawski, gr. 13, AiR
23
Równania momentów względem punktu B dla członów 2 i 3
L
M
P
R
L
P
M
L
R
M
B
B
B
i
21
.
1
2
)
sin(
0
)
sin(
2
2
2
2
2
2
12
2
2
2
2
2
12
)
(
2
=
⋅
−
⋅
=
=
⋅
⋅
−
+
⋅
=
Σ
ϕ
ϕ
τ
τ
L
M
R
M
L
R
M
B
i
2
.
0
0
3
3
03
3
3
03
)
(
3
=
=
=
−
⋅
=
Σ
τ
τ
I dalej:
0
03
03
2
2
12
12
=
+
+
+
+
+
n
n
R
R
P
B
R
R
τ
τ
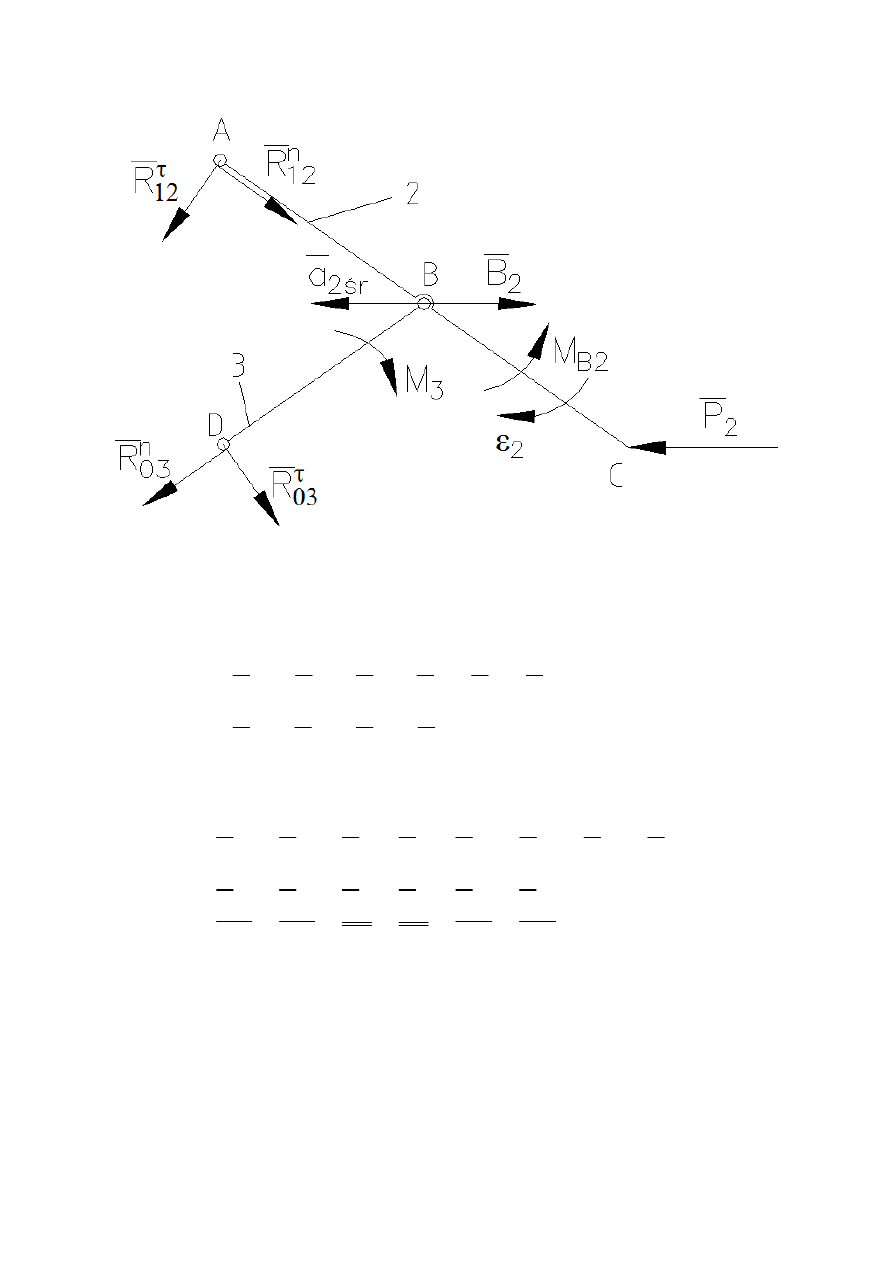
Graficznie wyznaczamy wartości sił normalnych reakcji
(podziałka sił w programie AutoCAD k
F
=0,1
N
/
mm
)
Rysunek 10 – plan sił działających na grupę strukturalną
Analiza mechanizmu dźwigniowego – Tomasz Olchawski, gr. 13, AiR
24
Odczytane wartości:
R
R
R
n
n
29
.
2
37
.
1
65
.
0
03
12
12
=
=
=
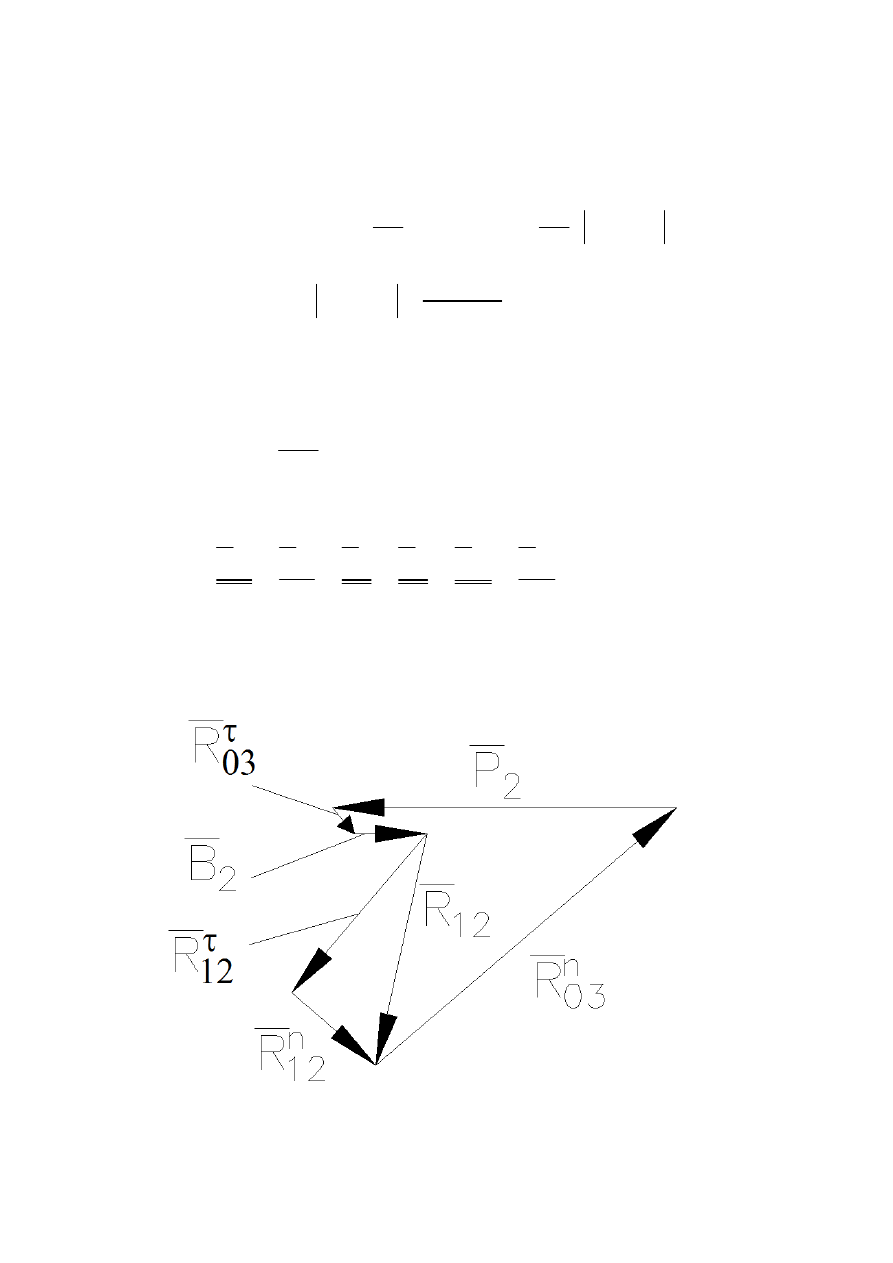
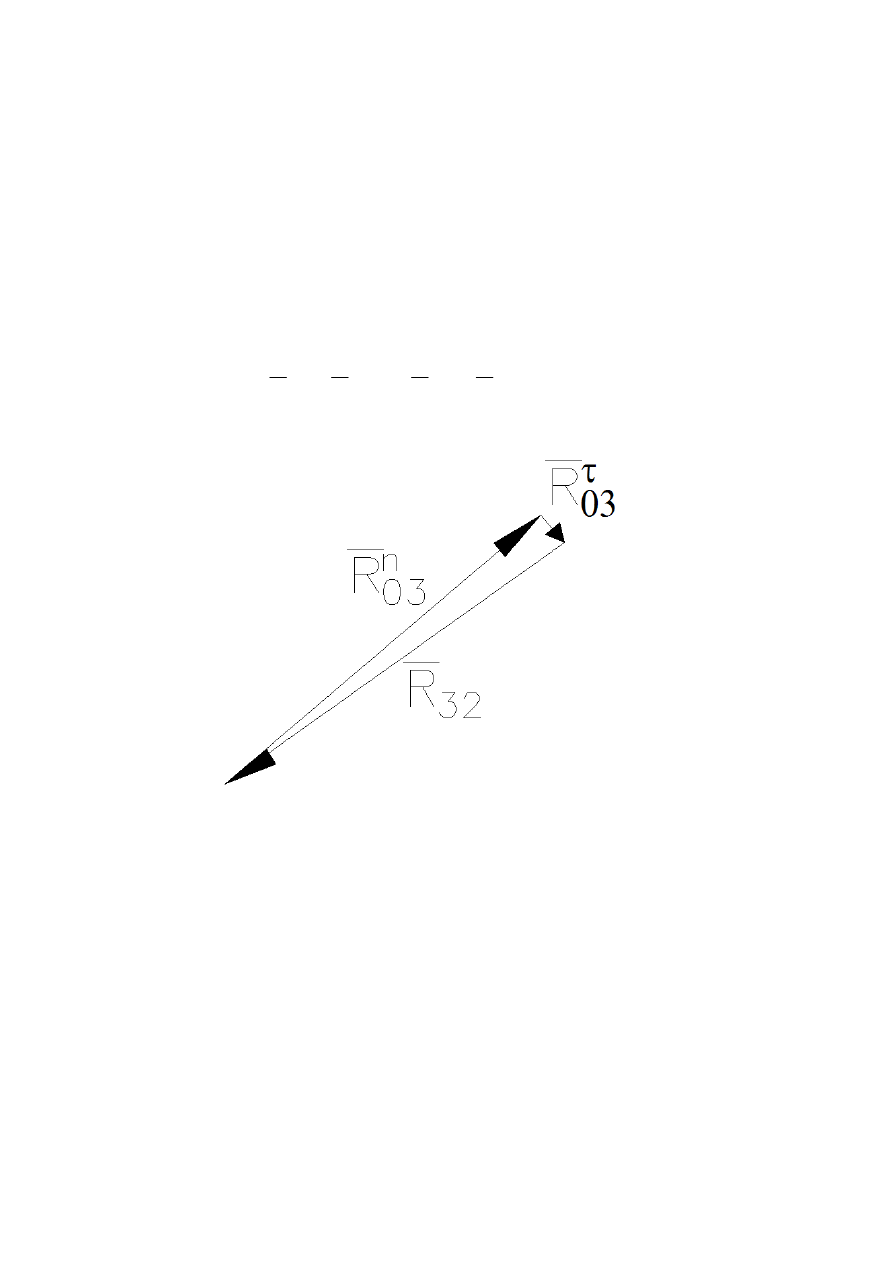
Oraz na podstawie równania sił członu 3:
32
23
03
03
R
R
R
R
n
=
−
=
+
τ
Rysunek 11 – siła reakcji członu 3 na człon 2
Odczytana wartość:
R
3
.
2
32
=
Analiza mechanizmu dźwigniowego – Tomasz Olchawski, gr. 13, AiR
25
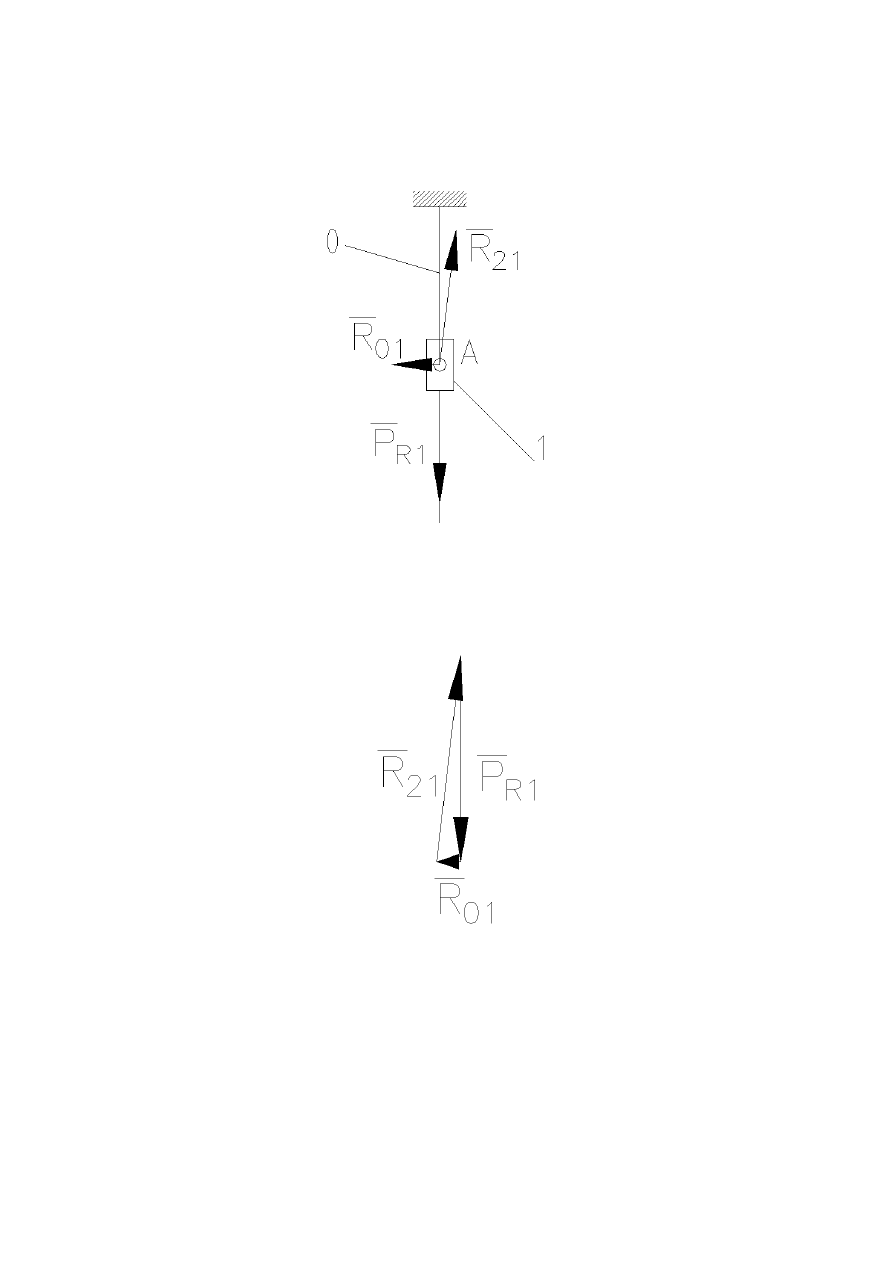
Następnie analizujemy człon napędzający uwalniając od więzów:
Rysunek 12 - układ sił przyłożonych do członu napędzającego
Podczas analizy nie uwzględniamy momentu ponieważ jest on równy
zero (wynika to z budowy członu 1)
Rysunek 13 – plan sił działających na człon napędzający
Odczytane wartości:
P
R
R
36
.
1
16
.
0
1
01
=
=
Analiza mechanizmu dźwigniowego – Tomasz Olchawski, gr. 13, AiR
26
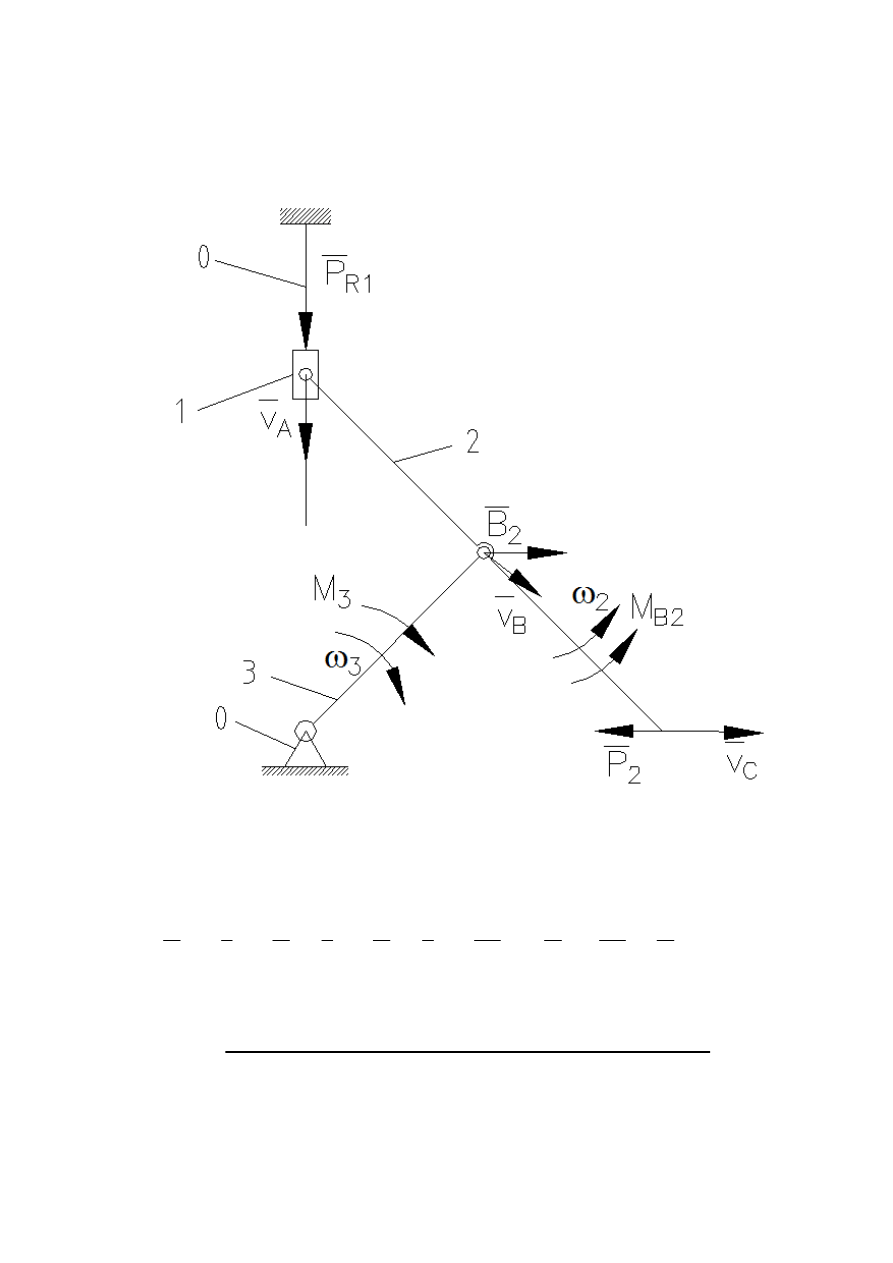
3.3. Wyznaczanie siły równoważącej metodą mocy
chwilowych
Rysunek 14 - schemat obliczeniowy mechanizmu metodą
mocy chwilowych
Równanie mocy chwilowych ma postać:
0
3
3
2
2
2
2
1
=
+
+
+
+
ω
ω
o
o
o
o
o
M
M
v
P
v
B
v
P
B
C
B
A
R
0
)
cos(
3
3
2
2
2
2
2
1
=
⋅
+
⋅
+
⋅
−
⋅
⋅
+
⋅
ω
ω
ϕ
M
M
v
P
v
B
v
P
B
C
B
a
R
A
B
B
C
R
v
v
B
M
M
v
P
P
)
cos(
2
2
2
2
3
3
2
1
ϕ
ω
ω
⋅
⋅
−
⋅
−
⋅
−
⋅
=
P
R
3378
.
1
1
=
Analiza mechanizmu dźwigniowego – Tomasz Olchawski, gr. 13, AiR
27
3.4. Wyznaczanie siły równoważącej w programie SAM
Model w programie SAM został uzupełniony o masę i moment
bezwładności członu 2 oraz obciążenie zewnętrzne
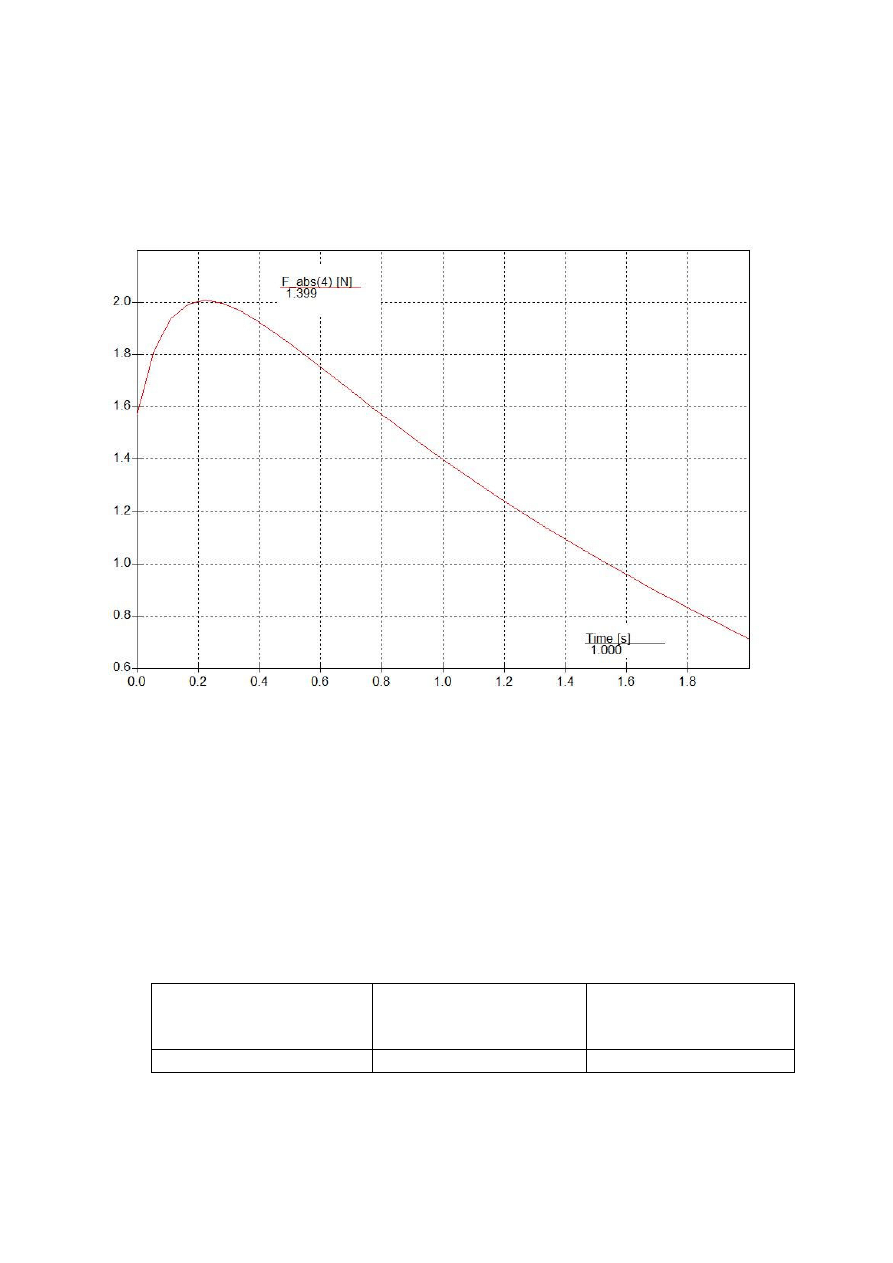
Wykres 9 – zależności siły równoważącej od czasu
Wartość odczytana:
P
R
399
.
1
1
=
3.5. Porównanie wyników obliczeń siły równoważącej
Tabela 3 zawiera wartości wyliczone siły równoważącej różnymi
metodami
Metoda
grafoanalityczna
P
R1
[N]
Metoda mocy
chwilowych
P
R1
[N]
SAM
P
R1
[N]
1.36
1.3378
1.399
Tabela 3
Zgodność wyników potwierdza poprawność obliczeń
Wyszukiwarka
Podobne podstrony:
TMM - PROJEKT 1B, Projekty, Teoria Maszyn i Mechanizmów
Projekt 1b
Tomasz Olchawski Sprawozdanie z Laboratorium 1
Tomasz Olchawski Sprawozdanie z Laboratorium 4
Fundamentowanie projekt 1B Paweł Widuliński
TMM PROJEKT 1B
Tomaszewicz,projektowanie urbanistyczne, DOKUMENTACJA PROJEKTOWA NORMY I PRZEPISY PRAWNE W PROJEKTOW
ADANIE 1b, Resources, Budownictwo, Fundamentowanie, Projekt, Fundamentowanie, Fundamentowanie-1, Pal
Tomaszewicz,projektowanie urbanistyczne, klasyfikacja terenów zielonych
Projekt 2 (Tomasza Krysińskiego)
Projekt - całyczesc 1b, Fizyka Budowli - WSTiP, fizyka budowli(4), fizyka budowli, Fizyka Budowli, K
tomek cw1, IŚ Tokarzewski 27.06.2016, V semestr ISiW, Kanalizacje, ćw proj, projekty Chudzicki, Zięt
Wzor opisu do projektu - sem 6 a, IŚ Tokarzewski 27.06.2016, VI semestr COWiG, Komputerowe Wspomagan
Tomaszewicz,projektowanie urbanistyczne, Walory?koracyjne roślinności i zasady kompozycji plastyczne
Tomaszewicz,projektowanie urbanistyczne, WNĘTRZA jako pierwszy stopień kompozycji
więcej podobnych podstron