Sito Eratosteresa

2,3,4,5,6….N

Usuwamy z naszego ciągu wszystkie liczby od p

1

= 2 i podzielne przez p

1

=2

Pierwszą nieusuniętą liczbą z naszego ciągu jest liczba p

2

= 3

Usuniemy z naszego ciągu liczby > p

2

= 3 będące wielokrotnościami 3.

Pierwszą nieusuniętą liczbą z naszego ciągu niepodzielną przez 2 i 3 jest teraz p

3

= 5. Mamy

teraz ciąg

2,3,5,7,11,13,17….

Postępowanie kontynuujemy i za n-tym razem otrzymujemy n-tą liczbę p

n

Usuniemy z naszego ciągu wszystkie wielokrotności liczby p

n

większe od p

n

Pierwszą nieusuniętą liczbą w naszym ciągu jest liczba pierwsza p

n + 1

Jeżeli ciąg jest skończony to postępowanie możemy zakończyć po otrzymaniu największej liczby
pierwszej p

k

≤ √. Wszystkie liczby większe od tej liczby p

k

pozostałe są liczbami pierwszymi.

równanie diofantyczne

– rozwiązań poszukujemy w liczbach całkowitych

4. Równania nieoznaczone

Twierdzenie 4.1

Niech a1,a2,..an oraz b ϵ ℤ, a12 + a22 + …an2 > 0

Na to by równanie a1x1 + a2x2 + anxn = b
miało rozwiązanie potrzeba i wystarcza by największy wspólny dzielnik a1 a2 … an dzielił b
czyli (a1,a2,…an)|b

Przykład 2x + 68y + 10z = 7
(2,68,10) = 2 , 2 ∤ 7

Twierdzenie 4.2

Jeśli (x0, y0) jest pewnym całkowitoliczbowym rozwiązaniem równanie

ax + by = c a,b,c ϵ ℤ

a2 + b2 > 0

wszystkie rozwiązania tego równania wyznaczymy wzorem

x = x

0

+

௕

(௔,௕)

∗

t ϵ ℤ

y = y

0

-

௕

(௔,௕)

∗

Przykłady:

20x + 502y = 3
(20,502) = 2

2 ∤ 3

czyli nie ma rozwiązań

28x + 15y = 2
(28,15) = 1
1 | 2
czyli rozwiązaniem jest

x = -1 +

ଵହ

(ଵହ,ଶ଼)

∗ x = -1 + 15t

t ϵ ℤ

y = 2 -

ଶ଼

(ଵହ,ଶ଼)

∗

y = 2 – 28t

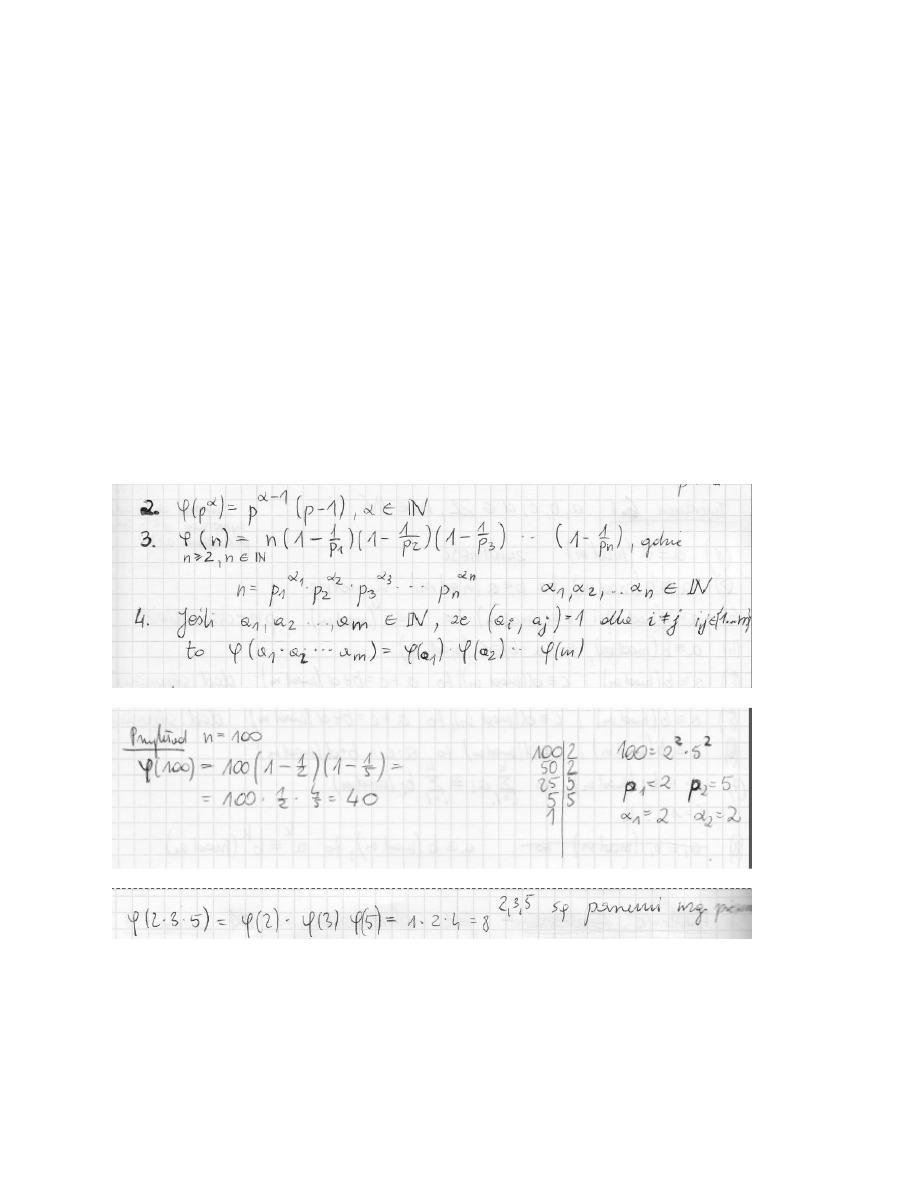
5. Funkcje Eulera

Wartością jest ilość liczb pierwszych
φ (n) = { ilość liczb naturalnych ≤ n względnie pierwszych ≥ n }

Przykłady
φ (1) = 1 bo

(1,1) = 1

φ (2) = 1 bo

(1,2) = 1 (2,2) = 2 (2 nie jest względnie pierwsze)

φ (3) = 2 bo

(1,3) = 1 (2,3) = 1 (3,3) = 3

φ (4) = 2 bo

(1,4) = 1 (2,4) = 2 (3,4) = 1 (4,4) = 4

φ (5) = 4
φ (6) = 2
φ (12) = 4

Funkcja Eulena nie jest monotoniczna

Twierdzenie 5.1

Niech φ będzie funkcją Eulera φ(p) = p -1 gdzie p to zbiór liczb pierwszych

Funkcja π(x) x ∈ IN
π(x) = {ilość liczb pierwszych ≤ x}

π(1) = 0

π(4) = 2

π(2) = 1

π(5) = 3

π(3) = 2

π(7) = π(8) = π(9) = π(10) = 4

6. Kongruencja

3 = 20 (mod 17)
20 = 12 (mod 8)
100 = 80 (mod 4)

Definicja : o dwóch liczbach całkowitych a,b mówimy że przystają do siebie modulo m, m ∈IN,
jeśli m | a-b czyli

Twierdzenie 6.1

a,b,c,d ∈ Z, m ∈ IN

1

2

3

4

5

6

7

8

9

10