Informatyka 1

Informatyka 1

Politechnika Białostocka

Politechnika Białostocka -- Wydział Elektryczny

Wydział Elektryczny

Elektrotechnika, semestr II, studia niestacjonarne I stopnia

Elektrotechnika, semestr II, studia niestacjonarne I stopnia

Rok akademicki 2011/2012

Rok akademicki 2011/2012

Wykład nr 2 (16.03.2012)

Wykład nr 2 (16.03.2012)

dr inż. Jarosław Forenc

Informatyka 1, studia niestacjonarne I stopnia

dr inż. Jarosław Forenc

Rok akademicki 2011/2012, Wykład nr 2

2/50

Plan wykładu nr 2

Plan wykładu nr 2

Systemy pozycyjne

systemy pozycyjne a język C

zastosowania systemów pozycyjnych

Systemy niepozycyjne

system rzymski

system rzymski

Kodowanie liczb

naturalny kod binarny (NKB), kod BCD,

kod 1 z N (pierścieniowy), kod 2 z 5

kod kołowy (Johnsona), kod Graya (refleksyjny)

Kodowanie znaków

kod ASCII, ISO/IEC 646, ISO/IEC 8859

EBCDIC, Windows-1250

Informatyka 1, studia niestacjonarne I stopnia

dr inż. Jarosław Forenc

Rok akademicki 2011/2012, Wykład nr 2

3/50

Systemy pozycyjne a język C

Systemy pozycyjne a język C

W języku C liczby mogą być zapisywane w trzech systemach:

dziesiętnym (domyślnie), np. 1239
ósemkowym (zaczynają się od zera -

0

), np. 011 (11

(8)

= 9

(10)

)

szesnastkowym (zaczynają się od

0x

lub

0X

), np. 0x11 (11

(16)

= 17

(10)

)

Do wyświetlenia liczby funkcją

printf()

stosowane są następujące

Do wyświetlenia liczby funkcją

printf()

stosowane są następujące

specyfikatory formatu:

liczba dziesiętna:

%d

,

%i

liczba ósemkowa:

%o

liczba szesnastkowa:

%x

,

%X

Do wczytania liczby funkcją

scanf()

stosowane są następujące

specyfikatory formatu:

liczba dziesiętna:

%d

(typ int),

%D

(typ long)

liczba ósemkowa:

%o

(typ int),

%O

(typ long)

liczba szesnastkowa:

%x

(typ int),

%X

(typ long)

Informatyka 1, studia niestacjonarne I stopnia

dr inż. Jarosław Forenc

Rok akademicki 2011/2012, Wykład nr 2

4/50

Systemy pozycyjne a język C

Systemy pozycyjne a język C

#include <stdio.h>

#include <stdlib.h>

int main()

{

int x1 = 456; /* system dziesietny

*/

int x2 = 0710; /* system osemkowy

*/

Dziesietny:

456

456

456

Osemkowy:

710

710

710

Szesnastkowy:

1c8

1c8

1c8

Szesnastkowy:

1C8

1C8

1C8

int x2 = 0710; /* system osemkowy

*/

int x3 = 0x1C8; /* system szesnastkowy */

printf("Dziesietny: %d %d

%d\n",x1,x2,x3);

printf("Osemkowy: %o %o

%o\n",x1,x2,x3);

printf("Szesnastkowy: %x %x

%x\n",x1,x2,x3);

printf("Szesnastkowy: %X %X

%X\n",x1,x2,x3);

system("pause");

return 0;

}

Informatyka 1, studia niestacjonarne I stopnia

dr inż. Jarosław Forenc

Rok akademicki 2011/2012, Wykład nr 2

5/50

System dwójkowy

System dwójkowy -- zastosowania

zastosowania

System dwójkowy, nazywany także binarnym:

p = 2

,

D = {0,1}

Powszechnie używany w elektronice cyfrowej i informatyce

Informatyka 1, studia niestacjonarne I stopnia

dr inż. Jarosław Forenc

Rok akademicki 2011/2012, Wykład nr 2

6/50

System ósemkowy

System ósemkowy -- zastosowania

zastosowania

Ósemkowy, oktalny, oktogonalny:

p = 8

,

D = {0,1,2,3,4,5,6,7}

Obecnie jego zastosowanie jest znikome

Przykład:

w systemie Linux/Unix do zmiany praw

user

group other

w systemie Linux/Unix do zmiany praw
dostępu do plików i katalogów stosowane
jest polecenie

chmod

chmod tryb plik ...

tryb może być liczbą ósemkową
lub wyrażeniem symbolicznym

r w x

/

+ - =

/

u g o a

chmod g+x data

tryb jako liczba ósemkowa jest sumą
wartości przedstawionych na rysunku

rwx rwx rwx

user

group other

001
002
004

010
020
040

100
200
400

Informatyka 1, studia niestacjonarne I stopnia

dr inż. Jarosław Forenc

Rok akademicki 2011/2012, Wykład nr 2

7/50

System ósemkowy

System ósemkowy -- zastosowania

zastosowania

Ósemkowy, oktalny, oktogonalny:

p = 8

,

D = {0,1,2,3,4,5,6,7}

Obecnie jego zastosowanie jest znikome

Przykład:

Obliczenia:

400 + 0 + 100 = 500
40 + 20 + 0 = 60
4 + 2 + 1 = 7

500 + 60 + 7 = 567

chmod 567 plik

r - x r w - r w x

1
2
4

0
20
40

100
0
400

Informatyka 1, studia niestacjonarne I stopnia

dr inż. Jarosław Forenc

Rok akademicki 2011/2012, Wykład nr 2

8/50

System dziesiętny

System dziesiętny -- zastosowania

zastosowania

Dziesiętny, dziesiątkowy:

p = 10

,

D = {0,1,2,3,4,5,6,7,8,9}

Podstawowy system stosowany w niemal wszystkich krajach

Od XVI wieku stosowano go obok systemu rzymskiego w:

nauce

księgowości

księgowości

bankowości

Zdaniem antropologów
o przyjęciu systemu
dziesiętnego przesądziło
posiadanie przez człowieka
10 palców ułatwiających
liczenie w systemie
dziesiętnym

Informatyka 1, studia niestacjonarne I stopnia

dr inż. Jarosław Forenc

Rok akademicki 2011/2012, Wykład nr 2

9/50

System dwunastkowy

System dwunastkowy -- zastosowania

zastosowania

Dwunastkowy:

p = 12

,

D = {0,1,2,3,4,5,6,7,8,9,A,B}

Uważany przez matematyków za system praktyczniejszy
niż dziesiętny, gdyż 12 ma 4 dzielniki naturalne (2,3,4,6)
a liczba 10 - tylko dwa (2,5)

Wcześniej był częściej stosowany, o czym świadczą

Wcześniej był częściej stosowany, o czym świadczą
niestandardowe nazwy liczebników

11

i

12

w niektórych

językach, np. w języku angielskim (11 - eleven, 12 - twelve)

Stosowany jest do pomiaru długości (USA):

stopa

= 12 cali

cal

= 12 linii

linia

= 12 punktów

Informatyka 1, studia niestacjonarne I stopnia

dr inż. Jarosław Forenc

Rok akademicki 2011/2012, Wykład nr 2

10/50

System dwunastkowy

System dwunastkowy -- zastosowania

zastosowania

Z systemu dwunastkowego wywodzą się pojęcia:

tuzin

(12 sztuk)

kopa

(5 tuzinów = 60 sztuk)

gros

(12 tuzinów = 144 sztuki)

Na systemie tym opiera się rachuba czasu:

Na systemie tym opiera się rachuba czasu:

rok

dzieli się na 12 miesięcy

doba

dzieli się na 24 godziny

godzina

na 60 minut

minuta

na 60 sekund

W niektórych kulturach liczba 12 ma szczególny status, np.

12 znaków zodiaku

12 bogów olimpijskich

12 plemion Izraela

12 apostołów

12 gwiazd na fladze UE

Informatyka 1, studia niestacjonarne I stopnia

dr inż. Jarosław Forenc

Rok akademicki 2011/2012, Wykład nr 2

11/50

System szesnastkowy

System szesnastkowy -- zastosowania

zastosowania

Szesnastkowy, heksadecymalny:

p = 16

,

D = {0,1,…,9,A,B,…,E,F}

Powszechnie używany w informatyce

Jeden bajt można zapisać za pomocą tylko dwóch cyfr w systemie
szesnastkowym:

0000 0000

(2)

00

(16)

0000 1111

(2)

0F

(16)

1111 1111

(2)

FF

(16)

1111 0000

(2)

F0

(16)

Dzięki powyższej właściwości system ten nadaje się do zapisu
bardzo dużych liczb, np. adresów w pamięci

Wiele programów wyświetla zawartość pamięci w systemie
szesnastkowym

Informatyka 1, studia niestacjonarne I stopnia

dr inż. Jarosław Forenc

Rok akademicki 2011/2012, Wykład nr 2

12/50

System szesnastkowy

System szesnastkowy -- zastosowania

zastosowania

Adresy sprzętowe

MAC

urządzeń sieciowych podawane są

w systemie szesnastkowym, np.

00:0A:E6:3E:FD:E1

Stosowany jest w HTML do zapisu 24-bitowych kolorów RGB

Informatyka 1, studia niestacjonarne I stopnia

dr inż. Jarosław Forenc

Rok akademicki 2011/2012, Wykład nr 2

13/50

System

System sześćdziesiątkowy

sześćdziesiątkowy -- zastosowania

zastosowania

Używany w Babilonie (1750 p.n.e.) skąd dotarł do Europy

Obecnie jest używany w związku z jednostkami czasu:

godzina

dzieli się na

60

minut

minuta

dzieli się na

60

sekund

Powszechnie występuje przy podawaniu miar kątów, a zwłaszcza

Powszechnie występuje przy podawaniu miar kątów, a zwłaszcza
długości i szerokości geograficznej

Zaletą tego systemu jest podzielność liczby 60 przez 2, 3, 4, 5, 6,
10, 12, 15, 20, 30 i 60

Dzięki powyższej podzielności ułamki mają formę liczb całkowitych

Przykład:

autobus jeździ 3 razy na godzinę
rozkład jazdy w systemie sześćdziesiątkowym: 7

00

; 7

20

; 7

40

; 8

00

rozkład jazdy w systemie dziesiętnym: 7,0; 7,3333…

Informatyka 1, studia niestacjonarne I stopnia

dr inż. Jarosław Forenc

Rok akademicki 2011/2012, Wykład nr 2

14/50

Przykład systemu

Przykład systemu niepozycyjnego

niepozycyjnego -- system rzymski

system rzymski

W systemie rzymskim posługujemy się siedmioma znakami:

I

- 1

V

- 5

X

- 10

L

- 50

C

- 100

D

- 500

M

- 1000

Za pomocą dostępnych symboli można określić liczby od

1

do

3999

System

addytywny

- wartość liczby określa się na podstawie sumy

wartości cyfr, np.

wartości cyfr, np.

II

(1 + 1 = 2),

XXX

(10 + 10 + 10 = 30)

CLX

(100 + 50 + 10 = 160),

MMXII

(1000 + 1000 + 10 + 1 + 1 = 2012)

Wyjątkiem od powyższej zasady są liczby do opisu których używa się
odejmowania, np.

IV

(5 - 1 = 4),

IX

(10 - 1 = 9),

XL

(50 - 10 = 40),

XC

(100 - 10 = 90)

Stosowany w łacińskiej części Europy do końca Średniowiecza

Niewygodny w prowadzeniu nawet prostych działań arytmetycznych,
brak ułamków

Informatyka 1, studia niestacjonarne I stopnia

dr inż. Jarosław Forenc

Rok akademicki 2011/2012, Wykład nr 2

15/50

Przykład systemu niepozycyjnego

Przykład systemu niepozycyjnego -- system rzymski

system rzymski

Zasady tworzenia liczb:

zestawiamy odpowiednie znaki od oznaczającego liczbę największą
do oznaczającego liczbę najmniejszą

XVI

= 10(

X

) + 5(

V

) + 1(

I

) = 16

jeżeli składnik liczby, którą piszemy, jest wielokrotnością liczby

jeżeli składnik liczby, którą piszemy, jest wielokrotnością liczby
nominalnej, wtedy zapisywany jest z użyciem kilku następujących
po sobie znaków

CCC

= 100(

C

) + 100(

C

) + 100(

C

) = 300

dodatkowo należy zachować zasadę nie pisania czterech tych
samych znaków po sobie, lecz napisać jeden znak wraz ze znakiem
oznaczającym wartość większą o jeden rząd liczbowy

CD

= 500(

D

) - 100(

C

) = 400

Informatyka 1, studia niestacjonarne I stopnia

dr inż. Jarosław Forenc

Rok akademicki 2011/2012, Wykład nr 2

16/50

Przykład systemu niepozycyjnego

Przykład systemu niepozycyjnego -- system rzymski

system rzymski

Zasady odczytu liczb:

cyfry jednakowe są dodawane

MMM

= 1000(

M

) + 1000(

M

) + 1000(

M

) = 3000

cyfry mniejsze stojące przed większymi są odejmowane od nich

CDXCIV

= 500(

D

) - 100(

C

) + 100(

C

) - 10(

X

) + 5(

V

) - 1(

I

) = 494

cyfry mniejsze stojące za większymi są do nich dodawane

MDCLX

= 1000(

M

) + 500(

D

) + 100(

C

) + 50(

L

) + 10 (

X

) = 1660

Informatyka 1, studia niestacjonarne I stopnia

dr inż. Jarosław Forenc

Rok akademicki 2011/2012, Wykład nr 2

17/50

Kodowanie

Kodowanie

Informacje przetwarzane przez komputer to liczby, ale także
inne obiekty, np. litery, wartości logiczne, obrazy, itp.

Każda informacja przetwarzana przez komputer musi być
reprezentowana za pomocą tylko dwóch stanów:

wysokiego (1 - jedynka)

wysokiego (1 - jedynka)

niskiego (0 - zero)

Konieczne są zatem reguły przekształcania różnych postaci
informacji na informację binarną (zero-jedynkową)

Proces przekształcania jednego rodzaju postaci informacji
na inną postać nazywamy

kodowaniem

Informatyka 1, studia niestacjonarne I stopnia

dr inż. Jarosław Forenc

Rok akademicki 2011/2012, Wykład nr 2

18/50

Kodowanie

Kodowanie

Informatyka 1, studia niestacjonarne I stopnia

dr inż. Jarosław Forenc

Rok akademicki 2011/2012, Wykład nr 2

19/50

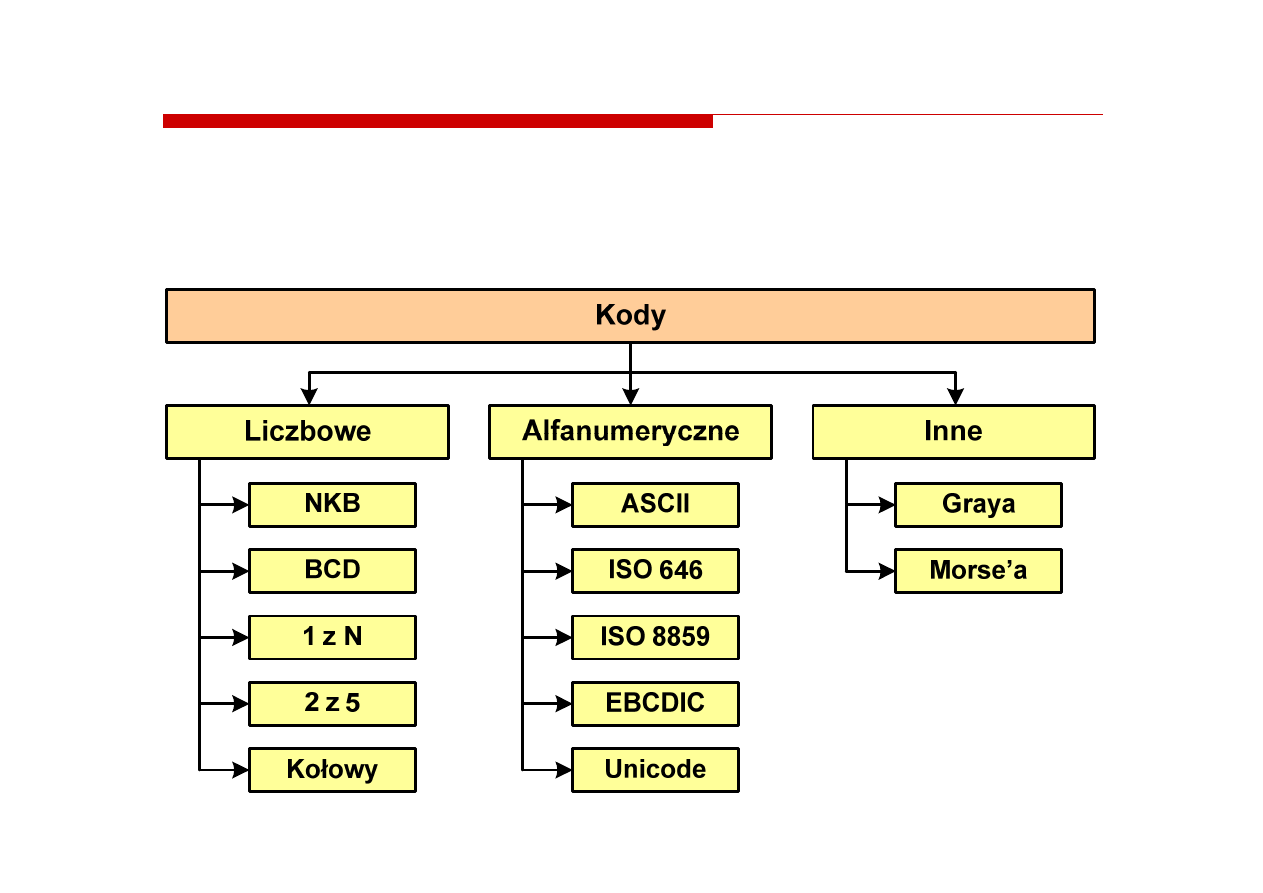
Kody liczbowe

Kody liczbowe -- Naturalny Kod Binarny (NKB)

Naturalny Kod Binarny (NKB)

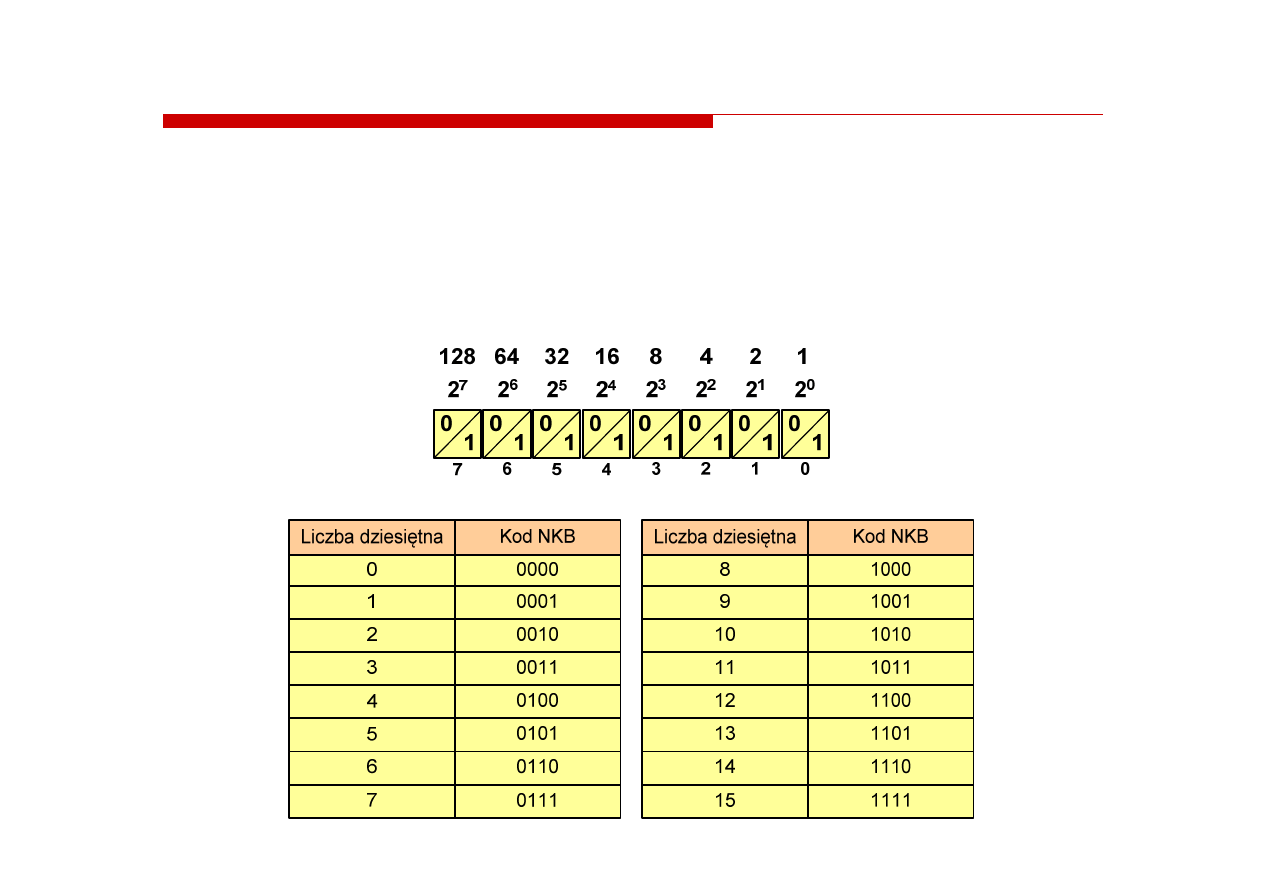
Jeżeli dowolnej liczbie dziesiętnej przypiszemy odpowiadającą
jej liczbę binarną, to otrzymamy

naturalny kod binarny

(NKB)

Informatyka 1, studia niestacjonarne I stopnia

dr inż. Jarosław Forenc

Rok akademicki 2011/2012, Wykład nr 2

20/50

Kody liczbowe

Kody liczbowe -- Naturalny Kod Binarny (NKB)

Naturalny Kod Binarny (NKB)

W naturalnym kodzie binarnym za pomocą

n

-bitów można zapisać

liczbę dwójkową z zakresu:

Największe liczby dwójkowe:

1

2

,

0

X

n

)

2

(

−

=

Największe liczby dwójkowe:

)

10

(

32

)

2

(

)

10

(

16

)

2

(

)

10

(

10

)

2

(

)

10

(

8

)

2

(

)

10

(

3

)

2

(

)

10

(

2

)

2

(

)

10

(

1

)

2

(

295

967

294

4

1

2

11111111

11111111

bity

32

535

65

1

2

11111111

11111111

bitów

16

023

1

1

2

1111111111

bitów

10

255

1

2

11111111

bitów

8

7

1

2

111

bity

3

3

1

2

11

bity

2

1

1

2

1

bit

1

=

−

=

−

=

−

=

−

=

−

=

−

=

−

=

−

=

−

=

−

=

−

=

−

=

−

=

−

K

L

Informatyka 1, studia niestacjonarne I stopnia

dr inż. Jarosław Forenc

Rok akademicki 2011/2012, Wykład nr 2

21/50

Kody liczbowe

Kody liczbowe -- Kod BCD

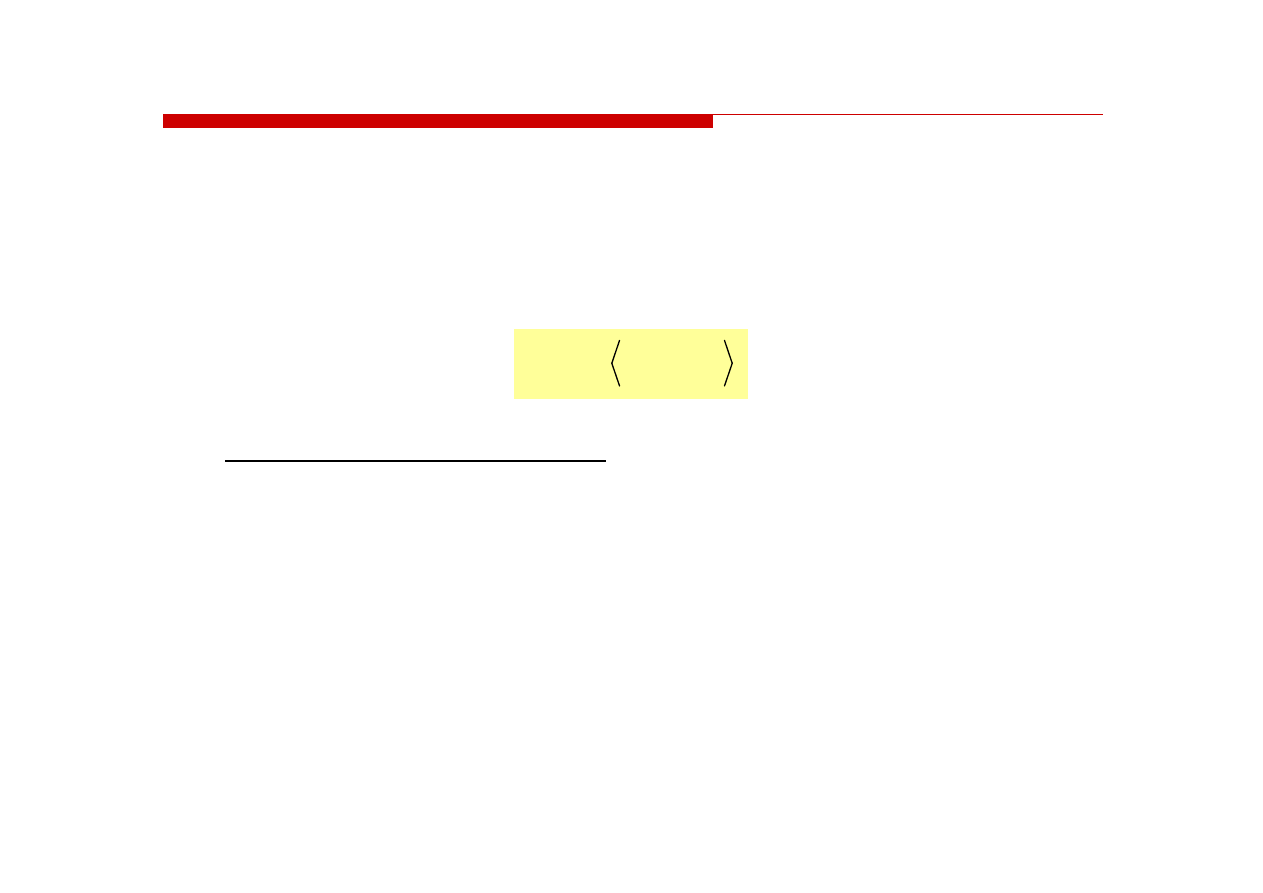
Kod BCD

B

inary-

C

oded

D

ecimal - dziesiętny zakodowany dwójkowo

BCD

- sposób zapisu liczb polegający na zakodowaniu kolejnych

cyfr liczby dziesiętnej w 4-bitowym systemie dwójkowym (NKB)

W ogólnym przypadku kodowane są tylko znaki

0 ÷ 9

Pozostałe kombinacje bitowe mogą być stosowane
do kodowania znaku liczby lub innych znaczników

Informatyka 1, studia niestacjonarne I stopnia

dr inż. Jarosław Forenc

Rok akademicki 2011/2012, Wykład nr 2

22/50

Kody liczbowe

Kody liczbowe -- Kod BCD

Kod BCD

Przykład:

}

}

}

8

6

1

)

BCD

(

)

10

(

00

0001011010

168

1000

0110

0001

?

168

=

=

{

{

{

3

5

9

)

10

(

)

BCD

(

953

11

1001010100

0011

0101

1001

?

0011

|

0101

|

1001

=

=

Zastosowania:

urządzenia elektroniczne z wyświetlaczem cyfrowym
(np. kalkulatory, mierniki cyfrowe)

przechowywania daty i czasu w BIOSie komputerów
(także wczesne modele PlayStation 3)

zapis części ułamkowych kwot (systemy bankowe)

)

BCD

(

)

10

(

00

0001011010

168

=

)

10

(

)

BCD

(

953

11

1001010100

=

Informatyka 1, studia niestacjonarne I stopnia

dr inż. Jarosław Forenc

Rok akademicki 2011/2012, Wykład nr 2

23/50

Kody liczbowe

Kody liczbowe -- Kod BCD: przechowywanie liczb

Kod BCD: przechowywanie liczb

Użycie 4 najmłodszych bitów jednego bajta, 4 starsze bity są
ustawiane na jakąś konkretną wartość:

0000

1111 (np. kod EBCDIC, liczby F0

(16)

÷ F9

(16)

)

0011 (tak jak w ASCII, liczby 30

(16)

÷ 39

(16)

)

0011 (tak jak w ASCII, liczby 30

(16)

÷ 39

(16)

)

Zapis dwóch cyfr w każdym bajcie (starsza na starszej połówce,
młodsza na młodszej połówce) - jest to tzw.

spakowane BCD

w przypadku liczby zapisanej na kilku bajtach, najmniej znacząca
tetrada (4 bity) używane są jako flaga znaku

standardowo przyjmuje się 1100 (C

(16)

) dla znaku plus (+) i 1101

(D

(16)

) dla znaku minus (-), np.

)

D

127

(

1101

0111

0010

0001

127

)

C

127

(

1100

0111

0010

0001

127

)

16

(

)

10

(

)

16

(

)

10

(

=

−

=

Informatyka 1, studia niestacjonarne I stopnia

dr inż. Jarosław Forenc

Rok akademicki 2011/2012, Wykład nr 2

24/50

Kody liczbowe

Kody liczbowe -- Kod BCD

Kod BCD

Zalety

BCD w stosunku do NKB:

prostsze obliczenia i zaokrąglanie liczb (podstawa systemu: 10)

prostsza konwersja do postaci dogodnej do wyświetlenia (wyświetlacz
7-segmentowy), konwersja wykonywana w czasie liniowym

niektóre wartości niecałkowite (np. 0,1) mają w BCD skończoną

niektóre wartości niecałkowite (np. 0,1) mają w BCD skończoną
reprezentację, dzięki czemu BCD wprowadza mniejsze błędy obliczeń

Wady

BCD w stosunku do NKB:

skomplikowane operacje arytmetyczne (dodawanie, mnożenie)

nadmiarowość - na 4 bitach można zapisać 16 różnych wartości,
a BCD wykorzystuje tylko 10 z nich

operacje wykonywane w praktycznie istniejących implementacjach
BCD są wolniejsze niż w NKB

Informatyka 1, studia niestacjonarne I stopnia

dr inż. Jarosław Forenc

Rok akademicki 2011/2012, Wykład nr 2

25/50

Kody liczbowe

Kody liczbowe -- Kod BCD

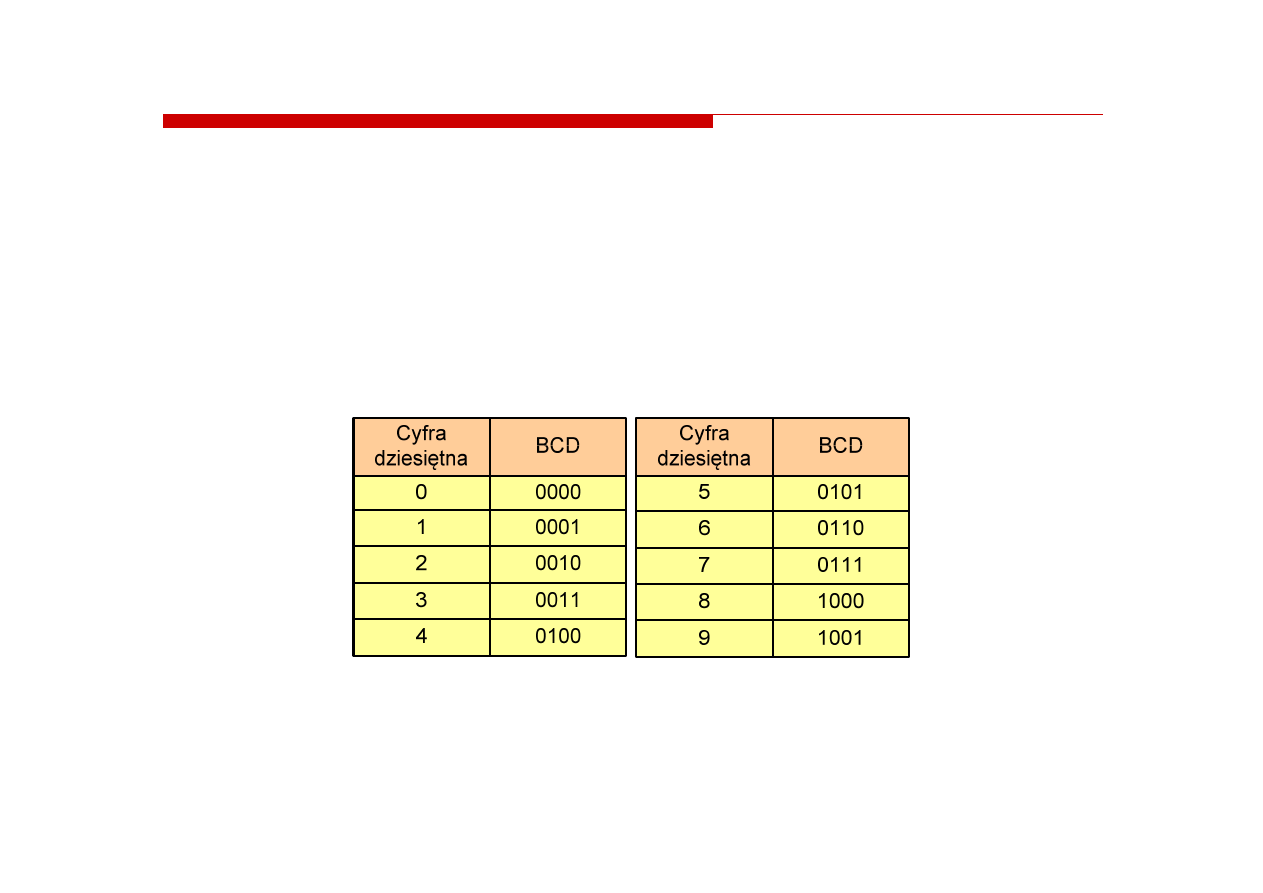
Kod BCD

Na poprzednich slajdach przedstawiono podstawową postać kodu
BCD -

BCD 8421

lub

SBCD

(Simple Binary - Coded Decimal)

Istnieją inne warianty kodu BCD, w których poszczególne cyfry
są kodowane w inny sposób

Informatyka 1, studia niestacjonarne I stopnia

dr inż. Jarosław Forenc

Rok akademicki 2011/2012, Wykład nr 2

26/50

Kody liczbowe

Kody liczbowe -- Kod 1 z N (pierścieniowy)

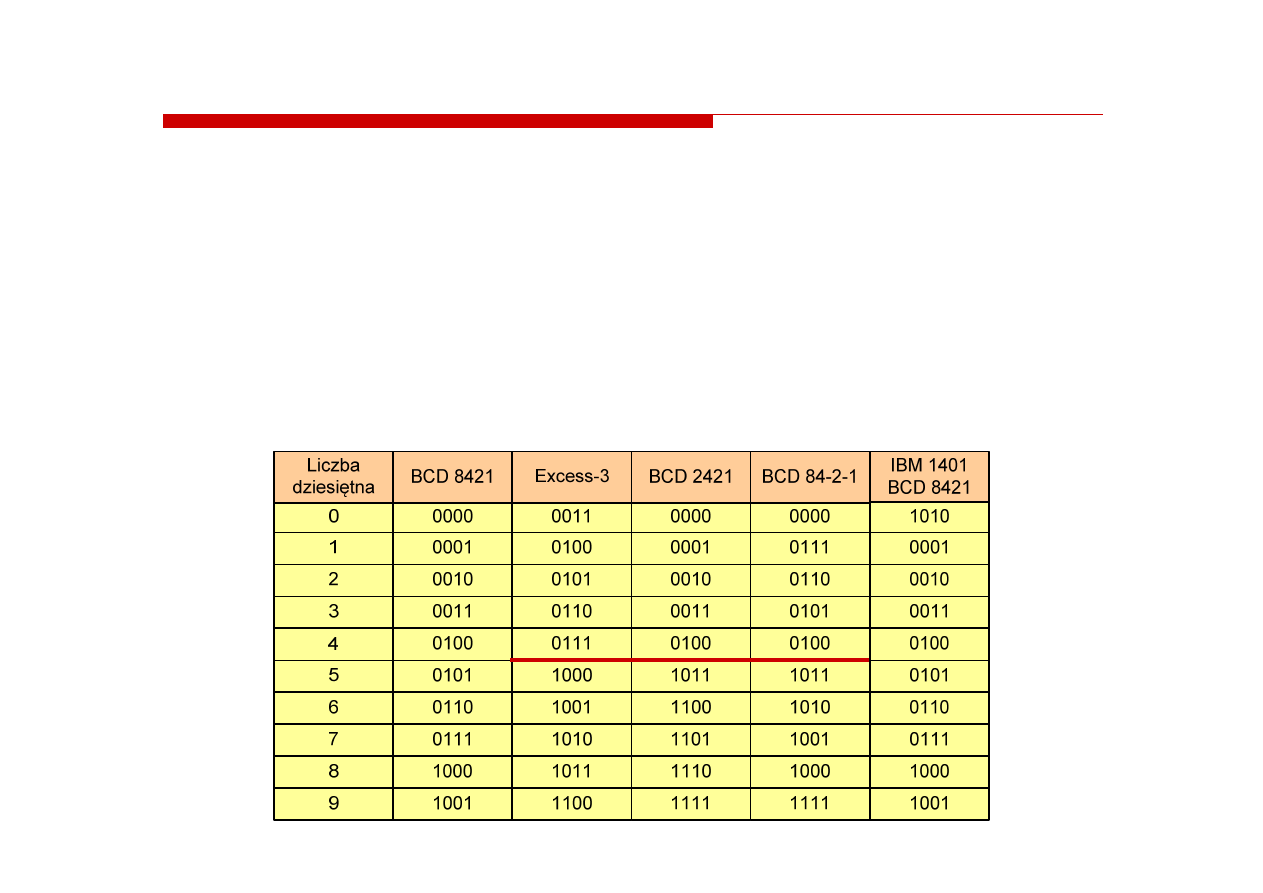
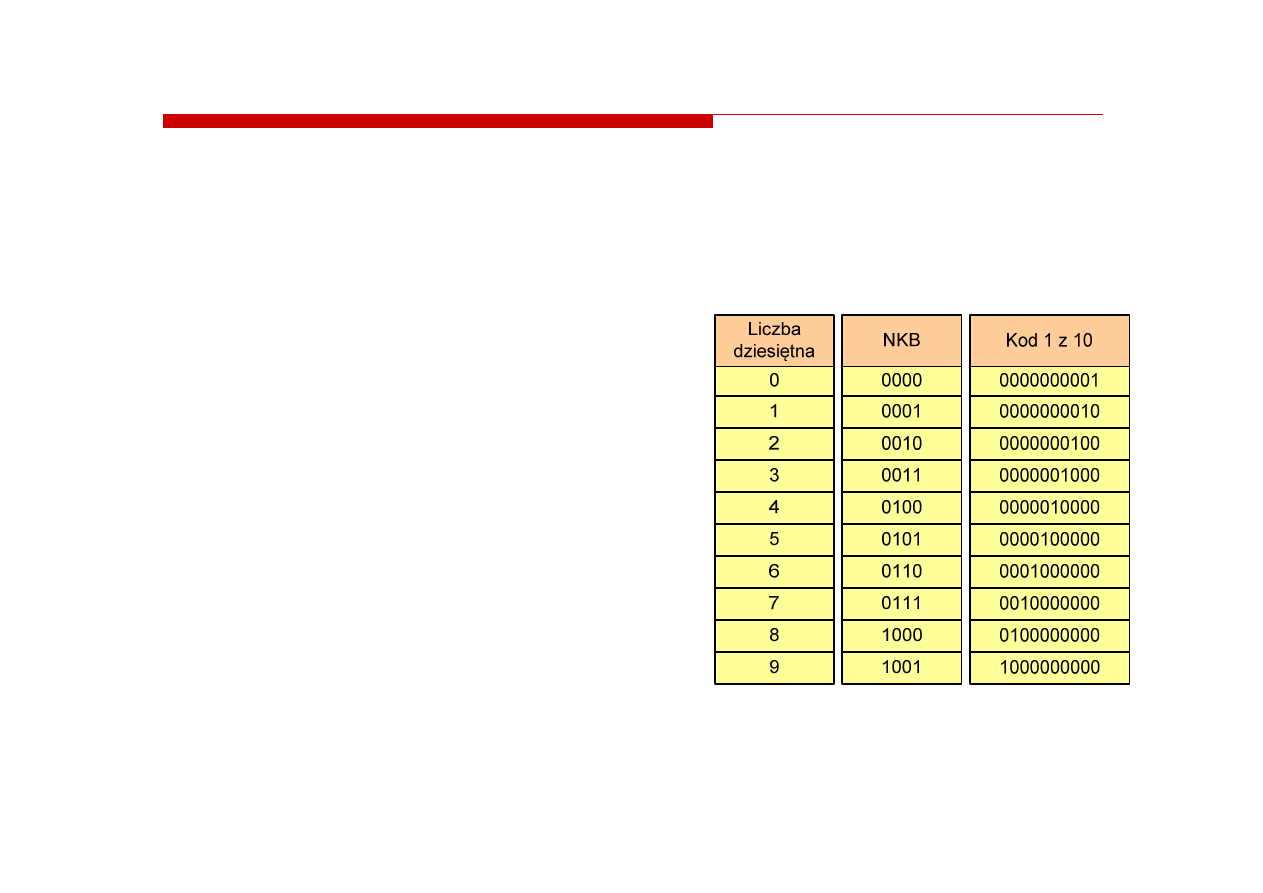
Kod 1 z N (pierścieniowy)

Najbardziej rozpowszechniony
jest

kod 1 z 10

Kod wagowy (9,8,7,6,5,4,3,2,1,0)

Kod detekcyjny

w czasie wykonywania
operacji można kontrolować
liczbę jedynek

wykrycie braku jedynki lub
wykrycie dwóch lub więcej
jedynek wskazuje na błąd

Informatyka 1, studia niestacjonarne I stopnia

dr inż. Jarosław Forenc

Rok akademicki 2011/2012, Wykład nr 2

27/50

Kody liczbowe

Kody liczbowe -- Kod 2 z 5

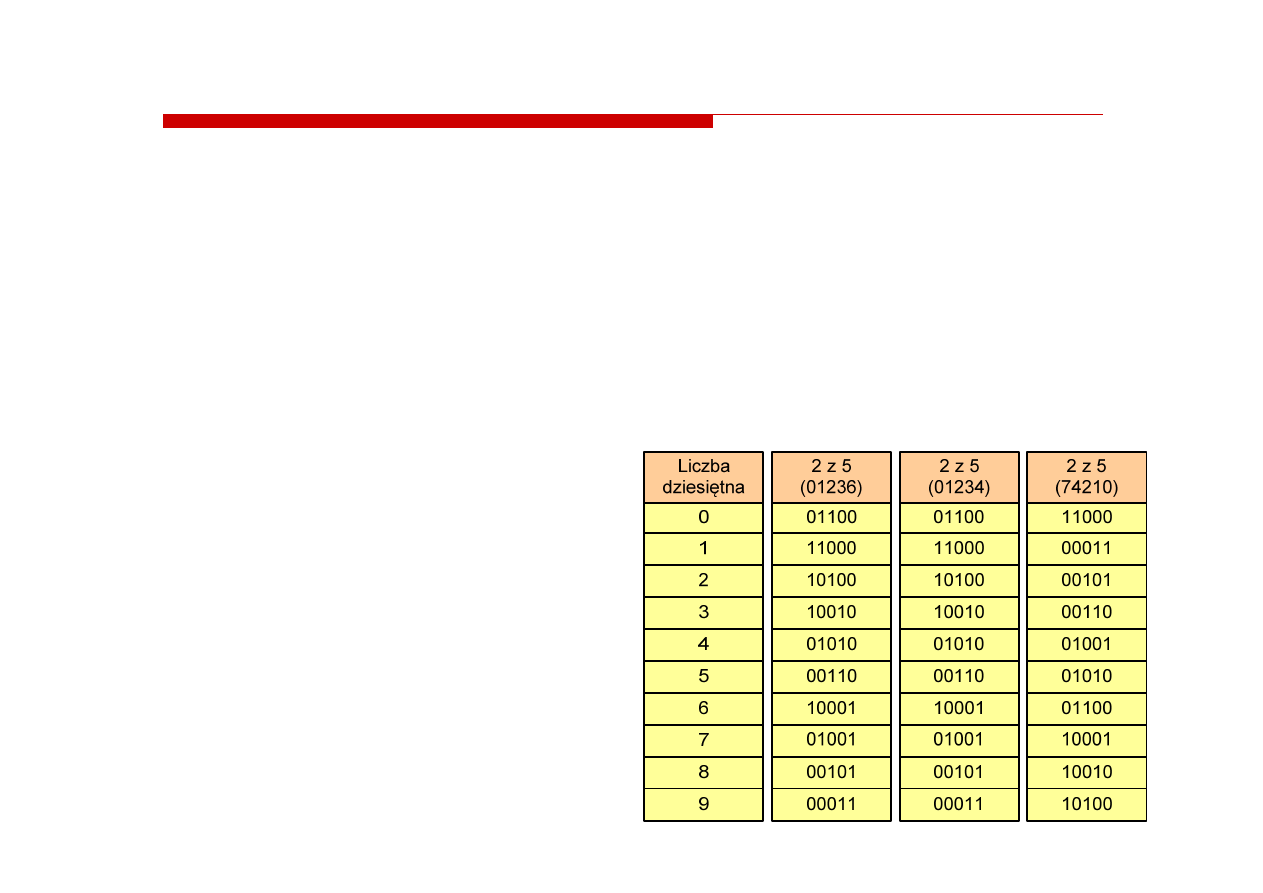
Kod 2 z 5

Kod 5-bitowy - jeden znak kodowany jest na 5 bitach (2 bity są
zawsze równe jeden, a 3 bity są zawsze równe zeru)

Można zakodować 10 znaków, koduje cyfry dziesiętne, kody nie są
wzajemnie jednoznaczne (ta sama wartość może być zakodowana
w różny sposób)

w różny sposób)

Kod stałowagowy, występuje
w wielu wersjach, np.
01236, 01234, 74210

Kod detekcyjny

Stosowany przede wszystkim
w

kodach kreskowych

Informatyka 1, studia niestacjonarne I stopnia

dr inż. Jarosław Forenc

Rok akademicki 2011/2012, Wykład nr 2

28/50

Kody liczbowe

Kody liczbowe -- Kod 2 z

Kod 2 z 5 Industrial (1960 r.)

5 Industrial (1960 r.)

Jednowymiarowy kod kreskowy
kodujący cyfry:

0

÷

9

Każdy znak składa się z 5 pasków
(2 szerokich i 3 wąskich),
odstępy pełnią rolę separatorów

odstępy pełnią rolę separatorów

Szeroki pasek jest wielokrotnością
wąskiego, szerokości muszą być
takie same dla całego kodu

Struktura kodu:

start: 11011010

numer

stop: 11010110

Może zawierać sumę kontrolną

Informatyka 1, studia niestacjonarne I stopnia

dr inż. Jarosław Forenc

Rok akademicki 2011/2012, Wykład nr 2

29/50

Kody liczbowe

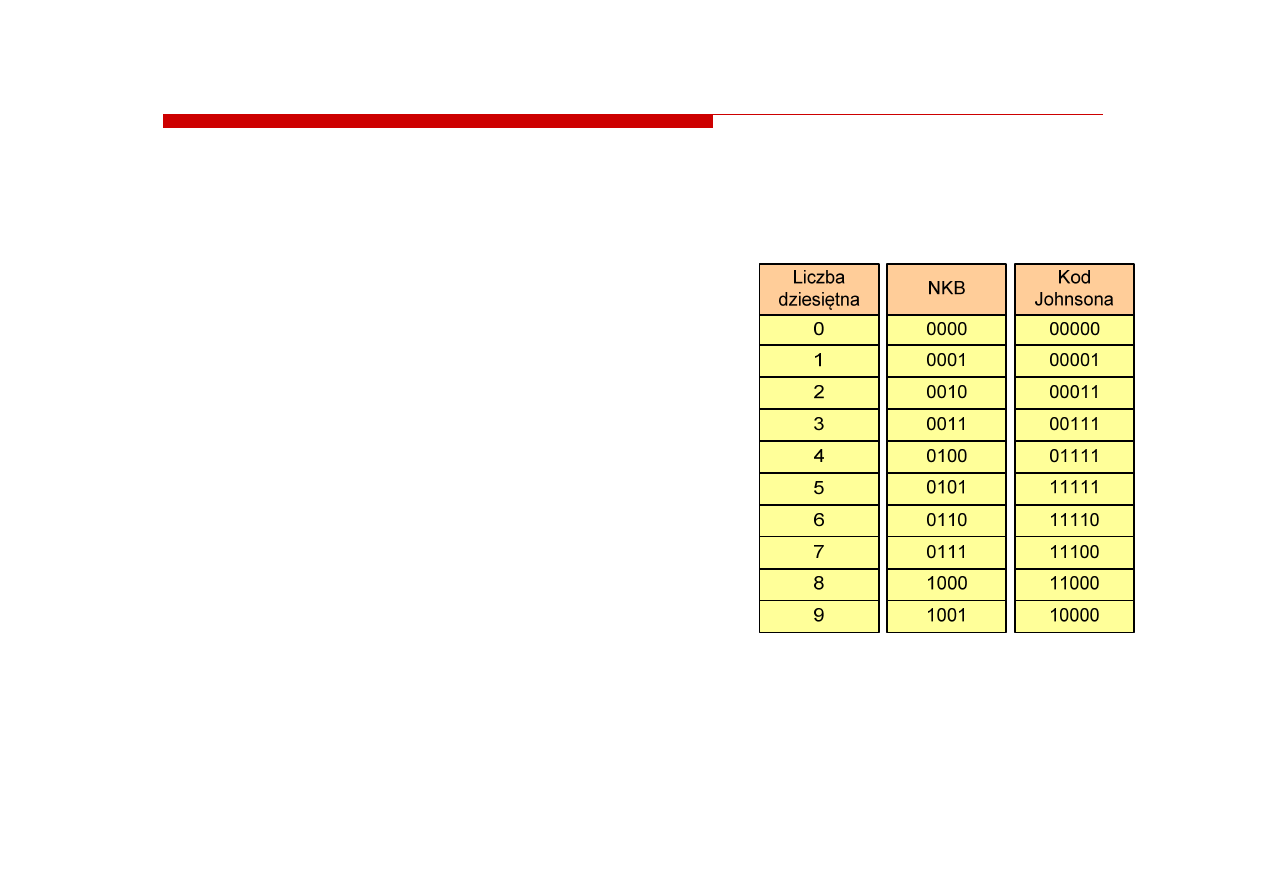
Kody liczbowe -- Kod

Kod kołowy

kołowy

5-bitowy kod kołowy nazywany jest

kodem Johnsona

Począwszy od najmniej znaczącego
bitu zwiększa się liczba stanów 1
aż do wszystkich bitów równych 1

aż do wszystkich bitów równych 1

Następnie stanów 1 zaczyna ubywać
(począwszy od najmniej znaczącego
bitu) aż do osiągnięcia wartości 10000

Kolejną wartością po 10000 będzie
ponownie 00000

Informatyka 1, studia niestacjonarne I stopnia

dr inż. Jarosław Forenc

Rok akademicki 2011/2012, Wykład nr 2

30/50

Kody liczbowe

Kody liczbowe -- Kod Graya (refleksyjny)

Kod Graya (refleksyjny)

Kod dwójkowy, bezwagowy, niepozycyjny

Dwa kolejne słowa kodowe różnią się stanem jednego bitu

Kod cykliczny - ostatni i pierwszy wyraz również różnią się stanem
jednego bitu

Konstrukcja n-bitowego kodu:

dopisz do (n-1)-bitowego kodu te
same słowa kodowe, ale w odwrotnej
kolejności (lustrzane odbicie)

do początkowych wyrazów dopisz bit
o wartości 0, natomiast do odbitych
lustrzanie bit o wartości 1

Informatyka 1, studia niestacjonarne I stopnia

dr inż. Jarosław Forenc

Rok akademicki 2011/2012, Wykład nr 2

31/50

Kody liczbowe

Kody liczbowe -- Kod Graya

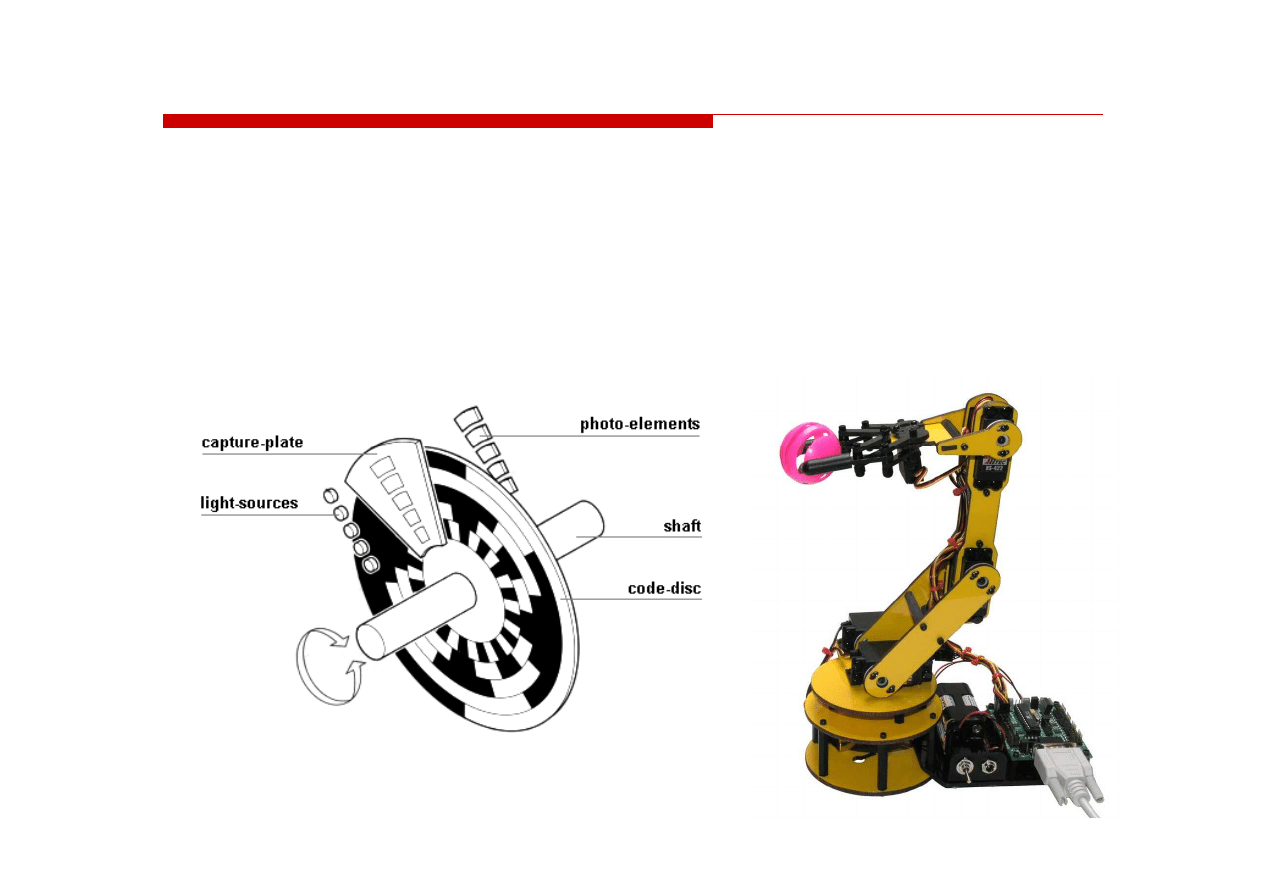
Kod Graya

Stosowany w przetwornikach analogowo-cyfrowych, do cyfrowego
pomiaru analogowych wielkości mechanicznych (przesuw liniowy,
kąt obrotu)

http://tams-www.informatik.uni-hamburg.de
/applets/hades/webdemos/10-gates/15-graycode/dual2gray.html

Informatyka 1, studia niestacjonarne I stopnia

dr inż. Jarosław Forenc

Rok akademicki 2011/2012, Wykład nr 2

32/50

Kod

Kod ASCII

ASCII

ASCII - A

merican

S

tandard

C

ode

for

I

nformation

I

nterchange

7-bitowy kod przypisujący
liczby z zakresu 0-127:
- literom (alfabet angielski)
- cyfrom

- cyfrom
- znakom przestankowym
- innym symbolom
- poleceniom sterującym

kody 0-31, 127 - 33 kody
sterujące służące do sterowania
urządzeniami typu drukarka
czy terminal

kody 32-126 - 95 kodów
tworzących zbiór znaków ASCII

Informatyka 1, studia niestacjonarne I stopnia

dr inż. Jarosław Forenc

Rok akademicki 2011/2012, Wykład nr 2

33/50

Kod ASCII

Kod ASCII -- Kody sterujące

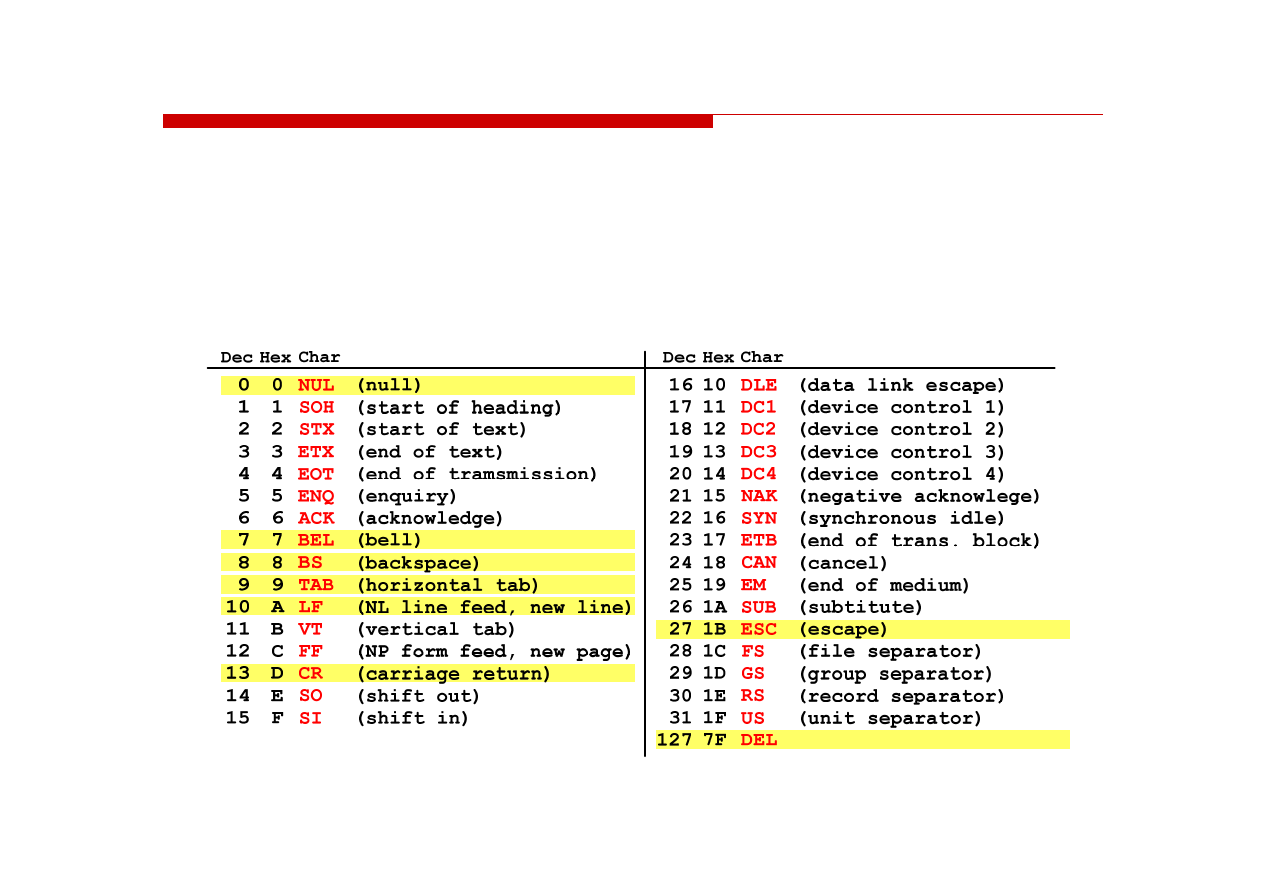
Kody sterujące

Kody sterujące - 33 kody, o numerach: 0-31, 127

Informatyka 1, studia niestacjonarne I stopnia

dr inż. Jarosław Forenc

Rok akademicki 2011/2012, Wykład nr 2

34/50

Kod ASCII

Kod ASCII -- Kody sterujące a język C

Kody sterujące a język C

0

(10)

= 0

(16)

NUL

- koniec łańcucha znaków, zapis:

\0

7

(10)

= 7

(16)

BEL

- alarm, dźwięk głośniczka, zapis:

\a

8

(10)

= 8

(16)

BS

- klawisz

Backspace

, zapis:

\b

9

(10)

= 9

(16)

TAB

- tabulacja (odstęp), zapis:

\t

9

(10)

= 9

(16)

TAB

- tabulacja (odstęp), zapis:

\t

10

(10)

= A

(16)

LF

- przejście do nowego wiersza, zapis:

\n

13

(10)

= D

(16)

CR

- powrót na początek wiersza, zapis:

\r

27

(10)

= 1B

(16)

ESC

- klawisz

Escape

127

(10)

= 7F

(16)

DEL

- klawisz

Delete

Informatyka 1, studia niestacjonarne I stopnia

dr inż. Jarosław Forenc

Rok akademicki 2011/2012, Wykład nr 2

35/50

Kod ASCII

Kod ASCII -- Pliki tekstowe

Pliki tekstowe

Elementami pliku tekstowego są

wiersze

, mogą one mieć różną długość

W systemie Windows każdy wiersz pliku zakończony jest parą znaków:

CR

, ang. carriage return - powrót karetki, kod ASCII -

13

(10)

=

0D

(16)

LF

, ang. line feed - przesunięcie o wiersz, kod ASCII -

10

(10)

=

0A

(16)

Załóżmy, że plik tekstowy ma postać:

Załóżmy, że plik tekstowy ma postać:

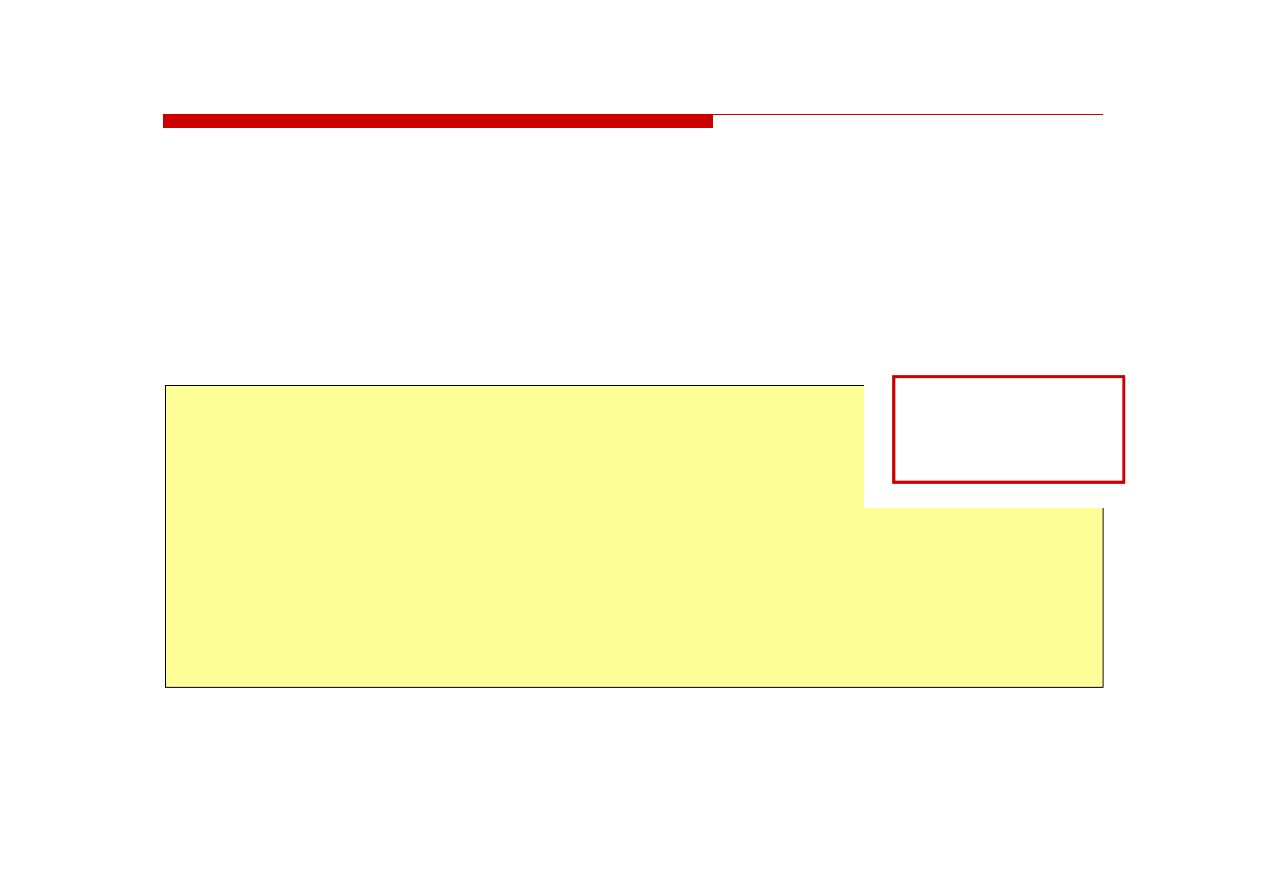
Rzeczywista zawartość pliku jest następująca:

Wydruk zawiera:

przesunięcie od początku pliku (szesnastkowo)
wartości poszczególnych bajtów pliku (szesnastkowo)
znaki odpowiadające bajtom pliku (traktując bajty jako kody ASCII)

Informatyka 1, studia niestacjonarne I stopnia

dr inż. Jarosław Forenc

Rok akademicki 2011/2012, Wykład nr 2

36/50

Kod ASCII

Kod ASCII -- Pliki tekstowe

Pliki tekstowe

W czasie wczytywania tekstu z pliku do pamięci komputera znaki

CR

i

LF

zastępowane są jednym znakiem -

LF

Znak

LF

w języku C reprezentowany jest przez

\n

, zaś

CR

- przez

\r

#include <stdio.h>

\n --> 10 A

\r --> 13 D

Przy zapisywaniu łańcucha znaków do pliku tekstowego mamy sytuację
odwrotną - znak

LF

zastępowany jest parą

CR

i

LF

int main()

{

printf("\\n --> %d %X\n",'\n','\n');

printf("\\r --> %d %X\n",'\r','\r');

return 0;

}

\r --> 13 D

Informatyka 1, studia niestacjonarne I stopnia

dr inż. Jarosław Forenc

Rok akademicki 2011/2012, Wykład nr 2

37/50

Kod ASCII

Kod ASCII -- Pliki tekstowe

Pliki tekstowe

W systemie Linux znakiem końca wiersza jest tylko

LF

o kodzie ASCII -

10

(10)

=

0A

(16)

Załóżmy, że plik tekstowy ma postać:

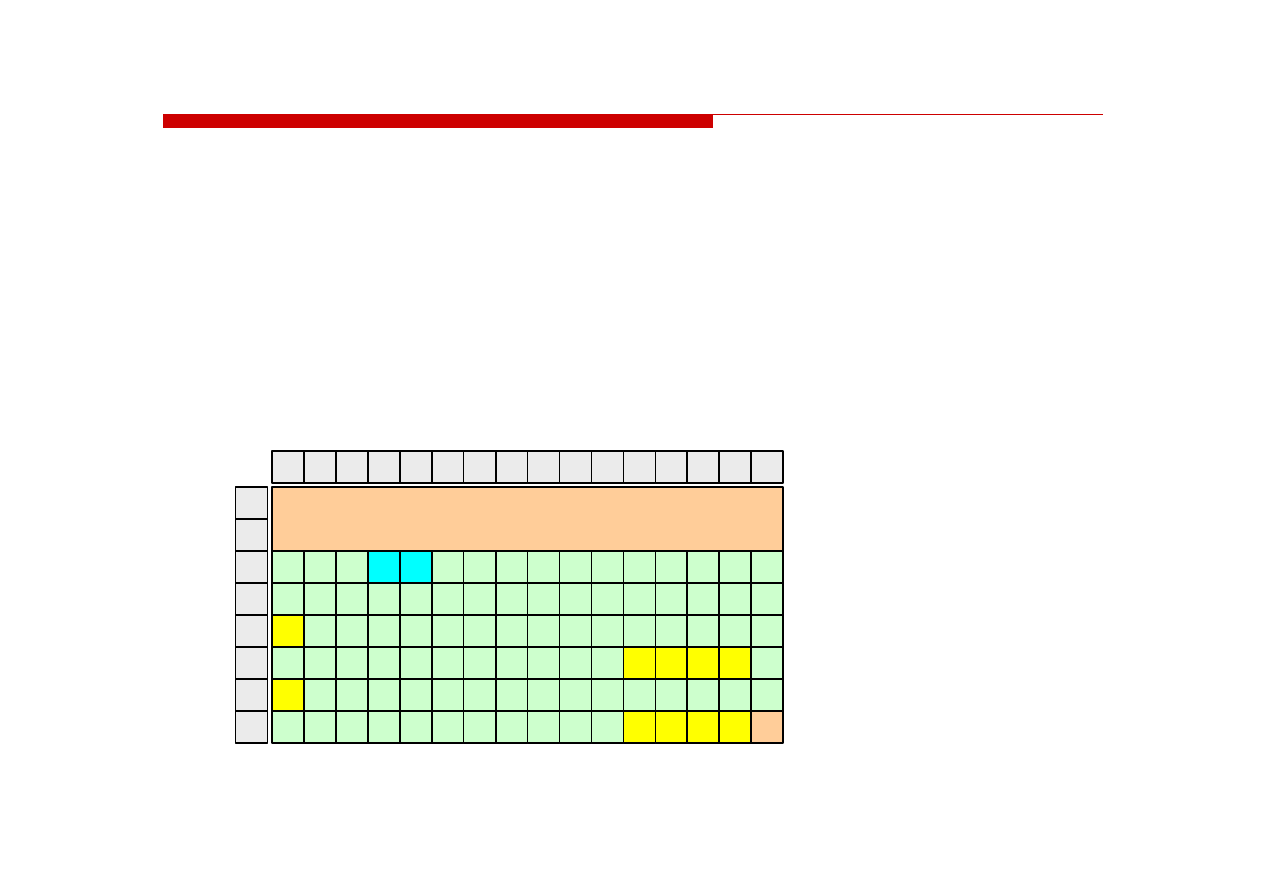
Rzeczywista zawartość pliku jest następująca:

Podczas przesyłania pliku tekstowego (np. przez protokół

ftp

) z systemu

Linux do systemu Windows pojedynczy znak

LF

zamieniany jest

automatycznie na parę znaków

CR

i

LF

Błędne przesłanie pliku tekstowego (w trybie binarnym) powoduje
nieprawidłowe jego wyświetlanie:

Informatyka 1, studia niestacjonarne I stopnia

dr inż. Jarosław Forenc

Rok akademicki 2011/2012, Wykład nr 2

38/50

ISO/IEC 646

ISO/IEC 646

ISO/IEC 646

- norma definiująca modyfikację 7-bitowego

kodowania ASCII, stosowana w latach 70-tych i 80-tych

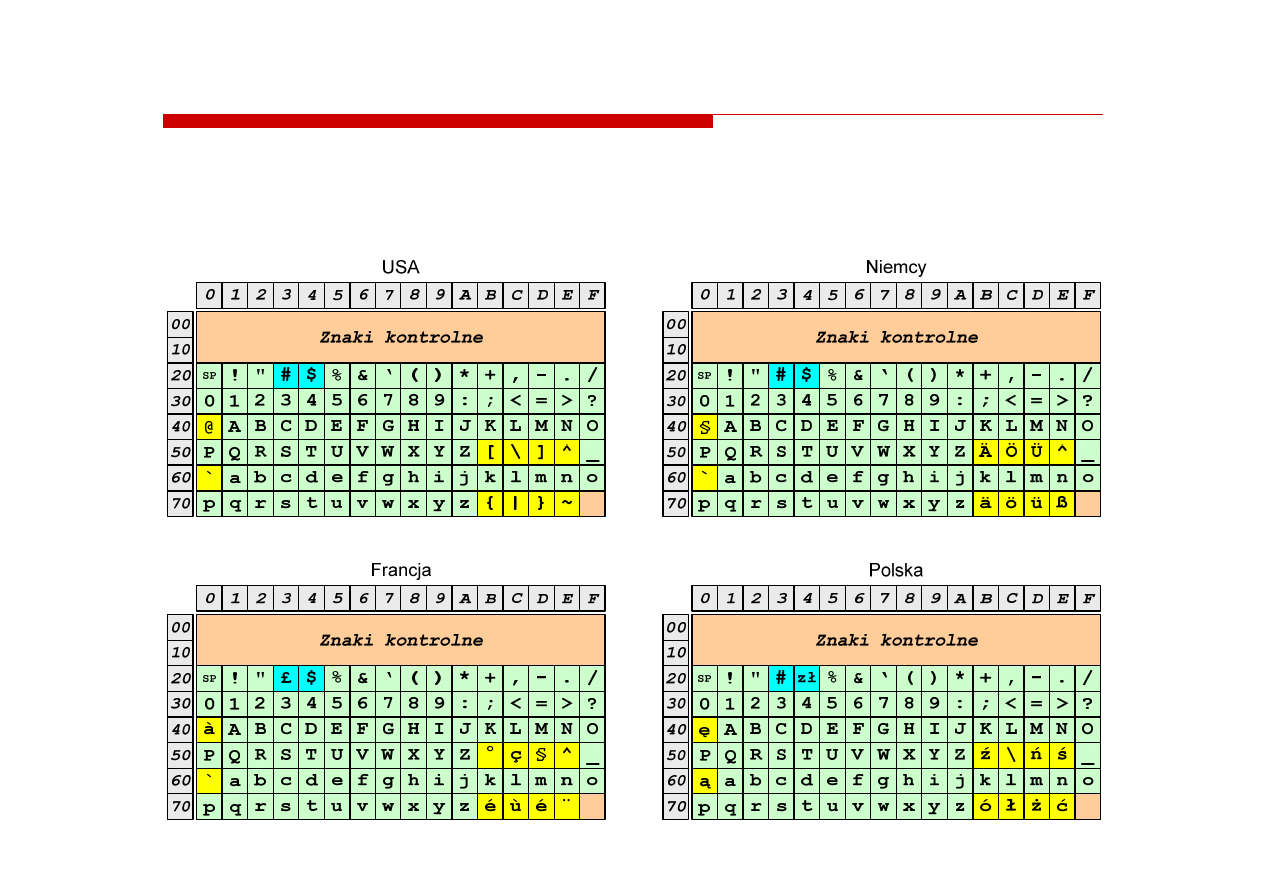
W normie określono 10 pozycji na znaki w języku kraju, który
przyjął tę normę oraz 2 pozycje na znaki walut

Wszystkie pozostałe znaki są zgodne z ASCII

! " # $ % & ‘ ( ) * + , - . /

SP

1 2 3 4 5 6

0

7 8 9 : ; < = > ?

A B C D E F G H I J K L M N O

@

Q R S T U V

P

W X Y Z [ \ ] ^ _

Znaki kontrolne

a b c d e f g h i j k l m n o

`

q r s t u v

p

w x y z { | } ~

0

1

2

3

4

5

6

7

8

9

A

B

C

D

E

F

00

10

20

30

40

50

60

70

żółty - znaki narodowe

niebieski - znaki walut

Informatyka 1, studia niestacjonarne I stopnia

dr inż. Jarosław Forenc

Rok akademicki 2011/2012, Wykład nr 2

39/50

ISO/IEC 646

ISO/IEC 646 -- odmiany

odmiany narodowe

narodowe

Norma: BN-74/3101-01

Informatyka 1, studia niestacjonarne I stopnia

dr inż. Jarosław Forenc

Rok akademicki 2011/2012, Wykład nr 2

40/50

ISO/IEC 8859

ISO/IEC 8859

ISO/IEC 8859

- zestaw standardów służących do kodowania

znaków za pomocą 8-bitów

Wszystkie zestawy ISO 8859 mają znaki

0

(10)

-127

(10)

(

00

(16)

-7F

(16)

)

takie same jak w kodzie ASCII

Pozycjom

128

-159

(

80

-9F

) przypisane są dodatkowe

Pozycjom

128

(10)

-159

(10)

(

80

(16)

-9F

(16)

) przypisane są dodatkowe

kody sterujące, tzw. C1 (obecnie nie są używane)

W czerwcu 2004 roku, grupa robocza odpowiedzialna za
utrzymanie zestawów znaków kodowanych ośmiobitowo została
rozwiązana, wstrzymane zostały prace związane z ISO 8859,
a skoncentrowano się na standardzie

Unicode

Informatyka 1, studia niestacjonarne I stopnia

dr inż. Jarosław Forenc

Rok akademicki 2011/2012, Wykład nr 2

41/50

ISO/IEC 8859

ISO/IEC 8859

Stosowane standardy ISO 8859:

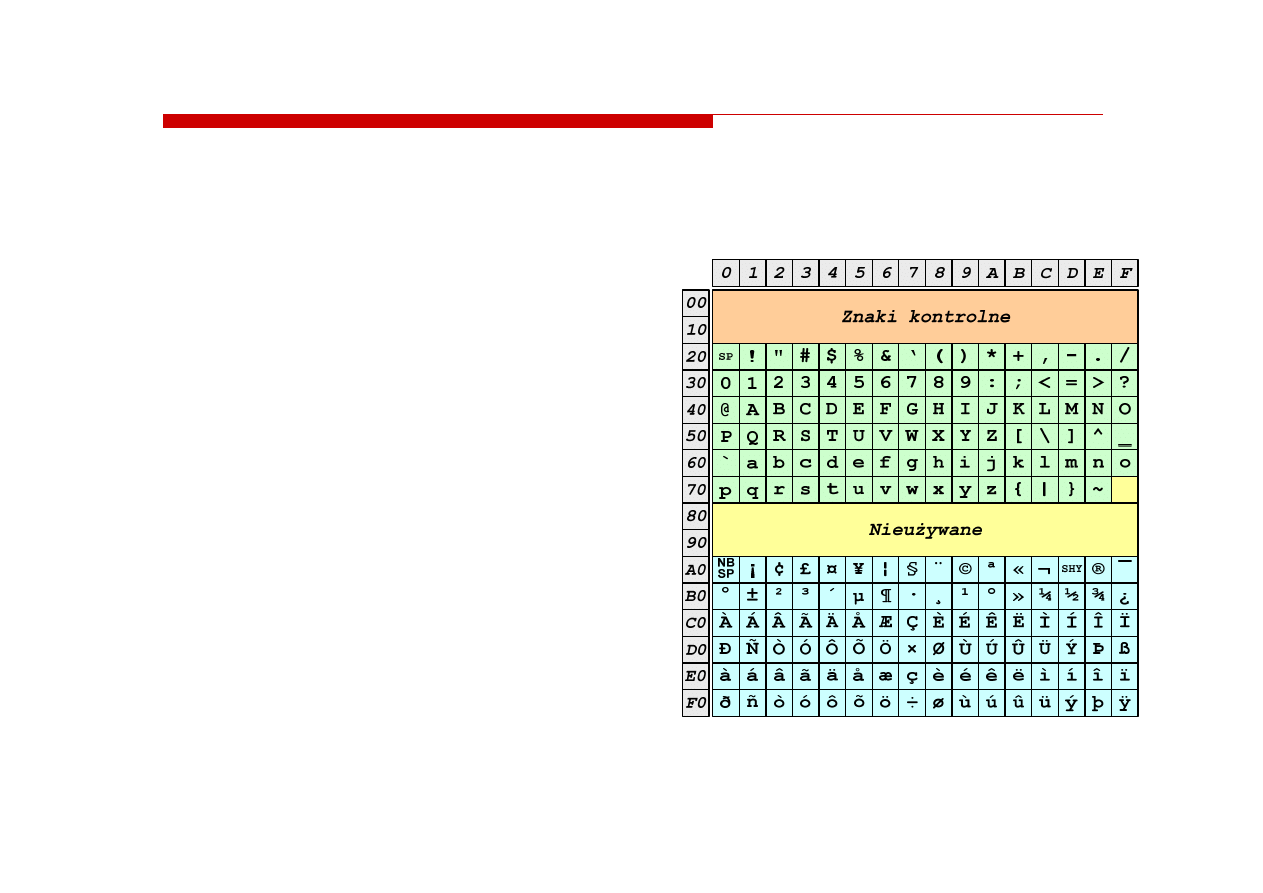
ISO 8859-1 (Latin-1) - alfabet łaciński dla Europy zachodniej
ISO 8859-2 (Latin-2) - łaciński dla Europy środkowej i wschodniej
ISO 8859-3 (Latin-3) - łaciński dla Europy południowej
ISO 8859-4 (Latin-4) - łaciński dla Europy północnej
ISO 8859-5 (Cyrillic) - dla cyrylicy

ISO 8859-5 (Cyrillic) - dla cyrylicy
ISO 8859-6 (Arabic) - dla alfabetu arabskiego
ISO 8859-7 (Greek) - dla alfabetu greckiego
ISO 8859-8 (Hebrew) - dla alfabetu hebrajskiego
ISO 8859-9 (Latin-5)
ISO 8859-10 (Latin-6)
ISO 8859-11 (Thai) - dla alfabetu tajskiego
ISO 8859-12 - brak
ISO 8859-13 (Latin-7)
ISO 8859-14 (Latin-8) - zawiera polskie znaki
ISO 8859-15 (Latin-9)
ISO 8859-16 (Latin-10) - łaciński dla Europy środkowej, zawiera polskie znaki

Informatyka 1, studia niestacjonarne I stopnia

dr inż. Jarosław Forenc

Rok akademicki 2011/2012, Wykład nr 2

42/50

ISO/IEC 8859

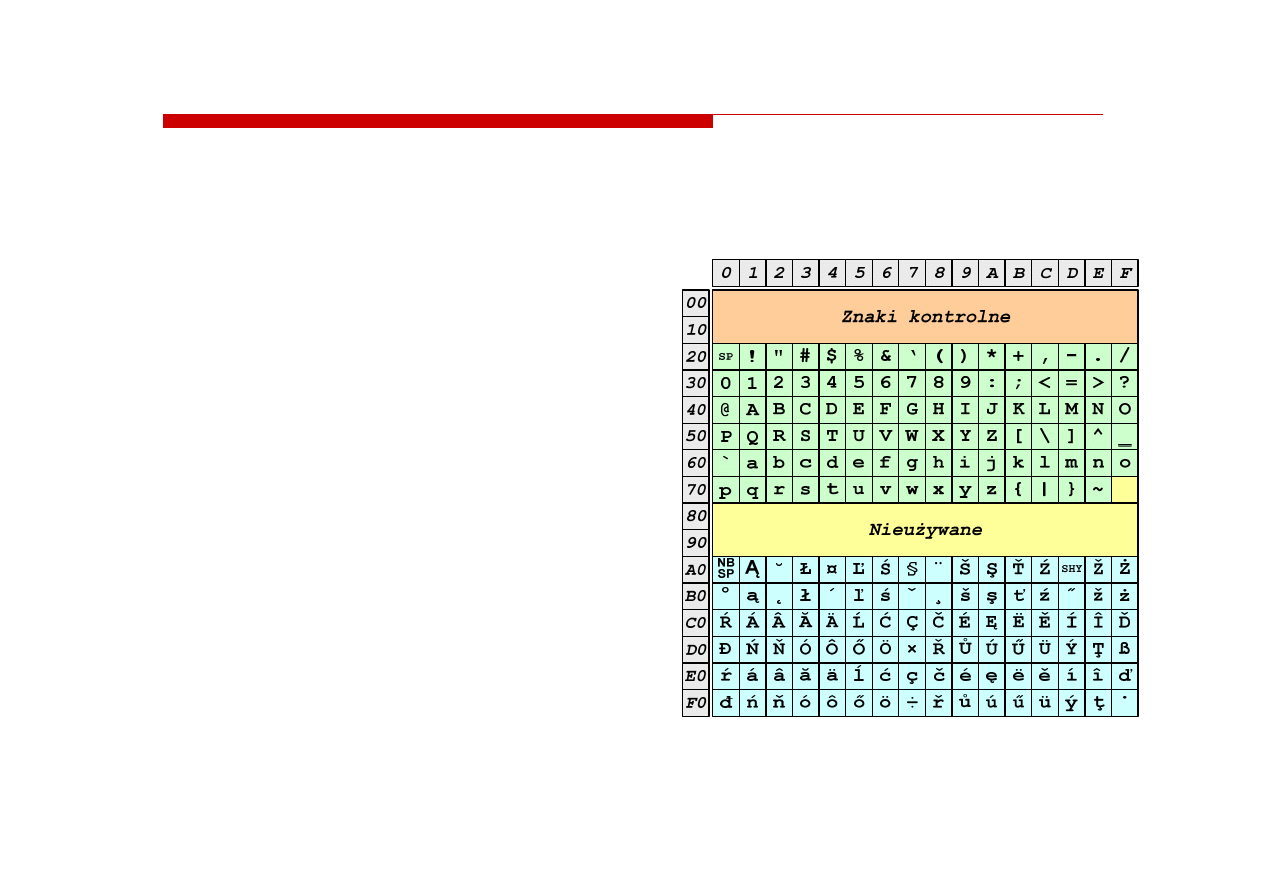
ISO/IEC 8859--1

1

ISO/IEC 8859-1, Latin-1
(„zachodnioeuropejskie”)

kodowanie używane w Amerykach,
Europie Zachodniej, Oceanii
i większej części Afryki

dostępne języki: albański, angielski,

dostępne języki: albański, angielski,
baskijski, duński, estoński, fiński,
francuski, hiszpański, irlandzki,
islandzki, kataloński, łaciński,
niderlandzki, niemiecki, norweski,
portugalski, retoromański, szkocki,
szwedzki, włoski

191 znaków łacińskiego pisma

SP

- spacja

NBSP - twarda spacja
SHY

- miękki dywiz (myślnik)

Informatyka 1, studia niestacjonarne I stopnia

dr inż. Jarosław Forenc

Rok akademicki 2011/2012, Wykład nr 2

43/50

ISO/IEC 8859

ISO/IEC 8859--2

2

ISO/IEC 8859-2, Latin-2 („środkowo”,
„wschodnioeuropejskie”)

dostępne języki: bośniacki,
chorwacki, czeski, węgierski,
polski, rumuński, serbski,
serbsko-chorwacki, słowacki,

serbsko-chorwacki, słowacki,
słoweński, górno- i dolnołużycki

możliwość przedstawienia znaków
w języku niemieckim i angielskim

191 znaków łacińskiego pisma

kody z przedziałów 00

(16)

-1F

(16)

oraz 7F

(16)

-9F

(16)

nie są używane

w ISO-8859-2

kodowanie zgodne z

Polską Normą

SP

- spacja

NBSP - twarda spacja
SHY

- miękki dywiz (myślnik)

Informatyka 1, studia niestacjonarne I stopnia

dr inż. Jarosław Forenc

Rok akademicki 2011/2012, Wykład nr 2

44/50

ISO/IEC 8859

ISO/IEC 8859--2

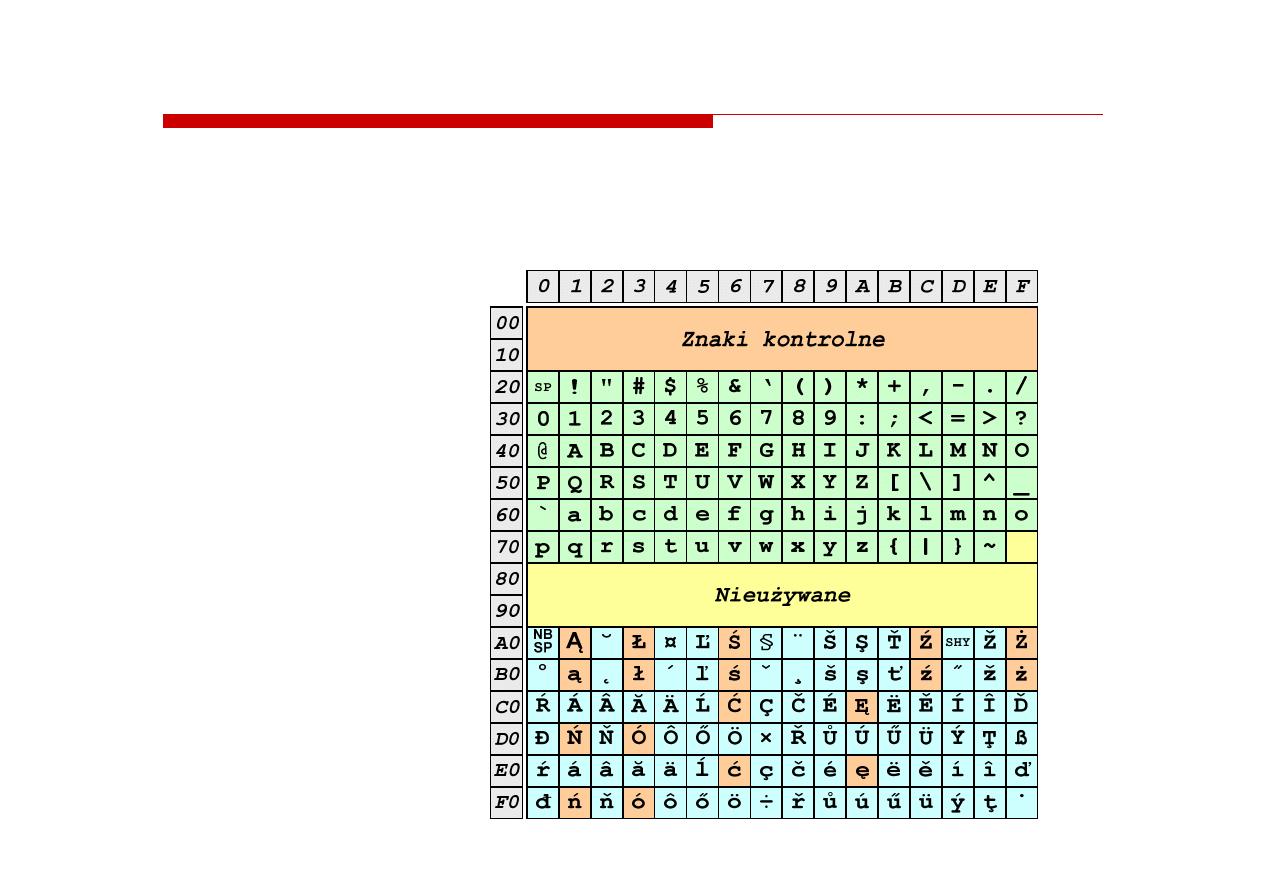
2 -- Kodowanie polskich znaków

Kodowanie polskich znaków

18 znaków:

Ą - ą

Ć - ć

Ę - ę

Ł - ł

Ł - ł

Ń - ń

Ó - ó

Ś - ś

Ź - ź

Ż - ż

Informatyka 1, studia niestacjonarne I stopnia

dr inż. Jarosław Forenc

Rok akademicki 2011/2012, Wykład nr 2

45/50

ISO/IEC 8859

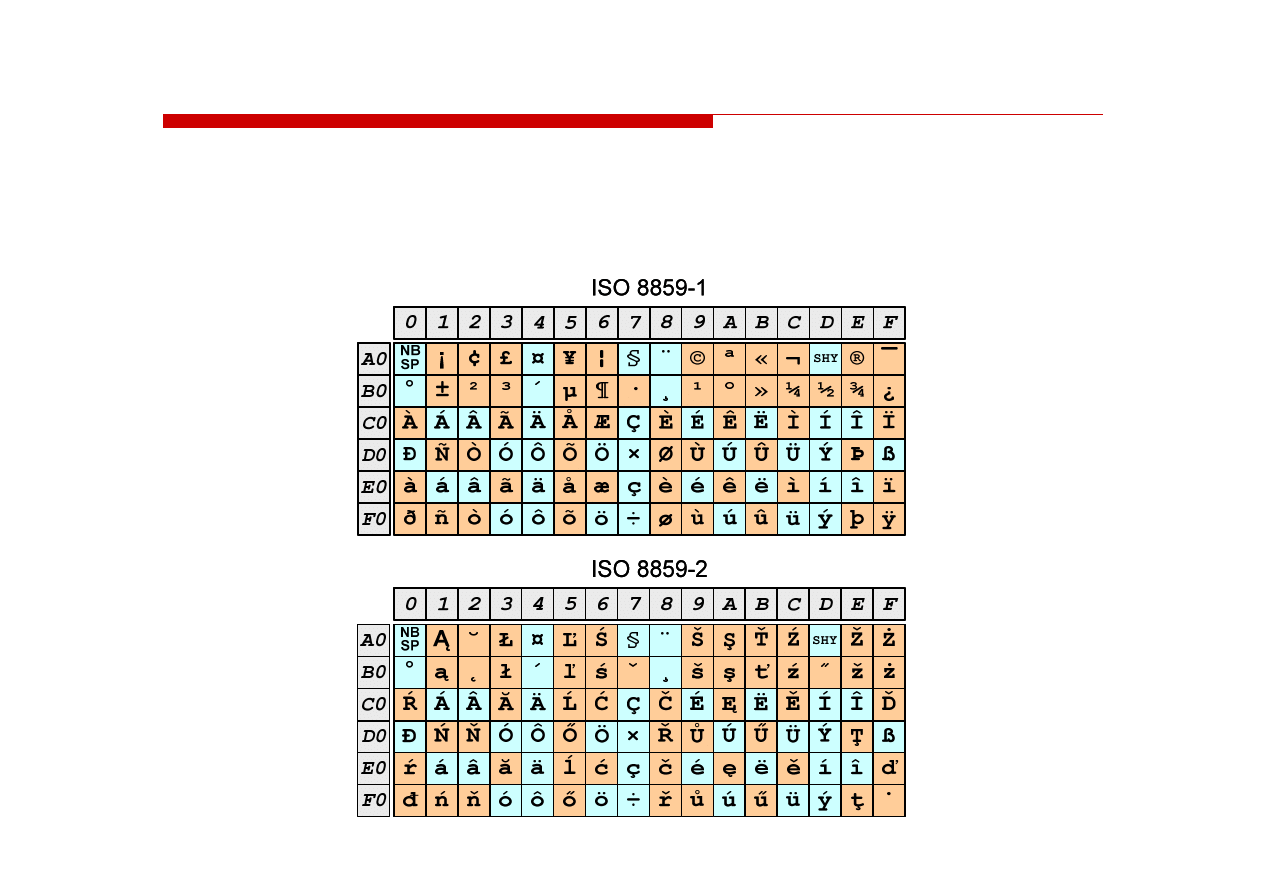
ISO/IEC 8859--1 i ISO/IEC 8859

1 i ISO/IEC 8859--2

2 -- porównanie

porównanie

Informatyka 1, studia niestacjonarne I stopnia

dr inż. Jarosław Forenc

Rok akademicki 2011/2012, Wykład nr 2

46/50

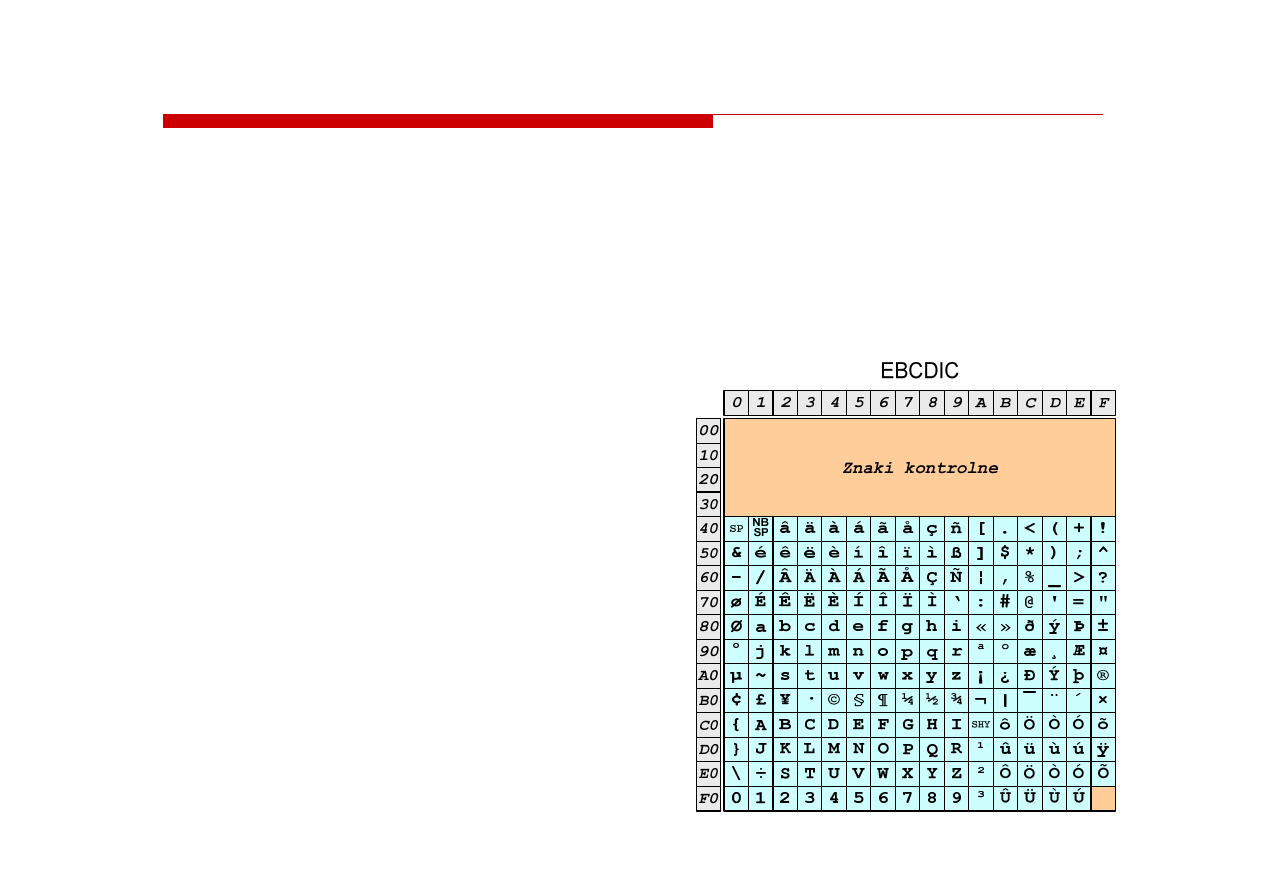
EBCDIC

EBCDIC

EBCDIC

- Extended Binary Coded Decimal Interchange Code

8-bitowe kodowanie znaków stworzone jako rozszerzenie
kodowania BCD

używane głównie w systemach
IBM w latach 60-tych XX wieku

IBM w latach 60-tych XX wieku

umożliwia zapisanie do 256
różnych symboli

brak zachowania kolejności
liter zgodnie z kolejnością
kodów, np. po R nie ma S

kody EBCDIC

nie są zgodne

z ASCII

Informatyka 1, studia niestacjonarne I stopnia

dr inż. Jarosław Forenc

Rok akademicki 2011/2012, Wykład nr 2

47/50

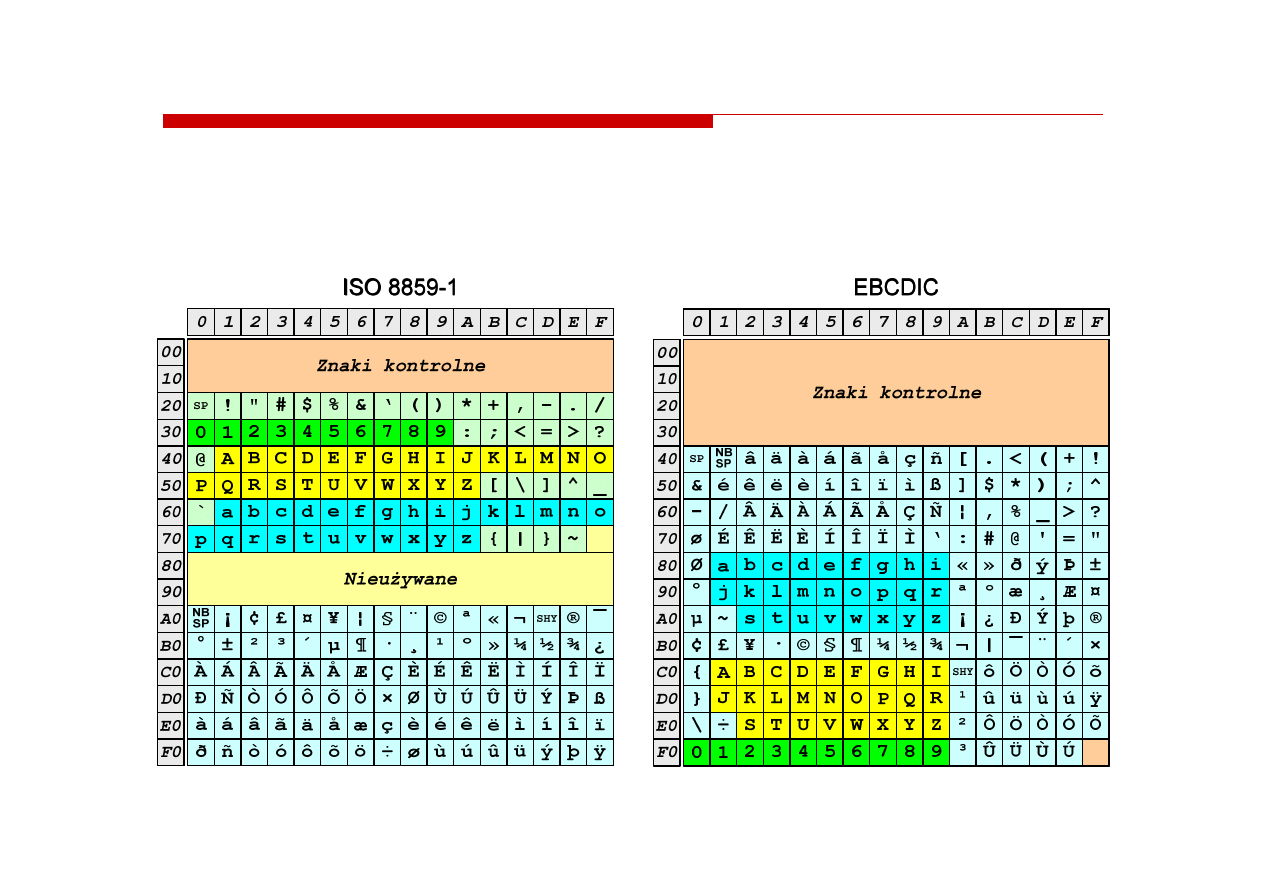
EBCDIC i

EBCDIC i ISO 8859

ISO 8859--1

1 -- porównanie

porównanie

Informatyka 1, studia niestacjonarne I stopnia

dr inż. Jarosław Forenc

Rok akademicki 2011/2012, Wykład nr 2

48/50

Windows

Windows--1250

1250

Windows-1250

(

CP-1250

) - strona kodowa używana przez system

Microsoft Windows do reprezentacji tekstów w językach
środkowoeuropejskich używających alfabetu łacińskiego

Obsługiwane języki: albański, chorwacki, czeski, polski, rumuński,
słowacki, słoweński, węgierski (ale także niemiecki)

słowacki, słoweński, węgierski (ale także niemiecki)

Windows-1250 jest podobny do ISO 8859-2 - posiada wszystkie
jego drukowalne znaki (a także kilka dodatkowych), lecz kilka
z nich zajmuje inne miejsca

Informatyka 1, studia niestacjonarne I stopnia

dr inż. Jarosław Forenc

Rok akademicki 2011/2012, Wykład nr 2

49/50

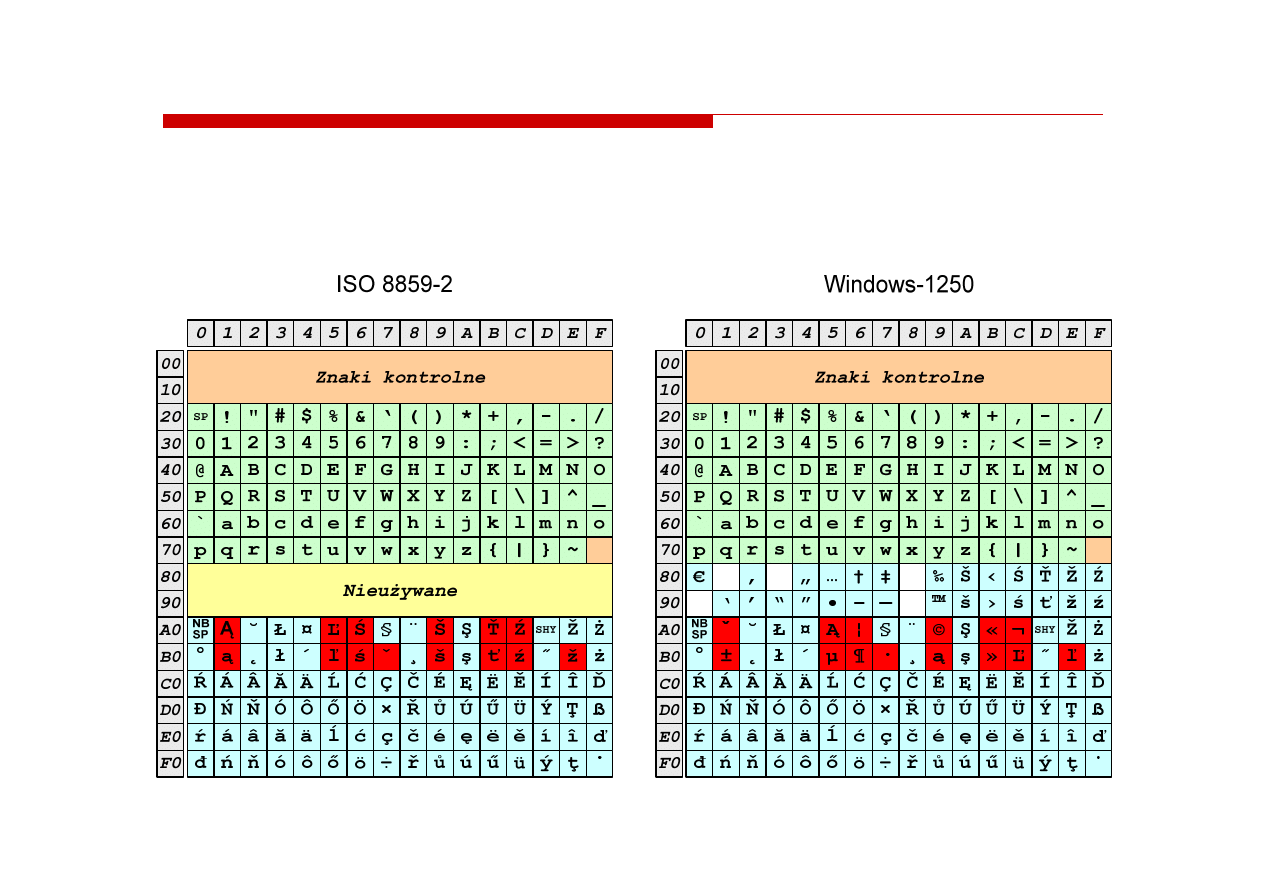
ISO 8859

ISO 8859--2 i Windows

2 i Windows--1250

1250 -- porównanie

porównanie

Informatyka 1, studia niestacjonarne I stopnia

dr inż. Jarosław Forenc

Rok akademicki 2011/2012, Wykład nr 2

50/50

Koniec wykładu nr 2

Koniec wykładu nr 2

Dziękuję za uwagę!

Dziękuję za uwagę!

Dziękuję za uwagę!

Dziękuję za uwagę!